Adaptive dose finding based on t-statistic for dose–response trials

SUMMARY

The goals of phase II dose–response studies are to prove that the treatment is effective and to choose the dose for further development. Randomized designs with equal allocation to either a high dose and placebo or to each of several doses and placebo are typically used. However, in trials where response is observed relatively quickly, adaptive designs might offer an advantage over equal allocation. We propose an adaptive design for dose–response trials that concentrates the allocation of subjects in one or more areas of interest, for example, near a minimum clinically important effect level, or near some maximal effect level, and also allows for the possibility to stop the trial early if needed. The proposed adaptive design yields higher power to detect a dose–response relationship, higher power in comparison with placebo, and selects the correct dose more frequently compared with a corresponding randomized design with equal allocation to doses.

1. INTRODUCTION

Among the possible goals of phase II clinical studies are (1) to demonstrate the response different from placebo; (2) to estimate the minimum effective dose (MED), that is, the smallest dose with discernible useful effect compared with placebo; (3) to identify the range of doses with high response rates; and (4) to assess the shape of the dose–response curve. Correct identification of the dose is the key in the entire process of drug development. Many dose–response studies use a randomized design where equal numbers of subjects are randomized to selected doses and placebo. For example, a dose–response study described by Bretz et al. [1] assigned 20 subjects to each of the four doses of the drug and 20 subjects to placebo. In some trials, the response can be observed relatively quickly. This allows for the possibility of using an adaptive design: adaptive with respect to allocation to doses and sequential monitoring with the possibility to stop the trial early for futility or efficacy. Berry et al. [2] suggested an adaptive design for a dose-finding study with the goal of estimating ED95, the smallest dose at which 95 per cent of the maximal response is achieved. Their method was proposed for trials where monotonicity could not be assumed. In many trials, it is reasonable to assume that the mean response is monotone (non-increasing or non-decreasing) with dose. This is typical of most efficacy endpoints. Utilizing this assumption in the design and estimation procedure increases the efficiency of the procedure. We suggest an adaptive design for dose-finding trials with monotone mean response and compare its performance with equal allocation. Section 2 provides notation and defines the basic adaptive method proposed. Section 3 specifies an adaptive method that can be used to estimate MED. Adaptive designs for multiple objectives are discussed in Section 4. The addition of futility assessment is in Section 5. Section 6 describes simulation studies that illustrate performance characteristics of the proposed adaptive designs, and Section 7 provides some discussion of the material from the previous sections.

2. NOTATION AND METHODS

Let D={d₁, …, d_K} be the set of ordered dose levels selected for a trial with d₁ denoting placebo. We assume that a subject’s response at d_j is distributed as N(μ_j, σ²), where μ=(μ₁, …, μ_K) is the mean vector corresponding to D. Observations from different subjects are independent. Only one observation per subject is taken. Let n=(n₁, …, n_K) be the vector of the number of subjects at each of the K doses. Let Y_ji be the observation taken at dose d_j from subject i . Let $\overline{Y}{}_j={\displaystyle {\sum }_{i=1}^{n_j}{Y}_{\mathit{\text{ji}}}/n_j}$ be the observed mean response, Ȳ=(Ȳ₁, …, Ȳ_K), and $S^2={\displaystyle {\sum }_{j=1}^K{\displaystyle {\sum }_{i=1}^{n_j}{(Y_{\mathit{\text{ji}}}-{\overline{Y}}_j)}^2/({\displaystyle {\sum }_{j=1}^K{n}_j-K})}}$ be the pooled variance estimator.

We first describe the analytical methods we will use in goals (1)–(4) mentioned in the Introduction assuming that data have already been collected.

2.1. Demonstrating dose response

To demonstrate treatment effect different from placebo, we use the likelihood ratio trend test [3], since it is the most powerful test under isotonic assumption.

2.2. Defining and estimating the dose(s) of interest

Among the doses of interest in a dose-finding study are [4] the MED, the peak dose, the maximum safe dose. The MED is the smallest dose with discernible useful effect compared with placebo. We define the MED as the lowest dose with the mean response of μ₁+C₁, where C₁ is a known constant determined by the clinical team. The peak dose is a maximal dose beyond which additional meaningful benefit will be unlikely to occur (ICH E9, 1998). Often, the peak dose is described as the lowest dose on the plateau of the response curve. Since it is statistically difficult to define the plateau, the peak dose is sometimes defined as the lowest dose with mean response μ_K − δ, where δ is the minimum clinically important difference in response specified by the clinical team. In some cases, δ could equal C₁, that is, MED is the smallest dose with minimum clinically important difference from placebo, and peak dose is a dose beyond which no minimum clinically important increase in response is observed. Alternatively the goal can be to estimate ED95, the smallest dose where 95 per cent of the maximal response is achieved, or to find the dose with mean response μ₁+C₂ with C₂>C₁, being a known constant representing the desirable effect over placebo that is believed to be close to the maximum effect. We will consider two target doses, the dose with mean response μ₁+C₁ and mean response μ₁+C₂. Other definitions of response can be addressed similarly to the way we address these.

In some trials it is of interest to pick one of the doses under consideration as the estimated target dose, in other trials the estimated target dose does not have to be among the doses studied. The former is relevant when only a fixed number of drug formulations are available for subsequent clinical use, for example, when only 1, 5, and 25 mg tablets are available. The latter is relevant when the exact dose of drug can be administered, as with an oral solution or an intra-venous formulation. Hence, we consider both discrete estimation and estimation on a continuous scale. Since monotonicity of the mean response is assumed, we will estimate the doses of interest by fitting isotonic regression to the observed responses. In the case when the dose is chosen from a discrete set D, the dose with the estimated mean response closest to the target is chosen. If there are several such doses the lowest of them is chosen if the estimated response at these doses is higher than the target, otherwise the highest of these doses is chosen. In this case when the estimated dose does not have to be among the doses studied, the only restriction is that the estimated dose is in (d₁, d_K]. In this case, the estimated dose is obtained by using linear interpolation between the doses with mean response right below and right above the target. Linear interpolation used with isotonic regression estimation has been shown to work well for studies with binary outcomes [5].

2.3. Assessing the shape of dose–response curve

To assess the shape of dose–response curve, we use the technique from [1]. They suggested selecting a set of M candidate shapes. For example, Bretz et al. [1] included models 2–6 (Table I) as the candidate shapes. They also considered a quadratic model that we do not include because of the underlying assumption of monotonicity of mean response. For each shape m,m=1, …, M, consider testing the null hypothesis $H_0^m:{\mathbf{c}}_m^{\prime }\mathbf{\mu }=0$ against one-sided alternative $H_1^m:{\mathbf{c}}_m^{\prime }\mathbf{\mu }>0$ for a given contrast vector ${\mathbf{c}}_m^{\prime }=(c_{m1},\dots ,c_{\mathit{\text{mK}}})$ of known constants subject to conditions ${\mathbf{c}}_m^{\prime }\mathbf{1}=0\text{and}\Vert {\mathbf{c}}_m^{\prime }\Vert =1$. The test statistics are $T_m={\mathbf{c}}_m^{\prime }\overline{\mathbf{Y}}/[S^2\sqrt{{{\displaystyle {\sum }_{j=1}^{K}c}}_{\mathit{\text{mj}}}^2/n_j}],m=1,\dots ,M$. The best fitting model is the model with the largest value of the test statistic. If the largest value of the test statistic is less than the critical value, none of the models are considered to be a good fit. See [1] for more details. For a given mean vector μ^(m) corresponding to shape m,m=1, …, M, the optimal contrast coefficients maximize the non-centrality parameter:

$${[\tau (\mathbf{c})]}^2=\frac{1}{{\sigma }^2}\frac{{({\mathbf{c}}^{\prime }{\mathbf{\mu }}^{(m)})}^2}{{\displaystyle {\sum }_{j=1}^K{c}_{\mathit{\text{mj}}}^2/n_j}}$$

Table I.

Data generating dose–response shapes as functions of d and values of μ_jcomputed for scenarios with seven doses.

Model	Specification of μ(d)
Constant			0.2
Emax			0.2+0.7d/(0.2+d)
Linear in log-dose			0.2+0.6log(5d+1)/log(6)
Linear			0.2+0.6d
Exponential			0.183+0.017exp[2d log(6)]
Logistic			0.193+0.607/{1+exp[10log(3)(0.4−d)]}
Step 1			0.2+0.6(d−0.6)/(1−0.6)I (0.6<d≤1)
Step 2			0.2+0.6(d−0.2)/(0.6−0.2)I (0.2<d<0.6)+0.6I (0.6≤d)
Step 3			0.2+0.6(d−0.05)/(0.2−0.05)I (0.05<d<0.2)+0.6I(0.6≤d)
	μj for a 7-dose scenario
Model	μ1	μ2	μ3	μ4	μ5	μ6	μ7
Constant	0.20	0.20	0.20	0.20	0.20	0.20	0.20
Emax	0.20	0.34	0.55	0.67	0.72	0.76	0.78
Linear in log-dose	0.20	0.27	0.43	0.57	0.66	0.74	0.80
Linear	0.20	0.23	0.32	0.44	0.56	0.68	0.80
Exponential	0.20	0.20	0.22	0.25	0.33	0.48	0.80
Logistic	0.20	0.21	0.25	0.50	0.74	0.79	0.80
Step 1	0.20	0.20	0.20	0.20	0.20	0.50	0.80
Step 2	0.20	0.20	0.20	0.50	0.80	0.80	0.80
Step 3	0.20	0.20	0.80	0.80	0.80	0.80	0.80

The values μ_j closest to the first target are in bold, and those closest to the second are in bold and italic. The values μ₄ at dose 0.4 and μ₆ at dose 0.8 that were added to a 5-dose scenario to make a 7-dose scenario are underlined.

The optimal contrast coefficients can be obtained using the following formula [6, pp. 117–118]:

$$\begin{array}{c}{\mathbf{\mu }}^{*}=\mathbf{n}({\mathbf{\mu }}^{(m)}-{\mu }^{**})\text{where}{\mu }^{**}={\displaystyle \sum _{j=1}^K{\mu }_j^{(m)}{n}_j/{\displaystyle \sum _{j=1}^K{n}_j}}\hfill \\ {\mathbf{c}}_{\text{opt}}={\mathbf{\mu }}^{*}/\Vert {\mathbf{\mu }}^{*}\Vert \hfill \end{array}$$

3. DAPTIVE ALLOCATION TO FIND THE MED

To develop a strategy for adaptation in a dose-finding trial with goals (1)–(4), we first note that our main objective is to estimate the MED with high precision; the secondary objective is to compare the estimated MED with placebo. In our simulation study, trials with sample sizes that provide acceptable quality of estimation of the target dose(s) have a power close to 100 per cent to demonstrate dose response or to show difference from placebo for an effective drug. That is, at least in set-ups that we considered, the goal of demonstrating dose response or demonstrating difference from placebo does not require as many subjects as the goal of estimating the dose(s) of interest well or the goal of assessing the shape of the dose–response curve. This is in accordance with the conclusions of [1]. Therefore, we focus on adaptive designs that improve the efficiency of estimation of the doses of interest. Also, the proposed adaptive allocation maximizes the number of subjects at the target dose and therefore maximizes power of treatment comparison. The doses of interest are the MED defined as the dose with the mean response μ₁+C₁, the second target is the dose with mean response μ₁+C₂, where C₁<C₂ are known constants.

3.1. Adaptive design to target the MED

The goal is to find the design that can be successfully used with a wide range of dose–response models. Therefore, no particular response curve is assumed, and the only assumption we are making is that the mean response is a non-decreasing function of dose. Ivanova et al. [7] proposed the cumulative cohort design for dose finding with binary outcome. The decision rule is very intuitive: the current dose is repeated if the estimated response rate at that dose is close to the target and changed otherwise. We will use a similar idea here: the dose is repeated if the current estimated difference in responses between the dose and placebo scaled by the variance is close to C₁ and changed otherwise. In the proposed procedure, at each step we compute the t-statistic comparing the difference between the mean response at the current dose with the mean response at placebo plus C₁. The proposed allocation rule is described as follows.

Subjects are assigned sequentially in cohorts with a certain proportion of subjects in each cohort assigned to placebo. The total number of subjects is equal to N. Let n(t)=(n₁(t), …, n_K (t)) be the number of subjects at each of the K doses right after subject t, t≤N,has been assigned, that is, n₁(t)+…+n_K (t)=t. Define T_j to be t-statistics comparing the mean response at dose d_j with the mean response at placebo, d₁, computed from observations Y_j1, …, Y_{jnj (t)} and Y₁₁, …, Y_1n1(t):

$$T_j=\frac{{\overline{Y}}_j(n_j(t))-{\overline{Y}}_1(n_1(t))-C_1}{S\sqrt{\frac{1}{n_j(t)}+\frac{1}{n_1(t)}}}$$

Suppose the most recent cohort of subjects was assigned to dose d_j, j =2, …, _K. The next cohort of subjects is assigned as follows:

1. if T_j≤−Δ, the next cohort of subjects is assigned to dose d_j+1;

2. if −Δ<T_j<Δ, the next cohort of subjects is assigned to dose d_j ;

3. if T_j≥Δ, the next cohort of subjects is assigned to dose d_j−1.

Appropriate adjustments are made at doses d₂ and d_K. Here Δ>0 is the design parameter. Ivanova et al. [7] studied the impact of the choice of Δ on design performance in a similar design for binary outcomes with the goal of finding the dose from the set D of doses studied with mean response closest to the target quantile. They recommended using a small Δ that is away from 0. In the trial we consider, one of the goals is to estimate the dose of interest by interpolation. Therefore, it is beneficial to accumulate data on the two nearby doses, which is accomplished by setting Δ to a value very close to 0, for example, Δ=0.01. Assuming that values Z_j are not in (−0.01, 0.01), this choice of Δ yields a very simple decision rule: increase the dose if Ȳ_j<Ȳ₁+C₁ and decrease otherwise; therefore, for this choice of Δ there is no need to estimate the variance.

4. DOSE SELECTION TRIALS WITH MULTIPLE OBJECTIVES

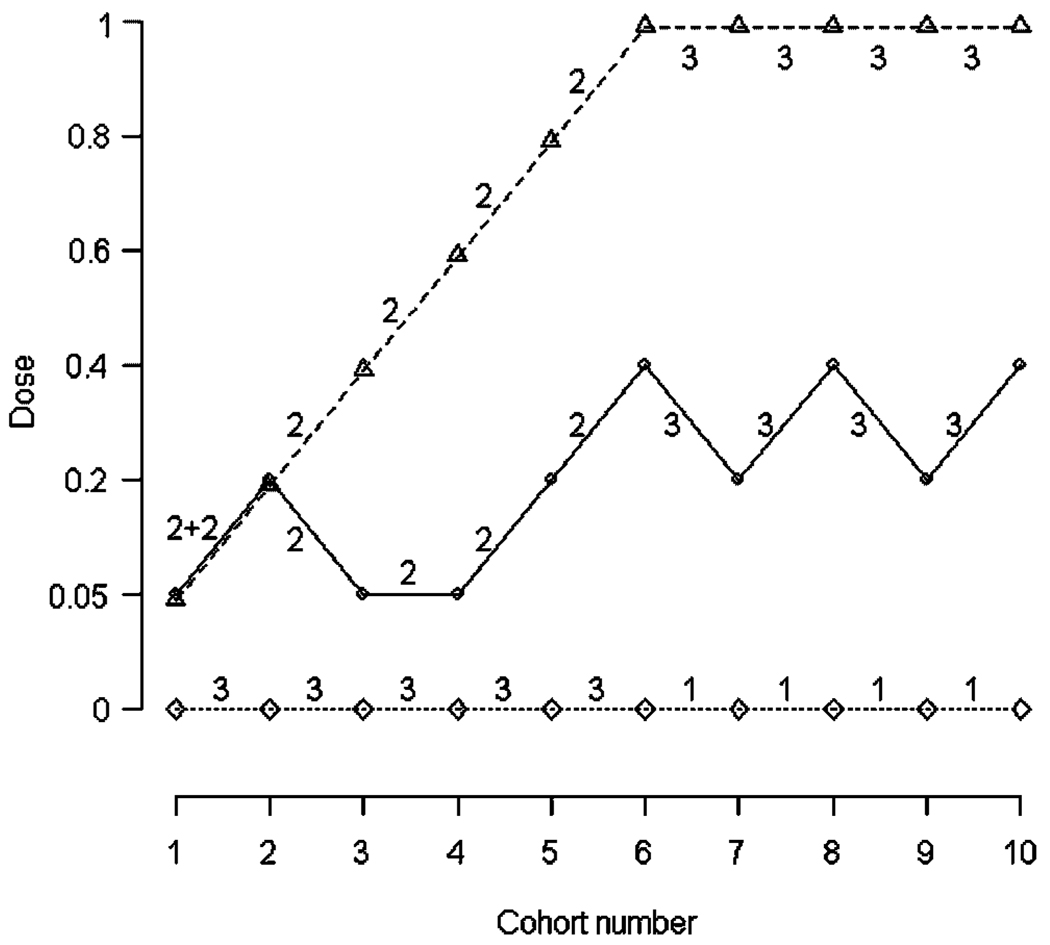
In many dose–response studies, the goal is to identify two or more doses of interest. Consider an example, where the doses of interest are the dose with mean response of μ₁+C₁ and the dose with the mean response of μ₁+C₂,C₁<C₂. For trials with two goals of interest, we split each cohort of subjects into three sub-cohorts: the first sub-cohort is assigned to placebo, the second targets the first dose of interest, and the last targets the second dose of interest. That is, two parallel adaptive sequences are run, each targeting the corresponding dose of interest. An example of a trial with two objectives is presented in Figure 1 and Table II. The data were generated from model 2 (Table I) with doses D={0,0.05,0.2,0.4,0.6,0.8,1} and σ=0.65. The mean vector is μ=(0.20,0.34,0.55,0.67,0.72,0.76,0.78) with the first target dose being dose 0.27 and the second target dose being very close to 1. Subjects were assigned in 10 cohorts of size 7 with a total of 20 subjects assigned to placebo and 50 to drug. More subjects were assigned to placebo in the beginning of the trial: in the first five cohorts there were three subjects assigned to placebo and two to each of the two target sequences; in the last five cohorts one subject was assigned to placebo and three to each of the target sequences.

Figure 1.

Dose assignment sequence illustrating the trial from Table II. The solid line represents the sequence targeting the first target dose (true first target dose is 0.27), and the dashed line the sequence targeting the second target dose (true second target dose is 1.00), and the dotted line the sequence of assignments to placebo. The numbers represent sub-cohort sizes of subjects assigned to placebo, sequence 1, and sequence 2.

Table II.

Example of an adaptive trial with Δ=0.01.

Cohort number	Cohort composition	Assignment for target 1	$\frac{{\overline{Y}}_i-{\overline{Y}}_1-C_1}{S\sqrt{1/n_i+1/n_1}}$	Assignment for target 2	$\frac{{\overline{Y}}_j-{\overline{Y}}_1-C_2}{S\sqrt{1/n_j+1/n_1}}$
1	(3,2,2)	0.05	−0.201	0.05	−0.550
2	(3,2,2)	0.2	0.005	0.2	−0.381
3	(3,2,2)	0.05	0.216	0.4	−0.117
4	(3,2,2)	0.05	−0.756	0.6	−1.448
5	(3,2,2)	0.2	−0.298	0.8	−0.690
6	(1,3,3)	0.4	1.037	1	−1.016
7	(1,3,3)	0.2	−1.058	1	−1.316
8	(1,3,3)	0.4	1.130	1	−1.151
9	(1,3,3)	0.2	−0.764	1	−0.443
10	(1,3,3)	0.4	−0.281	1	−0.193

Data were generated from model 2 with seven doses. Cohort composition is the number of subjects assigned to placebo and to sequences targeting target doses 1 and 2. The first target dose is the dose with the mean response μ₁+C₁ with C₁=0.4, and the second target is μ₁+C₂ with C₂=0.6. The current dose in the sequence targeting the first target dose is d_i, and in the sequence targeting the second target dose is d_j .

In a parallel dose trial with equal allocation to six doses of the drug and placebo, $\frac{1}{7}$ of the subjects are assigned to placebo. The goal of adaptive design is to increase allocation to doses in the range of interest; therefore, it is beneficial to increase allocation to placebo as well. On the basis of the simulation results, we recommend assigning about 30 per cent of subjects to placebo when adaptive design is used. Also, since the target dose is computed based on response to placebo, it is beneficial to have as precise an estimate of placebo response as early in the trial as possible. Hence, it is desirable to have a greater ratio of placebo to active drug in early cohorts. Then the ratio could be decreased for later cohorts since placebo information will already have accumulated, and emphasis could shift to the estimation of responses at targeted doses. Actual numbers and emphasis for switching choice points can be studied by simulation. In the implementation of our design, we increased the number assigned to placebo in each cohort by 1 in the first half of the trial and decreased this number by 1 in the second half of the trial.

5. STOPPING RULE FOR FUTILITY

An important feature of an adaptive dose-finding study is the possibility of stopping for futility before the total sample size is reached. If response rates of the drug are low at all doses, the adaptive allocation will reach the highest dose quickly. Therefore, under the assumption of non-decreasing mean response, we suggest to stop the trial if the hypothesis H₀ :μ_K>μ₁+C₁ is rejected. To ensure that we have enough data, the first check for futility is made after the sample size at the highest dose reaches N_stop subjects. Subsequently, the hypothesis is tested after responses from each new cohort of subjects are obtained. The trial is stopped as soon as the p-value for the test is less than α_stop, that is, the Pocock type boundary is used [8]. Although we assume monotonicity, it might be wise to take into account a possible downturn in the curve. This is accomplished by incorporating data from lower doses. The trial is stopped as soon as the p-value for comparison of the observed response at dose d_K with d₁ and p-value for comparison of combined samples at d_K−1 and d_K with d₁ are less than α_stop. The parameters N_stop and α_stop are selected to insure desirable features of the stopping rule. Since sample sizes n_K−1(t) and n_K (t) at d_K−1 and d_K are random variables, an exact overall type I error rate is impossible to compute. For each hypothesized value of n_K−1(t) and n_K (t), typical group sequential calculations can provide information on overall type I error rate. Our main goal was to insure that a trial investigating a promising treatment is stopped for futility with extremely low probability; therefore, we chose a very small α_stop, such as α_stop=0.005.

6. SIMULATION STUDY

To illustrate the performance of the adaptive design, we used models from Bretz et al. [1]. The data were generated from the models in Table I with σ=0.65 and 1.478 with 25,50,75,100, and 150 subjects allocated to each dose. Bretz et al. [1] considered trials with five doses, D={0,0.05,0.2,0.6,1}. To investigate what is the best number of doses to consider when adaptive design is used, we also examined scenarios with seven doses, D={0,0.05,0.2,0.4,0.6,0.8,1}, and with nine doses, D={0,0.1,0.2,0.4,0.5,0.6,0.7,0.8,1}. For the 7-dose model, two additional doses 0.4 and 0.6 were included. For the 9-dose model, the doses were chosen with equal increments as is typical (assuming that all the doses are on a log scale). To extend step shapes to 7- and 9-dose scenarios, we considered piecewise linear models (models 7–9 in Table I). The total sample size in the trial was set to 125,250,375,500, and 750 for 5-dose models; 126,252,371, 497, and 749 for 7-dose models; and 126,252,378, 504, and 747 for 9-dose models. In the adaptive design, subjects were assigned in groups of five with two to placebo and three to drug in 5-dose trials, groups of seven with two assigned to placebo and five to drug in 7-dose trials, and groups of nine with three to placebo and six to drug in 9-dose trials. Placebo mean response was μ₁=0.2 for all models. The first target dose was defined as the dose with the mean response μ₁+C₁ with C₁=0.4 and the second target as μ₁+C₂ with C₂=0.6. In adaptive trials stopped early for futility, both estimated doses were set equal to d₁. All simulation results are based on 5000 runs for each scenario/model combination.

6.1. Demonstrating dose response

The power of the likelihood ratio test (LRT) for 5-dose models with σ=1.478 is presented in Table III. Trials stopped for futility were counted as demonstrating no dose response. The size of the LRT was preserved under the adaptive design setting in all sample size/variance combinations except the scenario with total sample size of 125 (Table III, row 1). The adaptive design yielded much higher power of the LRT compared with equal allocation. This is because in the scenarios we considered, the second target dose was in the range of high doses, and adaptive allocation yielded an increase in the proportion of subjects assigned to high doses. For the sample size of 125, the power (averaged over eight models) for the adaptive design was 59 per cent compared with 49 per cent for the equal allocation; for a sample size of 250, the power was 88 per cent for the adaptive design compared with 76 per cent power for the equal allocation. As expected for σ=0.65, the power of the LRT was close to 1 for both adaptive and equal allocations for all models and scenarios.

Table III.

The power of the LRT and the power for comparison of estimated target dose 1 (discrete method) with placebo for a 5-dose scenario with σ=1.478.

		Model
N	Design	Const	Emax	LinL	Lin	Exp	Logist	Step 1	Step 2	Step 3
LRT
125	Adaptive	0.07	0.58	0.58	0.56	0.55	0.61	0.57	0.65	0.67
125	Equal	0.05	0.44	0.46	0.45	0.41	0.54	0.42	0.58	0.60
250	Adaptive	0.05	0.85	0.87	0.86	0.88	0.89	0.89	0.90	0.91
250	Equal	0.05	0.71	0.73	0.71	0.71	0.82	0.69	0.86	0.87
Comparison with placebo
250	Adaptive	0.04	0.46	0.44	0.44	0.46	0.47	0.49	0.46	0.47
250	Equal	0.03	0.26	0.23	0.19	0.16	0.26	0.16	0.29	0.37
375	Adaptive	0.04	0.66	0.67	0.66	0.62	0.66	0.65	0.63	0.66
375	Equal	0.03	0.46	0.43	0.37	0.32	0.47	0.35	0.50	0.58
500	Adaptive	0.03	0.81	0.79	0.78	0.70	0.77	0.71	0.75	0.75
500	Equal	0.03	0.66	0.60	0.54	0.44	0.60	0.47	0.61	0.69
750	Adaptive	0.03	0.92	0.91	0.90	0.79	0.86	0.79	0.83	0.84
750	Equal	0.03	0.87	0.83	0.76	0.62	0.77	0.63	0.75	0.82

6.2. Estimating the dose(s) of interest

First, we look at the power of comparison of the estimated target dose with placebo where the estimated dose is in D (Table III). We used a step-down procedure and performed the comparison with placebo only if a dose–response was demonstrated by the LRT. For trials with no dose response, the response at the target dose was considered to be not significantly different from placebo. The adaptive design yielded much higher power of comparison with placebo compared with equal allocation. For example, for 5-dose models with the sample size of 250, the power (averaged over models 2–9) was 46 per cent for adaptive design compared with 24 per cent for equal allocation; for the sample size of 375 the power was 65 and 43 per cent; and for the sample size of 500 the power was 76 and 58 per cent for the two designs correspondingly. Adaptive design resulted in much higher power because it assigned many more patients to both placebo and estimated target dose compared with equal allocation.

To compare the quality of estimation for the two targets, s=1 and 2, we measured the precision of estimation using relative deviation $R_s=100(\mu ({\widehat{d}}_s)-{\mu }_s^{*})/{\mu }_s^{*}$. Here d̂_s is the estimated target dose and ${\mu }_s^{*}$ is the targeted mean response, with ${\mu }_1^{*}=0.6\text{and}{\mu }_2^{*}=0.8$. The value μ(d̂_s) was calculated by substituting the value d̂_s in the formula for the corresponding true model (Table I). Bretz et al. [1] used a similar measure but their measure was computed on the dose scale not on the mean response scale. One of the reasons we computed the deviation on the mean response scale is because in several models (Table I) there was a range of doses with the mean response equal to ${\mu }_2^{*}$ . Relative deviations were computed for both estimators, discrete and continuous. Table IV presents the root mean-squared error (MSE), computed as the root of the average over models 2–9 of squared relative deviations for several sample sizes for σ=0.65. In all scenarios considered and for both σ=0.65 and 1.478 adaptive design had the smaller root MSE compared with the equal allocation for the estimation of targets 1 and 2.

Table IV.

The square root of MSE averaged over eight models with σ=0.65.

		Target 1		Target 2
N	Scenario	Adaptive	Equal	Adaptive	Equal
Continuous estimator
125	5-dose	21.7	24.5	12.5	15.1
126	7-dose	22.8	26.5	13.8	17.3
126	9-dose	22.0	28.0	15.4	19.3
250	5-dose	13.6	15.3	7.3	8.9
252	7-dose	14.7	17.2	7.7	9.9
252	9-dose	14.5	19.0	8.0	11.3
750	5-dose	10.4	11.6	5.3	6.4
749	7-dose	10.5	12.4	5.4	7.0
747	9-dose	10.9	14.0	5.6	8.0
Discrete estimator
125	5-dose	35.9	38.1	10.4	13.8
126	7-dose	28.3	31.0	14.2	17.7
126	9-dose	24.7	29.1	15.8	19.8
250	5-dose	30.0	31.8	5.0	5.8
252	7-dose	22.6	23.7	6.8	9.6
252	9-dose	20.2	22.4	7.5	11.4
750	5-dose	27.6	28.7	3.6	3.9
749	7-dose	20.6	20.9	4.2	5.8
747	9-dose	18.6	19.4	4.8	7.4

Next we try to answer the question of what is the optimal number of doses to consider in a trial where adaptive design is used for allocation. The answer depends on which type of estimation is of interest: continuous or discrete. For estimation on a continuous dose scale, the quality of estimation was the best with a 5-dose scenario compared with 7- and 9-dose scenarios. Note that all scenarios cover the same range of doses and that range contains both targets. The results might have been different if scenarios were covering different ranges some of which not containing target doses. For the discrete estimator, the quality of the estimator of target 1 is the highest for a 9-dose scenario; the estimation of target 2 is the best in a 5-dose scenario. This is because for discrete estimation, adding more doses increases the quality of estimation of a target if doses that are added have a mean response closer to the target than doses already considered. Target 2 was a dose with mean response 0.8. All models in a 5-dose scenario already had a dose with a mean response of 0.8. Therefore, adding more doses resulted in more doses to choose from and higher likelihood to make a mistake when selecting a dose. If both continuous and discrete estimations are of interest we would recommend using adaptive design with nine doses. Interestingly, in our simulations both adaptive design and equal allocation exhibited the same pattern of root MSE measure in relation to the number of doses considered.

6.3. Assessing the shape of dose–response curve

Table V presents the model selection results for the two designs for the case of five dose levels for σ=0.65. The adaptive design does not yield as good a model selection for E_max and logistic models compared with equal allocation; it selects the right model more frequently in the case of linear and exponential models. Similar conclusions were reached for σ=1.478.

Table V.

Correct model selection for a 5-dose scenario with σ=0.65.

		Model
N	Design	Emax	LinL	Lin	Exp	Logist
125	Adaptive	0.50	0.22	0.37	0.80	0.53
125	Equal	0.61	0.21	0.29	0.76	0.64
250	Adaptive	0.66	0.43	0.66	0.93	0.74
250	Equal	0.73	0.45	0.57	0.90	0.82
750	Adaptive	0.78	0.62	0.81	0.97	0.89
750	Equal	0.84	0.65	0.76	0.97	0.93

6.4. Stopping for futility

The stopping rule for futility was used with N_stop=25 and α_stop=0.005. These parameters were set to insure a very low probability of stopping for futility when the drug is in fact effective. Simulations show that among trials with a total planned sample size of 750, with data generated by models 2–9, 0.02 and 0.4 per cent of the trials were stopped early for futility for trials with σ=0.65 and 1.478 correspondingly. On the other hand, when data were generated from model 1 with a total sample size of 750 and σ=0.65, 100 per cent of the trials were stopped early for futility yielding the average total sample sizes of 110, 115, and 147 for 5-, 7-, and 9-dose models correspondingly. For σ=1.478, 91 per cent of the trials were stopped early for futility yielding the average total sample sizes of 328, 341, 393 for 5-, 7-, and 9-dose models correspondingly. Average total sample sizes for model 1 were very similar for smaller maximum sample sizes.

7. DISCUSSION

The adaptive design described here is flexible and can be used with continuous distributions other than normal or discrete distributions (for example, binomial). The strategy that we described can also be used when there is no placebo in the trial, and a particular mean response is targeted or to find the dose that is non-inferior to an active control, in which case some of the subjects in each group are assigned to control. When there is only one target dose of interest, the advantages of adaptive designs as far as the quality of estimation of the target dose and the power of its comparison with placebo are even more pronounced. At the same time if the target dose is in the low range of dose–response curve, the ability to select the correct dose response model is not nearly as good as for equal allocation. This is because only the lower part of the dose–response curve will be explored by the adaptive design.

We used isotonic estimation only to estimate the target doses after the trial. Isotonic estimates can be used in the adaptive design’s decision rule instead of sample means. Using isotonic estimates improves the performance of adaptive design further; however, improvements are not significant (results are available from the authors).