Modeling calcium waves in cardiac myocytes: importance of calcium diffusion

Abstract

Under certain conditions, cardiac myocytes engage in a mode of calcium signaling in which calcium release from the sarcoplasmic reticulum (SR) to myoplasm occurs in self-propagating succession along the length of the cell. This event is called a calcium wave and is fundamentally a diffusion-reaction phenomenon. We present a simple, continuum mathematical model that simulates calcium waves. The framework features calcium diffusion within the SR and myoplasm, and dual modulation of ryanodine receptor (RyR) release channels by myoplasmic and SR calcium. The model is used to illustrate the effect of varying RyR permeability, sarco/endoplasmic reticulum Ca²⁺ ATPase (SERCA) activity and calcium ion mobility in myoplasm and SR on wave velocity. The model successfully reproduces calcium waves using experimentally-derived variables. It also supports the proposal for wave propagation driven by the diffusive spread of myoplasmic calcium, and highlights the importance of SR calcium load on wave propagation.

2. INTRODUCTION

Intracellular Ca²⁺ waves are a form of Ca²⁺ signaling executed in many cell types (1). Ca²⁺ waves can occur in cardiac myocytes that have been ‘Ca²⁺ overloaded’ (2, 3). The appearance of waves is usually arrhythmogenic, as it activates inward currents such as that carried by Na⁺-Ca²⁺ exchange (NCX) (4). Waves are produced as a consequence of Ca²⁺ release through ryanodine receptor (RyR) channels expressed in the sarcoplasmic reticulum (SR), the myocyte’s reservoir of stored Ca²⁺. These release events do not occur simultaneously throughout the cell, but are triggered in succession, one release event acting as the trigger for an adjacent release event. After release, Ca²⁺ is taken back into the SR by the SERCA pump. The nature of this propagating mechanism means that a wave travels at a finite velocity. This is therefore dissimilar to the Ca²⁺ transient evoked by an action potential, which is a whole-cell release event, coordinated by depolarization-activated Ca²⁺ entry through L-type Ca²⁺ channels (5). Ca²⁺ diffusion inside myocytes is clearly a major factor that will determine Ca²⁺ wave velocity. Wave velocity, in turn, will determine the pace of Ca²⁺ release: faster velocity will produce a more coordinated release and a higher myoplasm-averaged rise in [Ca²⁺], which will exert a greater effect on membrane potential and contractile state.

In this study, we present a simple mathematical framework for understanding the importance of Ca²⁺ ion diffusion in the propagaton Ca²⁺ waves, with particular emphasis on their velocity, a readily-measureable wave parameter. Our spatial model features a continuum diffusion-reaction representation of free and buffered Ca²⁺ ions in both myoplasm and SR (6), and also incorporates a simplified (non-Markovian) but comprehensive representation of RyR channel modulation by myoplasmic and SR [Ca²⁺] (7-11). With these features, the model provides a first attempt at reconciling recent work on Ca²⁺ mobility with the mechanism for Ca²⁺ wave propagation.

2.1. Calcium mobility

The calcium ion is highly reactive and binds readily to buffer sites within cells. These buffer sites are held on large molecules, such as troponin in the myoplasm, and calsequestrin in the SR, as well as smaller molecules such as calmodulin and ATP (6, 10, 12). In myoplasm during diastole, it is estimated that only one in a thousand Ca²⁺ ions remains unbound (12, 13). This ratio is believed to be closer to one in ten for Ca²⁺ within the SR (6, 14). Figure 1 shows buffering capacity curves determined empirically for the myoplasm (13, 15, 16) and SR (14). Since most Ca²⁺ buffering is hosted by molecules considerably larger than the Ca²⁺ ion, effective Ca²⁺ ion mobility is predicted to be low. Overall Ca²⁺ mobility is the sum of free Ca²⁺ ion diffusion and buffered Ca²⁺ (buf) diffusion (17):

$$\frac{\partial \mathrm{Ca}}{\partial \mathrm{t}}+\frac{\partial \mathrm{buf}}{\partial \mathrm{t}}={\mathrm{D}}_{\text{free}}\cdot \frac{{\partial }^2\mathrm{Ca}}{\partial {\mathrm{x}}^2}+{\mathrm{D}}_{\mathrm{buf}}\cdot \frac{{\partial }^2\mathrm{buf}}{\partial {\mathrm{x}}^2}$$

This equation can be simplified using the chain rule,

$$\begin{array}{cc}\hfill & \frac{\partial \mathrm{buf}}{\partial \mathrm{t}}=\frac{\partial \mathrm{buf}}{\partial \mathrm{Ca}}\cdot \frac{\partial \mathrm{Ca}}{\partial \mathrm{t}};\frac{\partial \mathrm{buf}}{\partial \mathrm{x}}=\frac{\partial \mathrm{buf}}{\partial \mathrm{Ca}}\cdot \frac{\partial \mathrm{Ca}}{\partial \mathrm{x}}\hfill \\ \hfill & \therefore \frac{\partial \mathrm{Ca}}{\partial \mathrm{t}}\cdot \left(1+\frac{\partial \mathrm{buf}}{\partial \mathrm{Ca}}\right)=\left({\mathrm{D}}_{\text{free}}+{\mathrm{D}}_{\mathrm{buf}}\cdot \frac{\partial \mathrm{buf}}{\partial \mathrm{Ca}}\right)\cdot \frac{{\partial }^2\mathrm{Ca}}{\partial {\mathrm{x}}^2}\hfill \end{array}$$

In unbuffered media at 37°C, the diffusion coefficient for free Ca²⁺ (D_free) is ~1000μm²/s (18). However, in the presence of a non-diffusible buffer (concentration C and Ca²⁺ dissociation constant K), effective Ca²⁺ mobility (D_eff) is given by:

$${\mathrm{D}}_{\mathrm{eff}}={\mathrm{D}}_{\text{free}}\cdot {\left(1+\frac{\mathrm{C}\cdot \mathrm{K}}{{(\mathrm{K}+\left[{\mathrm{Ca}}^{2+}\right])}^2}\right)}^{-1}$$ Eq 1

Ca²⁺ mobility can be facilitated by parallel diffusion of Ca²⁺-bound, low molecular weight buffers. Such ‘facilitated diffusion’ also underpins cytoplasmic mobility of the H⁺ ion (19), another example of a buffered ionic species. To account for facilitated diffusion aboard buffers, Eq 1 can be expanded to include several buffers, each with a diffusion coefficient D:

$${\mathrm{D}}_{\mathrm{eff}}=\frac{{\mathrm{D}}_{\text{free}}+\sum _{\mathrm{i}}^{\mathrm{N}}\frac{{\mathrm{D}}_{\mathrm{i}}\cdot {\mathrm{C}}_{\mathrm{i}}\cdot {\mathrm{K}}_{\mathrm{i}}}{{({\mathrm{K}}_{\mathrm{i}}+\left[{\mathrm{Ca}}^{2+}\right])}^2}}{1+\sum _{\mathrm{i}}^{\mathrm{N}}\frac{{\mathrm{C}}_{\mathrm{i}}\cdot {\mathrm{K}}_{\mathrm{i}}}{{({\mathrm{K}}_{\mathrm{i}}+\left[{\mathrm{Ca}}^{2+}\right])}^2}}$$ Eq 2

Overall mobility can be reduced further by tortuosity due to geometrical restrictions and/or macromolecular crowding. This factor has been estimated to reduce ionic mobility by a factor of two in myoplasm (20) and over an order of magnitude in the SR (6). To account for tortuosity, Eq 2 should be scaled by a constant.

Figure 1.

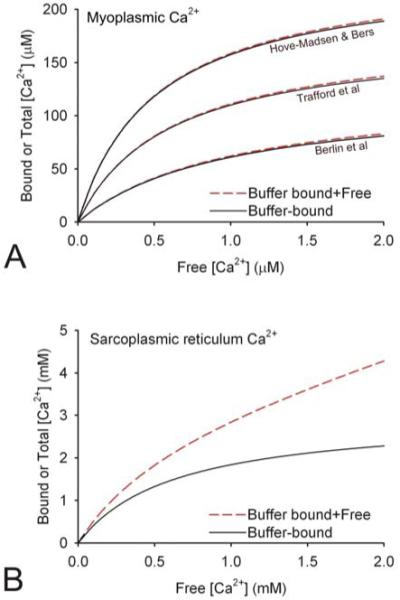
Experimentally-derived Ca²⁺ buffering capacity curves for (A) myoplasm (13, 15, 16) and (B) SR (14). Continuous black curves denote buffer-bound Ca²⁺ and dashed red curves denote total Ca²⁺. The marked difference between the three myoplasmic buffering curves may be accounted for by the time-frame within which buffering was measured. The lowest estimate (16) was obtained over a rapid time-scale and therefore represents fast buffering. The highest buffering capacity estimate (15) was determined over a much longer timescale and therefore also includes slow buffers.

Theoretical considerations, based on buffering and tortuosity, predict low effective Ca²⁺ mobility (D_eff<​<​D_free) in both myoplasm and SR. Experimental measurements have confirmed these predictions. Myoplasmic D_eff (D_Meff), estimated at diastolic levels of [Ca²⁺], is ~10-20μm²/s (20-22). Comparable estimates have been made for the cytoplasm of non-muscle cells (23, 24). A key precautionary measure that must be considered in such studies is the propensity for exogenous buffers (such as Ca²⁺ fluorophores, if present) to inflate D_Meff artefactually (24). Low myoplasmic Ca²⁺ mobility is consistent with the local nature of Ca²⁺ signaling in myocytes, within functional ‘units’ called couplons (5, 25). The fundamental SR release event is a Ca²⁺ spark (first described in (26)) which may involve simultaneous activation of a cluster of ~20 RyR channels (26). During this non-propagating SR release event, myoplasmic [Ca²⁺] rises to 200-300nM within ~10ms over a 2μm-wide space. Sustaining such a steep concentration gradient over a small distance requires Ca²⁺ to diffuse slowly (25). In isolation, such an event does not produce a contractile response. However, coordinated opening of tens of thousands of RyRs will generate sufficient Ca²⁺ to engage the contractile apparatus throughout the myocyte. Low Ca²⁺ mobility also ensures that the response can be graded by varying the number of activated release sites. However, in order to reach contractile proteins, Ca²⁺ must be adequately mobile. A mobility of 10-20μm²/s is a compromise between localization of Ca²⁺ signaling and Ca²⁺ penetrability into the myoplasm.

Two recent studies have tackled the issue of SR D_eff (D_SReff). As expected from SR luminal buffering and tortuosity, D_SReff was found to be lower than free Ca²⁺ mobility, D_free. The first study suggested a mobility of 60μm²/s at room temperature (~80μm²/s when corrected to 37°C) (27), i.e. considerably faster than myoplasmic Ca²⁺ mobility. However, the second study (6) estimated D_SReff to be 9μm²/s i.e. of similar order of magnitude to myoplasmic D_eff. The difference between these two studies may represent species differences (rabbit in (27) vs rat and guinea-pig in (6)), but it may also be explained by experimental design. The first study (27) measured relaxation of an intra-SR [Ca²⁺] gradient, imposed by a transient and local exposure to caffeine to empty SR regionally. The relaxation time-course was measured using an intra-SR Ca²⁺ dye (Fluo-5N), and fitted with diffusion equations to obtain mobility. The second study (6) used a caffeine-based protocol to empty the SR at one end of the cell and, after a delay, empty the remainder of the SR. SR content was assayed using measurements of myoplasmic [Ca²⁺], made under conditions that control for background SR leak, SR uptake and sarcolemmal transport. These experiments showed that SR Ca²⁺ mobility is similar to, or even smaller than myoplasmic Ca²⁺ mobility. Incidentally, when background SR leak was not allowed for, a much larger value for D_SReff was obtained, emphasizing the importance of controlling ‘reaction’ fluxes in diffusion-reaction phenomena, whenever the mathematics are simplified to a diffusive problem (6).

The exact value of D_SReff remains an actively researched and hotly debated topic (25, 28). It is noteworthy, however, that the lower estimate for D_SReff is in agreement with the rate of ‘Ca²⁺ blink’ recovery (29, 30) i.e. the relaxation of intra-SR [Ca²⁺] non-uniformity following a Ca²⁺ spark, the kinetics of which are believed to be diffusion-limited (31). Low SR Ca²⁺ mobility is also in agreement with the paradigm of local Ca²⁺ signaling. If D_SReff were larger than D_Meff, individual release sites would no longer be independent (25) because depletion at one site would promptly and significantly reduce the substrate for release elsewhere. To summarize, Ca²⁺ mobility in myoplasm and the SR have been shown, both experimentally and theoretically, to be much lower than free Ca²⁺ ion mobility in unbuffered medium.

2.2. Calcium waves

Intracellular Ca²⁺ waves were first inferred from spontaneous contractions observed under conditions of elevated [Ca²⁺] in skinned cardiac cells (32), and later in intact cells (33). With the advent of high-resolution imaging, Ca²⁺ waves were described as Ca²⁺ release events that propagate throughout the cell at constant velocity (3, 34). In cardiac myocytes, velocity has been estimated to be ~100μm/s (35).

The fundamental event that triggers a Ca²⁺ wave is a local Ca²⁺ release that, under a special set of conditions, elicits Ca²⁺ release from adjacent SR regions (Figure 2A). RyR channels are central to Ca²⁺ wave propagation, as they are sensitive to myoplasmic [Ca²⁺] (35, 36) and SR [Ca²⁺] (37, 38). The initial stimulus for RyR activation could be elevated myoplasmic [Ca²⁺] (39) or overloaded SR (40), or both.

Figure 2.

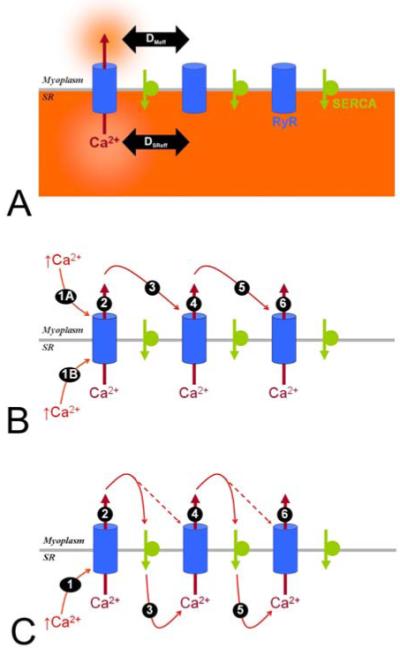
Postulated mechanisms underlying Ca²⁺ waves. (A). Local Ca²⁺ release from the SR, through locally-activated RyRs, leads to a depletion of SR [Ca²⁺] and a local rise in myoplasmic [Ca²⁺]. The spatial influence of these two microdomains is set by the Ca²⁺ diffusion coefficient in myoplasm and SR (D_Meff and D_SReff). (B). The classical model for Ca²⁺ wave propagation postulates that the stimulus for RyR channel opening is myoplasmic [Ca²⁺] (1A). An extension of this model takes into account modulation by the SR [Ca²⁺] load. Under certain conditions, SR ‘overload’ can trigger RyR channel opening (1B). The myoplasmic microdomain of released Ca²⁺ spreads diffusively to adjacent RyRs and triggers their activation. This cycle repeats and a wave of Ca²⁺ release events propagates along the myocyte. (C). An alternative model for Ca²⁺ wave propagation. Ca²⁺ released from the SR through activated RyR channels is re-sequestered by SERCA pumps. The locally-elevated intra-SR [Ca²⁺] spreads diffusively and sensitizes RyR channels en route. A rise in myoplasmic [Ca²⁺] then readily activates sensitized RyR channels. The advancing myoplasmic Ca²⁺ wavefront therefore moves behind a wavefront of elevated (RyR-sensitizing) SR [Ca²⁺]. For a wave to spread by this mechanism, intra-SR Ca²⁺ diffusion (3, 5...) cannot be slower than myoplasmic Ca²⁺ diffusion.

According to ‘classical’ models of wave propagation, the Ca²⁺ wave is driven forward by Ca²⁺ diffusion in the myoplasm (Figure 2B). Under this hypothesis, the myoplasmic Ca²⁺ wavefront will travel ahead of any SR Ca²⁺ wavefront. Recently, an alternative model of Ca²⁺ wave propagation (41) has been postulated. In this model, a Ca²⁺ wave arises as a result of the spread of an intra-SR Ca²⁺ overload that sensitizes RyR channels en route (Figure 2C). Ca²⁺ released into the myoplasm is resequestered back into the SR by SERCA pumps. The activity of these pumps raises intra-SR [Ca²⁺] locally. This ‘bolus’ of SR Ca²⁺ spreads diffusively and sensitizes downstream RyR channels, so that a rise in myoplasmic [Ca²⁺] opens RyRs more readily. Under this proposal, Ca²⁺ diffusion in the SR cannot be slower than in the myoplasm (27), i.e. the SR wavefront of RyR sensitization must travel ahead of the myoplasmic Ca²⁺ wavefront. In addition, a local rise in SR [Ca²⁺] is expected to precede the myoplasmic [Ca²⁺] wave. For either model, the propagation velocity will depend on

1. the distance between adjacent release sites,

2. the time taken for RyR channels to open.

These parameters are somewhat analogous to the length and time constants of membranes, which determine the velocity of action potential propagation in axons (42). An upper limit for the greatest spacing σ between adjacent release sites can be estimated by comparing Ca²⁺ wave velocity (v_Ca) with the Ca²⁺ diffusion coefficient (D_eff). The time taken for Ca²⁺ to diffuse distance σ must be shorter than the time-delay expected from the wave velocity, i.e.

$$\frac{{\sigma }^2}{2\cdot {\mathrm{D}}_{\mathrm{eff}}}<\frac{\sigma }{{\mathrm{v}}_{\mathrm{Ca}}}$$ Eq 3

It is important to note that the next adjacent release site must contain activatable RyR channels and sufficient substrate (i.e. SR [Ca²⁺] content) for release. Under such a model, fast Ca²⁺ wave velocity is favored by:

1. fast myoplasmic Ca²⁺ diffusion,

2. low RyR activation threshold,

3. rapid Ca²⁺ release,

4. an adequate SR Ca²⁺ store in adjacent regions.

It is clear from the postulated models of Ca²⁺ wave propagation that Ca²⁺ mobility in both SR and myoplasm must play a major role in setting Ca²⁺ wave velocity. Ca²⁺ mobility will also affect RyR channel modulation by Ca²⁺ ions on both the myoplasmic and luminal SR side. For instance, the local SR [Ca²⁺] load that modulates RyR channels will depend on the extent to which intra-SR Ca²⁺ has diffused, following a local release event elsewhere in the SR (6). Similarly, the dilution of myoplasmic [Ca²⁺] by diffusion will affect the rate at which the RyR opening threshold is reached, the time-course of channel inactivation, and the transmembrane Ca²⁺ gradient.

Mathematical models have been instrumental in our understanding of Ca²⁺ waves (43-47). To understand the importance of Ca²⁺ diffusion in determining Ca²⁺ wave velocity, we have constructed a simple continuum diffusion-reaction model. Our model allows for intra-SR Ca²⁺ diffusion and incorporates RyR modulation by both cis and trans [Ca²⁺]. The simplicity of the model renders it useful for didactic purposes, and for testing hypotheses for Ca²⁺ wave propagation.

3. METHODS

3.1. Measuring calcium mobility and calcium waves

Ventricular myocytes were isolated from rat hearts by a combination of mechanical and enzymic dispersion (see (6) for further details). All procedures were performed in line with UK Home Office regulations. Myocytes were loaded with the acetoxymethyl ester of the Ca²⁺-sensitive fluorophore Fluo-3 (10μM) and imaged in linescan mode along the myocyte’s long-axis under an inverted Leica IRBE microscope coupled to a Leica TCS NT confocal system (detecting fluorescence >515nm). Excitation at 488nm was provided by an argon laser. Fluorescence was reported as a pseudo-ratio F/F₀, normalized to starting fluorescence F₀. Cells were paced at 2Hz and superfused in a Perspex chamber at 37°C with normal Tyrode solution at pH 7.4, containing 135mM NaCl, 4.5mM KCl, 20mM Hepes, 2mM CaCl₂, 1mM MgCl₂ and 10mM glucose.

To assess Ca²⁺ diffusion in the myoplasm and SR, pacing was stopped and cells superfused with ‘solution A’ (0Na-0Ca): 140mM N-methyl-D-gluconate, 4.5mM KCl, 1mM MgCl₂, 10mM glucose, 0.5mM EGTA, 10μM cyclopiazonic acid (CPA, a SERCA inhibitor) and 0.3mM tetracaine (an RyR channel blocker). Under these conditions, the myocyte SR store was stabilized and sarcolemmal fluxes minimized (6). After 30s, one half of the myocyte was exposed to ‘solution B’ which was similar to ‘solution A’, but contained 10mM caffeine (RyR activator) instead of tetracaine. The other half of the cell remained exposed to ‘solution A’ (step 1 in Figure 3Ai). Sharp separation of the two solutions was possible with a dual microperfusion apparatus (6, 19). This maneuver evokes rapid Ca²⁺ release through RyR channels located in the caffeine-exposed part of the myocyte. SR Ca²⁺ release can be estimated from the myoplasmic Fluo-3 signal. After a 30s delay, the entire myocyte was exposed to ‘solution B’ (step 2 in Figure 3Ai). This maneuver evokes rapid Ca²⁺ release from the remainder of the cell. Details of this method have been validated and published elsewhere (6).

Figure 3.

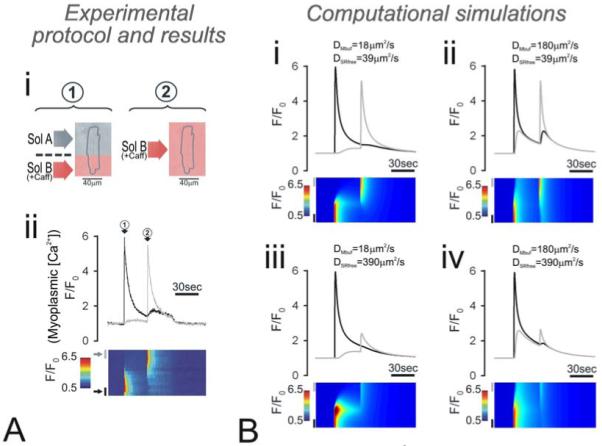
(A) Experimental evidence for low myoplasmic and SR Ca²⁺ mobility. (i) Protocol based on (6) executed on a rat cardiac myocyte, preloaded with Fluo-3 to measure myoplasmic Ca²⁺ fluorescence F/F₀. (ii) F/F₀ was collected in linescan mode (bottom panel), normalized to cell-length along the y-axis. F/F₀ time-courses were sampled on either end of the myocyte, in regions of length equal to 20% of cell length (top panel). Protocol: myocyte was superfused with Na⁺-free, Ca²⁺-free (+0.5mM EGTA) solution to minimize sarcolemmal Ca²⁺ flux, with 10μM cyclopiazonic acid to block SERCA and 0.3mM tetracaine to block RyR channels (‘solution A’). Arrow 1: One end of the myocyte was rapidly exposed to caffeine-containing ‘solution B’ (similar to ‘solution A’ but containing 10mM caffeine instead of tetracaine; caffeine-containing solutions have been shaded red). Remainder of the cell continued to be exposed to ‘solution A’. This generated a regional and rapid release of Ca²⁺ from the caffeine-exposed SR into the myoplasm, which was recorded as a rise in normalized myoplasmic Fluo-3 fluorescence (F/F₀). Relaxation of F/F₀ back to 1 was mediated by the plasmalemmal Ca²⁺-pump. The extent to which myoplasmic Ca²⁺ spread laterally was small, suggesting low Ca²⁺ mobility. Arrow 2: After a delay of 30s, the entire myocyte was bathed in ‘solution B’, thereby exposing the remainder of the myocyte to 10mM caffeine. This mobilized the remaining SR Ca²⁺, which was recorded as a second rise in Fluo-3 fluorescence. The peak rise in F/F₀ was similar during the first and second caffeine maneuver. This indicates that SR Ca²⁺ diffusion was minimal. (B) Computational simulations for the experimental protocol with different diffusion coefficients for myoplasmic buffer mobility (D_Mbuf) and SR free Ca²⁺ mobility (D_SRfree): (i) 18 and 39μm²/s, (ii) 180 and 39μm²/s, (iii) 18 and 390μm²/s, and (iv) 180 and 390μm²/s. The best-fit is obtained with low myoplasmic and SR Ca²⁺ mobility.

Myoplasmic Ca²⁺ mobility can be assessed from the spread of Ca²⁺ following the first, localized caffeine exposure (step 1 in Figure 3Ai). In the same cell, SR Ca²⁺ mobility can be derived from the relationship between the size of the F/F₀ rise during the localized caffeine exposure (step 1 in Figure 3Ai) versus the response evoked distally by whole-cell caffeine exposure (step 2 in Figure 3Ai). The latter will depend on the extent to which the SR has been drained by the first, localized caffeine pulse.

To trigger Ca²⁺ waves, pacing was stopped and cells were superfused with normal Tyrode solution containing elevated CaCl₂ at 7.5mM. Under these conditions, the SR is overloaded and the incidence of Ca²⁺ waves is greatly enhanced (40).

3.2. Mathematical model for calcium waves

One output of the Ca²⁺ wave model is a prediction of wave velocity under different experimental conditions. Our model is a continuum representation, featuring two compartments, the myoplasm (volume fraction v_myo) and SR (volume fraction v_SR) within which Ca²⁺ diffuses, with effective diffusion coefficients D_Meff and D_SReff, respectively. Myoplasmic Ca²⁺ is buffered by a fast, lumped myoplasmic buffer (flux J_Mbuf), described in (16). SR Ca²⁺ is buffered by calsequestrin (flux J_SRbuf), characterized in (14). To simplify the model, Ca²⁺ diffusion coefficients were set to a particular constant, independent of [Ca²⁺]. Indeed, few data are available to characterize fully the [Ca²⁺]-dependence of Ca²⁺-mobility. Ca²⁺ flux between the two compartments is mediated by SERCA (J_SERCA) working in forward or reverse mode (with a maximum rate of V_SERCA) (14) and RyR channels (J_RyR). The myoplasmic compartment is also in communication with the extracellular space via sarcolemmal flux (J_sl) that features a simplified model for Na⁺-Ca²⁺ exchange (NCX) and Ca²⁺ entry via a leak pathway (assuming extracellular [Ca²⁺]_e=1mM) (38).

The mathematical characterization of RyR channels is simplified to the minimum that is sufficient to encode the properties (7-10) of

• activation and inactivation by myoplasmic [Ca²⁺],

• threshold opening with high gain,

• modulation by SR [Ca²⁺].

To represent these features mathematically, RyRs were modeled as ‘release gates’, sensitive to myoplasmic and SR [Ca²⁺] (7). The simplified mathematics describe schematic population behavior of RyRs, rather than a Markovian channel representation of RyR channel clusters. Ca²⁺ flux across RyR ‘release gates’ is given by the product of their fractional activation and a permeability constant (k_RyR). Fractional activation is given by the difference in ‘occupancy’ of a fast, activation gate (S_α) and a slow, inactivation gate (S_β). By setting faster Ca²⁺ binding kinetics to S_α, the model encodes for time-dependent SR Ca²⁺ release: activation followed by inactivation, as proposed originally in (48). Occupancy of these two gates is described by Ca²⁺ dissociation constants K_α and K_β. The fast gate is assumed to be in equilibrium with myoplasmic Ca²⁺ whereas binding to the slow gate follows first order kinetics with on and off rate-constants k_β⁺ and k_β⁻, respectively.

Incorporation of the inactivation gate S_β is necessary to account for threshold. Threshold is encoded by ensuring that, below a certain rise in myoplasmic [Ca²⁺], S_β occupancy exceeds S_α occupancy, i.e. K_α>K_β at steady-state. For comparison, if K_α=K_β, any rise in myoplasmic [Ca²⁺] will trigger opening and, if K_α​<​K_β, RyR channels will open spontaneously. In other words, threshold is determined by the difference between K_α and K_β under resting conditions.

It is well-established that SR content affects Ca²⁺ wave threshold. A Ca²⁺ ‘overloaded’ SR is more prone to firing Ca²⁺ waves (40). At present, there is good experimental evidence to suggest that calsequestrin modulates RyR opening probability (8, 9). To account for RyR modulation by SR Ca²⁺ content in the model, k_β⁺ is set to be linearly-dependent on calsequestrin concentration (14, 38). By implementing this, K_β and hence Ca²⁺ wave threshold become dependent on SR [Ca²⁺].

The system of equations for the model is constructed to describe a vector u for the following species:

1. free myoplasmic [Ca²⁺],

2. Ca²⁺-bound myoplasmic buffer,

3. unbound myoplasmic buffer,

4. free SR [Ca²⁺],

5. Ca²⁺-bound calsequestrin,

6. unbound calsequestrin,

7. Ca²⁺-occupancy of (fast, activating) site S_α,

8. Ca²⁺-occupancy of (slow, inactivating) site S_β.

The model equations are as follows:

$$\begin{array}{c}\frac{\partial {\mathrm{u}}_1}{\partial \mathrm{t}}={\mathrm{D}}_1\cdot \frac{{\partial }^2{\mathrm{u}}_1}{\partial {\mathrm{x}}^2}-{\mathrm{J}}_{\mathrm{Mbuf}}+\frac{{\mathrm{J}}_{\mathrm{sl}}+{\mathrm{J}}_{\mathrm{RyR}}-{\mathrm{J}}_{\mathrm{SERCA}}}{{\mathrm{v}}_{\mathrm{m}}}\hfill \\ \frac{\partial {\mathrm{u}}_2}{\partial \mathrm{t}}={\mathrm{D}}_2\cdot \frac{{\partial }^2{\mathrm{u}}_2}{\partial {\mathrm{x}}^2}-{\mathrm{J}}_{\mathrm{Mbuf}}\hfill \\ \frac{\partial {\mathrm{u}}_3}{\partial \mathrm{t}}={\mathrm{D}}_3\cdot \frac{{\partial }^2{\mathrm{u}}_3}{\partial {\mathrm{x}}^2}+{\mathrm{J}}_{\mathrm{Mbuf}}\hfill \\ \frac{\partial {\mathrm{u}}_4}{\partial \mathrm{t}}={\mathrm{D}}_4\cdot \frac{{\partial }^2{\mathrm{u}}_4}{\partial {\mathrm{x}}^2}-{\mathrm{J}}_{\mathrm{SRbuf}}+\frac{{\mathrm{J}}_{\mathrm{SERCA}}-{\mathrm{J}}_{\mathrm{RyR}}}{{\mathrm{v}}_{\mathrm{SR}}}\hfill \\ \frac{\partial {\mathrm{u}}_5}{\partial \mathrm{t}}={\mathrm{D}}_5\cdot \frac{{\partial }^2{\mathrm{u}}_5}{\partial {\mathrm{x}}^2}-{\mathrm{J}}_{\mathrm{SRbuf}}\hfill \\ \frac{\partial {\mathrm{u}}_6}{\partial \mathrm{t}}={\mathrm{D}}_6\cdot \frac{{\partial }^2{\mathrm{u}}_6}{\partial {\mathrm{x}}^2}+{\mathrm{J}}_{\mathrm{SRbuf}}\hfill \\ {\mathrm{u}}_7=\frac{{\mathrm{u}}_1}{{\mathrm{u}}_1+{\mathrm{K}}_{\alpha }}\hfill \\ \frac{\partial {\mathrm{u}}_8}{\partial \mathrm{t}}={{\mathrm{k}}_{\beta }}^{+}\cdot {\mathrm{u}}_6\cdot {\mathrm{u}}_1\cdot (1-{\mathrm{u}}_8)-{{\mathrm{K}}_{\beta }}^{-}\cdot {\mathrm{u}}_8\hfill \end{array}$$

where

$$\begin{array}{c}{\mathrm{J}}_{\mathrm{Mbuf}}={\mathrm{k}}_{\mathrm{M}}\cdot ({\mathrm{u}}_1\cdot {\mathrm{u}}_3-{\mathrm{K}}_{\mathrm{M}}\cdot {\mathrm{u}}_2)\hfill \\ {\mathrm{J}}_{\mathrm{SRbuf}}={\mathrm{k}}_{\mathrm{SR}}\cdot ({\mathrm{u}}_4\cdot {\mathrm{u}}_6-{\mathrm{K}}_{\mathrm{SR}}\cdot {\mathrm{u}}_5)\hfill \\ {\mathrm{J}}_{\mathrm{RyR}}=\mathrm{R}({\mathrm{u}}_7,{\mathrm{u}}_8)\cdot ({\mathrm{u}}_4-{\mathrm{u}}_1)\hfill \\ {\mathrm{J}}_{\mathrm{SERCA}}=\frac{{\mathrm{V}}_{\mathrm{SERCA}}\cdot ({{\mathrm{u}}_1}^2-{({\mathrm{u}}_4∕\delta )}^2)}{{{\mathrm{K}}_{\mathrm{SERCA}}}^2+{{\mathrm{u}}_1}^2+{({\mathrm{u}}_4∕\delta )}^2}\hfill \\ {\mathrm{J}}_{\mathrm{sl}}={\mathrm{k}}_{\mathrm{sl}}\cdot ({\left[{\mathrm{Ca}}^{2+}\right]}_{\mathrm{e}}-{\mathrm{u}}_1)-\frac{{\mathrm{V}}_{\mathrm{NCX}}\cdot {\mathrm{u}}_1}{{\mathrm{K}}_{\mathrm{NCX}}+{\mathrm{u}}_1}\hfill \end{array}$$

The gating of RyR channels follows the condition:

$$\mathrm{R}=\{\begin{array}{cc}{\mathrm{k}}_{\mathrm{RyR}}\cdot ({\mathrm{u}}_7-{\mathrm{u}}_8)+{\mathrm{k}}_{\text{leak}}\hfill & \text{if}({\mathrm{u}}_7-{\mathrm{u}}_8)>0,\hfill \\ {\mathrm{k}}_{\text{leak}}\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

Recent measurements of the SR leak-load relationship (49) suggest that the rate-constant for background SR Ca²⁺ leak, k_leak, is not constant but varies with SR [Ca²⁺]. To implement this in the model, k_leak was set to vary with total SR [Ca²⁺] raised to 1.7^th power, and scaled to a level that balances SERCA flux to attain the desired steady-state SR [Ca²⁺] load (0.063 s⁻¹ for SR free [Ca²⁺]=500μM; (49)). Parameterization of SERCA flux was based on (38). Unless stated otherwise, resting myoplasmic and SR free [Ca²⁺] were set to 0.1μM and 500μM (6, 14, 38). The initial conditions vector is,

$$\left[\begin{array}{cccc}\hfill 0.1\hfill & \hfill \frac{0.1\cdot {\mathrm{C}}_{\mathrm{mbuf}}}{0.1+{\mathrm{K}}_{\mathrm{mbuf}}}\hfill & \hfill \frac{{\mathrm{K}}_{\mathrm{mbuf}}\cdot {\mathrm{C}}_{\mathrm{mbuf}}}{0.1+{\mathrm{K}}_{\mathrm{mbuf}}}\hfill & \hfill \dots \hfill \\ \hfill 500\hfill & \hfill \frac{500\cdot {\mathrm{C}}_{\mathrm{SRbuf}}}{500+{\mathrm{K}}_{\mathrm{SRbuf}}}\hfill & \hfill \frac{{\mathrm{K}}_{\mathrm{SRbuf}}\cdot {\mathrm{C}}_{\mathrm{SRbuf}}}{500+{\mathrm{K}}_{\mathrm{SRbuf}}}\hfill & \hfill \dots \hfill \\ \hfill \frac{0.1}{0.1+{\mathrm{K}}_{\alpha }}\hfill & \hfill \frac{0.1}{0.1+{\mathrm{K}}_{\beta }}\hfill & \hfill \hfill & \hfill \hfill \end{array}\right]$$

The six solutes modeled are assigned diffusion coefficients D₁ to D₆ (D₂=D₃, D₅=D₆) which determine ‘effective’ Ca²⁺ mobility:

$${\mathrm{D}}_{\mathrm{Meff}}=\frac{{\mathrm{D}}_1+\frac{{\mathrm{D}}_2\cdot {\mathrm{C}}_{\mathrm{Mbuf}}\cdot {\mathrm{K}}_{\mathrm{Mbuf}}}{{({\mathrm{K}}_{\mathrm{Mbuf}}+\left[{\mathrm{Ca}}^{2+}\right])}^2}}{1+\frac{{\mathrm{C}}_{\mathrm{Mbuf}}\cdot {\mathrm{K}}_{\mathrm{Mbuf}}}{{({\mathrm{K}}_{\mathrm{Mbuf}}+\left[{\mathrm{Ca}}^{2+}\right])}^2}}$$ Eq 4

$${\mathrm{D}}_{\mathrm{SReff}}=\frac{{\mathrm{D}}_4+\frac{{\mathrm{D}}_5\cdot {\mathrm{C}}_{\mathrm{SRbuf}}\cdot {\mathrm{K}}_{\mathrm{SRbuf}}}{{({\mathrm{K}}_{\mathrm{SRbuf}}+\left[{\mathrm{Ca}}^{2+}\right])}^2}}{1+\frac{{\mathrm{C}}_{\mathrm{SRbuf}}\cdot {\mathrm{K}}_{\mathrm{SRbuf}}}{{({\mathrm{K}}_{\mathrm{SRbuf}}+\left[{\mathrm{Ca}}^{2+}\right])}^2}}$$ Eq 5

Myoplasmic free Ca²⁺ mobility (D₁=D_Mfree) is estimated assuming a free Ca²⁺ mobility of 1000μm²/s and a tortuosity that reduced mobility by a factor of 2 (20). D₂ and D₃ describe myoplasmic buffer mobility (D_Mbuf), which was set to a single, lumped value that yields an effective Ca²⁺ mobility (D_Meff) of 20μm²/s at diastolic [Ca²⁺] (Eq 4). For a cell at diastolic myoplasmic [Ca²⁺]=100nM, D_Meff of 20μm²/s translates to a D_Mbuf 18μm²/s. Calsequestrin is assumed to be immobile, therefore D₅=D₆=0. Intra-SR free Ca²⁺ mobility (D₄=D_SRfree) is estimated from data for effective intra-SR Ca²⁺ mobility. At half-filled SR, D_SReff has been estimated to be 9μm²/s, therefore D_SRfree=39μm²/s (Eq 5). To simulate changes in myoplasmic and SR Ca²⁺ mobility, variables D_Mbuf and D_SRfree were varied independently.

Since cell width and height are considerably smaller than length, the mathematics can be reduced to a one-dimensional space. The wave model is solved over a linear space x= [0,100]μm with reflection boundaries set on either end. Table 1 lists values of constants used in the modeling.

Table 1. Constants used for simulating Ca²⁺ waves.

Symbol	Parameter description	Value
vmyo	Volume fraction of myoplasm (6, 38)	0.65
vSR	Volume fraction of SR (6, 38)	0.035
Cmbuf	Myoplasmic buffer concentration (6, 13)	175μM
Kmbuf	Myoplasmic buffer dissociation constant (6, 13)	590nM
km	Myoplasmic buffer on rate constant*	100/μM/s
CSRbuf	SR buffer concentration (6, 14)	4.0mM
KSRbuf	SR buffer binding constant (6, 14)	630μM
kSRbuf	SR buffer on rate constant*	100/μM/s
VSERCA	Maximum flux on SERCA (14, 38)	500μM/s
δ	Max SR/myoplasm [Ca2+]-gradient (14, 38)	7000
KSERCA	SERCA Ca2+ dissociation constant (14, 38)	0.25μM
VNCX	Maximum flux on NCX (38)	1.2mM/s
KNCX	NCX Ca2+ dissociation constant (38)	36μM
ksl	Sarcolemmal leak rate constant#	0.0033/s
kleak	Background RyR channel flux constant at filled SR, scaled to fit leak-loak data (49)#	0.063/s
kα+	Sα on-rate constant	Not limiting
kα−	Sα off-rate constant	Not limiting
kβ+	Sβ on-rate constant at loaded SR [Ca2+]=500μM#	5/μM/s
kβ−	Sβ off-rate constant#	0.59/s
kRyR	Activated RyR channel flux constant#	18/s
D1	Free Ca2+ diffusion coefficient in myoplasm	500μm2/s
D2	Ca2+-bound myoplasmic buffer diffusion coefficient	18μm2/s
D3	Unbound myoplasmic buffer diffusion coefficient	18μm2/s
D4	Free Ca2+ diffusion coefficient in SR	39μm2/s
D5	Ca2+-bound calsequestrin diffusion coefficient	0μm2/s
D6	Unbound calsequestrin diffusion coefficient	0μm2/s

^*parameter assumed to be diffusion-limited

^#parameter best-fitted to data

To trigger a simulated Ca²⁺ wave, SR release was activated in a 2μm-wide region, midway along the length of the model cell. This was performed by one of three maneuvers: (i) introducing an additional SR-membrane flux term, with permeability constant k_act in parallel to k_RyR and k_leak, (ii) by locally elevating myoplasmic [Ca²⁺] (raising k_sl for 20msec) or (iii) by locally over-loading SR [Ca²⁺] (introducing a constant gain in SR free [Ca²⁺] for 20ms). Maneuvers (ii) and (iii) (but not (i)) increase, albeit temporarily, the total amount of Ca²⁺ in the cell. Unless stated otherwise, in silico Ca²⁺ waves were triggered by (i).

4. RESULTS

4.1. Calcium mobility in myoplasm and SR is low

Low Ca²⁺ mobility has been measured in previous studies for both myoplasm (20-22) and SR (6). Figure 2A shows an experiment from (6), illustrating low Ca²⁺ mobility in SR and myoplasm. The cell was first stabilized under conditions where sarcolemmal and SR Ca²⁺ fluxes are minimized (absence of superfusate Na⁺ and Ca²⁺, presence of CPA and tetracaine). Using a dual microperfusion apparatus (6, 19), one half of the myocyte was exposed to caffeine to open RyR channels locally (arrow 1, Figure 3Aii). This produced a local Ca²⁺ release into the myoplasm, reported by the rise in Fluo-3 signal (F/F₀). The black trace in Figure 3Aii shows the fluorescence rise averaged in the proximal, caffeine-exposed region and the grey trace shows the fluorescence rise at the other (distal) end. Note that the spread of Ca²⁺ to the distal end was small, indicating low myoplasmic Ca²⁺ mobility. After a delay of 30s, the rest of the cell was also exposed to caffeine, releasing any Ca²⁺ that had remained within the SR. Again, the spread of Ca²⁺ along the myoplasm was small, arguing for low myoplasmic Ca²⁺ mobility. This experiment also confirms low SR Ca²⁺ mobility. The whole-cell caffeine exposure (arrow 2, Figure 3Aii) produced a large release of Ca²⁺, peaking at a level similar to that during the first, regional caffeine exposure (arrow 1, Figure 3Aii). If SR Ca²⁺ mobility were high, the local caffeine exposure would have drained distal SR regions and reduced overall [Ca²⁺] load. Since the F/F₀ peaks indicated by the two circled arrows in Figure 3Aii were of similar magnitude, SR mobility is unlikely to be fast.

Figure 3B shows model simulations for the experimental maneuver, based on the modeling framework published and validated elsewhere (6). Panel (i) shows the simulation for the best-fitting effective myoplasmic and SR Ca²⁺ mobility of D_Mbuf=18 and D_SRfree=39μm²/s, respectively. These are equivalent to D_Meff and D_SReff of 20μm²/s (at diastolic myoplasmic [Ca²⁺]=100nM) and 9μm²/s (at half-filled SR), respectively. To confirm the goodness-of-fit, the model was run for different values for D_Mbuf and D_SRfree: (ii) 180 and 39μm²/s, (iii) 18 and 390μm²/s, and (iv) 180 and 390μm²/s. By inflating D_Mbuf and/or D_SRfree by one order of magnitude, the predicted F/F₀ time-courses no longer fit the data. These and similar data confirm low D_Meff and D_SReff in myocytes.

In a second set of experiments, myocytes were exposed to high superfusate Ca²⁺ (7.5mM) to induce SR Ca²⁺ overload and elicit Ca²⁺ waves (40). Figure 4 shows an experiment in which a myocyte spontaneously fired a Ca²⁺ wave (Figure 4A). After a 1s delay, the cell was field-stimulated for 2ms to evoke a Ca²⁺ transient (Figure 4B). The Ca²⁺ wave propagated at a velocity of 89μm/s (average for 10 cells=78±5μm/s), in agreement with previous estimates for cardiac myocytes of ~100μm/s (35). The time-course of the Ca²⁺ wave was velocity-corrected (time-frame for F/F₀ averaging was aligned with the onset of the wave, along the region denoted by the grey bar on the left of the linescan, (44)) and compared with the time-course of the Ca²⁺ transient. The time-course of the Ca²⁺ wave was similar to that of a Ca²⁺ transient. The Ca²⁺ wave onset, peak and duration were marginally slower than the corresponding parameters for the Ca²⁺ transients. The time-to-peak for the wave was ~100ms and its half-maximal width was ~180ms. Assuming a Fluo-3 dissociation constant of 850nM (6, 50), the peak rise in fluorescence corresponds to ~1μM [Ca²⁺].

Figure 4.

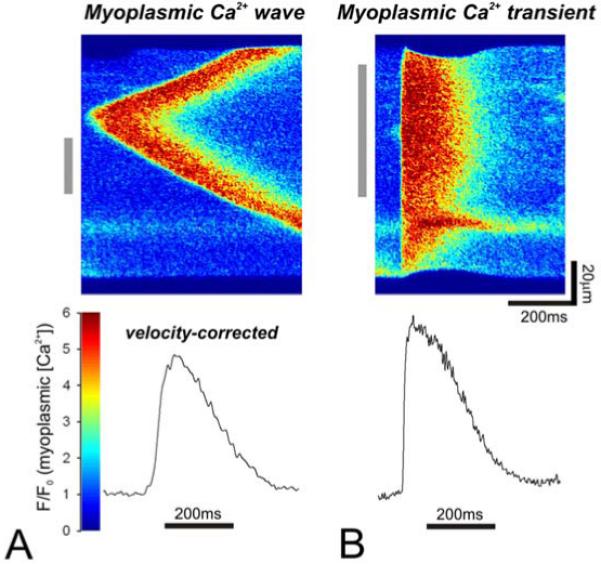
Comparison of a myoplasmic Ca²⁺ wave and myoplasmic Ca²⁺ transient. A rat myocyte, bathed in normal Tyrode solution with elevated Ca²⁺ (7.5mM) to produce SR overload. Under these conditions, myocytes exhibit a high probability of firing Ca²⁺ waves. The linescans show Fluo-3 fluorescence (myoplasmic [Ca²⁺] signal) along a myocyte (y-axis) over time (x-axis). (A). Top: Around mid-length of the myocyte, a Ca²⁺ wave was triggered spontaneously, propagating along either sides of the myocyte at 89μm/s. Bottom: The velocity-corrected time-course of a fragment of the wave (indicated by the grey bar, left of linescan). (B). Top: The myocyte, bathed in the same solution, was field-stimulated to produce a Ca²⁺ transient. Bottom: The averaged time-course of a fragment of the transient (indicated by the grey bar, left of linescan).

4.2. Modeling calcium waves

Ca²⁺ waves were simulated to generate an estimate for their velocity, which was then correlated with the Ca²⁺ diffusion coefficients. First, several model parameters (denoted by ^# in Table 1) were adjusted to obtain Ca²⁺ wave velocity and time-course similar to that measured experimentally (Figure 4). The interaction of Ca²⁺ with the S_α and S_β gates was described with dissociation constants K_α and K_β that were set to be within the experimentally-determined range of 300-700nM (38, 51). The difference between K_α and K_β determines threshold for Ca²⁺ wave initiation. Under resting conditions, release events that raise myoplasmic [Ca²⁺] locally to >200nM trigger waves (44), therefore under resting conditions ([Ca²⁺]_SR=500μM, [Ca²⁺]_M=0.1μM), K_α and K_β were set to 400nM and 300nM, respectively. The value for activated RyR permeability (k_RyR) was derived by best-fitting to Ca²⁺ wave velocity and the rate of myoplasmic [Ca²⁺] rise (Figure 4A, (44)). The magnitude of k_RyR, together with the threshold for RyR channel activation, will set the time-delay for triggering Ca²⁺ release. These parameters will therefore affect Ca²⁺ wave velocity.

The model also predicts Ca²⁺ wave propagation failure when free [Ca²⁺] in the SR falls below 365μM, i.e. 73% of resting [Ca²⁺]. This is in agreement with experimental data (52) that have shown Ca²⁺ wave propagation failure when total SR load falls by >25% (absence of Ca²⁺ waves for total SR [Ca²⁺]<90μmol/ (L cytosol), assuming total [Ca²⁺] in filled SR of 120μmol/(L cytosol)).

The model output is presented in Figure 5 in the form of linescans for myoplasmic and SR [Ca²⁺]. SR release was triggered locally (middle 2μm-wide region) by introducing an additional, exponentially-decaying term for SR Ca²⁺ permeability k_act (t) in parallel to k_RyR and k_leak. The initial amplitude of k_act was varied to probe for the threshold for Ca²⁺ wave generation. Below the threshold, SR release produced a local event that resembled a Ca²⁺ spark in the myoplasm (Figure 5Ai) and an associated Ca²⁺ blink (local luminal depletion) in the SR (Figure 5Bi). By setting the time-constant for k_act to 10ms, the spark and blink recovery time-constants were 25 and 75ms, within the experimentally-determined range (26, 29, 31). Above the threshold, the model generated a Ca²⁺ wave of velocity 78μm/s in the myoplasm (Figure 5Aii) and SR (Figure 5Bii). The model predicts a [Ca²⁺] rise in the myoplasm during the wave, accompanied by a simultaneous wave of [Ca²⁺] depletion in the SR. The time-courses of the myoplasmic release and SR depletion waves are plotted, together with the time-courses of the simulated Ca²⁺ ‘spark’ and ‘blink’. To compare the simulated time-course with experimental data, myoplasmic and SR [Ca²⁺] were converted to normalized Fluo-3 and Fluo-5 fluorescence (Figure 5C), assuming dissociation constants of 850nM (6, 50) and 400μM (27), respectively. The myoplasmic Ca²⁺ time-course is in agreement with experimental data (Figure 4A). The maximum local SR [Ca²⁺] depletion (~60%) is also in agreement with predictions based on experiments (38).

Figure 5.

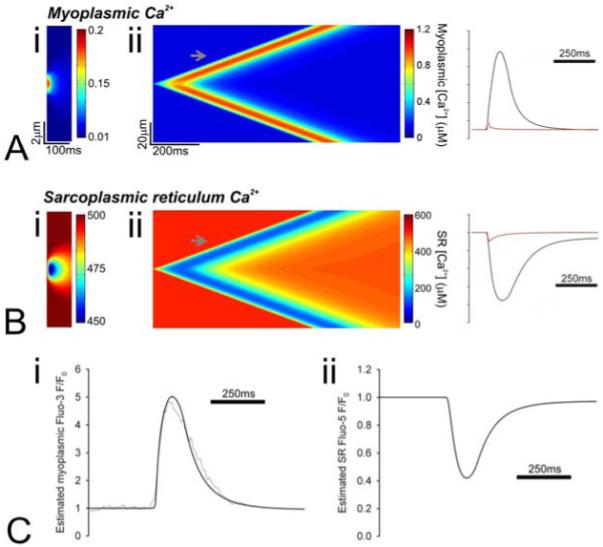
Simulated Ca²⁺ in (A) the myoplasm and (B) SR. Ca²⁺ release from the SR was triggered by introducing an additional, exponentially decaying (time-constant 10ms) permeability (k_act) in the SR membrane in a 2μm-wide region mid-way along the model cell. (i) Below a critical level, k_act generates a unitary and isolated event that fails to propagate. This event is similar to a Ca²⁺ spark in myoplasm and a Ca²⁺ blink in the SR. (ii) Above a critical level, k_act triggers a Ca²⁺ wave that spreads to either end of the cell at 78μm/s. The time-plots (right) show the Ca²⁺ rise in myoplasm and the corresponding fall in the SR during the sub-threshold events (red trace) and during the triggered Ca²⁺ wave (black trace, plotted at the position indicated by the grey arrow on the linescans). (C) (i) Myoplasmic [Ca²⁺] measured during a simulated Ca²⁺ wave was converted to Fluo-3 F/F₀ assuming a dye dissociation constant of 850nM. Superimposed on the prediction is the experimentally-determined Ca²⁺ wave time-course from Figure 4. (ii) SR [Ca²⁺] measured during a simulated Ca²⁺ wave was converted to Fluo-5N F/F₀ assuming a dye dissociation constant of 400μM.

The trigger for the simulated waves in Figure 5 was RyR activation imposed by an additional term for permeability. Physiologically, RyR activation can occur as a result of a rise in myoplasmic [Ca²⁺] or a rise in SR [Ca²⁺]. These were implemented mathematically by introducing a constant Ca²⁺ flux in the myoplasm or SR for 20ms in a central, 2μm-wide region in the myocyte. The magnitude was set to a supra-threshold level for wave generation. The outcome of the two triggering protocols was very similar (Figure 6). This is not surprising, given that the unified model uses the same equations for both modes of triggering. It is noteworthy that the simulated wave of SR [Ca²⁺] depletion is sharp, as determined experimentally (28, 53) and as expected from slow SR Ca²⁺ mobility (6) (but cf (27, 41)).

Figure 6.

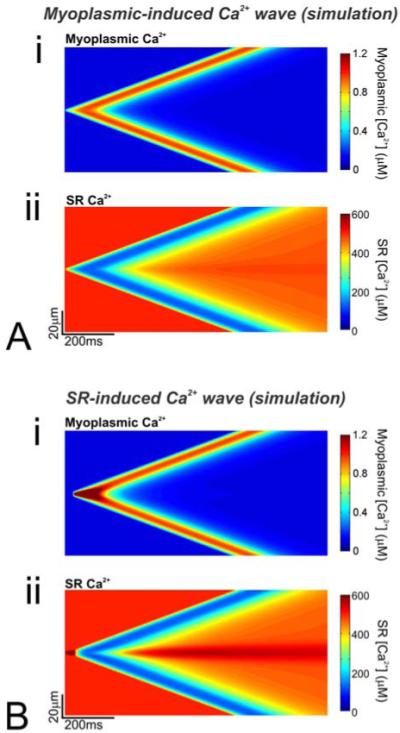
(A) Simulated Ca²⁺ wave was triggered by raising myoplasmic Ca²⁺ locally (central 2μm region) above a critical level, beyond which local Ca²⁺ release is sufficiently large to open adjacent release sites in a propagating manner. Linescans for (i) myoplasmic and (ii) SR [Ca²⁺]. (B) Simulated Ca²⁺ wave triggered by raising SR [Ca²⁺] locally (central 2μm region) to a level at which release occurs spontaneously at resting myoplasmic [Ca²⁺], i.e. the release threshold is lowered. Linescans for (i) myoplasmic and (ii) SR [Ca²⁺]. Note that the wave velocity (78μm/s) is the same with both simulations. Also, the time-course of the myoplasmic and SR [Ca²⁺] are very similar (away from the trigger site).

4.3. Modeling calcium waves at different calcium diffusion coefficients

In this set of simulations, effective Ca²⁺ mobility in myoplasm (D_Meff) and SR (D_SReff) were varied independently. This was performed by varying D_Mbuf between zero and 100μm²/s (D_Meff=102μm²/s) and D_SRfree between zero and 500μm²/s (D_SReff=160μm²/s). Ca²⁺ waves were triggered by opening RyR channels (introducing permeability k_act). At constant, control D_SRfree=39μm²/s, increasing D_Mbuf (and D_Meff) increased wave velocity sub-linearly over the range studied (Figure 7A). This is expected, as increasing mobility will decrease the time-delay due to diffusion between adjacent release sites. According to the model, velocity is proportional to the square root of diffusion coefficient D_Mbuf (Figure 7A). This is expected from continuum models (46). In fire-diffuse-fire models with discrete release sites, velocity has been proposed to vary proportionally with diffusion coefficient (47, 54) because the rate of wave progression is limited by the diffusion delay between discrete release sites rather than the release kinetics. In the presented continuum model, the slope of the mobility-velocity relationship (Figure 7A) falls at high Ca²⁺ mobility because the time-delay incurred by the opening of RyR channels becomes a more significant limiting factor towards overall Ca²⁺ wave velocity.

Figure 7.

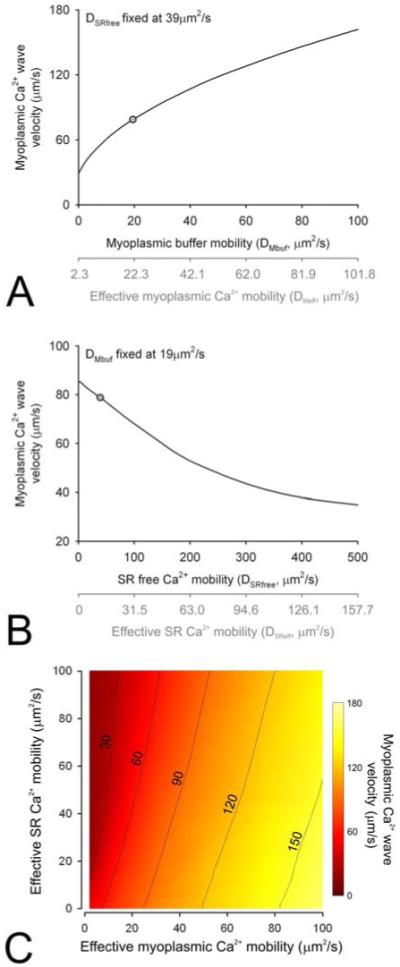
(A) Simulated relationship between myoplasmic buffer mobility (D_Mbuf) and Ca²⁺ wave velocity, at fixed SR free Ca²⁺ mobility (D_SRfree=39μm²/s). Grey circle: control conditions. (B) Simulated relationship between D_SRfree and Ca²⁺ wave velocity, at fixed D_Mbuf=18μm²/s. Grey circle: control conditions. The triggering protocol is the same as in Figure 5. Also plotted in grey is a secondary axis with mobility converted to effective myoplasmic Ca²⁺ mobility (D_Meff) at 100nM and effective SR Ca²⁺ mobility (D_SReff) at half-filled SR. (C) Contour maps showing the relationship between wave velocity, D_Meff and D_SReff.

At constant D_Mbuf=18μm²/s, increasing D_SRfree​ decreased wave velocity (Figure 7B) proportionately with the square root of D_SRfree. At high D_SRfree (as proposed for the model illustrated in Figure 2C), waves propagate at a velocity much slower than measured experimentally. This observation is somewhat less intuitive than the relationship in Figure 7A. Following a local SR release event, low D_SRfree (hence low D_SReff) will protect adjacent SR regions from diffusive dissipation. This will preserve Ca²⁺ substrate for SR release and hence wave propagation. Conversely, at high D_SReff, a local SR release will lead to depletion of adjacent SR regions. Consequently, myoplasmic Ca²⁺ will have to travel a longer distance (i.e. longer time-delay) to the next available SR region that can support release. This phenomenon is emphasized by the modulation of S_α-Ca²⁺ interaction kinetics by SR [Ca²⁺]. However, even without this additional cross-talk, the negative slope between D_SRfree and velocity remains qualitatively true.

Figure 7C shows the results of simulations in the form of a contour map. To summarize, the modeling predicts that increasing myoplasmic Ca²⁺ mobility and decreasing SR Ca²⁺ mobility will favor faster Ca²⁺ wave propagation.

4.4. Modeling calcium waves at different SERCA pump rates and RyR permeability

The local SR [Ca²⁺] available for release is dependent on diffusive dissipation and also on the replenishing activity of the SR Ca²⁺ pump, SERCA. Experimental results have yielded apparently conflicting inferences on the effect of SERCA inhibitors on wave velocity (a decrease (41, 55) or an increase (40)). As highlighted by others (55), the effect of SERCA inhibitors is two-fold. On the one hand, inhibition of SERCA reduces Ca²⁺ uptake from myoplasm, and therefore permits myoplasmic Ca²⁺ to diffuse a longer distance to reach more distant release sites. This factor increases wave velocity. From this point of view, SERCA behaves like a ‘Ca²⁺ buffer’ (indeed, increasing the dose of the Ca²⁺ buffer EGTA decreases wave velocity (56)). On the other hand, inhibition of SERCA will also reduce SR load and reduce the substrate for release. Furthermore, since SR Ca²⁺ modulates RyR channels (37, 38), a fall in local SR load will reduce the likelihood of RyR channel opening. These factors will tend to reduce Ca²⁺ wave velocity.

The model was configured with V_SERCA manipulated to between 0.2- and 2-fold of control activity, while D_Mbuf and D_SRfree were maintained at 18 and 39μm²/s. A Ca²⁺ wave was triggered (activating permeability k_act) immediately after manipulating V_SERCA or after a delay of 0.3, 0.6, 1 or 1.5s. The output of the model is shown in Figure 8Ai. If the Ca²⁺ wave is triggered early (<0.4s) after SERCA manipulation, the model predicts a negative relationship between V_SERCA and velocity. Over this short time-delay, the SR Ca²⁺ load will not change significantly. However, the altered activity of SERCA will have an immediate effect on the spatial spread of myoplasmic Ca²⁺. Under these conditions, the higher the SERCA activity, the smaller the spatial spread of myoplasmic Ca²⁺ and hence the slower the wave (40), as expected from the EGTA-like ‘buffer’ effect of SERCA (56). If the Ca²⁺ wave is triggered after a longer delay (>0.4s) following SERCA inhibition, the SR load has had enough time to change, particularly when the starting SR [Ca²⁺] is high (the SR leak-load relationship is exponential, (49)). Under these conditions, the spatial range of myoplasmic Ca²⁺ diffusion will be secondary to the effect of SR load on RyR channels: the lower the SR load, the slower the wave velocity. Our model therefore highlights the complexity of factors that affect Ca²⁺ wave velocity. Interpretation of experimental data must be made carefully in order to produce a unified hypothesis for the mechanism of Ca²⁺ waves. The star symbol indicates mean, normalized Ca²⁺ wave velocity, measured experimentally after 1s of inhibiting SERCA to a level that slows Ca²⁺ recovery 2.4-fold (41) (equivalent to 70% reduction in V_SERCA). The data are in good agreement with the mathematical prediction, i.e. SERCA inhibition slows wave velocity. Moreover, the slowing can occur without a major change in wave amplitude, as the smaller Ca²⁺ release (due to reduced SR load) is balanced by the slower SERCA kinetics that allow myoplasmic [Ca²⁺] to stay elevated for longer.

Figure 8.

(A) (i) Simulated relationship between control-normalized myoplasmic Ca²⁺ wave velocity and maximal SERCA flux (scaling V_SERCA by a factor of 0.2 to 2.0), calculated from myoplasmic Ca²⁺ waves triggered immediately after manipulation of V_SERCA or after a delay of 0.3, 0.6, 1s or 1.5s. D_Mbuf=18μm²/s; D_SRfree=39μm/s. Grey circle: control conditions. Green star: data from Keller et al (41). (ii) Simulated relationship between control-normalized wave velocity and SR free [Ca²⁺]. Different levels of SR load were obtained by varying V_SERCA. Grey circle: control conditions. Green star: data converted from Keller et al (41). Red triangle: data converted from Stokke et al (57). (B) (i) Simulated relationship between control-normalized myoplasmic Ca²⁺ wave velocity and RyR channel permeability. In one set of simulations (black curve), only activated RyR channel permeability (k_RyR) was varied, by scaling the control value by between 0.2 and 2.0. In a second set of simulations (red curve), leak RyR channel permeability (k_leak) was varied by scaling between 0.2 and 2.0 and allowing for the system to attain a new steady-state SR [Ca²⁺] load. In a third set of simulations, both parameters were varied simultaneously, and the system was allowed to attain a new steady-state (green curve). D_Mbuf=18μm²/s; D_SRfree=39μm²/s. Grey circle: control conditions. Stars indicate conditions at which waves fail to propagate. (ii) Simulated relationship between control-normalized wave velocity and peak Ca²⁺ amplitude, measured at 5μm away from trigger site, obtained by varying k_RyR. Grey circle: control conditions. Green stars: data from Trafford et al (39). Red triangles: data from Smith & O’Neill (59).

To illustrate the importance of SR load on Ca²⁺ wave velocity, the model was used to plot Ca²⁺ wave velocity against SR [Ca²⁺] (measured at 5μm from the trigger site). Reducing SERCA activity reduces SR free [Ca²⁺] and increases k_β⁺ which, in turn, elevates the threshold for Ca²⁺ release and reduces wave velocity. The experimental result (41) plotted in Figure 8Ai (green star) has been re-plotted in Figure 8Aii, again showing agreement with the predicted slowing of wave velocity. This prediction is also in agreement with recent experimental data (57) showing that a reduction in SERCA expression (42% reduction in rate) reduces Ca²⁺ wave velocity (red triangle, Figure 8Aii).

SR Ca²⁺ is released into the myoplasm through both a triggered and a leak pathway. There is good evidence to suggest that both pathways are mediated by RyR channels, but it is possible that the SR background leak occurs, at least partly, via ‘rogue’ RyR channels located outside couplons (58). In our model, Ca²⁺ fluxes are described by constants k_RyR and k_leak, respectively, and can be varied independently. Experimentally, however, pharmacological modulation of RyR channels with drugs such as tetracaine (an inhibitor) or caffeine (an activator) may affect both k_RyR and k_leak. Perhaps not surprisingly, the effect of tetracaine on Ca²⁺ wave velocity is complex. In some studies, tetracaine has been reported to slow wave velocity (59). Other studies have proposed a dose-dependence (60), such that lower tetracaine doses (<0.5mM) accelerated Ca²⁺ waves and higher doses (>0.5mM) tended to slow propagation.

In an attempt to reconcile the above findings with the proposed model for Ca²⁺ wave propagation, we performed two simulations. In the first, k_RyR was varied between 20% and 200% of its control rate while D_Mbuf and D_SRfree were fixed at 18 and 39μm²/s. This computational maneuver altered the population permeability of activated RyR channels. The black curve in Figure 8Bi shows the output of this simulation. Ca²⁺ wave velocity increased with increasing activated RyR permeability. This is predicted intuitively, as a faster development of RyR conductance will lead to faster Ca²⁺ release, which in turn will have a knock-on effect in reducing the time-delay associated with triggering the adjacent SR release event. Such a positive-slope relationship has been obtained experimentally with low doses of caffeine which increases wave velocity (39, 61) or, under certain conditions, with tetracaine which decrease wave velocity (59, 60). By increasing the rate of Ca²⁺ release, increasing k_RyR will also increase overall Ca²⁺ wave amplitude. The model was used to plot Ca²⁺ wave velocity versus peak myoplasmic [Ca²⁺] during a Ca²⁺ wave measured at 5μm from the trigger site (Figure 8Bii). The positive velocity-amplitude relationship is backed by experimental data (39, 59). Conversely, when k_RyR is reduced below 45% of its control value, Ca²⁺ waves fail to propagate (black star, Figure 8Bi). Experimentally, tetracaine doses in excess of 0.75mM have been shown to abolish waves within 1 min of application (60). This is equivalent to a 58% reduction in k_RyR (60), in approximate agreement with the model prediction.

In a second set of simulations, k_leak was varied instead of k_RyR. The model equations were first allowed to attain steady-state at the new value for k_leak. This was necessary in order to re-adjust diastolic SR [Ca²⁺], which is set by the balance between background SR leak and SERCA activity. The output of this simulation is shown as the red curve in Figure 8Bi. This relationship is strikingly different from the previous simulation. As k_leak decreases, Ca²⁺ wave velocity increases. This relationship has been reported at low doses of tetracaine (60). The dominant factor in shaping the difference between the two curves in Figure 8Bi is most likely to be SR [Ca²⁺] load. Alterations to k_leak, unlike k_RyR, change diastolic SR [Ca²⁺]. Since SR [Ca²⁺] modulates RyR sensitivity to myoplasmic [Ca²⁺], k_leak will affect the threshold for triggering SR Ca²⁺ release. High SR Ca²⁺ leak will lower SR [Ca²⁺] which, in turn, will elevate the threshold for Ca²⁺ release by raising k_β⁺. This will favor slower Ca²⁺ wave propagation, as predicted by the model. If k_leak is raised >1.8-fold, free [Ca²⁺] in the SR drops to <365μM and Ca²⁺ waves fail to propagate (red star, Figure 8Bi), in agreement with experimental data (52).

In a third set of simulations, k_RyR and k_leak were manipulated simultaneously (Figure 8Bi, green curve) and the system was allowed to attain a new steady-state at the new value for k_leak. Under steady-state conditions, adding RyR inhibitors or openers are likely to produce parallel changes in both k_RyR and k_leak. The predicted relationship is positive and approximately linear, indicating that the rate of Ca²⁺ rise (k_RyR) is the major determinant of Ca²⁺ wave velocity.

The effect of k_RyR+k_leak on Ca²⁺ wave velocity was studied further at different values of D_Mbuf and D_SRfree. The purpose of this final set of simulations was to identify the combination of RyR permeability and Ca²⁺ diffusion in myoplasm and SR at which Ca²⁺ wave velocity is 78μm/s. The output of the model is presented in Figure 9A. This figure can be used to identify the set of conditions that is compatible with normal Ca²⁺ wave velocity. If, for example, D_SReff were higher than 9μm²/s, then a higher D_Meff and/or higher k_RyR+k_leak would be necessary to predict a wave velocity of 78μm/s. Specifically, if D_SReff were 60μm²/s (as measured in (27)) and D_Meff were 20μm²/s, wave velocity of 78μm/s would require k_RyR and k_leak to be 1.6-fold higher, i.e. the rising slope of the myoplasmic Ca²⁺ wave would be steeper (due to k_RyR) and SR [Ca²⁺] load would be smaller (due to k_leak). Conversely, if present estimates for D_Meff have been under-estimated, D_SReff will need to be higher and/or k_RyR lower to obtain the desired 78μm/s velocity. It is noteworthy that the model predicts the experimentally measured wave velocity using an experimentally-derived wave rising-slope and independently-derived diffusion coefficients.

Figure 9.

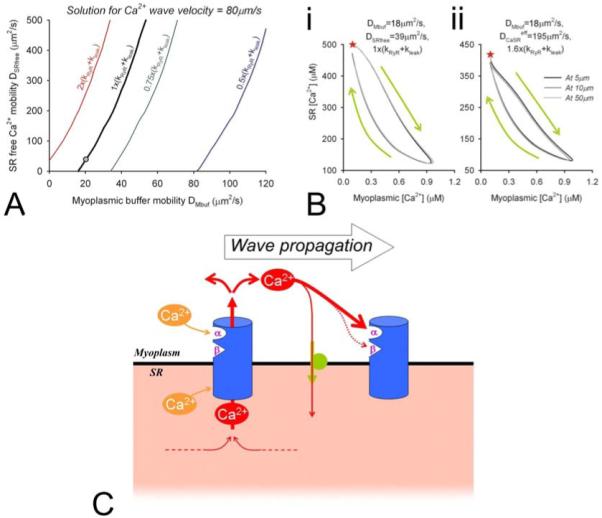
(A) Solution curves for the combination of D_SRfree, D_Mbuf and k_RyR+k_leak that predict wave velocity of 78μm/s. (B) Hysteresis loops for myoplasmic [Ca²⁺] versus and SR [Ca²⁺] during a Ca²⁺ wave, plotted at 5, 10 and 50μm away from the midpoint of the cell (trigger site). Green arrows indicate direction of hysteresis. Red stars indicate the start of the hysteresis. The model was parameterized to give a wave velocity of 78μm/s. (i) Hysteresis loop obtained for a Ca²⁺ wave under conditions of low Ca²⁺ mobility (D_Mbuf=18μm²/s, D_SRfree=39μm²/s) at control k_RyR+k_leak. (ii) Hysteresis loop obtained for a Ca²⁺ wave under conditions of high SR Ca²⁺ mobility (D_SRfree=195μm²/s) with 1.6-fold higher k_RyR+k_leak to yield the desired 78μm/s wave velocity. In all cases, the hysteresis is clockwise, indicating that the rise in myoplasmic [Ca²⁺] was not preceded by a rise in SR [Ca²⁺]. NB: hysteresis was not due to buffering, as this was fast. (C) Proposed model for Ca²⁺ wave propagation, inferred from comparing experimental data with the present mathematical modeling. RyR channels (blue icon) contain two myoplasmic Ca²⁺-sensitive ‘gates’: α (fast activation) and β (slow inactivation) and an inhibitory, SR-facing calsequestrin-sensitive site. To trigger the wave, Ca²⁺ occupancy of β cannot exceed that of α. Once RyR channel is open, the magnitude of Ca²⁺ release depends on RyR permeability, the transmembrane [Ca²⁺] gradient and the volume over which SR [Ca²⁺] is drawn by diffusive dissipation (i.e. D_SReff). Ca²⁺ diffusion within the SR will affect the substrate for Ca²⁺ release and calsequestrin-RyR interaction elsewhere in the SR. In the myoplasm, the spatial spread of released Ca²⁺ will be determined by Ca²⁺ diffusion (D_Meff) and uptake by SERCA pumps (green icon). If a supra-threshold myoplasmic [Ca²⁺] is delivered to an adjacent, activatable RyR channel (site α occupancy>site β occupancy) and if SR [Ca²⁺] is sufficiently high to provide release substrate and sufficiently low to maintain low (calsequestrin) locally, Ca²⁺ will flux out of the SR. A Ca²⁺ wave is propagated.

As a final point, we investigated the temporal relationship between myoplasmic and SR [Ca²⁺] in an attempt to identify whether a myoplasmic or SR wavefront drives the Ca²⁺ wave. This underpins the difference between classical (Figure 2B) and the more recent (Figure 2C, (41)) proposals for the mechanism for Ca²⁺ wave propagation. The Ca²⁺ wave simulated in Figure 5 was analyzed first. This wave was triggered under conditions of control Ca²⁺ mobility and RyR permeability (D_Mbuf=18μm²/s; D_SRfree=39μm²/s; wave velocity=78μm/s). Myoplasmic and SR [Ca²⁺], at different distances from the trigger site, were plotted as hysteresis loops, shown in Figure 9Bi. The loops were clockwise, indicating that the rise in myoplasmic [Ca²⁺] occurred before the fall in SR [Ca²⁺], i.e. a component of the myoplasmic [Ca²⁺] rise is due to diffusion from elsewhere within the myoplasm. Also, the slope of the loops over the rising phase of the Ca²⁺ wave was consistently negative, indicating that a rise in SR [Ca²⁺] never traveled ahead of the rise in myoplasmic [Ca²⁺]. Our second simulation attempted to address an alternative proposal for Ca²⁺ wave propagation, in which fast intra-SR Ca²⁺ diffusion produces a wavefront of sensitized RyR channels ahead of the myoplasmic [Ca²⁺] wavefront (Figure 2C, (41)). The wave was simulated under conditions of fast SR mobility (D_SRfree=195μm²/s giving D_SReff=60μm²/s for half-filled SR) and appropriately elevated k_RyR to obtain 78μm/s wave velocity (see Figure 9A). The hysteresis loops for this simulation are shown in Figure 9Bii. Again, the hysteresis loops were clockwise. Thus, the rising phase of the myoplasmic Ca²⁺ wave was not preceded by a rise of SR [Ca²⁺], excluding the possibility that a wavefront of RyR sensitization travels ahead of the myoplasmic [Ca²⁺] wavefront. These loops, generated under two different simulation conditions, strengthen the hypothesis that Ca²⁺ waves are driven by a myoplasmic Ca²⁺ wavefront (Figure 9C) that is not preceded by elevated (RyR-sensitizing) SR [Ca²⁺].

5. DISCUSSION

5.1. Role of Ca²⁺ mobility and SR Ca²⁺-load in wave propagation

Ca²⁺ waves play a significant role in cardiac myocyte physiology, particularly under pathological conditions such as Ca²⁺ overload. It has been argued that Ca²⁺ waves may serve to eliminate SR overload by stimulating Na⁺-Ca²⁺ exchange to extrude excess Ca²⁺ although, paradoxically, the very same process underlies their arrhythmogenic properties (62). Experimental studies of Ca²⁺ waves have helped to refine our understanding of Ca²⁺ signaling mechanisms (35, 36). Analyses of Ca²⁺ waves have also offered novel approaches to calibrating dyes (50) and for measuring SERCA kinetics (44).

The benefits of our modeling are four-fold. Firstly, the model offers a simple mathematical framework to accompany experimental investigations into the mechanism of Ca²⁺ waves. A key output of the model is wave velocity which is a readily-measurable parameter. The model can be used to test if a particular cellular parameter (such as a Ca²⁺ flux rate or diffusion coefficient) is consistent with measured velocity. For instance, Figure 9A can be used as a look-up table to derive the missing parameter if the other two are known (among Ca²⁺ diffusion in SR, Ca²⁺ diffusion in myoplasm, RyR permeability). Although many combinations of D_SReff and D_Meff predict a wave velocity of 78μm/s, only a narrow range also satisfies the criterion for RyR permeability which can be estimated experimentally from the time-course of the Ca²⁺ wave.

Secondly, the model illustrates the importance of ionic mobility in determining Ca²⁺ wave velocity. Our simulations confirm the well-established importance of myoplasmic Ca²⁺ diffusion in setting wave velocity (Figure 7A). In addition, the simulations show that Ca²⁺ wave velocity is very sensitive to the Ca²⁺ diffusion coefficient in the SR (Figure 7B). This finding is both novel and important, as SR Ca²⁺ mobility has only recently been measured (6, 27). Many previous models have made assumptions of zero SR Ca²⁺ mobility (e.g. (43, 44)) or finite mobility (e.g. (46)) with no strong experimental backing.

Thirdly, the model offers a unifying framework which can explain seemingly conflicting observations. One illustration of this has been presented in Figure 8A for the effects of SERCA activity on wave velocity. Experiments have determined that inhibition of SERCA either decreases (41, 55) or increases (40) wave velocity. The model can predict both responses, depending on the circumstances. Another example of the usefulness of the model is in the interpretation of experiments in which RyR channels are modulated pharmacologically. In Figure 8B, we have shown that such modulation can either increase or decrease wave velocity. This is because there are potentially two effects of RyR-targeting drugs (such as tetracaine or caffeine). One will be a modulation of the background SR Ca²⁺ leak, and the other will be a modulation of the rate of Ca²⁺ release through triggered RyR channels during the rising phase of a Ca²⁺ wave. The onset of the latter effect will be immediate. The former effect will change wave velocity by adjusting SR [Ca²⁺] load. This, however, will take longer to develop. If the background leak is affected, the dominant influence on wave velocity will be via SR [Ca²⁺] load, and thus the sensitization of RyR channels to myoplasmic [Ca²⁺]. Otherwise, if modulation of triggered RyR channels prevails, wave velocity will be affected by the myoplasmic [Ca²⁺] rise-time, i.e. the time-delay to threshold. Such a mechanism may explain the positive relationship between caffeine dose and Ca²⁺ wave velocity (61) and the slowing effect that tetracaine has on Ca²⁺ waves (59, 60) (albeit at higher doses in (60)). It is possible that inhibition of background leak requires a more sustained but lower tetracaine dose, explaining why, in one study, low doses of the drug (<0.5mM) accelerated Ca²⁺ waves (60).

Fourthly, the model can help in testing for the feasibility of proposed hypotheses for Ca²⁺ wave propagation. For instance, an earlier finding that SERCA inhibition leads to wave slowing has spawned an alternative hypothesis for the mechanism of Ca²⁺ waves (41), in which a wave of elevated SR [Ca²⁺] (supported, for example, by advance SERCA activity) travels ahead of the myoplasmic [Ca²⁺] wavefront. This hypothesis (Figure 2C) would necessitate fast SR Ca²⁺ mobility (D_SReff). Our model can predict a fall in wave velocity when SERCA is down-regulated, without having to assume a high D_SReff. Indeed even at high D_SReff, simulated Ca²⁺ waves follow the classical model of propagation illustrated in Figure 2B, i.e. myoplasmic-driven Ca²⁺ wave propagation without a preceding wavefront of elevated SR [Ca²⁺]. A plot of myoplasmic [Ca²⁺] versus SR [Ca²⁺] during a simulated Ca²⁺ wave (Figure 9B) reveals a clock-wise hysteresis, indicating that the rise in myoplasmic Ca²⁺ occurs before a fall in SR [Ca²⁺]. None of the simulations performed using our model predicted a rise in SR [Ca²⁺] that would drive wave propagation. Moreover, the simulated SR [Ca²⁺] wavefront is sharp and biphasic (Figures 5, 6) in agreement with experimental evidence obtained with intra-SR Ca²⁺ dyes (28, 53), an observation that supports the presence of low SR Ca²⁺ mobility. Although high SR Ca²⁺ mobility would favor faster spread of an intra-SR Ca²⁺ overload, once the SR Ca²⁺ wave encounters sensitized RyR channels, SR Ca²⁺ is released and the intra-SR diffusion gradient for wavefront progression will be abolished, or even reversed.

5.2. Model limitations

The present work presents a simplified, continuum, common-pool model for a Ca²⁺ wave (for criticism of common-pool models, see (63); for criticism of continuum models, see (47)). The model was deliberately simple to reduce the number of uncertain or unresolved variables and to reduce computational time to the order of tens of seconds on a 2GHz processor. More sophisticated models should include a fuzzy space between SR and myoplasm (e.g. (38)). Although the introduction of a third compartment is mathematically justifiable, it would be difficult to parameterize fully, e.g. with respect to buffering and Ca²⁺ mobility. The model does not encode for a precise geometrical relationship between RyR channels and SERCA and does not distinguish between junctional and network SR. At the scale of this fine detail, a continuum approximation is valid given that diffusion delays between junctional and network SR (64) and between RyR and SERCA (65) are likely to be small. As discussed earlier, however, the continuum approximation will generate a nonlinear dependence of wave velocity on diffusion coefficient (Figure 7A) (46, 66). In fire-diffuse-fire models with discrete release sites, wave velocity has been proposed to vary proportionally with diffusion coefficient (47, 54). In cardiac myocytes, the 1.8μm spacing between RyR release sites (67) is sufficiently large to support a discrete fire-diffuse-fire model. Moreover, some studies have hinted at discrete release sites during wave propagation (56). The relationship predicted by our model may under-estimate wave velocity at very high mobility. On the other hand, measurements of the temperature dependence of Ca²⁺ wave velocity (66) suggest an activation energy that is 28% higher than the activation energy predicted for Ca²⁺ diffusion. This implies a diffusion-independent step affects Ca²⁺ wave velocity. This may suggest that the mobility-velocity relationship may be sub-linear for high Ca²⁺ diffusion coefficients. A rigorous validation of the mobility-velocity relationship must await a full experimental characterization of the Ca²⁺ diffusion coefficient-dependence of Ca²⁺ wave velocity.

Finally, the RyR gating model used in the present Ca²⁺ wave model is simple and not intended to present a fully mechanistic Markovian representation for the binding and gating events in the RyR (cf (68)). It does, however, comply with the desired properties of threshold, activation by myoplasmic Ca²⁺ and subsequent inactivation, and modulation by SR Ca²⁺.

5.3. Conclusions

We have constructed a mathematical framework for simulating myoplasmic and SR Ca²⁺ waves. By simplifying the mathematical representation for RyR channel gating and by reducing the in silico cell to two 1-D compartments, it was possible to parameterize the equation variables using experimental data obtained for rat myocytes in the present work (Figure 4) or from previous studies (e.g. (6, 14, 38)). Using experimentally-derived effective myoplasmic and SR Ca²⁺ mobility values of 20 and 9μm²/s (Figure 3), the model predicts Ca²⁺ wave velocity of 78μm/s, in agreement with independent experimental observations. A wave velocity of 78μm/s is not given uniquely by the measured Ca²⁺ mobility (Figure 9B). However, other combinations would significantly alter the time-course of the Ca²⁺ wave, which would no longer confirm with experimental data. A supra-threshold rise in myoplasmic [Ca²⁺], SR [Ca²⁺] (SR overload), or both, give indistinguishable Ca²⁺ wave characteristics away from the trigger site (Figure 6). The model also explains seemingly conflicting data obtained by pharmacological manipulation of the SERCA pump or of RyR channels (40, 41, 55, 59-61). It emphasizes the importance of SR [Ca²⁺] load, which cross-talks with the myoplasmic-facing activating sites on RyR channels (Figure 8) (8, 9). Our model also tests the feasibility of opposing hypotheses for the mechanism of wave propagation (Figure 2B vs C). We show that high SR Ca²⁺ mobility favors slow wave propagation (Figure 6). The spread of an intra-SR [Ca²⁺] overload cannot drive a Ca²⁺ wave since this would be self-limiting. Diffusive progression of an intra-SR [Ca²⁺] wave will be terminated the instant that RyR channels open, thereby abolishing, or even reversing, the intra-SR driving force for the SR [Ca²⁺] wavefront. Our modeling indicates a myoplasmic rather than an SR-driven model of Ca²⁺ wave propagation (Figure 9C), a conclusion supported by recent proposals for slow SR Ca²⁺ mobility (6, 31).