Abstract
We present a population model to examine the forces that determined the quality and quantity of human life in early agricultural societies where cultivable area is limited. The model is driven by the non-linear and interdependent relationships between the age distribution of a population, its behavior and technology, and the nature of its environment. The common currency in the model is the production of food, on which age-specific rates of birth and death depend. There is a single nontrivial equilibrium population at which productivity balances caloric needs. One of the most powerful controls on equilibrium hunger level is fertility control. Gains against hunger are accompanied by decreases in population size. Increasing worker productivity does increase equilibrium population size but does not improve welfare at equilibrium. As a case study we apply the model to the population of a Polynesian valley before European contact.
Keywords: paleodemography, demography, density dependence, population regulation, carrying capacity, food ratio, hunger, fertility control, feedback, quality of life, taxation
Introduction
Population dynamics are important in human genetic and cultural adaptation and our ecological interactions, but our tools for exploring these relationships remain limited. We follow Lee (1986) and Wood (1998) in a demographic and economic approach to preindustrial societies and present and analyze an age-structured model of an early agricultural society. Central to the dynamics of this model is the feedback between the hunger level of a population and its agricultural productivity.
The condition of a human population living at equilibrium has interested scientists, statisticians and writers for a long time. More than 2,000 years ago Aristotle urged abortion and infanticide for citizens and expulsion of slaves and aliens as means of stabilizing the population and reducing the threat of hunger. More recently the Marquis de Condorcet (1795) proposed that over time humans would maximize welfare by progressively limiting population growth. In response Thomas Malthus (1798) argued that humans could not realistically constrain fertility and predicted periodic catastrophes in which starvation checked population growth. Ester Boserup (1965) has argued that increasing population density drives an increasing rate of innovation, which will in turn increase population density. These questions have often been phrased in terms of human carrying capacity. Joel Cohen (1995) concluded that attempts to estimate Earth’s carrying capacity are doomed to failure because “carrying capacity” is both multi-dimensional and conditional. In particular, Cohen argues, turning caloric potential into people depends on cultural norms and expectations. There are examples in human history where each of the scenarios described by Condorcet, Malthus and Boserup may have played out, suggesting that none of these ideas is complete. Here we present and analyze a framework that allows us to incorporate the first two. Boserup’s is not an equilibrium model, but we can explore the relationship between population dynamics and innovation.
We build on Lee and Tuljapurkar (in review): in our model vital rates (fertility and survival) are functions of caloric intake that fall with available food, but cannot be increased above some (biologically and culturally determined) maximum values even with abundant food. Food availability is a function of the productivity of the environment and the nature of the workforce. Lee and Tuljapurkar (in review) describe an initial colonization phase when a population has access to unlimited space. Here we examine the consequences of living in limited space and achieving a “density-dependent” equilibrium. Our analysis also yields information about the level of hunger in the population and life expectancy, two measures of well being. We use this information to examine options prehistoric populations may have had to alter quality of life, including altering the amount of work by individuals, controlling fertility, practicing infanticide or geronticide, changing patterns of food sharing, investing effort in new agricultural technology or exploring alternate food sources.
Our space-limited population has at most a single stable equilibrium in which population growth rate is zero and agricultural output is sufficient to maintain the population. Using data from human populations we find that the level of hunger at equilibrium is typically substantial. Effective levers to reduce hunger include fertility control and infanticide. Both generate gains in welfare accompanied by a reduction in population, highlighting a basic tradeoff between population size and average individual well being. Geronticide has no effect on equilibrium hunger levels and lowers life expectancy, but does decrease the fraction of non-workers in the population through an effective exchange of older individuals for younger ones. Improving agricultural production can have a variety of effects on population measures, depending on how the gains are achieved; such improvements increase equilibrium population size but often with diminishing returns.
Wood (1998) addresses five fundamental questions about the dynamics of preindustrial populations. He builds logical general arguments that integrate economic theory and population dynamics. Our approach allows us to take a significant step forward from his groundbreaking work by defining an explicit link between food availability and demographic rates. As a result we can move from generalities to generalizable functions. Our goal is not to predict how many people might be supported by a particular patch of ground but to see how much leverage there is in environmental, demographic and cultural elements that bear on the quality and quantity of life. This model may be used to estimate equilibrium population densities but to do so requires answering many specific questions about environment, demography and culture to address Cohen’s points regarding multidimensionality and conditionality. As such this model is neither strictly Malthusian or Condorcetian.
The space-limited food ratio
We measure food availability by the food ratio, E, the ratio of available calories to the calories at which vital rates achieve their maximum values. These maximum vital rates will be denoted mx(1) and px(1) for fertility rate and survival probability, respectively, at age x when E = 1. Denote caloric consumption needed to achieve maximal rates by J ρx at age x, where J is daily caloric need at the age with the largest nutritional need, ρx = 1 for ages x at which consumption equals J, and ρy < 1 at all other ages y. Maximum total consumption is J < ρ, n(t) > = J Σx ρx nx(t), where the population vector n(t) records the number of individuals of age x at time t. The notation < a, b > refers to the scalar product of vectors a and b. Total population size is N(t). In our numerical examples we assume the group with the greatest need demands 2,785 Kcal/day to achieve maximal survival and fertility. See Table 1 for parameter values, and the appendix for more information. The food ratio represents the level of hunger experienced by the entire population if food were distributed in proportion to need. Other allocations of food by age include, for example, buffering individuals with the greatest labor potential or in their reproductive prime from hunger at the expense of the youngest and oldest in the population. Such alternate methods of allocation are considered later.
Table 1.
Parameters and variables used in most numerical examples.
| Parameter or variable |
|||
|---|---|---|---|
| ID | Description | Value | Units |
| J | max. food required by most needy age | 2,785 | Kcal/day |
| Y | agricultural potential of the land | 13,100 | Kcal/ha/day |
| Am | total arable land | 1000 | ha |
| H | labor contribution of typical adult (M or F) | 5 | hours/individual/day |
| k | conversion from time to annual area cultivated | 0.0944 | ha-days/hour/yr |
| ρx | relative consumption by age | 0.294-1 | |
| φx | relative labor output by age | 0 or 1 | |
| γ(1) | baseline fertility elas. at any reproductive age | 0.135 | |
| β1(1) | baseline elasticity of survivorship in first year | 0.057 | |
| β26(1) | baseline elasticity of survivorship at age 25 | 0.19 | |
| β66(1) | baseline elasticity of survivorship at age 65 | 0.47 | |
| νG | mean baseline elasticity of vital rates | 0.332 | |
| e0(1) | baseline life expectancy | 45 | years |
| e0(Ê) | equilibrium life expectancy | 30.3 | years |
| e10(1) | baseline life expectancy at age 10 | 49.1 | years |
| e10(Ê) | equilibrium life expectancy at age 10 | 38.0 | years |
| TFR(1) | baseline total fertility | 2.44 | daughters |
| TFR(Ê) | baseline total fertility | 2.08 | daughters |
| Ê | equilibrium food ratio | 0.680 | |
| N̂ | equilibrium total population size | 4,752 | individuals |
Calories available per time unit depend on Y, the daily caloric yield per unit area cultivated, averaged over a year or other discrete time unit of interest; k, a constant that converts daily person-hours of labor to area; H, the hours worked per day by the age class working the longest hours; and φx ≤ 1, the hours contributed by an individual of age x, relative to H. As a vector, φ = {φx}. When there is plenty of available land, Hk φx is the total area that can be cultivated annually by an individual of age x, and Hk < φ, n(t) > is the total area that can be cultivated by the population. The values of H and φ, which define the level and age distribution of work, may vary by culture. The value of k reflects agricultural technology, as well as topography, the patchiness of arable land and the like.
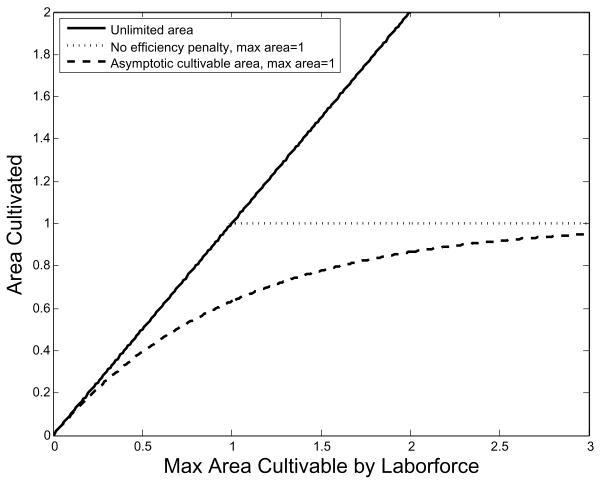
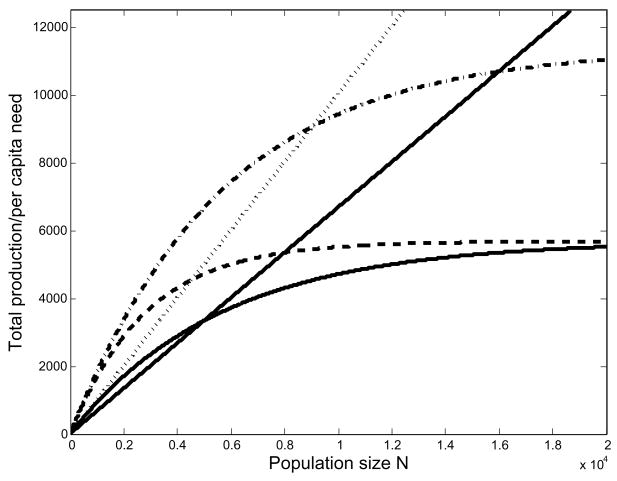
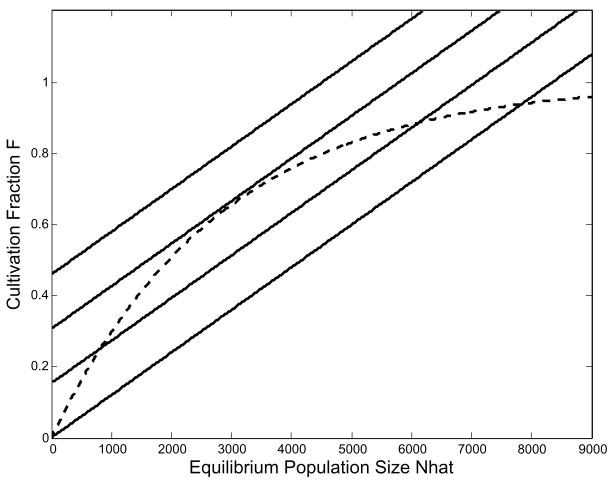
We describe space limitation by the fraction F of maximum area (Am) in active cultivation, a function of labor efficiency and the population vector, F = F (H k < φ, n(t) >/Am). Writing z = (H k < φ, n(t) >/Am), we assume that function F(z) is zero when z = 0 and is concave increasing, saturating at 1 as z increases. Thus we have a non-linear relationship between population and area in cultivation (Fig. 1). As the population increases, food production becomes increasingly limited by space and each new worker adds less to the production total than the one before him. However, per capita caloric need is constant, so that total caloric requirement increases linearly with N. In numerical examples we use .
Fig. 1.
The solid line represents the case of unlimited area. As much land as the population is capable of cultivating is put to use. The dotted line represents the case where cultivated area is a piecewise linear function of labor. Cultivated area is increased until it is all in use. The dashed line represents the case in which it becomes increasingly difficult to put additional area into cultivation the closer the population gets to the maximum. The function F describes the fraction of maximum area in cultivation.
With these definitions the food ratio, the ratio of available calories to maximal consumption, is
| (1) |
When E < 1 the population experiences some degree of food deprivation and so we call E the hunger level. In the denominator of equation (1), F is an increasing function of N but is bounded by 0 and 1. The denominator increases in proportion to N. Hence as N increases, E declines, and vice versa (assuming fixed population structure). This inverse relationship describes a tradeoff between equilibrium population size and quality of life at equilibrium, as defined by hunger level and hence by expected lifespan. This is a result of space limitation and does not appear when land is unlimited (as in LT).
The response of vital rates to hunger is described by their elasticities with respect to E. Denote elasticities with respect to E at age x by αx for survival rate px and γx for fertility rate mx. The elasticity of survivorship, lx, is , and β1 = 0. We index survivorship such that l1 = 1.
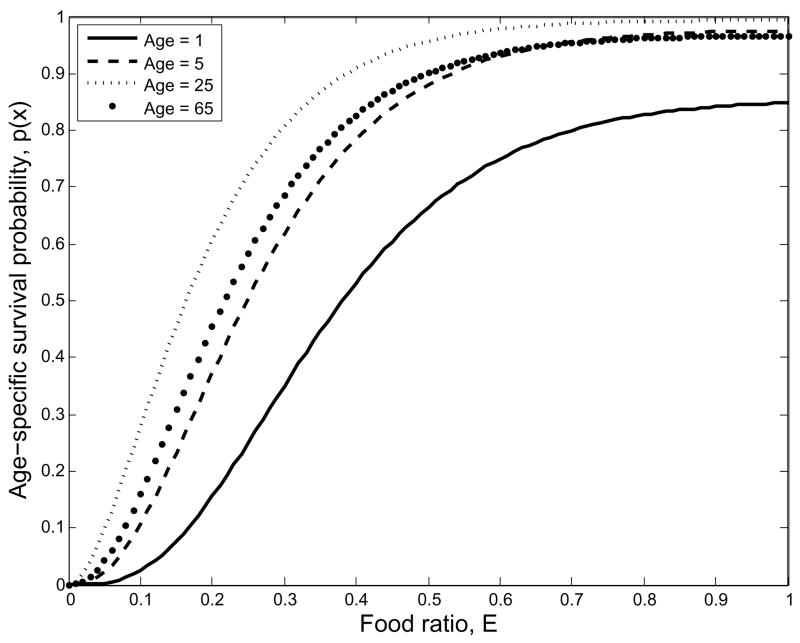
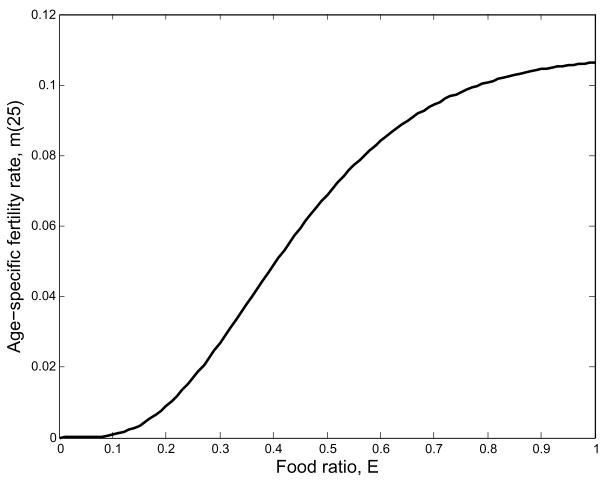
Fertility and survival rates are zero when E = 0, increase monotonically in E and approach their maximum values as E → 1 (Figs. 3, 4). We expect that survival and fertility rates decline slowly as E falls below 1, and then more rapidly toward zero as daily caloric availability approaches the basal metabolic rate. Caloric requirement for basal metabolism is approximately half of the caloric requirement to maximize vital rates (Cunningham, 1980). We use historical demographic data to estimate age-specific elasticities (see appendix for details) for fertility mx and mortality qx, where qx is the probability of death for age class x. Because survival probability px = 1 − qx, the elasticity of px equals the product of (1 − px)/px and the elasticity of mortality. In our analyses we explore three different schedules of maximum survival, with maximal e0 increasing from 30 to 60 years. We keep the elasticity of mortality fixed, so the elasticities of survival rate decrease with increasing maximal e0. Maximal fertility and survival rates depend on the physical and disease environment, cultural characteristics and technological factors. Maximal mortality may respond to changes in the interaction between a society and its environment, e.g., the draining of swampy areas to reduce the incidence of malaria, advances in cooking technology or practice, changes in sanitation, or the adoption of advantageous or injurious medical practices from another group.
Fig. 3.
Survival probability declines slowly from its maximum with E when hunger is small, but the risk of mortality increases quickly as E approaches the basal metabolic rate at approximately E = 0.5.
Fig. 4.
Fertility responds in a way that is similar to survival probability. We have assumed that the elasticity of fertility is identical for all ages.
The response of survival to food shortage includes, first, a biological response in the risk of death. Although the human body appears to have a large capacity to withstand short-term food shortage with little or no long-term ill effects (see Dyson and O Grada (2002) and Bengtsson et al. (2004)) we are interested in the case of a stable environment in which some level of hunger is persistent. The short-term ability of an individual to withstand occasional famine becomes irrelevant in the face of enduring shortage. A second component of survival consists of behavioral changes in response to food availability. While E describes the population’s mean hunger level weighted by need, some groups may be more insulated or exposed as a result of behavior. Examples include the disproportionate increased mortality of young or old in times of scarcity due to neglect or willful murder. The type of situational infanticide discussed in Clutton-Brock (1991) could be described by larger elasticities of survival with respect to food for the youngest age classes. Similarly, part of the response of fertility rates to hunger can be attributed directly to food limitation, and a lower conception success rate or higher risk of miscarriage due to inadequate prenatal nutrition, for example (Scott and Duncan, 2002). But fertility rates may also change with behavioral responses to hunger (e.g., a reduced frequency of intercourse or a change in expected ages of first marriage (Bongaarts, 1978)).
The food-dependent vital rates mx(E) and px(E) generate a projection matrix A(E), with age-specific fertilities in the first row and survival probabilities along the subdiagonal, that describes the dynamics of the population,
| (2) |
We assume that when food is plentiful and maximal vital rates apply, the population increases, i.e., the dominant eigenvalue of A(1) > 1.
Equilibrium conditions
An equilibrium of this model consists of a population n̂ and a food ratio Ê such that n̂ = A(Ê) n̂. Thus Ê determines a matrix A(Ê) whose dominant eigenvalue is 1 and whose corresponding right eigenvector is proportional to n̂. This means that the population does not grow or shrink and that the population’s distribution among age classes remains fixed. We can describe the equilibrium population vector in terms of total population size N̂ and the population structure û, whose elements sum to 1. Doing so gives n̂ = N̂ û.
Equilibrium is defined by two conditions. The first uses the characteristic equation of demography: since Ê is the food ratio at which the population just replaces itself,
| (3) |
Ê is calculated using only maximal fertility and survival and their elasticities with respect to E. Since E measures the downward pressure on vital rates, Ê is the level of hunger at which vital rates fall to replacement levels. Given Ê, the corresponding survivorship l̂x determines life expectancy (e.g., ê0 and ê10) and the equilibrium population structure, û. From û we can determine dependency ratios and other properties of the equilibrium population.
Once we have Ê and û, equation (1) determines N̂ as the solution to
| (4) |
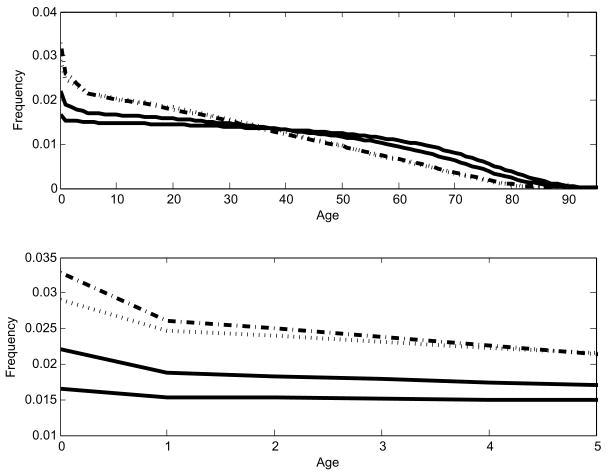
The parameter values we use to illustrate the model are in Table 1 (1). Wherever possible they are taken from sources that describe early Polynesian societies, where both the food-limited case described in Lee and Tuljapurkar (in review) and the space-limited case described here were applicable at different times and places. See the appendix for more information on sources. Using these parameters (including e0(1) = 45 years) yields an equilibrium food ratio Ê = 0.680, meaning that all individuals in the population receive 68 percent (corresponding to 1,869 Kcal/day for the most energetic age class) of the calories required to achieve maximal fertility and survival. Solving equation (4) gives a population of N̂ = 4, 752 individuals on 1,000 ha (or 2,471 acres) of cultivable land. Fig. 7 compares the equilibrium population structure û with the stationary population structure u(1) we would obtain if survival rates were at their maximal values. In the figure we show results for two different maximal survival schedules, e0(1) = 45 and e0(1) = 60. The upper panel shows that û and u(1) differ significantly at all ages when e0(1) = 60 but the maximal age structure begins to resemble the equilibrium one when e0(1) = 45. The lower panel shows in detail the differences for ages up to 5 years, which is where the greatest divergence in structure occurs. Life expectancy decreases by 32.6% in the shift from maximal rates to equilibrium rates when e0(1) = 45. Life expectancy at equilibrium falls 42.7% when we assume e0(1) = 60. We now discuss the determinants of such equilibria.
Fig. 7.
At birth the lowest solid line in each panel represents e0(1) = 60, and the next lowest is e0(1) = 45. The dotted line is the ê0 = 60 schedule and the dot-dash-dot line represents ê0 = 45. The panels are drawn from the same data, but the lower panel highlights the differences in the first five years of life. The effect of changing the maximum survival schedule is most pronounced in the youngest age classes. Elsewhere the equilibrium age structures are very similar.
Understanding equilibrium hunger
At equilibrium, the net reproductive rate R0(Ê) = 1. In our model, as is typical in human demography (Preston et al., 2001), the net reproductive rate at any value of E is well approximated by R0(E) ≈ lμ(E) M (E), where μ is the mean age of reproduction and M is the total fertility rate. We find that the equilibrium hunger level Ê is accurately approximated (see appendix for derivation) by the equation,
| (5) |
| (6) |
Here (βμ(1) + γ(1)) is the elasticity of the product lμ(E) M (E) when E = 1. The parameter K describes the rate of growth of the elasticity of this product as E falls. In all our numerical examples K ≈ 7.4, and the value of K changes little with the other parameters, so we treat it as constant. When maximum expected lifespan is 45 years the approximation yields Ê ≈ 0.677 compared with an exact value of 0.680, an error of 0.4%. This is the largest percentage error in equation (6) over the parameter range we examined.
We may draw three important conclusions from this approximation:
-
Ê decreases when the maximal net reproductive rate R0(1) increases. For example, suppose that maximal fertility doubled so as to increase the maximal R0(1) from 1.05 to 2.1. This changes log(log R0(1)) from −3.02 to −0.299. Assuming elasticities are held constant, Ê would decrease by (0.299–3.02)/K ≈ 0.37. Indeed, equation (6) shows that the elasticity of Ê to R0(1) is
which is −0.10 when R0(1) = 2 but rises to −0.24 when R0(1) = 1.5. It is clear that if a population could lower its maximum total fertility rate it could make significant headway against hunger. In fact the closer the maximum total fertility rate gets to replacement level the greater the response of E. When the maximum TFR is high, the response of E is weakest. A lower maximal fertility rate increases the effect of fertility reductions.
Ê increases with the elasticities of vital rates at E = 1. In our numerical examples, (βμ(1) + γ(1)) fall from 0.51 to 0.22 as maximum e0(1) increases from 30 to 60 years. From equation (6), the elasticity of Ê to (βμ(1) + γ(1)) ranges from −0.26 to −0.61. This is due to the role of the elasticities as modifiers of the vital rates. When elasticities are small, the decline in vital rates with declining E is shallow. It therefore requires a greater drop from E = 1 to achieve vital rates that correspond to zero growth compared to system with larger elasticities.
Ê responds to a change in maximal survival via the resulting increases in both R0(1) and the elasticity βμ(1). As maximal e0 increases from 30 to 60, log(logR0(1)) increases from −1.96 to −0.33, which acts to decrease Ê via the last term on the right of equation (6). But log(βμ(1) + γ(1)) decreases from −0.66 to −1.53, which acts to decrease Ê via the second term on the right of equation (6). The combined effect is to decrease Ê from 0.9 to 0.57.
Understanding equilibrium population
Given Ê from equation (3), calculate the equilibrium age distribution û, and rearrange equation (4) as
| (7) |
The left-hand side describes a straight line with a slope of Ê (Fig. 5) and the right-hand side is an increasing concave function due to the nonlinearity in the cultivation fraction F, whose second derivative is negative for all N. Because both curves pass through the origin and F is monotone and all other terms are linear in N, there will be at most one non-trivial equilibrium.
Fig. 5.
Equilibrium N is determined by the intersection of the solid lines, representing the left- and right-hand sides of equation (7). This example, calculated from the parameters in Table 1, generates a population of 4,752 individuals at a hunger level of 0.680 on 1,000 ha of arable land. The dotted line is EmN, the line above which the population is no longer viable as no straight line passing through the origin will intersect the curved line. The upper curved line (dot-dash-dot) shows what happens to the RHS if we double Y, raising the asymptote. The dashed line represents a doubling of the product Hk, increasing the saturation rate, but not the asymptote. Each change increases N̂, but increasing terms outside of F is more effective.
The slope of the right-hand side as N → 0 is the maximum food ratio that can be generated by this equilibrium population and its resources and is Em = (Y Hk < φ, û >/J < ρ, û >). If Ê ≥ Em there will be no non-trivial equilibrium because the calories required to maintain a workforce cannot be produced. Em, the population feasibility threshold, depends on Y Hk as a product, so multiplicative changes to any of the three will have an identical effect on this threshold.
As N → ∞, the cultivation fraction F → 1 and the right-hand side of equation (7) approaches (Y Am/J< ρ, û >). Thus there are two fundamental ways the equilibrium population may be altered, given Ê. The terms within F (specifically H, k, φ) will affect the rate at which the right-hand side of equation (7) changes, and the terms outside (Y, Am, J, φ) will affect the asymptotic level (Fig. 5). Because F ≤ 1 the maximum value of N̂ is (Y Am/Ê J< ρ, û >). When F is near 1 at equilibrium this maximum may serve as a first-pass approximation of the actual equilibrium population size. This maximum is the number of individuals who can be supported at a particular hunger level if all land is in cultivation.
Whether F is in its non-linear (far from 1) or linear (close to 1) regime is determined by the population size and the parameters that determine F’s rate of saturation, c = (Hk < φ, û >/Am). If N ≈ (1/c) (or less) it is in the non-linear zone, and if N ≫ (1/c) then the equilibrium is in the linear zone. In our e0(1) = 45 parameterization N̂ = 4, 752, less than (1/c) = 5, 661, and in the non-linear regime.
Marginal production of labor
Wood (1998) in his reevaluation of Malthus discussed marginal production, which is the change in calories produced with respect to a change in population size. In our model marginal production is
| (8) |
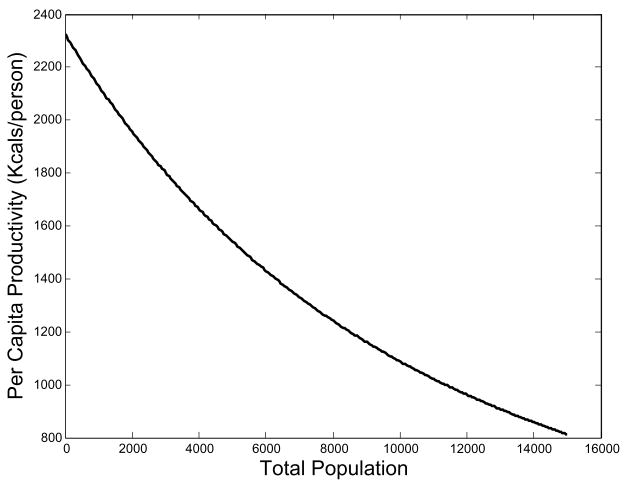
where z = (H k < φ, n >/Am). As in Wood (1998), here the per capita caloric production decreases as the population increases (compare his Fig. 4 to our Fig. 2). For the working ages, (∂F/∂nx), the change in the fraction of area cultivated as a result of a adding workers age x, decreases in N, meaning diminishing returns from the labor of new individuals. As φx = 0 for non-working age classes, their marginal productivity is always zero.
Fig. 2.
Per capita productivity decreases with population size. Equilibrium is achieved when caloric output drops to the point where fertility and survival schedules result in a zero-growth population.
The importance of knowing whether F has become linear is that as F → 1, the terms within F, in particular the characteristics of labor, become less important to the equilibrium. When the vast majority of land is in use, increasing worker productivity through H or k has little effect on caloric production. However, terms that occur outside of F, including Y and Am will have an effect on equilibrium population size N̂, regardless of F.
Equilibrium and yield
Yields may increase for several reasons: selection on existing crop varieties, adoption of new higher-yielding crops, collective irrigation works, mulching, fertilization, and climate change. How does the equilibrium population size depend on crop yield? The answer depends on the amount of vacant land at equilibrium, which is large when N̂ ≈ (1/c) and small when N̂ ≫ (1/c), as discussed earlier. From equation (4),
| (9) |
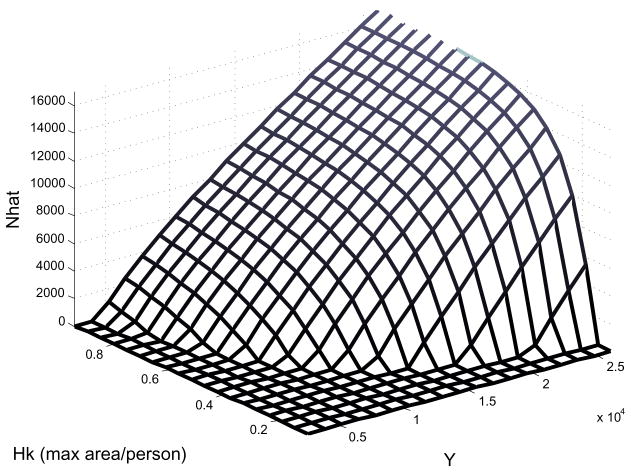
Equation (9) reveals that when F is near 1, so that (∂F/∂N) ≈ 0, we have (∂N̂/∂Y) ≈ (N̂/Y). In this regime, equation (4) shows that N̂ α Y, meaning that N̂ increases linearly with yield. However, when F is much below 1, equation (9) shows that (∂F/∂N) > (N̂/Y), and equation (4) shows that (N̂/Y) α F, so (∂F/∂N) increases with increasing yield. The result is an initially steep increase in N̂ when yield increases, which flattens, converging to a line with slope (Am/ÊJ < ρ, û >). In Fig. 8, for any fixed worker productivity Hk, we see that N̂ increases with Y as described above.
Fig. 8.
Equilibrium population as a function of yield per hectare and the number of hectares that can be worked by the most productive age class, a measure of worker productivity. The non-linearity when population is low is due to the fact that the cultivation fraction F is not near 1 and worker productivity can have a large impact.
Equilibrium and technological innovation
Technological innovation can affect a population in three ways in this model. The first concerns changes that affect demographic rates, and thus Ê, in equation (3). Examples include the adoption of a medical technology or a practice (e.g., safer boats for fishing) that increases the maximum level of survival at one or more ages. Changes that increase the maximum expected lifespan have the effect of reducing the equilibrium food ratio, while increasing the population size. The effect of such changes on the equilibrium lifespan at birth can be counter intuitive. Table 3 shows the effect of increasing maximum age-specific survival rates. If we double the maximum life expectancy from 30 to 60 years, the food ratio drops by 37% and equilibrium life expectancy only increases by 7.5 years, or 28%. Population increases by 62% at the same time. Altering the terms in equation (3) will also have an effect on the equilibrium age structure, û, although the only appreciable effect is in the first few age classes (Fig. 7).
Table 3.
Changing maximum expected lifespan at birth.
| e0(1) | NRR(1) | λ1(1) | ê0 | ê10 | Ê | N̂ |
|---|---|---|---|---|---|---|
| 30 | 1.15 | 1.01 | 26.9 | 38.1 | 0.902 | 12,619 |
| 45 | 1.63 | 1.02 | 30.3 | 38.0 | 0.680 | 17,132 |
| 60 | 2.05 | 1.03 | 34.4 | 37.9 | 0.567 | 20,545 |
Other forms of innovation can alter the terms inside the non-linear cultivation fraction F, or those outside of F in equation (7). Unlike changes to demographic parameters, these will only change the size of the equilibrium population. The effect of technological advances that increase maximum per capita land cultivation (H, k, φ) will be muted by the function F as N increases, as above. Where there is significant uncultivated land at equilibrium, the initial response of N̂ to innovation will be steep, but approach zero as these terms are increased. Advances that improve the caloric potential of the land Y were discussed earlier. Altering the other terms outside of F in equation (4) (Am, ) will have a similar effect, their response being initially steep and converging to a line with positive slope as F saturates, unlike innovations that increase terms within F. We can visualize the combined effect of these two forms of innovation as a surface in yield-efficiency-N̂ space (Fig. 8). The figure illustrates that as yield increases the slope decreases, converging to a line with a positive slope vs. N̂. Improving worker productivity (Hk) provides diminishing returns approaching zero, as predicted. Note that when total production is too low, no non-trivial equilibrium is possible and N̂ = 0. This is also illustrated in Fig. 5, where the dotted line representing the maximum slope of the right-hand side of equation (7) isn’t steep enough to allow an intersection with the ÊN line. This maximum slope is defined in part by the product Y Hk, illustrating the equivalent role these parameters play in determining population viability.
Equilibrium and human behavior
There are two ways that behavioral changes can affect the equilibrium food ratio. The first alters the maximal vital rates themselves. These were discussed in the context of medical innovation earlier, but these rates may change as a result of a number of behavioral adaptations, some of which may be considered innovations. These include changes to the background risk of death, independent of the effects of hunger. Examples include the reduction of exposure to risky agricultural or hunting practices, altering rite-of-passage rituals to make them more or less dangerous, making peace with neighbors and thus reducing war-related mortality, and the sorts of communal works that may increase sanitation or safety for large groups of people (e.g., pest eradication, waste disposal systems, defensive earthworks). If such efforts increase the maximum survival rates they will in turn increase the maximum net reproductive rate R0(1), and equation (6) predicts increased hunger at equilibrium (Table 3). This effect is accelerated by the fact that increasing maximum survival of age classes through μ ≈ 27 decreases the survival elasticities that contribute to βμ(1) in equation (6). This depresses Ê even further.
We may also think of the effect of behavior on maximum fertility rates. The biological maximum of human fertility is estimated at 16 children per woman, or 8 daughters per woman (Preston et al., 2001), but fertilities near this limit have rarely been observed. Total fertility rates are functions of the age of marriage, the likelihood of sexual activity outside of marriage, the degree of male and female cohabitation, the availability of contraceptive and abortifacient substances, and the culturally determined age at weaning, among other things (Bongaarts, 1978). Typical high-fertility populations have 3.5 daughters per woman or fewer. MacArthur (1967) suggests a total fertility rate of less than 2.5 daughters was more typical for Polynesia. We distinguish the alteration of maximal rates from the alteration of fertility elasticities by the fact that the former are not a direct response to hunger. We find that increasing maximum TFR, like an increase in maximal survival rates, increases R0(1), generating a Malthusian feedback that lowers the equilibrium rates through the effect of hunger. However, unlike survival, altering the maximal fertility rates does not alter their elasticities.
While the kinds of behavioral change required to shift maximal vital rates likely occurred only over long periods, changes to the elasticities of survival and fertility with respect to hunger could have occurred on a much shorter time scale. The former pushes the survival or fertility envelope to a new extreme, where the latter requires either buffering one or more age classes against the effects of hunger or engaging in behavior that decreases survival or fertility of some ages in an effort to improve the lot of others. We assume here that the food ratio is a general indicator of the plentitude of food, but that elasticities reflect both the physiological and the behavioral response to hunger, including the culturally mediated age-related food distribution scheme. For example, workers may get a greater percentage of the calories they require than other groups, or in a gerontocracy the old may be fed first. Fertility may be similarly affected, e.g., in response to hunger the age distribution may remain unchanged, but all couples are expected to halve the number of children they would otherwise bear; or, marriage and childbearing is delayed to shift the fertility distribution up in age and thus reduce the total fertility rate. See Wrigley (1967) for a discussion of fertility control in response to density-dependent constraints.
Recognizing the constraints on vital rates as functions of food availability, it only makes sense to think of global changes to elasticities. A change that increases the elasticity of survival at some value of E steepens the px(E) curve at that point, but because px(1) and px(0) are fixed, the entire curve must be adjusted to compensate. One way this may be accomplished is by altering the single input parameter by modifying the empirical estimates of the elasticities near E = 1. When elasticities through the reproductive ages are increased in this manner, the equilibrium food ratio increases, following equation (6). We find that one method of maximizing human welfare, as measured by Ê and equilibrium life expectancy at birth, is to increase the elasticity of fertility at all ages to the point where the total fertility rate approaches replacement level.
We find that infanticide, accomplished by increasing the elasticities of survival of the youngest age classes, has an effect similar to fertility control in terms of life expectancy at age 10. The term βμ(1) is the sum of all the age-specific survival elasticities before it, and thus an increase in α1(1) will increase Ê, as in equation (6). However, geronticide, the reduction of survival of post-reproductive age classes has no effect on Ê, as the reproductive value of these ages is zero and thus their survival is irrelevant to equation (3) and equation (6). Manipulating the age structure will have an effect on the total population size N̂, even if it is small. The effect will depend on the labor and consumption patterns of the age classes in question. In our parameterization of the model for pre-European contact Hawai’i increasing the survival elasticities of the age classes that do not contribute to production has little effect on the total population size. The equilibrium population size decreases by less than 0.025% in response to a steep decrease in survival at those ages. The loss of older individuals results in proportional increases in all younger age classes. Geronticide does accomplish an exchange of older individuals for younger ones, with some loss due to the fact that the oldest age classes have survived the hazards of previous age classes and are being exchanged for those who have not. On the other hand, if post-reproductive individuals performed work outside of agricultural production (e.g., childcare or the performance of other essential societal tasks) those services would be lost for little apparent gain. Additionally, in a geronticide scenario life expectancy would decrease as a result of the socially imposed wall of mortality at late ages.
Another question we can address here is the effect of our assumptions regarding the age distribution of labor. In equation (7), changes to the relative age-specific expectations regarding work can be recorded in the vector φ. Increasing the number of age classes that contribute labor or the amount of labor that each age contributes will tend to increase the rate at which F saturates. The curved line in Fig. 5 will move upwards as a result and there will be some increase in equilibrium population size. This increase may be quite small if F is near 1 at equilibrium (or N ≫ (1/c)), illustrating that adding more labor to an agricultural system when it is working near capacity provides little benefit with regard to population size. On the other hand if field labor could be reduced with little effect on subsistence population size and were invested with higher benefit elsewhere, there may be a net benefit to the group. We do not consider such alternate economies here, but they may well have existed in human history.
The effect of taxation
One common feature of hierarchical societies is the existence of some form of taxation. From the point of view of the agricultural class taxation represents a loss of available calories. Taxes can be calculated either on per capita basis or as a lump sum, in the manner of rent. The two methods have profoundly different consequences for the population’s dynamics. The total tax burden is ϒ, measured in Kcal; If levied per capita, ϒ = υN. Equation (4) becomes
| (10) |
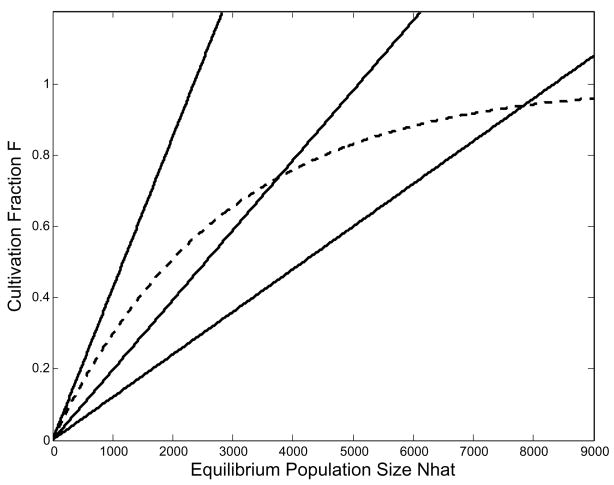
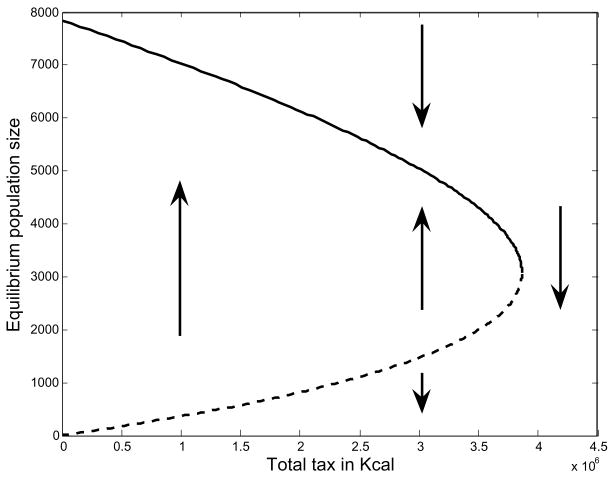
It is important to remember that demographic rates and elasticities fix Ê in equation (3), so taxation only affects equilibrium population size N̂. Rewrite equation (10) as F = (ÊN̂J < ρ, û > +ϒ)/(Y Am). With taxes assessed per capita, their burden increases the slope of the solid line in Fig. 9, shifting the intersection with F function (if one still exists) to the left and reducing equilibrium population size. The imposition of a fixed tax, however, shifts the intercept of the solid line upward and creates the possibility of two nontrivial equilibria (Fig. 10). In cases where there are two equilibria the lower one is unstable and if the population drops below the associated value of N̂ the population will be drawn toward zero (Fig. 11). Above the unstable equilibrium the population is drawn toward the upper equilibrium point. If the two equilibrium points are not far apart, a fixed taxation scheme could provide a hole a population might fall into in hard times and never find its way out of. In such a case the population is too small to pay the tax and feed itself at the equilibrium hunger level, resulting in diminished vital rates and a negative growth rate, which accelerates as the population plummets toward extinction.
Fig. 9.
A per capita tax increases the slope of the solid line and if an intersection with the F function’s curve still exists, the equilibrium population is decreased.
Fig. 10.
In the case of a fixed tax, the solid line is shifted upward, increasing the intercept. This represents the tax burden, which is constant, even when the population is zero. The shifting solid line creates several possibilities. There may be two non-trivial equilibria, one or none. The solid lines represent increasing tax burden as the intercept increases.
Fig. 11.
In the case of a fixed tax there may be two non-trivial equilibria, being a saddle-node bifurcation. The upper half of the curve represents the stable equilibrium solutions and the lower part represents the unstable ones. Perturbation of an equilibrium on the lower half of the curve will draw the population to the stable upper equilibrium solution at the same taxation level, or to a population of zero, as the arrows indicate.
Stability of equilibria
We find that an equilibrium is both globally and locally stable under our assumptions and expected parameter ranges, although stability criteria are difficult to interpret (see appendix). Stability arises generally because when the population is below the equilibrium size, assuming the population is near its equilibrium distribution, per capita resources exceed those at equilibrium and vital rates increase, as in the Lee and Tuljapurkar (in review) model. However in our model as the population approaches equilibrium the growth rate approaches zero due to the reduction in vital rates as per capita food availability falls. Above equilibrium population size per capita resources fall such that the growth rate of the population becomes negative and it is drawn back toward equilibrium. When elasticities become large the population overshoots equilibrium and may oscillate around it.
’Opunohu Valley, a case study
Our model may be used to estimate equilibrium population densities of real groups in real places, but to do so requires estimation of a large number of parameters. In this section we use best available information about the environment, culture and technological nature to examine what an equilibrium population on the Polynesian island of Mo’orea might have been before European contact. Specifically we use data collected by Hamilton and Kahn (2007) to address the question of population density in the ’Opunohu Valley of Mo’orea precisely.
The valley is located on the northern side of Mo’orea, one of the Society Islands of French Polynesia. The tall volcanic island lies within sight of the bigger island of Tahiti. The valley sweeps up from ’Opunohu Bay and is contained by steep ridges of the mountain on either side. There are numerous house sites, terraces and religious structures called marae within the valley, some of which have been excavated for evidence of settlement patterns. The alluvial plain at the base of the valley is made up of rich soil and the vegetation that covers much of the valley today is quite lush. There are several estimates of the island and valley’s population at about the time of European contact, but these are quite contradictory.
Our analysis begins with the characteristic equation and the equilibrium food ratio, Ê. We employ a standard one-sex model here for simplicity, meaning that we don’t track men and women separately, but assume the sexes can both be described by a single set of vital rates. It is difficult enough to agree on generalized patterns of mortality for modern populations, and even more so for a group that has not existed in its native form for more than 250 years and for whom skeletal records (with their attendant problems) are difficult to be had. We assume that in the absence of hunger, early inhabitants of Mo’orea had an expected lifespan of 45 years, following the Coale-Demeny West pattern, female mortality level 11. The age-distribution of fertility rates is derived from MacArthur (1967). Fertility begins at age 14 and ends by age 50, with the peak of the distribution between 25 and 30 years of age. The elasticities of survival rates are derived from Bengtsson et al. (2004), and fertility elasticities from Lee (1987). The result is an equilibrium hunger level of E = 0.6795. This means that a worker who needs 3,000 Kcal/day (following Hamilton and Kahn (2007)) to maximize vital rates, receives only 2,039. We must also calculate the equilibrium age structure, û.
Hamilton and Kahn (2007) divide the valley’s total cultivable area into 10 combinations of soil and slope and they have estimated the yield in tons of starch in a typical year (see their Table 8.9). The cultivars were chosen from among local options to maximize the starch production for each cultivation zone. Wetland taro production in the rich alluvial soil of the valley bottom and in the terraced areas was the most productive, providing 25 tons per hectare. The least productive zone was the semi-cultivation of a plantain species in the mountainous interior, which provided 1.25 tons per hectare. The mean productivity for the entire valley was 11.61 tons of starch per hectare, which was converted to 35,478 Kcal per hectare for our yield parameter, Y. The sum of all agricultural areas was 823.03 ha, providing our maximum area, Am.
We assume that half of the population participates directly in agricultural production, approximating the sexual division of labor typical of many Polynesian societies, and that an adult can cultivate 0.9443 ha over the course of year using traditional methods and working a traditional day. The relative labor contributions by age, the vector φ, represent a simple step function in which young adults begin agricultural work at age 14 and stop after age 44. During those years we assume all age classes contribute an identical amount and quality of labor. Our estimates are not particularly sensitive to this assumption because the availability of land, rather than of labor, defines the equilibrium. Finally, we assume that land use efficiency is described by the function . We now solve equation (4) numerically for N̂.
The equilibrium population under our assumptions is 17,132 persons, or an average density of 720 p/km2. This density seems quite high and begs the question where all these people would have lived if such a population ever existed. The part of the valley not dedicated to agriculture is only 15.6 km2, half of which is too steep for habitation. This leaves 8.3 km2 of area, some fraction of that being fern-covered, for people to use for habitation. Thus average density of habitable space would be 2,064 p/km2, or 484 m2/p. The space-limited model’s equilibrium population exceeds by a factor of almost 2 the carrying capacity of ’Opunohu Valley estimated by Hamilton and Kahn (2007). Labor efficiency is a minor factor in this scenario, and the fraction of land in cultivation exceeds 99%, after excluding fallow.
Hamilton and Kahn (2007) used these figures to calculate a “maximum carrying capacity” for comparison to other estimates of ’Opunohu’s population. They arrived at a maximum carrying capacity of 9,750 individuals maximum based on agricultural capacity and uniform per capita need, and 1,252 minimum population based on house site counts.
There are two reasons why our estimates will likely exceed such carrying capacities. Carrying capacity estimates generally assume the population is made of a single age class, typically the most energetically needy one. We include children and older people, who generally consume less than the young adults on whom the carrying capacity is based, and thus end up with a greater population from the same number of calories. Additionally, the inclusion of hunger in our model further reduces the number of calories per person by not requiring that every person gets all the calories they desire. In our model the lower the value of Ê, the greater the equilibrium population size.
Adding realism will generally decrease our estimate of the equilibrium population. We might assume 10% crop losses to waste, rot and the like and perhaps an additional 15% taken from the remainder to support a ruling class. This leaves a total yield of 27,141 Kcal/ha and generates an equilibrium population of 12,819. This figure is much closer to the maximum carrying capacity from Hamilton and Kahn (2007), but still exceeds it by 31%.
What if the population practiced fertility control such that hunger is minimized? When we increase (by greater than four-fold in this case) the elasticity of fertility to the point where equilibrium fertility is low enough to generate an equilibrium at E = 1, ’Opunohu Valley’s equilibrium population number falls to 11,012, a 36% decrease from the initial projection of 17,132. The total fertility rate in this scenario drops from 2.1 to 1.5 children per parent. At E = 1, age-specific survival is maximized and the life expectancy at birth will be maximized as well.
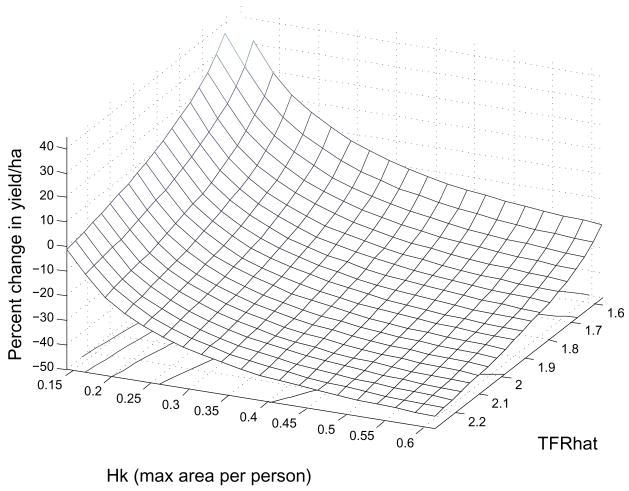
As an exercise we can ask what combinations of fertility elasticity (as reflected in total fertility rate), yield reduction and worker efficiency generate an equilibrium population equal to the Hamilton and Kahn (2007) carrying capacity. The results are shown in Fig. 12.
Fig. 12.
These are the combinations of total fertility rate, worker productivity and percent change in yield per ha that generate an equilibrium population of 9,750 for ’Opunohu Valley. At the levels of productivity and fertility in our parameter set, yield would have to be reduced by approximately 40% to arrive at the population predicted by K.
In general, decreasing the expected maximum lifespan increases per capita food availability at equilibrium. If we change the maximum life expectancy at birth to 30 years, Ê rises to 0.902 and N̂ falls to 12,619. At e0(1) = 60 years Ê drops precipitously to 0.567 and N̂ climbs to 20,545. Despite the dramatic differences in our assumptions regarding the life expectancy without food limitation, adult lifespan in all three scenarios is identical (Table 3). This is a reflection of the fact that while adult mortality levels are relatively stable between scenarios, juvenile mortality changes tremendously. Given that the remains of the young are generally less well preserved than those of adults we may be unable to determine the true maximum lifespan from skeletal remains, even given a perfect estimate of equilibrium adult lifespan. Without a sense of the childhood mortality levels we may not be able to tell the difference between a smaller, well-fed population and a large, hungry one from their mortality signatures.
Conclusions
Our space-limited model of human population dynamics provides a picture of human quality of life in early agricultural societies. Our model is not a one-dimensional logistic (e.g., Verhulst (1838)). Nor is it directly analogous to two-species models (e.g., predator-prey, Lotka (1925) Volterra (1926), host-parasite Anderson and May (1978), or consumer-resource Caughley and Lawton (1981). Instead, our model links food-dependent vital rates to the labor supply available to produce food in a space-limited agricultural system. The model reveals key tradeoffs between quality of life and demographic parameters, some of which were under human control, and provides a tool for examining cultural, ecological and evolutionary interactions in an early agricultural society.
We find that the hunger level at equilibrium is determined largely by two factors: the maximum growth rate that the population can achieve if food is plentiful, and the responsiveness of the demographic rates to hunger. In consequence, a society can only change hunger level and welfare at equilibrium by either increasing mortality of the working ages or younger, or decreasing fertility. Our analyses show that the most effective lever an early society would have had to improve well being at equilibrium is fertility control. By depressing total fertility a population could increase both per capita food availability and life expectancy at birth. Infanticide would also lead to a decrease in hunger and an increase in adult lifespan, but is a practice that many cultures find abhorrent. The size of the population that can be maintained at equilibrium depends on arable land area, the labor supply and efficiency of workers, the productivity of the soil, and the marginal gain in area obtained by adding new workers. We examined technological innovation as it affects two aspects of production. An increase in worker productivity, and thus in the area an individual can cultivate, will increase equilibrium population size, but the effect is limited by the amount of uncultivated land remaining at equilibrium.
Innovations that directly increase productivity while using only surplus labor, such as mulching or irrigation, will increase in equilibrium population size. A similar effect can be obtained from innovations that indirectly raise food supply, such as fishing and hunting, or the manufacture of trade items that can be used to procure additional calories. Innovations that increase the caloric yield per unit area have an effect equivalent to increasing the total arable area, and both increase equilibrium population almost linearly. None of these innovations directly affects the hunger level at equilibrium. Taxation can be incorporated into the model as a reduction in the caloric availability to the population. We find that a fixed-tax system provides the possibility of multiple equilibria and has important implications for stability.
With these results in hand it let us revisit the five fundamental questions proposed by Wood (1998).
Is the growth of preindustrial populations “regulated” in any meaningful sense of the word? Our answer is yes, they were if access to cropland was limited.
Is there an optimal population size, and do preindustrial populations tend to equilibrate at the optimum? To discuss optimality in a meaningful way requires specification of the quantity we aim to maximize, but we find that in a deterministic environment a population will approach an equilibrium. If we compare equilibrium states, there is a fundamental tradeoff between equilibrium welfare (measured by hunger level, life expectancy, or fertility at equilibrium) and the population size at equilibrium. However, any notion of an optimal equilibrium must be driven by factors outside the model, such as cultural preferences and choices. For example, a society that defined a certain level of welfare measured in terms of infant mortality or adult life expectancy would be able to move towards that target by manipulating its demographic behavior. The agricultural environment, productive technology and labor would then drive the population size to the corresponding equilibrium level.
What is the relationship between population growth and economic change? The answer depends on how we define “economic change” with regard to the parameters of the model. Wood focuses on Boserupian technological advances that come as a result of economic pressure. We examine the consequences of improving technology to either increase the amount of area an individual may cultivate or alternately to increase the caloric potential of the soil. In the first case, the effect on the size of the population is muted by the constraints on cultivation of new land, while in the second the increase in population size is almost linear.
What are the implications of population growth and economic change for individual health and well being? We have addressed these questions directly. In terms of well being, a population’s hunger level will decrease as its numbers increase towards an equilibrium level. Economic growth that alters the productivity of land (or otherwise increases the caloric returns to labor via other forms of economic activity) will result in an increase in equilibrium population size. Economic growth that alters demographic conditions will affect the equilibrium level of hunger. The tradeoff between population size and individual well being at equilibrium is sensitive to changes in technology.
What is the role of crisis mortality in preindustrial population dynamics? The answer to this question depends on the duration of the crisis. For a population at equilibrium, a single short-lived crisis, such as a famine that lasts a few years, will drive population below its equilibrium level. The response of hunger and welfare depends on the nature of the crisis: excess mortality of the young and old will temporarily increase the food ratio and lower hunger. But this gain will dissipate as the population recovers and moves back towards equilibrium. On the other hand, excess mortality in the working ages may increase hunger as it decreases population, exacerbating the crisis until the labor force recovers through population renewal. A long-lived crisis, such as a multi-decade drought, effectively lowers agricultural productivity. Absent a change in demographic behavior, such a crisis will drive the population to a new equilibrium at lower population size but at the same level of hunger. But a response of demographic rates is certainly likely in such a scenario, with increased mortality and lower fertility. In that case, the equilibrium hunger level can rise and the equilibrium population size fall much farther than it would without a demographic response. To fully address this question requires an analysis of the dynamics in a variable environment, in which we take account of crises of variable impact and duration. The deterministic dynamics analyzed here are an essential step towards understanding dynamics in a variable world.
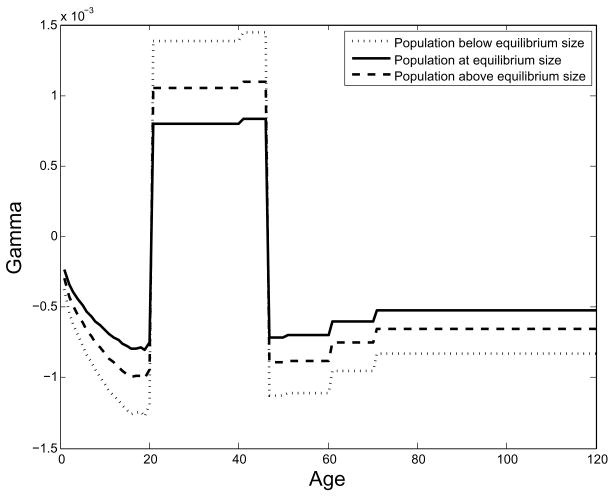
Fig. 6.
The working age classes are net producers in all three scenarios, and adding individuals in those age classes will increase E, as indicated by a positive marginal productivity Γx in those ages. However, the net effect of adding a typical individual, in which we examine the scalar product of the Γ vector and the stable age structure, is always negative. This indicates that welfare is maximized when population is small and per capita productivity is maximized.
Table 2.
Parameters and variables from ’Opunohu case study.
| Parameter or variable |
|||
|---|---|---|---|
| ID | Description | Value | Units |
| J | max. food required by most needy age | 3,000 | Kcal/day |
| Y | agricultural potential of the land | 35,465 | Kcal/ha/day |
| Am | total arable land | 823 | ha |
| H | labor contribution of typical adult (M or F) | 5 | hours/individual/day |
| k | conversion from time to annual area cultivated | 0.0944 | ha-days/hour/yr |
| ρx | relative consumption by age | 0.294-1 | |
| φx | relative labor output by age | 0 or 1 | |
| γ(1) | baseline fertility elas. at any reproductive age | 0.135 | |
| β1(1) | baseline elasticity of survivorship in first year | 0.057 | |
| β26(1) | baseline elasticity of survivorship at age 25 | 0.19 | |
| β66(1) | baseline elasticity of survivorship at age 65 | 0.47 | |
| νG | mean baseline elasticity of vital rates | 0.332 | |
| e0(1) | baseline life expectancy | 45 | years |
| e0(Ê) | equilibrium life expectancy | 30.3 | years |
| e10(1) | baseline life expectancy at age 10 | 49.1 | years |
| e10(Ê) | equilibrium life expectancy at age 10 | 38.0 | years |
| TFR(1) | baseline total fertility | 2.44 | daughters |
| TFR(Ê) | baseline total fertility | 2.08 | daughters |
| Ê | equilibrium food ratio | 0.680 | |
| N̂ | equilibrium total population size | 17,132 | individuals |
Acknowledgments
The authors would like to thank Charlotte Lee for her valuable contributions throughout the creation of this manuscript. We also thank Marc Feldman, Jamie Jones, Pat Kirch, Ron Lee and Peter Vitousek. CP thanks the Stanford University Archaeology Center for funding his research. ST thanks the National Institute on Aging and the National Science Foundation Biocomplexity program for support.
Appendix
Parameter values
Our baseline age-specific survival rates are derived from Coale and Demeny (1983) using their West mortality schedule. We used three mortality levels to examine the range of model responses, corresponding to a life expectancy at birth of 30, 45 and 60 years. Fertility schedules were based upon the age distribution described in MacArthur (1967), which was adjusted proportionally to generate the desired total fertility rate. The age-specific elasticities of mortality were derived from Bengtsson et al. (2004) and fertility elasticities from Lee (1987). Following Lee and Tuljapurkar (in review) fertility elasticity is assumed to be identical for all reproductive ages. Each set of elasticities represents the mean response of these vital rates to some proxy for a decrease in caloric availability across several locations and times. Mortality elasticities were converted to elasticities of survival. A discussion of how these elasticities were used to generate specific survival and fertility rates as a function of food availability is found in the following subsection.
We use a schedule of age-specific daily caloric requirements from FAO/WHO (1973) as our baseline caloric need. The age group with the greatest need requires 2,785 Kcal per day, defining parameter J. The vector ρ describes the FAO/WHO baseline caloric need of each age with respect to J. We chose to make the labor contribution by age a simple step function for ease of interpretation. Before the 20th year and after the 45th year relative labor contribution φx = 0. In the working years the relative contribution is 1. The labor output of a reference worker (in area) is the product Hk, which from ethnographic sources is estimated to be 0.472 ha/person (or 1.17 acres/person) after accounting for the assumption that only men (approximately half the population) are directly involved in agricultural production (Kamakau, 1976). These figures were estimated for sweet potato farming, a major source of calories across much of Polynesia. If we assume that is the product of H = 10 hours of daily labor per man, then the typical adult works half of that and the conversion from labor to land k = 0.0944 ha/hour over the course of a year.
Elasticities
Following Caswell (2004), elasticities of survival, αx, and of fertility, γx, are defined
| (A-11) |
Survivorship lx = p1p2 ···px−1 so the elasticity of lx is
| (A-12) |
where we index survivorship such that l1 = 0, and the elasticity of l1, β1 = 0.
We estimate the values of αx, γ from the historical data. We assume they apply at E ≈ 1. Write for these estimated values, assumed to apply at E = 1. These values are independent of any model we use for the functional dependence of elasticity on E. The αx will depend on the baseline survival rates because we are actually starting with mortality elasticities and translating to survival elasticity. The values of βx(E) and γ (E) rise rapidly as E falls below 1.
How elasticities change with E
In general, we can write the vital rates as a product of their maximal values and a factor that changes with E. For example, px(E) = px(1) G(E). We require that G(E) is a continuous function that is very close to 1 at E = 1 and is zero at E = 0. So, in general, pick a probability density function (pdf) g(E) on (0, ∞) such that g(0) = 0, |g(1) − 1| ≪ 1. Let G be the cumulative distribution function (cdf) corresponding to g, so that g = dG/dE, and then set px(E) = px(1) G(E). The elasticity of px is
| (A-13) |
Fix the parameters by of G by setting α(1) to the historically estimated value at E = 1. Now observe that
| (A-14) |
We write g′ = dg/dE. The requirement that G(1) is close to 1 means that the density g must fall rapidly as E approaches 1. For a gamma pdf, this means that b ≫ 1; for a normal pdf, we’d need μ + 3σ < 1; and so on.
Since all the elasticities are small (≪ 1) at E = 1, we can approximate equation (A-14) by
| (A-15) |
Gamma CDF Elasticities
For the gamma pdf,
| (A-16) |
Since the elasticities are small (≪ 1) at E = 1, we approximate equation (A-14) by
| (A-17) |
say. This leads to the approximation
| (A-18) |
Numerical analysis show that this approximation captures the behavior of the elasticities quite well. Equation (A-18) shows that elasticities double when the hunger level drops by (1/K). The range of values of K is 6.4 for fertility and around 8 for mortality, so elasticities double when we go from E = 1 to E ≈ 0.88, and elasticities will increase by a factor of nearly 32 by E = 0.5 and by a factor of 500 by E = 0.1.
For βx use equation (A-12) to write
and approximate this by
| (A-19) |
where kβ is an average,
The numbers show that when x = 29 or so, kβ will be about 7 or so.
Note the general qualitative fact that since we want g to be close to zero at E = 1, as E decreases we will “ride up” the curve of increasing g and elasticities will change very fast. For the gamma pdf, we know that the right tail of the gamma near E = 1 is e(−E/b) = e−10E which is the basis for the exponential changes described above. A similar feature will occur with any other pdf model because we will always have the tail of g falling fast near E = 1.
Equilibrium with gamma cdf elasticities
Given the maximal rates mx(1), lx(1) compute the mean age of reproduction,
and the Total Fertility Rate M = Σx mx. Then at E = 1 the Net Reproductive Rate
Numerics show that for all values of E,
| (A-20) |
Because the elasticities of the mx are equal, just call it γ, we have
| (A-21) |
Since E is close to 1 we can approximate this (getting an underestimate) by
Approximating Ê
The final step is to use equation (A-19) and write
Here
We expect that K ≈ 7 and numerical work conforms this.
This will give us
Now use this to integrate equation (A-21) from lower limit E to upper limit 1 and find
where
At Ê we have R(Ê) = 1 so
Given how large K is, ignore the second term on the right to get the final result
| (A-22) |
The Stability Matrix
At equilibrium if we were to increase the population by an amount proportional to û, the per capita change in log E would be proportional to < û, Γ >, where
| (A-23) |
The first term on the RHS is the marginal gain in cultivated area obtained by adding an individual of age x, and the second is the concomitant increase in baseline consumption. At equilibrium we expect that < û, Γ >= Σx uxΓx < 0. In Lee and Tuljapurkar (in review) the per capita increase in cultivable area increases linearly with population size once the stable age structure has been achieved. This difference is essential to the regulation of space-limited populations. The result is that E always decreases with an increase in N (assuming stable age structure), reflecting the fact that well being is maximized when density-dependent pressure is minimized, near where the population is zero. The net change in E is always negative when N increases proportional to û.
Consider what happens when we perturb the population away from equilibrium by a small vector which we write as
| (A-24) |
The first effect of this is that log Ê changes to
| (A-25) |
where the elements of Γ are defined as in equation (A-23). The elements of the matrix A(t) = A(log E(t)) change to
| (A-26) |
where
| (A-27) |
Inserting equation (A-26) into the dynamic equation (2) and eliminating higher order terms we obtain
| (A-28) |
We will rewrite this approximation as
| (A-29) |
where
| (A-30) |
where the prime on a vector indicates its transpose.
Local stability of the equilibrium requires that H(t) → 0 as t increases, which requires that the eigenvalues of S must be less than 1 in magnitude. We introduce the diagonal matrix
| (A-31) |
We will study the eigenvalues of a transformation of S that has the same eigenvalues,
| (A-32) |
The first matrix on the right of (A-32) is
| (A-33) |
where gx = lx(Ê) mx(Ê). Matrix (A-33), like Â, has a dominant eigenvalue 1, and all its rows sum to 1.
The second matrix on the right of (A-32) needs to be considered in bits. First, use equation (A-11) and equation (A-27) to find
| (A-34) |
From this conclude that
| (A-35) |
The equilibrium age structure is proportional to the survivorship,
| (A-36) |
where a is a constant that ensures Σx ûx = 1.
Using (A-36) and the definition l̂ = {lx(Ê)}, we have
where e is a vector of ones. Then use equation (A-35) to find
| (A-37) |
Finally,
| (A-38) |
Putting all this together the second matrix on the right of equation (A-32) becomes the product
| (A-39) |
The transformed stability matrix L−1SL is thus explicitly given by the sum of the matrices in equation (A-33) and equation (A-39). The population equilibrium n̂ in our model will be locally stable (meaning that the population will return to the equilibrium if it is perturbed from it by small numbers) if the eigenvalues of S (equivalently of the transformed matrix in (A-32)) are all less than 1 in absolute value. The characteristic equation of the transformed matrix can be written explicitly (see below) but does not seem to yield useful stability criteria. The usual localization theorems for eigenvalues do not yield useful criteria, and the general problem of finding eigenvalues for a sum of matrices such as (A-34) and (A-39) does not appear to have useful solutions.
Applying standard perturbation theory to the matrix S changes the dominant eigenvalue to
| (A-40) |
This is a first-order approximation that gets less accurate as the magnitude of the perturbation gets larger. Since we know that the elasticities and the gx are positive, and the scalar product in the numerator of the last term is negative, the fraction on the RHS of equation (A-40) must be negative. So, |λ1(S)| < 1 if the fraction on the RHS of equation (A-40) is between zero and −2. The denominator in the last term of equation (A-40) equals the mean generation time T̂ in the equilibrium population (typically 25 < T̂ < 30) and so will simply act to reduce the effect of the perturbations in the numerator.
We conclude that when elasticities of survival and fertility are much less than 1 the system should be locally stable around the equilibrium. We can imagine circumstances in which the elasticities are very large, which could drive a sustained instability as the population overshoots and undershoots equilibrium. We have not found such instabilities numerically using parameters that describe typical early agricultural populations. In fact we must increase the baseline elasticities of fertility and survival by more than 24 times to increase λ1(S) to 1.
The Generalized Characteristic Equation
The perturbation H(t) may be rewritten as a linear combination of any of the right eigenvectors and a vector of other numbers, c.
Vectors ui and vi are the right and left eigenvectors of equilibrium projection matrix  respectively, corresponding to eigenvalue λi.
| (A-41) |
| (A-42) |
Substituting into equation (A-29)
| (A-43) |
| (A-44) |
| (A-45) |
Multiply through on the left by .
| (A-46) |
Define the matrix Λ as a matrix with the eigenvalues of  along the diagonal in descending order and zeros elsewhere. Define the matrix Θ as follows.
| (A-47) |
The dynamics of the vector c may be described in terms of these two matrices.
| (A-48) |
The eigenvalues of the matrix (Λ + Θ), call them zi, are the roots of the equation
| (A-49) |
Define the following terms for simplicity
| (A-50) |
| (A-51) |
Working from equation (A-49) in the 2×2 case we get the equation
| (A-52) |
| (A-53) |
| (A-54) |
| (A-55) |
In the 3×3 case we get
| (A-56) |
Solving for the determinant of the 3×3 matrix, we get
| (A-57) |
For ease of interpretation, define εi = (z − λi). This gives characteristic equations in the 2×2, 3×3 and 4×4 cases, respectively,
| (A-58) |
| (A-59) |
| (A-60) |
For a k×k matrix the characteristic equation may be written
| (A-61) |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson RM, May RM. Regulation and stability of host-parasite population interactions: I. Regulatory processes. Journal of Animal Ecology. 1978;47 (1):219–247. [Google Scholar]
- Bengtsson T, Campbell C, Lee J. Life Under Pressure: Mortality and Living Standards in Europe and Asia, 1700–1900. MIT Press; Cambridge, MA: 2004. [Google Scholar]
- Bongaarts J. A framework for analyzing the proximate determinants of fertility. Popul Dev Rev. 1978;4(1):105–132. [Google Scholar]
- Boserup E. The Conditions of Agricultural Growth: The Economics of Agrarian Change under Population Pressure. Aldine; Chicago: 1965. [Google Scholar]
- Caswell H. Matrix Population Models. 2. Sinauer; Sunderland, Mass: 2004. [Google Scholar]
- Caughley G, Lawton JH. Plant-herbivore systems. In: May RM, editor. Theoretical Ecology. Blackwell; Oxford: 1981. pp. 132–166. [Google Scholar]
- Clutton-Brock TH. Evolution of Parental Care. Princeton Univ. Press; Princeton: 1991. [Google Scholar]
- Coale AJ, Demeny P. Regional Model Life Tables and Stable Populations. 2. Academic Press; New York: 1983. [Google Scholar]
- Cohen JE. How Many People Can the Earth Support? W. W. Norton & Co.; New York: 1995. [Google Scholar]
- Condorcet M. Outlines of an Historical View of the Progress of the Human Mind: Being a Posthumous Work of the Late M. de Condorcet. J. Johnson; London: 1795. Translated from the French. [Google Scholar]
- Cunningham JJ. A reanalysis of the factors influencing basal metabolic rate in normal adults. American Journal of Clinical Nutrition. 1980;33 (11):2372–2374. doi: 10.1093/ajcn/33.11.2372. [DOI] [PubMed] [Google Scholar]
- Dyson T, O'Grada C. Famine Demography: Perspectives from the Past and Present. Oxford University Press; New York: 2002. [Google Scholar]
- FAO/WHO. Joint Ad Hoc Expert Committee Technical Report 522. Food and Agriculture Organization and World Health Organization; 1973. Energy and protein requirements. [PubMed] [Google Scholar]
- Hamilton BK, Kahn JG. Pre-contact population in ’opunohu valley, mo’orea. In: Kirch PV, Rallu J-L, editors. The Growth and Collapse of Pacific Island Societies. Ch 8. University of Hawai’i Press; Honolulu: 2007. pp. 129–159. [Google Scholar]
- Kamakau S. The Works of the People of Old. Bernice Pauahi Bishop Museum; Honolulu: 1976. [Google Scholar]
- Lee CT, Tuljapurkar S. Population and prehistory I: Food-limited population growth in constant environments. Theoretical Population Biology. doi: 10.1016/j.tpb.2008.03.001. in review. [DOI] [PubMed] [Google Scholar]
- Lee RD. Malthus and Boserup: A dynamic synthesis. In: Coleman D, Schofield R, editors. The State of Population Theory. Blackwell; Oxford: 1986. pp. 96–130. [Google Scholar]
- Lee RD. Population dynamics of humans and other animals, presidential address to the population association of america. Demography. 1987;24:443–466. [PubMed] [Google Scholar]
- Lotka AJ. Elements of Physical Biology. Williams and Wilkins Co; Baltimore: 1925. [Google Scholar]
- MacArthur N. Island Populations of the Pacific. Australian National University Press; Canberra: 1967. [Google Scholar]
- Malthus TR. An Essay on the Principle of Population as it Affects the Future Improvements of Society. With Remarks on the Speculations of Mr. Goodwin, M. Condorcet, and Other Writers. J. Johnson; London: 1798. [Google Scholar]
- Preston SH, Heuveline P, Guillot M. Demography: Measuring and Modeling Population Processes. Blackwell; Malden, Mass: 2001. [Google Scholar]
- Scott S, Duncan CJ. Demography and Nutrition: Evidence from Historical and Contemporary Populations. Blackwell Publishing; Oxford: 2002. [Google Scholar]
- Verhulst PF. Notice sur la loi que la population suit dans son accroissement. Correspondance Math Phys. 1838;10:113–121. [Google Scholar]
- Volterra V. Fluctuations in the abundance of a species considered mathematically. Nature. 1926;118:558–560. [Google Scholar]
- Wood JW. A theory of preindustrial population dynamics: Demography, economy, and well-being in Malthusian systems. Current Anthropology. 1998;39 (1):99–135. [Google Scholar]
- Wrigley EA. Demographic models and geography. In: Chorley RJ, Haggett P, editors. Models in Geography. Ch 6. Methuen & Co; London: 1967. pp. 189–216. [Google Scholar]