Temperature jump induced force generation in rabbit muscle fibres gets faster with shortening and shows a biphasic dependence on velocity

Abstract

We examined the tension responses to ramp shortening and rapid temperature jump (<0.2 ms, 3–4°C T-jump) in maximally Ca²⁺-activated rabbit psoas muscle fibres at 8–9°C (the fibre length (L₀) was ∼1.5 mm and sarcomere length 2.5 μm). The aim was to investigate the strain sensitivity of crossbridge force generation in muscle. The T-jump induced tension rise was examined during steady shortening over a wide range of velocities (V) approaching the V_max (V range ∼0.01 to ∼1.5 L₀ s⁻¹). In the isometric state, a T-jump induced a biphasic tension rise consisting of a fast (∼50 s⁻¹, phase 2b) and a slow (∼10 s⁻¹, phase 3) component, but if treated as monophasic the rate was ∼20 s⁻¹. During steady shortening the T-jump tension rise was monophasic; the rate of tension rise increased linearly with shortening velocity, and near V_max it was ∼200 s⁻¹, ∼10× faster than in the isometric state. Relative to the tension reached after the T-jump, the amplitude increased with shortening velocity, and near V_max it was ∼4× larger than in the isometric state. Thus, the temperature sensitivity of muscle force is markedly increased with velocity during steady shortening, as found in steady state experiments. The rate of tension decline during ramp shortening also increased markedly with increase of velocity. The absolute amplitude of T-jump tension rise was larger than that in the isometric state at the low velocities (<0.5 L₀ s⁻¹) but decreased to below that of the isometric state at the higher velocities. Such a biphasic velocity dependence of the absolute amplitude of T-jump tension rise implies interplay between, at least, two processes that have opposing effects on the tension output as the shortening velocity is increased, probably enhancement of crossbridge force generation and faster (post-stroke) crossbridge detachment by negative strain. Overall, our results show that T-jump force generation is strain sensitive and becomes considerably faster when exposed to negative strain. Thus the crossbridge force generation step in muscle is both temperature sensitive (endothermic) and strain sensitive.

Introduction

The underlying basis of active muscle contraction and force development is the cyclic interaction of myosin heads (crossbridges) of the thick filaments with actin of the thin filaments during which the chemical energy from ATP hydrolysis is transduced into mechanical work (Huxley, 1957; Geeves & Holmes, 1999). Examination of the tension response to rapid perturbations has helped to elucidate the mechanism of crossbridge force generation in active muscle. Thus, Huxley & Simmons (1971) attributed the quick tension recovery after a rapid shortening step (length release) to the force-generating transition, or the power stroke, in the attached crossbridges and a number of subsequent studies have supported this interpretation (Ford et al. 1977; Piazzesi et al. 2002a,b, 2003; Huxley et al. 2006). The experimental studies that used a step increase of temperature (T-jump) – on maximally Ca²⁺-activated skinned fibres (Davis & Harrington, 1987; Goldman et al. 1987; Bershitsky & Tsaturyan, 1992) and also on tetanised intact muscle fibres (Coupland & Ranatunga, 2003) – have shown that crossbridge force generation is endothermic; force rises when heat is absorbed. In isometric muscle, a small T-jump leads to a biphasic tension rise to a new steady level in which the faster component (phase 2b) is identified as the endothermic force generation in attached crossbridges, and it has been compared to a component part of the quick tension recovery after length release (Davis, 1998; Ranatunga et al. 2002). Subsequent studies examined the T-jump force generation in relation to the actomyosin ATPase cycle and identified phase 2b as a molecular step in the actomyosin crossbridge cycle before the release of inorganic phosphate (P_i) (see refs in Coupland et al. 2005).

An issue that remains unresolved is why the T-jump force generation in muscle is considerably slower than the quick tension recovery after a length release as in the Huxley & Simmons (1971) type of experiment. It has been suggested that, in isometric muscle, T-jump and length release perturb different molecular steps in the crossbridge cycle and that the T-jump force generation is strain independent (see Bershitsky & Tsaturyan, 2002; Davis & Epstein, 2009). On the other hand, we reported recently that the T-jump force generation in active muscle is not observed during steady lengthening whereas it is enhanced during steady shortening, suggesting that the endothermic force-generating process is indeed strain sensitive, inhibited by positive strain and enhanced by negative strain (Ranatunga et al. 2007). However, the velocity range used in our previous study (0.0–0.2 L₀ s⁻¹), although adequate to cover the full force–lengthening velocity relation, in the shortening direction, only reduced the force to ∼0.5P₀ (isometric force).

The goal of the present study was to extend our previous findings to higher velocities, approaching the maximum shortening velocity (V_max). Results show that both the rate of tension decline during ramp shortening and the rate of T-jump induced tension rise during steady shortening increase markedly with increase of shortening velocity. The present findings support the view that crossbridge force generation is both endothermic and strain sensitive.

Some preliminary data from this study were reported at the European Muscle Conference, Oxford (Ranatunga & Roots, 2008).

Methods

The experiments used segments of single skinned fibres from rabbit psoas muscle. Adult male rabbits were killed by an intravenous injection of an overdose of sodium pentobarbitone (Euthatal, Rhone, Merieux), in accordance with the UK Home Office (Schedule 1) humane killing procedure of animals (Drummond, 2009). Fibre bundles from the psoas muscle were prepared and chemically skinned using 0.5% Brij 58, as described previously (Fortune et al. 1991). The procedures were approved by the University of Bristol Ethical Review Committee for animal use and care.

Information on fibre dissection and mounting for tension recording, the compositions of buffer solutions and the trough assembly have been published in detail before (see refs in Ranatunga et al. 2002; 2007). Briefly, a single fibre segment was mounted between, and fibre ends glued to, two metal hooks, one attached to a force transducer (resonant frequency, ∼14 kHz) and the other to a motor to apply ramp length changes to the fibre end. Using He–Ne laser diffraction, the fibre length was adjusted to give a sarcomere length of 2.5–2.6 μm. A fibre, held isometric, was maximally Ca²⁺ activated in the front trough where the temperature was clamped at 8–9°C and monitored by a thermocouple placed close to the muscle fibre. A laser pulse of 0.2 ms duration and 1.32 μm in wavelength was used to induce a T-jump in the fibre and the solution bathing it in the front trough (see Ranatunga, 1996, for details); care was taken to shadow the transducer hooks from the laser radiation to minimise thermal expansion effects. As reported previously (see Goldman et al. 1987), the thermocouple output showed an initial overshoot due to heating of the thermocouple wires by direct absorption of laser light. Measured subsequent to the overshoot (and decay), the raised solution temperature remained constant for ∼0.5 s after the laser pulse (see Ranatunga, 1996). The amplitude of the T-jump used in the experiments was 3–4°C and, in a typical experiment, tension responses to a standard T-jump were recorded both when the fibre was held isometric and when it was shortening at a range of ramp velocities. The timing of the laser pulse with respect to the beginning of a ramp was adjusted for each velocity such that a T-jump occurred when the force during a ramp shortening reached an approximately steady level.

In a few experiments, the sarcomere length change was also monitored by a diffractometer, constructed using a 10 mW He–Ne laser (see Mutungi & Ranatunga, 1996; Ranatunga, 2001). An assembly of cylindrical and bi-convex lenses (basically as described by Goldman & Simmons, 1984) changed the laser beam cross-section into a rectangle, passed it through the fibre and focused it on a photo-detector beyond, such that an area of ∼0.5 mm (along the fibre) × 0.05 mm (across the fibre) was illuminated. Equatorially scattered light from the fibre was collected on the photo-detector by a cylindrical lens to monitor the first-order diffraction. The photo-detector was a one-dimensional position sensitive detector (Hamamatsu, Photonics, S3932) coupled to an analog divider circuit, and it provided a voltage signal proportional to the position of the diffraction. Some intrinsic noise and drift in the diffractometer signal precluded accurate estimate of in-series end-compliance. However, from measurements of the signal, both during and after the ramp, the amplitude of the sarcomere length change (mean ±s.e.m.) was 0.89 (0.03, n= 20, 3 fibres) of the ramp length change applied to the fibre end. Hence, the average sarcomere shortening due to end-compliance would be ∼11%, somewhat higher than ∼5–7% sarcomere shortening obtained on maximal fibre activation in our previous studies (Mutungi & Ranatunga, 2000; Ranatunga et al. 2002). Analyses will be made with regard to fibre length and the corresponding sarcomere length change will be only briefly considered. The fibres were regularly examined under the microscope and an experiment terminated if fibres developed irregularities or showed damage.

The outputs of the tension transducer, the thermocouple, the motor (fibre length) and, in some experiments, the diffractometer (sarcomere length change) were examined on two cathode ray oscilloscopes and digital voltmeters and, using a CED micro-1401 (Mk II) laboratory interface and Signal 3 software (Cambridge Electronic Design Ltd, Cambridge, UK), collected and stored on a personal computer. Subsequent analyses, including measurements of force, temperature and length and curve-fitting to tension records were made using Signal software and further analyses made with Fig.P software (Biosoft, Great Shelford, Cambridgeshire, UK).

Simulating T-jump tension responses during shortening

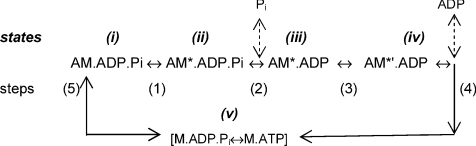
To simulate the basic trends indicated in our T-jump experiments, we used a minimal kinetic Scheme 1 given below. It consists of five steps (1–5) in an unbranched cycle and is essentially similar to the scheme used previously (Ranatunga et al. 2007). Step 1 is the force generation step, step 2 is release of inorganic phosphate (P_i) and steps 3 and 4 represent a two-step ADP release; step 5 is initial attachment/detachment. The rigor [AM] state is not identified in the scheme since in the presence of millimolar level of [ATP] its life time would be very short. Thus, ADP release step (step 4) represents crossbridge detachment on cycle-completion and, to identify it from the initial detachment (k₋₅) in step 5, step 4 (ADP release) will be referred to as end-detachment.

Scheme 1.

In step 1, the forward rate constant (k₊₁) is temperature sensitive (endothermic force generation or power stroke) and, for the present study, k₊₁ was assumed to be strain sensitive and enhanced by shortening (negative strain). For the isometric state at ∼10°C, k₊₁ was 10 s⁻¹. The reverse rate constant (k₋₁) was 100–125 s⁻¹, insensitive to both temperature (as in Dantzig et al. 1992; Zhao & Kawai, 1994) and negative strain; it would be enhanced by positive strain as in lengthening muscle (see Roots et al. 2007), which is not considered here. In step 2, k₊₂ is rapid P_i release (∼1000 s⁻¹) and, assuming the P_i-binding constant to be 1 × 10⁵–2 × 10⁵m⁻¹ s⁻¹ and 0.5 mm P_i to be present in active muscle, k₋₂ was 50–100 s⁻¹. The forward/reverse rate constants for steps 3 and 5 were 40/2.5 and 15/10, respectively. Steps 2, 3 and 5 were assumed to be insensitive to shortening and temperature. The end-detachment rate (k₊₄) was small (∼2–3 s⁻¹) for isometric muscle; k₋₄ was <0.7 s⁻¹. For simulating a certain shortening velocity, k₊₄ was increased, since the ADP release step is thought to determine speed of shortening (see He et al. 1999). During steady shortening (filament sliding), all attached crossbridge states will be exposed to a velocity dependent negative strain (Huxley, 1957). Furthermore, when crossbridges in state i (i.e. AM.ADP.P_i, pre-stroke state) become negatively strained, they would undergo the force generating transition (the power-stroke) more readily/rapidly, as proposed by Huxley & Simmons (1971) from length-release experiments. To incorporate this feature, k₊₁ was increased in simulating muscle shortening. Dragging to negative strain of the force bearing (post-stroke) crossbridge states (states ii, iii and iv) during steady shortening will decrease their average force contribution, but this feature was not incorporated into our simplistic kinetic simulation.

The post-stroke states ii, iii and vi (i.e. AM*.ADP.P_i, AM*ADP and AM*′.ADP) were taken to be equal-force bearing states and the sum of their fractional occupancy is taken as force (see Coupland et al. 2005 for other details). The unbranched kinetic Scheme 1 above was solved by the matrix method using Mathcad 2000 Professional software (Mathsoft) as described previously (Gutfreund & Ranatunga, 1999). Simulations involved two stages. Firstly, after the steady state in the occupancy is reached for the isometric state, shortening was simulated by increasing k₊₄ (up to 128 s⁻¹) and k₊₁ by up to twofold. Secondly, once a steady state is reached for each shortening, a T-jump relaxation was simulated by increasing k₊₁ with a Q₁₀ of 4 as in previous studies and the approach to the new steady state at the higher temperature obtained. As found previously (Coupland et al. 2005), making k₊₄ (ADP release) also temperature sensitive (Q₁₀ of 1.3) in simulating T-jumps did not lead to marked changes in the responses, but a detailed examination remains to be done. The amplitude and the rate were measured from the simulated T-jump tension responses. For qualitative description, the data will be examined against ‘shortening velocity’, assuming k₊₄ of ∼128 s⁻¹ nearly leads to maximum shortening velocity (V_max) and taking shortening velocity (L₀ s⁻¹) to be given by:

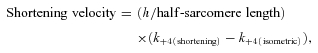where the half-sarcomere length was 1250 nm and h (stroke distance) was 10 nm (an approximate adaptation from He et al. 1999).

Some general considerations

For describing T-jump tension responses, we adopted a nomenclature that to some extent accommodates findings from different types of rapid perturbation (see Coupland & Ranatunga, 2003). Briefly, the tension change that occurs concomitant with a perturbation is referred to as phase 1, where the extreme force reached is T₁, as used in length perturbation experiments (Huxley & Simmons, 1971). After a length perturbation, the tension recovers quickly from the T₁ to T₂ level and this quick tension recovery can be resolved into two exponential components (Davis & Harrington (1993)) and are referred to as phase 2a (very fast) and phase 2b. The tension rise above the pre-perturbation level (endothermic force generation) following a T-jump corresponds to phase 2b (see Ranatunga et al. 2002). Sensitivity to increased P_i and MgADP also suggests that the phase 2b in length perturbation and in T-jump experiments may be comparable processes (Coupland et al. 2005). In T-jump experiments where a prominent phase 1 was seen due to thermal expansion in some series elasticity (see Goldman et al. 1987; Ranatunga, 1999), a quick tension recovery corresponding to phase 2a was seen which partially recovered the phase 1 force-drop, as in length perturbation. In the T-jump experiments reported here, the phase 1 and the quick phase 2a are not obtained. In isometric fibres, the approach to a higher steady force after a T-jump is biphasic with a moderately fast phase 2b and a slow phase 3. In shortening fibres, a T-jump leads to a tension rise to a higher steady (shortening) force but the tension rise is monophasic.

The tension decline during ramp shortening is described basically as in Roots et al. (2007) and Roots & Ranatunga (2008). In brief, the initial inflection soon after the onset of ramp shortening is referred to as the P₁ transition. The P₁ transition is thought to represent the force generating transition in the attached, pre-stroke, crossbridges on exposure to negative strain (see Ford et al. 1977). The subsequent tension decline undergoes a gradual decrease in slope in reaching a nearly steady shortening force. This is referred to as the P₂ transition. Mechano-kinetic modelling has shown that the detachment of (post-stroke) crossbridges that were originally attached in the isometric phase is nearly complete after the P₂ transition (see Roots et al. 2007). In mammalian muscle fibre experiments, a continued slow tension decline is often observed (P₃ tension) after the P₂ transition and is thought to be due to decay of elastic tension in some stretched non-crossbridge elements. Since, in the present experiments, a T-jump was applied soon after the P₂ transition, contribution from P₃ tension is ignored. The rate and amplitude of tension decline during the P₂ transition are determined by an exponential curve fit.

Experimental data presented for T-jumps in the paper were collected from nine fibres; the mean (±s.e.m.) length (L₀) of the fibre segments was 1.48 (±0.13) mm. The mean (±s.e.m.) maximum Ca²⁺-activated steady isometric tension (P₀) at 8–9°C was 180 (±12) with a range of 132–250 kN m⁻², comparable to those in our previous studies at similar temperatures (Ranatunga et al. 2002, 2007). The rate of T-jump induced tension rise in isometric fibre (either from a double exponential fit or from a single exponential fit) was not correlated (P > 0.05) with fibre force. Also, analysis of various data for different velocities from individual fibres showed the trends seen in the pooled plots presented. Nevertheless, whether the large variability in our various measurements is due to different fibre types in the pool cannot be excluded.

Results

Tension responses to ramp shortening and T-jump

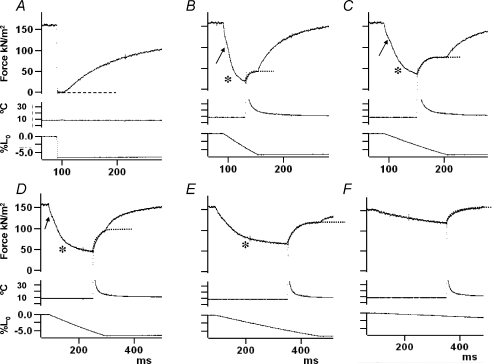
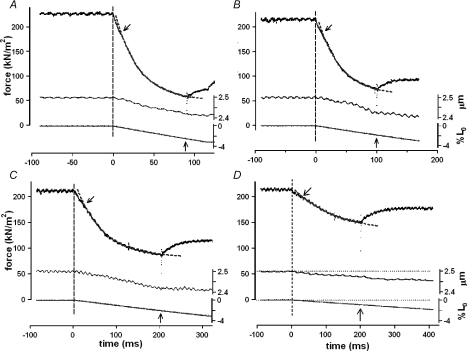
Figure 1 shows sample experimental records from one experiment where the amplitude of the ramp shortening was 7%L₀. The tension response (top trace in Fig. 1A) to a rapid ramp shortening, where the tension drops and then redevelops after a delay, was used for determining the zero tension level in the fibre (dotted line). Figure 1B–F shows the tension responses to a range of different ramp shortening velocities. In each case a T-jump of 3°C was applied during near-steady shortening, i.e. when the tension had reached an approximate steady level while shortening. Note that the initial overshoot in the temperature record is due to direct laser heat absorption by the thermocouple and does not represent solution temperature (see Goldman et al. 1987; Ranatunga, 1996). Figure 2 shows experimental records from another preparation in which the tension response and also the sarcomere length change (middle trace in each frame) during ramp shortening was recorded. The sarcomere length change essentially followed the ramp length change of the fibre but, perhaps due to signal noise and because the sarcomere length change is not clamped, some discrepancies are noticeable.

Figure 1. Tension responses to ramp shortening and to T-jump during shortening.

The fibre was maximally Ca-activated at ∼8°C and during the isometric tension plateau (top trace), a ramp shortening of ∼7%L₀ was applied (bottom trace); middle trace is the temperature of the trough solution monitored close to the fibre. A, a rapid ramp shortening (>3 L₀ s⁻¹), with no T-jump, leads to unloaded shortening, fall in tension and subsequent tension re-development; the dashed line denotes zero tension. B–F, tension responses to ramp shortening at five different velocities, decreasing from B (∼1 L₀ s⁻¹) to F (0.04 L₀ s⁻¹). Note that frames D, E and F are displayed on a slower time scale. An asterisk denotes the gradual decrease of tension slope (the P₂ transition) towards a shortening steady tension. As first described in frog fibres by Ford et al. (1977), an initial inflection (arrow, referred to as the P₁ transition) is seen in a tension decline during ramp shortening and its amplitude is larger at the higher velocities (see Roots et al. 2007, in rat fibres). In each case, a T-jump of ∼3°C was induced by a laser pulse during the subsequent steady shortening after the P₂ transition; the middle trace is the thermocouple output where the initial overshoot and slow decay are due to direct laser light absorption by the thermocouple (see Goldman et al. 1987; Ranatunga, 1996). Note that, as the velocity is increased from F to B, the tension rise after T-jump (see the superimposed dotted line) becomes faster and its amplitude increases and then decreases.

Figure 2. Sample records of tension and sarcomere length change in an experiment.

Each frame shows records of tension (upper trace) and displacement of the first order He–Ne fibre diffraction (sarcomere length change – middle trace) during a ramp shortening (bottom trace) from a fibre preparation (at ∼9°C). The ramp shortening begins at time zero (the vertical dashed line); the shortening velocities decreased from ∼0.3 L₀ s⁻¹ in A to ∼0.04 L₀ s⁻¹ in D and the display time scales are different. The slanting arrow above a tension trace denotes the P₁ transition (see Fig. 1) and application of a ∼3°C T-jump is shown by a vertical arrow displayed above the abscissa. The dotted curve extended through the tension trace is a single exponential fitted to tension data points between the P₁ transition and the T-jump. Note that despite the noisy recording, the sarcomere length remains steady during the isometric phase (before the vertical dashed line) but decreases approximately in parallel to the fibre shortening. The tension decline during shortening (fitted curve) is faster at higher shortening velocities.

The tension records in Figs 1 and 2 show a number of features of interest. Firstly, during a ramp shortening, the tension decline undergoes a gradual decrease in slope, or a transition, to reach a near-steady tension that is lower than the isometric tension (P₀). This gradual decrease in slope is referred to as the P₂ transition (Roots et al. 2007) and its occurrence is indicated by the asterisks in Fig. 1. Tension records also show the occurrence of an inflection (indicated by an arrow) soon after the onset of a ramp and before the P₂ transition; referred to as the P₁ transition, this inflection is more pronounced and occurs earlier at the higher velocities. The P₁ transition is thought to represent the force generating transition in the attached, pre-stroke, crossbridges on exposure to negative strain (see Ford et al. 1977; Roots et al. 2007) but its analysis is not reported here. Secondly, the tension records show that the post-P₁ inflection tension decline is faster at the higher velocities and it could be fitted with an exponential function (Fig. 2) to determine the rate of the tension decline during ramp shortening. Thirdly, application of a T-jump after the P₂ transition is nearly complete, i.e. during near-steady shortening, leads to a characteristic tension rise. As shown by the superimposed dotted curves in Fig. 1, the T-jump induced tension rise is faster at higher velocities but its amplitude is larger at intermediate velocities (compare C, D and E with F and B in Fig. 1). Although the main emphasis of the study was to examine T-jump force generation, in order to gain a fuller picture, some characteristics of the tension decline during ramp shortening and the force–velocity relationship will be outlined first.

Tension decline during shortening and the force–velocity relation

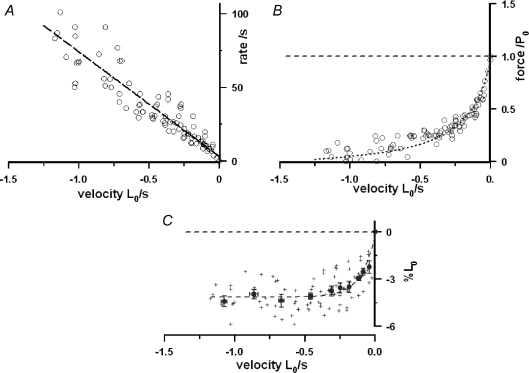
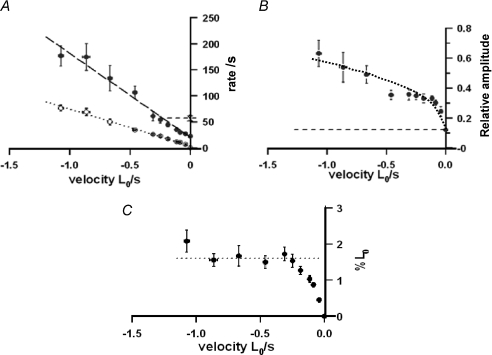
Figure 3A illustrates pooled data for the rate of tension decline during ramp shortening, as determined from curve fits to the post-P₁ inflection tension trace prior to T-jump (see Fig. 2). Despite the scatter in the data, the rate of tension decline is linearly correlated with shortening velocity. The fitted line gives a significant intercept (i.e. an apparent rate for isometric) of ∼3 s⁻¹ (see figure legend). Figure 3B shows the pooled data for the force–shortening velocity relation at the pre-T-jump temperature; the relation has a V_max∼ 1.5 L₀ s⁻¹ and a high curvature (a/P₀∼ 0.1). These data are basically similar to those previously reported from intact and skinned mammalian fast muscle fibres at low temperatures (∼8–10°C; Ranatunga, 1984; Ranatunga et al. 2007). Determining the length change that accompanies a tension change has often been useful in muscle mechanics studies. The extent of shortening at which the P₂ transition is nearly complete was calculated as velocity (L₀ s⁻¹) × 3τ₁ (τ₁= time constant from curve fit), representing the shortening from the isometric state to ∼95% of the tension decline towards the steady shortening state. The results (Fig. 3C) show that the extent of shortening at which the tension reaches the steady shortening state (i.e. when P₂ transition is complete) increases with velocity and remains at ∼4%L₀ at velocities higher than ∼0.5 L₀ s⁻¹.

Figure 3. Force decline during ramp shortening and the force–shortening velocity relation.

Pooled data from nine fibres in each of which tension responses were examined at 8–9°C during ramp shortening at a series of velocities. Shortening velocity (L₀ s⁻¹) is plotted on a negative abscissa. A, rate of force decline. The reciprocal time constant (1/τ₁) of the exponential curve fitted to the post-P₁ tension decline prior to the T-jump (see Fig. 2) is plotted as a rate on the ordinate. The rate is correlated with velocity (r > 0.9, n= 106) and increases approximately linearly with velocity. The line fitted with no constraint to pass through the origin (as shown), gives a slope (±s.e.m.) of 71.1 (±2.78)/L₀ and a significant intercept of 3.16 (±1.4) s⁻¹. With the intercept fixed at zero, the slope is 75.8 (±1.86)/L₀. B, the force–shortening velocity relation. The approximate steady force reached (after the P₂ transition) during ramp shortening at different velocities (V), obtained by direct measurement or, in some cases, from extrapolation of the pre-T-jump tension trace. Force is plotted as a ratio of isometric force, P₀, and the dotted curve is A. V. Hill's hyperbolic relation (Hill, 1938), fitted as P=a(V_max−V)/(V+b), where a and b are constants, a/P₀ is ∼0.1 and V_max is ∼1.5 L₀ s⁻¹. Despite scatter, the data distribution is basically similar to our previous findings (see Ranatunga et al. 2007). C, the extent of shortening. The extent of shortening from the beginning of the ramp to ∼95% tension decline towards the steady state (i.e. approximate completion of the P₂ transition) was calculated as velocity × 3τ₁ and is plotted as %L₀. Crosses are individual data points (n= 106) and filled symbols means (±s.e.m., n= 5–18) from pooled data. The required extent of shortening increases with velocity and reaches a steady level of ∼4%L₀ at velocities higher than 0.5 L₀ s⁻¹.

T-jump induced force generation during steady shortening

Figure 4 illustrates the velocity dependence of different features of the T-jump induced tension response. A single exponential could be fitted to the tension rise induced by a T-jump and Fig. 4A shows data for the rate of tension rise so determined. As seen from the fitted linear regression (dotted line), the rate of tension rise increases linearly with increase of shortening velocity so that, at velocities higher than ∼1 L₀ s⁻¹, i.e. approaching V_max, it is ∼10 times faster than the monophasic isometric rate (∼20 s⁻¹). As in previous studies, the T-jump tension response in isometric state – but not in steady shortening state (Ranatunga et al. (2007)– consists of two phases, a fast phase 2b and a slow phase 3, that could be isolated by fitting a double exponential to the tension trace. Phase 2b is considered to represent the force generating process and, for comparison, its rate (∼50 s⁻¹) is shown by the horizontal dashed line in Fig. 4A. Compared to phase 2b, the tension rise is slower at shortening velocities <0.25 L₀ s⁻¹, as indeed found in the previous study where only velocities up to ∼0.2 L₀ s⁻¹ were used. The present results show that, near V_max, the rate of T-jump induced tension rise is 4–5 times faster than isometric phase 2b.

Figure 4. Characteristics of T-jump induced tension rise during steady shortening.

Pooled data from nine fibres in each of which tension responses to a 3–4°C T-jump were examined over a range of shortening velocities at 8–9°C, as in Fig. 1. A single exponential curve was fitted to the post-T-jump tension rise to extract the rate of tension rise (1/τ₂ (time constant)) and the amplitude. The mean (±s.e.m., n= 5–18) data are plotted against shortening velocity as in Fig. 3. A, rate of tension rise. Filled symbols show the rate of T-jump induced tension rise, where the dashed line is the fitted linear regression to the pool of original data (excluding values for isometric; r > 0.7, n= 95). The rate increases approximately linearly with increase of shortening velocity, reaching >200 s⁻¹ at ∼V_max. Assuming monophasic tension rise, the isometric value is 22 (±2.5) s⁻¹ (filled symbol on the ordinate); phase 2b from biphasic analysis was ∼55 s⁻¹ (× on the ordinate and short-dashed horizontal line). For comparison, the open symbols show the data for the rate of tension decline during ramp shortening as in Fig. 3, but plotted as means (±s.e.m.). B, normalised amplitude of tension rise. The amplitude is plotted as a ratio of the post T-jump tension during steady shortening; the horizontal dashed line denotes the isometric value and the dotted curve through the points is fitted by eye. With increase of shortening velocity, the amplitude increases steeply at low velocities (as in our previous study) and then increases more slowly but remains above the isometric value at higher velocities. C, extent of shortening during tension rise. The extent of shortening was calculated using velocity (L₀ s⁻¹) and time constant (τ₂) from curve fit to tension rise, as (velocity × 3τ₂). It is an approximate estimate of ∼95% of the T-jump tension rise. The extent of shortening increases with velocity and remains at ∼1.6%L₀ (dotted line, fitted by eye) at velocities > −0.25 L₀ s⁻¹.

The amplitude of the T-jump tension response, normalised to the post-T-jump tension in the isometric state and during shortening, as normally done in kinetics relaxation studies, is shown in Fig. 4B. Compared to the tension increment by T-jump in the isometric state, the amplitude is increased at low velocities, as fully characterised in our previous study (Fig. 3B in Ranatunga et al. 2007). The present data show that the relative amplitude remains higher than isometric over the full range of velocities and is ∼4 times that of isometric near ∼V_max. Thus, the force in the steady shortening state becomes more temperature sensitive as the velocity is increased. As in Fig. 3C, an approximate estimate of shortening when the tension rise after a T-jump is nearly (∼95%) complete (i.e. after 3 ×τ₂) may be calculated as velocity × 3 τ₂, where τ₂ is the time constant from exponential curve fit to the T-jump tension rise. Figure 4C shows that the extent of shortening increases with velocity but remains at ∼1.6%L₀ (dotted line, fitted by eye) at velocities >0.25 L₀ s⁻¹ which is <0.5 times the extent of shortening for the P₂ transition (∼4%L₀, Fig. 3C). Taking the half-sarcomere length as 1.25 μm, these translate to ∼20 nm per half-sarcomere (1250 nm × 1.6%) for T-jump tension rise and ∼50 nm per half-sarcomere (1250 nm × 4%) for completion of the P₂ transition. Due to an end compliance of ∼11% (see Methods), the sarcomere length change would be 0.89 times the length change applied to the fibre end and hence the above values will be lower, ∼18 nm (0.89 × 20 nm) and ∼45 nm (0.89 × 50 nm), respectively. With no sarcomere length clamping, no allowance made for the sarcomere non-uniformity and filament compliance, these values represent upper estimates for the extent of half-sarcomere shortening, but the apparent difference between the two may be useful.

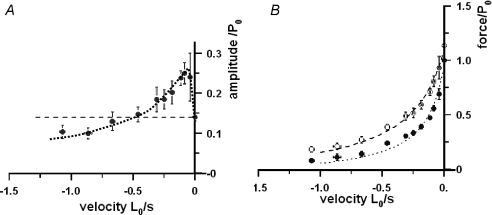
Our previous study showed that the absolute amplitude of the T-jump induced tension rise increased above that of isometric as the shortening velocity increased to ∼0.05 L₀ s⁻¹ and, within the low velocity range employed, it remained higher than that of isometric force (Fig. 5A in Ranatunga et al. 2007). In Fig. 5A, the amplitude data in Fig. 4B are re-plotted as a ratio of the isometric force of each fibre. It is seen that, when examined over a wider range of velocities, the velocity dependence of the amplitude is biphasic. The amplitude is higher than in the isometric state at the low velocities (a peak of ∼2-times the isometric value) as in our previous study, but it decreases to be below the isometric amplitude at higher velocities. Figure 5B shows pooled data for the post-T-jump tension (open symbols) and pre-T-jump tension (filled symbols) at various velocities representing the approximate steady state force-shortening velocity relations at ∼12°C and ∼9°C, respectively. The fitted force–velocity curves (see Fig. 5 legend) show that the extrapolated V_max is higher and the curvature lower at the post-T-jump temperature than at the pre-T-jump temperature.

Figure 5. Absolute amplitude of tension rise and the force-shortening velocity curves.

A, amplitude of T-jump tension rise. The data in Fig. 4B are re-plotted. To pool data from different fibres, the T-jump induced tension amplitude was normalised to isometric force (P₀ at the pre-T-jump temperature of ∼8–9°C) and the dotted curve through the data is fitted by eye. The data show that the absolute amplitude of tension rise for a standard T-jump is higher than isometric (horizontal dashed line) at low velocities (as reported in the previous study), but decreases below isometric at higher velocities (> ∼0.5 L₀ s⁻¹). Thus, the temperature sensitivity of force in steady shortening muscle suggests a biphasic force–shortening velocity relation. B, the force–shortening velocity curves. Pooled force data (means ±s.e.m.) at different velocities for post-T-jump (∼12°C – open circles) and pre-T-jump (8–9°C – filled circles) temperatures; force is normalised to the (pre-T-jump) isometric force (P₀). A force–velocity curve is fitted separately to each pool (n= 106, as in Fig. 3B). The curve for 8–9°C data (dotted curve) is the same as in Fig. 3B and the curve for ∼12°C data (dashed curve) gives a V_max of ∼2.5 and a/P₀ of ∼0.14.

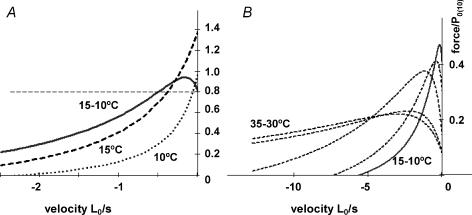
Figure 5B basically illustrates that, in muscle fibres shortening at different steady velocities, the tension increment produced by a standard T-jump can be used to generate the force–shortening velocity curves for a high (post-T-jump) temperature and a low (pre-T-jump) temperature. Figure 5A basically shows that the difference between the two sets of data or the two curves (or the velocity dependence of the T-jump induced tension increment) is biphasic. Moreover, the differences seen between the high and the low temperature curves (a lower curvature and a higher V_max at the higher temperature) from T-jump experiments are the same as obtained in previous steady state experiments on intact rat muscle fibre bundles, in which force–velocity curves were characterized for a range of different temperatures including the high physiological temperatures. It is therefore of interest to examine whether such steady state force–velocity data from intact rat muscle at different temperatures (Ranatunga, 1984) show a biphasic character in the temperature sensitivity of force during shortening. Figure 6A shows the force–velocity curves at 10 and 15°C (dotted and dashed curves), constructed using the mean data for fast muscle in that study (Ranatunga, 1984; see Fig. 6 legend), together with the 15–10°C difference between the two curves. The difference curve is biphasic, as found in the present study from T-jump experiments. Interestingly, the biphasic nature of temperature sensitivity of the force–shortening velocity curve is also seen in the difference curves for other temperatures (see Fig. 6B). Thus, the steady state data at different temperatures also illustrate the basic features of the T-jump experiments in Fig. 5.

Figure 6. Force–shortening velocity curves at different temperatures from steady state experiments.

A, the steady-state force versus shortening velocity curves for intact rat fast (extensor digitorum longus) muscle at 10°C (dotted curve) and 15°C (dashed curve). The curves were constructed using the mean V_max and a/P₀ data given in Table 1 of Ranatunga (1984) in which the isotonic release method was used to determine the force–shortening velocity relations. For comparison with Fig. 5A and B, force is normalised to P₀ at 10°C (on the basis of the temperature dependence of the tetanic force of rat fast muscle (Coupland & Ranatunga, 2003). The continuous curve is the tension difference between 15°C and 10°C; for clarity in presentation, 2 × tension difference is plotted, where the horizontal dashed line is the isometric force difference The data from steady state experiments show the basic features of the T-jump amplitude data in Fig. 5A and B, particularly, that the force increment for a standard 5°C increase of temperature is larger than in the isometric state at low velocities (<0.5 L₀ s⁻¹), but decreases below that of isometric at higher velocities. B, 5°C difference force versus shortening velocity curves for a range of temperatures from the same study. Note that the biphasic temperature sensitivity of force in shortening muscle is evident at all temperatures, although the curves are shifted to higher velocities at the higher temperatures (e.g. 30–35°C). Since force in lengthening muscle was insensitive to T-jump (Ranatunga et al. 2007), the difference–tension curves would remain near zero on the positive side of the abscissa.

Model simulations

Using a five-step crossbridge/AM-ATPase kinetic scheme (Scheme 1) that included a two-step P_i release, where step 1 (only) generates force and is temperature sensitive (endothermic) and a subsequent slow, two-step, MgADP release, we could qualitatively simulate the temperature-dependent features of isometric force (see Coupland et al. 2005). Increasing the ADP release rate (k₊₄) simulated some findings at low shortening velocities (Ranatunga et al. 2007). Here we assumed that the endothermic force generation step (k₊₁) is strain sensitive and increased with shortening velocity.

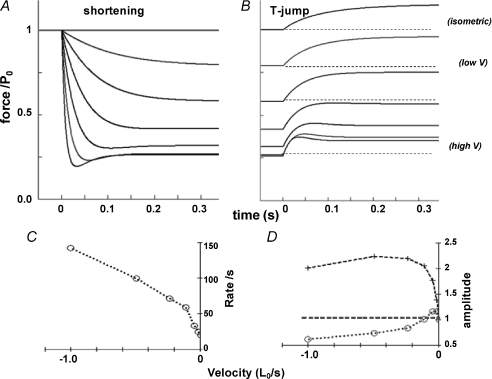
Figure 7A shows simulated tension responses to shortening (see Methods for detail). Force decreases to ∼20%P₀ as the velocity is increased. Figure 7B shows tension responses to a simulated T-jump after the pre-T-jump force reached a steady state, by simulated shortening. The T-jump-induced tension rise becomes faster with velocity (from top to bottom). Also, the amplitude of the T-jump tension rise is larger than that of the isometric state at the low velocities. Figure 7B shows the rate of tension rise and Fig. 7C shows the amplitude data, plotted against velocity (see Methods). A marked increase with velocity of the rate (Fig. 7B) and the biphasic dependence on velocity of the amplitude (circles in Fig. 7C) are clear. Figure 7C (crosses) shows that the amplitude normalised to post-T-jump (steady or peak) tension increases with velocity; the shortening muscle force is more temperature sensitive. Thus, although the extent of the velocity-dependent changes is less marked, a linear un-branched kinetic scheme models the main trends in our T-jump tension responses. Simulation of tension decline by ramp shortening would require mechano-kinetic modelling.

Figure 7. Simulations using a five-state kinetic model.

Simulations were carried out using the kinetic model in Scheme 1 where the sum of the fractional occupancy of attached states ii, iii and iv was taken as force (see Methods). A, after the isometric steady state was achieved, a shortening was induced at time zero by increasing k₊₄ and k₊₁. The force responses to six ramp shortening velocities (the velocity increasing from top to bottom) are shown. At the highest velocity, the sum of all attached states decreased to 0.58 of that in the isometric state. B, after the steady state is reached at a given velocity, and in the isometric state (top), a T-jump of ∼5°C is introduced at time zero, by increasing k₊₁ (Q₁₀ of ∼4). The traces show the approach to the new steady state of the simulated force and the dashed lines show the pre-T-jump force levels for some traces. Note that the rate of T-jump tension rise is faster at high velocity. The amplitude is largest at the low shortening velocities (second and third traces from top). C, the rate of T-jump tension rise (from direct measurement of the time constant from tension traces) is plotted against k₊₄, arbitrarily converted to a velocity for illustrating the data (see Methods). D, the absolute amplitude (open circles) shows a biphasic dependence on velocity; it is ∼15% larger than in the isometric state at low velocities but decreases to below the isometric level at the higher velocities. When normalised to the post-T-jump tension level (crosses), the amplitude increases with velocity to ∼2 times the T-jump tension amplitude in isometric state. The above are qualitatively similar to the experimental findings from T-jumps.

Discussion

The present study extends our previous findings to higher shortening velocities, approaching the maximal shortening velocity (V_max). The results show that the tension decline during ramp shortening and the T-jump force generation during steady shortening become faster with increasing shortening velocity. The amplitude of the T-jump tension rise when normalised to final tension at the post-T-jump temperature increased with shortening velocity whereas the absolute amplitude of tension rise shows a biphasic dependence on velocity.

T-jump force generation

Following a T-jump, the tension rises to a new steady level. In isometric muscle the tension rise is biphasic consisting of a fast (phase 2b) and a slow (phase 3) component, where phase 2b is P_i-sensitive. During steady shortening, however, the tension rise is monophasic (see Figs 1 and 2 here and Fig. 1 in Ranatunga et al. 2007). The underlying basis for the complexity in the isometric case is not exactly clear but it probably arises from the slow flux through the cycle, so that the reverse steps contribute more to a relaxation resultant from a rapid perturbation (e.g. T-jump).

T-jump tension response during steady shortening

The present study shows that, treating the tension rise as monophasic, the T-jump force generation becomes faster as the shortening velocity is increased. At high velocity, when the steady force is near zero, it is ∼10 times faster than in the isometric state (Fig. 5A) – as expected from our previous study (Ranatunga et al. 2007). In comparison with the isometric state, the processes that have changed to determine the steady state force during shortening are the following. (a) The crossbridge cycle would be operating faster than in the isometric case due to faster end-detachment of post-stroke crossbridges (Huxley, 1957). (b) The resultant filament sliding at a certain constant speed would drag all attached crossbridges – including those after attachment, or in the pre-stroke state, to a negative strain. Both (a) and (b) will lead to a lower, velocity-dependent, steady state force in shortening muscle. (c) On the basis of the Huxley–Simmons (1971) proposal for the mechanism of crossbridge force generation, the force generation would be faster during steady shortening due to the increased negative strain in the pre-stroke state. This effect (c) would lead to a speeding with velocity of the tension rise after a T-jump, if T-jump force generation is strain sensitive. This is what is seen in our experiments. That the amplitude of tension rise normalised to the post-T-jump (shortening) force is markedly increased with shortening velocity (Fig. 4B) is in keeping with this thesis. Thus, the overall implication is that the force in shortening muscle would be more temperature sensitive than isometric force. This was indeed found in a recent study in which the steady force at a selected number of ramp shortening velocities was examined at a range of temperatures. Analyses showed that the activation enthalpy (ΔH) was 100 kJ mol⁻¹ for isometric force and it was higher, 140 kJ mol⁻¹, during shortening at 0.5–0.9 L₀ s⁻¹ (see Fig. 7 in Roots & Ranatunga, 2008).

Our conclusion that the force generation induced by a T-jump is strain sensitive is at variance with that made by Bershitsky & Tsaturyan (2002) from some careful muscle fibre experiments. They found that, when preceded by step-length changes of different amplitude and sign, the time course of the T-jump tension response remained similar and, hence, concluded that the T-jump force generation is strain independent. The reason for the discrepancy between their findings and ours is not clear. It may be argued, however, that there is some uncertainty in their experiments whether crossbridges remained at a different strain when a T-jump was applied, since the changed crossbridge strain after a length-step would be transient and would largely disappear on quick tension recovery. During steady shortening or lengthening, as in our previous and present experiments, crossbridges would be exposed continually to a changed strain and hence any differences seen in the T-jump force response at different velocities are due to strain differences. Our findings lead to the unambiguous conclusion that the T-jump force generation is indeed strain sensitive, as also suggested in an earlier study by Bershitsky & Tsaturyan (1990).

The biphasic force–velocity relation

The absolute amplitude of the T-jump tension response increased above that for the isometric state at low velocities but decreased when the velocity was increased further (Fig. 5A). The picture that emerges is that the force–shortening velocity relation has a biphasic character. Interestingly, the biphasic character was evident from re-analysis of the previous steady state force–velocity data at a wide range of different temperatures including the high physiological temperatures (see Fig. 6). During steady shortening, the process (a) (fast end-detachment of post-stroke crossbridges) and process (b) (increased negative strain in them) will tend to decrease muscle force below isometric as the velocity is increased. On the other hand, process (c) (enhancement by negative strain of force generation in newly attached crossbridges) will tend to increase muscle force. The interplay of two such opposing tendencies as shortening velocity is increased can cause a biphasic velocity dependence of the amplitude of T-jump force generation. At some low velocity, the effect of process (c) may become more pronounced.

The biphasic nature of the force–velocity relation at constant temperature is well known from the original studies of Edman (1988) on frog muscle fibres. The deviation from a single hyperbola occurred at low velocity. Also, from detailed analysis of tension transients to load-clamps in frog muscle fibres, Piazzesi et al. (2007) postulated a molecular basis for the force–shortening velocity relation. Interestingly, the average force per crossbridge at low velocities is somewhat higher than in the isometric state and decreases below isometric at higher velocities (Fig. 4B in their paper), a biphasic character as in our T-jump experiments (Fig. 5A).

Kinetic modelling

The simulations using a simplistic kinetic model where the force generation step was both endothermic and sensitive to shortening velocity show the basic trends in our findings from T-jumps on shortening muscle. With increased velocity, the rate and the normalised amplitude of tension rise increase markedly and the absolute amplitude shows biphasic behaviour (Fig. 7). However, mechano-kinetic modelling with specific consideration given to the strain and temperature sensitivities of various steps in the crossbridge cycle would be required to validate the conclusions.

The extent of shortening during T-jump tension rise

Our results in Fig. 4C indicate that, during steady shortening over a range of higher velocities, the length change associated with a T-jump tension rise is ∼1.6%L₀ (or ∼18 nm per half-sarcomere). Although the observation is of interest, an exact interpretation remains difficult. Contributory factors include the following. (i) The stroke distance per se may be velocity dependent (Piazzesi et al. (2002a). (ii) Although in isometric muscle the number of attached crossbridges is thought to remain similar at different temperatures and after a T-jump (Bershitsky & Tsaturyan, 1992; Piazzesi et al. 2003; Colombini et al. 2008; Roots & Ranatunga, 2008), crossbridge recruitment may occur after a T-jump during shortening. (iii) Higuchi & Goldman (1991) determined the sliding distance between actin and myosin filaments per ATP molecule hydrolysed (i.e. per crossbridge cycle) during shortening and found that it increased from ∼20 nm at low velocity to ∼40 nm at high velocity. They argued that crossbridges during shortening would generate positive force and also bear negative drag force, so that the sliding distance was the sum of the working and drag distances. From fast stretching of muscle fibres, Bagni et al. (2005) also suggested that crossbridges may bear negative force during shortening. Occurrence of a drag distance or negative bias in crossbridge strain would also apply to our findings. Thus, although the T-jump induced tension rise during steady shortening is monophasic, involvement of processes/steps additional to the endothermic power-stroke perhaps cannot be excluded.

Tension decline during ramp shortening

The tension decline during a ramp shortening represents the transition from the isometric to the steady shortening state. It would be complex involving changes in the processes (a), (b) and (c), identified above. Of particular interest here is the tension decline after the P₁ transition; it is approximately exponential (Fig. 2) and its rate increases with shortening velocity (Fig. 3A). This tension decline would be dominantly due to loss of force by process (a), fast end-detachment of crossbridges that were originally present in isometric state as force bearing states, before attachment and force generation in new crossbridges takes over to establish a new shortening steady state (Roots et al. 2007). The scatter in our data in Fig. 3A, perhaps, does not exclude the possibility that the relationship between rate and velocity may be non-linear. The trend seen in our data, however, is reminiscent of the linear relationship shown between the rate constant of crossbridge detachment and filament sliding velocity in the load-clamp experiments of Piazzesi et al. (2007) on frog fibres (their Fig. 4D). An outcome of a linear relationship is that the extent of shortening (say to the completion of the P₂ transition) remains similar over a wide range of velocities, as seen from Fig. 3C. Examining the tension decline during ramp shortening at a range of temperatures (10–35°C), we previously found that its rate is rather temperature insensitive (Q₁₀ < 1.5) and also the Q₁₀ values decreased at the higher velocities. This implies that, at higher temperatures, the relation between the rate of tension decline and shortening velocity (as in Fig. 3A) would be shifted upwards slightly (low Q₁₀) but the shift would be less at higher velocities. In other words, the slope of the rate versus shortening velocity (Fig. 3A) will decrease and the intercept at zero velocity (isometric) would increase at higher temperatures. Such information as above should be useful for understanding in situ muscle performance at the high physiological temperatures.

Conclusion

Our previous T-jump studies on isometric muscle identified that the force generation is endothermic and occurs in an early molecular step in the actomyosin ATPase cycle (see Introduction), broadly consistent with the findings from a variety of other mechano-kinetic studies on muscle (Fortune et al. 1991; Kawai & Halvorson, 1991; Dantzig et al. 1992; He et al. 1999; Siththanandan et al. 2006; West et al. 2009) and mechano-kinetic modelling (Smith & Sleep, 2004; Roots et al. 2007). Our recent experiments (Ranatunga et al. 2007 and the present paper) demonstrate that the T-jump induced force generation is inhibited/depressed during lengthening but become enhanced and significantly fast during shortening, in a velocity-dependent manner. Thus, although the structural mechanism(s) remain unclear and there may be other temperature-sensitive steps in the muscle crossbridge cycle (see West et al. 2009), our findings from T-jump studies lead to the conclusion that the force generation process itself is both temperature sensitive (endothermic) and strain sensitive.

Glossary

Abbreviations

A

actin

L

fibre length

L₀

optimal fibre length

M

myosin

P

force or tension

P₀

steady isometric tension

P₁, P₂

tensions during ramp shortening at the initial inflection and at the tension decline to a steady level

phase 2b, phase 3

fast and slow components of tension rise after T-jump in isometric muscle

P_i

inorganic phosphate

T-jump

step increase of temperature

V, V_max

velocity and maximum velocity of shortening

Author contributions

K.W.R. was responsible for design, execution of experiments, analyses and writing; H.R. made essential contributions to experimental preparations, data analyses and discussion; G.W.O. played a crucial role in data interpretation, discussion and writing.