A Review of Standards and Statistics Used to Describe Blood Glucose Monitor Performance

Abstract

Glucose performance is reviewed in the context of total error, which includes error from all sources, not just analytical. Many standards require less than 100% of results to be within specific tolerance limits. Analytical error represents the difference between tested glucose and reference method glucose. Medical errors include analytical errors whose magnitude is great enough to likely result in patient harm. The 95% requirements of International Organization for Standardization 15197 and others make little sense, as up to 5% of results can be medically unacceptable. The current American Diabetes Association standard lacks a specification for user error. Error grids can meaningfully specify allowable glucose error. Infrequently, glucose meters do not provide a glucose result; such an occurrence can be devastating when associated with a life-threatening event. Nonreporting failures are ignored by standards. Estimates of analytical error can be classified into the four following categories: imprecision, random patient interferences, protocol-independent bias, and protocol-dependent bias. Methods to estimate total error are parametric, nonparametric, modeling, or direct. The Westgard method underestimates total error by failing to account for random patient interferences. Lawton's method is a more complete model. Bland–Altman, mountain plots, and error grids are direct methods and are easier to use as they do not require modeling. Three types of protocols can be used to estimate glucose errors: method comparison, special studies and risk management, and monitoring performance of meters in the field. Current standards for glucose meter performance are inadequate. The level of performance required in regulatory standards should be based on clinical needs but can only deal with currently achievable performance. Clinical standards state what is needed, whether it can be achieved or not. Rational regulatory decisions about glucose monitors should be based on robust statistical analyses of performance.

Introduction

Glucose testing plays an important role in the diagnosis and treatment of patients with diabetes. Sadly, all laboratory tests, including glucose measurements, contain some error. This article largely describes the magnitudes and types of error that represent the analytical properties of the test. These analytical properties are important to manufacturers and to clinical laboratories. The clinical properties of a test, diagnostic sensitivity and specificity, also known as diagnostic efficacy, will be impaired with large enough test errors, regardless of the error source. To the clinician, the only important error measure is the total error of the assay—the combination of all possible errors.¹ In this review, patients who perform and interpret self-monitoring of blood glucose (SMBG) testing act as clinicians. This review focuses on SMBG and SMBG devices that are run in the point of care (POC) environment.

Total error is the difference between the observed value and true glucose value. This difference can be caused not just by analytical error, but also by pre- and postanalytical errors. Preanalytic errors are those errors that occur before the analytical measurement and include insufficient cleaning of the finger before capillary collection, collection of a nonrepresentative capillary blood specimen from a hypotensive patient, dilution of the capillary blood due to excess manipulation of the punctured digit, and so on. Postanalytical errors are those that occur after testing. In a clinical laboratory, they are usually represented by reporting delays or delivery of incorrect or garbled information to the clinician. Whereas postanalytical errors might seem unlikely for SMBG, they have been occurring too often, with SMBG systems displaying glucose results in millimoles per liter rather than milligrams per deciliter and vice versa (see the following recalls: http://www.accessdata.fda.gov/scripts/cdrh/CFdocs/cfRES/res.cfm?ID=52985, http://www.accessdata.fda.gov/scripts/cdrh/CFdocs/cfRES/res.cfm?ID=41682 and http://www.accessdata.fda.gov/scripts/cdrh/CFdocs/cfRES/res.cfm?ID=38282) and for one meter system displaying a misleading error message in which results over 500 mg/dl were called ER1 instead of HI (see http://www.devicelink.com/mddi/archive/01/03/008.html).

To frame the discussion about glucose performance standards and accuracy, it is helpful to classify medical errors into either discrete or continuous variables.² An error such as wrong site surgery can be thought of as a discrete error—it either occurs or does not. A glucose assay always has error, which can be measured on a continuous scale. Because small errors are unimportant clinically (e.g., reporting 91 mg/dl when truth is 90 mg/dl), performance standards attempt to set limits to distinguish between unimportant and important errors.

There are two ways that diagnostic assays can harm patients: (1) assays that have too much error and (2) time critical assays that fail to provide a result. Most standards neglect the latter cause.

Performance standards are used commonly either as part of a regulatory process or for clinical acceptability. Within the regulatory process, there are two groups: regulatory providers and regulatory consumers. Providers are regulatory agencies who create and use performance standards as part of the approval process for new systems. Regulatory consumers are manufacturers who must meet standards to sell products and clinical laboratories that may use adaptations of these standards to evaluate newly manufactured reagents periodically before using them for regular analysis.

The level of performance required in regulatory standards should be based on clinical needs but can only deal with a currently achievable performance. Clinical standards state what is needed, whether it can be achieved or not. An example of a standard based on clinical needs and not achievable was the 1987 American Diabetes Association (ADA) glucose standard.³ Many standards for discrete events (e.g., wrong site surgery) are set for zero error rates, although they are not achieved when measured across all hospitals.

Published Glucose Standards

Standards can be characterized according to Table 1.

Table 1.

Published Glucose Standards

	Percent of data specified
	<100%	100%
One set of limits	ISO 15197 CLSI C30A FDA (SMBG) CLIA 88 ADA 1996	ADA 1997
Multiple limits	—	Error grid

Standards That Specify Less than 100% of Data

International Organization for Standardization (ISO) 15197⁴ and Clinical and Laboratory Standards Institute (CLSI) C30A⁵ have been written for SMBG and POC systems, respectively. C30A cites the ISO standard for acceptance criteria.

International Organization for Standardization 15197 states that for minimum acceptable accuracy,

“Ninety-five percent (95%) of the individual glucose results shall fall within ± 0.83 mmol/liter (15 mg/dl) of the results of the manufacturer's measurement procedure at glucose concentrations ≤4.2 mmol/liter (75 mg/dl) and within ±20% at glucose concentrations >4.2 mmol/liter (75 mg/dl).” (The 95% limits are not confidence limits. They are percentiles. This means that the requirement is for the 95th percentile of the distribution of the differences to be less than the limit stated.)

Note 1 of ISO 15197⁴ adds that this requirement is “based on the medical requirements for glucose monitoring.”

One must first understand what is meant by accuracy. ISO 15197 uses metrology terminology⁶ with accuracy meaning “closeness of agreement between a test result and the accepted reference value.” Per ISO 15197, accuracy “involves a combination of random error components and a common systematic error or bias component.” Hence, these are total error limits.

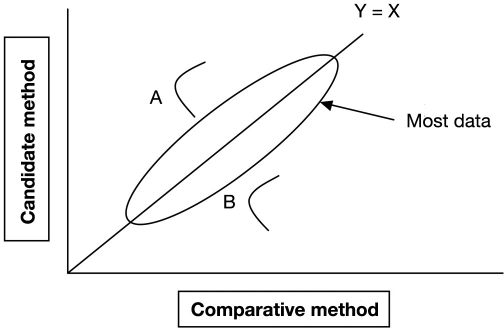
The problem with this standard is simple: up to 5% of the results can be medically unacceptable. Consider what this means for SMBG. If a subject tests his (her) blood glucose four times daily, then on average there could be a medically unacceptable result every 5 days (once per 20 measurements). Another problem can be seen in Figure 1, which compares the Taguchi loss function to an attempt to dichotomize a continuous variable.⁷ Here, the ISO limits imply the dashed lines, whereby all values inside total error limits are considered acceptable and all values outside of limits are unacceptable. The problem with this specification can be deduced by comparing values “A” and “B,” which are just outside and just inside of the limit, respectively. These two values have about the same amount of error and should have about the same potential to either cause or not cause patient harm. A more realistic model is seen by the curved line in Figure 1 where the potential for patient harm increases with increasing error.

Figure 1.

The problem with dichotomous limits. Points A and B have about the same amount of error. Their potential for patient harm is better expressed on the solid rather than dashed line. This is a conceptual representation of error, as real error is unlikely to be symmetric or so smooth.

It is unrealistic to specify a single set of limits. A wide set of limits would prevent very large errors, but nevertheless would allow smaller magnitude but still too large errors. A much narrower set of limits, such as the ISO 95% standard, allows too many (up to 5%) large errors.

Another problem can be inferred from details in the ISO protocol, which suggest that the ISO total error specification is for the analytical subset of total error. ISO 15197 has a separate section called “User performance evaluation.” Here, a separate evaluation is to be carried out comparing results between a user and a trained health care professional, but the only analysis requirements are that “Results shall be documented in a report.” However, SMBG users experience pre- and postanalytical error in addition to analytical error alone.^8,9 With user errors unspecified (and not quantified), the ISO specification fails to inform clinicians of the true performance of SMBG.

Finally, there is the problem of glucose monitors that fail periodically to provide a result. Whereas this can merely be an inconvenience, it can occur during a situation when the glucose level is needed emergently. The ISO standard does not deal with this.

One can ask, who wrote the ISO 15197 standard? One will not find a list of authors or committee members in this or any ISO standard. Through our presentations and correspondence with the ISO 15197 working group, we determined that the principal author of ISO 15197 was a regulatory affairs person from industry.

The SMBG U.S. Food and Drug Administration (FDA) draft guidance (see http://www.fda.gov/downloads/Medical Devices/Device Regulation and Guidance/GuidanceDocuments/ucm071439.pdf) cites the ISO 15197 standard for total error and user performance, but also suggests that linearity and interferences be assessed with CLSI standards.

The Clinical Laboratory Improvement Amendments of 1988 (CLIA 88) goal applies to all in vitro glucose testing performed in the United States with the exception of SMBG testing. CLIA 88 requires external proficiency testing results to be within 10% of target values or <0.3 mmol/liter (6 mg/dl), whichever is larger. CLIA values have to be met 80% of the time (see http://www.cdc.gov/clia/regs/subpart_i.aspx#493.931). This standard applies to U.S. federally mandated proficiency surveys.

Standards That Specify 100% of Data

In 1987, the ADA recommended a goal for total error (user plus analytical) of <10% at glucose concentrations of 1.7–22.2 mmol/liter (30–400 mg/dl) 100% of the time.³ In addition, the ADA proposed that glucose measurements should not differ by more than 15% from those obtained by a laboratory reference method. The recommendation was modified in 1996, for the maximum analytical error to be <5%.¹⁰ This is confusing because by specifying a quantitative goal only for analytical error, in that case, user error and hence total error are unspecified. By using one set of limits, the ADA requirement has the problem shown in Figure 1. The much tighter ADA error limits can probably be partially attributed to the constituency of the advisory panels, being primarily clinicians and laboratorians.

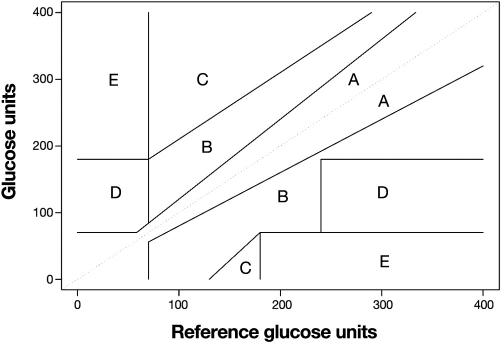
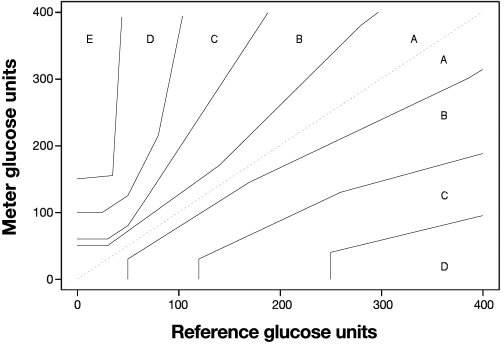
Clarke and colleagues¹¹ (Figure 2) and later Parkes and associates¹² (Figure 3) presented error grids as a way of specifying glucose performance needed for clinical purposes. The error grid is well known for glucose but not for other assays. Although the error grid has not been adopted by either ADA or ISO 15197, it is often cited in studies and thus can be considered a standard. The FDA requires an error grid for any assay seeking waiver approval (see http://www.fda.gov/MedicalDevices/DeviceRegulationandGuidance/GuidanceDocuments/ucm079632.htm).

Figure 2.

The Clarke error grid for glucose.

Figure 3.

The Parkes consensus error grid for glucose.

The value of an error grid is that it informs the clinician about the severity of errors. A problem with the Clarke grid (Figure 2) is that the “A” zone (acceptable result) is contiguous to a “D” zone (dangerous result). This means that the illogical situation in Figure 1 could occur whereby two results with almost the same amount of error could have very different clinical outcomes. The Parkes grid (Figure 3) avoids this by having an intervening “B” zone between the “A” and any higher zone. Whereas “B” zone results are still acceptable, their presence provides a warning.

Although error grids are appealing because they provide multiple limits based on the potential for wrong treatment decisions, care must be used in interpreting error grid studies. Most SMBG evaluations are conducted over relatively short periods; as such, infrequent events may not occur and yield significant grid outliers. Also, consider a case where one result had a large error but fell in the “B” zone and no results were in higher letter zones. It is possible that this large error was observed at a “benign” concentration by chance and that a future error of this percentage magnitude could place the result in a more dangerous zone. For example, for the Clarke grid, a 25% error can be both: Y = 500 mg/dl, X = 400 mg/dl zone = “B”; Y = 69 mg/dl, X = 86 mg/dl zone = “D.” For the Parkes grid, an 80% error can be both: Y = 450 mg/dl, X = 250 mg/dl zone = “B”; Y = 50 mg/dl, X = 90 mg/dl zone = “C.” Therefore, errors of a given percentage magnitude tend to be tolerated less in the lower physiologic range of glycemia and better tolerated in the high range.

Error Grid Details

Clarke and Parkes grids are used to assess the accuracy of glucose monitoring. Other error grids can be designed for use in diabetes screening, or diagnosis. In setting the zones, one must distinguish between medical need, which may be difficult to reach by consensus, and currently achievable performance. Misclassifications can have either a low or a high potential to cause incorrect treatment decisions. When the true glucose value is at a medical decision point, the misclassification rate will be 50%. For example, if the true glucose value is 126 mg/dl, imprecision will cause half of the observed values to be lower and half higher than this medical decision point.

A common specification for the percentages allowed for each zone is:

• 95% for the innermost error zone (the “A” zone), also called allowable total error (ATE) in FDA guidance

• 0% for the outermost error zone (the “C” or higher letter zones), also called limits for erroneous results (LER) in FDA guidance

• 5% for the “B” zone, which is the error zone greater than the “A” zone but less than the “C” zone.

Although it can be demonstrated statistically that 95% of results are in the ATE zone, it can never be proven that 0% of results are in the LER zone. For example, if one assays 10,000 specimens and observes 0 results in the LER zone, the 95% confidence limit for the number of possible results in the LER zone is 0.0369% or 369 results per million tries.¹³ In a simple method comparison or even in a multicenter comparison, an excessive (impractical) sample size would be needed to determine performance, where performance means not just values in zone A in an error grid but confidence in the number of observations (if any) in higher zones. Thus, in addition to method comparison, which provides information about data in zone A, risk management is required, including failure mode effects analysis (FMEA) and fault trees. As a result, the word protocol is used in a generic sense, e.g., FMEA is a protocol.

Analytical Error Sources

Analytical error sources that comprise total analytical error can be divided into four categories¹⁴: imprecision, random patient interferences, protocol-independent bias, and protocol-dependent bias.

Imprecision is the dispersion among replicates and is measured as short-term (within-run) imprecision and long-term (total) imprecision. ISO calls short-term imprecision repeatability and long-term imprecision reproducibility. Imprecision is estimated by repeatedly analyzing aliquots of a blood specimen (real or artificial) and either calculating the standard deviation or using analysis of variance to determine the components of imprecision.

Random patient interferences are nonspecific reactions that add bias to results. There can be more than one interfering substance in a patient specimen, with the final bias equal to the combination of these nonspecific effects. Random patient interferences are estimated by either directly testing candidate interfering substances sequentially or indirectly with regression analysis to assess a global random patient interference effect.

Bias is the average difference between two assays, usually a candidate and comparative assay. A protocol-independent bias means that bias exists regardless of the order in which samples are run. Protocol-independent bias is usually estimated with regression for paired samples assayed by a candidate and comparative assay. For example, some prostate-specific antigen assays have demonstrated biases up to 20% as a result of standardization differences.¹⁵ In a College of American Pathologists survey,¹⁶ suspected calibrator inaccuracy explained a 9.6% difference between glucose methods.

Protocol-dependent bias refers to bias that depends on the way the sample was assayed. For example, the amount of between-lot bias depends on the bias in each lot and the specific lot in use. Another example is a loss of high-end linearity toward the end of the shelf life of a reagent. The amount of bias depends on reagent degradation and the number of days remaining in the shelf life. Protocol-dependent bias can be estimated using multifactor protocols¹⁷ or by special studies that isolate each effect. For example, drift can be estimated by measuring the same sample repeatedly over the desired length of time and then regressing results vs time.

This taxonomy for analytical error helps one think about error sources. These sources may not be mutually independent. For example, imprecision is not always the same as random error. Thus, if an assay has linear drift, the apparent imprecision from calculating the standard deviation will be a combination of random error and bias due to drift.¹⁴ On a similar note, the bias estimated from regression is the combined average bias from random patient interferences, protocol-independent bias, and protocol-dependent bias.

Methods Used to Estimate Total Error

Methods for estimating total error can be classified as shown in Table 2. In modeling methods, total error components are estimated and combined in a model. Parametric analyses require that data follow known distributions (usually a normal distribution). Compared to nonparametric methods (no assumptions are made about the distribution of data), the confidence intervals for parametric methods are smaller for the same sample size. However, if the assumption about the distribution is incorrect, the confidence interval will be incorrect. Modeling is appealing because it often simplifies the estimation of performance. For example, it is relatively easy to estimate glucose average bias and imprecision. Using these estimates, one can construct total error requirements and simulate combinations of average bias and imprecision that satisfy requirements. However, if the model is incorrect, such simulations can be misleading.

Table 2.

Methods Used to Estimate Total Error

Method	Parametric	Nonparametric
Modeling	Westgard Lawton	—
Direct	Bland–Altman	Mountain plot Error grid

Westgard

Westgard and colleagues proposed a model¹⁸ widely used and shown in Equation (1).

$$\%\text{TE}=\text{\%Bias}+1.96\left({\text{CV}}_{\text{T}}\right),$$ (1)

where %TE is percent total error, %Bias is percent average bias, and CV_T is total coefficient of variation due to imprecision.

This model is incomplete and underestimates total error because it fails to account for nonspecificity in patient samples. Figure 4 illustrates the problem. Sample A has a positive bias and sample B has a negative bias, both caused by interferences. The average bias is zero but these individual patients will have large glucose errors. Krouwer¹⁷ and Miller and associates¹⁹ showed that the Westgard model underestimates total error for total and low-density lipoprotein (LDL)–cholesterol. The LDL–cholesterol example was particularly revealing because the National Cholesterol Education Program²⁰ uses a similar standard to the ISO 15197 glucose standard (95% of values must have <12% error) with limits based on the Westgard model. Miller and colleagues¹⁹ showed that three of four commercial LDL–cholesterol assays achieved the National Cholesterol Education Program guidelines when data were analyzed according to the Westgard model, but all four assays failed these limits when data were analyzed by Lawton's method, which is discussed in the next section.

Figure 4.

Replicating sample A gives a distribution of values due to assay imprecision, all with positive bias. Sample B results all have negative bias. Regression estimates no average bias.

Boyd and Bruns²¹ used the Westgard model to propose glucose requirements for average bias and imprecision. Krouwer²² pointed out that their model was inadequate, which was acknowledged by Boyd and Bruns.²³ The Westgard model has been used by an expert committee²⁴ with a 1.65 (one-sided) multiplier in Equation (1). The Westgard model continues to be popular as it is intuitively appealing, simple, and used by influential researchers and consultants.

Lawton

The model of Lawton and colleagues²⁵ is more complete in that it accounts for nonspecificity [Equation (2)]:

$$\%\text{TE}=\text{\%Bias}+1.96\left({\text{CV}}_{\text{T}}\right)+1.96\left({\text{CV}}_{\text{RI}}\right),$$ (2)

where CV_RI is the total coefficient of variation due to random interferences.

The calculations are more complicated because the CV_RI term is estimated indirectly. Although the term CV_RI is attributed to interferences in patient samples, it will reflect any error that occurs for one sample. For example, a defective reagent strip can result in a large error for a patient sample that does not have interferences.

Bland–Altman

Bland and Altman used a more direct approach²⁶ and graphed the differences between a candidate and a comparative method, where a candidate method is the method under test and the comparative method is the existing method. “Comparative” is preferred over “reference” because “reference” also means a specific procedure (such as isotope dilution mass spectrometry). The Bland–Altman plot is useful by itself. To estimate the limits containing 95% of data, normally distributed differences are needed.

In this method and all direct methods, the imprecision of the comparative method contributes to the difference. This effect can be minimized by repeating the comparative method and using its average. The reduction in imprecision equals one over the square root of the number of replicates.

Mountain Plots

A mountain plot^27,28 is a nonparametric method that simply orders differences between a candidate and comparative method to arrive at the 2.5th and 97.5th percentiles (limits that contain 95% of data). Separate mountain plots are sometimes used for low concentrations (using absolute differences) and higher concentrations (using percentage differences). The mountain plot can handle large amounts of data and demonstrate large errors. It is less useful for small data sets (<40 points).

Error Grids

Error grids, discussed previously, are a simple way of estimating total error—one just tallies the number of observations into each zone. Confidence limits can be calculated for each percentage. An important feature of an error grid (and also a mountain plot) is that one can estimate the location of 100% of data.

The CLSI guideline EP21A²⁹ uses Bland–Altman and mountain plots, and the CLSI guideline EP27P³⁰ uses error grids.

Methods That Estimate Total Error Components

Clinical and Laboratory Standards Institute protocols have been developed to estimate various analytical performance parameters relevant to glucose and include imprecision EP5A2,³¹ linearity EP6A,³² interferences EP7A2,³³ average bias EP9A2,³⁴ and reagent stability EP25P.³⁵

Correlation Coefficient

The correlation coefficient is a measure of the linear association between the candidate and the comparative method.³⁶ The problem with this measure is that a high degree of linear association is expected, but it is not easy to describe differences in correlation coefficients in meaningful terms. For example, if method A has a correlation coefficient of 0.932 and method B has a correlation coefficient of 0.865, it is hard to know what this means. Compare this with a statement such as method A has an average bias of 11% and method B has 2%.

Locally Smoothed Median Absolute Differences (LS MAD)

The goals of LS MAD curves are to demonstrate continuous regions of the entire glucose range where performance, by any standard, is unacceptable. These curves have been used to relate poor performance and high risk to tight glucose control intervals.³⁷

Total Error Evaluation Protocol

The purpose of estimating total error is to predict glucose performance in routine use, whether for SMBG or POC. The “total” in total error can be thought of as referring to the protocol, i.e., the set of conditions under which the evaluation is carried out determines which error sources can be observed. This creates complications as the following types of performance must be assessed: (1) throughout the range of the assay, especially in the hypoglycemic and hyperglycemic ranges; (2) under representative assay conditions, which can include rare combinations; and (3) obtained by actual users.

Generally, three types of protocols are employed: (1) assaying consecutive samples by a candidate and comparative method with actual users, (2) conducting special studies as part of risk management, and (3) monitoring performance of existing meters.

The goal in any assay evaluation is to estimate (all) error that will be observed by clinicians in routine use. Because of the usual brevity of protocol 1 (method comparison), rare conditions are unlikely to be sampled. By assessing performance with actual users, preanalytical errors such as accessing capillary blood from poorly cleaned finger will be sampled. If glucose is present on the site, this glucose will contaminate the blood sample. The reported result is the combination of all errors regardless of their source. A simple analysis of the first protocol is to graph the results in an error grid and calculate the percentage of results in each zone. The rate that no result is obtained should also be determined. As stated previously, enormous sample sizes would be required to prove that the number of large-sized errors is below a specified low limit. However, method comparison studies provide useful information about the location of most differences. Comparing one meter to another yields differences not errors, as error can only be estimated by comparing a meter to a glucose reference procedure.

In addition to estimating all analytical properties, performance must be assessed with combinations of factors such as abnormal glucose concentrations, different reagents lots, temperature variation, extremes of hematocrit, and so on. It is possible to expedite this type of testing through the use of factorial designs (protocol 2).³⁸ A factorial design is used to evaluate two or more factors simultaneously. The advantages of factorial designs over one-factor-at-a-time experiments are that they are more efficient and they allow interactions between factors to be detected.

Risk management (also protocol 2) means enumerating all possible failure modes during the measurement process that could lead to errors or failure to obtain a result and assessing their risk.³⁹ Protocol 2 is performed by manufacturers, although risk management can also be performed by clinical laboratories.

Protocols 1 and 2 are performed before meters are released. Recall data show that errors still occur for meters that have been released to customers (see http://www.accessdata.fda.gov/scripts/cdrh/CFdocs/cfRES/res.cfm). Protocol 3 is a suitable monitoring method used to assess performance after release.

Conclusions

An adequate glucose specification for either POC or SMBG needs to state quantitative limits for total error for 100% of data. Neither the ADA nor the ISO specifications do this. Ideally, a glucose specification should also include a protocol, which prevents exclusion of typically encountered conditions that could cause errors. Manufacturers can test combinations of potential error causes through factorial studies and also by using risk management. The opportunity exists to leverage data from SMBG and POC monitors in general use. A good understanding of the statistics used to describe the performance of SMBG monitors is necessary for the development of sound performances standards.

Abbreviations

ADA

American Diabetes Association

ATE

allowable total error

CLIA 88

Clinical Laboratory Improvement Amendments of 1988

CLSI

Clinical and Laboratory Standards Institute

CV

coefficient of variation

FDA

Food and Drug Administration

FMEA

failure mode effects analysis

ISO

International Organization for Standardization

LDL

low-density lipoprotein

LER

limits for erroneous results

LS MAD

locally smoothed median absolute differences

POC

point of care

SMBG

self-monitoring of blood glucose

TE

total error