Ontology Matching with Semantic Verification

Abstract

ASMOV (Automated Semantic Matching of Ontologies with Verification) is a novel algorithm that uses lexical and structural characteristics of two ontologies to iteratively calculate a similarity measure between them, derives an alignment, and then verifies it to ensure that it does not contain semantic inconsistencies. In this paper, we describe the ASMOV algorithm, and then present experimental results that measure its accuracy using the OAEI 2008 tests, and that evaluate its use with two different thesauri: WordNet, and the Unified Medical Language System (UMLS). These results show the increased accuracy obtained by combining lexical, structural and extensional matchers with semantic verification, and demonstrate the advantage of using a domain-specific thesaurus for the alignment of specialized ontologies.

1. Introduction

An ontology is a means of representing semantic knowledge [20], and includes at least a controlled vocabulary of terms, and some specification of their meaning [43]. Ontology matching consists in deriving an alignment consisting of correspondences between two ontologies [8]. Such an alignment can then be used for various tasks, including semantic web browsing, or merging of ontologies from multiple domains.

Our main motivation lies in the use of ontology matching for the integration of information, especially in the field of bioinformatics. Nowadays there is a large, ever-growing, and increasingly complex body of biological, medical, and genetic data publicly available through the World Wide Web. This wealth of information is quite varied in nature and objective, and provides immense opportunities to genetics researchers, while posing significant challenges in terms of housing, accessing, and analyzing these data sets [10]. The ability to seamlessly access and share large amounts of heterogeneous data is crucial towards the advancement of genetics research, and requires resolving the semantic complexity of the source data and the knowledge necessary to link this data in meaningful ways [27]. Semantic representation of the information stored in multiple data sources is essential for defining correspondence among entities belonging to different sources, resolving conflicts among sources, and ultimately automating the integration process [36]. Ontologies hold the promise of providing a unified semantic view of the data, and can be used to model heterogeneous sources within a common framework [25]. The ability to create correspondences between these different models of data sources is then critical towards the integration of the information contained in them.

In the biomedical and bioinformatics knowledge domain, efforts at deriving ontology alignments have been aided by the active development and use of vocabularies and ontologies. The Unified Medical Language System (UMLS) is a massive undertaking by the National Library of Medicine to create a single repository of medical and biological terminology [4]. Release 2007AB of the UMLS contains over 1.4 million biomedical concepts and 5.3 million concept names from more than 120 controlled vocabularies and classifications, including the NCI Thesaurus developed by the National Cancer Institute as a comprehensive reference terminology for cancer-related applications [18].

In this paper, we describe the Automated Semantic Matching of Ontologies with Verification (ASMOV) algorithm for ontology matching. Most current approaches handle only tree-like structures, and use mainly elemental or structural features of ontologies [14]. ASMOV is designed to combine a comprehensive set of element-level and structure-level measures of similarity with a technique that uses formal semantics to verify whether computed correspondences comply with desired characteristics. We begin with a discussion of the current state of the art in ontology matching. Following, we present a brief definition of the problem and a general description of the algorithm. Next, we provide details of the similarity measure calculations, of the semantic verification executed after an alignment is obtained, and of the conditions for algorithm termination. Then, we provide the results of two sets of experiments; the first set shows the accuracy of the algorithm against the OAEI 2008 benchmark tests, and the second set analyzes the results of running the algorithm against two sets of anatomy ontologies, using both the general-purpose WordNet thesaurus (wordnet.princeton.edu) and the UMLS Metathesaurus (www.nlm.nih.gov/research/umls/). Finally, the limitations of the system and the direction of future work are discussed, and our conclusions are stated.

2. Background and Related Work

Ontology matching is an active field of current research, with a vigorous community proposing numerous solutions. Euzenat and Shvaiko [14] present a comprehensive review of current approaches, classifying them along three main dimensions: granularity, input interpretation, and kind of input. The granularity dimension distinguishes between element-level and structure-level techniques. The input interpretation dimension is divided into syntactic, which uses solely the structure of the ontologies; external, which exploits auxiliary resources outside of the ontologies; and semantic, which uses some form of formal semantics to justify results. The kind of input dimension categorizes techniques as terminological, which works on textual strings; structural, which deals with the structure of the ontologies; extensional, which analyzes the data instances; and semantic, which makes use of the underlying semantic interpretation of ontologies.

Most work on ontology matching has focused on syntactic or structural approaches. Early work on ontology alignment and mapping focused mainly on the string distances between entity labels and the overall taxonomic structure of the ontologies. However, it became increasingly clear that any two ontologies constructed for the same domain by different experts could be vastly dissimilar in terms of taxonomy and lexical features. Recognizing this, systems such as FCA-Merge [39] and T-Tree [12] analyze subclass and superclass relationships for each entity as well as the lexical correspondences, and additionally require that the ontologies have instances to improve comparison. PROMPT consists of an interactive ontology merging tool [35] and a graph based mapping dubbed Anchor-PROMPT [34]. It uses linguistic “anchors” as a starting point and analyzes these anchors in terms of the structure of the ontologies. GLUE [11] discovers mappings through multiple learners that analyze the taxonomy and the information within concept instances of ontologies. COMA [29] uses parallel composition of multiple element- and structure-level matchers. Corpus-based matching [28] uses domain-specific knowledge in the form of an external corpus of mappings which evolves over time. RiMOM [41] discovers similarities within entity descriptions, analyzes instances, entity names, entity descriptions, taxonomy structure, and constraints prior to using Bayesian decision theory in order to generate an alignment between ontologies, and additionally accepts user input to improve the mappings. Falcon-AO [19] uses a linguistic matcher combined with a technique that represents the structure of the ontologies to be matched as a bipartite graph. IF-Map [22] matches two ontologies by first examining their instances to see if they can be assigned to concepts in a reference ontology, and then using formal concept analysis to derive an alignment. Similarity flooding [32] uses a technique of propagation of similarities along the property relationships between classes. OLA [15] uses weighted averages between matchers along multiple ontology features, and introduces a mechanism for computation of entity-set similarities based on numerical analysis; the approach used in ASMOV for the calculation of similarities at a lexical, structural and extensional level is similar to OLA, but affording more flexibility to the design of similarity measure calculations for different features.

In the particular realm of ontology matching in the biological domain, the AOAS system developed by the U.S. National Library of Medicine [5][44], designed specifically to investigate the alignment of anatomical ontologies, uses the concept of “anchors” and implements a structural validation that seeks to find correspondences in relationships between anchors. Sambo [24] uses a similar approach to lexical and structural matching, and complements it with a learning matcher based on a corpus of knowledge compiled from published literature. Notably, both AOAS and SAMBO take advantage of the part-of relation between entities, widely used in biomedical ontologies but not defined in general languages such as OWL; such a relation would be modeled as a property in a general ontology.

Semantic techniques for ontology matching have received recent attention in the literature. Semantic reasoning is by definition deductive, while the process of ontology matching is in essence an inductive task [14]. Semantic techniques therefore need a preprocessing phase to provide an initial seeding alignment, which is then amplified using semantic methods. This initial seeding can be given by finding correspondences with an intermediate formal ontology used as an external source of common knowledge [1]. Deductive techniques for semantic ontology matching include those used in S-Match [17], which uses a number of element-level matchers to express ontologies as logical formulas and then uses a propositional satisfiability solver to check for validity of these formulas; and CtxMatch [6], which merge the ontologies to be aligned and then uses description logic techniques to test each pair of classes and properties for subsumption, deriving inferred alignments.

Semantic techniques have also been used to verify, rather than derive, correspondences. The approach by Meilicke et.al. [30] uses model-theoretic semantics to identify inconsistencies and automatically remove correspondences from a proposed alignment. This model, however, only identifies those correspondences that are provably inconsistent according to a description logics formulation. The same authors have extended this work to define mapping stability as a criterion for alignment extraction [31]; the approach in ASMOV introduces additional rules that seek to find positive verification that consequences implied by an alignment are explicitly stated in the ontologies.

3. Ontology Matching Algorithm

3.1 Ontology Matching

In this section, we present a succinct definition of the concepts of correspondences between entities and ontology matching; the reader is referred to [14] for a more formal definition. An ontology O contains a set of entities related by a number of relations. Ontology entities can be divided in subsets as follows: classes, C, defines the concepts within the ontology; individuals, I, denotes the object instances of these classes; literals, L, represents concrete data values; datatypes, T, defines the types that these values can have; and properties, P, comprises the definitions of possible associations between individuals, called object properties, or between one individual and a literal, called datatype properties. Four specific relations form part of an ontology: specialization or subsumption, ≤; exclusion or disjointness, ⊥; instantiation or membership, ∈; and assignment, =.

The Web Ontology Language (OWL), a World Wide Web Recommendation, is fast becoming the standard formalism for representing ontologies. In particular, the OWL-DL sublanguage of OWL supports those users who want the maximum expressiveness without losing computational completeness and decidability [38], by restricting type separation so that the sets C, P, L, I, and T in the ontology are disjoint. The ASMOV alignment algorithm presented in this paper assumes that the ontologies to be aligned are expressed in OWL-DL.

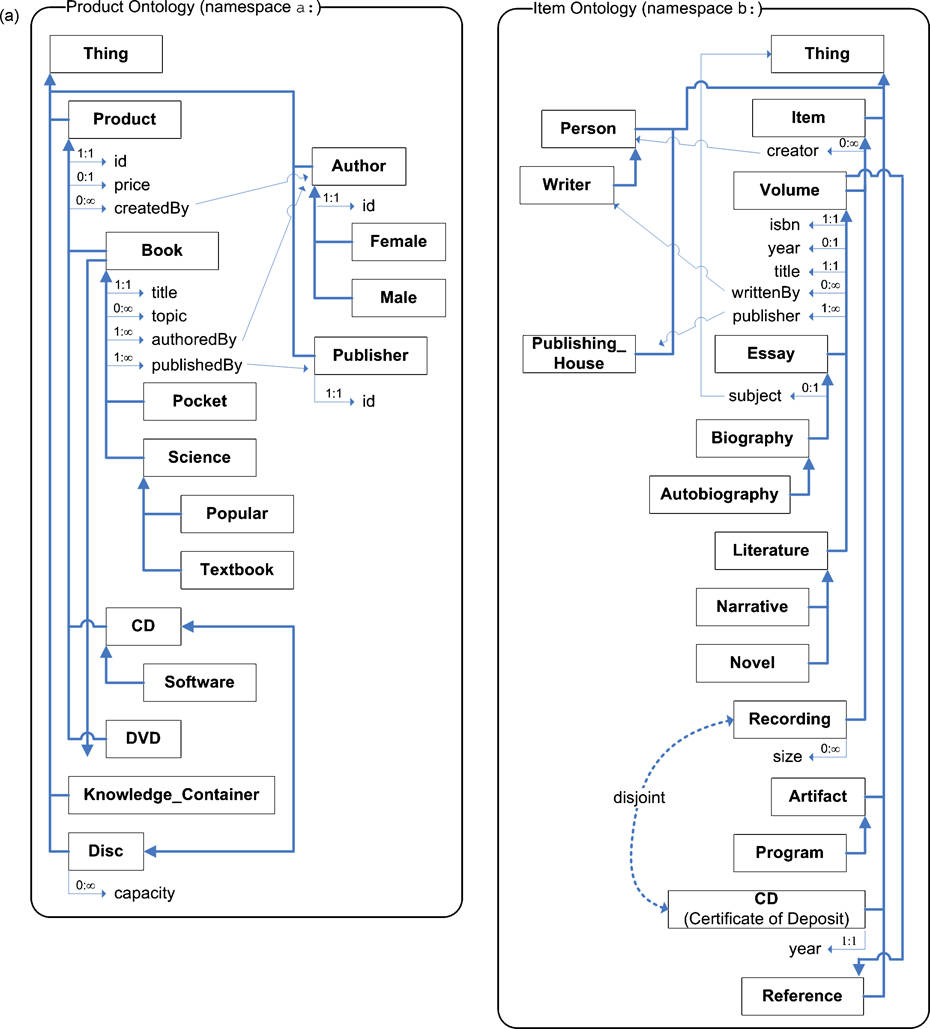
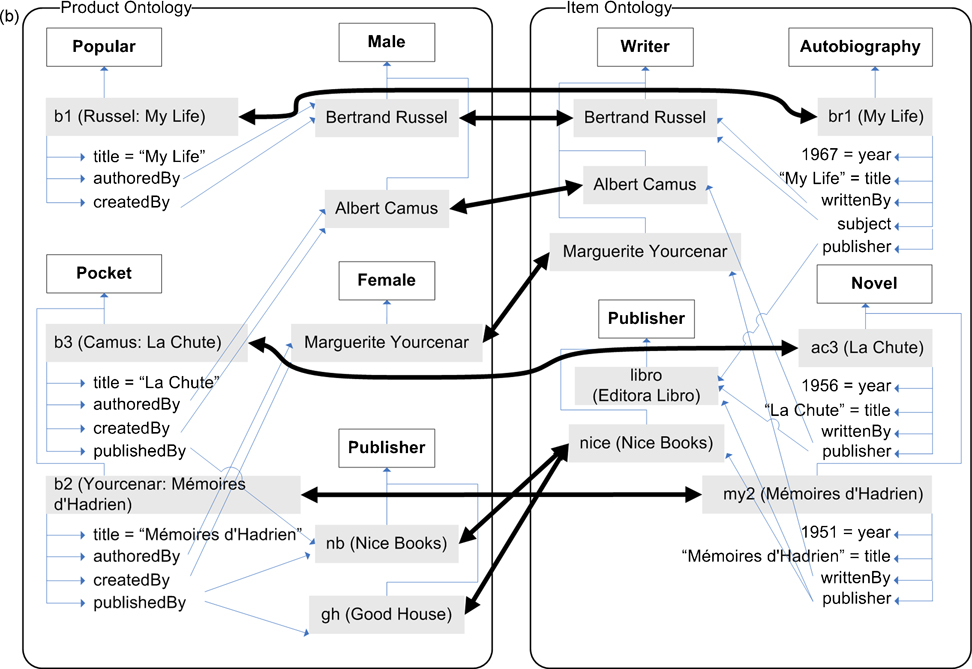
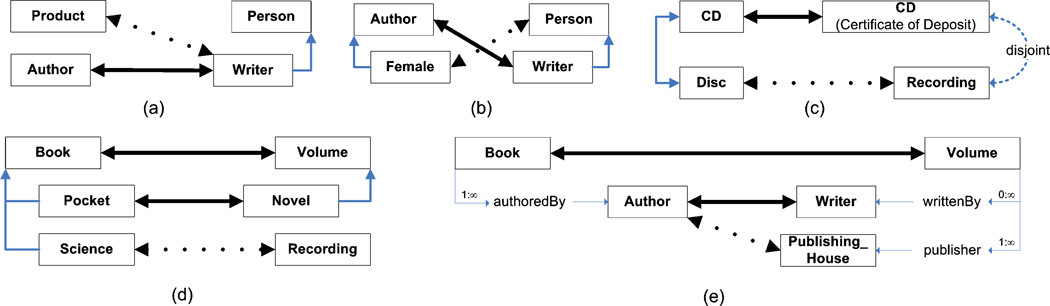
The objective of ontology matching is to derive an alignment between two ontologies, where an alignment consists of a set of correspondences between their elements. Given two ontologies, O and O’, a correspondence between entities e in O and e’ in O’, which we denote as 〈e, e’〉, signifies that e and e’ are deemed to be equivalent. Consider the two example ontologies in fig. 1; based upon the meaning of the labels of the elements, it would be expected that an ontology matching algorithm will find an alignment that would include, for example, the correspondences 〈a:Book, b:Volume〉 and 〈a:publishedBy, b:publisher〉.

Fig. 1. Example Ontologies.

Entities are identified by their id; where the label is different, it is shown in parenthesis. Comments for entities are not shown. Subsumption is indicated by a directional arrow; equivalence by a bidirectional arrow, and disjointness by a dotted arrow. Cardinalities are shown next to each property. (a) shows the classes and properties of the ontology; (b) shows individuals belonging to each ontology. The ontologies themselves and graphical notation are based on an example in [14], modified to illustrate multiple inheritance, compound property domains, disjointness, multiple cardinalities, and individual matching.

3.2 ASMOV Algorithm

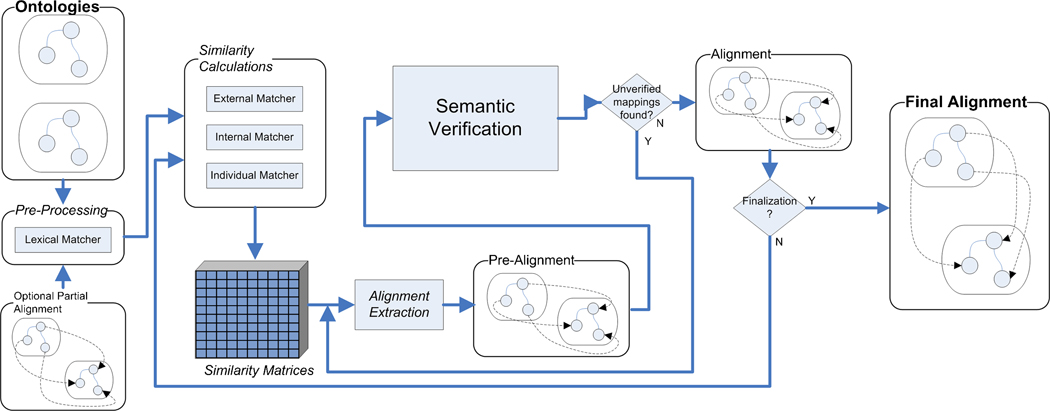
The ASMOV process, illustrated in the block diagram in fig. 2, is an iterative process divided into two main components: similarity calculation, and semantic verification. ASMOV receives as input two ontologies to be matched, such as the two ontologies shown in the example in fig. 1, and an optional input alignment, containing a set of predetermined correspondences.

Fig. 2. ASMOV Block Diagram.

First, the similarity calculation process computes a similarity value between all possible pairs of entities, one from each of the two ontologies, and uses the optional input alignment to supersede any calculated measures; the details of this calculation, including the description of the different attributes examined for each pair of entities, are provided in Section 4. This process results in a similarity matrix containing the calculated similarity values for every pair of entities; partial views of this matrix for the ontologies in fig. 1 are shown in Table 1.

Table 1. Partial similarity matrices.

for (a) classes, (b) properties, and (c) individuals after iteration 1 for example in fig. 2.

(a)
	Item	Volume	Essay	Literature	Narrative	Novel	Biography	Autobiography
Product	0.194	0.531	0.115	0.218	0.056	0.434	0.055	0.052
Book	0.210	0.849	0.346	0.353	0.292	0.523	0.219	0.205
Pocket	0.242	0.523	0.050	0.050	0.051	0.449	0.050	0.047
Science	0.248	0.068	0.143	0.358	0.072	0.072	0.070	0.065
Popular	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
Textbook	0.126	0.432	0.000	0.000	0.000	0.365	0.000	0.000

(b)
	subject	publisher	creator	writtenBy	title
id	0.228	0.051	0.177	0.000	0.174
price	0.279	0.126	0.160	0.000	0.289
createdBy	0.000	0.000	0.000	0.500	0.000
authoredBy	0.000	0.000	0.000	0.500	0.000
title	0.301	0.056	0.230	0.000	1.000
publishedBy	0.000	0.000	0.000	0.500	0.000

(c)
	Bertrand_ Russel	Albert_ Camus	Marguerite_ Yourcenar
myourcenar	0.000	0.000	0.625
acamus	0.000	0.625	0.000
brussel	0.625	0.000	0.000

From this similarity matrix, a pre-alignment is extracted, by selecting the maximum similarity value for each entity. For example, 〈a:Product, b:Volume〉 has the highest value for a:Product, while 〈a:Book, b:Volume〉 has the highest value for b:Volume; both are included in the pre-alignment. This pre-alignment is passed through a process of semantic verification, detailed in Section 5, which eliminates correspondences that cannot be verified by the assertions in the ontologies, resetting the similarity measures for these unverified correspondences to zero. For example, the potential correspondence 〈a:Science, b:Recording〉 is eliminated due to the existence of 〈a:Book, b:Volume〉, because a:Science is a subclass of a:Book, while b:Recording is not asserted to be a subclass of b:Volume.

This process results in a semantically verified similarity matrix and alignment, which are then used to evaluate a finalization condition as detailed in Section 6. If this condition is true, then the process terminates, and the resulting alignment is final. Fig. 3 shows the alignment obtained from running the ASMOV process over the ontologies in fig. 1, which includes expected correct correspondences in terms of our interpretation of the ontologies, such as 〈a:Book, b:Volume〉, but also includes other correspondences such as 〈a:price, b:year〉 that do not agree with a human interpretation of their meaning. The accuracy of ASMOV has been evaluated against a set of well-established tests, as presented in section 7.

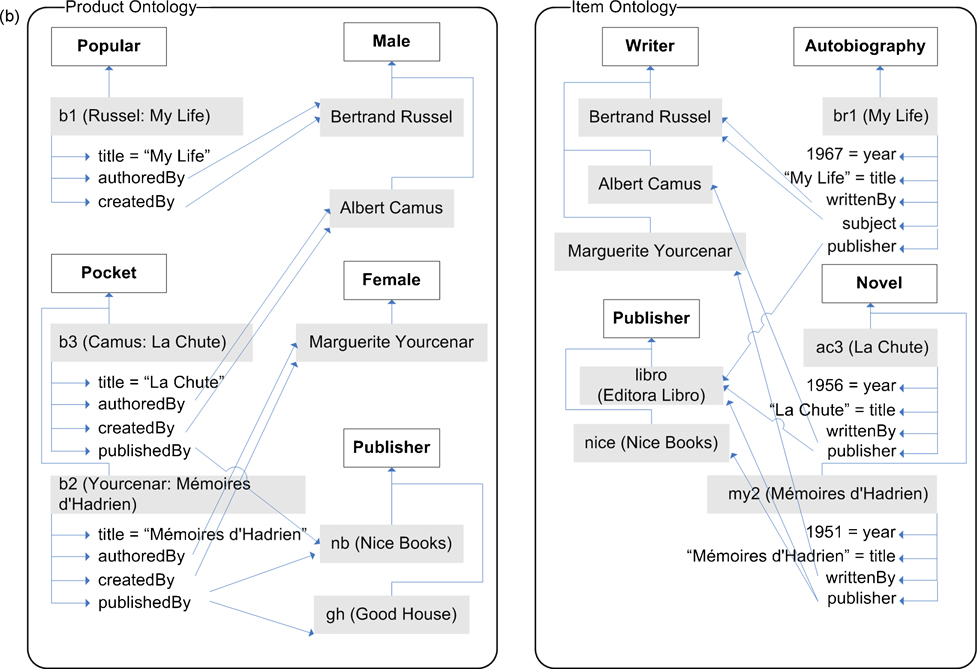
Fig. 3. Example Alignments.

(a) shows the alignment obtained by ASMOV between classes and properties of the ontology; (b) shows alignment between individuals.

4. Similarity Calculations

The ASMOV similarity calculation is based on the determination of a family of similarity measures which assess the likelihood of equivalence along three different ontology kinds of input as classified in [14]. The nature of this calculation process is similar to the approach used in OLA [15], both in its use of a normalized weighted average of multiple similarities along different ontology facets, and especially in its use of similarities between entity sets. OLA, however, uses a graph structure to represent the ontology, and performs its set of calculations based on entity sets identified from this graph; ASMOV uses a more diversified approach, working from the OWL-DL ontology directly and proposing ad-hoc calculations designed specifically for each ontology facet. In addition, the ASMOV process is made more tolerant of the absence of any of these facets in the ontologies to be matched, by automatically readjusting the weights used in the weighted average calculation. ASMOV also is designed to accept an input alignment as a partial matching between the ontologies.

At each iteration k, for every pair of entities e ∈ O, e’ ∈ O’, ASMOV obtains a calculated similarity measure σ_k(e,e’), as a weighted average of four similarities:

• a lexical (or terminological) similarity, s^L(e,e’), using either an external thesaurus or string comparison;

• two structural similarities:

  • a relational or hierarchical similarity s^H_k (e,e’), which uses the specialization relationships in the ontology; and
  • an internal or restriction similarity s^R_k (e,e’), which uses the established restrictions between classes and properties.
  an extensional similarity, s^E_k(e,e’), which uses the data instances in the ontology. The lexical similarity does not vary between iterations and is therefore calculated only once, during pre-processing. Consider F={L,E,H,R} to be the set of similarity facets used in the calculation; σ_k(e,e’) is computed as

  $${\sigma }_k(e,e\prime )=\{\begin{array}{c}\frac{{\displaystyle \sum _{f\in F}(w_f\cdot s_k^f(e,e\text{'}))}}{{\displaystyle \sum _{f\in F}{w}_f}},\text{if}e\text{and}e\text{'}\text{are}\text{the}\text{same}\text{type}\text{of}\text{entity};\hfill \\ 0.0,\text{otherwise}\hfill \end{array}$$ (1)

where w_f are weights assigned to each of the features in the calculation. Using fixed weights presents a problem, as noted in [2]: if a given facet f is missing (e.g., if an entity in an ontology does not contain individuals), the corresponding similarity value s^f_k is marked as undefined, and its weight w_f is changed to zero.

In addition, ASMOV accepts an optional input alignment A_o as a set of correspondences, A_o = {〈e,e’〉}, where each correspondence in A_o has a confidence value n₀(e,e’). This input alignment is used to supersede any similarity measures, defining a total similarity measure s_k(e,e’) as follows:

$$s_k(e,e\prime )=\{\begin{array}{c}{n}_0(e,e\prime ),\text{if}\langle e,e\prime \rangle \in A_0\hfill \\ {\sigma }_k(e,e\prime ),\text{otherwise}\hfill \end{array}$$ (2)

The initial calculated similarity value between entities, σ₀(e,e’), is given by the lexical similarity between the entities multiplied by the lexical similarity weight. The total similarity measures for every possible pair of entities e in O and e’ in O’ define a similarity matrix S_k = {s_k(e, e’)} for each iteration k.

4.1 Lexical Similarity

The lexical feature space consists of all the human-readable information provided in an ontology. Three such lexical features are considered in OWL ontologies: the id, the label, and the comment.

4.1.1 Lexical Similarity for Labels and Ids

Let the two labels being compared be l and l’, belonging respectively to entities (classes or properties) e and e’. ASMOV is capable of working with or without an external thesaurus; if an external thesaurus is not used, only string equality is used as a measure. Let Σ denote a thesaurus, and syn(l)the set of synonyms and ant(l) the set of antonyms of label l; the lexical similarity measure between the labels of e and e’, s^L(e,e’), is then given as follows:

$$s^L(e,e\prime )=\{\begin{array}{c}\hfill \\ 1.0,\text{if}l=l\text{'}\hfill \\ 0.99,\text{if}l\prime \in \text{syn}(l)\hfill \\ 0.0,\text{if}l\prime \in \text{ant}(l)\hfill \\ \text{Lin}(l,l\prime ),\text{if}l\in \text{Σ}\wedge l\text{'}\in \text{Σ}\wedge l\prime \notin \text{syn}(l)\hfill \\ \frac{|\text{tok}(l)\cap \text{tok}(l\prime )|}{\text{max}(|\text{tok}(l)|,|\text{tok}(l\prime )|)},\text{otherwise}.\hfill \end{array}$$ (3)

The similarity measure for synonyms is set slightly lower than the measure for actual string equality matches, in order to privilege exact matching between terms. Lin(l,l’) denotes the information-theoretic similarity proposed by Lin in [26]; it provides a good measure of closeness of meaning between concepts within a thesaurus. The tokenization function tok(l) extracts a set of tokens from the label l, by dividing a string at punctuation and separation marks, blank spaces, and uppercase changes; when at least one of the labels to be compared is not found in the thesaurus, and if they are not exactly equal, the lexical similarity is computed as the number of overlapping tokens.

ASMOV optionally finds a lexical similarity measure between identifiers of entities e and e’, s^id(e,e’), in the same way as with labels, except that the Lin function is not used; in case that the identifiers are not found to be synonyms or antonyms, the number of overlapping tokens is computed. In principle, identifiers in OWL are meant to be unique, and do not necessarily have a semantic meaning [38], and thus the similarity measurement is made to be more restrictive.

The lexical similarity measure s^L(e,e’) is designed to privilege labels (and ids) that can be found within the thesaurus used by the system; thus, it avoids using other commonly used metrics such as string edit or n-grams. While this design choice results in less tolerance for spelling mistakes, on the other hand it avoids influencing the matching process with similarities between identifiers that happen to share the same letters or n-grams. Nevertheless, as part of our future work, we are exploring the inclusion of non-language-based techniques within a weighted average with the thesaurus-based measure.

Examples of lexical similarity measures for both labels and ids for some classes in the ontologies in fig. 1, are provided in Table 2, where the results have been calculated using WordNet as the thesaurus.

Table 2. Examples of lexical similarity calculations.

a:	b:	sid	slabel	Notes
Book	Volume	0.99	0.99	Same id and label, both synonyms.
CD	CD	1.0	0.99	Labels are “CD” for a:CD, and “Certificate of Deposit” for b:CD.
Book	Reference	0.0	0.955	Not synonyms, but closely related
Male	Female	0.0	0.0	Antonyms (as example only: b:Female does not exist in example ontologies).

4.1.2 Lexical Similarity for Comments

Comments are processed differently, since they usually consist of a phrase or sentence in natural language. In this case, we compute the similarity between the comments of entities e and e’, s^c(e,e’), as a variation of Levenshtein distance but applied to tokens. First, an ordered set of tokens is obtained from the comment of each of the entities; then, we calculate the number of token operations (insertions, deletions, and substitutions of tokens) necessary to transform one of the comments into the other. Let x, x’ be the comments of e, e’ respectively, and let op(x, x’) denote the number of token operations needed, and tok(x) denote the number of tokens in a comment,

$$s^c(e,e\text{'})=1-\frac{\text{op}(x,x\text{'})}{\text{max}(|\text{tok}(x)|,|\text{tok}(x\prime )|)}$$ (4)

Consider for example the comments for classes a:Book and b:Volume. The comment for a:Book is “A written work or composition that has been published, printed on pages bound together.” For b:Volume, it is “A physical object consisting of a number of pages bound together.” Each of these phrases is tokenized, where a:Book results in 14 tokens and b:Volume in 11 tokens. The total number of token operations necessary to transform a token into another is 10, 7 substitutions and three insertions (or deletions). The lexical similarity for these two comments then is 1 − (10/14) = 0.286.

4.1.3 Lexical similarity measure calculation

The lexical similarity measure is calculated as the weighted average of the label, id, and comment similarities. The weights used in this calculation have been determined experimentally, as label weight w^label = 0.5, id weight w^id = 0.3, and comment weight w^comment = 0.2. From the results given above, then, the lexical similarity measure between a:Book and b:Volume can be calculated as 0.849.

4.2 Entity Set Similarity

For the calculation of the structural and extensional similarities, in several cases it is necessary to determine a single similarity measure for sets of entities; in this section we provide the details of this calculation. Let E and E’ be a set of entities from ontology O and O’, and let S={s(e,e’)} denote a matrix containing a set of similarity values from each e ∈ E, e’ ∈ E’. The procedure to obtain this single measure for these sets is as follows:

• First, a greedy selection algorithm is used to obtain a set of correspondences A^S = {〈e_i,e’_j〉}. This algorithm iteratively chooses the largest s(e_i,e’_j) in S and eliminates every other similarity for e_i and e’_j from S, until all e_i or all e’_j are eliminated.

• Next, a similarity measure s^set(E,E’,S) is calculated using the following formula:

  $$s^{set}(E,E\prime ,S)=\frac{2\times {\displaystyle \sum _{\langle e_i,e_j,s(e_i,e_j)\rangle \in A^S}s\mathit{(}{e}_i,{e\prime }_j\mathit{)}}}{|E|+|E\prime |}$$ (5)

This normalization accounts for any difference in size between E and E’; some entities from the larger set will not have a correspondence and will reduce the overall similarity measure. Note that Eq. (5) will always yield values between 0 and 1, since the total number of correspondences in A^S cannot be greater than the average size of the two sets E and E’.

4.3 Relational Similarity

The relational similarity is computed by combining the similarities between the parents and children of the entities being compared. As classes or properties may contain multiple parents and children, the similarity calculation is calculated as the average of the similarities of all parents or children, in order to restrict the results between 0 and 1.

Let e and e’ be two entities belonging to ontologies O and O’ respectively, and let U, U’ be the sets of entities that are parents of e and e’. Let e = a:Book and e’ = b:Volume; then U = {a:Product, a:Knowledge_Container} and U’ = {b:Reference, b:Item}. If the sets U and U’ are both empty, the parent similarity measure between e and e’ is undefined and ignored; if only one is empty, the measure is 0.0. Otherwise, we construct a parent similarity matrix UP_(k−1)(e,e’) containing the similarity measures at the (k−1)th iteration between each u ∈ U and u’ ∈ U’. The parent similarity measure s^U_k(e,e’) for the kth iteration is then calculated as s^set(U,U’, UP_(k−1)(e,e’)). A similar calculation is performed for the children sets, resulting in the children similarity measure s^V_k(e,e’).

The total relational similarity s^H_k(e,e’) is then calculated as the weighted sum of the parent and children similarity calculations; ASMOV uses equal weights for both sets. If both the parent and children similarity measure are undefined, then the total relational similarity itself is undefined and ignored. If one of them is undefined, then the other is used as the relational similarity.

The relational similarity between properties and between individuals is calculated in an analogous manner; in the case of individuals, the calculation considers the classes to which individuals are asserted members as their parents. Examples of these calculations for classes, properties, and individuals are presented in Table 3.

Table 3. Relational Similarity Calculations.

a:			b:			Relational Similarity
Entity	Parent set	Children set	Entity	Parent Set	Children     Set	Parent	Children	Total
Book	{Product, Knowledge_ Container}	{ Essay, Literature}	Volume	{ Item, Reference }	{Pocket, Science}	0.3562	0.4433	0.3997
createdBy	{ authoredBy }	-	creator	{ writtenBy }	-	0.5198	undef.	0.5198
b1	{ Popular }	-	br1	{ Auto- biography }	-	0.2450	undef.	0.2450

4.4 Internal Similarity

The internal similarity is calculated differently for classes and properties in the ontology.

4.4.1 Internal Similarity for Properties

For properties, the internal similarity s^R is calculated as a weighted sum of the domain and range similarities using equation (1). For the domain of all properties and for the range of object properties, the similarity is calculated as the similarity between the classes that define the domain and range. If these consist of the union of multiple classes, the best matched pair is used. Consider properties p and p’, and let their domain be dom(p) and dom(p’) respectively. Further, let dom(p) = (c₁ ◡…◡ c_M), and dom(p’) = (c’₁ ◡…◡ c’_N). First, the pair (c_m, c’_n) with the highest similarity value at the (k−1)th iteration is chosen; note that if N=M=1, c_m = dom(p), c_n = dom(p’). The domain similarity for properties at the kth iteration is then given by

$$s_k^{RD}(p,p\text{'})=s_{(k-1)}(c_m,c{\text{'}}_n)$$ (6)

The range similarity for object properties s^RR(p,p’) is calculated analogously. The total internal similarity for properties is then calculated as the weighted average between the domain and range similarities; ASMOV uses equal weights for both. To calculate the range similarity of two datatype properties p and p’, Wu-Palmer similarity [42] is calculated over the canonical taxonomy structure of XML Schema datatypes [3].

Table 4 illustrates two examples for the calculation of internal similarity for properties, one for object properties and the other for datatype properties with multiple domain classes.

Table 4. Internal Similarity for Properties.

Note that in the similarity between a:id and b:year, the domain similarity is obtained from the highest similarity, in this case, between a:Product and b:Volume.

a:			b:			Internal Similarity
Entity	Domain	Range	Entity	Domain	Range	Domain	Range	Total
authoredBy	Book	Author	writtenBY	Volume	Writer	0.4649	0.3330	0.3974
id	{ Product, Author, Publisher}	xsd:anyURI	year	{ Volume, CD }	xsd:int	0.3423	0.4444	0.3934

4.4.2 Internal Similarity for Classes

For classes, the internal similarity s^R_k(c,c’) for the kth iteration is calculated by taking into account the similarities of all local property restrictions associated to a class, considering the similarity between the properties themselves, and the cardinality and value restrictions for these properties. Let c and c’ be two classes belonging to ontologies O and O’, and let P(c) and P(c’) be the sets of properties whose domain includes c and c’ respectively. If both P(c) and P(c’) are empty, the internal similarity between c and c’ is undefined and ignored in the calculation of equation (1). Otherwise, for each pair of properties p_m ∈ P(c) and p’_n∈P(c’), we calculate a property restriction similarity s^RP_k(p_m,p’_n) as the weighted average of three values:

• The first value, s_(k−1)(p_m,p’_n), is the similarity between the two properties at the (k−1)th iteration.

• The second value, s^card(p_m,p_n), is a measure of the agreement in cardinality restrictions: if the two properties are restricted to the same minimum and maximum cardinality, this measure is 1.0, otherwise, it is 0.0.

• The third value, s^value(p_m,p’_n), is a measure of the similarity in value restrictions. Two types of value restrictions are considered: restrictions on particular property values, called enumerations, and restrictions on the class of the allowable values, which are called range restrictions. If one of the property value restrictions is defined as an enumeration of possible individual values, and the other is not, the value restriction similarity measure is 0.0. If both are enumerations, then this measure is calculated as the proportion of the enumerated individuals that match from one property restriction to another with respect to the total number of possible matches. If neither property being compared is restricted by enumerations, then their value restriction similarity measure is calculated by comparing the classes defined by the range restriction on the properties, as in the case of property internal similarity detailed in subsection 4.4.1 above.

We then construct an property restriction similarity matrix R_k(c,c’), containing all s^RP_k(p_m,p’_n) between each p_m ∈ P(c) and p’_n ∈ P(c’), and calculate the relational similarity measure s^R_k(c,c’) = s^set(P(c),P(c’),R_k(c,c’)). Table 5 shows an example of the calculation of internal class similarity between a:Book and b:Volume.

Table 5. Internal similarity calculation for classes a:Book and b:Volume.

(a) similarities at first iteration; (b) cardinality restriction similarities; (c) value restriction similarities; (d) matrix of property restriction similarities, calculated as a weighted average using weights w^prev = 0.5, w^card = 0.1, w^value = 0.4. (e) correspondences derived by the entity set similarity calculation. The resulting internal class similarity s^R_k(a:Book,b:Volume) = 0.524.

(a)
	year	publishe r	title	isbn	writtenB y
authoredBy	0.000	0.189	0.000	0.000	0.520
id	0.325	0.017	0.457	0.399	0.000
topic	0.431	0.019	0.692	0.616	0.000
price	0.510	0.042	0.422	0.325	0.000
createdBy	0.000	0.118	0.000	0.000	0.449
publishedBy	0.000	0.613	0.000	0.000	0.511
title	0.431	0.019	0.950	0.616	0.000

(b)
	year	publishe r	title	isbn	writtenB y
authoredBy	0.000	1.000	0.000	0.000	0.000
id	0.000	0.000	1.000	1.000	0.000
topic	0.000	0.000	0.000	0.000	1.000
price	1.000	0.000	0.000	0.000	0.000
createdBy	0.000	1.000	0.000	0.000	0.000
publishedBy	0.000	1.000	0.000	0.000	0.000
title	0.000	0.000	1.000	1.000	0.000

(c)
	year	publishe r	title	isbn	writtenB y
authoredBy	0.000	0.000	0.000	0.000	0.330
id	0.000	0.000	0.000	0.000	0.000
topic	0.444	0.000	1.000	1.000	0.000
price	0.000	0.000	0.000	0.000	0.000
createdBy	0.000	0.000	0.000	0.000	0.000
publishedBy	0.000	0.764	0.000	0.000	0.062
title	0.444	0.000	1.000	1.000	0.000

(d)
	year	publishe r	title	isbn	writtenB y
authoredBy	0.000	0.194	0.000	0.000	0.392
id	0.163	0.008	0.329	0.300	0.000
topic	0.393	0.009	0.746	0.708	0.100
price	0.355	0.021	0.211	0.163	0.000
createdBy	0.000	0.159	0.000	0.000	0.225
publishedBy	0.000	0.712	0.000	0.000	0.280
title	0.393	0.009	0.975	0.808	0.000

(e)
a:	b:	Similarity
authoredBy	writtenBy	0.392
topic	isbn	0.708
price	year	0.355
publishedBy	publisher	0.712
title	title	0.975

4.4.3 Internal Similarity for Individuals

Let d.p denote the value of property p for individual d; the internal similarity s^R_k(d,d’) between two individuals d and d’ is calculated by comparing the values of their properties, as follows:

• For any two datatype properties p and p’ with values for d and d’ respectively, a value similarity s^value_k(d,p,d’,p’) is set to s_(k−1)(p,p’), the total similarity between the properties at the previous iteration, if their corresponding values are lexically equivalent, otherwise it is set to undefined.

• For any two object properties p and p’ with values O and O’ for d and d’ respectively, a value similarity s^value_k(d,p,d’,p’) is set to s_(k−1)(O,O’), the total similarity between O and O’ at the previous iteration.

The similarities between properties then define a matrix S^value(d, d’). Let P(d) and P’(d’) be the sets of both datatype and object property values for d and d’; then the relational similarity between the individuals is calculated using the entity set similarity evaluation algorithm as s^R_k(d,d’) = s^set(P(d),P’(d’), S^value(d, d’)). Table 6 shows the calculation of similarity between individuals a:b2 and b:my2.

Table 6. Internal similarity calculation for individuals a:b2 and b:my2.

(a) matrix of property value similarities; (b) correspondences derived by the entity set similarity calculation. The resulting internal class similarity s^R_k(a:b2,b:my2) = 0.437.

(a)
	title: Mémoires d'Hadrien	year: 1951	writtenBy: Marguerite _Yourcenar	publisher: nice	publisher: libro
title: Mémoires d'Hadrien	0.950	0.000	0.000	0.000	0.000
authoredBy: myourcenar	0.000	0.000	0.217	0.000	0.000
publishedBy: nb	0.000	0.000	0.062	0.469	0.330
publishedBy: gh	0.000	0.000	0.062	0.330	0.330

(b)
a:	b:	Similarity
title: Mémoires d'Hadrien	title: Mémoires d'Hadrien	0.950
authoredBy: myourcenar	writtenBy: Marguerite_ Yourcenar	0.217
publishedBy: nb	publisher: nice	0.469
publishedBy: gh	publisher: libro	0.330

4.5 Extensional Similarity

4.5.1 Extensional Similarity between Classes

The extensional similarity measure for two classes is calculated in the same way as the children hierarchical similarity. Let I(c) and I’(c’) be the sets of individuals members of classes c and c’, and let IS_(k−1)(c,c’) be the similarity matrix formed by the total similarity values for each pair of individuals d ∈ I(c), d’ ∈ I(c’). The extensional similarity measure for classes c and c’ is then given by s^D_k(c,c’) = s^set(I(c),I(c’), IS_(k−1)(c,c’)). An example calculation for classes a:Male and b:Writer is shown in Table 7.

Table 7. Extensional similarity calculation for classes a:Male and b:Writer.

(a) matrix of similarity values for instances in previous iteration ; (b) correspondences derived by the entity set similarity calculation. The resulting extensional class similarity s^R_k(a:Male,b:Writer) = 0.171. Note the reduction effect due to the existence of a third individual in ontology b:.

(a)
	Bertrand_ Russel	Albert_ Camus	Margoeme _ Yourcenar
acamus	0.074	0.213	0.074
brussel	0.213	0.074	0.074

(b)
a:	b:	Similarity
acamus	Albert_Camus	0.213
brussel	Bertrand_Russel	0.213

4.5.2 Extensional Similarity between Properties

To determine extensional similarity between properties, all individuals that contain a value for a given property are analyzed to determine a list of possible matches. Only properties which are both object or both datatype can have an extensional similarity; otherwise, the similarity is undefined.

Given two properties p in O and p’ in O’, let the sets I(p) and I(p’) denote the set of individuals that contain one or more values for each property, and let I’ denote the set of all individuals in O’. Further, for a given individual d, let d.p denote the value of the property p for individual d. The individual similarity calculation is performed by finding a set of individual correspondences B^D = {〈d.p, d’.p’’〉}, d ∈ I(p), d’ ∈ I’. A correspondence belongs to B^D if

• for p and p’´ object properties, s_k(d.p, d’.p’’), the total similarity measure between individuals d.p and d’.p’’ at the previous iteration, is greater than zero.

• for p and p’’ datatype properties, d.p and d’.p’’ are lexically equivalent.

A second set A^D ⊆ B^D, is obtained by restricting it to correspondences where the property at the second individual p’’ = p’. Then, the individual similarity between properties p and p’, s^D_k(p,p’), is given by the ratio of the sizes of sets A^D and B^D.

In the example in fig. 1, there are three different values for the property a:authoredBy: a:brussel, a:acamus, and a:myourcenar. Each of these values has a non-zero similarity at iteration 1 with one individual each from ontology b: b:Bertrand_Russel, b:Albert_Camus, and b:Marguerite_Yourcenar. Each of these occurs once as the value of b:writtenBy, and b:Bertrand_Russel occurs additionally as a value for b:subject. The individual similarity between a:authoredBy and b:writtenBy is then 0.75.

5. Semantic Verification Process

5.1 Pre-alignment Extraction

In order to perform semantic verification, a pre-alignment B_k is first extracted from the similarity matrix S_k that results from the similarity calculations. This pre-alignment is obtained using a greedy algorithm as follows. A correspondence 〈e, e’〉 is inserted into the alignment B_k if it has not been previously eliminated through the process of semantic verification, and if s_k(e,e’) is maximal to within a similarity threshold λ either for e or for e’; that is, if there does not exist an e_i such that 〈e_i,e’〉 has not been eliminated and |s_k(e_i,e’) − s_k(e,e’)| ≤ λ, or there does not exist an e’_j such that 〈e,e’_j〉 has not been eliminated and |s_k(e,e’_j) − s_k(e,e’)| ≤ λ. Note that if two elements e_a and e_b have similarity values such that |s_k(e_a,e’) − s_k(e_b,e’)| ≤ λ, then both 〈e_a, e’〉 and 〈e_b, e’〉 are inserted into the pre-alignment.

5.2 Semantic Verification

The pre-alignment B_k is then passed through a process of semantic verification, designed to verify that certain axioms inferred from an alignment are actually asserted in an ontology, removing correspondences that lead to inferences that cannot be verified. It is important to underline that the idea is not to find semantically invalid or unsatisfiable alignments, but rather to remove correspondences that are less likely to be satisfiable based on the information present in the ontologies. This approach is similar to the notion of mapping instability defined in [31], where mappings are considered to be stable when subsumptions implied by the merge of the mapped ontologies and their mapping can be verified in the ontologies themselves. It is also similar to the approach used in [23] to derive ontology fragments based on an existing alignment by verifying subsumptions as well as domain and range axioms. In addition to these axioms, ASMOV uses equivalence and disjointness relationships.

Let O and O’ be two ontologies, let B_k be a pre-alignment between O and O’, and let B₁₂={〈e₁, e’₁〉, 〈e₂, e’₂〉} be an alignment consisting of a single pair of correspondences, B₁₂ ⊆ B_k. Consider O^Mto be an ontology defined by the merge of O, O’, and B₁₂, where the correspondences in B₁₂ are transformed into equivalence axioms. Suppose that an axiom α involving only entities in O can be inferred in O^M from the relations derived from the correspondences in B₁₂; B₁₂ is said to be verified in O if α is independently asserted by O. If B₁₂ cannot be verified, the correspondence with the lowest confidence value is eliminated from B_k and set in a list of removals, with the other correspondence stated as the cause for elimination; if both correspondences have the same measure, neither is eliminated.

Let e₁, e₂ be two distinct entities in O, and e’₁, e’₂ distinct entities in O’. The following kinds of inferences are examined by the ASMOV semantic verification process:

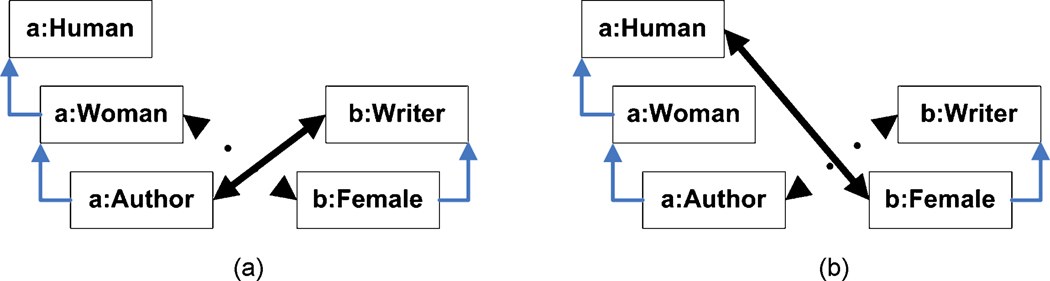
• Multiple-entity correspondences: A multiple-entity correspondence, illustrated in fig. 4(a), occurs when an alignment contains both 〈e₁,e’₁〉 and 〈e₂,e’₁〉. Such an alignment implies that (e₁ = e₂), so if this axiom is not asserted, the alignment cannot be verified.

• Crisscross correspondences: Suppose that e₂ • e₁ and e’₂ • e’₁. A crisscross correspondence, shown in fig. 4(b), occurs when an alignment contains both 〈e₁,e’₂〉 and 〈e₂,e’₁〉: [(e₂ • e₁) ∧ (e₁ = e’₂) ∧ (e₂ = e’₁) ∧ (e’₂ • e’₁)] implies both (e₁ = e₂) and (e’₁ = e’₂). If both equivalences are not actually asserted in O or O’ respectively, then the alignment cannot be verified.

• Disjointness-subsumption contradiction: Suppose that (e₂ • e₁) and (e’₂ ⊥ e’₁). If an alignment contains both 〈e₁,e’₂〉 and 〈e₂,e’₁〉, this implies (e₂ ⊥ e₁) and (e’₂ • e’₁), which are both invalid and therefore cannot be verified. This contradiction is illustrated in fig. 4(c); note that since (e₂ = e₁) → (e₂ • e₁), this also holds for equivalences.

• Subsumption and equivalence incompleteness: If an alignment contains both 〈e₁,e’₁〉 and 〈e₂,e’₂〉, then (e₂ • e₁) and (e’₂ • e’₁) mutually imply each other; subsumption incompleteness occurs when one of the two is not asserted in its corresponding ontology, as shown in fig. 4(d). Equivalence incompleteness is similar.

• Domain and range incompleteness: Let c, c’ be classes and p, p’ be properties in O and O’ respectively, let dom(p) denote the domain of a property p, and suppose c ∈ dom(p). If an alignment contains both 〈c,c’〉 and 〈p,p’〉 this implies (c’ ∈ dom(p); domain incompleteness occurs when this axiom cannot be verified, as illustrated in fig. 4(e). A similar entailment exists for ranges.

Fig. 4. Kinds of semantic verification inferences.

(a) Multiple-entity correspondences; (b) crisscross correspondences; (c) disjointness-equivalence contradiction; (d) subsumption incompleteness: 〈a:Pocket, b:Novel〉 is kept, while 〈a:Science, b:Recording〉 is eliminated; (e) domain and range incompleteness: 〈a:Author, b:Writer〉 is kept, while 〈a:Author, b:Publishing_House〉 is eliminated.

Every unverified correspondence is added to a list of removals; then, all existing unverified correspondences are checked to determine whether the cause of elimination subsists, removing correspondences from the list if the cause has disappeared. If at least one correspondence is newly unverified or at least one previously unverified correspondence has been removed from the list of removals, then a new pre-alignment is extracted from the existing similarity matrix, and the semantic verification process is restarted from this new pre-alignment. Otherwise, the semantically verified alignment A_k and matrix T_k are obtained, the first by removing all unverified correspondences from the pre-alignment B_k provided as input to the semantic verification process, and the second by resetting to zero the similarity values of all unverified correspondences in the list of removals.

6. Algorithm Termination and Convergence

6.1 Finalization Condition

The semantically verified alignment A_k and matrix T_k are subjected to the evaluation of a finalization condition, in order to determine whether the algorithm should terminate, or whether a new iteration should be started by recomputing the similarity values. Two finalization conditions are potentially used to determine when the iterative process should stop. The most stringent condition requires that the resulting matrix T_k be repeated to within the same similarity threshold λ used for pre-alignment extraction in section 5.1; that is, that for some iteration x < k, and for every s_k(e,e’) in T_k s_x(e,e’) in T_x, |s_x(e,e’) − s_k(e,e’)|≤ λ.

In practice, we have found that it is enough to require that the resulting alignment be repeated, that is, that for some iteration x < k, A_x = A_k. Although it cannot be guaranteed that this looser condition will necessarily result in the same alignment as if the matrix itself were repeated, we posit that for most practical cases the results will be very similar, at a much lesser processing cost.

Due to the iterative nature of the ASMOV alignment algorithm, it is important to determine if these finalization conditions guarantee its termination. For this, we determine that under most circumstances the algorithm converges, and that this convergence guarantees termination. We also show that if a cyclic condition is encountered, termination is also ensured.

6.2 Convergence without Semantic Verification

We first examine the case where no correspondences are ever eliminated through the semantic verification processes. To prove convergence, we will show that the similarities increase monotonically and have an upper bound. Assuming that for iteration k > 0, for any e in O, e’ in O’, s_k(e,e’) ≥ s_(k−1) (e,e’), an investigation of each of the similarity calculations shows that s_(k+1)(e,e’) ≥ s_k(e,e’), since all calculations are based either on values that remain constant throughout iterations, or on the similarities between two related entities, which cannot decrease. For example, the parent relational similarity measure is based on the similarity measures of the parents at the previous iteration, which cannot decrease. Thus, the total similarity measure cannot decrease. Now observe that the initial calculated similarity value σ₀(e,e’) = w_L · s^L(e,e’); from eq. (1) it is clear that σ₀(e,e’) is the lowest possible value that any s_k(e,e’) may take. Since similarity values are upper-bound to 1.0, s_k(e,e’) converges to some s_∞(e,e’) ≤ [1 − w_L (1 − s^L(e,e’))]. The use of a non-zero threshold λ in the stringent finalization check described in section 3.2 ensures that the algorithm terminates, since for large enough k, |s_k+1(e,e’) − s_k(e,e’)| ≤ λ. Since equivalent matrices generate equivalent alignments, the looser finalization check also guarantees termination.

6.3 Convergence with Semantic Verification

When an unverified correspondence is eliminated, the similarity measure of this correspondence, which was some positive value at the previous iteration, is forced to 0.0. This in turn could cause other similarity measures to decrease in value. As long as these eliminated correspondences are not restored, then the algorithm will eventually converge for the reasons espoused in section 6.1.

It is possible that “unverified hunting” situations arise, however, especially for ontologies that are not well modeled or those from very different knowledge domains. Suppose the example in fig. 5, where a crisscross correspondence is discovered in the first iteration in (a). The second iteration finds a new set of correspondences as in (b), and eliminates 〈a:Author, b:Writer〉 in favor of 〈a:Human, b:Female〉; since 〈a:Author, b:Writer〉 is no longer a correspondence, this could lead again to the matching in (a). Under this situation, it is possible that the algorithm does not converge, but rather that it enters a cyclic situation. Provided that the similarity threshold λ is non-zero, the number of possible matrices is finite, and therefore the algorithm is guaranteed to terminate. The number of possible alignments is also finite, even if the threshold is zero, therefore termination is also ensured under the looser condition. Note that termination will occur much faster, under a cyclic situation, by requiring only that an alignment be repeated.

Fig. 5. Example of unverified hunting situation.

7. Experimental Results

A prototype of ASMOV has been implemented as a Java application. Using this prototype, two sets of experiments were carried out. The first set of experiments was done using the 2008 benchmark series of tests created by the Ontology Alignment Evaluation Initiative (OAEI) [7], in order to determine the accuracy of the ASMOV algorithm. The second set of experiments was performed using the NCI Thesaurus (describing the human anatomy) and the Adult Mouse Anatomy ontologies, which are also part of the OAEI 2008 contest, in order to analyze the algorithm using different thesauri.

The experiments were carried out on a PC running SUSE Linux Server with two quad-core Intel Xeon processors (1.86 GHz), 8 GB of memory, and 2×4MB cache.

7.1 Evaluation of Accuracy

The goal of ontology matching is to generate an alignment that discovers all correct correspondences, and only correct correspondences, where correctness is judged with respect to a human interpretation of meaning. In some cases, either incorrect correspondences are discovered, or correct correspondences are not. For example, in fig. 3, the correspondence 〈a:price, b:year〉 is incorrect in terms of our interpretation of the meaning of “price” and “year.” Nevertheless, since these two concepts are not antonyms, since their structural characteristics are similar, and since there do not exist semantic clues to reject their equivalence, the correspondence is included by ASMOV in the alignment.

To evaluate accuracy of ontology matching, it is necessary to quantify both the number of correct correspondences not found, and the number of incorrect correspondences found. This is done by using a gold standard alignment between two ontologies previously derived by human experts, running the algorithm on the ontologies, and then calculating precision (p), the percentage of gold standard correspondences that exist within the extracted alignment, recall (r), the percentage of correct extracted correspondences that exist within the gold standard, and F₁, the harmonic mean of precision and recall. Let G be the gold standard alignment, and A be the alignment extracted by the ontology matching algorithm,

$$p=\frac{|A\cap G|}{A},r=\frac{|A\cap G|}{|G|},F_1=\frac{2pr}{p+r}$$ (7)

We have evaluated the accuracy of ASMOV using the well-established OAEI benchmark series of tests, in their 2008 version, and we have compared these results with those of other algorithms that competed in the OAEI challenge. These tests are confined to the domain of bibliographic references (BibTeX). The benchmark tests start from a reference ontology to a multitude of alterations. As ontologies may be modeled in a different manner by different developers, the variations between the tests highlight how well the algorithm would perform in the real world.

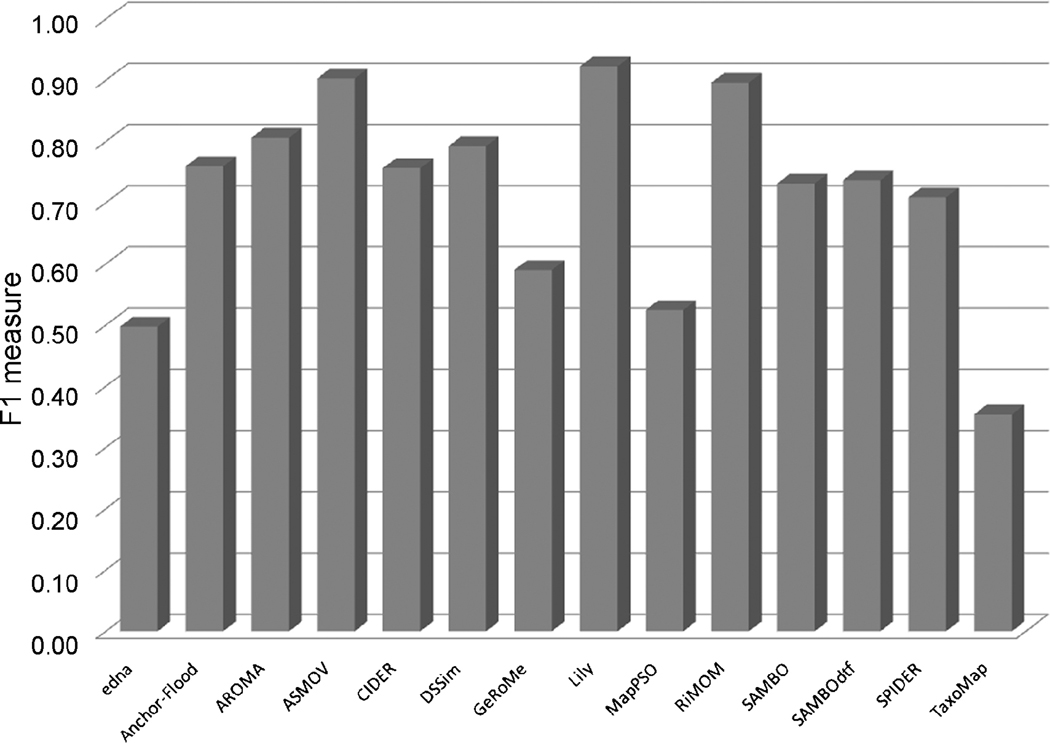
Fig. 6 graphs these values for ASMOV against all other entrants in the OAEI 2008 campaign. As mentioned in the OAEI 2008 results [7], ASMOV was one of the three best performing systems; this mirrors our success during the OAEI 2007 evaluations [13]. The total time required to run all benchmarks was 76 sec., an order of magnitude improvement over our 2007 implementation [21]. Total memory used to run these tests was 23.5MB, including the Java Virtual Machine.

Fig. 6. Accuracy of ASMOV vs. OAEI 2008 entrants.

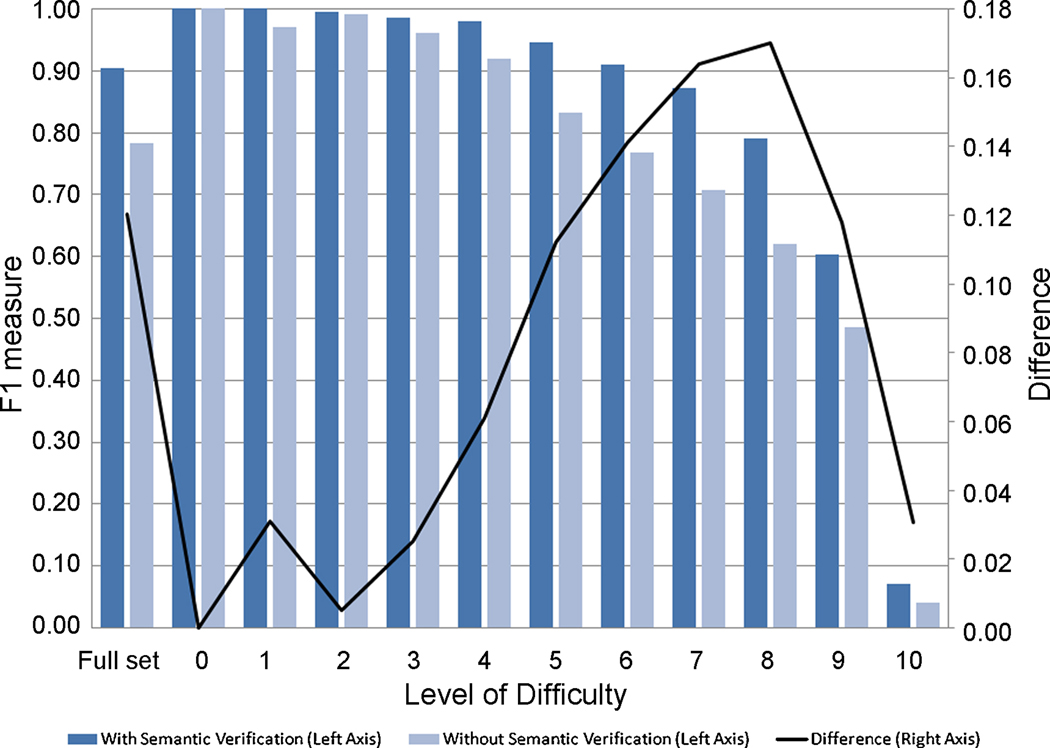
The OAEI 2008 benchmark tests are divided into ten levels of difficulty, where the most difficult tests have less information on which to base an alignment; we have run experiments to determine F₁ for each of these sets of benchmarks. Furthermore, to gauge the effect of our semantic verification process, we have run the experiments both using the full ASMOV implementation, as well as using a system without the semantic verification. The results of these experiments are shown graphically in fig. 7. It can be clearly seen that, as expected, the accuracy of ASMOV decreases as the tests become more difficult. It can also be seen from the plot of the difference between the two measures, shown in fig. 7 as a line graph with the scale on the right axis, that the semantic verification process produces an important improvement on the overall F₁ measure, and that this improvement is more significant for matching situations where there are sparse cues available.

Fig. 7. Effect of semantic verification on accuracy, by level of difficulty.

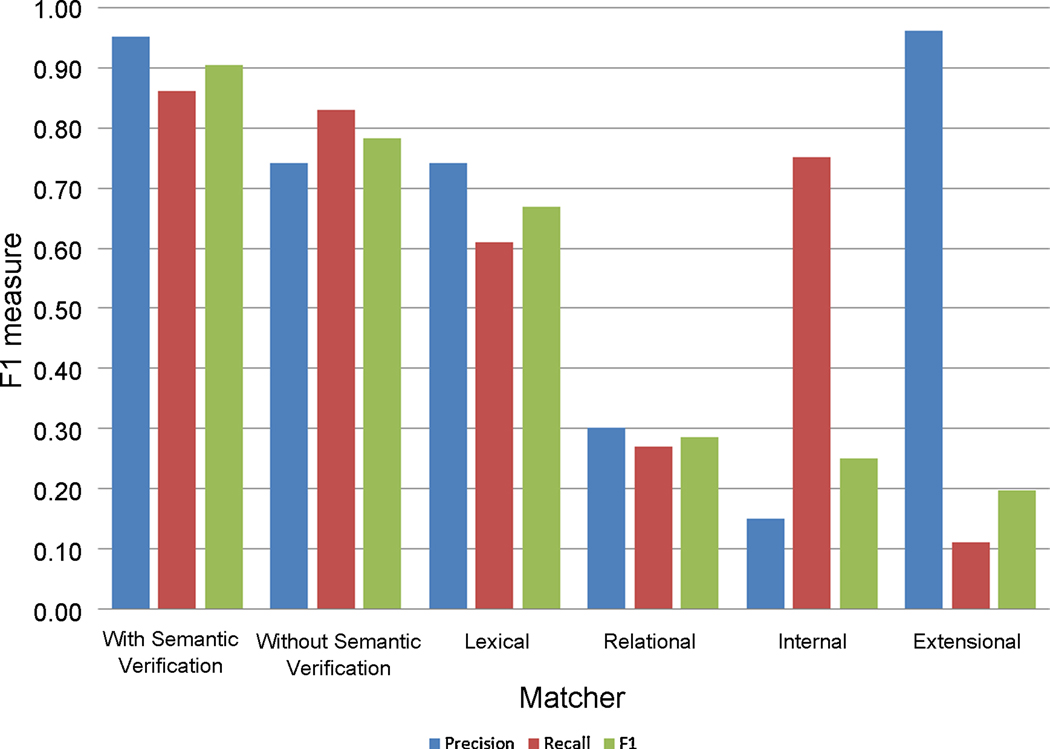
To better analyze the influence of the various matchers used in ASMOV in the overall accuracy, we have also run the algorithm using only one of the four similarity matchers at a time, without semantic verification; the lexical matcher is always used as seeding value for the iterative algorithm. The results of these tests are shown in fig. 8. It can clearly be seen that the combination of all four matchers produces a more accurate result than the use of any individual matcher. It is interesting to note that most of the accuracy is still being given by the entity-level lexical matching, while the other matchers act as complements to enhance precision and/or recall.

Fig. 8. Effect of matchers on accuracy.

7.2 Comparison of Alignments using UMLS and WordNet

The implementation of the ASMOV ontology alignment algorithm contemplates the use of a standardized thesaurus adapter application programming interface (API), to enable the interchangeability of thesauri and therefore the use of the algorithm in different domains. This thesaurus adapter API has been derived from the implementation of the Java WordNet library (http://jwn.sourceforge.net/), an open-source implementation for connectivity to WordNet version 2.0. The interface used in this library has been expanded and modified to incorporate features from WordNet 2.1, as well as to allow for the implementation of other thesauri.

This API contains six interfaces: Dictionary database, Index word, Synonym set, Word, Pointer, and Pointer type.

• Dictionary database: this interface is a bridge between the application and the lexical reference database, providing independence from the actual database implementation. It exposes one method that lets an application lookup index words from the underlying database.

• Index word: the index word is the text being queried, tagged with its synonym sets and its part-of-speech (POS). Depending on the implementation of the thesaurus, the text may actually represent a combination of words, such as “heart attack”.

• Synonym set: A synonym set represents a concept and contains a set of words that are alternative names for that concept. A synonym set can also contain a description that describes it in a human readable format.

• Word: the word interface wraps a word, its description and its intended meaning through a synonym set.

• Pointer: a pointer encodes a semantic relationship between words. These relationships are directional, with a source, a target and a pointer type.

• Pointer type: this interface describes a type of semantic relationship between concepts. Each thesaurus defines its own set of pointer types through this interface; at a minimum, a thesaurus adapter must provide a synonym, antonym, hypernym (or parent), and hyponym (or child) relationship.

We have implemented this standardized API for two different thesauri: WordNet and the UMLS Metathesaurus. The implementation for WordNet has been achieved by updating the existing JWordNet library. In the case of the UMLS Metathesaurus, the implementation of the API leverages the Java library created by the UMLS in order to retrieve concepts. Thus, the implementation of the Dictionary database interface queries the UMLS library in order to retrieve a set of concepts associated with a given text. These concepts represent synonym sets and are combined to form a UMLS Index word. Since concepts in UMLS are non-linguistic entities, no POS is tagged to the Index word. Concepts in UMLS are tied to their various names; each of these names is wrapped by the implementation of the word interface.

Since UMLS does not provide an antonym relationship between concepts, the UMLS thesaurus adapter for ASMOV investigates whether two concepts are related in some way, either as synonyms, hypernym-hyponym, or by some of the other UMLS relationships such as the ‘related’ relationship. If no relationship other than ‘sibling’ is found, then the two concepts are treated as if they were antonyms for purposes of the lexical similarity calculation, to avoid mapping closely related but antonymous concepts such as ‘Man’ and ‘Woman’. This antonymy assumption is similar to the strong disjointness assumption used in [37] for correcting ontologies. Currently, it is only used in ASMOV to provide completeness to UMLS; however, this assumption could be more widely applicable for semantic verification, as discussed under Future Work.

Additionally, it is well-known that UMLS exhibits some semantic inconsistencies, in particular circular hierarchical relations [33], which causes problems when calculating some lexical similarity measures such as Lin [26]; where there exists a circular hierarchy, it is not possible to determine which of the elements within the circularity is actually the root. For these tests, we have used the naïve approach outlined in [33] in order to resolve eq. (3) when terms are neither synonyms nor antonyms. This approach works well in order to find a common hypernym between two terms even if circular relations are found. However, the distance from this common hypernym to the root of the thesaurus may not be computable. In order to avoid this issue, we have used a subset of the UMLS Metathesaurus containing only references to the NCI Thesaurus; this ensured that all concepts retrieved would have the ‘NCI Thesaurus’ concept (C1140168) as the common root concept. We have manually verified that all terms involved in the tests have at least one path to this root. The implementation of the formal approach outlined in [33] is a matter of future work.

Alignment results using these two different thesauri have been compared using two real-world anatomy ontologies: a subset of the NCI Thesaurus encoding the human anatomy, and the Adult Mouse Anatomy developed by the Jackson Laboratory Mouse Genome Informatics. We have specifically used the versions of these ontologies presented for evaluation at the OAEI 2007 and 2008 challenges; the authors in [5] present a report on an alignment of previous versions of these ontologies using other techniques.

The accuracy of ASMOV using UMLS Metathesaurus and WordNet is shown in Table 8. This overall accuracy evaluation of the algorithm using both thesauri was computed through independent testing by the evaluators of the OAEI challenge. Total time elapsed for the execution of ASMOV was 3 hours and 50 min., using 600MB of memory. As can be appreciated, the accuracy of ASMOV using UMLS for these specialized anatomy ontologies is substantially greater than its accuracy using the generic WordNet thesaurus. This result illustrates the advantages to be gained from the use of domain-specific knowledge in order to enhance ontology alignments. In order to explore the accuracy of these mappings further, we analyzed a sample set of mappings from [5], and results from the partial alignments provided by OAEI 2008.

Table 8. Accuracy for OAEI Anatomy test.

	WordNet	UMLS
Precision	0.431	0.787
Recall	0.453	0.652
F1	0.442	0.713

7.2.1 Sample of Ontology Correspondences

In [5], some examples of correct correspondences and one example of an incorrect correspondence between terms in previous versions of these two ontologies are presented by the authors. We have tabulated these mappings in Table 9, comparing them with the mappings obtained by ASMOV using both UMLS and WordNet. As can be seen, UMLS as a thesaurus provides much better results for this small sample. While we believe this higher accuracy is partially due to the fact that the lexical features in the NCI anatomy are codified as concepts in UMLS, the ability to find accurate correspondences in the mouse anatomy is the result of the help provided by the UMLS Metathesaurus in relating medical and biological concepts not found in WordNet.

Table 9. Examples of Ontology Mappings.

Mouse Anatomy Concept	[5]		UMLS		WordNet
	Mapped NCI concept	Valid?	Mapped NCI concept	Correct?	Mapped NCI concept	Correct?
uterine cervix	Cervix Uteri	Yes	Cervix	Yes	Ectocervix	No
tendon	tendon	Yes	Tendon	Yes	Tendon	Yes
urinary bladder urothelium	Transitional Epithelium	Yes	Gallbladder Epithelium	No	Nothing	No
lienal artery	Splenic Artery	Yes	Splenic Artery	Yes	Nothing	No
Alveolus Epithelium	Alveolar Epithelium	Yes	Alveolar Epithelium	Yes	Alveolar Epithelium	Yes
cervical vertebra 1	C1 Vertebra	Yes	Nothing	No	Cervical Vertebra	No
cerebellum lobule I	lingula of the lung	No	Nothing	Yes	Cerebellar Cortex	No

7.2.2 Partial Alignments

For the OAEI 2008 challenge, a partial alignment for these two ontologies was given, to be used as input for one of the tasks for this test. This partial alignment contained all correspondences considered trivial, i.e., those that could be found by simple string comparison, and a set of 54 non-trivial correspondences [7]. The evaluation for the task using partial alignments was done by the OAEI committee as follows: consider G^p to be the partial alignment provided, G to be the full reference alignment, and A to be the alignment obtained by the system under evaluation. Then, the precision and recall are calculated for an alignment A − G^p, against a gold standard A − G. The results obtained for ASMOV are shown in Table 10. While the results obtained leave substantial margin for improvement, we should note that there was a marked increase in the overall accuracy of the system when using a partial alignment.

Table 10. OAEI Anatomy Test results for ASMOV using partial alignments.

	Without Partial	Using Partial
Precision	0.339	0.402
Recall	0.258	0.254
F1	0.293	0.312

In order to investigate further the performance of ASMOV against the OAEI anatomy tests, we used the provided partial alignment as a gold standard, We then ran ASMOV using two different combinations of weights: the first set is the one used for the OAEI contest, which had to be the same set as those used for the benchmark, and the second set was derived experimentally to improve accuracy. The results of this further investigation are presented in Table 11; it is clear that the variation in weights resulted in a substantial increase in correct correspondences found. Nevertheless, there is still an important number of correspondences that were not found in this partial alignment. We believe that the main cause for this is the semantic verification process, and more specifically in the evaluation of subsumption incompleteness between entities that have multiple parents. Some correspondences are being eliminated unless all possible assertions of subsumption exist; this condition seems too stringent, and needs to be reevaluated. In addition, other systems such as SAMBO make use of more of the semantic knowledge included within UMLS, especially the relation part-of; this shows an important avenue for improvement to ASMOV’s semantic verification. The OAEI organizers have offered to open their reference alignment after the 2008 challenge; this will enable us to make a more in-depth analysis of this issue.

Table 11. Total number of correspondences found for partial alignment in Anatomy test.

The standard weights used were w^L = 0.2, w^H = 0.3, w^R = 0.4, w^E = 0.1, w^label = 0.5, w^id = 0.3, w^comment = 0.2. The optimized weights used were w^L = 0.4, w^H = 0.1714, w^R = 0.2571, w^E = 0.15, w^label = 0.58, w^id = 0.12, w^comment = 0.3.

	Standard Weights	Optimized Weights
Correct Correspondences Found	855	891
Correspondences Found But Not in Gold Standard	407	431
Correspondences in Gold Standard Not Found	114	78
Precision	0.678	0.674
Recall	0.882	0.920

8. Limitations and Future Work

The evaluations of ASMOV presented in the Experimental Results section show the potential of our algorithms in deriving useful alignments even when relatively little information is present in the ontologies being matched. In particular, we have been able to show that the combination of similarity matchers in multiple dimensions, with a process for semantic verification of the resulting alignments, results in a system with high accuracy. Nevertheless, there is room for continued improvement in our algorithms. In the following sections, we present some of the limitations of our current algorithm implementation, and the direction of our ongoing work.

8.1 Evaluation of other OAEI Results

The OAEI anatomy test results show that, under dissimilar ontologies, the accuracy of ASMOV is reduced. We believe this is mostly due to stringiness in the semantic verification process; further evaluation is merited in this regard.

In addition, we should note that ASMOV participated in three additional tracks in both OAEI 2007 and OAEI 2008: the directory tests, the fao tests, and the conference tests. All these tests are blind; thus, it is difficult to make comprehensive evaluations of the results. The results for the directory tests show that ASMOV had the highest precision but low recall. We believe this may be because the semantic verification process is eliminating too many potential correspondences, in particular where multiple entities in one ontology are being mapped to a single entity in the other ontology without an equivalence assertion; if corroborated, this may show that the multiple-entity verification is too strict, and it also may show that ontology pre-processing may be required. In the fao tests, we did not report any correspondences found; this was due to our understanding that correspondences should be reported only on classes. After re-running these tests to include matching of individuals, we found a substantial number of correspondences in most of the tests; however, it was not possible to verify which of these are actually correct with respect to the gold standard. The conference tests do not have a complete reference alignment, and the evaluations are being done over tentative alignments. The results from 2008 show that ASMOV had the best accuracy of the three systems that were able to complete this test.

We should further note that ASMOV did not participate in the multilingual directory (mldirectory), library, and very large crosslingual resources (vlcr) tests during OAEI 2008. In the first case, this non-participation was because we have not yet implemented an interface to a multilingual thesaurus, without which the mldirectory test would have given poor results. In the case of library and vlcr, these tests are designed using the SKOS ontology language, while ASMOV is specifically designed to work with OWL-DL.

8.2 Computational cost and complexity

The implementation of ASMOV used in the OAEI 2008 tests produced an improvement of an order of magnitude with respect to our 2007 implementation. Nevertheless, the run time of over 3 hours for the anatomy tests still suggests that improvements in execution efficiency are needed.

While a formal derivation of computational complexity for ASMOV is beyond the scope of this paper, we present here an initial analysis. Let O and O’ be the ontologies being matched, and let N and N’ be the number of entities in O and O’ respectively. Further, consider that most similarity calculations between two entities e ∈ O and e’ ∈ O’ entail the comparison of entity subsets related to e and e’. It is reasonable to assume that in most cases the size of each of these entity subsets is much smaller than N and N’. For example, for the relational similarity calculation between e and e’, the size of the parent and children sets of e and e’ can be assumed to be much smaller than the overall size of each ontology. With this assumption, such comparisons can be approximated as constant time with respect to the size of the ontologies. Thus, the overall complexity for each similarity calculation can be approximated as O(N·N’).

The complexity of the semantic verification process can be estimated by recognizing that this entails the comparison between pairs of entities from each ontology. The total number of pairs of entities in O is N(N−1)/2; thus, the upper bound on this process is O(N²·N’²).

These processes are repeated iteratively until a finalization condition is reached. The above two results show that each iteration for ASMOV is performed in polynomial time. As has been noted in section 6, the algorithm converges under most circumstances, but may encounter cyclical conditions under others. The total number of iterations required for termination depends especially on the internal characteristics of the ontologies being aligned. An upper bound for the number of iterations is given by either the number of possible matrices or alignments; the latter is a much smaller number, but both are exponential over the number of terms in the ontologies. This indicates that the number of iterations that ASMOV needs to execute must be closely studied in order to reduce computational cost. With this aim, then, we are currently performing a formal evaluation of the complexity of the ontology matching problem and of ASMOV in particular.

8.3 Direction of ongoing work

Our ongoing work is focused on the improvement in the performance and capabilities of ASMOV. One interesting avenue of exploration is the preprocessing of ontologies to reduce the number of required iterations; [40] have examined the performance of ASMOV and other systems under such preprocessing, obtaining some evidence that it could increase accuracy. A particular type of preprocessing is the semantic clarification by pinpointing detailed in [37], which could be used to provide more comprehensive information within the ontologies and thus enhance the process of semantic verification.

We are also investigating the expansion of the semantic rules used for semantic verification, especially where it concerns sets of more than two correspondences; pairwise verification is only an approximation of an overall verification of the resulting alignment [31]. Also, the method used for the extraction of the initial pre-alignment is being further examined.

In terms of the similarity calculations, we are studying the inclusion of non-language-based techniques in the lexical similarity, such as the combination of cosine similarity and Jaro-Winkler functions presented in [9]. We are working to improve and streamline the implementation of ASMOV, and we are researching and designing capabilities to allow the algorithm to work with larger ontologies through partitioning algorithms. In addition, we are developing mechanisms to implement a more formal approach to resolve circular relations in the UMLS Metathesaurus adapter. Finally, ASMOV, coupled with algorithms for ontology creation and for semantic querying, is currently being applied in the development of a system for the integration of heterogeneous biological and biomedical data sources.

9. Conclusion

In this paper, we have presented the ASMOV ontology matching algorithm, including a detailed discussion of the calculations used to determine similarity between two entities from different ontologies. We have also shown that the algorithm converges to a solution. The experimental results presented illustrate that ASMOV outperforms most existing ontology matching algorithms, and obtains accuracy values for the OAEI 2008 benchmarks on par with the best system in the contest. We have also shown that the process of semantic verification enhances the performance of the system, especially under sparser information in the ontologies to be matched. Additional experimental results demonstrate the adaptability of ASMOV through the use of a thesaurus adapter API. Tests on the alignment of a human anatomy with a mouse anatomy ontology show that the use of a specialized thesaurus such as UMLS significantly improves the alignment of ontologies of a particular knowledge domain. There are still important avenues for the further improvement in the performance of ASMOV, in particular, the pre-processing of ontologies to provide more complete information for semantic verification.