Allelic-Based Gene-Gene Interaction Associated With Quantitative Traits

Abstract

Recent studies have shown that quantitative phenotypes may be influenced not only by multiple single nucleotide polymorphisms (SNPs) within a gene but also by the interaction between SNPs at unlinked genes. We propose a new statistical approach that can detect gene-gene interactions at the allelic level which contribute to the phenotypic variation in a quantitative trait. By testing for the association of allelic combinations at multiple unlinked loci with a quantitative trait, we can detect the SNP allelic interaction whether or not it can be detected as a main effect. Our proposed method assigns a score to unrelated subjects according to their allelic combination inferred from observed genotypes at two or more unlinked SNPs, and then tests for the association of the allelic score with a quantitative trait. To investigate the statistical properties of the proposed method, we performed a simulation study to estimate type I error rates and power and demonstrated that this allelic approach achieves greater power than the more commonly used genotypic approach to test for gene-gene interaction. As an example, the proposed method was applied to data obtained as part of a candidate gene study of sodium retention by the kidney. We found that this method detects an interaction between the calcium-sensing receptor gene (CaSR), the chloride channel gene (CLCNKB) and the Na, K, 2Cl cotransporter gene (CLC12A1) that contributes to variation in diastolic blood pressure.

INTRODUCTION

It has been widely recognized that gene-gene interaction is likely to have an important role in the variation of quantitative traits for complex disease. Most ongoing genetic studies focus on the identification of single gene effects and do not attempt to identify more complex genetic interactions. Unfortunately, it is quite possible that some important genetic effects may be missed because they do not have a main effect that can be identified; rather the effect of the gene may only be observed when modeled as an interaction with the other relevant genes. The failure to replicate significant association results across studies using single locus-based analysis may be due to the failure to include gene-gene interactions in the genetic analyses.

Many statistical methods have been proposed to detect gene-gene interactions contributing to disease-associated quantitative traits. Combinatorial partitioning methods [Nelson et al., 2001], restricted partitioning methods (RPM) and multivariate adaptive regression splines [Cook et al. 2004] have all been proposed to cluster genotype combinations at multiple loci into subgroups to account for the variation caused by the genetic interactions. Moreover, a standard regression method is commonly used to detect multiplicative interaction effects on a quantitative trait.

There are several shortcomings associated with the currently available methods. First, some of these methods are computationally intensive, especially when more than 10 single nucleotide polymorphisms (SNPs) are included in the interaction model [Ritchie et al., 2001]. Second, the results from these methods can be difficult to interpret biologically because there are no meaningful interpretations of the genotypes clustered together and found to affect the quantitative trait. Third, high dimensionality from multi-locus combinations and small sample size can lead to many sparse or empty cells, thereby reducing the power to identify an interaction effect unless the cell is combined with other cells.

In this article, we propose a statistical method to identify the interaction of multiple unlinked genes defined by the nonrandom association of alleles which occurs when a particular allele in one gene and a particular allele in another unlinked gene contribute to the variation in a quantitative trait through their interaction. Our proposed method assigns a score to a subject according to the allelic combinations inferred from multi-locus genotypes and then tests for the association of these allelic scores with a quantitative trait. We evaluate the analytical properties of our test statistic based on non-centrality parameter approximation and additionally perform a simulation study to compare our method with a genotype-based approach which is a standard regression method. The application of our approach to real data demonstrates its utility to detect the interaction of three genes associated with sodium retention by the kidney.

METHODS

Most of the previously described methods start with all 3 × 3 genotypic combinations obtained when analyzing bi-allelic markers such as SNPs. The basic idea is to group genotypic combinations of the two markers into subgroups having similar quantitative trait mean values. The primary difficulty in implementing the cell clustering approach using the nine genotypic combinations is to discriminate main effects and interaction effects from the clustered cell combinations. For instance, the highlighted cells on the 3 × 3 cell genotype table in Figure 1A can be interpreted as demonstrating either main or interaction effects of the two markers. When using more than two loci, the significant cell clusters become even harder to interpret biologically.

Fig. 1.

Cell combinations of two unlinked markers; M₁ has A and a alleles, and M₂ has B and b alleles. (A) 3 × 3 combinations of genotypes; (B) 2 × 2 cell combinations of alleles.

We propose to employ SNP alleles rather than SNP genotypes in our test of interaction. As shown in Figure 1B, the AB allelic combination (A allele at M₁ marker and B allele at M₂ marker) has an increased or decreased trait mean as compared with the other allelic combinations. Linear trend implies that a subject having higher score (probability) at AB allelic combination tends to have a high (or low) quantitative trait value which presents disease susceptibility. Our proposed method can detect any interaction created by any allelic combination at M₁ and M₂ globally, then can find specific allelic combinations.

ALLELIC SCORE FOR STATISTICAL MODEL

The underlying principle of our method is to identify the association of allelic combination between two unlinked markers with a quantitative trait so that subjects are assigned an allelic score given their observed genotype information. The score is a conditional probability of obtaining the particular allelic combination given the observed genotypes at the two loci of each subject. For example, a subject with AA (at marker M₁) and Bb (at marker M₂) genotype has $\frac{1}{2}$ in the AB combination and $\frac{1}{2}$ in the Ab combination, $X_{AB}=P(AB\mid M_1=AA,M_2=Bb)=\frac{1}{2}$ and $X_{Ab}=P(Ab\mid M_1=AA,M_2=Bb)=\frac{1}{2}$. Table I presents the allelic scores of a subject whose genotype is given. The number of allelic combinations at two markers is 2² but the probability of a particular allelic combination is a function of the three remaining probabilities, so the number of independent probabilities is 2²−1. The null hypothesis is that there is no association caused by gene-gene interaction; therefore, the mean of the quantitative trait at the four allelic combinations is equal to population mean of trait. Rejecting the null hypothesis would indicate there are particular allelic combinations associated with the quantitative trait. We can further investigate which allelic combinations are interacting to influence the quantitative trait based on our model. In the extension to multiple markers, the assignment of allelic score to each subject is straightforward, i.e. X_c = P(c|M₁, …, M_k). The number of independent probabilities associated with the allelic combination from k loci is 2^k − 1.

TABLE I.

Allelic scores given genotypes of individual

	Allelic score
Genotype	AB	Ab	aB	ab
(AA, BB)	1	0	0	0
(AA, Bb)	$\frac{1}{2}$	$\frac{1}{2}$	0	0
(AA, bb)	0	1	0	0
(Aa, BB)	$\frac{1}{2}$	0	$\frac{1}{2}$	0
(Aa, Bb)	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$
(Aa, bb)	0	$\frac{1}{2}$	0	$\frac{1}{2}$
(aa, BB)	0	0	1	0
(aa, Bb)	0	0	$\frac{1}{2}$	$\frac{1}{2}$
(aa, bb)	0	0	0	1

STATISTICAL MODEL AND PROPERTIES

We consider two disease-associated quantitative trait loci (QTL) $Q_1^{\ast },Q_2^{\ast }$ underlying a quantitative trait. Both are in Hardy-Weinberg equilibrium and unlinked, but interacted to influence variation of the trait. Let Q₁ and q₁ be the two alleles at the first QTL, $Q_1^{\ast }$ with frequencies p_Q1 and p_Q1, respectively. Let Q₂ and q₂ be the two alleles at the second QTL, $Q_2^{\ast }$ with frequencies p_Q2 and p_q2. We consider two genotyped bi-allelic marker loci with marker M₁ in linkage disequilibrium (LD) with susceptibility locus $Q_1^{\ast }$ and marker M₂ in LD with $Q_2^{\ast }$. Marker M₁ has two alleles (A, a) with frequencies p_A and p_a respectively, and M₂ has two alleles (B, b) with frequencies p_B and p_b respectively. Let LD_AQ1 = P(AQ₁) − P_AP_Q1 be the measure of LD between $Q_1^{\ast }$ and M₁, and LD_BQ2 = P(BQ₂) − P_BP_Q2 be LD measure between QTL $Q_2^{\ast }$ and M₂.

Let μ_mnrs be the mean of a quantitative trait of two genotype combinations m, n = (Q₁, q₁) and r, s = (Q₂, q₂) at two loci, $Q_1^{\ast },Q_2^{\ast }$. Let μ_nm, μ_rs be the mean of the quantitative trait for genotype m, n = (Q₁, q₁) at $Q_1^{\ast }$ and r, s = (Q₂, q₂) at $Q_2^{\ast }$, respectively. The mean of the quantitative trait for two allelic combinations Q₁ and Q₂ can be calculated by μ_Q1Q2= μ_Q1Q1Q2Q2p_Q1p_Q2 + μ_Q1Q1Q2q2p_Q1p_q2 + μ_Q1q1Q2Q2p_q1p_Q2 + μ_Q1q1Q2q2p_q1p_q2, and μ_Q1q2, μ_q1Q2, μ_q1q2 are calculated in the same way. Let α₁ = μ_Q1Q1 − (μ_Q1Q1 + μ_q11q1)/2, δ₁ = μ_Q1q1 − (μ_Q1Q1 + μ_q1q1q₁)/2 be additive and dominance effect of the first QTL $Q_1^{\ast }$, and α₂ = μ_Q2Q2 − (μ_Q2Q2 + μ_q2q2)/2, δ₂ = μ_Q2q2 − (μ_Q2Q2 + μ_q2q2)/2 be those of the second QTL $Q_2^{\ast }$. Additive and dominance variances of each locus, ${\sigma }_{ga1}^2=2P_{Q_1}{P}_{q_1}{\alpha }_1^2,{\sigma }_{gd1}^2={(P_{Q_1}{P}_{q_1})}^2{\delta }_1^2,{\sigma }_{ga2}^2=2P_{Q_2}{P}_{q_2}{\alpha }_2^2,{\sigma }_{gd2}^2={(P_{Q_2}{P}_{q_2})}^2{\delta }_2^2$ can be derived [Falconer and Mackay, 1996]. We assume that dominance variances at each locus are negligible. The total variance is ${\sigma }^2={\sigma }_1^2+{\sigma }_2^2+{\sigma }_{\text{interaction}}^2+{\sigma }_{\text{e}}^2$, where ${\sigma }_1^2,{\sigma }_2^2$ are the total variances at each locus, ${\sigma }_{\text{interaction}}^2={\sum }_{i=(Q_1{Q}_2,\dots ,q_1{q}_2)}{({\mu }_i-\mu )}^2{p}_i$ is the interaction variance and ${\sigma }_{\text{e}}^2$ is the error variance.

Let y_i be the trait value of ith individual with observed genotypes M₁ and M₂ (i = 1, …, N). Under the assumption of normality of y, the interaction effect of two genes on a trait can be modeled as

$$\begin{array}{l}{y}_i=w_i\gamma +X_{i,AB}{\beta }_{AB}+X_{i,Ab}{\beta }_{Ab}+X_{i,aB}{\beta }_{aB}\\ +X_{i,ab}{\beta }_{ab}+e_i,\end{array}$$ (1)

where X_i,AB = P(AB|M₁, M₂) is the AB allelic score derived from M₁ and M₂ genotypes at ith subject and β_{j∈{AB,Ab,aB,ab}} is the interaction effects of jth ∈ {AB, Ab, aB, ab} allelic combination. w_i is a covariate such as age or gender and γ is the coefficient of the covariate. We assume e_i is the error term following the normal distribution $N(0,{\sigma }_{\text{e}}^2)$. Table I presents allelic scores calculated according to the conditional probability, given the genotypes at the two markers.

For simplicity, no covariate variables are considered. The regression coefficients of model (1) is

$$\begin{array}{l}\beta =K^{-1}[\mu \left(\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right)+({\mu }_{Q_1{Q}_2}-{\mu }_{Q_1{q}_2}-{\mu }_{q_1{Q}_2}+{\mu }_{q_1{q}_2})\\ \times \left(\begin{array}{c}{D}_{{AQ}_1}{D}_{{BQ}_2}/P_A{P}_B\\ D_{{AQ}_1}{D}_{{bQ}_2}/P_A{P}_b\\ D_{{aQ}_1}{D}_{{BQ}_2}/P_a{P}_B\\ D_{{aQ}_1}{D}_{{bQ}_2}/P_a{P}_b\end{array}\right)+({\mu }_{Q_1}-{\mu }_{q_1})\\ \times \left(\begin{array}{c}{D}_{{AQ}_1}/P_A\\ D_{{AQ}_1}/P_A\\ D_{{aQ}_1}/P_a\\ D_{{aQ}_1}/P_a\end{array}\right)+({\mu }_{Q_2}-{\mu }_{q_2})\left(\begin{array}{c}{D}_{{BQ}_2}/P_B\\ D_{{bQ}_2}/P_b\\ D_{{BQ}_2}/P_B\\ D_{{bQ}_2}/P_b\end{array}\right)],\end{array}$$ (2)

where (μ_Q1 − μ_q1), (μ_Q2 − μ_q2) are the average effect of the gene substitution at each $Q_1^{\ast },Q_2^{\ast }$ respectively [Falconer and Mackay, 1996], (μ_Q1Q2 − μ_Q1q2 − μ_q1Q2 + μ_q1q2) is the magnitude of interaction effect between two loci. The coefficients are functions of the LD between the marker and the putative QTL and the interaction effect as well as main effects. In Appendix A, we show the detailed derivation of regression coefficients of model (1). Assigning allelic scores with more than two markers is straightforward; for example, with K markers, the allelic score is X_i,C = P(C|M₁, M₂, …, M_K) and the statistical model with 2^k of the number of allelic combinations is y_i = w_iγ + Σ_C X_i,Cβ_C + e_i with the extension of (1).

TEST STATISTIC AND NON-CENTRALITY PARAMETER APPROXIMATIONS

Let us denote $X=(X_{AB}^{\tau },\dots ,X_{ab}^{\tau })$, X_AB = (X_1,AB, …, X_N,ab), y = (y₁, …, y_N)^t and β = (β_AB, β_Ab, β_aB, β_ab)^t. Based on the null hypothesis (global test) H₀: β_AB = β_Ab = β_aB = β_ab = μ, a test matrix H is defined as follows:

$$H=\left(\begin{array}{cccc}1& -1& 0& 0\\ 1& 0& -1& 0\\ 1& 0& 0& -1\end{array}\right).$$

The global test statistic for interaction effect is

$$F_{\text{allele}}=\frac{{(H\widehat{\beta })}^t{[H{(X^{t}X)}^{-1}{H}^t]}^{-1}(H\widehat{\beta })}{Y^t[I_N-X{(X^{t}X)}^{-1}{X}^t]Y}\frac{N-4}{3},$$ (3)

where I_N is the N × N identity matrix and (Hβ)^t = (β_AB − β_Ab, β_AB − β_aB, β_AB − β_ab). The non-centrality parameter λ_allele = 1/σ²(Hβ)[H(X^τX)⁻¹H^τ]⁻¹(Hβ)^τ of the above F-statistic (3) is

$$\begin{array}{l}{\lambda }_{\text{allele}}\approx \frac{N}{{\sigma }^2}({\beta }_{AB}-{\beta }_{Ab},{\beta }_{AB}-{\beta }_{aB},{\beta }_{AB}-{\beta }_{ab})\\ \times {[HE{(X^{t}X)}^{-1}{H}^t]}^{-1}\\ \times {({\beta }_{AB}-{\beta }_{Ab},{\beta }_{AB}-{\beta }_{aB},{\beta }_{AB}-{\beta }_{ab})}^t,\end{array}$$

where the total variance ${\sigma }^2={\sigma }_1^2+{\sigma }_2^2+{\sigma }_{\text{interaction}}^2+{\sigma }_{\text{e}}^2$.

Under the null hypothesis, F_allele test statistic follows F(3, N − 4) with λ_allele = 0. Under the alternative hypothesis, F_allele is noncentral to F(3, N − 4, λ_allele) with its non-centrality parameter λ_allele. Once significant interaction is detected using the global test, one may want to test which specific allelic combinations cause interaction effect on the trait. We propose to test each allelic interaction effect of β_{C∈{AB,Ab,aB,ab}} as follows:

$$y_i=\mu +w_i\gamma +X_{i,C}{\beta }_C+e_i,$$

which provides H₀: β_C = 0 with F(1, N − 4). With k multiple markers, the F-test statistic used in the global test H₀: β₁ = · · · = β_2^k = μ at all allelic combinations follows F(2^k − 1, N − 2^k) and F-test statistic of allelic specific-interaction test H₀: β_C = 0 has F(1, N − 2^k).

$$K=\left(\begin{array}{cccc}(1-0.5P_a)(1-0.5P_b)& 0.5P_b(1-0.5P_a)& 0.5P_a(1-0.5P_b)& 0.25P_b{P}_a\\ 0.5P_B(1-0.5P_a)& (1-0.5P_a)(1-0.5P_B)& 0.25P_a{P}_B& 0.5P_a(1-0.5P_B)\\ 0.5P_A(1-0.5P_b)& 0.25P_A{P}_b& (1-0.5P_A)(1-0.5P_b)& 0.5P_b(1-0.5P_A)\\ 0.25P_A{P}_B& 0.5P_A(1-0.5P_B)& 0.5P_B(1-0.5P_A)& (1-0.5P_A)(1-0.5P_B)\end{array}\right).$$

We can also derive a likelihood ratio test (LRT) for the global interaction test H₀: β_AB = · · · = β_ab = μ, which is 2(L_HA − L_H0) following ${\chi }_{\text{df}=3}^2$. L_HA is a likelihood function of maximum likelihood estimates (MLE) β̂_AB, β̂_Ab, β̂_aB, β̂_ab under the alternative hypothesis and L_H0 is a likelihood function of MLE of μ̂ under the null hypothesis. For each allelic combination test of H₀: β_C = 0, LRT follows ${\chi }_{\text{df}=1}^2$. In a similar fashion, k multiple markers interaction can be tested.

RESULTS

TYPE I ERROR RATES

To evaluate the robustness of the proposed model, we performed simulations to examine the type I error rates at the 1% and 5% significance levels. Eight models of interaction between two unlinked QTL were considered (see Table II). Most of the models were designed based on the combination of dominant and recessive inheritance at the genotypic level at each marker. These models are (1) Dominant or Dominant (Dom ∪ Dom), (2) Dominant or Recessive (Dom ∪ Rec), (3) Modified model, (4) Dominant and Dominant (Dom ∩ Dom), (5) Recessive or Recessive (Rec ∪ Rec), (6) Threshold model, (7) Dominant and Recessive (Dom ∩ Rec), (8) Recessive and Recessive (Rec ∩ Rec). For each model, we simulated 5,000 datasets using SNaP [Nothnagel, 2002]. Each dataset has 500 unrelated subjects with two unlinked QTL under no LD between markers and QTLs ( $D_{{AQ}_1}^{\prime }=D_{{AQ}_1}/D_{max}=0;D_{{BQ}_2}^{\prime }=D_{{BQ}_2}/D_{max}=0;R_{{AQ}_1}^2=R_{{BQ}_2}^2=0$) and disease associated allele frequencies at the two loci are 0.2 (P_Q1 = P_Q2 = 0.2), and the two markers allele frequencies are P_A = P_B = 0.3. Quantitative trait values at genotypic combination of two loci were generated from normal distribution with a mean value indicated as a number (0 or 1) in Table II. Standard deviation is 1 for all models. Table III presents the results of the empirical type I error rates of the F-test statistic and LRT calculated from 5,000 datasets at 1% and 5% significance level. It showed that all type I error rates of both test statistics for each model were close to the nominal values 1 and 5% suggesting that the proposed method is statistically robust. For different parameters such as 0.5 disease associated alleles frequencies (P_Q1 = P_Q2 = 0.5) and the equal allelic frequencies of the two markers (P_A = P_B = 0.5), all models achieved nominal values of 1% and 5% as in Table III (results not shown).

TABLE II.

The interaction models: 0, 1 stand for a quantitative trait mean given the genotypes

		Second locus					Second locus
Models	First locus	Q2Q2	Q2q2	q2q2	Models	First locus	Q2Q2	Q2q2	q2q2
Dom ∪ Dom	Q1Q1	1	1	1	Rec ∪ Rec	Q1Q1	1	1	1
	Q1q1	1	1	1		Q1q1	1	0	0
	q1q1	1	1	0		q1q1	1	0	0
Dom ∪ Rec	Q1Q1	1	1	1	Threshold	Q1Q1	1	1	0
	Q1q1	1	1	1		Q1q1	1	0	0
	q1q1	1	0	0		q1q1	0	0	0
Modified	Q1Q1	1	0	1	Dom ∩ Rec	Q1Q1	1	0	0
	Q1q1	1	0	1		Q1q1	1	0	0
	q1q1	0	0	0		q1q1	0	0	0
Dom ∩ Dom	Q1Q1	1	1	0	Rec ∩ Rec	Q1Q1	1	0	0
	Q1q1	1	1	0		Q1q1	0	0	0
	q1q1	0	0	0		q1q1	0	0	0

TABLE III.

Result of type I error rate (%) at 1 and 5% significance level from 5,000 datasets, each has 500 subjects

	Type I error rates (%) for F		Type I error rates (%) for LRT
Model	α = 0.01	α = 0.05	α = 0.01	α = 0.05
Dom ∪ Dom	1.06	4.24	1.12	4.54
Dom ∪ Rec	0.84	4.36	0.94	4.58
Modified	0.74	4.80	0.88	5.02
Dom ∩ Dom	1.06	5.10	1.26	5.48
Rec ∪ Rec	1.16	4.96	1.24	5.10
Threshold	1.00	5.02	1.10	5.22
Dom ∩ Rec	1.14	5.80	1.30	6.14
Rec ∩ Rec	1.30	4.96	1.34	5.62

ANALYTICAL POWER AND SAMPLE SIZE CALCULATION

To further evaluate the performance of the proposed model at the parameters affecting power, we examined the analytical power and the required sample size of the proposed approach based on the non-centrality parameter approximation across a range of each parameter. The power to detect interaction effect was influenced by various parameters such as LD between marker and the putative QTL (D_AQ1, D_BQ2) and trait loci allele frequencies (p_Q1, p_Q2), observed marker allele frequencies (p_A, p_B), and heritability $h_{Q_1}^2={\sigma }_{ga1}^2/{\sigma }_1^2,h_{Q_2}^2={\sigma }_{ga2}^2/{\sigma }_2^2$ of the two putative QTLs. Based on the eight two-loci interaction models, we calculated additive variances at two loci and the total variance for non-centrality parameter λ_allele to estimate power and the required sample size.

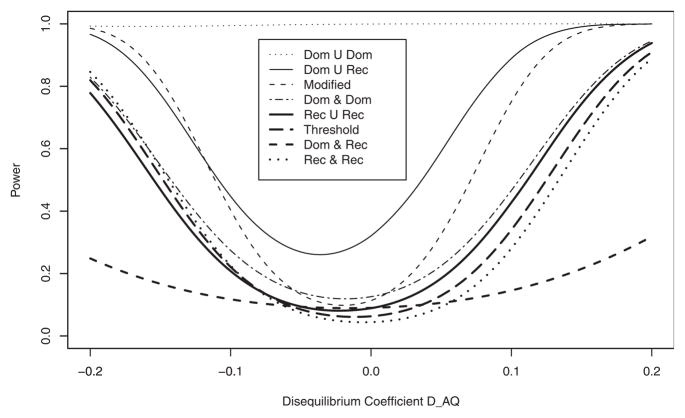
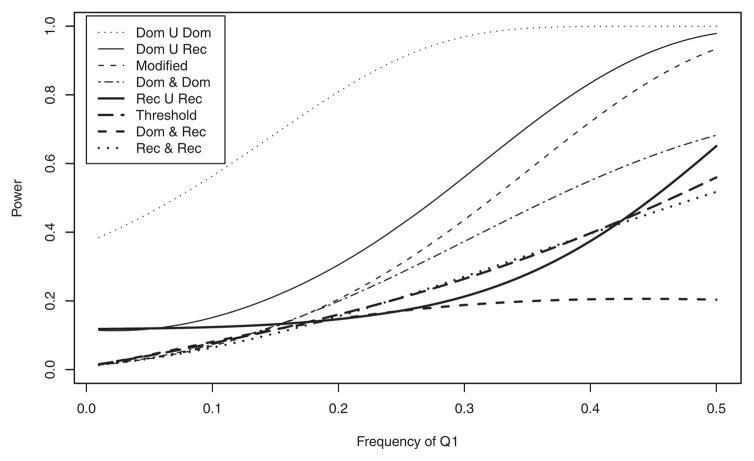
Figure 2 shows the analytical power curves of the test statistic F_allele plotted against LD coefficient D_AQ1 with the fixed value D_{BQ2 = 0.05} at the 1% significance level. Power is calculated under $h_{Q_1}^2=h_{Q_2}^2=0.2$; P_A = P_a = 0.5; P_B = P_b = 0.5 and sample size, N = 100. The power of “Dom ∪ Dom” model achieves 100% power over all range of LD. Powers are higher in the order of “Dom ∪ Rec”, “Modified”, “Dom ∩ Dom”, “Rec ∪ Rec”, “Threshold” at D_AQ1 −0.05, D_AQ1 0.05, whereas at −0.05 < D_AQ1 < 0.02, “Dom ∩ Rec” model is more powerful than “Threshold” and “Rec ∩ Rec”. Figure 3 illustrates power curves over the frequency of Q₁ allele (p_Q1) at $Q_1^{\ast }$ when fixed p_Q2 = 0.5 at 1% significance level. All parameters used for Figure 3 are the same as those used in Figure 2 except D_AQ1 = {min(P_Q1, P_A) − P_Q1 P_A}/2 according to p_Q1. Likewise as shown in Figure 2, the power of “Dom ∪ Dom” is the highest over all models at all range of p_Q1. “Dom ∪ Rec” has higher power than “Modified”, which in turn has higher power than “Dom ∩ Dom” at p_Q1 > 0.2. The patterns of power are very similar to those of powers shown in Figure 2 except “Rec ∪ Rec” whose power is lower than that of all models except “Dom ∩ Rec”. “Threshold” and “Rec ∩ Rec” achieve almost identical power.

Fig. 2.

Analytical power against D_AQ1 when D_BQ2 = 0.05 at 1% significance level. Dominant or Dominant model is indicated by Dom ∪ Dom, Dominant or Recessive model by Dom ∪ Rec, Dominant and Dominant model by Dom ∩ Dom, Recessive or Recessive model by Rec ∪ Rec, Dominant and Recessive model by Dom ∩ Rec and Recessive and Recessive model by Rec ∩ Rec. P_Q1 = 0.5; P_Q2 = 0.5; P_A = 0.5; P_B = 0.5; heritabilities $h_{Q_1}^2=0.2;h_{Q_2}^2=0.2$; the sample size N = 100.

Fig. 3.

Analytical power against frequency of Q₁ when P_Q2 = 0.5 at 1% significance level. P_A = 0.5; P_B = 0.5; D_AQ1 = {min(P_Q1, P_A) − P_Q1 P_A}/2; D_BQ2 = 0.05; heritabilities $h_{Q_1}^2=0.2;h_{Q_2}^2=0.2$; the sample size N = 100. Model notations are the same as in Figure 2.

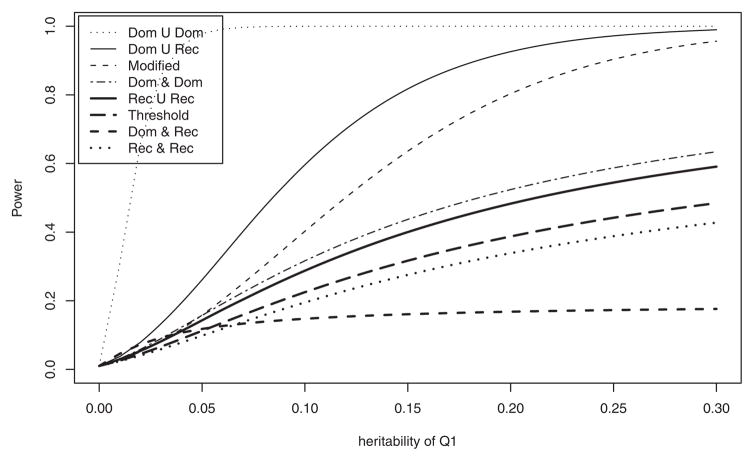
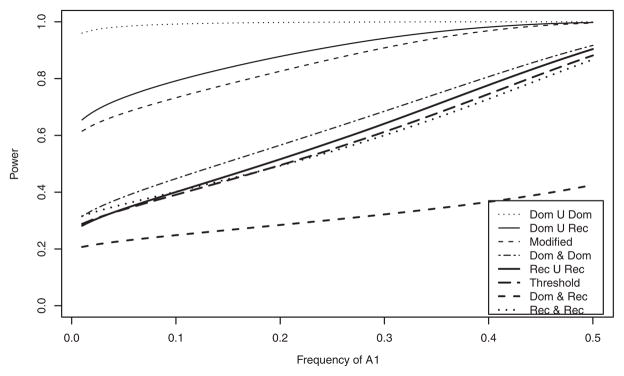
Figure 4 presents power curves against heritability ( $h_{Q_1}^2$) of QTL $Q_1^{\ast }$ when $h_{Q_2}^2=0.2$. Similarly the power of “Dom ∪ Dom” achieved the highest power over all models, and the “Dom ∪ Rec” has the second highest power. The power of all models follows the order stated from the top to the bottom in the legend, except that “Dom ∩ Rec” has the lowest power at $h_{Q_1}^2>0.05$. The powers for the interaction test with the A allele frequency of M₁, p_A when p_B = 0.5 are shown in Figure 5. As in the previous results, the power of “Dom ∪ Dom” has the highest power, and “Dom ∩ Rec” has the lowest power across all range of p_A < 0.5. “Threshold” and “Rec ∩ Rec” have almost the same power.

Fig. 4.

Analytical power against heritability of Q₁ when h_Q2= 0.2 at 1% significance level. P_Q1= 0.5; P_Q2 = 0.5; P_A = 0.5; P_B = 0.5; D_AQ1 = 0.1; D_BQ2= 0.05; heritabilities $h_{Q_1}^2=0.2;h_{Q_2}^2=0.2$; the sample size N = 100. Model notations are the same as in Figure 2.

Fig. 5.

Analytical power against frequency of A when P_B = 0.5 at 1% significance level. P_Q1 =0.5; P_Q2 = 0.5; D_AQ1 = {min(P_Q1, P_A) − P_Q1P_A}/2, D_BQ2 = 0.05; heritabilities $h_{Q_1}^2=0.1;h_{Q_2}^2=0.1$; the sample size N = 70. Model notations are the same as in Figure 2.

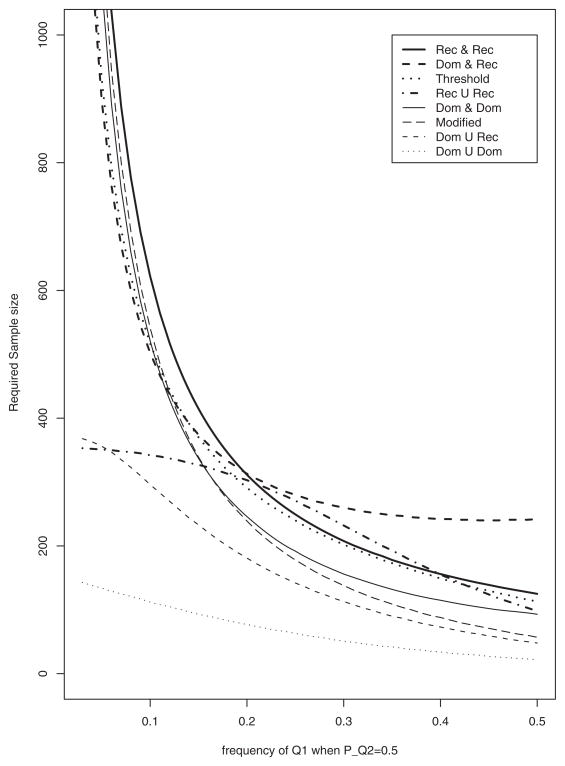
Figure 6 shows the required sample size of test statistic F_allele across the frequency of Q₁ allele (p_Q1) at $Q_1^{\ast }$ when fixed p_Q2 < 0.5 in order to achieve 80% power at 1% significance level. The sample size was calculated under $h_{Q_1}^2=h_{Q_2}^2=0.2$; P_A = P_a = 0.5; P_B = P_b = 0.5. Shown in Figure 6, at p_Q1 < 0.2 “Rec ∩ Rec” needs the largest sample size with over 400 subjects, whereas “ Dom ∩ Rec” requires the largest sample size over all model at p_Q1 > 0.2. “Dom ∪ Rec”, “Dom ∪ Dom” and “Rec ∪ Rec” need less than 400 subjects over all range.

Fig. 6.

The required sample size against P_Q1when P_Q2 = 0.5 for 80% power achievement at 1% significance level. P_A = 0.5; P_B = 0.5; D_AQ1 = {min(P_Q1, P_A) − P_Q1 P_A}/2; D_BQ2 = 0.05; heritabilities $h_{Q_1}^2=0.2;h_{Q_2}^2=0.2$. Model notations are the same as in Figure 2.

POWER COMPARISON WITH GENOTYPIC BASED METHOD USING SIMULATION STUDY

In order to compare the allelic-based gene-gene interaction method with the genotypic-based method, we modeled the genotypic-based method as follows. There are several genotypic-based approaches such as RPM, but these are not directly comparable. Therefore, we restricted our analysis to a regression method that takes into account the genotypic combinations of the two markers as follows. For ith subject,

$$y_i=w_i\gamma +\sum _{k=1}^9{Z}_{i,k=(jl,mn)}{\beta }_k+e_i,$$

where

$$\begin{array}{c}{Z}_{i,k=(jl,mn)}=\{\begin{array}{ll}1\hfill & \text{if}{G}_k=(jl,mn)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\text{and}\\ j,l=(A,\text{or}a),m,n=(B,\text{or}b)\end{array}$$

for example,

$$Z_{i,k=(AA,BB)}=\{\begin{array}{ll}1\hfill & \text{if}{G}_k=(AA,BB),\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

Under the null hypothesis of no interaction between two unlinked loci, H₀: β₁ = · · · = β₉ = μ and (Hβ)^t = (β₁ − β₂, β₁ − β₃, …, β₁ − β₉), the F-test statistic follows a F(8, N − 9) with λ = 0. Under the alternative hypothesis, the F is noncentral to F(8, N − 9, λ_genotype), with non-centrality parameter given by,

$$\begin{array}{l}{\lambda }_{\text{genotype}}\approx \frac{N}{{\sigma }^2}({\beta }_1-{\beta }_2,{\beta }_1-{\beta }_3,\dots ,{\beta }_1-{\beta }_9)\\ \times {[HE{(Z^{t}Z)}^{-1}{H}^t]}^{-1}\\ \times {({\beta }_1-{\beta }_2,{\beta }_1-{\beta }_3,\dots ,{\beta }_1-{\beta }_9)}^t.\end{array}$$

Likewise, we can also use the LRT, 2(L_HA − L_H0, where L_HA is the likelihood function under the alternative hypothesis, L_H0 is the likelihood function under the null hypothesis of H₀: β₁ = · · · = β₉ = μ. The LRT has chi-square distribution ${\chi }_8^2$.

We performed simulation studies to compare the empirical power between the allelic-based method and the genotypic-based methods. Using SNaP, we simulated 2,000 datasets with two scenarios of LD between markers and QTLs under 0.2 of disease associated quantitative allele (P_Q1 = P_Q2 = 0.2), and two markers allelic frequencies P_A = P_B = 0.3 in order to understand power in a more realistic situation: the first situation is relatively high LD between QTL and markers, $D_{{AQ}_1}^{\prime }=D_{{BQ}_2}^{\prime }=0.8;R_{{AQ}_1}^2=R_{{BQ}_2}^2=0.4$ and the second situation is low LD, $D_{{AQ}_1}^{\prime }=D_{{BQ}_2}^{\prime }=0.65;R_{{AQ}_1}^2=R_{{BQ}_2}^2=0.25$. Each dataset has 500 subjects. We explored the eight interaction models in Table II. Tables IV and V present the empirical power at the 1 and 5% significance level of both scenarios using both F-test and LRT statistics. We found that all models in the allelic-based method achieved higher power than those in the genotypic-based method except “Rec ∪ Rec”. The powers at “Dom ∪ Dom”, “Dom ∪ Rec”, “Dom ∩ Rec” and “Rec ∩ Rec” models are slightly higher in the allelic-based method or similar at both methods. The power of F-test and LR test are almost identical. Furthermore, we explored more scenarios such as perfect LD ( $R_{{AQ}_1}^2=R_{{BQ}_2}^2=1$) and very low LD ( $R_{{AQ}_1}^2=R_{{BQ}_2}^2<0.1$). Both scenarios do not provide information of powers over the models because some of the models achieve equally 100% for perfect LD scenario and some of models achieve almost no power for low LD scenario.

TABLE IV.

Power (%) at 1 and 5% significance level at $D_{{AQ}_1}^{\prime }=D_{{BQ}_2}^{\prime }=0.8;R_{{AQ}_1}^2=R_{{BQ}_2}^2=0.4$ from 2,000 datasets, each has 500 subjects

	Allelic-based method				Genotype-based method
	F-test		LR test		F-test		LR test
Model	α = 0.01	α = 0.05	α = 0.01	α = 0.05	α = 0.01	α = 0.05	α = 0.01	α = 0.05
Dom ∪ Dom	99.2	99.9	99.2	99.9	96.0	99.3	95.7	99.2
Dom ∪ Rec	99.2	99.9	99.3	99.9	98.1	99.4	98.0	99.3
Modified	89.4	97.0	89.8	97.2	81.6	93.2	80.8	93.0
Dom ∩ Dom	64.7	83.7	65.8	84.3	47.0	72.0	46.3	71.2
Rec ∪ Rec	18.4	38.6	18.9	39.4	26.0	48.4	25.5	48.1
Threshold	6.8	18.1	7.1	18.5	5.7	16.6	5.6	16.4
Dom ∩ Rec	2.0	7.5	2.3	7.8	1.9	8.2	1.9	8.2
Rec ∩ Rec	1.2	5.2	1.3	5.6	1.1	5.0	1.1	4.9

TABLE V.

Power (%) at 1 and 5% significance level at $D_{{AQ}_1}^{\prime }=D_{{BQ}_2}^{\prime }=0.65;R_{{AQ}_1}^2=R_{{BQ}_2}^2=0.25$ from 2,000 datasets, each has 500 subjects

	Allelic-based method				Genotype-based method
	F-test		LR test		F-test		LR test
Model	α = 0.01	α = 0.05	α = 0.01	α = 0.05	α = 0.01	α = 0.05	α = 0.01	α = 0.05
Dom ∪ Dom	88.6	96.6	89.3	96.7	73.1	89.6	72.1	89.3
Dom ∪ Rec	91.5	97.9	92.1	97.9	80.2	93.0	79.4	92.7
Modified	66.5	83.7	67.7	84.2	50.3	72.7	48.8	71.8
Dom ∩ Dom	36.9	61.2	38.8	62.1	24.2	46.8	23.2	45.7
Rec ∩ Rec	10.0	26.5	10.4	27.3	11.6	28.4	11.2	27.9
Threshold	4.2	13.3	4.4	13.7	3.4	12.2	3.4	12.0
Dom ∩ Rec	1.4	6.9	1.5	7.1	1.3	6.6	1.3	6.5
Rec ∩ Rec	1.0	5.6	1.0	5.8	0.9	4.2	0.9	4.1

APPLICATION TO GENETIC STUDY OF SODIUM RETENTION BY KIDNEY

Our proposed method is applicable to many different genotyping experiments including whole genome-wide association data or candidate gene studies. Here, we apply our method to a candidate gene study of renal sodium reabsorption and blood pressure (BP). An increase in sodium retention by the kidney has been shown to underlie an increased level of BP. Furthermore, African Americans (AA) retain more sodium in the kidney and have a higher prevalence of hypertension than European Americans [Guyton et al., 1972; Meneton et al., 2003].

Subjects consisted of 95 unrelated AAs aged 18–36 years. BP was measured under controlled conditions in an inpatient facility, the General Clinical Research Center at Indiana University–Purdue University at Indianapolis. We genotyped 67 SNPs in five genes which are known to regulate sodium reabsorption by the Na, K, 2Cl cotran-sporter in the kidney’s thick ascending limb [Hebert, 1998]: (1) a gene for a protein that facilitates Cl- transport (BSND: 10 SNPs), (2) the calcium-sensing receptor gene (CaSR: 17 SNPs), (3) a chloride channel kb gene (CLCNKB: 14 SNPs), (4) a potassium channel gene (KCNJ1: 11 SNPs), and (5) the gene for the cotransporter itself (CLC12A1: 15 SNPs). The procedure of the proposed method to search for the best interaction model consists of multiple steps: First, each SNP was individually tested for association with systolic and diastolic BP using a standard additive model [Fan et al., 2006] after we tagged SNPs using Hclust.R program [Rinaldo et al., 2005]. SNPs were ranked according to the P-values corresponding to the association test with diastolic BP as the quantitative phenotype. Second, the 20 SNPs that had the smallest P-values were selected. The 20 SNPs consisted of 8 SNPs with P-value <0.05 and 12 SNPs with P-value between 0.05 and 0.2. The SNPs created 2,400 cases of 5 way (five SNPs) combinations when choosing one SNP from each gene. We applied our method to 2,400 cases of 5 way interaction and found that only 4 cases of the 5 way combinations were statistically significant after the application of a Bonferroni correction for multiple comparisons (α<=0.0002) using LRT statistics. Third, we then employed a backward elimination model selection method to search for the best model as we dropped one SNP from the selected 5 way interaction model. We applied the same procedure to all four cases chosen from the second step. The P-value from the F-test statistic from the full (5 way) and reduced model (4 way) was calculated by

$$\begin{array}{l}F=\frac{\text{RSS}(\text{reduced})-\text{RSS}(\text{full})}{\text{RSS}(\text{full})}\\ \times \frac{n-\text{df}(\text{full})}{\text{df}(\text{full})-\text{df}(\text{reduced})},\end{array}$$

where RSS(·) denotes the residual sum of square and df is degree of freedom. We also calculated Bayesian information criterion (BIC), which is a criterion for model selection as it takes into account a penalty to an increase of the number of parameters. Based on P-value of the full-reduced F-test statistic (adjusted Bonferroni correction at significance level 0.05) and smallest BIC including P-value of the 4 way interaction analysis, we chose the two significant models of the 4 (SNPs) way interaction from the four cases of 5 ways; (1) BSND, CaSR, CLCNKB, CLC12A1 genes, (2) BSND, CLCNKB, CLC12A1, KCNJ1 genes. Fourth, we continued this procedure until 2 way interaction analysis performed and the best interaction models are determined by the criteria (significance of interaction model, full-reduced F-test statistic and BIC). Among the five unlinked genes, the 3 way interaction model consisting of rs3749204 from CaSR, rs2297727 from CLCNKB and rs2279366 from SLC12A1 was determined to be the best interaction model (P-value = 0.02 in LRT of the interaction model, P-value = 0.07 in the full-reduced F). Rs3749204 has 0.1 of P-value, and both rs2297727 and rs2279366 have 0.047 of P-value. Additionally, we investigated which combination of alleles among three SNPs creates the interaction effect and identified that allele A at rs3749204, allele T at rs2297727 and allele C at rs2279366 are associated interactively with diastolic BP (β_ATC = 22.11, LRT = 9.95, P-value = 0.002).

DISCUSSION

Advanced genotyping technologies make genome-wide association studies possible for many common complex diseases. It has been known that multiple genes along with the environment play interactive roles contributing to the development of complex diseases. Single marker association tests often fail to identify causal association with disease due to biological complexity or lack of a strong association signal due to the small sample size. Therefore, the search for genetic interactions has become a reasonable next step. Most of the current approaches test for interaction at the genotype level. In this article, we proposed a method to identify gene-gene interaction at the allelic level for QTL. The allelic approach provides several advantages for detecting genetic interactions contributing to a quantitative trait: (1) This method can detect the interaction of SNPs when the contribution to disease of a particular allele inherited in one gene depends on a particular allele inherited at other unlinked genes, which is a novel definition for the allelic-based gene-gene interaction. (2) The method can identify the interaction of important SNPs with or without main effects when important SNPs may not be detected using a single marker test. (3) The biological interpretation may be more straightforward at the allelic rather than the genotypic level because the interacting alleles can be explained by combinations of disease-associated alleles, whereas the genotypic method cannot explain the interaction simply due to a lack of an interpretable relationship between the genotypes combined in a cluster.

There are several criteria by which the genotype-based and allelic-based methods can be compared. Genotype-based approaches can increase the degrees of freedom of a test statistic, resulting in a concomitant loss of power when multiple unlinked markers (i.e. more than 3) are tested for interaction. In contrast, the allelic-based method can reduce the number of degrees of freedom by accounting for allelic levels. Furthermore, the power of the genotype-based method may be compromised by sparse or empty combination caused by multiple markers with small sample sizes and a lower minor allele frequency (<0.1). However, the allelic-based method is relatively robust even with lower minor allele frequencies and small sample sizes. The application to renal sodium reabsorption and BP demonstrates the feasibility of our proposed method. The reported results of gene-gene interaction associated with the Na, K, 2Cl cotransporter in the kidney’s thick ascending limb is novel. Subsequent studies must be performed based on more phenotypes related to the sodium retention. In addition, regardless of the type of test used to evaluate gene-gene interaction, molecular studies will need to be performed to test whether and how the statistical interactions reflect an underlying biological interactions.

Our approach to detect interaction effect is different from the more conventional models such as the method of Wang and Zheng [2006] and that of Fan et al. [2006]. We do not implement the main additive and dominance effect on the model. Additionally, the interaction terms in the traditional methods were modeled by multiplication of two main effect variables (i.e. additive × additive, additive × dominance, dominance × dominance). The method of Wang and Zheng [2006] allowed Hardy-Weinberg and LD among two markers, which would be more appropriate to test an interaction among linked genes. The test of interaction is limited to the way to score the additive and dominance variables in the model (i.e. in additive variable X₁ = 0, 1, 2, X₂ = 0, 1, 2 according to the number of copies of any allele and the interaction variable is X₁ × X₂ = 0, 1, 2, 4). We performed simulation study to compare the power between the commonly used model, y_i = μ + β_AX₁ + β_BX₂ + β_AB (X₁ * X₂) + ε_i, and our proposed model (1) and found that both methods achieved the same power under the null hypothesis of no genetic effects regardless of the source of effects. However, the parameters in the two methods explain the different genetic effects: all three parameters in our model are associated with interaction effects and tested for interactions, but one of three parameters in the traditional model is associated with an interaction and tested for the interaction effect. Further simulation was carried out for the power comparison between the two models under the null hypothesis of no genetic interaction effect. The result shows that the interaction effect (β_AB) in the commonly used model does not achieve high power to detect interaction effect compared with the allelic-based method (results not shown). Moreover, the traditional model can only test for an interaction caused by the specified alleles of markers, which depends on a dosage of the alleles at X₁, X₂ in the model. In contrast with that, our proposed method can test all possible allelic interaction between two markers which may or may not have main effects. However, the issue of multiple comparisons still remains in the high dimensionality, which is inherent in a genome-wide association approach. Devlin et al. [2003] presented a procedure to control the false discovery rate in multiple markers analysis under the assumption of independence of SNPs, but there remains in ongoing studies the need to resolve the challenge of dependent P-values that may be created due to the LD between markers. In our currently proposed approach, we suggest a two-stage analysis; initially, individual marker analysis followed by selection of the 5–10% of markers with marginal main effects. The selected markers are then used to identify gene-gene interaction at the allelic level.

Detection of gene-gene interaction is an important procedure in genome-wide association research, but is a complex concept due to a variety of definition. Furthermore, one may want to test for association of quantitative traits measured in case-control based ascertained genome-wide association data subsequently after case and control genome scan. Even our method is designed for randomly ascertained data, the approach could be extended to incorporate the case/control status in the model. Integration of biological knowledge of pathway into gene-gene interaction may help select high-priority candidate genes that potentially play a role in physiological and genetic meaning of interactions. Future work is needed to develop and evaluate more statistical methods that can handle various study designs such as case-control data at the allelic level.

APPENDIX A

Under the assumption of no covariates for simplification, we multiply both sides by $X=(X_{AB}^{\tau },X_{Ab}^{\tau },X_{aB}^{\tau },X_{ab}^{\tau })$, where X_AB = (X_1,AB, X_2.AB, …, X_N,AB)^τ and take the expectation in order to derive regression coefficients in Equation (1)

$$\begin{array}{l}E\left(\begin{array}{c}{X}_{AB}y\\ X_{Ab}y\\ X_{aB}y\\ X_{ab}y\end{array}\right)=E\left(\begin{array}{cccc}{X}_{AB}^2& X_{AB}{X}_{Ab}& X_{AB}{X}_{aB}& X_{AB}{X}_{ab}\\ X_{Ab}{X}_{AB}& X_{Ab}^2& X_{Ab}{X}_{aB}& X_{Ab}{X}_{ab}\\ X_{aB}{X}_{AB}& X_{aB}{X}_{Ab}& X_{aB}^2& X_{aB}{X}_{ab}\\ X_{ab}{X}_{AB}& X_{ab}{X}_{Ab}& X_{ab}{X}_{aB}& X_{ab}^2\end{array}\right)\\ \times \left(\begin{array}{c}{\beta }_{AB}\\ {\beta }_{Ab}\\ ⋮\\ {\beta }_{ab}\end{array}\right).\end{array}$$ (A1)

The expectation of each element in matrix E(X′X) is calculated as follows:

$$\begin{array}{l}E(X_{AB})=P_A{P}_B,E(X_{Ab})=P_A{P}_b,E(X_{aB})=P_a{P}_B,\\ E(X_{ab})=P_a{P}_b,\\ E(X_{AB}{X}_{Ab})=0.5P_A{P}_B{P}_b(1-0.5P_a),\\ E(X_{AB}{X}_{aB})=0.5P_A{P}_B{P}_b(1-0.5P_a),\dots ,\\ E(X_{aB}{X}_{ab})=0.5P_a{P}_B{P}_b(1-0.5P_A).\end{array}$$

Therefore,

$$\begin{array}{l}E(X^{\prime }X)\\ =\left(\begin{array}{cccc}{P}_A{P}_B(1-0.5P_a)(1-0.5P_b)& 0.5P_A{P}_B{P}_b(1-0.5P_a)& 0.5P_A{P}_B{P}_a(1-0.5P_b)& 0.25P_A{P}_B{P}_b{P}_a\\ 0.5P_A{P}_B{P}_b(1-0.5P_a)& P_A{P}_b(1-0.5P_a)(1-0.5P_B)& 0.25P_A{P}_B{P}_b{P}_a& 0.5P_A{P}_a{P}_b(1-0.5P_B)\\ 0.5P_A{P}_B{P}_a(1-0.5P_b)& 0.25P_A{P}_B{P}_b{P}_a& P_a{P}_B(1-0.5P_A)(1-0.5P_b)& 0.5P_a{P}_B{P}_b(1-0.5P_A)\\ 0.25P_A{P}_B{P}_b{P}_a& 0.5P_A{P}_a{P}_b(1-0.5P_B)& 0.5P_a{P}_B{P}_b(1-0.5P_A)& P_a{P}_b(1-0.5P_A)(1-0.5P_B)\end{array}\right).\end{array}$$

The expectation $E(X_{C}y)={\sum }_{\mathit{ijkl}}{\sum }_C{\mu }_{\mathit{ijkl}}P(C\mid M_1,M_2)\times P(Q_1^{\ast },Q_2^{\ast },M_1,M_2)$, where P(C_m|M₁, M₂) is an allelic combination score given the genotype markers M₁, M₂ and

$$y=\{\begin{array}{ll}{\mu }_{\mathit{ijkl}}& i,j=(Q_1,q_1),k,l=(Q_2,q_2),\\ 0& \text{otherwise}.\end{array}$$

For example, the expectation

$$\begin{array}{l}E(X_{AB}y)=1\times \{{\mu }_{1111}\times P(Q_1^{\ast }=Q_1{Q}_1,Q_2^{\ast }=Q_2{Q}_2,\\ M_1=AA,M_2=BB)+\cdots +{\mu }_{2222}\\ \times P(q_1{q}_1,q_2{q}_2,AA,BB)\}\\ +\frac{1}{2}\times \{{\mu }_{1111}\times P(Q_1{Q}_1,Q_2{Q}_2,AA,Bb)\\ +\cdots +{\mu }_{2222}\times P(q_1{q}_1,q_2{q}_2,AA,Bb)\}\\ +\frac{1}{2}\times \{{\mu }_{1111}\times P(Q_1{Q}_1,Q_2{Q}_2,Aa,BB)\\ +\cdots +{\mu }_{2222}\times P(q_1{q}_1,q_2{q}_2,Aa,BB)\}\\ +\frac{1}{4}\times \{{\mu }_{1111}\times P(Q_1{Q}_1,Q_2{Q}_2,Aa,Bb)\\ +\cdots +{\mu }_{2222}\times P(q_1{q}_1,q_2{q}_2,Aa,Bb)\}\\ ={\mu }_{1111}\{p{({AQ}_1)}^{2}P{({BQ}_2)}^2+\frac{1}{2}\\ \times 2p{({AQ}_1)}^{2}P({BQ}_2)P({bQ}_2)\\ +\frac{1}{2}\times 2p({AQ}_1)p({aQ}_1)P{({BQ}_2)}^2\\ +\frac{1}{4}\times 4p({AQ}_1)p({aQ}_1)P({BQ}_2)P({bQ}_2)\}\\ +\cdots +{\mu }_{2222}\{p{({Aq}_1)}^{2}P{({Bq}_2)}^2\\ +\frac{1}{2}\times 2p{({Aq}_1)}^{2}P({Bq}_2)P({bq}_2)\\ +\frac{1}{2}\times 2p({Aq}_1)p({aq}_1)P{({Bq}_2)}^2\\ +\frac{1}{4}\times 4p({Aq}_1)p({aq}_1)P({Bq}_2)P({bq}_2)\},\\ E(X_{AB}y)=P({AQ}_1)P({BQ}_2)\{{\mu }_{1111}P(Q_1)P(Q_2)\\ +{\mu }_{1112}P(Q_1)P(q_2)\\ +{\mu }_{1211}P(q_1)P(Q_2)+{\mu }_{1212}P(q_1)P(q_2)\}\\ +P({AQ}_1)P({Bq}_2)\{{\mu }_{1112}P(Q_1)P(Q_2)\\ +{\mu }_{1122}P(Q_1)P(q_2)\\ +{\mu }_{1212}P(q_1)P(q_2)+{\mu }_{1222}P(q_1)P(q_2)\}\\ +P({Aq}_1)P({BQ}_2)\{{\mu }_{1211}P(Q_1)P(Q_2)\\ +{\mu }_{1212}P(Q_1)P(q_2)\\ +{\mu }_{2211}P(q_1)P(Q_2)+{\mu }_{2212}P(q_1)P(q_2)\}\\ +P({Aq}_1)P({Bq}_2)\{{\mu }_{1212}P(Q_1)P(Q_2)\\ +{\mu }_{1222}P(Q_1)P(q_2)\\ +{\mu }_{2212}P(q_1)P(Q_2)+{\mu }_{2222}P(q_1)P(q_2)\}.\end{array}$$

Utilizing P(AQ₁) = D_AQ1+P_AP_Q1; P(Aq₁) = D_Aq1 + P_AP_q1; P(BQ₂) = D_BQ2 + P_BP_Q2; P(bq₂) = D_bq2 + P_bP_q2 and μ_Q1Q2 = μ₁₁₁₁ P(Q₁)P(Q₂) μ₁₁₁₂ P(Q₁)P(q₂) + μ₁₂₁₁P(q₁)P(Q₂) + μ₁₂₁₂P(q₁)P(q₂), similarly derived μ_Q1q2, μ_q1Q2, μ_q1q2give

$$\begin{array}{l}E(X_{AB}y)=(D_{{AQ}_1}+P_A{P}_{Q_1})\times (D_{{BQ}_2}+P_B{P}_{Q_2}){\mu }_{Q_1{Q}_2}\\ +\cdots +(D_{A{d}_1}+P_A{P}_{d_1})\times (D_{{Bq}_2}+P_B{P}_{q_2}){\mu }_{q_1{q}_2}\\ =\mu P_A{P}_B+({\mu }_{Q_1{Q}_2}-{\mu }_{Q_1{q}_2}-{\mu }_{q_1{Q}_2}+{\mu }_{q_1{q}_2})D_{{AQ}_1}{D}_{{BQ}_2}\\ +({\mu }_{Q_1}-{\mu }_{q_1})D_{{AQ}_1}{P}_B+({\mu }_{Q_2}-{\mu }_{q_2})D_{{BQ}_1}{P}_A.\end{array}$$

With the same derivation of E(X_Aby);E(X_aBy);E(X_aby) and

$$\begin{array}{l}{D}_{{AQ}_1}=-D_{{aQ}_1}=-D_{{Aq}_1},D_{{AQ}_1}=D_{{aq}_1},\\ D_{{BQ}_2}=-D_{{bQ}_2}=-D_{{Bq}_2},D_{{BQ}_2}=D_{{bq}_2},\end{array}$$

$$\begin{array}{l}E(Xy)=\left(\begin{array}{c}{P}_A{P}_B\\ P_a{P}_B\\ P_A{P}_b\\ P_a{P}_b\end{array}\right)\mu +({\mu }_{Q_1{Q}_2}-{\mu }_{Q_1{q}_2}-{\mu }_{q_1{Q}_2}+{\mu }_{q_1{q}_2})\\ \times \left(\begin{array}{c}{D}_{{AQ}_1}{D}_{{BQ}_2}\\ D_{{AQ}_1}{D}_{{bQ}_2}\\ D_{{aQ}_1}{D}_{{BQ}_2}\\ D_{{aQ}_1}{D}_{{bQ}_2}\end{array}\right)+({\mu }_{Q_1}-{\mu }_{q_1})\left(\begin{array}{c}{D}_{{AQ}_1}{P}_B\\ D_{{AQ}_1}{P}_b\\ D_{{aQ}_1}{P}_B\\ D_{{aQ}_1}{P}_b\end{array}\right)\\ +({\mu }_{Q_2}-{\mu }_{q_2})\left(\begin{array}{c}{D}_{{BQ}_2}{P}_A\\ D_{{bQ}_2}{P}_A\\ D_{{BQ}_1}{P}_a\\ D_{{bQ}_1}{P}_a\end{array}\right).\end{array}$$

Equation (A.1) can be expressed as follows:

$$\begin{array}{l}\stackrel{⌢}{\beta }=E{(X^{t}X)}^{-1}[\left(\begin{array}{c}{P}_A{P}_B\\ P_a{P}_B\\ P_A{P}_b\\ P_a{P}_b\end{array}\right)\mu \\ +({\mu }_{Q_1{Q}_2}-{\mu }_{Q_1{q}_2}-{\mu }_{q_1{Q}_2}+{\mu }_{q_1{q}_2})\left(\begin{array}{c}{D}_{{AQ}_1}{D}_{{BQ}_2}\\ D_{{AQ}_1}{D}_{{bQ}_2}\\ D_{{aQ}_1}{D}_{{BQ}_2}\\ D_{{aQ}_1}{D}_{{bQ}_2}\end{array}\right)\\ +({\mu }_{Q_1}-{\mu }_{q_1})\left(\begin{array}{c}{D}_{{AQ}_1}{P}_B\\ D_{{AQ}_1}{P}_b\\ D_{{aQ}_1}{P}_B\\ D_{{aQ}_1}{P}_b\end{array}\right)+({\mu }_{Q_2}-{\mu }_{q_2})\left(\begin{array}{c}{D}_{{BQ}_2}{P}_A\\ D_{{bQ}_2}{P}_A\\ D_{{BQ}_2}{P}_a\\ D_{{bQ}_2}{P}_a\end{array}\right)]\\ =K^{-1}[\mu \left(\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right)\\ +({\mu }_{Q_1{Q}_2}-{\mu }_{Q_1{q}_2}-{\mu }_{q_1{Q}_2}+{\mu }_{q_1{q}_2})\left(\begin{array}{c}{D}_{{AQ}_1}{D}_{{BQ}_2}/P_A{P}_B\\ D_{{AQ}_1}{D}_{{bQ}_2}/P_A{P}_b\\ D_{{aQ}_1}{D}_{{BQ}_2}/P_a{P}_B\\ D_{{aQ}_1}{D}_{{bQ}_2}/P_a{P}_b\end{array}\right)\\ +({\mu }_{Q_1}-{\mu }_{q_1})\left(\begin{array}{c}{D}_{{AQ}_1}/P_A\\ D_{{AQ}_1}/P_A\\ D_{{aQ}_1}/P_a\\ D_{{aQ}_1}/P_a\end{array}\right)+({\mu }_{Q_2}-{\mu }_{q_2})\left(\begin{array}{c}{D}_{{BQ}_2}/P_B\\ D_{{bQ}_2}/P_b\\ D_{{BQ}_2}/P_B\\ D_{{bQ}_2}/P_b\end{array}\right)],\end{array}$$

where

$$K=\left(\begin{array}{cccc}(1-0.5P_a)(1-0.5P_b)& 0.5P_b(1-0.5P_a)& 0.5P_a(1-0.5P_b)& 0.25P_b{P}_a\\ 0.5P_B(1-0.5P_a)& (1-0.5P_a)(1-0.5P_B)& 0.25P_a{P}_B& 0.5P_a(1-0.5P_B)\\ 0.5P_A(1-0.5P_b)& 0.25P_A{P}_b& (1-0.5P_A)(1-0.5P_b)& 0.5P_b(1-0.5P_A)\\ 0.25P_A{P}_B& 0.5P_A(1-0.5P_B)& 0.5P_B(1-0.5P_A)& (1-0.5P_A)(1-0.5P_B)\end{array}\right).$$

The ${\alpha }_{Q_1^{\ast }}=({\mu }_{Q_1}-{\mu }_{q_1}),{\alpha }_{Q_2^{\ast }}=({\mu }_{Q_2}-{\mu }_{q_2})$ can be defined by the average effect of the gene substitution and (μ_Q1Q2 − μ_Q1q2 − μ_q1Q2 + μ_q1q2) is the magnitude of interaction effect.