Abstract
Pollinator-mediated stabilizing selection (PMSS) has been proposed as the driver of the evolutionary shift from radial to bilateral symmetry of flowers. Studies have shown that variation in flower size is lower in bilateral than in radial species, but whether bilateral flowers experience more stabilizing selection pressures by employing fewer, more specialized pollinators than radial flowers remains unclear. To test the PMSS hypothesis, we investigate plant–pollinator interactions from a whole community in an alpine meadow in Hengduan Mountains, China, to examine: (i) variance in flower size and level of ecological generalization (pollinator diversity calculated using functional groups) in 14 bilateral and 13 radial species and (ii) the role pollinator diversity played in explaining the difference of variance in flower size between bilateral and radial species. Our data showed that bilateral species had less variance in flower size and were visited by fewer pollinator groups. Pollinator diversity accounted for up to 40 per cent of the difference in variance in flower size between bilateral and radial species. The mediator effect of pollinator diversity on the relationship between floral symmetry and variance in flower size in the community is consistent with the PMSS hypothesis.
Keywords: bilateral and radial, variance in flower size, pollinator diversity, ecological specialization, pollinator-mediated stabilizing selection, mediator effect
1. Introduction
Pollinator-mediated selection has been considered as one key factor moulding the evolution of floral traits (Stebbins 1974). The shift in flower symmetry from radial to bilateral, important in the evolution of flowering plants, is thought to have occurred as a consequence of strong selection exerted by specialized pollinators (Neal et al. 1998; Endress 2001). Bilateral flowers, which are often visited by one type of pollinator (Stebbins 1951; Fenster et al. 2004), may obtain higher pollination efficiency because of the accuracy of the physical fit between flower and pollinator (Wolfe & Barrett 1987; Harder & Barrett 1993). This specialized pollinator system might mediate stabilizing selection, and thus variation in flower size would be lower in species with bilateral flowers than radial flowers (Armbruster et al. 1999; Wolfe & Krstolic 1999), as postulated by the pollinator-mediated stabilizing selection (PMSS) hypothesis (Wolfe & Krstolic 1999). In contrast, radial flowers are often pollinated by a wider range of animal species because of their simpler structures (Cronk & Möller 1997; Richards 1997). The diversity of pollinators causes radial symmetry to be associated with unstable selection and correspondingly permits large variation in phenotypes (Fisher 1958; Lande & Arnold 1983). Variation in flower size and lack of specific pollinators could reduce pollination efficiency per visit of radial species (Faegri & van der Pijl 1979; Ingrouille 1992; Endress 1999).
Several comparisons of variation in floral traits have demonstrated that bilateral flowers were less variable in size than radial flowers (Armbruster et al. 1999; Wolfe & Krstolic 1999; Ushimaru et al. 2007; Herrera et al. 2008; van Kleunen et al. 2008), supporting the PMSS hypothesis. However, it remains unclear whether variance in the flower size is associated with pollinator diversity. One would expect bilateral species to employ few specialized pollinators compared with radial species. If large variation in flower size is associated with high pollinator diversity, and less variation in flower size is associated with low pollinator diversity, it would provide evidence to support the PMSS hypothesis.
To further test the PMSS hypothesis, it is necessary to evaluate the difference of pollinator diversity between bilateral and radial species. We initially performed a multivariate analysis to illustrate preferences of pollinator groups for different floral symmetries. Then, we quantified the level of pollination generalization or specialization (as a measure of pollinator diversity), given pollination systems ranging from specialized to generalized in species with both bilateral and radial flowers (Ollerton et al. 2007; Lázaro et al. 2008). The approach of characterizing ecological generalization in plant pollination systems (Sahli & Conner 2006) permits us to estimate the level of pollinator generalization using functional groups. Here, we investigate variance in flower size and the level of ecological generalization in plant–pollinator interactions in an alpine meadow in Hengduan Mountains, China, using data from 14 bilateral and 13 radial species from one community to: (i) estimate the difference of variance in flower size and preference of pollinators between bilateral and radial species, (ii) evaluate the role of pollinator-mediated selection in variance in flower size between bilateral and radial species and (iii) examine the relationships between variance in flower size and ecological generalization (pollinator diversity) across levels of floral symmetry.
2. Material and methods
(a). Study community
We investigated flower size and plant–pollinator interactions in a species-rich montane meadow in Shangri-La Alpine Botanical Garden in Hengduan Mountains, Yunnan Province, China (27°54′230″ N, 99°38′298″ E, 3250 m in altitude), in one of the world's biodiversity hotspots. The meadow is about 40 × 100 m2 and is fenced by the wall of the garden, so disturbance by human beings and livestock is avoided. We recorded a total of 41 insect-pollinated flowering species during fieldwork in 2008 within the study community. Thirty-three of these species flowered simultaneously at peak flowering in August. Table 1 shows the 27 plant species included in the analysis (for details of the selection of species, see §2c). Bumblebees (Bombus spp.), muscoid flies (Muscidae) and hoverflies (Syrphidae) were the most frequent pollinators and accounted for 36.1 per cent, 34.8 per cent and 17.4 per cent of the total 35 894 visits that we recorded (see below), respectively. Other pollinator groups included solitary bees (Halictidae, 7.0%), ants (Formicidae, 3.2%), wasps (Ichneumonidae, 0.6%), butterflies (Lepidoptera, 0.4%), beetles (Coleoptera, 0.3%) and beeflies (Bombylius minor, 0.2%).
Table 1.
Basic characteristics of the 27 plant species in the study community. ‘Visual units’ are S for single flower, I for inflorescence. ‘Flower formulae’ for the measurement of area of floral visual units: L × W (length × width) for square-shaped floral visual units, πR2 (R = radius) for flowers with circular outlines, 4πR2 for three-dimensional orbicular floral visual units, and for floral visual units with a depth dimension, D, we used 2πRD + πR2 (D = depth). ‘All visits’ are the total numbers of visits of the pollinator groups recorded to each plant species. ‘Main visitor’ shows the insect group that visited a species most frequently. PG is the level of pollinator generalization and CV is the coefficient of variation of the floral visual unit area of each plant species.
| study species | family | visual unit | flower formula | all visits | main visitor | PG | CV |
|---|---|---|---|---|---|---|---|
| Bilateral symmetry | |||||||
| Ajuga forrestii | Lamiaceae | S | L × W | 1356 | bumble-bees | 1.052 | 0.191 |
| Astragalus pullus | Fabaceae | I | 4πR2 | 843 | bumble-bees | 1.012 | 0.129 |
| D. asperoides | Dipsacaceae | I | 4πR2 | 1969 | bumble-bees | 1.467 | 0.177 |
| Oreorchis foliosa | Orchidaceae | S | L × W | 32 | muscoid flies | 2.547 | 0.173 |
| Origanum vulgare | Lamiaceae | I | L × W | 1077 | bumble-bees | 2.737 | 0.318 |
| Pedicularis confertiflora | Orobanchaceae | S | L × W | 9 | bumble-bees | 1 | 0.236 |
| Pedicularis densispica | Orobanchaceae | S | L × W | 5080 | bumble-bees | 1 | 0.178 |
| P. tricolor | Orobanchaceae | S | L × W | 325 | bumble-bees | 1 | 0.163 |
| Phlomis forrestii | Lamiaceae | S | L × W | 9 | bumble-bees | 1.528 | 0.268 |
| Phlomis melanantha | Lamiaceae | S | L × W | 12 | bumble-bees | 1.600 | 0.355 |
| Salvia przewalskii | Lamiaceae | S | 2πRD + πR2 | 2105 | bumble-bees | 1.002 | 0.213 |
| Tibetia himalaica | Fabaceae | S | L × W | 97 | bumble-bees | 1 | 0.232 |
| Trigonella pubescens | Fabaceae | S | L × W | 74 | solitary bees | 1.513 | 0.201 |
| Vicia tibetica | Fabaceae | S | L × W | 460 | bumble-bees | 1 | 0.161 |
| Radial symmetry | |||||||
| Anaphalis yunnanensis | Asteraceae | I | πR2 | 24 | hoverflies | 2.165 | 0.527 |
| Aster yunnanensis | Asteraceae | I | πR2 | 900 | hoverflies | 2.123 | 0.255 |
| C. approximata | Convolvulaceae | I | 4πR2 | 1 | hoverflies | 1 | 0.301 |
| Daucus carota | Apiaceae | I | πR2 | 3371 | muscoid flies | 1.996 | 0.309 |
| E. brevifolium | Onagraceae | S | πR2 | 16 | solitary bees | 2.612 | 0.514 |
| Halenia elliptica | Gentianaceae | S | 2πRD + πR2 | 427 | bumble-bees | 1.019 | 0.253 |
| Ixeridium biparum | Asteraceae | I | πR2 | 401 | solitary bees | 2.965 | 0.486 |
| L. andersonii | Asteraceae | I | L × W | 3 | diverse insects | 3 | 0.574 |
| O. confertum | Boraginaceae | S | 2πRD + πR2 | 99 | bumble-bees | 1 | 0.139 |
| Pleurospermum davidii | Apiaceae | I | πR2 | 15 401 | muscoid flies | 2.215 | 0.307 |
| P. lancinata | Rosaceae | S | πR2 | 1723 | solitary bees | 2.444 | 0.186 |
| Spenceria ramalana | Rosaceae | S | πR2 | 36 | muscoid flies | 3.028 | 0.274 |
| Stellaria graminea | Caryophyllaceae | S | πR2 | 44 | solitary bees | 1.148 | 0.318 |
(b). Measurements of flower visual size
Flower measurements were conducted in the field using digital calipers and a portable anatomical lens on one flower per plant. We measured the area of one ‘floral visual unit’ on each of 20 randomly selected plants of each species to represent flower size following the method of Wolfe & Krstolic (1999) since several studies have established that the intraplant variance in flower size was substantially smaller than the variance among individuals (Wolfe & Krstolic 1999; Ushimaru et al. 2007; Herrera et al. 2008). A floral visual unit acted as a functional unit for pollinator attraction (Dafni 1994; Hegland & Totland 2005), which was identified as a solitary flower (e.g. Epilobium brevifolium) or an inflorescence (e.g. Dipsacus asperoides) with individual florets clustering together which cannot be easily counted in the field (table 1). Floral symmetry was classified according to flower characteristics of each species. Species in the Asteraceae that contain both bilateral ray florets and radial disc florets have been assigned to radial species following Hegland & Totland (2005) and Lázaro et al.'s (2008) classifications. Following Dafni (1994) and Hegland & Totland (2005), the area in one plane of floral visual units of each species was calculated according to the shape of the flower. For circular ones (e.g. Potentilla lancinata), we calculated the area using the formula πR2, and for other flat floral visual units (e.g. Pedicularis tricolor), we used the formula L × W (length × width). Deviating from Hegland & Totland's (2005) formulae, 4πR2 was used for convex or domed floral visual units (e.g. Cuscuta approximata), and for other three-dimensional ones with a depth dimension, D (e.g. Onosma confertum), we used 2πRD + πR2. The last two formulae are different from those used by Hegland & Totland (2005) but adjust more accurately to the shape of the flowers (S. J. Hegland 2007, personal communication; see table 1 for formulae used for each species).
(c). Observations of pollinator assemblages
Pollinator visitation was observed, in 12 permanent 2 × 2 m2 plots, from July to August 2008 because this period covered the flowering season of most plant species in the community, and thus the main period for pollinator activity. The plots are located in the community in four rows and three lines and the distance between adjacent plots is 10 m in a row and 20 m in a line. Within each plot, we counted the number of visits of the nine visitor groups to flowering units for each plant species during 30 min observation periods. All observations were made on sunny days without strong wind. In total, we conducted 108 observation periods (i.e. 3240 min in total) during the flowering season. We considered as pollinators those flower visitors that actually landed on the flowering head or contacted the sexual organs for more than 1 second searching for pollen and/or nectar (Memmott 1999; Hegland & Totland 2005). Those plant species that were observed in fewer than six periods throughout the study period were not included in the final analysis, yielding a sample of 27 plant species. We recorded the number of floral visual units of each plant species within the plot before each observation period.
(d). Pollinator diversity and the coefficient of variation of flower size
Pollinator generalization (PG) level (table 1) was measured as the pollinator diversity for each plant species, using the total number of visits recorded during their flowering period. We classified pollinators into nine functional groups including bumble-bees (Bombus spp.), muscoid flies (Muscidae), hoverflies (Syrphidae), solitary bees (Halictidae), ants (Formicidae), wasps (Ichneumonidae), butterflies (Lepidoptera), beetles (Coleoptera) and beeflies (Bombylius minor). Functional groups were used instead of pollinator species because our observations indicated that the members of each functional group behaved similarly in flowers, and so would exert similar selection on flowers (Fenster et al. 2004). Following Sahli & Conner (2006), we used Simpson's (1949) diversity index
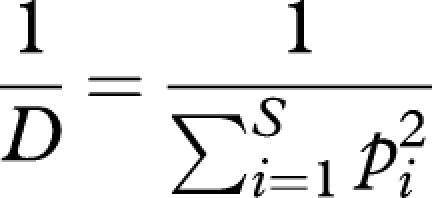 |
where pi is the proportion of visits made by pollinator group i and S is the number of pollinator groups visiting a plant species. A value of 1 means absolute specialization on one pollinator group.
The relative amount of variation in the area of floral visual units of each plant species can be expressed by the coefficient of variation (CV; the s.d. divided by the mean) (Wolfe & Krstolic 1999).
(e). Statistical analysis
To compare pollinator preference with respect to floral symmetry, multivariate analysis (performed by CANOCO v. 4.5) was used. To decide the ordination method, we first conducted a detrended correspondence analysis (DCA). The maximum gradient length was about 3, indicating that both linear and unimodal methods worked reasonably (Ter Braak & Smilauer 2002), so we chose a linear method. We conducted a redundancy analysis with plant species as samples, percentage of the visits to a particular plant species attributed to each functional group as the response variable and floral symmetry (re-coded into dummy variables) as the explanatory variable. Total visits recorded for each plant species and plant species’ abundance were entered as covariables to prevent the possible under-sample effects and the influence of composition of the visitor assemblage (Herrera, C. M. 2005; Lázaro et al. 2008). Log (y + 1) was used to transform the response variables. To test the significance of the full model, 4999 Monte Carlo permutations were used.
We performed a mediational analysis to examine the mediator effect of PG on the relationship between floral symmetry and CV of flower size. A mediator is defined as a variable that explains the relationship between a predictor and an outcome (Baron & Kenny 1986; Frazier et al. 2004). In other words, a mediator is the mechanism through which a predictor is able to influence an outcome (Baron & Kenny 1986). Following Baron & Kenny's (1986) method, four steps were conducted using three regression equations. In the first step, the predictor (floral symmetry) must be significantly associated with the outcome (CV of flower size). In the second step, the predictor must be significantly associated with the mediator (PG). In the third step, the mediator must be associated with the outcome variable, when the effects of predictor on the outcome are controlled. The final step is to show that the strength of the association between the predictor and the outcome is significantly reduced when the mediator is added to the model. If perfect mediation is obtained, the predictor effect will become zero, showing that PG fully mediates the relationship between floral symmetry and CV of flower size. If the predictor effect remains significant, it suggests that PG is a partial mediator. The first two steps were implemented separately using simple linear regressions. The last two steps were implemented together using a multiple regression.
A moderator analysis was conducted to test whether floral symmetry moderated the influence of PG on CV of flower size using hierarchical multiple regression. Following standard procedure, predictor (PG) was centred to maximize interpretability and minimize potential problems with multi-collinearity (West et al. 1996). Floral symmetry was coded using effects coding (code–1 for bilateral and code 1 for radial; see Frazier et al. 2004). In the first step, we regressed CV of flower size on floral symmetry and centred PG. In the second step, we entered the two-way interaction (floral symmetry × centred PG).
To reduce the effect of phylogeny, we used a pairwise comparative method (Møller & Birkhead 1992) executed by paired-samples t-tests to compare PG and CV of flower size between radial and bilateral flowers. Pairs of closely related taxa differing in symmetry were compared, so the phylogenetic constraints on PG and CV of flower size are reduced (Møller & Birkhead 1992). We constructed the phylogeny for the 27 species following Bremer et al. (2003), yielding six paired family groups. In the analysis, we compared family means. The PG and CV values of bilateral Lamiaceae and Orobanchaceae were averaged because both are from the order Lamiales.
3. Results
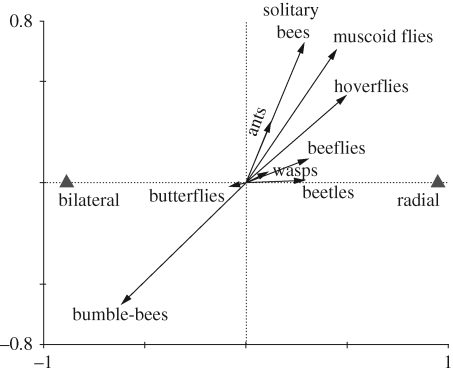
The result of the DCA model was significant (F = 8.037, p < 0.01), indicating that floral symmetry had a significant effect on the composition of pollinator groups. Floral symmetry explained 25.9 per cent of the variance in pollinator visits. The solid triangles (representing bilateral and radial) can be projected perpendicularly onto the line overlaying the arrow of each particular pollinator group (figure 1). Projection points are in the order of predicted increase in the relationship between floral traits and the pollinator group. The increase is predicted to occur in the direction indicated by the arrow. The length of the arrow tells how accurately its correlation with floral traits can be read form the biplot (Ter Braak 1994). The biplot (figure 1) shows that the percentage of bumble-bee visits is higher in bilateral flowers, but muscoid flies, hoverflies, solitary bees, ants, beeflies and beetles are more associated with radial than bilateral flowers. Butterflies tend to visit bilateral flowers and wasps prefer radial flowers. These two relationships can not be interpreted accurately because of the relatively short length of the arrows.
Figure 1.
Biplot indicating the relationships between floral symmetry (bilateral and radial represented by solid triangles) and nine pollinator functional groups (arrows). The solid triangles can be projected perpendicularly onto the line overlaying the arrow of particular pollinator group; the direction of the arrow indicates the increase in the degree of associations between floral traits and the pollinator group. See text for details.
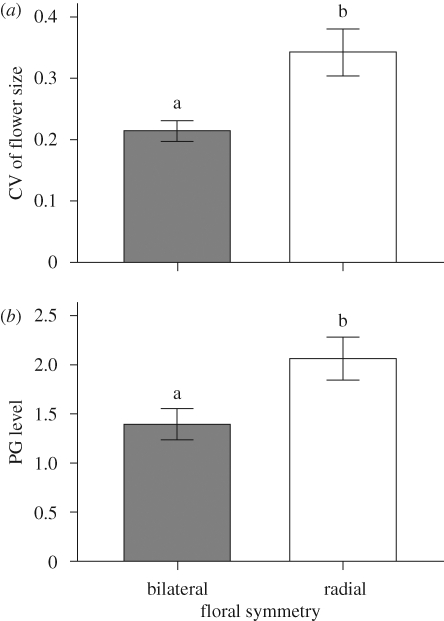
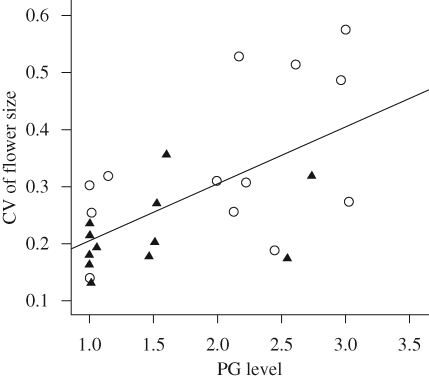
Table 2 shows the results of the mediational analysis. In the first step, floral symmetry was positively related to CV of flower size (B = 0.128, t = 3.128, p < 0.01; figure 2a), suggesting that the variance of flower size was higher in radial than in bilateral species. In the second step, PG was significantly regressed on floral symmetry (B = 0.665, t = 2.524, p < 0.05; figure 2b), indicating that PG was significantly higher in species with radial flowers than in species with bilateral flowers. In the third step, floral symmetry and PG were entered simultaneously in the equation as predictor variables. The relationship between PG and CV of flower size (controlling for floral symmetry) was also significant (B = 0.077, t = 2.822, p < 0.01; figure 3). So far, the requirements for mediation in the first three steps have all been met. The third regression equation also provided an estimate of the relationship between floral symmetry and CV of flower size (controlling for PG), which was not significant (B = 0.076, t = 1.885, p > 0.05), indicating that the mediator effect of PG on the relationship between floral symmetry and CV of flower size is significant. The unstandardized regression coefficient for floral symmetry on the CV of flower size decreased from 0.128 to 0.065 in the third step, showing that 40.6 per cent (1 − [0.076/0.128] = 0.406) of the variability in the relationship between floral symmetry and the CV of flower size was explained as a function of the PG mediator.
Table 2.
Regression analyses to test the mediator effect of PG on floral symmetry prediction of CV of flower size. CI, confidence interval; floral symmetry (0, bilateral; 1, radial); n.s., not significant.
| predictor variable | B | s.e. | 95% CI | β | t | criterion variable |
|---|---|---|---|---|---|---|
| all species included | ||||||
| step 1 | ||||||
| floral symmetry | 0.128 | 0.041 | 0.044, 0.212 | 0.530 | 3.128** | CV of flower size |
| step 2 | ||||||
| floral symmetry | 0.665 | 0.264 | 0.122, 1.208 | 0.451 | 2.524* | PG |
| step 3 | ||||||
| PG | 0.077 | 0.027 | 0.021, 0.134 | 0.474 | 2.822** | CV of flower size |
| floral symmetry | 0.076 | 0.040 | −0.007, 0.160 | 0.317 | 1.885 (n.s.) | CV of flower size |
| two species excluded | ||||||
| step 1 | ||||||
| floral symmetry | 0.110 | 0.040 | 0.028, 0.192 | 0.502 | 2.786* | CV of flower size |
| step 2 | ||||||
| floral symmetry | 0.675 | 0.262 | 0.134, 1.216 | 0.474 | 2.581* | PG |
| step 3 | ||||||
| PG | 0.067 | 0.029 | 0.006, 0.127 | 0.432 | 2.295* | CV of flower size |
| floral symmetry | 0.065 | 0.041 | −0.020, 0.151 | 0.298 | 1.584 (n.s.) | CV of flower size |
*p < 0.05, **p < 0.01.
Figure 2.
Comparisons of (a) CV in flower size and (b) pollinator generalization (PG) level between species with radial and bilateral flowers. Different letters indicate significant differences between two groups. Values are mean ± s.e.
Figure 3.
The relationship between the CV in flower size and the pollinator generalization level of 14 species with bilateral (filled triangles) and 13 species with radial (open circles) flowers. Both the mediational analysis and the moderator analysis indicate a significant relationship. See text for details.
Two plant species (C. approximata and Leontopodium andersonii) in our community received fewer than five visits during the whole study period, potentially causing an underestimate of generalization levels (Hingston & McQuillan 2000). To avoid this inaccuracy, we performed an alternative mediational analysis with these two species excluded. The result was largely similar. PG showed a significant mediator effect on the relationship between floral symmetry and CV of flower size because all requirements for mediation in the four steps were met (table 2). This model indicated that 40.9 per cent (1 − [0.065/0.110] = 0.409) of the variability in the relationship between floral symmetry and the CV of flower size was explained as a function of the PG mediator.
In the first step of the moderator analysis, the first-order effect of PG was significant (B = 0.077, t = 2.822, p < 0.01), meaning that there was a significant positive relationship between PG and CV of flower size (figure 3). Floral symmetry × centred PG interaction did not serve as a significant predictor of CV of flower size (B = 0.044, t = 1.251, p > 0.05). According to the framework proposed by Baron & Kenny (1986), the absence of this interaction is indicative of no moderator effect of floral symmetry on the relationship between PG and CV of flower size. In other words, there was no significant difference between bilateral and radial species in the strength and direction of the influence of PG on the CV of flower size. Similar results were obtained when we excluded the above-mentioned two plant species: PG had a positive effect on the CV of flower size (B = 0.067, t = 2.295, p < 0.05) and the interaction effect between floral symmetry and centred PG on the CV of flower size was not significant (B = 0.027, t = 0.747, p > 0.05).
The result of six pairwise comparisons indicated that the variance in flower size of radial species was higher than that of bilateral species (t = −2.792, d.f. = 5, p = 0.038), consistent with the conclusion of the random analysis presented above. In this pairwise comparison, however, PG was not significantly different between radial and bilateral species (t = −2.071, d.f. = 5, p = 0.093).
4. Discussion
Our community survey demonstrated that variation of flower visual size was larger in bilateral than in radial symmetry species, consistent with previous studies (Wolfe & Krstolic 1999; Ushimaru et al. 2007; Herrera et al. 2008; van Kleunen et al. 2008). Furthermore, we found that the pollinator generalization level was lower in bilateral than in radial symmetry species in the second step of the mediational analysis. These results indicate that flowers visited by a more specialized pollinator fauna show less variance in flower size, providing substantial evidence for the hypothesis that PMSS is responsible for the erosion of variance in flower size (Berg 1960; Fenster 1991; Armbruster et al. 1999; Wolfe & Krstolic 1999).
Both our randomly and pairwise selected comparisons revealed that bilateral species showed less variance in flower size than radial species. Similarly, previous studies have shown that variation in flower size was higher in species with radial rather than bilateral flowers, using various plant species from numerous families. Such a trend has been found in different countries, although different studies have used different measures of flower size, such as flower or corolla length (table 3), but the trend was not found in the analysis by Herrera et al. (2008) using a random sample. However, phylogenetically pairwise comparisons conducted by them, as well as Wolfe & Krstolic (1999), revealed this significant trend. Unlike previous studies, we used area measurements of floral visual units, a functional unit for pollinator attraction (Dafni 1994; Hegland & Totland 2005), to calculate flower size. Thus, it is not surprising to see a higher value of CV in our study (table 3).
Table 3.
Basic information and among-individual CV in flower size for bilateral and radial flowers in five related studies. p-value indicates the significance of the difference between bilateral and radial flowers with respect to among-individual CV in flower size. n.s., not significant.
| studies | location | index of flower size | family number | species number | CV |
||
|---|---|---|---|---|---|---|---|
| bilateral | radial | p-value | |||||
| Wolfe & Krstolic | America | petal/corolla length | 20 | 31 | 0.091 | 0.121 | *** |
| Ushimaru et al. | Japan | petal/corolla length | 16 | 27 | 0.088 | 0.121 | * |
| Herrera et al. | Spain | petal/corolla length | 11 | 22 | 0.061 | 0.093 | * |
| petal/corolla length | 16 | 38 | 0.076 | 0.105 | n.s. | ||
| van Kleunen et al. | Switzerland | flower length | 11 | 28 | 0.064 | 0.117 | *** |
| flower width | 11 | 28 | 0.085 | 0.122 | * | ||
| this study | China | flower visual size | 13 | 27 | 0.214 | 0.342 | ** |
*p < 0.05, **p < 0.01, ***p < 0.001.
We found that pollinator diversity was significantly higher in radial rather than bilateral species in a natural community, indicating that the level of ecological generalization was higher in species with radial flowers. Other studies have shown that a higher percentage of zygomorphic than actinomorphic flowers was pollinated by a single pollinator group (see Fenster et al. 2004). In our community, only bumble-bees preferred bilateral flowers while radial flowers attracted more pollinator groups such as muscoid flies, hoverflies, solitary bees, ants, beeflies and beetles. Compared with bilateral species, radial species are usually pollinated by diverse pollinator groups (e.g. Leppik 1953; McCall & Primack 1992; Hingston & McQuillan 2000; Wolfe & Sowell 2006; Lázaro et al. 2008). The complex (bilateral) flowers are expected to be the most ecologically specialized within a community because their complexity may reflect selection by narrower pollinator groups (Herrera 1988; Johnson & Steiner 2000; Fenster et al. 2004). Although we demonstrated that bilateral species employed few pollinator groups and thus possessed a low level of ecological generalization, which serves as a supporting evidence for above prediction, several studies have shown that the ecological generalization level of plant species can vary across years and communities because of community context variation (Ollerton et al. 2007; Alarcón et al. 2008; Lázaro et al. 2008; Olesen et al. 2008; Petanidou et al. 2008; Dupont et al. 2009). Thus, measuring only one season of PG in our study is a limitation. For example, some plant or pollinator species appear as specialists in 1 year, but tend to be generalists in other years (Alarcón et al. 2008; Petanidou et al. 2008). Whereas flower size may not vary significantly from year to year because it might be the result of consistent selection through the years. Given data from several years to test this hypothesis are unavailable now, we suppose that the year to year variation of PG in our community could be relatively low. We recorded plant–pollinator interactions in this meadow and found that the abundance and diversity of plants and pollinators were relatively stable from 2006 to 2008 (Y.-B. Gong & S.-Q. Huang 2006–2008, unpublished data). Furthermore, even if variation in pollinator species is high from year to year, variation in functional groups may be not so high (Dupont et al. 2009).
On the other hand, in some situations such as in communities lacking diverse pollinator functional groups, bilateral species can be more generalized than radial species (Ollerton et al. 2007; Lázaro et al. 2008). However, this may not argue against the validity of the PMSS hypothesis since evolutionary specialization (bilateral symmetry) is a historical process of evolution towards greater specialization in response to PMSS, whereas ecological specialization refers to selection exerted by pollinators in the present time (Fenster et al. 2004; Armbruster et al. 2006). In addition, other floral traits such as tube length, colour, clustering, scent, nectar and pollen production may also have an influence on pollinator visits (Faegri & van der Pijl 1979; Lázaro et al. 2008). So even though we have demonstrated the overall trend of greater PG in radial than bilateral flowers, two radial species, Halenia elliptica and O. confertum, showed relatively lower PG, perhaps because they are the only two radial species having a corolla tube. Aside from a small number of paired family groups, the non-significant results of pairwise comparison of PG between radial and bilateral flowers may be a consequence of leaving out of consideration the influences other floral traits on PG level.
Our community survey revealed a positive relationship between pollinator diversity (ecological generalization level) and variance of flower size at the interspecific level. This relationship was not moderated by floral symmetry, indicating that both bilateral and radial species experienced pollinator-mediated selection at similar intensity. In other words, if PG for bilateral and radial species is equal, there should be no difference in the variance of flower size between them. In accordance with the above inference based on the results of moderator analysis, the mediator effect of PG on the relationship between floral symmetry and CV of flower size is significant, supporting the PMSS hypothesis. However, even though pollinator-mediated selection could account for up to 40 per cent of the difference in variance in flower size between bilateral and radial species, it may not be the only mediator. Other non-pollinator factors could also be mediators (Strauss & Whittall 2006). In addition, only among-individual variance in flower size was investigated in our study, which may not adequately reflect the phenotypic variation in response to pollinator-mediated selection because of the existence of multiple levels of floral variation, including among populations, among individuals within populations and among flowers within individuals (Armbruster 1991; Williams & Conner 2001; Herrera, J. 2005). These considerations suggest that future comparative studies designed to test the PMSS hypothesis need a more rigorous methodology for the investigation of pollinator diversity and the measurement of variance in flower size.
Acknowledgements
The authors thank laboratory members Ji-Fan Sun, Xiao-Xin Tang, Qiang Fang, Yun-Yun Mao, Jiao-Kun Li, Yang Lu, Cai Wei, Huan-Le Liu, Chang-Qiu Liu and Ming-Kai Guo for their help in the field study, Zhen-Dong Fang, Qin Xu, Zong-Ling Ma and Zi-Quan Pu from Shangri-La Alpine Botanical Garden for their logistical support, Lawrence D. Harder for comments on experimental design, Stein Joar Hegland and Zhi-Gang Zhao for help in data analysis, the associate editor and two anonymous reviewers for their detailed and constructive comments on the manuscript. Grants from National Science Foundation of China (30770135 and 30825005) to S.Q.H. supported this work.
References
- Alarcón R., Waser N. M., Ollerton J.2008Year-to-year variation in the topology of a plant–pollinator interaction network. Oikos 117, 1796–1807 (doi:10.1111/j.0030-1299.2008.16987.x) [Google Scholar]
- Armbruster W. S.1991Multilevel analysis of morphometric data from natural plant populations: insights into ontogenetic, genetic, and selective correlations in Dalechampia scandens. Evolution 45, 1229–1244 (doi:10.2307/2409730) [DOI] [PubMed] [Google Scholar]
- Armbruster W. S.2006Evolutionary and ecological aspects of specialized pollination: views from the Arctic to the Tropics. In Plant–pollinator interactions. From specialization to generalization (eds Waser N. M., Ollerton J. M.), pp. 260–282 Chicago, IL: University of Chicago Press [Google Scholar]
- Armbruster W. S., Stilio V. S. D., Tuxill J. D., Flores T. C., Runk J. L. V.1999Covariance and decoupling of floral and vegetative traits in nine Neotropical plants: a re-evaluation of Berg's correlation-pleiades concept. Am. J. Bot. 86, 39–55 (doi:10.2307/2656953) [PubMed] [Google Scholar]
- Baron R. M., Kenny D. A.1986The moderator–mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J. Pers. Soc. Psychol. 51, 1173–1182 (doi:10.1037/0022-3514.51.6.1173) [DOI] [PubMed] [Google Scholar]
- Berg R. L.1960The ecological significance of correlation pleiades. Evolution 14, 171–180 (doi:10.2307/2405824) [Google Scholar]
- Bremer B., et al. 2003An update of the Angiosperm Phylogeny Group classification for the orders and families of flowering plants: APG II. Bot. J. Linn. Soc. 141, 399–436 (doi:10.1046/j.1095-8339.2003.t01-1-00158.x) [Google Scholar]
- Cronk Q., Möller M.1997Genetics of floral symmetry revealed. Trends Ecol. Evol. 12, 85–86 (doi:10.1016/S0169-5347(97)01028-8) [DOI] [PubMed] [Google Scholar]
- Dafni A.1994Note on side advertisement in flowers. Funct. Ecol. 8, 136–138 [Google Scholar]
- Dupont Y. L., Padrón B., Olesen J. M., Petanidou T.2009Spatio-temporal variation in the structure of pollination networks. Oikos 118, 1261–1269 (doi:10.1111/j.1600-0706.2009.17594.x) [Google Scholar]
- Endress P. K.1999Symmetry in flowers: diversity and evolution. Int. J. Plant Sci. 160, S3–S23 (doi:10.1086/314211) [DOI] [PubMed] [Google Scholar]
- Endress P. K.2001Evolution of floral symmetry. Curr. Opin. Plant Biol. 4, 86–91 (doi:10.1016/S1369-5266(00)00140-0) [DOI] [PubMed] [Google Scholar]
- Faegri K., van der Pijl L.1979The principles of pollination ecology, 3rd edn Oxford, UK: Pergamon Press [Google Scholar]
- Fenster C. B.1991Selection on floral morphology by hummingbirds. Biotropica 23, 98–101 (doi:10.2307/2388696) [Google Scholar]
- Fenster C. B., Armbruster W. S., Wilson P., Dudash M. R., Thomson J. D.2004Pollination syndromes and floral specialization. Annu. Rev. Ecol. Evol. Syst. 35, 375–403 (doi:10.1146/annurev.ecolsys.34.011802.132347) [Google Scholar]
- Fisher R. A.1958The genetical theory of natural selection New York, NY: Dover Publications [Google Scholar]
- Frazier P. A., Tix A. P., Barron K. E.2004Testing moderator and mediator effects in counseling psychology research. J. Coun. Psychol. 51, 115–134 (doi:10.1037/0022-0167.51.1.115) [Google Scholar]
- Harder L. D., Barrett S. C. H.1993Pollen removal from tristylous Pontederia cordata: effects of anther position and pollinator specialization. Ecology 74, 1059–1072 (doi:10.2307/1940476) [Google Scholar]
- Hegland S. J., Totland Ø. 2005Relationships between species’ floral traits and pollinator visitation in a temperate grassland. Oecologia 145, 586–594 (doi:10.1007/s00442-005-0165-6) [DOI] [PubMed] [Google Scholar]
- Herrera C. M.1988Variation in mutualisms: the spatiotemporal mosaic of a pollinator assemblage. Biol. J. Linn. Soc. 35, 95–125 (doi:10.1111/j.1095-8312.1988.tb00461.x) [Google Scholar]
- Herrera C. M.2005Plant generalization on pollinators: species property or local phenomenon? Am. J. Bot. 92, 13–20 (doi:10.3732/ajb.92.1.13) [DOI] [PubMed] [Google Scholar]
- Herrera J.2005Flower size variation in Rosmarinus officinalis: individuals, populations and habitats. Ann. Bot. 9, 431–437 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrera J., Arista M., Ortiz P. L.2008Perianth organization and intra-specific floral variability. Plant Biol. 10, 704–710 (doi:10.1111/j.1438-8677.2008.00091.x) [DOI] [PubMed] [Google Scholar]
- Hingston A. B., McQuillan P. B.2000Are pollination syndromes useful predictors of floral visitors in Tasmania? Aust. J. Ecol. 25, 600–609 [Google Scholar]
- Ingrouille M.1992Diversity and evolution of land plants London, UK: Chapman & Hall [Google Scholar]
- Johnson S. D., Steiner K. E.2000Generalization versus specialization in plant pollination systems. Trends Ecol. Evol. 15, 140–143 (doi:10.1016/S0169-5347(99)01811-X) [DOI] [PubMed] [Google Scholar]
- Lande R., Arnold S. J.1983The measurement of selection on correlated characters. Evolution 37, 1210–1226 (doi:10.2307/2408842) [DOI] [PubMed] [Google Scholar]
- Lázaro A., Hegland S. J., Totland Ø. 2008The relationships between floral traits and specificity of pollination systems in three Scandinavian plant communities. Oecologia 157, 249–257 (doi:10.1007/s00442-008-1066-2) [DOI] [PubMed] [Google Scholar]
- Leppik E. E.1953The ability of insects to distinguish number. Am. Nat. 87, 229–236 (doi:10.1086/281778) [Google Scholar]
- Memmott J.1999The structure of a plant–pollinator food web. Ecol. Lett. 2, 276–280 (doi:10.1046/j.1461-0248.1999.00087.x) [DOI] [PubMed] [Google Scholar]
- McCall C., Primack R. B.1992Influence of flower characteristics, weather, time of the day, and season on insect visitation rates in three plant communities. Am. J. Bot. 79, 434–442 (doi:10.2307/2445156) [Google Scholar]
- Møller A. P., Birkhead T. R.1992A pairwise comparative method as illustrated by copulation frequency in birds. Am. Nat. 139, 644–656 (doi:10.1086/285348) [Google Scholar]
- Neal P. R., Dafni A., Giurfa M.1998Floral symmetry and its role in plant–pollinator systems: terminology, distribution, and hypotheses. Annu. Rev. Ecol. Syst. 29, 345–373 (doi:10.1146/annurev.ecolsys.29.1.345) [Google Scholar]
- Olesen J. M., Bascompte J., Elberling H., Jordano P.2008Temporal dynamics in a pollination network. Ecology 89, 1573–1582 (doi:10.1890/07-0451.1) [DOI] [PubMed] [Google Scholar]
- Ollerton J., Killick A., Lamborn E., Watts S., Whiston M.2007Multiple meanings and modes: on the many ways to a generalist flower. Taxon 56, 717–728 [Google Scholar]
- Petanidou T., Kallimanis A. S., Tzanopoulos J., Sgardelis S. P., Pantis J. D.2008Long-term observation of a pollination network: fluctuation in species and interactions, relative invariance of network structure and implications for estimates of specialization. Ecol. Lett 11, 564–575 (doi:10.1111/j.1461-0248.2008.01170.x) [DOI] [PubMed] [Google Scholar]
- Richards A. J.1997Plant breeding systems London, UK: Chapman & Hall [Google Scholar]
- Sahli H. F., Conner J. K.2006Characterizing ecological generalization in plant–pollination systems. Oecologia 148, 365–372 (doi:10.1007/s00442-006-0396-1) [DOI] [PubMed] [Google Scholar]
- Simpson E. H.1949Measurement of diversity. Nature 163, 688 (doi:10.1038/163688a0) [Google Scholar]
- Stebbins G. L.1951Natural selection and differentiation of angiosperm families. Evolution 5, 299–324 (doi:10.2307/2405676) [Google Scholar]
- Stebbins G. L.1974Flowering plants: evolution above the species level Cambridge, MA: Belknap Press [Google Scholar]
- Strauss S. Y., Whittall J. B.2006Non-pollinator agents of selection on floral traits. In Ecology and evolution of flowers (eds Harder L. D., Barrett S. C. H.), pp. 120–138 Oxford, UK: Oxford University Press [Google Scholar]
- Ter Braak C. J. F.1994Canonical community ordination. Part I: basic theory and linear methods. Ecoscience 1, 127–140 [Google Scholar]
- Ter Braak C. J. F., Smilauer P.2002CANOCO reference manual and CanoDraw for Windows user's guide: software for canonical community ordination (version 4.5) Ithaca, NY: Microcomputer Power [Google Scholar]
- Ushimaru A., et al. 2007The influence of floral symmetry and pollination systems on flower size variation. Nord. J. Bot. 24, 593–598 (doi:10.1111/j.1756-1051.2004.tb01644.x) [Google Scholar]
- van Kleunen M., Meier A., Saxenhofer M., Fischer M.2008Support for the predictions of the pollinator-mediated stabilizing selection hypothesis. J. Plant Ecol. 1, 173–178 (doi:10.1093/jpe/rtn017) [Google Scholar]
- West S. G., Aiken L. S., Krull J. L.1996Experimental personality designs: analyzing categorical by continuous variable interactions. J. Pers. 64, 1–49 (doi:10.1111/j.1467-6494.1996.tb00813.x) [DOI] [PubMed] [Google Scholar]
- Williams J. L., Conner J. K.2001Sources of phenotypic variation in floral traits in wild radish, Raphanus raphanistrum (Brassicaceae). Am. J. Bot. 88, 1577–1581 (doi:10.2307/3558401) [PubMed] [Google Scholar]
- Wolfe L. M., Barrett S. C. H.1987Pollinator foraging and pollen collection on the floral morphs of tristylous Pontederia cordata. Oecologia 74, 347–351 (doi:10.1007/BF00378928) [DOI] [PubMed] [Google Scholar]
- Wolfe L. M., Krstolic J. L.1999Floral symmetry and its influence on variance in flower size. Am. Nat. 154, 484–488 (doi:10.1086/303249) [DOI] [PubMed] [Google Scholar]
- Wolfe L. M., Sowell D. R.2006Do pollination syndromes partition the pollinator community? A test using four sympatric morning glory species. Int. J. Plant Sci. 167, 1169–1175 (doi:10.1086/507651) [Google Scholar]