Abstract
Recent advances in testing mediation have found that certain resampling methods and tests based on the mathematical distribution of 2 normal random variables substantially outperform the traditional z test. However, these studies have primarily focused only on models with a single mediator and 2 component paths. To address this limitation, a simulation was conducted to evaluate these alternative methods in a more complex path model with multiple mediators and indirect paths with 2 and 3 paths. Methods for testing contrasts of 2 effects were evaluated also. The simulation included 1 exogenous independent variable, 3 mediators and 2 outcomes and varied sample size, number of paths in the mediated effects, test used to evaluate effects, effect sizes for each path, and the value of the contrast. Confidence intervals were used to evaluate the power and Type I error rate of each method, and were examined for coverage and bias. The bias-corrected bootstrap had the least biased confidence intervals, greatest power to detect nonzero effects and contrasts, and the most accurate overall Type I error. All tests had less power to detect 3-path effects and more inaccurate Type I error compared to 2-path effects. Confidence intervals were biased for mediated effects, as found in previous studies. Results for contrasts did not vary greatly by test, although resampling approaches had somewhat greater power and might be preferable because of ease of use and flexibility.
The concept of indirect or mediated effects has a long history in the social sciences (Alwin & Hauser, 1975; MacCorquodale & Meehl, 1948; Woodworth, 1928). These effects occur when some intermediate variable is held to be part of a causal chain, such that the independent variable achieves all or part of its effect on the dependent variable by first changing the intermediate construct. This mediator variable then affects the outcome (Sobel, 1990). These effects are important for experimental and nonexperimental studies, and are useful for both basic and applied research questions (Baron & Kenny, 1986; MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002; Shrout & Bolger, 2002). The addition of a mediator to a simple cause–effect relationship adds to researchers’ understanding of how an effect is achieved by adding detail to the causal sequence.
Although adding a mediator to a simple bivariate cause-and-effect model increases knowledge about how effects are achieved, extensions of this model might further enhance understanding of complex relationships. For example, adding multiple mediators might reveal multiple influences of behavior, each one a mediator of some other overarching variable or event such as program exposure or experience of abuse in childhood (Banyard, Williams, & Siegel, 2001; MacKinnon et al., 2001). Additionally, mediation can be a multiple-step process that extends beyond the normal three-variable chain; there can be additional mediators or intervening variables that have influence on “downstream” mediators, resulting in a causal process with three or more paths from the primary cause to the outcome. Although methods to evaluate mediation have received a great deal of attention recently (e.g., MacKinnon et al., 2002; MacKinnon, Lockwood, & Williams, 2004; Pituch, Whittaker, & Stapleton, 2005; Shrout & Bolger, 2002), most investigations have been confined to variations of the three-variable mediation model. Because many theories of behavior posit models with two or more mediators or indirect effects with more than one mediator in the causal chain, it is important to know the properties of tests of mediation in such models. This article explores the statistical properties of recent advances in testing mediation, using the basic three-variable mediation model as a starting point.
TESTING MEDIATION
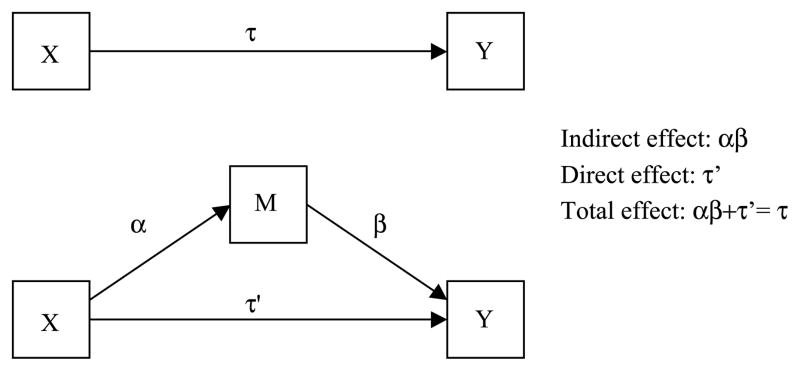
The basic mediation model is shown in Figure 1 and includes three variables: X, the principle independent variable, Y, the outcome or dependent variable, and M, the mediator. This model is expressed by the following equations:
| (1) |
| (2) |
and
FIGURE 1.
Basic mediation model.
| (3) |
The first equation estimates τ̂, the overall effect of the predictor X on the outcome, Y. Equation 2 estimates the effect of X on the mediator, expressed as the α̂ regression coefficient. Equation 3 models the effect of the mediator on the outcome, the β̂ coefficient, also estimating any remaining direct or nonmediated effect of X on Y (τ̂′). Intercepts are expressed by β̂0(1), β̂0(2), and β̂0(3), and error variances by ε1, ε2, and ε3.
Although there are several general methods of testing mediation (see Mac-Kinnon et al., 2002, for an overview), this study focuses on the product of coefficients method that requires only the second and third equations. The point estimate of the mediated effect is the product of α̂ and β̂ and can be tested for significance by dividing α̂β̂ by its standard error and comparing the result to the standard normal distribution. This is the standard z method for testing mediation. The most commonly used standard error for the product method was given by Sobel (1982), who used the multivariate delta method based on a Taylor series approximation. This standard error is programmed into many covariance matrix programs and is expressed as:
| (4) |
Confidence limits for the mediated effect can be formed using the point estimate and standard error using the formula:
| (5) |
where z1−ω/2 is the z score for the value 1 minus half the nominal Type I error rate, ω.
Simulation studies have shown that this standard error is unbiased at relatively small sample sizes (~100; MacKinnon, Warsi, & Dwyer, 1995; Stone & Sobel, 1990). However, the same studies and others (e.g., MacKinnon et al., 2004) have shown that confidence limits based on this standard error do not perform well. For positive values of αβ confidence intervals (CIs) show a negative bias in their placement, resulting in a greater proportion of true values falling to the right of the interval than to the left.
The Distribution of the Product
The standard z method assumes that the product of normally distributed variables divided by its standard error is normally distributed. As detailed in statistical theory (Craig, 1936; Meeker, Cornwell, & Aroian, 1981; Springer & Thompson, 1966) and simulation studies (MacKinnon, Lockwood, & Hoffman, 1998; MacKinnon et al., 2002; MacKinnon et al., 2004), the product of two normal random variables is not itself normally distributed in most circumstances. When both random variables have a mean of zero the distribution is symmetric with a kurtosis of six (Craig, 1936). When the product is nonzero, the distributions continue to have excess kurtosis and are skewed as well. As the ratio of at least one variable’s mean to its standard error increases, the distribution approaches normality (Aroian, 1947; Aroian et al., 1978).
Although the distribution of the product is complex, several statisticians (Meeker et al., 1981; Springer & Thompson, 1966) have tabled some of the critical values of this function. Springer and Thompson (1966) presented tables of the product when both coefficients are equal to zero. A more extensive presentation is found in Meeker et al. (1981), containing tables of the distribution of two random normal variables. These tables contain fractiles for the standardized function for varying values of α, β, σα, and σβ. The standard error of the product in these tabled values is the exact, second-order Taylor series approximation given in Aroian (1947). Entries are in terms of the ratio of each coefficient to its standard error, α/σα and β/σβ, giving two delta values: δα and δβ. The tabled values assume that the quantities are population values, but sample values can be used (Meeker et al., 1981, p. 8).
ALTERNATIVES TO THE Z TEST
Recently, MacKinnon and colleagues (MacKinnon, Fritz, Williams, & Lockwood, 2007; MacKinnon et al., 2002; MacKinnon et al., 2004) have proposed two improvements to significance testing and confidence limit formation for indirect effects. The first is a single-sample test that uses the critical values from the distribution of the product (Meeker et al., 1981). The second uses resampling methods, in particular, two types of percentile bootstrap, to overcome some of the problems that arise from the assumption of normality inherent in the z test for indirect effects.
The M Test
The sample estimates of δα and δβ, δ̂α and δ̂β can be used together with critical values from the distribution of the product to find mediated effect confidence limits, power, and Type I error rates (MacKinnon et al., 1998; MacKinnon et al., 2002). This method forms asymmetric CIs and has been called the M test (MacKinnon et al., 2004). First, delta values are computed from sample values and these are then used to find critical values of the product distribution. These critical values are rarely equidistant from zero for any pair of coefficients and approach symmetry only when both coefficients are very small or very large. M test CIs are then formed by
| (6) |
| (7) |
where Mupper and Mlower correspond to the critical values of the distribution of the product and σ̂α̂β̂ is the standard error from Equation 4. The M test has been evaluated in several large simulation studies with increasingly more precise critical values for the distribution of the product (e.g., MacKinnon et al., 2002; MacKinnon et al., 2004). Earlier studies used the tables in Meeker et al. (1981), so critical values were only available in increments of .4 for most delta values. MacKinnon et al. (2004) used a table that had been augmented with critical values for deltas in increments of .2. Even with these relatively imprecise critical values, the M test showed greater power at smaller sample sizes than the standard z, without inflated Type I error rates. Like the z test, the M test had inaccurate (too low) Type I error rates when the true mediated effect was zero. Although the proportions of true values outside these CIs were more balanced than those formed with Equation 5, M intervals were also biased, with more true values falling to the right of the empirical interval than to the left (for positive mediated effects).
As implemented thus far, the M test has two notable drawbacks: the lack of exact critical values for any pair of observed deltas and the lack of any critical values for the product of more than two variables, which are required for mediated effects with more than two paths. One solution to limited critical values was the use of empirically based values derived by simulation. This empirical M (Emp-M) test performed somewhat better than the M in MacKinnon et al. (2004) and can be generalized to indirect effects with more than two component paths. The need for empirically based critical values for two-path effects has recently been rendered unnecessary as MacKinnon et al. (2007) detailed a program (PRODCLIN, available in SAS, SPSS, and R) that uses sample-derived deltas to calculate the exact critical values from the distribution of the product. Indirect effects with three or more paths currently still lack critical values from anything other than simulation.
Resampling Methods
Resampling approaches have also been offered as a possible solution to the distributional irregularities of the mediated effect (Bollen & Stine, 1990; Lockwood & MacKinnon, 1998; MacKinnon et al., 2004; Shrout & Bolger, 2002). Approaches such as the nonparametric bootstrap make fewer assumptions about the data than do traditional, asymptotic tests. Rather than relying on assumed distributional properties of test statistics, resampling techniques generate their own test distributions against which to test hypotheses and generate CIs. This is done by generating a large number of pseudo datasets through resampling observations from the original sample. Because resampling is done with replacement, each pseudo dataset will tend to be different from all others. Several large simulation studies (e.g., MacKinnon et al., 2004) have examined a variety of resampling approaches for testing the mediated effect, including the percentile bootstrap and the bias-corrected bootstrap.
Lockwood and MacKinnon (1998) found bootstrapped standard errors for the mediated effect comparable to those from the multivariate delta solution. Type I error rates were too small for small effect sizes of α and β. Confidence limits were again biased with an imbalance in the proportions of true values to the left and right of the interval, a finding similar to that of Bollen and Stine (1990). An extensive simulation study of resampling approaches (MacKinnon et al., 2004) found that the percentile bootstrap outperformed the z test, but confidence limits were biased, with a greater proportion of true values falling to the right of the percentile interval. Although it had greater power and more accurate Type I error rates than the z test, the basic percentile bootstrap did not outperform the M test.
A variant of the simple percentile bootstrap, the bias-corrected bootstrap, seems especially appropriate for estimating CIs for the mediated effect because this effect often has a distribution with considerable skewness. Correcting for bias in the bootstrap intervals might remove some of the inaccuracies found in other methods that assume a normal distribution of the mediated effect. MacKinnon et al. (2004) and Pituch, Stapleton, and Kang (2006) found the bias-corrected bootstrap had greater power and more accurate Type I error rates than single-sample and other resampling methods. However, the Type I error rates were occasionally too high under some conditions.
COMPARISONS OF MEDIATED EFFECTS
More complex models of behavior raise questions of how two or more indirect effects within the same model compare. In these models, it is likely that some mediators are more central to theory or are easier to measure and change than others. Such concerns are of particular importance in applied areas such as evaluation of prevention and intervention programs. Typically, multiple constructs such as various risk and protective factors are targeted to achieve change in the ultimate outcome (e.g., smoking). Some of these mediators might be far more costly or difficult to change than others. Given that many funding agencies now require cost-effectiveness analyses as a part of program evaluation, it is useful to compare the mediated effects of individual mediators to help inform researchers and agencies about which components are most effective relative to others. Groups of related mediators, such as risk factor mediators and protective factor mediators, can also be compared to help modify and focus programs.
Interest in contrasts of indirect effects dates back at least to Wright (1934), when he compared mediated effects of litter size on birth weight of guinea pigs. Wright examined competition for growth and gestational period as mediators, and concluded that the mediated effect for growth was three times that of length. Although comparing mediated effects has a long history, formal methods for doing so are sparse and relatively recent. Research questions such as Wright’s can be addressed by contrasts of two or more mediated effects using methods given by MacKinnon (2000). Contrasts range from simply comparing two mediated effects to complicated comparisons such as those contrasting groups of multiple effects or inclusion of effects with different numbers of paths. Comparing mediated effects, calculated as the product of two (or more) regression coefficients (α̂ and β̂), is possible because any two effects with the same outcome variable will be in the same metric (MacKinnon, 2000).
To test the differences between mediated effects, it is necessary to have an estimate of the variance of the contrast. The multivariate delta method, the same technique used to find the most commonly used standard error of the mediated effect, can be used to find this quantity (MacKinnon, 2000). As an example, consider a basic multiple mediator model with one independent variable, one outcome, and two mediators. This model yields two indirect effects, α̂1β̂1 and α̂2β̂2, as well as the direct effect τ̂′. Several potentially useful comparisons arise from this simple model. For example, a researcher might wish to test one mediated effect compared to the other (e.g., α̂1β̂1 − α̂2β̂2), either indirect effect compared to the remaining direct effect (e.g., α̂iβ̂i − τ̂′), and the total indirect effect compared to the direct effect (e.g., α̂1β̂1 + α̂2β̂2 − τ̂′). The first contrast will be used to demonstrate how to compare two mediated effects. Pre- and postmultiplying the covariance matrix of the elements of the function (α1β1 − α2β2) by the first-order derivatives yields the variance:
| (8) |
The difference between the mediated effects, Δ, is found through subtraction and is then tested by dividing this difference by the square root of the variance estimate, σΔ. Confidence limits can be formed using the formula Δ ± 1.96σΔ (for σ = .05). Just as with the standard z test of mediation, both the significance test and confidence limits assume a normal distribution of the contrast. However, given the nonnormal distribution of the product of two normal variables discussed earlier, this assumption might not be correct (MacKinnon, 2000).
THIS STUDY
Previous research has demonstrated that the widely used standard z test for mediation has serious drawbacks such as low power and biased confidence limit coverage. Tests based on the distribution of products and resampling methods (notably the percentile and bias-corrected bootstraps) have greater power and less biased CIs in single mediator models. However, the basic mediation model is somewhat limited in its applicability to more complex research questions. Many studies examine multiple behaviors or constructs that are thought to be related to the primary independent variable and the ultimate outcome of interest. It is therefore necessary to evaluate the performance of these newer tests for mediation in more complex models if they are to be successfully and appropriately applied to such data. Additionally, these methods might be useful for mediated effects with more than two paths and contrasts of indirect effects, but their performance in these applications has not been examined. Neither three-path mediation nor contrasts of mediated effects have been extensively studied previously and alternative methods for these situations are sparse.
This study was conducted to clarify these issues and extend the findings on alternative mediation tests. First, it evaluated tests of two-path effects within the context of a more complex model. Second, it extended the distribution of products and bootstrap approaches to three-path indirect effects and compared these to the performance of the standard z method described by Taylor, MacKinnon, and Tein (in press). Third, it replicated and extended the impact of the exact critical values for the M test based on the PRODCLIN program of MacKinnon et al. (2007). Finally, it evaluated the performance of MacKinnon’s (2000) test of contrasts of mediated effects, and compared this to resampling methods to test contrasts.
METHODS
Model and Simulations
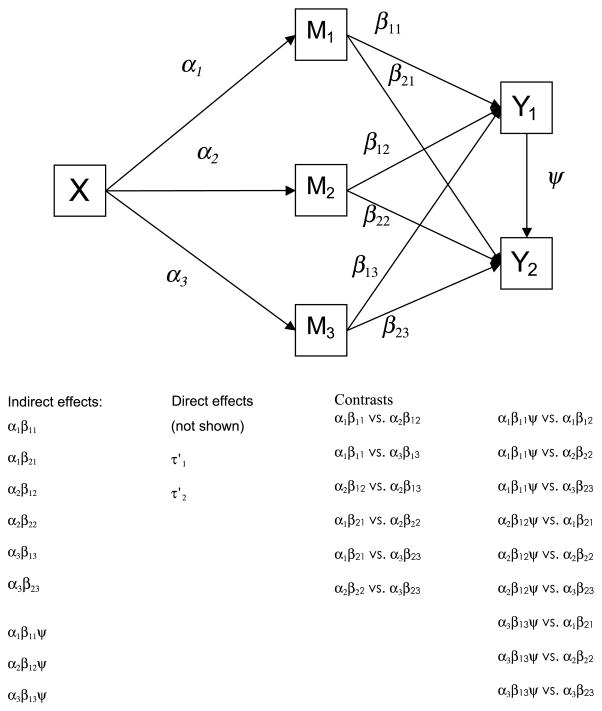
The model used for this study is shown in Figure 2. There are three mediators, two outcomes, and a single independent variable. All indirect effects examined in this study have causal paths that begin with X, for a total of six two-path mediated effects, three three-path mediated effects, and two direct effects. Variables and paths in the model were named to correspond to common identification schemes in the mediation literature (e.g., MacKinnon et al., 2002; Shrout & Bolger, 2002). Paths corresponding to the effect of the independent variable, X, are denoted as αm, where the subscript m indicates at which of the three mediators the path terminates. The paths from the mediators (M1, M2, and M3) to the outcomes (Y1 and Y2) are indicated by βym. The m subscript indicates the mediator from which the path originated and the y subscript indicates the outcome variable of the path. The direct effects from X to the outcomes are included in the model as . Because direct effects are represented by c or c′ in many models when not using Greek notation, it is necessary to call the path from Y1 to Y2 by another letter, in this case y or ψ. Specific mediated effects from the path model can be identified by the combination of two or three of these paths. For example, the indirect effect of X on Y1 through the second mediator is given by α2β12. The effect of X on Y2 through M3 and Y1 can be written as α3β13ψ. Note that the ψ path has no subscript as it is the only path in this model that forms a three-path indirect effect. Greek letters are used to represent population or true values, Greek letters with hats (^) denote estimates.
FIGURE 2.
Multiple mediator/multiple outcome path model.
This model results in the following equations predicting mediators and the two outcomes. For clarity, intercepts and the direct effect of X are omitted. Each mediator Mm is given by:
| (9) |
In Figure 2, m takes on values of 1, 2, and 3. The two outcomes Y1 and Y2 are given by:
| (10) |
and
| (11) |
Monte Carlo simulations were used to evaluate the performance of five tests of mediation and three tests of contrasts of mediated effects in a path model with multiple mediators and two- and three-path indirect effects. Simulations were conducted using the SAS software package (version 8.2). Data corresponding to the true values of α, β, and ψ parameters of interest were generated from covariance matrices with elements calculated with covariance matrix algebra and Equations 9, 10, and 11. A separate covariance matrix for each complete set of mediation parameters was found and used to simulate raw data. A parameter set consisted of the true values of the path coefficients that were needed for the full model in Figure 2: three α paths, six β paths, and a single ψ path coefficient. Previous simulation studies of mediation have suggested that estimates are not affected by the magnitude of direct effects so and were set to zero to simplify the model (MacKinnon et al., 2004). Path coefficients were chosen so that each distinct set of parameters would yield mediated effects (two-path, three-path, or both) that corresponded to combinations found in previous work (e.g., MacKinnon et al., 2002; MacKinnon et al., 2004) and contrasts that would address power or Type I error in a number of ways (e.g., null contrasts between two zero indirect effects, null contrasts from equal nonzero mediated effects). Path coefficients were set to 0, .14, .39, or .59 in varying combinations of α, β, and ψ, again to correspond to previous research. For two-path mediation models studied in previous simulations, these values corresponded to effect sizes of zero, small, medium, and large (Cohen, 1988). In all, 12 sets of parameters were necessary to test indirect effects and contrasts of interest. The full range of possible combinations was not explored, as this would have increased the number of parameter sets. Two-path combinations included zero/zero, zero/small, zero/medium, zero/large, small/small, medium/medium, medium/large, and large/large. Three-path effects were zero/zero/zero, zero/zero/small, zero/zero/medium, zero/zero/large, small/zero/zero, small/small/zero, medium/zero/zero, medium/medium/zero, large/zero/zero, large/large/zero, small/small/small, small/small/large, medium/medium/medium, large/large/small, and large/large/large.
Previous simulation studies (MacKinnon et al., 2002; MacKinnon et al., 2004) have found that many methods of testing mediation converge in their estimates of power and Type I error rates at sample sizes of around 500, so this study focused on samples of 50, 100, and 200. Three sample sizes for each of the 12 parameter sets yielded 36 unique combinations, for which 1,000 replication datasets were generated. For the resampling tests, each of these 36,000 datasets was resampled 1,000 times.
Confidence Intervals
CI calculation varied according to the method used, but all were evaluated as follows. The CI for each replication was found and compared to the true value of the mediated effect. To examine interval bias and coverage, the proportion of times that the true value fell to the left and right of the computed interval was found for each test. To gauge how close this proportion was to the expected value, .5ω, the liberal robustness criterion proposed by Bradley (1978) was used. Proportions were considered robust if they were between .25ω and .75ω, or ± half the expected proportion.
CIs were also used to evaluate statistical power and Type I error rates. Power was obtained as the proportion of replications for true nonzero effects whose CIs did not include zero. Type I error rate was calculated as the proportion of true zero parameter replications whose CI did not include zero. These proportions were also evaluated with the liberal robustness criterion and were considered robust if it fell between .025 and .075. Power and Type I error of contrasts were evaluated in a similar manner as mediated effects.
Single Sample Methods
Standard z
The standard z method for creating CIs used the standard errors from Equation 4 for two-path mediated effects. Three-path mediated effects, αβψ, have a more complicated variance estimate described by Taylor et al. (in press). The variance estimate, derived from the multivariate delta method, is given as:
| (12) |
CIs were formed by using Equation 5 with a value of 1.96 for z1−ω/2 using the appropriate standard error estimate.
M test
M test CIs were created using Equations 6 and 7. Upper and lower critical values were obtained by submitting the two delta estimates from each simulation replication to the PRODCLIN program (MacKinnon et al., 2007).
Empirical-M
Although the PRODCLIN program overcomes the lack of available exact critical values for two path-mediated effects, it does not enable application of the M to indirect effects with more than two paths. The Emp-M, however, can be applied to such effects, with the expectation (based on the comparability between the M and Emp-M found by MacKinnon et al., 2004) that the Emp-M results closely approximate results that would be obtained with a three-path M test. Critical values were generated from the empirical distributions of the product of three variables generated through simulations. Values for each of the three delta variables were varied in increments of .5 to reduce the total number of combinations. This increment was comparable to the intervals of .4 for the distribution of the product of two variables tabled in Meeker et al. (1981) and originally used with the M test.
Resampling Methods
Percentile bootstrap
The percentile bootstrap was proposed by Efron (1979) and is described by Efron and Tibshirani (1993). It assumes that there is a transformation, known or unknown, that will convert the bootstrapped distribution of the estimator to a normal distribution (Bollen & Stine, 1990; Manly, 1997) and might therefore be more accurate than the standard z method, which assumes a normal distribution to the mediated effect. To find the 100(1 − ω)% CI for a quantity, θ, a large number of bootstrap samples are taken, with replacement, from the original dataset. An estimate of θ, θ̂b, is found in each of the bootstrap samples and these are sorted from least to greatest. The confidence limits are then the values of θ̂b at the ω/2 and 1 − ω/2 cumulative frequency of this distribution.
Bias-corrected bootstrap
The effectiveness of the percentile method is largely dependent on the assumption that there is a transformation for θ̂, f (θ̂), such that the transformed variable is normally distributed with a mean equal to the population parameter of interest, θ. If this assumption does not hold, coverage will be distorted and error rates will not be equal to ω. The bias-corrected bootstrap has a weaker assumption and allows the mean of the transformed estimate to differ from the population mean. Formally, there exists a transformation of θ̂, f (θ̂), such that f (θ̂) is normally distributed with a mean, f (θ) − z0η. In this equation z0 is the bias correction and η is the standard deviation of f (θ̂).
The bias correction, z0, is calculated from the bootstrap sampling distribution. The original sample estimate, θ̂, is compared to the bootstrap sample estimates, θ̂b, and the proportion of bootstrap estimates that exceed the original estimate is denoted by p. Next, z0 is calculated as the z score for the probability 1 − p. For example, if there was no discrepancy between the bootstrap mean and the population mean, p = 0 and z0 = 0.
Limits for bias-corrected CIs are formed using Equation 13:
| (13) |
where the parameter φL is the probability of finding a value of 2z0 − zω/2 on the standard normal distribution and ψU is the probability of 2z0 + zω/2. Multiplying both φL and φU by 100 yields the correct quantiles from the bootstrap distribution to use as the upper and lower confidence limits.
Contrasts of Mediated Effects
Contrasts were evaluated with three methods. First, the technique for testing contrasts of mediated effects detailed by MacKinnon (2000) was used. This method formed CIs using an estimate of the contrast (the difference between two effects) and an estimate of this quantity’s standard error, derived using the multivariate delta method described earlier. The percentile and bias-corrected bootstrap were also used to evaluate contrasts. The distribution of the product methods is not directly applicable as tests of contrasts because their reference distribution is of the product, not the difference between two products. It might be possible to empirically generate a distribution based on a contrast to create confidence limits (e.g., the distribution of the difference between two product variables). It is likely that this method would be very similar to the resampling methods described in this article.
Comparisons included contrasts between a pair of two-path effects as well as contrasts between a single two-path and a single three-path mediated effect. Each parameter set entered into the path model yielded six contrasts between pairs of two-path contrasts and nine contrasts that included a three-path effect (tables of specific comparisons from each set are available from the first author). Power was found for comparisons between unequal effects and Type I error rates were found for all included comparisons of two zero indirect effects and comparisons of identical nonzero effects. Robustness intervals were used to evaluate whether the observed Type I error rates approximated the nominal error rate.
RESULTS
Initial analyses explored inadmissible solutions and other problems. Although there were no instances of failure to converge or improper solutions, there were replications with undefined standard errors for some contrasts. Approximately 46% of the three-path versus two-path effect contrast combinations had at least one replication with a negative contrast error variance based on the multivariate delta method. The number of replications with negative error variances tended to be small (under 5%) and decreased as sample size increased. Inspection of replication-level variance-covariance estimates suggested that negative variance estimates were most common when a covariance between parameters was negative and the true value of the contrast was equal to zero. Replications with negative variances for a contrast did not contribute to estimates for the z test method for testing that contrast. Bootstrap estimates were not affected by negative error variances. None of the standard errors for contrasts of pairs of two-path effects were undefined.
Mediated Effects
Each of the 12 sets of parameters yielded six two-path mediated effects and three three-path effects, for a total of 72 two-path and 36 three-path effects. Many combinations of the α and β (and ψ for three-path effects) paths were duplicated within a set of parameters or across sets. Results for power and Type I error are given in Table 1 with entries combined across two-path and three-path effects separately. Type I error results in Table 1 are further broken down by the number of zero paths effect. Complete tables of individual effects are available online at http://www.public.asu.edu/~davidpm/ripl/mediate.htm.
TABLE 1.
Average Type I Error and Power, Mediated Effects
| Sample Size |
||||
|---|---|---|---|---|
| Effect Type | Test | 50 | 100 | 200 |
| Null two-path, two zero paths | Standard z | .00020a | .00030a | .00000a |
| M | .00400a | .00350a | .00250a | |
| Percentile bootstrap | .00440a | .00250a | .00220a | |
| Bias-corrected bootstrap | .01360a | .01130a | .01160a | |
| Null two-path, one zero path | Standard z | .02050a | .02540 | .03140 |
| M | .05020 | .04910 | .04940 | |
| Percentile bootstrap | .04200 | .04620 | .05070 | |
| Bias-corrected bootstrap | .06900 | .06760 | .07130 | |
| Null two-path, overall | Standard z | .01410a | .01750a | .02150a |
| M | .03570 | .03480 | .03470 | |
| Percentile bootstrap | .03020 | .03250 | .03540 | |
| Bias-corrected bootstrap | .05160 | .04990 | .05260 | |
| Null three-path, three zero paths | Standard z | .00000a | .00000a | .00000a |
| Empirical M | .00000a | .00000a | .00000a | |
| Percentile bootstrap | .00150a | .00000a | .00000a | |
| Bias-corrected bootstrap | .00600a | .00150a | .00400a | |
| Null three-path, two zero paths | Standard z | .00000a | .00000a | .00007a |
| Empirical M | .00364a | .00350a | .00386a | |
| Percentile bootstrap | .00307a | .00143a | .00214a | |
| Bias-corrected bootstrap | .01736a | .01650a | .01343a | |
| Null three-path, one zero path | Standard z | .00860a | .02013a | .02847a |
| Empirical M | .05413 | .05393 | .05627 | |
| Percentile bootstrap | .03467 | .04433 | .04587 | |
| Bias-corrected bootstrap | .08093a | .07820a | .07860a | |
| Null three-path, overall | Standard z | .00416a | .00974a | .01381a |
| Empirical M | .02784 | .02768 | .02897 | |
| Percentile bootstrap | .01826a | .02210a | .02316a | |
| Bias-corrected bootstrap | .04739 | .04539 | .04435 | |
| Nonzero two-path | Standard z | .48360 | .66690 | .73090 |
| M | .58050 | .71140 | .78430 | |
| Percentile bootstrap | .53510 | .69740 | .76920 | |
| Bias-corrected bootstrap | .57820 | .72080 | .80460 | |
| Nonzero three-path | Standard z | .19480 | .38380 | .50240 |
| Emp-M | .35520 | .47540 | .58720 | |
| Percentile bootstrap | .29080 | .45120 | .55500 | |
| Bias-corrected bootstrap | .37400 | .50020 | .61960 | |
Proportion outside Bradley (1978) robustness interval.
Type I Error
Two-path mediated effects
When both α and β were zero, all methods estimated the Type I error at below the nominal rate. The bias-corrected bootstrap performed best, but all methods were below the robustness interval at all sample sizes. For null mediated effects with one nonzero path, the M and bootstrap methods performed better than the z, with no error rates outside the robustness interval. The M and percentile bootstrap were close to the nominal Type I error rate, but the bias-corrected bootstrap was somewhat higher than .05. For some combinations of sample size and α and β paths, the bias-corrected bootstrap was too high (approximately .08). However, the bias-corrected bootstrap had the most accurate overall Type I error rates, followed by the M. The z test was inaccurate, consistently underestimating the Type I error rate.
Three-path mediated effects
The Emp-M replaced the M test for three-path effects. In general, all methods displayed inaccurate, too-low Type I error rates across all zero three-path effects. Two nonzero paths were necessary for estimates from any test to fall within robustness intervals. When two paths were of medium size or larger, the bias-corrected bootstrap again had instances of excess Type I errors (e.g., over .08 for all sample sizes for zero/medium/medium and zero/large/large). The Emp-M also had excess Type I errors, though in fewer cases. Overall, the bias-corrected bootstrap had the most accurate Type I error across all zero three-path effects, followed by the Emp-M. Both were within robustness for all sample sizes across all null three-path mediated effects.
The influence of several factors on mediated effects’ Type I error rate were modeled using analysis of variance (ANOVA). Both between-groups and repeated-measures models were examined and gave similar results, but results from the former are presented. Factors included the number of paths in the mediated effect (two or three), which test was used to evaluate the effect (standard z, M/Emp-M, percentile bootstrap, bias-corrected bootstrap), sample size (50, 100, 200), and the number of zero paths in the effect (one, two, or three). All interactions were included except for any involving both number of zero paths and number of paths as these overlapped.
Two main effects were significant. There was significant variation of Type I error by test, F(3, 744) = 10.80, p < .001, partial η2 = .04. The bias-corrected bootstrap was closest to the nominal Type I error rate, followed by the percentile and M tests. The z method had the lowest overall error rate. Type I error was also influenced by the number of zero paths in the effect, F(2, 744) = 538.99, p < .001, partial η2 = .59. The rate was most accurate across all other conditions when there was only a single zero path. The interaction of test and number of zero paths in the effect was significant, F(6, 744) = 19.24, p < .001, partial η2 = .13, and suggested that as the number of zero paths increased to two or three, differences between tests diminished and all four methods were generally inaccurate. With a single zero path, the M and bias-corrected bootstrap were both more accurate than the other methods and close to the nominal error rate. The interaction of test and number of paths in the mediated effect was also significant, F(3, 744) = 4.24, p < .01, partial η2 = .02. Type I error for the percentile bootstrap and z tests were impacted more than the bias-corrected bootstrap when the number of paths increased from two to three.
Power
Two-path mediated effects
In contrast to previous findings, the bias-corrected bootstrap was not consistently the most powerful method. Overall, this method and the M test with exact critical values from PRODCLIN had very similar power, with one method performing somewhat better for some combinations of sample size and paths and the other having slightly higher power for the others. The exception to this was for small/small mediated effects, where the M had considerably less power than the bias-corrected bootstrap. The percentile bootstrap performed better than the z, which lagged behind the other tests, especially at smaller sample and effect size.
Three-path mediated effects
Consistent with previous studies, the bias-corrected bootstrap had the greatest power to detect an effect. The z had the lowest power, especially when one or more paths were small and when sample size was low. The test based on the distribution of the product (Emp-M) again had superior power to the percentile bootstrap.
Just as with Type I error, factors that might impact power were included in an ANOVA. The model for power did not include the number of zero effects, but all other factors were retained. Two main effects emerged. Increasing sample size increased power, F(2, 480) = 7.28, p < .001, partial η2 = .03, and three-path effects were lower in power than two-path effects, F(1, 480) = 19.04, p < .001, partial η2 = .04. No interactions were significant.
Confidence Intervals
Confidence Interval Coverage
The performance of each method’s CI was assessed by calculating the coverage of each interval as 1 − (proportion of true values to the left + proportion of true values to the right). Under ideal conditions, a method should yield a coverage value of .95 when ω is set to .05. An ANOVA was conducted that included test, number of paths of the effect, sample size, and whether the effect was zero or nonzero. All interactions were included in the model. There was a main effect of zero versus nonzero effects, F(1, 1248) = 471.89, p < .001, partial η2 = .27. Across all other parameters, zero effects were above the optimal coverage of .95, whereas nonzero effects were somewhat below .95. Tests also significantly affected interval coverage, F(3, 1248) = 14.07, p < .001, partial η2 = .03, but all tests had overall estimated coverage within 1% of the optimal 95%. Two interactions were significant. The interaction of test and zero versus nonzero mediated effects was significant at p < .001, F(3, 1248) = 26.26, partial η2 = .06). Tests had greater variability in their coverage for null effects than for nonzero effects, with the bias-corrected bootstrap showing the least impact of effect type and the z the greatest. The second significant interaction was the type of mediated effect (zero vs. nonzero) by number of paths in the effect, F(1, 1248) = 27.30, p < .001, partial η2 = .02. Three-path effects were more variable than two-path ones, with intervals for null effects that were larger than those for null two-path effects and intervals for nonzero effects that were smaller than those two-path effects greater than zero. However, both two- and three-path mediated effects had coverage that was above .95 when the effect was equal to zero and coverage that was below .95 when the effect was nonzero.
Confidence Interval Bias
Table 2 shows the average proportion of true values that fell to the outside of each method’s CI, either to the left or the right, for two-path and three-path effects. Expected proportions are .025 to each side at a nominal ω = .05. For two- and three-path zero effects the intervals are relatively unbiased, with comparable proportions to the left and right of the interval. In terms of accuracy compared to expected values however, the z test performs poorly on average, with percentages that are too low and outside the robustness interval. The percentile bootstrap performs better but is still inaccurate overall. The bias-corrected bootstrap and Emp-M methods perform better, with proportions that are both balanced and within robustness intervals a greater number of times. When the true mediated effect was nonzero, confidence limits were often biased, with proportions of true values to the right that were too large and outside the robustness interval. Table 3 contains counts of proportions to the left and right of the interval for each test, combined across sample size, for each of the four types of mediated effects examined. The total left and right counts are out of a possible 69 nonrobust estimates on each side (138 total). The bias-corrected bootstrap had the lowest number of proportions that were too far from expected values, followed by the percentile method and M/Emp-M. The standard z test had approximately one third more values than the bias-corrected bootstrap that were too far from expected values.
TABLE 2.
Average Confidence Limits
| Sample Size |
|||||||
|---|---|---|---|---|---|---|---|
| 50 |
100 |
200 |
|||||
| Effect Type | Test | True to Left | True to Right | True to Left | True to Right | True to Left | True to Right |
| Null two-path, two zero paths | Standard z | .00000a | .00018a | .00027a | .00000a | .00000a | .00000a |
| M | .00255a | .00145a | .00209a | .00145a | .00155a | .00091a | |
| Percentile bootstrap | .00155a | .00282a | .00136a | .00109a | .00091a | .00127a | |
| Bias-corrected bootstrap | .00682a | .00682a | .00491a | .00636a | .00545a | .00618a | |
| Null two-path, one zero path | Standard z | .01042a | .01013a | .01308 | .01233a | .01492 | .01650 |
| M | .02571 | .02450 | .02488 | .02425 | .02363 | .02579 | |
| Percentile bootstrap | .02029 | .02171 | .02263 | .02358 | .02363 | .02704 | |
| Bias-corrected bootstrap | .03592 | .03308 | .03338 | .03425 | .03450 | .03683 | |
| Null two-path overall | Standard z | .00714a | .00700a | .00906a | .00846a | .01023a | .01131a |
| M | .01843 | .01726 | .01771 | .01709 | .01669 | .01797 | |
| Percentile bootstrap | .01440 | .01577 | .01594 | .01651 | .01649 | .01894 | |
| Bias-corrected bootstrap | .02677 | .02483 | .02443 | .02549 | .02537 | .02720 | |
| Null three-path, three zero paths | Standard z | .00000a | .00000a | .00000a | .00000a | .00000a | .00000a |
| Emp-M | .00000a | .00000a | .00000a | .00000a | .00000a | .00000a | |
| Percentile bootstrap | .00000a | .00150a | .00000a | .00000a | .00000a | .00000a | |
| Bias-corrected bootstrap | .00350a | .00250a | .00100a | .00050a | .00200a | .00200a | |
| Null three-path, two zero paths | Standard z | .00000a | .00000a | .00000a | .00000a | .00000a | .00007a |
| Emp-M | .00236a | .00129a | .00157a | .00193a | .00179a | .00207a | |
| Percentile bootstrap | .00064a | .00243a | .00071a | .00071a | .00086a | .00129a | |
| Bias-corrected bootstrap | .00993a | .00743a | .00729a | .00921a | .00800a | .00543a | |
| Null three-path, one zero path | Standard z | .00387a | .00473a | .01000a | .01013a | .01533 | .01313 |
| Emp-M | .02647 | .02767 | .02707 | .02687 | .02527 | .03100 | |
| Percentile bootstrap | .01493 | .01973 | .02353 | .02080 | .02407 | .02180 | |
| Bias-corrected bootstrap | .04060a | .04033a | .04047a | .03773a | .04060a | .03800a | |
| Null three-path, overall | Standard z | .00187a | .00229a | .00484a | .00490a | .00742a | .00639a |
| Emp-M | .01387 | .01396 | .01381 | .01387 | .01303 | .01594 | |
| Percentile bootstrap | .00752a | .01074a | .01171a | .01039a | .01203a | .01113a | |
| Bias-corrected bootstrap | .02435 | .02303 | .02294 | .02245 | .02339 | .02097 | |
| Nonzero two-path | Standard z | .00814a | .06346a | .01011a | .06592a | .01230a | .05719a |
| M | .01678 | .05046a | .01738 | .05519a | .01892 | .04338a | |
| Percentile bootstrap | .01449 | .04162a | .01754 | .04173a | .01986 | .04438a | |
| Bias-corrected bootstrap | .02219 | .04054a | .02376 | .04322a | .02505 | .03532 | |
| Nonzero three-path | Standard z | .00160a | .07620a | .00700a | .08920a | .00680a | .08300a |
| Emp-M | .01000a | .06780a | .01600 | .08100a | .01440 | .07320a | |
| Percentile bootstrap | .00920a | .03580 | .01420 | .04320a | .01620 | .05920a | |
| Bias-corrected bootstrap | .01960 | .05300a | .02660 | .05720a | .02420 | .04640a | |
Value outside Bradley (1978) robustness interval.
TABLE 3.
Count of Nonrobust Proportions of True Values to the Left and Right of Confidence Interval
| Type of Mediated Effect |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Null Two-Path |
Nonzero Two-Path |
Null Three-Path |
Nonzero Three-Path |
Combined |
|||||||
| Test | Left | Right | Left | Right | Left | Right | Left | Right | Left | Right | Total |
| Standard z | 8 | 8 | 6 | 11 | 27 | 28 | 13 | 15 | 54 | 62 | 116 |
| M/Emp-M | 6 | 5 | 3 | 7 | 26 | 27 | 7 | 14 | 42 | 53 | 95 |
| Percentile | 5 | 6 | 3 | 10 | 25 | 24 | 8 | 13 | 41 | 53 | 94 |
| Bias-corrected | 6 | 8 | 0 | 4 | 26 | 27 | 3 | 10 | 35 | 49 | 84 |
Contrasts
Type I Error
Average estimates for contrast power and Type I error are shown in Table 4. Type I error was evaluated for three types of null contrast: (a) two two-path effects that are both zero, (b) two equal nonzero two-path effects, and (c) one zero three-path and one zero two-path effect. The percentile bootstrap was closest to the nominal error rate across the types of contrasts and sample sizes. No overall estimates of Type I error were outside robustness intervals for any test or type of contrast at any sample size. Full tables of Type I error rates for each specific contrast are available at http://www.public.asu.edu/~davidpm/ripl/mediate.htm and show that estimates were generally accurate so long as one effect was not composed of two zero paths. Type I error was most seriously underestimated by all tests when both effects had only zero or small effect sizes in their paths (e.g., zero/zero vs. zero/small).
TABLE 4.
Average Contrast Type I Error and Power
| Sample Size |
||||
|---|---|---|---|---|
| Contrast | Test | 50 | 100 | 200 |
| Two two-path, both null | Standard z | .02911 | .03800 | .03594 |
| Percentile bootstrap | .03917 | .04839 | .04711 | |
| Bias-corrected bootstrap | .05539 | .06078 | .05528 | |
| Two equal nonzero two-path | Standard z | .03880 | .04060 | .04280 |
| Percentile bootstrap | .05220 | .04820 | .05600 | |
| Bias-corrected bootstrap | .05960 | .05920 | .05980 | |
| Three- vs. two-path, both null | Standard z | .07328 | .07415 | .06900 |
| Percentile bootstrap | .03548 | .03959 | .04420 | |
| Bias-corrected bootstrap | .05885 | .05698 | .06067 | |
| Two two-path, one null | Standard z | .39694 | .55668 | .64468 |
| Percentile bootstrap | .40785 | .56732 | .65871 | |
| Bias-corrected bootstrap | .43668 | .58332 | .67638 | |
| Two two-path, both nonzero | Standard z | .46000 | .67587 | .84500 |
| Percentile bootstrap | .46427 | .67567 | .84060 | |
| Bias-corrected bootstrap | .48927 | .68807 | .84233 | |
| One three-path, one null effect | Standard z | .37997 | .57003 | .66559 |
| Percentile bootstrap | .37807 | .58017 | .68498 | |
| Bias-corrected bootstrap | .42645 | .60743 | .71183 | |
| One three-path, both nonzero | Standard z | .35800 | .56175 | .69650 |
| Percentile bootstrap | .38675 | .55325 | .65450 | |
| Bias-corrected bootstrap | .42300 | .57125 | .66450 | |
When comparing two equal nonzero effects, there were few differences between tests. The error rate was underestimated by the z and percentile (N = 50 only) when two small/small effects were compared; otherwise the error estimate was comparable across test and there was little difference between contrasts of two medium/medium effects and two large/large ones. The percentile bootstrap had rates closest to the nominal rate.
Comparisons of zero three-path and zero two-path effects showed a similar pattern of results as contrasts of two null two-path effects, with more variability across tests and effects. In dramatic contrast to its previous conservative estimates, the z yielded Type I error rates of around .10 for some combinations, typically when all paths were zero except for one or two. Increased sample size appeared to exacerbate these problems. For example, the z gave an estimate of .188 for zero/zero/medium compared to zero/zero at N = 50 but at N = 200 the Type I error rate was .242. The resampling methods both somewhat underestimated the error rate for these same contrasts. The z method appeared to stabilize only when both effects had at least one path that was medium or greater and sample size was 100 or more. Although not as excessive as the z, the bias-corrected bootstrap had instances where it had Type I error beyond robustness, primarily when one or both of the effects had a path with a large effect size. Overall, however, the bias-corrected bootstrap had the most accurate Type I error rate across all sample sizes for this type of contrast, followed by the percentile.
The Type I error rates of all null contrasts were examined with an ANOVA. A 2×3×3 factorial model was examined where the factors were: (a) the contrast was between two two-path effects or between a three-path and a two-path effect, (b) number of observations (50, 100, 200), and (c) the type of test used to test the contrast (standard z, percentile bootstrap, or bias-corrected bootstrap). All interactions were included in the model.
Results indicated there were two main effects: number of paths in effect 1 (3 vs. 2), F(1, 603) = 14.26, p < .001, partial η2 = .02, and the type of test used, F(2, 603) = 10.94, p < .001, partial η2 = .04. The percentile bootstrap had the most accurate overall Type I error across all other conditions, followed by the bias-corrected bootstrap and then the z test. Contrasts with two two-path effects had an overall error rate slightly below the nominal .05 level, whereas contrasts with a three-path effect were slightly above .05. These two effects made up the only significant interaction, F(2, 603) = 23.68, p < .001, partial η2 = .07. Whereas the resampling methods had roughly equivalent (nonsignificant by simple effect test) error rates regardless of the number of paths in the first effect, the z method was inconsistent, with lower than .05 error rate with two paths and greater than .05 when there were three paths. The simple effect test for the z test across number of paths was highly significant, F(1, 603) = 59.55, p < .001, partial η2 = .10.
Power
Power was estimated for four types of contrasts. These included two two-path effects with one zero effect, two two-path effects that were both nonzero but unequal, one two-path and one three-path effect where one was zero, and one two-path and one three-path where they were both nonzero but unequal. Table 4 shows the average estimated power for each of these types of contrasts. All three tests had similar power except for when sample size was very small, in which case the bias-corrected bootstrap was more powerful.
The ANOVA model for examining effects on power was an expanded version of the one used to test the Type I error rate. The true difference of the contrast was entered as a factor, and all interactions introduced by this fourth factor were included in the model.
Number of paths in effect 1 was again significant, F(1, 963) = 87.58, p < .001, partial η2 = .08, with lower power in contrasts with a three-path effect. Sample size significantly affected power as well, F(2, 963) = 53.07, p < .001, partial η2 = .10, with larger sample size resulting in more power to detect the contrast difference. The true magnitude of the difference between effects was also highly significant, F(1, 963) = 452.05, p < .001, partial η2 = .32. Power did not differ by test.
There was again only a single significant interaction, this time between the true difference of effects and the number of paths in effect 1, F(1, 963) = 143.11, p < .001, partial η2 = .13. At high negative differences between effects, there was little effect of number of paths in effect 1 on power. When the difference was low (either positive or negative) and large and positive there was greater power when effect 1 had three paths.
The absolute value of the difference between effects was substituted for the true difference in an identical ANOVA. Number of paths in effect 1 and sample size were again significant with similar direction of effects, F(1, 963) = 20.47, p < .001, partial η2 = .02, F(2, 963) = 74.70, p < .001, partial η2 = .14, respectively. The absolute difference between effects was highly significant as well, F(1, 963) = 3591.95, p < .001, partial η2 = .79. Instead of the interaction of difference and number of paths being significant, there was a significant interaction of sample size and the absolute difference, F(2, 963) = 5.80, p < .01, partial η2 = .01. Increases in sample size did not have uniform increases in power across differing absolute differences between mediated effects. At small differences, there was not much increase in power with increased sample size. Similarly, large differences resulted in considerable power, and thus benefited less from added cases.
DISCUSSION
This study largely corroborated findings and recommendations from earlier studies of tests of mediated effects (MacKinnon et al., 2002; MacKinnon et al., 2004; Shrout & Bolger, 2002) and generalizes these to more complex models with multiple mediators and three-path effects. In addition, bootstrap alternatives to the standard z test for contrasts of mediated effects were explored. Results for contrasts were generally more uniform than those for mediated effects and are discussed first.
Method had little impact on conclusions about contrasts. Power to detect differences between mediated effects did not significantly differ by test. Sample size and the difference between effects were the primary determinants of power. On average, all Type I error rates were accurate as well. The percentile bootstrap was closest to the nominal error rate across conditions. The bias-corrected bootstrap tended to be similar to the percentile bootstrap but with somewhat higher estimates for both power and Type I error rate. The z test had lower power and Type I error as well as some other disadvantages. In some situations the z test substantially exceeded ω. Larger than expected Type I error rates were observed for contrasts whose distributions were not normally distributed, such as the contrast of zero/zero/medium and zero/zero and small/small/zero and zero/zero. The z test also suffers from an important computational problem. Almost half (46.6%) of the contrasts of a three-path effect to a two-path effect had at least one replication sample with an undefined standard error calculated using the multivariate delta method. Calculation of the z statistic is not possible without this standard error. The bootstrap methods are not susceptible to this problem, and both might be easier to use than calculating the formula for the standard error for each contrast of interest. In addition to the type of method used, Type I error was influenced by the number of paths in the first mediated effect.
As in previous studies, the z test was a conservative test of mediation, with the lowest power and Type I error rates that were often considerably below ω. The test based on the distribution of the product (M or Emp-M) outperformed both the z and the percentile bootstrap for both two- and three-path mediated effects. The exact critical values for the M test from the PRODCLIN program resulted in an increase in power for the M but the Emp-M, with relatively coarse deltas for critical values, also had better performance than the percentile bootstrap. However, overall differences between the percentile bootstrap and M/Emp-M were typically minimal. Across all conditions the bias-corrected bootstrap had the greatest power, the most accurate Type I error rates, and the fewest nonrobust CIs. This is counterbalanced somewhat by the slightly higher risk of making a Type I error with this method.
Although the properties of three-path mediated effects have not been extensively explored, this study sheds some light on their properties. Three-path mediated effects had low observed Type I error rates that were below the robustness interval for accurate estimates in most conditions. At least two nonzero paths (out of the three total) were needed for the Type I error rate to be within robustness criteria for accuracy. Large effect size and large sample sizes were required for sufficient power. Although all tests had inaccurate Type I error rates, the standard z method was far below the bootstraps and Emp-M. Power was much greater in the alternative tests as well.
CIs were often biased, as found in earlier studies. Bias was more likely at small sample sizes, for small effect sizes, and when the true mediated effect was nonzero. Tests performed differentially depending on whether the true mediated effect was equal to zero or not. When the true effect was zero, proportions of true values outside confidence limits were more often balanced with the percentile bootstrap or M test. When the true effect was nonzero, the bias-corrected bootstrap had the best balance. Overall, very few confidence limits were within robustness criteria for three-path effects.
Although this study extends previous investigations into alternative methods for testing mediation, there are several limitations. Many multiple mediator models similar to the one examined in this study will be in applied areas of research, particularly intervention or prevention program evaluation, that use binary variables as either predictors (e.g., treatment group vs. control) or outcomes (e.g., smoker status). Only continuous variables were investigated in this study. MacKinnon et al. (1995) compared continuous and binary independent variables using simulation methods and found little difference in point estimates between the two conditions. Standard errors were somewhat larger in the binary independent variable situation, but were quite similar. Comparability of estimates and standard errors suggest that results of this study can be generalized to program evaluations with treatment–control dichotomies for independent variables. Results for the bootstrap tests might be especially generalizable to binary independent variables because they rely only on repeated estimation of the point estimate of the effect, which was shown to not differ by independent variable type (MacKinnon et al., 1995). Dichotomous outcomes complicate estimation of mediated effects because the coefficients and standard errors are scaled differently (MacKinnon & Dwyer, 1993). Mediated effects can be tested by the product of coefficients or bootstrap tests but the estimated effect is not scaled identically to all other effects such as the direct effect. Standardization is required for contrasts, as each mediated effect must be scaled in the same metric for accurate tests of the difference between effects. Unless the coefficients from logistic regression are standardized, the two mediated effects (and the direct effect as well, if it is in the contrast) will not be identically scaled and the value of the contrast will be inaccurate.
A potential drawback of this study might be that 1,000 bootstrap samples are insufficient for estimating CIs, particularly for effects that are composed of more than three paths. Efron (1987) noted that confidence limits might require as many as 2,000 bootstrap samples even though as few as 200 were sufficient for a point estimate of a statistic. To test mediation and contrasts in this study, both the percentile and bias-corrected bootstrap rely on percentiles of the bootstrap distribution to form CIs. A commonly stated requirement for proper use of nonparametric bootstraps is that the resampling distribution should be representative of the sampling distribution of the statistic being examined, or at least be transformable to a normal distribution (Hall, 1992, Manly, 1997). Just as with “regular” sampling, a greater number of bootstrap samples or draws from the population yields a more accurate distribution of the statistic. For the percentile bootstrap, more resamples permits estimation of the 2.5th and 97.5th percentiles (for ω = .05) with greater precision. Although the percentile bootstrap performed well for contrasts and was superior to the standard z for mediated effects, its performance might increase with more bootstrap samples. A limited number of resamples is potentially more problematic for the bias-corrected bootstrap. Because it forms CIs by using a correction based on bias in the median to modify the upper and lower limits away from the simple 2.5th and 97.5th percentiles, it is possible that these limits might be adjusted to more extreme ends of the bootstrap distribution than they would be with a finer grained adjustment that would be possible with more resamples. This becomes more likely as the difference between the original estimate of the statistic and the median of the bootstrap distribution of estimates increases. Conceivably, the limits could be adjusted to one of the endpoints of the distribution, depending on whether the original estimate was greater or less than the median of the bootstrap distribution. The likelihood of adjusting either confidence limit to its extreme decreases with more and more bootstrap samples to absorb the correction for bias. Similarly, if one limit is close to zero, the adjustment might shift the interval so that it either encompasses zero more times than it should or it might not include zero when the effect is truly equal to zero. In the latter situation, Type I error would be overestimated, and this was the case with the bias-corrected bootstrap, especially when one path was large and others were equal to zero. Further work on bootstrap methods should determine if the excessive Type I error rate sometimes found with the bias-corrected bootstrap can be improved with more bootstrap samples. A small simulation study was performed to examine these issues about the limits of the bias-corrected bootstrap intervals. Preliminary simulation results suggest that 1,000 bootstrap samples might indeed be too few. Type I error rates were greater, and often above the nominal value when one effect size was large or medium, when only 1,000 bootstrap samples were used compared to 2,000. More work is needed to examine the appropriate number of bootstrap samples for the bias-corrected bootstrap when used for indirect effects, especially because it seems to be a promising technique in other respects in this and other studies (MacKinnon et al., 2004).
Although this study generalized results from single-mediator applications of alternative tests for mediation to a more complex model with multiple mediators, multiple outcomes, and contrasts of mediated effects, other complexities were not addressed and might prove fertile ground for future endeavors. First, the model studied used variables that were normally distributed. Alternative distributions with skew and kurtosis, or binary predictors, mediators, and outcomes can contribute further to understanding of how these newer methods perform. For example, the two nonparametric bootstrap methods examined here might be more robust to distributional anomalies in variables, just as they appear to be more robust to the nonnormality of the distribution of the product that comprises the mediated effect. Another potential contribution would be to introduce measurement error and other model misspecification to examine how each test performs under these less perfect conditions. Further exploration of some of these tests is warranted as well. The distribution of products test based on empirically derived critical values can be refined further with smaller intervals between delta values. The role of the number of bootstrap samples taken remains unclear at this point and would be a beneficial area for future exploration.
In sum, there are compelling alternatives to the standard z test that offer greater power and more accurate Type I error. When the raw data are available, the bias-corrected bootstrap offers the best power and CI placement, and the best overall Type I error. Both resampling tests are available in SAS macros using PROC REG (for single-mediator models) and PROC CALIS (for path models with multiple mediators) and have been incorporated into the Mplus (Muthén & Muthén, 2006) covariance matrix program. Contrasts seem particularly well suited to resampling if the data are available because these methods do not require unique standard errors, some with complex derivations and some that are undefined, for each type of contrast examined. In the absence of raw data, the M or Emp-M tests based on the distribution of the product are good alternatives for indirect effects but not contrasts. In light of these results, the z test is not recommended for either mediated effects or contrasts when sample size is not large. Superior alternatives are readily available and should be used instead. At larger sample sizes, differences between tests decrease, so large samples might render the choice of test to one of convenience as they have similar performance.
Acknowledgments
This research was supported by National Institute on Drug Abust grant R01DA09757 (David P. MacKinnon, Principal Investigator) and the Health, Social and Economics Research Unit, RTI International (Al Miedema, Vice President). We gratefully acknowledge the contributions of Sanford Braver, Siek-Toon Khoo, Alex Zautra, and Roger Millsap to this work, which was based on the first author’s doctoral dissertation.
Contributor Information
Jason Williams, RTI International.
David P. MacKinnon, Department of Psychology, Arizona State University
References
- Alwin DF, Hauser RM. The decomposition of effects in path analysis. American Sociological Review. 1975;40:37–47. [Google Scholar]
- Aroian LA. The probability function of the product of two normally distributed variables. Annals of Mathematical Statistics. 1947;18:265–271. [Google Scholar]
- Aroian LA, Taneja VS, Cornwell LW. Mathematical forms of the distribution of the product of two normal variables. Communications in Statistics: Theory and Methods. 1978;A7:165–172. [Google Scholar]
- Banyard VL, Williams LM, Siegel JA. The long-term mental health consequences of child sexual abuse: An exploratory study of the impact of multiple traumas in a sample of women. Journal of Traumatic Stress. 2001;14:697–715. doi: 10.1023/A:1013085904337. [DOI] [PubMed] [Google Scholar]
- Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Bollen KA, Stine R. Direct and indirect effects: Classical and bootstrap estimates of variability. Sociological Methods. 1990;20:115–140. [Google Scholar]
- Bradley JV. Robustness? British Journal of Mathematical and Statistical Psychology. 1978;31:144–152. [Google Scholar]
- Cohen J. Statistical power for the behavioral sciences. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc; 1988. [Google Scholar]
- Craig CC. On the frequency function of xy. Annals of Mathematical Statistics. 1936;7:1–15. [Google Scholar]
- Efron B. Computers and statistics: Thinking the unthinkable. SIAM Review. 1979;21:460–480. [Google Scholar]
- Efron B. Better bootstrap confidence intervals. Journal of the American Statistical Association. 1987;76:312–319. [Google Scholar]
- Efron B, Tibshirani R. An introduction to the bootstrap. New York: Chapman & Hall; 1993. [Google Scholar]
- Hall P. The bootstrap and Edgeworth expansion. New York: Springer-Verlag; 1992. [Google Scholar]
- Lockwood CM, MacKinnon DP. Bootstrapping the standard error of the mediated effect. Paper presented at the 23rd annual meeting of SAS User’s Group International; Cary, NC. 1998. Mar, [Google Scholar]
- MacCorquodale K, Meehl PE. On a distinction between hypothetical constructs and intervening variables. Psychological Review. 1948;55:95–107. doi: 10.1037/h0056029. [DOI] [PubMed] [Google Scholar]
- MacKinnon DP. Contrasts in multiple mediator models. In: Rose JS, Chassin L, Presson CC, Sherman SJ, editors. Multivariate applications in substance use research. Mahwah, NJ: Lawrence Erlbaum Associates, Inc; 2000. pp. 141–160. [Google Scholar]
- MacKinnon DP, Dwyer JH. Estimating mediated effects in prevention studies. Evaluation Review. 1993;17:144–158. [Google Scholar]
- MacKinnon DP, Fritz MS, Williams J, Lockwood CM. Distribution of the product confidence limits for the indirect effect: Program PRODCLIN. Behavior Research Methods. 2007;39(3):384–389. doi: 10.3758/bf03193007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Goldberg L, Clarke GN, Elliot DL, Cheong J, Lapin A, et al. Mediating mechanisms in a program to reduce intentions to use anabolic steroids and improve exercise self-efficacy and dietary behavior. Prevention Science. 2001;2(1):15–28. doi: 10.1023/a:1010082828000. [DOI] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CL, Hoffman J. A new method to test mediation. Paper presented at the annual meeting of the Society for Prevention Research; Park City, UT. 1998. Jun, [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7(1):83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CL, Williams J. Confidence limits for the indirect effect: Distribution of the product and resampling approaches. Multivariate Behavioral Research. 2004;39:99–128. doi: 10.1207/s15327906mbr3901_4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Warsi G, Dwyer JH. A simulation study of mediated effect measures. Multivariate Behavioral Research. 1995;30:41–62. doi: 10.1207/s15327906mbr3001_3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manly BFJ. Randomization, bootstrap and Monte Carlo methods in biology. London: Chapman & Hall; 1997. [Google Scholar]
- Meeker WQ, Jr, Cornwell LW, Aroian LA. The product of two normally distributed random variables. In: Kennedy WJ, Odeh RE, editors. Selected table in mathematical statistics. VII. Providence, RI: American Mathematical Society; 1981. [Google Scholar]
- Muthén LK, Muthén BO. Mplus user’s guide. 4. Los Angeles: Muthén & Muthén; 2006. [Google Scholar]
- Pituch KA, Stapleton LM, Kang JY. A comparison of single sample and bootstrap methods to assess mediation in cluster randomized trials. Multivariate Behavioral Research. 2006;41(3):367–400. doi: 10.1207/s15327906mbr4103_5. [DOI] [PubMed] [Google Scholar]
- Pituch K, Whittaker TA, Stapleton LM. A comparison of methods to test for mediation in multisite experiments. Multivariate Behavioral Research. 2005;40:1–23. doi: 10.1207/s15327906mbr4001_1. [DOI] [PubMed] [Google Scholar]
- Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: New procedures and recommendations. Psychological Methods. 2002;7:422–445. [PubMed] [Google Scholar]
- Sobel ME. Asymptotic confidence intervals for indirect effects in structural equation models. In: Leinhardt S, editor. Sociological methodology 1982. Washington, DC: American Sociological Association; 1982. pp. 290–312. [Google Scholar]
- Sobel ME. Effect analysis and causation in linear structural equation models. Psychometrika. 1990;55:495–515. [Google Scholar]
- Springer MD, Thompson WE. The distribution of independent random variables. SIAM Journal on Applied Mathematics. 1966;14:511–526. [Google Scholar]
- Stone CA, Sobel ME. The robustness of estimates of total indirect effects in covariance structure models estimated by maximum likelihood. Psychometrika. 1990;55:337–352. [Google Scholar]
- Taylor AB, MacKinnon DP, Tein J-Y. Standard error of the three-path mediated effect. Organizational Research Methods (in press) [Google Scholar]
- Woodworth RS. Dynamic psychology. In: Murchison C, editor. Psychologies of 1925. Worcester, MA: Clark University Press; 1928. pp. 111–126. [Google Scholar]
- Wright S. Physiological and evolutionary theories of dominance. American Naturalist. 1934;67:24–53. [Google Scholar]