Model-free estimation of the psychometric function

Abstract

A subject's response to the strength of a stimulus is described by the psychometric function, from which summary measures, such as a threshold or slope, may be derived. Traditionally, this function is estimated by fitting a parametric model to the experimental data, usually the proportion of successful trials at each stimulus level. Common models include the Gaussian and Weibull cumulative distribution functions. This approach works well if the model is correct, but it can mislead if not. In practice, the correct model is rarely known. Here, a nonparametric approach based on local linear fitting is advocated. No assumption is made about the true model underlying the data, except that the function is smooth. The critical role of the bandwidth is identified, and its optimum value estimated by a cross-validation procedure. As a demonstration, seven vision and hearing data sets were fitted by the local linear method and by several parametric models. The local linear method frequently performed better and never worse than the parametric ones. Supplemental materials for this article can be downloaded from app.psychonomic-journals.org/content/supplemental.

INTRODUCTION

The psychometric function is central to the theory and practice of psychophysics (Falmagne, 1985; Klein, 2001). It describes the relationship between the level of a stimulus and a subject's response, usually represented by the probability of success on a certain number of trials at that stimulus level, where success is interpreted broadly—that is, a particular response out of two possible forms (e.g., “present” or “absent”, “longer” or “shorter”, “above” or “below”). The actual psychometric function underlying the data is, of course, not directly accessible to the experimenter, and it needs to be estimated. The most common way of doing this is to assume that the true function can be described by a specific parametric model and then estimate the parameters of that model by maximizing the likelihood.

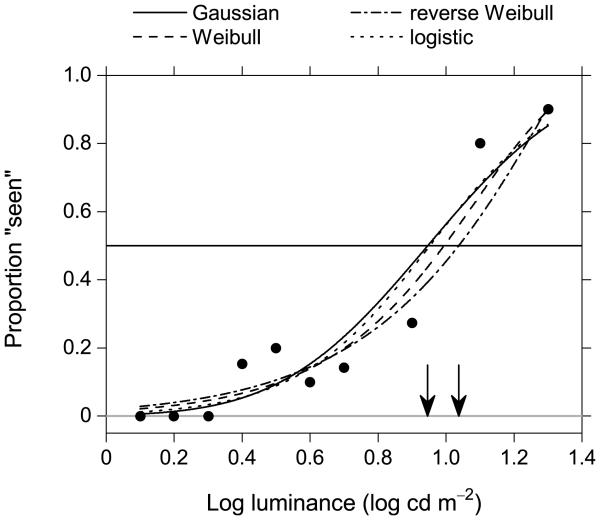
Figure 1 shows a typical example from an experiment on frequency of seeing (Miranda & Henson, 2008). A flash of light of variable intensity was presented repeatedly at a fixed location in the visual field of a subject who reported whether the flash was visible. The symbols show the proportion of responses “seen”, and the solid curve is the estimated psychometric function. This curve was modeled with a Gaussian cumulative distribution function (cdf), Φ_μ,σ, which has two parameters, the mean μ and the standard deviation σ, whose values were obtained by maximizing the likelihood. This function has a long history of usage in modeling frequency-of-seeing data, partly on the basis of theoretical considerations (Blackwell, 1946; Crozier, 1950). The other curves in Figure 1 are discussed shortly.

Figure 1.

Parametric estimation of a psychometric function for frequency of seeing. The proportion of responses “seen” is plotted against log stimulus luminance. Filled circles are data from Miranda and Henson (2008) and are based on 3–20 trials at each stimulus level. The curves are parametric fits, as identified in the key. The horizontal solid line indicates the criterion level for a 50% threshold, and the arrows mark the extreme estimated thresholds, which were for the Gaussian and reverse Weibull cumulative distribution functions.

From the estimated psychometric function, predictions of performance at other stimulus levels can be obtained. It is also possible to construct summary measures of performance, such as the threshold value of the stimulus for a certain criterion level of performance or the spread or slope of successful responses around that threshold value. More generally, it may be used to test models of the underlying physiological or psychological processes.

All this depends on the correctness of the specified model, but, in practice, the correct model is rarely known with certainty. The curves in Figure 1 illustrate why uncertainty about the correct model might be a problem. Each represents a plausible model, fitted by maximum likelihood. Along with the Gaussian cdf, there are Weibull, reverse Weibull, and logistic cdfs, whose formal definitions are given in Table 1. All four functions have different shapes; yet it is difficult to choose between them on the basis of the goodness of their individual fits, all of which are acceptable, given the number of data points. The small differences in a measure of lack of fit — the deviance, which is defined later — are not diagnostic. Estimates of a threshold stimulus level, corresponding to a criterion level of performance of 50% seeing, indicated by the solid horizontal line in Figure 1, varied from 0.946 log cd m⁻² (Gaussian cdf) to 1.037 log cd m⁻² (reverse Weibull cdf)—that is, by 10.1% of the non-deterministic part of the stimulus range. Here and elsewhere, log denotes logarithm to the base 10. Whether these differences in threshold estimates are important depends on the application, but it is clear that in parametric modeling, the choice of the model may lead to bias in the estimator.

Table 1.

Definitions of model cumulative distribution functions F(x) in standard form. The general form of each function is obtained by transforming x to y = a₀ + a₁x, where −∞ < a₀ < ∞ and a₁ > 0; then y has the distribution F((x − a₀)/a₁). For example, the standard Gaussian cdf Φ has the general form Φ_μ,σ, where the parameters a₀ and a₁ are the mean μ and standard deviation σ, respectively.

Model cdf F(x)	Definition
Gaussian	(2π)−1/2 ${\int }_{-\infty }^x$ exp (−z2/2) dz	−∞ < x < ∞
Weibull*	0, 1 − exp(−xβ),	−∞ < x ≤ 0 0 < x < ∞ and β > 0
reverse Weibull	exp(−(−x)β), 1,	−∞ < x ≤ 0 and β > 0 0 < x < ∞
logistic	(1 + exp(−x))−1,	−∞ < x < ∞

^*The Weibull cdf is sometimes written as 1 − exp(−x), with x > 0, after suitable transformation of variables (Strasburger, 2001); cdf, cumulative distribution function.

The difficulty of specifying the best parametric model was noted previously by Strasburger (2001), who used both Weibull and logistic cdfs to analyze data on character recognition as a function of character contrast in a 10-alternative forced-choice experiment. The resulting estimates of slope and threshold were not the same for the two models, but goodness of fit could not be used to decide which model best captured performance over the stimulus range (Strasburger, 2001, pp. 1371-1372).

How, then, should a model for a psychometric function be chosen? The approach advocated here is to use a nonparametric method¹ that is based on local linear fitting. In that no assumption is made about the shape of the true function underlying the experimental data, except for the basic requirement that it should be smooth², the approach may be considered, for psychophysical purposes, as model free. If necessary, the requirement could be added that the function should depend monotonically on the stimulus level, but this is usually satisfied automatically in the present applications. Although response measures other than quantal ones may be used (e.g., reaction times), only response proportions are considered. They are treated as being distributed binomially, but this assumption can be relaxed³.

Using a local linear method removes the burden of deciding about the parametric model when there is insufficient knowledge about the underlying processes. In a statistical sense, the local linear method also has the important property that its consistency, and hence lack of asymptotic bias, does not rely on the correctness of the model assumed by the experimenter (see, e.g., Fan & Gijbels, 1996, Section 5.4). Thus, as the sample size increases, the estimated function necessarily approaches the true function.

As shown by the examples presented later, local linear fitting gives reliable results for a wide range of real and simulated data. The requirement that the psychometric function be smooth is not really restrictive, and most parametric methods assume the same. The local linear method can also adjust automatically to unknown upper and lower limits on a subject's performance, including the conventional guessing rate and lapsing rate, but if these limits are known, they can be incorporated explicitly in the local linear fit. Any summary measures, such as the threshold or slope, can be readily extracted from the fitted function.

Local linear fitting is not the only nonparametric method available for modeling psychometric functions, but it does offer several advantages over alternatives such as kernel smoothing, smoothing splines, Fourier-series estimates, and wavelet approximations (see discussions in, e.g., Fan & Gijbels 1996; Härdle, Müller, Sperlich, & Werwatz 2004; Hart 1997; Simonoff 1996).

The organization of this article is as follows. First, the essentials of the parametric method and the local linear method are described, with particular attention given to the role of the bandwidth in determining the local linear fit. A measure of goodness of fit is formulated, which is then combined with a cross-validation procedure to obtain an estimate of the optimum bandwidth. The effects of guessing and lapsing are next analyzed, and their impact on derived statistics, such as the threshold and slope, illustrated. Finally, a range of real data sets posing varying difficulty in fitting are modeled by the local linear method, and the results are compared with those from parametric methods.

PARAMETRIC ESTIMATION

By way of preparation, it is useful to summarize the key features of the psychometric function and how it is fitted in a parametric approach based on maximum likelihood. The general form of the psychometric function is typically given as

$$P\left(x\right)=\gamma +(1-\gamma -\lambda )F\left(x\right)$$ (1)

where P(x) is the probability of a successful response at stimulus level x, the function F is a smooth, monotonic function of x taking values between 0 and 1, and the constants γ and λ define the lower and upper asymptotes (Treutwein & Strasburger, 1999). The independent variable x is assumed to be one-dimensional, but this assumption is not essential. The lower asymptote may be interpreted as a guessing rate, where, by the design of the experiment, performance is expected to be no better than chance; and the upper asymptote may be interpreted as a lapsing rate, where, because of errors unconnected with the task itself (e.g., blinking when the stimulus appears or making an error in signaling the response), performance is occasionally at chance level. For example, for a two-alternative forced-choice task, γ = 0.5, and if the subject fails to respond on, say, 1% of occasions, λ = 0.01. Necessarily, P(x) can only take values between γ and 1−λ.

As has already been indicated, the most common method of estimating a psychometric function is to fit a specific parametric model, essentially a generalized linear model (GLM; McCullagh & Nelder, 1989). A GLM has three components: a random component from the exponential family—for example, a binomial distribution with mean μ, which depends on the explanatory variables (e.g., x); a systematic component consisting of a linear predictor η, which is a linear transform of the explanatory variables; and a monotonic differentiable link function g that relates the two [i.e., η = g(μ)]. Certain distributions have canonical link functions that have some interesting statistical properties and simplify the calculation of iterative weighted least squares; for example, the canonical link for the binomial distribution Bi(m, μ), with probability of success μ in m trials, is the logit function η = ln(μ/(1-μ)), although other link functions are also used (McCullagh & Nelder, 1989). The inverse of each of these link functions is constrained to fall in the interval [0, 1], necessary for a probability. The parameters of the GLM are estimated by maximizing the appropriate likelihood function.

Accordingly, the psychometric function P(x) is modeled as

$$\eta \left(x\right)=g\left[P\left(x\right)\right].$$ (2)

By making the link function g a transformed logit or other inverse cdf⁴, the values of the psychometric function are constrained to the interval [γ, 1−λ] for known guessing and lapsing rates. The function η is almost always a polynomial in x of degree 1, so that η(x) = a₀ + a₁x. The coefficients a₀ and a₁ are simply related to the threshold and slope of the psychometric function.

The experimental data consist of the number r_i of successful responses out of m_i trials at each of n stimulus levels x_i, with 1≤ i ≤ n. For convenience, the responses are assumed to have a binomial distribution (see ​Footnote 3) Bi(m_i, P(x_i)) at each level x_i, so that the log-likelihood takes the form (McCullagh & Nelder, 1989):

$$\begin{array}{cc}\hfill l(a_0,a_1)& =\underset{i=1}{\overset{n}{\Sigma }}\ln \left[P^{r_i}\left(x_i\right){(1-P\left(x_i\right))}^{m_i-r_i}\right]\hfill \\ \hfill & =\underset{i=1}{\overset{n}{\Sigma }}{r}_i\ln P\left(x_i\right)+(m_i-r_i)\ln \left[1-P\left(x_i\right)\right]\hfill \\ \hfill & =\underset{i=1}{\overset{n}{\Sigma }}{r}_i\ln g^{-1}(a_0+a_1{x}_i)+(m_i-r_i)\ln \left[1-g^{-1}(a_0+a_1{x}_i)\right],\hfill \end{array}$$

where g⁻¹ is the inverse of g, so that g⁻¹[g(q)] = q for all q. The coefficients a₀ and a₁ are then estimated by maximizing l(a₀, a₁), usually by iterative weighted least squares, which proceeds by adjusting the fitted values and weights in turn, typically converging in just a few iterations. For more details, see McCullagh & Nelder (1989, Section 4.4). A generalized nonlinear framework for modeling psychometric functions has been described by Yssaad-Fesselier & Knoblauch (2006), but the approach is still parametric, since an appropriate link function needs to be chosen.

The link function g does most of the work of fitting in a GLM, but, as was indicated in the introduction, there is seldom sufficient information to make a correct choice. If the chosen link function is not the true one, the function η(x) might not be a polynomial in x of degree 1. A wrongly chosen link function can therefore result in a poor fit and misleading inferences (Czado & Santner, 1992). The problem cannot be obviated by dealing with a family of link functions in some general way, since it is unclear how the family should be parameterized, although Aranda-Ordaz (1981) and Morgan (1985) have proposed two particular families that contain the logistic function as a special case. The local linear method described in the next section avoids this problem and any dependency on a specific parametric model.

LOCAL LINEAR ESTIMATION

In the local linear method, the work in fitting is shifted from the link function g to the function η, assumed in Equation 2 to be linear in its parameters.

Suppose, for the moment, that g₁ is the correct link function for a particular psychometric function P so that P(x) = g₁⁻¹[η₁(x)] with η₁(x) = a₀ + a₁x for all x. Now suppose that g₁ is replaced by an incorrect link function g₂. Then P can still be represented as P(x) = g₂⁻¹[η₂(x)], but for some other function η₂ with η₂(x) = g₂{g₁⁻¹[η₁(x)]}. Although η₂(x) cannot, in general, be written as b₀ + b₁x, it is safe to assume that it is smooth. An alternative approach to the problem, therefore, is to accept a given link function g and concentrate on estimating the required function η, which is generally a nonlinear function of x. The link function g is still required, but merely to ensure that the transformed value of x—that is, g⁻¹[η(x)]—behaves as a probability and falls in the interval [0, 1].

One way to estimate the nonlinear function η is by polynomial regression of suitably high degree, but the difficulties of this approach are well documented. It can introduce large biases in the fit; individual observations can have an undue influence on remote parts of the curve; the degree of the polynomial cannot be controlled continuously; and the high value required for a good fit may lead to excessive variability in the estimated coefficients (Fan & Gijbels, 1996).

The principle of local linear fitting (Fan, Heckman, & Wand, 1995) is to approximate the function η locally, point by point, with the aid of a Taylor expansion. That is, for a given point x, the value η(u) at any point u in a neighborhood of x is approximated by

$$\eta \left(u\right)\approx \eta \left(x\right)+(u-x){\eta }^{\prime }\left(x\right),$$ (3)

where η′ is the first derivative of η. The accuracy of this approximation depends on the distance between u and x: the smaller |u − x|, the better the approximation. The actual estimate of the value of η(x) is obtained by fitting this approximation to the data over the prescribed neighborhood of x. The order of the Taylor expansion in Equation 3 could be higher than 1, but usually (see, e.g., Simonoff, 1996) it need not be more than 3. The linear approximation used here (i.e., order 1) has the particular merit that, if required, it guarantees the monotonicity of the estimated psychometric function if the neighborhood is large enough, as explained in the next section. It is emphasized that this local linear fit is not a concatenation of straight-line segments, but a smooth fit whose value at a particular point is obtained by performing a locally weighted linear fit at that point.

In more detail, local linear fitting proceeds as follows. Suppose that the link function is the canonical one for the binomial distribution—that is, the logit, g(q) = ln[q/(1 − q)], with inverse, the logistic function^†, g⁻¹(x) = [1 + exp(−x)]⁻¹. Although the logistic function has some advantages, the choice, as already indicated, is not critical. For a given point x, set α₀ = η(x) and α₁ = η′(x) in Equation 3. Then the values of the coefficients α₀ and α₁ can be estimated by maximizing the local log-likelihood l(α₀, α₁; x) ⁵, which is similar to the log-likelihood defined earlier but now includes a neighborhood weight function w(x, x_i). The local log-likelihood takes the form

$$\begin{array}{cc}\hfill l({\alpha }_0,{\alpha }_1;x)& =\underset{i=1}{\overset{n}{\Sigma }}\ln \left[P^{r_i}\left(x_i\right){(1-P\left(x_i\right))}^{m_i-r_i}\right]w(x,x_i)\hfill \\ \hfill & =\underset{i=1}{\overset{n}{\Sigma }}\left[r_i\ln P\left(x_i\right)+(m_i-r_i)\ln (1-P\left(x_i\right))\right]w(x,x_i)\hfill \\ \hfill & =\underset{i=1}{\overset{n}{\Sigma }}\left[r_i\ln g^{-1}({\alpha }_0+{\alpha }_1{x}_i)+(m_i-r_i)\ln (1-g^{-1}({\alpha }_0+{\alpha }_1{x}_i))\right]w(x,x_i)\hfill \\ \hfill & =\underset{i=1}{\overset{n}{\Sigma }}\left[r_i\ln \left\{{(1+\exp (-({\alpha }_0+{\alpha }_1{x}_i)))}^{-1}\right\}+(m_i-r_i)\ln \left\{1-{(1+\exp (-({\alpha }_0+{\alpha }_1{x}_i)))}^{-1}\right\}\right]w(x,x_i)\hfill \\ \hfill & =-\underset{i=1}{\overset{n}{\Sigma }}\left[r_i\ln \left\{1+\exp (-({\alpha }_0+{\alpha }_1{x}_i))\right\}+(m_i-r_i)\ln \left\{1+\exp ({\alpha }_0+{\alpha }_1{x}_i)\right\}\right]w(x,x_i).\hfill \end{array}$$ (4)

If α̂₀ is the estimated value of α₀, then the estimate of the function η at x is η̂(x) = α̂₀. The estimate of the psychometric function P at x is $\widehat{\mathit{P}}\left(\mathit{x}\right)$ = g⁻¹(α̂₀). This process is repeated at sufficiently many values of x that the estimates $\widehat{\mathit{P}}\left(\mathit{x}\right)$ provide the required level of detail in the description of P for the task in hand. The logit function was used as the link in all the examples of local linear fitting in this work.

The weight function w assigns a weight to each stimulus level x_i according to its distance from the point x, the points closest to x having the greatest influence on the estimate. It has the general form

$$w(x,x_i)=\frac{1}{h}K\left(\frac{x-x_i}{h}\right),$$

where K is the kernel and h is the bandwidth characterizing the size of the neighborhood. The kernel is a function usually assumed to be symmetric about zero and compactly supported, but this is not necessary for the validity of the method. How the kernel is chosen and the bandwidth is estimated are considered in the next section.

Figure 2 shows a local linear fit to the frequency-of-seeing data shown in Figure 1. The weight function was based on a Gaussian density function, with bandwidth h = 0.296 log cd m⁻² chosen by a cross-validation method. The shape of this weight function for the estimate at the particular stimulus level x₀ = 1.0 log cd m⁻² is shown in the left panel of Figure 3 by the solid curve. The data points at the lowest three stimulus levels, x = 0.1, 0.2, 0.3, make a negligible contribution to the fit at x₀.

Figure 2.

Local linear estimation of a psychometric function for frequency of seeing. The proportion of responses “seen” is plotted against log stimulus luminance. Filled circles are data from Miranda and Henson (2008), based on 3–20 trials at each stimulus level (as in Figure 1), and the curve is a local linear fit with Gaussian kernel and cross-validation bandwidth h_CV = 0.296 log cd m⁻². The horizontal solid line shows the criterion level for a 50% threshold, and the arrow marks the estimated threshold.

Figure 3.

Effect of the weight function on a local linear estimate. The proportion of responses “seen” is plotted against log stimulus luminance. Filled circles are data from Miranda and Henson (2008), as in Figures 1 and 2. In the left panel, the dotted and dashed curves are (scaled) Gaussian weight functions with, respectively, very small and very large bandwidths h = 0.12 log cd m⁻² and h = 0.6 log cd m⁻², centered at the point x₀ = 1.0 log cd m⁻², indicated by the vertical line. In the right panel, the dotted and dashed curves are the corresponding fits obtained at x₀, where they almost coincide, and over the rest of the stimulus range. The solid curve in the left panel shows for comparison the weight function at x₀ with the cross-validation bandwidth h_CV = 0.296 log cd m⁻² used in Figure 2.

The estimated 50% threshold was 0.974 log cd m⁻² (indicated by the arrow in Figure 2), which is similar to the value obtained with a parametric Gaussian cdf, but the local fit is better than any of the parametric fits in the top right part of the curve (cf. Figure 1), and it is no worse in the remaining part of the curve.

KERNEL AND BANDWIDTH

It is known that the influence of the weight function w depends less on the shape of the kernel K than on the bandwidth h (see, e.g., Härdle, et al., 2004). But for data where the levels are widely spaced, it is best if K has unbounded support, for then the influence of points as they are included or excluded from the fit does not lead to a rapidly changing estimate (see, e.g., Simonoff, 1996). This may be achieved with a Gaussian kernel—that is, K(u) = exp(−u²/2)—as in the local linear fit shown in Figure 2. A Gaussian kernel was used in all the examples of local linear fitting in this work.

Deciding on the bandwidth h is more problematic⁶. The choice is crucial, since h controls the domain of influence of w and, hence, the smoothness of the local linear estimate of the function η in Equation 2. For small h, the estimate of η at each x is based on a linear fit to just a few neighboring points of x, with the result that the estimate follows the data very closely and is therefore susceptible to the random variations in the data. For large h, the estimate of η at each x is based on a linear fit with most points in the data set receiving nearly equal weight, with the result that the estimate is very smooth, close to that obtained by a parametric method and, therefore, potentially biased.

Figure 3 illustrates how the bandwidth influences the weights assigned to each point in arriving at the local linear estimate. The dotted and dashed curves in the left panel are Gaussian weight functions with very small and very large bandwidths, respectively. The corresponding fits are shown in the right panel: the dotted curve, obtained with the very small bandwidth, almost interpolates between points, and the dashed curve, obtained with the very large bandwidth, almost coincides with the parametric fit with a logistic cdf (cf. Figure 1).

Ideally, the bandwidth should be chosen so that the resulting estimate is neither too variable nor too biased. A measure of the goodness of fit is thus needed to establish what constitutes an optimum bandwidth.

GOODNESS OF FIT

The goodness of fit of an estimated psychometric function can be measured in several ways. One measure is the deviance D (McCullagh & Nelder, 1989, Section 4.4), which is twice the difference between the maximum achievable log-likelihood and the log-likelihood under the fitted model—that is,

$$D=2\underset{i=1}{\overset{n}{\Sigma }}{r}_i\ln \frac{r_i}{m_i\widehat{P}\left(x_i\right)}+(m_i-r_i)\ln \frac{m_i-r_i}{m_i-m_i\widehat{P}\left(x_i\right)},$$ (5)

where $\widehat{\mathit{P}}$ is the estimate of the psychometric function P. When the deviance is defined for responses that have a normal, rather than a binomial, distribution at each level x_i, it coincides with the residual sum of squares. An alternative measure of goodness of fit is Pearson's X² statistic, which for the binomial distribution is given by

$$X^2=\underset{i=1}{\overset{n}{\Sigma }}\frac{{(r_i-m_i\widehat{P}\left(x_i\right))}^2}{m_i\widehat{P}\left(x_i\right)(1-\widehat{P}\left(x_i\right))}.$$

Other measures of goodness of fit are described in Read & Cressie (1988), Hart (1997), and Collett (2003).

Large values of D indicate a discrepancy between the fitted model and the data. But the significance of these differences can be interpreted only in relation to the distribution of the statistic. Asymptotically, D is distributed as χ²(n − k), where k is the number of fitted parameters, but the justification for this result relies on assumptions (McCullagh & Nelder, 1989) that, in practice, may be uncertain for many psychophysical experiments. In particular, if the model has a nonlinear part, as with the Weibull cdf or when the guessing and lapsing rates are estimated, then the asymptotic distribution may also depend on the unknown parameters (see, e.g., Hart, 1997).

These uncertainties are greater still for nonparametric models, where the definition of the number of fitted parameters — the degrees of freedom of the fit — has to be adjusted for local linear fitting, with the result that k is no longer integer (see, e.g., Hastie & Tibshirani, 1990, Appendix B). Notwithstanding these caveats, the χ² distribution can still be used as a rule-of-thumb reference distribution for the deviance (Hastie & Tibshirani, 1990, Section 6.8). That is, the value of D obtained for the fit is compared with χ²(n − k), and if D falls sufficiently far into the tail, it is concluded that the fit is unacceptable. It is emphasized that the reported values of D and estimated p values are not intended to decide between a local linear fit and the corresponding parametric fits, but simply to indicate the conventional plausibility of the fits.

For the local linear fit to the data in Figure 2, the value of D was 3.91, for which p = 0.78. For the parametric fits to the same data in Figure 1, the values of D ranged from 6.58 for the Gaussian to 4.52 for the reverse Weibull cdf, for which p = 0.58 and p = 0.72, respectively.

CROSS-VALIDATION

The bandwidth that yields the fitted curve closest to the true one depends on the unknown function being estimated; hence, it cannot be found explicitly. Instead, it can be chosen by one of several automatic methods. The three most popular ones are the plug-in (Ruppert, Sheather & Wand, 1995), cross-validation (Xia & Li, 2002), and the bootstrap (Faraway, 1990). Only cross-validation was used here. Although no method can be guaranteed always to work, cross-validation generally estimates the optimum bandwidth well (Loader, 1999), and it is not as computationally intensive as the bootstrap. A detailed discussion of the advantages and disadvantages of different approaches to bandwidth selection can be found in Loader, 1999. As a preliminary to this analysis, all three methods were tested in large-scale simulations with symmetric and asymmetric synthetic psychometric functions. Cross-validation performed no worse than either of the other methods.

Motivation for using cross-validation comes from considering a superficially simpler approach. Suppose that the deviance in Equation 5 were used directly as a criterion for bandwidth selection. Then the bandwidth h for which the deviance reaches its minimum is h = 0, where the fitted values are exactly the same as the observed ones. Thus, the deviance is zero, and the solution is degenerate. Cross-validation overcomes this problem in the following way (see, e.g., Silverman, 1986). Suppose that there were another independent sample drawn from a distribution identical to that of the original data. Then this second sample could be used to create an independent estimate ${\breve{\mathit{P}}}_{\mathit{h}}$of the psychometric function P (the dependence of estimators on the bandwidth h is made explicit for emphasis). This independent estimate can now replace ${\widehat{\mathit{P}}}_{\mathit{h}}\left({\mathit{x}}_{\mathit{i}}\right)$ in the deviance (Equation 5), since it estimates the same psychometric function P. Because the estimate ${\breve{\mathit{P}}}_{\mathit{h}}$ does not depend on the original observations, minimizing this modified deviance does not lead to a degenerate solution. In general, however, additional independent samples are not available. Instead, cross-validation employs a leave-one-out estimator, in which the fit ${\widehat{\mathit{P}}}_{-\mathit{i,h}}\left({\mathit{x}}_{\mathit{i}}\right)$ at each x_i is calculated with the i^th observation omitted to define the cross-validated deviance:

$$D_{\mathrm{CV}}\left(h\right)=\frac{2}{n}\underset{i=1}{\overset{n}{\Sigma }}{r}_i\ln \frac{r_i}{m_i{\widehat{P}}_{-i,h}\left(x_i\right)}+(m_i-r_i)\ln \frac{m_i-r_i}{m_i-m_i{\widehat{P}}_{-i,h}\left(x_i\right)}.$$

The value of the cross-validation bandwidth h_CV that minimizes D_CV(h) is the estimate of the optimum bandwidth.

Note that the cross-validated deviance is not being used to decide between different models but to estimate the best possible bandwidth, much as in the parametric method, where the parameter values are estimated by maximizing the likelihood.

In practice, the values of the cross-validated deviance D_CV are calculated for a finite number of values of the bandwidth h. A plausible lower limit for these values is the maximum distance between neighboring stimulus levels, and an upper limit, a multiple of the data range. Figure 4 shows the cross-validated deviance plotted against the bandwidth h for the data in Figure 2. The location of the minimum h_CV = 0.296 log cd m⁻², used to estimate the optimum bandwidth, is indicated by the arrow.

Figure 4.

Estimation of the optimum bandwidth. The cross-validated deviance D_CV for the data in Figure 2 is plotted against the bandwidth h. The location of the minimum defining the cross-validation bandwidth h_CV = 0.296 log cd m⁻² is indicated by an arrow. The function is plotted on a log-log scale for clarity.

It is possible to allow the bandwidth h to vary with x, so that it adapts to the density of the data points (Fan & Gijbels, 1992), but in the examples analyzed here, it is constant over the whole data range; that is, the estimation is performed in the same way at each data point. This contrasts with the parametric method where the asymptotes need special treatment.

ASYMPTOTES

The guessing rate γ and lapsing rate λ (Equation 1) have decisive roles in the parametric fitting of a psychometric function (Treutwein & Strasburger, 1999; Wichmann & Hill, 2001). Typically, in an M-alternative forced-choice task, the guessing rate γ = 1/M, and, in a yes-no task, γ = 0. But, depending on the response choices available, the guessing rate may deviate from the nominal value, and the form of the component F in the psychometric function (Equation 1) may change with changes in γ (Klein, 2001). Worse still, the lapsing rate λ cannot be predicted unless trials are specifically conducted to target this asymptote. It is often set arbitrarily to a small value (between 0 and 0.05) (Harvey, 1986; Strasburger, 2001; Treutwein & Strasburger, 1999), but, in fact, there is no reason to believe that it is equal to any prescribed value. The value of λ can strongly influence the estimated function F (Klein, 2001; Strasburger, 2001; Wichmann & Hill, 2001).

Both guessing and lapsing rates need to be either forced in parametric fitting or estimated by maximizing the likelihood. The latter approach is safer, in that it is free from bias due to incorrectly assumed values, but it increases the number of parameters in the fit, with the potential for deterioration in convergence (Treutwein & Strasburger, 1999). It also complicates the calculations, for the asymptotes appear in the log-likelihood in a nonlinear way, with the result that the model then falls outside the GLM framework. Nonlinearity also implies that the solution cannot be found by iterative weighted least squares (Treutwein & Strasburger, 1999). By contrast, the local linear method estimates the asymptotic values automatically, without the need to specify them explicitly in the likelihood, providing that there are sufficient data available in the required regions.

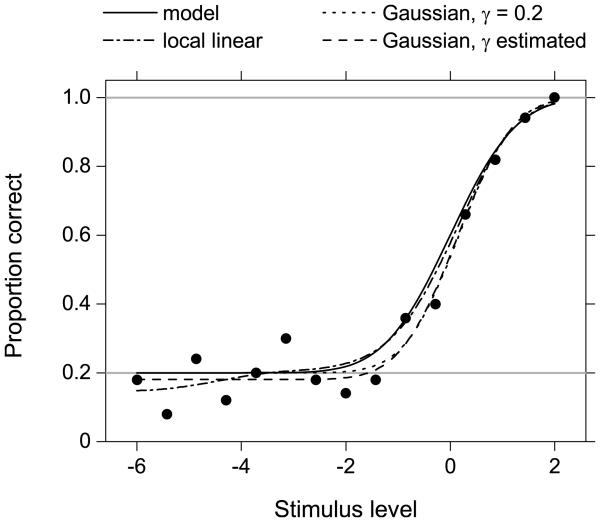
As an example, Figure 5 shows parametric and local linear fits to synthetic data generated from a model psychometric function (Equation 1) with the function F set to the standard Gaussian cdf Φ_0,1 (solid curve). The guessing rate γ = 0.2 corresponds to a five-alternative forced-choice paradigm. The stimulus levels were 15 equally spaced points in the interval [−6, 2], and there were 50 trials at each stimulus level. About half of the data points are in the region where the function reaches the guessing rate. Two parametric models were fitted, each with the (correct) Gaussian cdf: one with guessing rate fixed at the true value 0.2 (dots, largely obscured), and the other in which the guessing rate was estimated by maximizing the log-likelihood function (dashes). Both functions are quite close to the true function (solid curve), although the second parametric model slightly underestimated the guessing rate. The local linear fit, with cross-validation bandwidth h_CV = 1.032 (dashes–dots), stabilizes around the same value of the guessing rate as the global model with explicitly estimated guessing rate. Although the underlying psychometric function in the guessing region is essentially a horizontal line, the local linear fit has no prior knowledge of this behavior, so that some variation in the fit is to be expected, possibly leading to a departure from monotonicity. If more accurate modeling in this region is needed, the bandwidth could be varied adaptively with location (Fan & Gijbels, 1992), but this approach is not taken further.

Figure 5.

Effect of known and estimated guessing rates. Filled circles are synthetic data from a model psychometric function Φ_0,1 (solid curve). The other curves are for parametric fits of a correctly assumed Gaussian cumulative distribution function with correctly assumed guessing rate γ = 0.2 (dots) and estimated guessing rate (dashes), and for a local linear fit with cross-validation bandwidth h_CV = 1.032 (dashes–dots).

Figure 6 illustrates the risks of attempting to force a lapsing rate onto a parametric fit without knowing the correct rate. In the left panel, synthetic data were taken from a model psychometric function (Equation 1) with the function F again set to the standard Gaussian cdf Φ_0,1 with guessing rate γ = 0.2 and lapsing rate 0.02 (solid curve). The stimulus levels were 15 equally spaced points in the interval [−2.5, 2.5]. Three parametric models with fixed guessing and lapsing rates were fitted each with the correctly assumed Gaussian cdf and guessing rate γ = 0.2, but with incorrectly assumed lapsing rates λ = 0 (dots), λ = 0.01 (dashes), and λ = 0.05 (dashes–dots). All three fitted curves depart noticeably from the true curve, not only in the regions where the psychometric function reaches its asymptotes but importantly also in the main body of the curve.

Figure 6.

Effect of incorrectly assumed and estimated lapsing rates. In both panels, the filled circles are synthetic data from a model psychometric function Φ_0,1 with guessing rate γ = 0.2 and lapsing rate λ = 0.02 (solid curve). The other curves in the left panel are for parametric fits of a correctly assumed Gaussian cumulative distribution (cdf) function with correctly assumed guessing rate γ = 0.2 and lapsing rate fixed at λ = 0 (dots), λ = 0.01 (dashes), and λ = 0.05 (dashes–dots). The other curves in the right panel are for a parametric fit of a correctly assumed Gaussian cdf with estimated guessing and lapsing rates (dots), and for a local linear fit with cross-validation bandwidth h_CV = 0.930 (dashes).

The right panel of Figure 6 shows the fitted curves for a correctly assumed Gaussian cdf with estimated guessing and lapsing rates (dots) and for a local linear fit with cross-validation bandwidth h_CV = 0.930 (dashes). Both methods estimated the guessing and lapsing rates well, and the local fit fell reasonably close to the true psychometric function (solid curve) in the remaining part of the stimulus range. The departure of the parametric estimate from the true psychometric function over the interval [−1.5, 0.5] was presumably due to all the data in this interval falling below the true curve.

As an exercise, parametric fits to the frequency-of-seeing data of Figure 1 were repeated, but with guessing and lapsing rates estimated using an optimization routine. The deviances were D = 3.52 for the logit link and D = 3.55 for the probit link; for both, p = 0.74. These deviances are considerably lower than those for fits with fixed guessing and lapsing rates, but this is to be expected with the increase in the number of parameters from 2 to 4 (with more sparse data sets still, the fits can become degenerate). The estimated guessing rates were γ = 0.115 for the logit link and γ = 0.117 for the probit link. Yet, on inspection of the data (Figure 1), it is obvious that these asymptotes are inconsistent with the zero scores obtained at the lowest three stimulus levels, x = 0.1, 0.2, 0.3. For most of the other data sets considered here, parametric estimates of guessing and lapsing rates were very sensitive to the choice of initial values in the optimization, often leading to degenerate results, and they are not considered further.

From a psychophysical standpoint, the particular roles of the guessing rate γ and lapsing rate λ are treated more coherently within the context of a specific theory of performance, such as signal detection theory (Macmillan & Creelman, 2005).

SIGNAL-DETECTION THEORY

The importance of signal-detection theory in estimating the psychometric function has been emphasized by Klein (2001). In signal-detection theory, the guessing rate is incorporated into a discrimination measure d′, defined as the difference at each x between the linearized hit rate p_H(x) and the linearized false alarm rate p_FA. The latter is, in the theory, independent of x; that is, d' = g[p_H(x)] − g(p_FA), where g = Φ_0,1⁻¹ is the inverse of the standard Gaussian cdf. The symbol z is often used for Φ_0,1⁻¹, and the discrimination index is accordingly written d′ = z[p_H(x)] − z(p_FA). The link function g need not be restricted to Φ_0,1⁻¹ and may be replaced by the logit or any other function in the GLM family (DeCarlo, 1998). With the correct link function, d′ is a polynomial in x of degree 1. Transforming the data in this way does not, of course, change the nature of the problem—namely, finding the correct link function.

ESTIMATING THRESHOLD AND SLOPE

Recall that in parametric modeling, the psychometric function is uniquely determined by the link function and the parameters a₀ and a₁ through the relationship P(x) = g⁻¹(a₀ + a₁x) (Equation 2). Therefore, there exist closed-form expressions for statistics, such as the threshold and slope, whose estimates may be obtained by plugging the estimated parameters into these expressions. In local linear modeling, the psychometric function is estimated at each point of interest x, but there is no closed-form expression. Nevertheless, these statistics can easily be obtained from the fitted curve.

For example, for a criterion level of performance of 50%, the corresponding threshold stimulus level x_0.5 can be approximated by the value ${\widehat{\mathit{x}}}_{0.5}$ at which the estimated psychometric function $\widehat{\mathit{P}}$ takes a value closest to 0.5. Similarly, if the slope is defined as the first derivative P′(x_0.5) of P at x = x_0.5, it can be approximated by the discrete first derivative ${\widehat{\mathit{P}}}^{\prime }\left({\widehat{\mathit{x}}}_{0.5}\right)$ at x = ${\widehat{\mathit{x}}}_{0.5}$. Standard errors for each may be estimated by a bootstrap method (Efron & Tibshirani, 1993; Foster & Bischof, 1991).

To illustrate how this method works in practice, values of the 60% threshold and the slopes corresponding to these thresholds were obtained from the synthetic data in Figure 5. The estimates, along with their standard errors estimated by a bootstrap, are given in Table 2. For comparison, the true values of the threshold and slope are also shown.

Table 2.

True and estimated thresholds and slopes for the synthetic data of Fig. 5. Criterion level of performance was 60%.

Psychometric function	Threshold (SE)	Slope (SE)
Model	0	0.319
Gaussian cdf* with known guessing rate	0.166 (0.100)	0.386 (0.053)
Gaussian cdf* with estimated guessing rate	0.150 (0.101)	0.381 (0.054)
Local linear fit	0.070 (0.115)	0.328 (0.032)

^*cdf, cumulative distribution function

EXAMPLES

Six data sets, taken from studies of vision and hearing, were fitted by the local linear method, with cross-validation bandwidth, and, for comparison, by the four parametric models considered earlier (see Table 1). In the figures, the parametric fits are shown by interrupted curves: the Gaussian cdf by dots, the Weibull by dashes, the reverse Weibull by dashes–dots, and, when different from the Gaussian, the logistic cdf by short dashes. The local linear fit is shown by a solid curve.

The first two examples demonstrate that the local fit behaves much as parametric models do when they fit the data well. The second example also illustrates the ability of the local linear method to adjust automatically to the guessing rate. The remaining examples reveal the distinct strengths of the local fit when parametric fits are poor.

Visual detection of path deviation

Figure 7 shows results from a study of path deviation of a moving visual stimulus (Levi & Tripathy, 2006). The subject was presented with the image of a dot moving rightwards on a linear path until it reached the mid-line of the display, when it changed direction either upwards or downwards. The subject had to indicate the direction. The symbols in Figure 7 show the proportion of correct responses on 30 trials as the deviation varied from −3 to 3 units (Levi & Tripathy, 2006).

Figure 7.

Visual detection of path deviation. The proportion of correct responses in detecting the path deviation of a moving dot is plotted against the size of the deviation. Filled circles are data from Levi and Tripathy (2006) and are based on 30 trials at each stimulus level. The curves are parametric and nonparametric fits, as identified in the key.

All the parametric models gave acceptable fits, with the deviance ranging from D = 0.894 for the Weibull cdf to D = 3.57 for the Gaussian cdf. For all the parametric models, p > 0.61. As with the parametric fits in Figure 1, there are variations in the estimated 50% threshold, which ranged from −0.568 for the Weibull cdf to −0.0751 for the Gaussian cdf. The deviance for the local linear fit, with cross-validation bandwidth h_CV = 2.22, was D = 2.06, p = 0.77, and the estimated 50% threshold was −0.220.

Discrimination of pitch

Figure 8 shows data from a three-alternative forced-choice experiment on pitch discrimination (unpublished data from S. Carcagno, Lancaster University, July 2008). The subject had to identify the interval containing a tone whose fundamental frequency was different from that in the other two intervals. The symbols in Figure 8 show the proportion of correct responses as the difference between the tones varied. There were 3–49 trials at each stimulus level.

Figure 8.

Discrimination of pitch. The proportion of correct responses in identifying the interval containing a tone whose fundamental frequency was different from that in the other two intervals is plotted against the logarithm of the percentage difference in frequency. Filled circles are unpublished data from S. Carcagno (Lancaster University) and are based on 3–49 trials at each level. The curves are parametric and nonparametric fits, as identified in the key.

With the assumed guessing rate of 1/3, all the parametric models gave acceptable fits. The deviance ranged from D = 2.82 for the logistic cdf to D = 2.98 for the Gaussian cdf (for all the parametric models, p > 0.7). The deviance for the local linear fit, with cross-validation bandwidth h_CV = 0.562, was similar, with D = 2.64, p = 0.72, but the local method required no assumption about the guessing rate. It also provided a less-biased fit at small frequency differences (x = 2.0 to x = 3.0).

Discrimination of “porthole” views of natural scenes

Figure 9 shows data from an experiment on the visual perception of fragmented images (unpublished data from Xie & Griffin, 2007). The subject was presented with a display split into two parts, one containing a pair of patches from the same image, the other a pair from different images, and the subject had to judge which pair came from the same image. The symbols in Figure 9 show the proportion of correct responses on 200 trials as a function of patch separation.

Figure 9.

Discrimination of “porthole” views of natural scenes. The proportion of correct same-different judgments of patches of images from natural scenes is plotted against the logarithm of the separation of the patches in pixels. Filled circles are unpublished data from Xie and Griffin (2007) and are based on 200 trials at each stimulus level. The curves are parametric and nonparametric fits, as identified in the key.

Of the four parametric models, only the Weibull cdf gave an acceptable fit, with deviance D = 12.6, p = 0.084. For the other parametric models, D > 18, p < 0.012. For the local linear fit with cross-validation bandwidth h_CV = 2.44 log₂ pixels with D = 9.28, p = 0.23.

Induction of a visual motion aftereffect

Figure 10 shows results from a study of a dynamic visual motion aftereffect (Schofield, Ledgeway, & Hutchinson, 2007). The subject was presented with a moving adaptation stimulus, followed by a test stimulus. The symbols in Figure 10 show the proportion of responses in which the subject indicated motion of the test stimulus in the same direction as the adapting stimulus, either up or down, as a function of relative modulation depth. There were 10 trials at each stimulus level.

Figure 10.

Induction of a visual motion aftereffect. The proportion of responses in which motion of the test stimulus appeared in the same direction as the adapting stimulus is plotted against the relative modulation depth. Filled circles are data from Schofield, Ledgeway, and Hutchinson (2007) and are based on 10 trials at each stimulus level. The curves are parametric and nonparametric fits, as identified in the key.

None of the parametric models gave an acceptable fit, with the deviance ranging from D = 10.6, p = 0.031, for the Weibull cdf to D = 17.3, p = 0.004, for the Gaussian cdf. The local linear fit with cross-validation bandwidth h_CV = 23.2% was evidently better, with deviance D = 4.75, p = 0.24.

Note that the proportions of “same” responses all take either very low (≤ 0.1) or high (≥ 0.7) values, and therefore, the model curve has to be very steep to fit well. This was impossible with the constraints on the forms of the parametric models, but the local linear fit was able to adapt better. It did exhibit a slight variation from monotonicity near the lower asymptote, but, as noted earlier, deviations of this kind are often present in the guessing region where, ideally, the psychometric function would be constant. The local fit may be improved in this region by constraining the function to be monotonic.

Discrimination of image approximations

Figure 11 shows data from a two-alternative forced-choice visual discrimination task (unpublished data from Nascimento, Foster, & Amano, 2005). The subject was shown an image of a natural scene and an approximation of this image based on a principal component analysis. The task was to distinguish between the images. The symbols show the proportion of correct responses as a function of the number of components in the approximation. There were 200 trials at each level, pooled over a range of natural scenes.

Figure 11.

Discrimination of image approximations. The proportion of correct discriminations of an image of a natural scene and an approximation of this image based on principal component analysis is plotted against the number of components in the approximation. Filled circles are unpublished data from Nascimento, Foster, and Amano (2005) and are based on 200 trials at each level. The curves are parametric and nonparametric fits, as identified in the key.

Again, none of the parametric models fitted the data well: the deviance ranged from D = 18.8, p = 0.002, for the Weibull cdf to D = 33.1, p << 0.0001, for the logistic cdf. The local linear fit with cross-validation bandwidth h_CV = 1.13 was better, with deviance D = 16.7, p = 0.003, although still not conventionally acceptable. Nevertheless, it was obviously less biased over the region x = 5 to x = 8 and had slightly more of an inflexion at x = 3. Similar conclusions were drawn in Foster & Żychaluk (2007), where the same data were fitted by a local linear estimator with bandwidth chosen by a bootstrap method.

Auditory detection of a gap in noise

Figure 12 shows results from a study of auditory detection of a gap in noise (Baker, Jayewardene, Sayle, & Saeed, 2008). A 300-msec noise burst containing either a gap of 2–8 msec duration or no gap was presented to one ear of a subject. The symbols in Figure 12 show the proportion of “gap” responses as a function of gap duration. There were 12 trials with each gap duration and 84 trials with no gap.

Figure 12.

Auditory detection of a gap in noise. The proportion of responses indicating the presence of a gap is plotted against the duration of the gap. Filled circles are unpublished data from Baker, Jayewardene, Sayle, and Saeed (2008) and are based on 12 trials at each nonzero stimulus and 84 trials at zero stimulus level. The curves are parametric and nonparametric fits, as identified in the key.

None of the parametric models gave an acceptable fit, with the deviance ranging from D = 11.5, p = 0.042, for the reverse Weibull cdf to D = 17.2, p = 0.009, for the Gaussian cdf. The estimated 50% threshold ranged from 2.87 msec for the Weibull cdf to 3.51 msec for the Gaussian cdf.

The local linear fit with cross-validation bandwidth h_CV = 2.06 msec was clearly better, with deviance D = 7.5, p = 0.15. The estimated 50% threshold was 3.11 msec.

There is evidence of a nonzero lapsing rate with the longer gaps, x > 4 msec, which was estimated automatically by the local linear method but ignored by the global models. The local method was also less biased at intermediate and shorter gaps.

CONCLUSION

Fitting a wrong model function to a set of data can clearly give misleading inferences. But the problem of model uncertainty cannot be properly resolved by fitting several different parametric models, with or without estimates of the guessing and lapsing rates, and then appealing to a goodness-of-fit measure to decide between them. Differences in goodness of fit may be difficult to interpret, and systematic biases may still persist in the best-fitting parametric curve, as has been illustrated in the examples analyzed here. As a consequence, derived statistics, such as the threshold and slope, may also be biased away from the true value.

By contrast with parametric modeling, the local linear method needs no assumption about the true model, except its smoothness. The method adjusts automatically to unknown guessing and lapsing rates, which need not be treated specially, thereby avoiding the risk of misspecification, which, in a parametric model, may have a disproportionate impact on the rest of the curve. The threshold and slope may be readily extracted from the locally fitted function, along with estimates of their standard errors, which may be used to test the equality or otherwise of these parameters from multiple data sets. Critically, as the size of the data set increases, the locally fitted function necessarily approaches the true, albeit unknown, function.

The success of the local linear method does depend on the choice of bandwidth, but fortunately there are several methods of estimation, and the cross-validation method used in this work led to good estimates. The local linear method may be extended to sets of data in which there are several independent variables—for example, within the framework a generalized additive model (Hastie & Tibshirani, 1990).

As a matter of principle, a correct parametric model will always do better than a nonparametric one, simply because the parametric model assumes more about the data, but given an experimenter's ignorance of the correct model, the local linear method provides an impartial and consistent way of addressing this uncertainty.