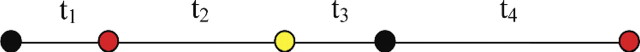An Evolutionary Analysis of Lateral Gene Transfer in Thymidylate Synthase Enzymes

Abstract

Thymidylate synthases (Thy) are key enzymes in the synthesis of deoxythymidylate, 1 of the 4 building blocks of DNA. As such, they are essential for all DNA-based forms of life and therefore implicated in the hypothesized transition from RNA genomes to DNA genomes. Two evolutionally unrelated Thy enzymes, ThyA and ThyX, are known to catalyze the same biochemical reaction. Both enzymes are sporadically distributed within each of the 3 domains of life in a pattern that suggests multiple nonhomologous lateral gene transfer (LGT) events. We present a phylogenetic analysis of the evolution of the 2 enzymes, aimed at unraveling their entangled evolutionary history and tracing their origin back to early life. A novel probabilistic evolutionary model was developed, which allowed us to compute the posterior probabilities and the posterior expectation of the number of LGT events. Simulation studies were performed to validate the model's ability to accurately detect LGT events, which have occurred throughout a large phylogeny. Applying the model to the Thy data revealed widespread nonhomologous LGT between and within all 3 domains of life. By reconstructing the ThyA and ThyX gene trees, the most likely donor of each LGT event was inferred. The role of viruses in LGT of Thy is finally discussed.

Thymidylate synthase (Thy) is a fundamental enzyme in DNA synthesis because it catalyzes the formation of deoxythymidine 5′-monophosphate (dTMP) from deoxyuridine 5′-monophosphate (dUMP). For decades, only one family of thymidylate synthase enzymes was known, and its presence was considered necessary to maintain all DNA-based forms of life. Then, a gene encoding an alternative enzyme was discovered and characterized (Dynes and Firtel 1989; Myllykallio et al. 2002), and the novel enzyme was named ThyX, whereas the other enzyme was renamed ThyA. The 2 enzymes, ThyA and ThyX, were found to have distinctly different sequences and structures, thus alluding to independent evolutionary origins.

By virtue of their function and phyletic distribution, Thys are ancient enzymes, implying 1) the likely participation of one or both enzymes during the transition from an RNA world to a DNA world (based on protein catalysts: Joyce 2002) and 2) the probable presence of a gene encoding Thy in the genome of the common ancestors of eukaryotes, bacteria, and archaea (Penny and Poole 1999; Woese 2002; Koonin 2003; Kurland et al. 2006). Thus, tracing back the evolutionary pathway of genes encoding ThyA and ThyX may shed light on the actively debated wider issue regarding the origins of viral and cellular DNA (Hendrix et al. 1999; Leipe et al. 1999; Villarreal and DeFilippis 2000; Bell 2001; Forterre 2002; Bamford 2003; Filee et al. 2003; Forterre 2005; Koonin and Martin 2005; Forterre 2006a; Kurland et al. 2006).

The sole known exception of an organism lacking Thy is the protist Giardia lamblia, which was reported incapable of synthesizing pyrimidines de novo and depends solely on obtaining dTMP from the environment via the thymidine salvage pathway (Jarroll et al. 1989). The distribution of ThyA and ThyX across the 3 domains of life is best described as mutual exclusiveness (i.e., in a given organism, the presence of one enzyme implies the lack of the other), but a few organisms have been found to code both thyA and thyX (Myllykallio et al. 2002). The evolutionary phenomenon whereby the same archaeon or bacterium encodes 2 structurally distinct enzymes performing the same function is postulated to be a possible transition stage in lateral gene transfer (LGT) and subsequent gene loss (Doolittle et al. 2003). We have previously observed and characterized this phenomenon in the context of archaeal and bacterial lysine aminoacyl-tRNA synthetases (Shaul et al. 2006).

Here, we present an evolutionary analysis of ThyA and ThyX using a probabilistic evolutionary model developed with the aim to study nonhomologous LGT events. The model is general and may be applied to the study of LGT events categorized as nonhomologous gene displacements (i.e., where 2 or more nonhomologous proteins performing the same function are interchanged). The model has 4 parameters representing the rates of gain and loss of each gene (here thyA and thyX), which are estimated from the data using maximum-likelihood (ML) techniques. A null model, which does not allow for LGT, enables statistical testing of the hypothesis that the distribution of the genes resulted solely from gene loss. Furthermore, the model allows us to estimate the posterior probability that an LGT event occurred in a certain lineage and enables calculating the expected number of LGT events that occurred along each edge of the phylogeny.

Using our model, we show that the distribution of Thy is characterized by frequent LGT events. We evaluate the performance of our method using computer simulations and by comparing the results of our ML-based method to those of a simpler method based on maximum parsimony (MP). We further infer the most probable occurrences of LGT throughout the phylogeny. We conclude that LGT of thy genes is exceptionally widespread between and among archaea and bacteria and that it has also occurred in Eukarya. We determine some of the most likely paths and several of the origins of these LGT events.

MATERIALS AND METHODS

Mapping thy Identity onto the Tree of Life

The phylogenetic tree of life (both the topology and the edge lengths) inferred by Ciccarelli et al. (2006) was used as a reference tree in this study. Giardia lamblia was removed from the tree because of the exceptional absence of thyA and thyX from its genome. For each species (a leaf in the tree), the identity of Thy (thyA, thyX, or both) was determined by using a BLAST search (Altschul et al. 1990) with multiple seeds (listed in the online supplementary material available from http://www.sysbio.oxfordjournals.org) against each species genome, available on the NCBI Web page (http://www.ncbi.nlm.nih.gov), and an E-value cutoff of 10⁻⁴. In 35 genomes, neither thyA nor thyX was detected using this stringent cutoff, but one or both were detected using a less stringent cutoff. To avoid errors in our annotation, we also removed these organisms from our analysis.

A Likelihood-Based Evolutionary Model for Inferring LGT Events

A Markov model of evolution over a 3-state alphabet $\{A,X,AX\}$ was developed to describe the presence of thyA, thyX, or both. The model assumes that simultaneous gain and loss events are impossible (i.e., an organism cannot encode for thyA and within an infinitesimal time swap it for thyX or vice versa). Thus, the transition between the 2 thy gene types must occur via a state where both are present. The model is represented by a continuous-time Markov process, defined by the instantaneous rate matrix Q, where the rate of change from state i to state j is defined as follows:

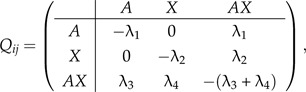(1)

where ${\lambda }_1$ and ${\lambda }_2$ denote the intrinsic rate of gaining the alternative thy gene while being at states A or X, respectively, and ${\lambda }_3$ and ${\lambda }_4$ are the intrinsic rates of loss of the corresponding genes from the transition state AX. According to our model, the probabilities of gene loss and gene gain events are not necessarily equal. Furthermore, time reversibility is not assumed, so the results are conditional on the location of the root (which was chosen to be at the node connecting the 3 domains).

We note that our analysis relies on a given tree topology with a given set of edge lengths. Because in our model the rate matrix is not normalized (i.e., the average rate of change does not equal one), the edge lengths of the given species tree are free to vary by a scaling factor. This factor determines the ratio between amino acid substitution units in the sequences used to construct the species tree and gain/loss event units of the Thy data. The scaling factor is assumed to be uniform across the topology. Because the root frequencies cannot be estimated (based on one character, they will always be estimated at either one or zero, they are set to the limiting stationary distribution of the rate matrix. Given the data (the assignment of the 3 possible states to the leaves), the phylogenetic tree, and the edge lengths, the model parameters were estimated using Brent's optimization scheme (Press et al. 2002). In order to avoid being trapped in local maxima, 100 random starting points were used during the optimization process.

Under a null model of evolution, no LGT occurs, so the taxonomic distribution of thyA and thyX may be explained by gene loss only. This can be modeled by assuming that ${\lambda }_1={\lambda }_2=0$. Because under the null model A and X are absorbing states, the only possible state at the root is AX, so the root frequency of state AX was fixed at one. We note that under these settings, a likelihood-ratio test cannot be used to compare different hypotheses. There are 2 reasons for this: 1) because of the way root frequencies are estimated, the model enabling gain events (hereby termed the LGT model) and the null model are not nested and 2) because only one character is analyzed (the type of the Thy enzyme), the limiting distribution of the maximum log-likelihoods difference is not necessarily chi-square distributed. Thus, a parametric bootstrap approach (Whelan and Goldman 1999) was used to generate the distribution suitable for comparing the maximum log-likelihoods of the 2 models developed here. To this end, 1000 data sets were simulated under the null model with the same parameters as those inferred by the null model on the Thy data set. Then, the parameters of the null model and the LGT model were optimized for the simulated data sets until convergence of the likelihood function. The LGT and null models were implemented in C++. The program is available at http://www.tau.ac.il/∼talp/threeStateLGT/lgt.html.

Calculating the Expectation and Probabilities of LGT Events

The evolutionary model allows us to compute the posterior expectation of the number of LGT events across the whole phylogeny and the posterior probability of LGT events occurring along individual edges of the phylogeny. An LGT event may be 1 of the 2 types: gain of thyA (represented by a transition from state X to state AX) or gain of thyX (represented by a transition from state A to state AX). The total number of transitions from state u to state v throughout the phylogeny is given by

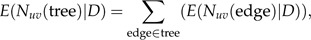(2)

where D represents the data and $E(N_{uv}\left(\text{edge}\right)\left|D\right)$ is the posterior expectation of $N_{uv}$ (the number of transitions from state u to state v) along a given edge. This can be calculated using the following formula:

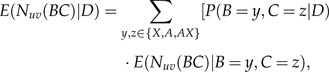(3)

BC is the edge that starts at node B and ends at node C. The summation over y and z represents all possible character assignments to nodes B and C, respectively. The left term of the summation in Equation (3) is the joint probability of observing states y and z at the tips of this edge, given the data, and can be calculated using an elaboration of Felsenstein's (1981) pruning algorithm for a nonreversible model (see Appendix). The right term of the summation is the posterior expectation of $N_{uv}$, given specific assignments y and z to nodes B and C, respectively, and may be calculated analytically in a reversible model or more generally in a model with real eigenvalue decomposition of its rate matrix Q (Minin and Suchard 2008). However, in our model, real eigenvalue decomposition is not necessarily achieved for all values of λ. Hence, simulations were used to assess the expected number of transitions, given the terminal states at the tips of an edge (elaborated in the Appendix). The posterior probability that a transition from state u to state v has occurred allows us to estimate along what edges LGT most probably took place. This is calculated as follows:

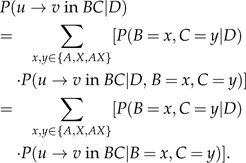(4)

Here, as for Equation (3), the summation over x and y represents all possible character assignments to nodes B and C. $P(B=x,C=y|D)$ is calculated as in Equation (3), and the right term, the probability given specific nodes assignments, is once again calculated using simulations (see Appendix).

Assessing Method Accuracy

The ability of the ML model to accurately infer LGT events was assessed in a number of ways: 1) by using simulation studies, 2) by comparing the results of our ML-based approach to those obtained using an MP-based approach, and 3) by testing the accuracy of the method as a function of the accuracy of the tree topology. These are elaborated on in the following sections.

Simulation studies.—

Simulations were conducted to determine how effective our method is at detecting LGT events. We generated 100 data sets by simulation under a model where the rates of gain (${\lambda }_1$ and ${\lambda }_2$) are low and the rates of loss (${\lambda }_3$ and ${\lambda }_4$) are high. The actual rates used were the values inferred for the Thy data in this study because rates of gain are low, and the ability to distinguish between the null model and the LGT model is not trivial. The root frequencies, the tree topology, and the edge lengths were identical to those inferred for the original Thy data. We simulated a continuous-time Markov chain (see Appendix) along the tree. During the simulation process, the points along each edge where a transition occurred between one state and another were precisely recorded. Thus, the exact number of transitions between each pair of states along the entire phylogeny is known. We then tested our method on these simulated data sets in order to assess whether it succeeds in finding significant support for the LGT model. We evaluated the accuracy of our method with regard to the error and the bias in the inference of the expected number of LGT events. Let $\text{True}(N_{uv}\left(\text{tree}\right){)}_i$ and $E(N_{uv}\left(\text{tree}\right)|D{)}_i$ represent the exact and inferred number of transitions in the ith simulation, and let ε represent the error of E, where ${\epsilon }_i=E(N_{uv}\left(\text{tree}\right)|D{)}_i-True(N_{uv}\left(tree\right){)}_i$. The mean square error, 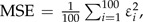and the mean error, 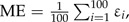were used to measure the error and bias, respectively, of our inference method.

We finally assessed the method's ability to accurately infer the exact location where LGT occurred, given a certain posterior probability cutoff. To this end, for each simulated data set, we calculated the rate of true and false positives and true and false negatives. For example, the rate of true positives was calculated as the average number of true positives over the 100 simulations, divided by the average number of true events in the simulations (i.e., the sum of true positives and false negatives). The other 3 rate values were calculated similarly.

Comparison of results obtained using the ML- and MP-based approaches.—

We also compared the performance of our method with that of an MP-based method. In the latter method, we commenced by using Sankoff's (1975) algorithm to reconstruct the ancestral states (the algorithm assumes that the costs of gain and loss are equal). We then counted the number of gains along the entire phylogeny. We inferred the number of gains in the simulated data sets described above using both the MP and the ML approaches and compared the ME and the MSE of the ML-based method with the equivalent of ME and MSE of the MP-based method.

Uncertainty in tree topology.—

In order to assess the robustness of the results to errors in the tree topology, 50 trees were generated. This was achieved by using a nonparametric bootstrap approach applied to the original multiple sequence alignment used to reconstruct the species tree (Ciccarelli et al. 2006). The original reconstruction used the PhyML software (Guindon et al. 2005), assumed evolution under the Jones–Taylor–Thornton (JTT) model of amino acid substitutions (Jones et al. 1992), and among-site rate variation was modeled using a discrete gamma distribution with 4 rate categories. We repeated the phylogenetic analysis under the same conditions for each of the 50 pseudo–data sets. The Thy data were then mapped onto each phylogeny thus obtained. The impact of the uncertainty in tree topology was finally assessed by comparing the number of gains inferred for each bootstrapped phylogeny with that inferred with the original phylogeny.

Reconstruction of Gene Trees

The species tree analysis allowed us to map the location of a gain event while the donor species remained unknown. Thus, the donor sequence was inferred to be the sequence most similar to the LGT recipient. Notably, this inference is only an approximation, due to limited availability of genomic sequences and the fact that the LGT events may have occurred a long time ago, while the donor is assumed to be an ancestor of one of the other taxa considered. To infer the donor sequence, ThyA and ThyX gene trees were reconstructed. PSI-BLAST (Altschul et al. 1997) searches with an E-value cutoff of $10^{-4}$ were performed against the NCBI nonredundant (nr) database (http://www.ncbi.nlm.nih.gov/BLAST/). Multiple seeds were used (listed in the online supplementary material) until the convergence of the searches to 2 data sets of 459 ThyA and 200 ThyX sequences. Following this, a filtering procedure was applied and sequences were removed according to the following criteria: 1) sequences that deviate from their known motifs (Prosite signature PS00091 for ThyA, Bairoch and Bucher 1994; RHRX₇S for ThyX, Myllykallio et al. 2002) by more than 2 dissimilar amino acids, 2) sequences shorter than 100 amino acids, and 3) to avoid redundancy and thus to reduce computational time, if a pair of sequences from the same genus shared more than 95% identity, one was removed. The filtering procedure left a total of 366 ThyA sequences and 184 ThyX sequences.

Sequences were aligned using the MAFFT program version 5.861 with the accuracy-oriented option E-INS-i (Katoh et al. 2005). A matched-pairs test of symmetry (Ababneh et al. 2006) was applied to the alignments of ThyA and ThyX in order to determine whether the sequences could be assumed to have evolved under time-reversible conditions. There was nothing in these data that suggested the sequences had evolved under more complex conditions (i.e., the matched-pairs test of symmetry produced 35 [out of 66,795 possible tests] and 0 [out of 16,836 possible tests] P values $<0.05$ for ThyA and ThyX, respectively), so it was deemed safe to use time-reversible substitution models in the ensuing phylogenetic analyses. Given Akaike's information criterion, the most appropriate time-reversible substitution models were then identified using ProtTest (Abascal et al. 2005): WAG + I + Γ (Whelan and Goldman 2001) for ThyA and WAG + I + Γ + F for ThyX. These models were then used for ML-based phylogenetic reconstruction, which was performed using PhyML version 3 (Guindon et al. 2005). The program was run using the most accuracy-oriented option (both nearest-neighbor interchange and subtree pruning and regrafting searches were performed). Node supports were determined by performing 100 bootstrap replicates (Felsenstein 1985). The ThyA and ThyX alignments, together with all relevant accession numbers and the corresponding phylogenetic trees, are available as part of the online supplementary material and in the TreeBASE database (http://www.treebase.org; ID numbers M4804 and M4805 for ThyX and ThyA, respectively).

G + C% Content Analysis

When LGT was inferred to have occurred along a terminal edge (leading to an extant organism), the G + C% content of the sequence (GC_s) was compared with that of the surrounding genome (i.e., the genomic sequence without the thy gene [ GC_g-s]). The latter is calculated by using the known lengths of the genome and the gene (l_g and l_s, respectively) and is calculated as follows:

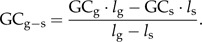(5)

As a rule of thumb, in cases where 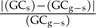> 0.10, this provided support for a scenario whereby the LGT event occurred recently (Supplementary Table S1). Genomic G + C% values were taken from the Genome Project section in NCBI (http://www.ncbi.nlm.nih.gov/), whereas gene-specific G + C% values were calculated using a Perl script.

RESULTS

Widespread LGT throughout ThyA and ThyX Evolution

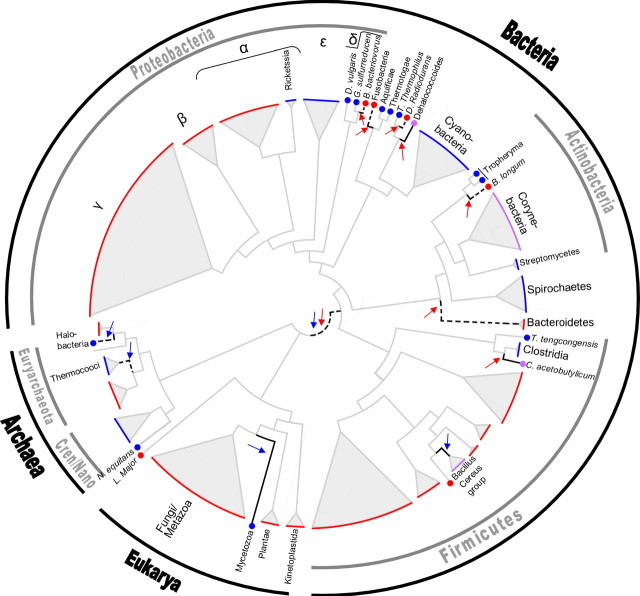
In order to study the evolution of ThyA and ThyX, the distribution of the 2 enzymes throughout the species tree of life was first characterized. Each organism (a leaf in the species tree) was color coded according to the gene it encodes (Fig. 1), revealing a patchy distribution of ThyA and ThyX across the tree. Two different scenarios may explain this distribution pattern: 1) H₀: the existence of both enzymes in the common ancestor of all 3 domains, followed by differential gene loss, and 2) H₁: the existence of LGT events, that is, gene gains and gene losses occurred throughout evolution. In order to test these 2 hypotheses, we developed a probabilistic evolutionary model (see Materials and Methods section) that considers 3 possible states at each tree node: ThyA, ThyX, or both. The transition probabilities among the states were estimated by maximizing the probability of the data, given the tree and model parameters. Specifically, in the general model, 2 parameters were used to account for gain events—one for the gain of ThyA and one for the gain of ThyX. In the null model, only gene loss events were allowed, so both of these gain parameters were set to zero. Additionally, the null model necessitated fixing the root frequency of the double state AX to one (see Materials and Methods section). Because the character frequencies at the root in the general model were determined by the limiting distribution of the Markov process, the models were not nested. We therefore used a parametric bootstrap approach (rather than the standard likelihood-ratio test) to assess whether one model fits the data significantly better than the other. To this end, the distribution of differences between the maximum log-likelihood values of the 2 models was estimated using 1000 simulations under the null model. Under a Type I error of either 5% or 1%, any difference in log-likelihood values higher than 0.04 or 0.7 points, respectively, results in rejection of the null model in favor of the LGT model.

FIGURE 1.

Mapping of the thymidylate synthase enzymes ThyA and ThyX onto the species tree. Posterior probabilities of an LGT event are coded onto the edges. A black line represents a probability of LGT higher than 0.75, and a dashed line represents a probability between 0.5 and 0.75. The states at the extant organisms are color coded onto the tips of the tree as follows: ThyA in red, ThyX in blue, and cases in which an organism codes both ThyA and ThyX simultaneously are in violet. Colored arrows represent an LGT event, with the color of the arrow standing for the gained gene. The tree is presented using the FigTree software (http://tree.bio.ed.ac.uk/) as a cladogram, and edge lengths are not shown to scale. Cren, Crenarchaeota; Nano, Nanoarchaeota.

The maximized log-likelihood values of the 2 models, given the Thy data, and the corresponding ML estimates of their parameters are summarized in Table 1. The difference in maximized log-likelihoods between the models allows us to reject the null hypothesis with a p value $<0.001$. Furthermore, out of 1000 data sets simulated, the highest difference obtained for any data set was 3.7. In comparison to the observed difference ($16=75.1-59.1$), this result emphasizes just how much better the alternative hypothesis (i.e., LGT model) fits the Thy data. Noteworthy, in 782 of the 1000 simulated data sets, the null model obtained higher likelihood values than the LGT model, further strengthening our confidence that allowing for gene gains reflects biological reality for the analyzed Thy data.

TABLE 1.

The assumptions, maximum-likelihood estimates (MLE) of free parameters, and maximum log-likelihood values of the null and LGT models applied to the thymidylate synthase (Thy) data

Model	Assumptions	MLEs	Maximum log-likelihood
Null	λ1 = 0	λ3 = 1.85	− 75.1
	λ2 = 0	λ4 = 1.45
	πA = 0
	πX = 0
	πAX = 1
LGT	πA = 0.64	λ1 = 0.38	− 59.1
	πX = 0.29	λ2 = 1.24
	πAX = 0.07	λ3 = 3.28
		λ4 = 4.92

We then computed the posterior expectation of the number of transitions between the 3 states (A X, and AX) throughout the phylogeny. Accordingly, a total of $\sim 23$ gene acquisition events occurred: 7 acquisitions of ThyX and 16 acquisitions of ThyA. These were accompanied by an expectation of $\sim 31$ gene loss events: 13 losses of ThyX and 18 losses of ThyA. Our next aim was to identify the edges along which LGT was most likely to have occurred (i.e., edges with a high posterior probability of a gain of either ThyA or ThyX). We focused on those edges with a posterior probability higher than 0.75 (marked with solid black lines in Fig. 1) or between 0.5 and 0.75 (marked with dashed black lines in Fig. 1). This yielded a total of 12 edges where a suspected LGT occurred. This number is evidently lower than the posterior expectation of the number of LGT events calculated above, most likely reflecting the difficulty in determining where older LGT events occurred in the phylogeny. We elaborate on these inferred LGT events and their possible donors in the section below.

In the edge leading from the root to the bacterial domain, both a gain of ThyA and a gain of ThyX were inferred to have occurred with probabilities around 0.7. This most likely stems from the long edge that leads to bacteria (note that this edge is not shown to scale in Fig. 1), in which our model predicts multiple substitutions.

Assessing the Accuracy of the ML-Based Methodology

The low gain rates inferred for the Thy data in this study (Table 1) imply that distinguishing between the null model and the LGT model is a difficult task. To this end, simulation studies were conducted to assess the efficacy of the method to detect isolated cases of LGT dispersed across a broad phylogeny. Under these simulations, the number and the location of LGT events are known, and thus, the capability of the methodology to detect these events can be tested. The simulations we performed purposely mimicked the Thy data at hand, where the probability of an LGT event is low across the phylogeny (see Materials and Methods section).

Encouragingly, the simulation results revealed that the ML methodology can accurately map LGT events. For all of the 100 data sets, the null hypothesis of loss only was rejected (P value $<0.001$ in all cases). The ME for the posterior expectation of LGT events was found to be 0.26. Because this number is near zero, this suggests that the method does not over- or underestimate the number of events in a consistent manner. The MSE for the posterior expectation of LGT events was found to be 24.11. In order to assess how good this value is, we compared the performance of our ML-based method with that of a simpler MP-based method. In the latter method, the ancestral states are reconstructed under the parsimony criterion and LGT events are inferred when the following character-state changes are observed: $X\to AX,X\to A,A\to AX$, or $A\to X$. Not surprisingly, the MP-based method consistently underestimated the number of events that occurred in all of the 100 simulated data sets (ME $=-11.48$). The MSE of inferred LGT events based on the parsimony reconstruction was 205.3, more than 8 times higher than the error obtained with the ML-based method.

We further used the simulated data sets to evaluate the ML-based methodology's ability to determine along which edges LGT events had occurred. This was achieved by computing the posterior probability of an LGT at an edge and assigning LGT events to edges with a probability higher than a certain cutoff. The false-positive rate and the false-negative rate were inferred for the 2 cutoff boundaries of 0.5 and 0.75, respectively (Table 2). Accordingly, the false-positive rates for these 2 boundaries were found to be 0.0082 and 0.0024, respectively, and the false-negative rates were found to be 0.54 and 0.66, respectively. Despite the high rate of false-negative inference, we preferred remaining with the exceptionally low rates of false-positive inference obtained with both cutoff levels rather than lowering the posterior cutoff at the risk of raising the probability of false inference of LGT. We suggest that the relatively high rate of false negatives stems from the difficulty of locating LGT events that occurred in earlier edges of the phylogeny because the posterior distribution is “diffused” around closely related edges. To conclude, our simulation study shows that the LGT events reported in this study are of high confidence.

TABLE 2.

Type I and Type II error rates (averaged over 100 simulated data sets) for cutoff values of the posterior probability that an LGT event occurred at an edge

Posterior probability cutoff	True positives	False positives (Type I error)	True negatives	False negatives (Type II error)
0.5	0.459	0.008	0.992	0.541
0.75	0.338	0.002	0.998	0.662

Uncertainty in Tree Topology

The method developed here relies on an input tree topology. We thus tested the sensitivity of the ML methodology to 1) the location of the root and 2) the accuracy of the tree topology. Seven different root locations were tested: the node connecting the 3 domains, the 3 nodes at the base of each domain, and 3 random nodes within each of the 3 domains. All 7 root positions yielded essentially the same results when analyzing the Thy data (data not shown).

We further tested the sensitivity of the method to possible errors in the species tree used in the study. To this end, 50 different trees were reconstructed by bootstrapping the original multiple sequence alignment used for reconstructing the species tree of Ciccarelli et al. (2006). This allowed us to make sure that the uncertainty in tree topology is not randomly distributed but rather that the occurrence of a split in the simulated trees is proportional to its bootstrap support in the real phylogeny used. The distance between every bootstrapped tree and the species tree used was calculated using the symmetric difference metric of Robinson and Foulds (1981), which counts the number of splits not shared between 2 trees. The average distance was found to be 28 (9.2% of all internal splits), indicating that the bootstrapped trees are somewhat different from the original tree. We mapped the original Thy data on the 50 trees obtained. Reassuringly, the null hypothesis that no LGT occurred was significantly rejected in all these alternative trees (p value $<0.001$). Thus, our conclusion that LGT prevails in the Thy data is robust in regard to the assumed tree topology. On the original species tree of Ciccarelli et al. (2006), the posterior expectation of gains is 23. On the 50 trees, this number ranged from 11.34 to 26.34. The inferred number of 23 is within the 92% confidence interval. This result suggests that the exact number of LGT events may vary depending on the input tree topology, pointing to the importance of a reliable tree topology for mapping LGT events. Nevertheless, this analysis clearly shows that the overall qualitative and quantitative conclusions drawn from the LGT analysis of Thy hold true.

Retracing the LGT Events

In order to elucidate the origins of each LGT event, gene trees were reconstructed for both ThyA and ThyX (collapsed versions are shown in Figs. 2 and 3, respectively; the full-length trees are available as part of the online supplementary material). The major trends for each domain are described below.

FIGURE 2.

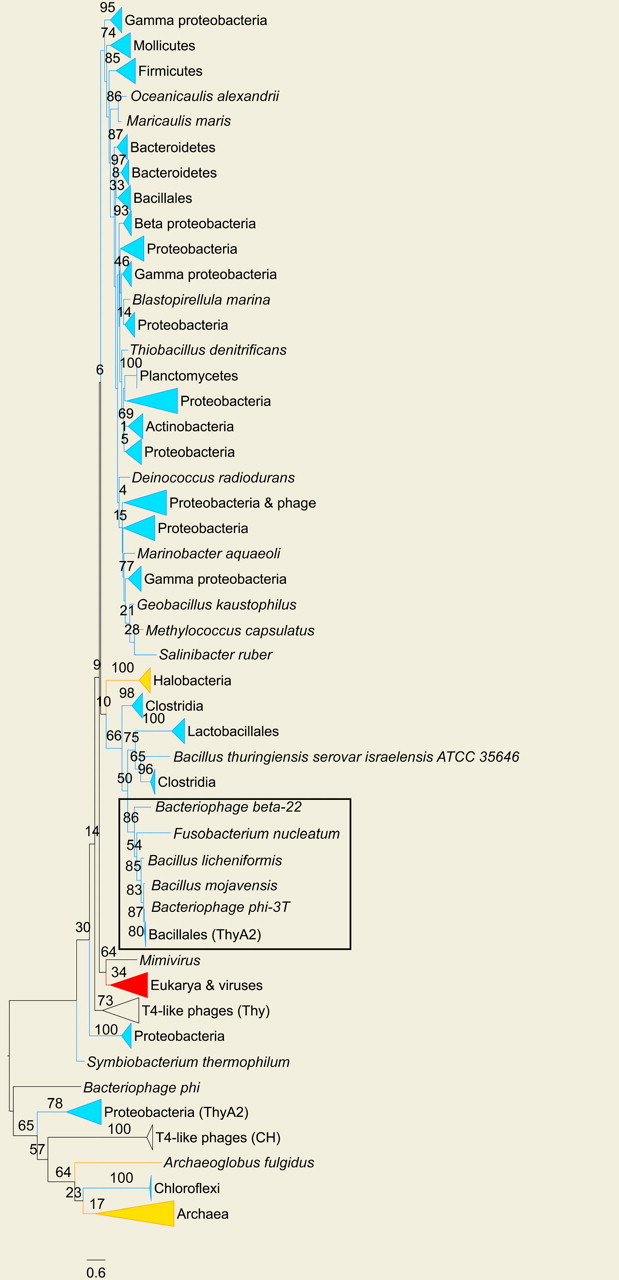
Unrooted collapsed ML gene tree of ThyA. Collapsed clades are color-coded according to their phylogenetic inclusion: blue, red, and orange stand for Bacteria, Eukarya, and Archaea, respectively. Node supports are presented as percentage of support out of 100 bootstrap iterations. One edge length unit is equivalent to an average of one substitution per site. An example of LGT involving Bacillus subtilis and the bacillus infecting phages φ-3T and β-22 is boxed in black. The tree is presented using the FigTree software (http://tree.bio.ed.ac.uk/). The full tree is available as part of the online supplementary material.

FIGURE 3.

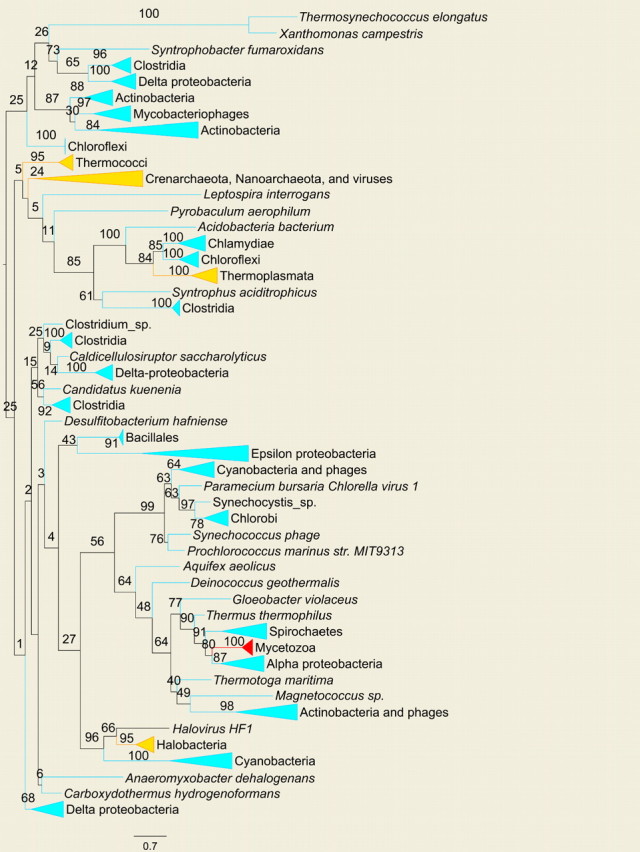
Unrooted collapsed ML gene tree of ThyX. Collapsed clades are color-coded according to their phylogenetic inclusion: blue, red, and orange stand for Bacteria, Eukarya, and Archaea, respectively. Node supports are presented as percentage of support out of 100 bootstrap iterations. One edge length unit is equivalent to an average of one substitution per site. The tree is presented using the FigTree software (http://tree.bio.ed.ac.uk/). The full tree is available as part of the online supplementary material.

ThyA/ThyX LGT in Eukarya.—

Until recently, LGT events were assumed to be very rare in Eukarya and of little evolutionary significance. However, accumulating evidence suggests that LGT has played a role in the evolution of unicellular eukaryotes, especially protists (Andersson 2005). Most eukaryotic genomes encode thyA, whereas the genomes of the mycetozoa clade, which includes the protist Dictyostelium discoideum (Dynes and Firtel 1989; Myllykallio et al. 2002), encode thyX. Thus, in Eukarya, a single LGT event is inferred, accounting for the acquisition of thyX in mycetozoa. This LGT event is highly supported by our model with a posterior probability of 0.97. The ThyX gene tree (Fig. 3) suggests that Rickettsiales or Rhodobacterales may have been the source of this gene acquisition. In light of the proposition that the origin of mitochondria is an α-proteobacterial ancestor (Gray et al. 2001), it is tempting to link this suggestion to the endosymbiotic theory. Specifically, members of the rickettsial subdivision are considered to be among the closest known eubacterial relatives of mitochondria (Andersson et al. 1998). According to this view, the source of thyX in mycetozoa may have been an α-proteobacterial ancestor from which mitochondria evolved. The ancestral mycetozoan was apparently the only known eukaryote to have integrated this thyX homolog into its genome. However, the fact that mycetozoa feed off bacteria via phagocytosis (Rupper and Cardelli 2001) hints at an alternative mechanism for the transfer between mycetozoa and bacteria. Consequently, DNA from an ancestral bacterium containing thyX may have been ingested by a mycetozoan and then taken up permanently by the nucleus. Indeed, most reported eukaryal LGT events involve protists with a phagotrophic lifestyle (Andersson 2005). The latter hypothesis is further favored by an analysis of G + C content, which supports a relatively recent acquisition of thyX by mycetozoa (online Supplementary Table S1).

ThyA/ThyX LGT in bacteria.—

Using our model, we pinpointed 8 LGT events, which are inferred to have occurred in the bacterial clade. The abundance of LGT events in bacteria coupled with the low resolution of the bacterial species tree (where resolution is defined here in terms of bootstrap support; but see Jermiin et al. [2005] for a cautious note on the interpretation of bootstrap support scores), as well as the low resolution of the bacterial clades in the thyA and thyX gene trees, render it difficult to determine the precise origin of many gene transfers in this domain. Furthermore, the large number of LGT events occurring in bacteria is also reflected in the disordered gene trees. The ThyA and ThyX gene trees do not reflect the taxonomic grouping expected according to the species tree of Ciccarelli et al. (2006), implying that orthologous LGT events also may have occurred. One such example is the apparent LGT of thyX between anaerobic δ-proteobacteria and Clostridia, as is evident by the several mixed clusters they form in the ThyX gene tree (Fig. 3). However, in most cases, the low bootstrap values in the relevant regions of the gene trees render the reliable inference of these LGT events difficult.

ThyA/ThyX LGT in archaea.—

Our analysis supports 2 displacements of thyA by thyX in Thermococci and in Halobacteria (see online Supplementary Table S1). Interestingly, the ThyX halobacterial sequences are located as a sister group of their phage Halovirus HF-1, supporting a possible role of the virus as an LGT vector (elaborated below). The small sample of archaeal genomes currently available does not permit us to assess the full extent of LGT in archaea, but our results imply that it prevails there as well. In fact, when normalizing the posterior expectation of the number of LGT events to the extent of species sampling (by dividing the number of LGTs by the sum of edge lengths in each domain), a similar ratio of $\sim 0.8$ LGT events per unit edge length (average number of amino acid substitutions per site) is obtained.

ThyA/ThyX LGT in viruses.—

Our gene tree analysis reveals that viruses encoding their own Thy are widespread. Seventy-five viral Thy sequences are found in our data set, the majority belonging either to Herpesviridae or to Myoviridae. Not surprisingly, all of these are double-stranded DNA viruses with large genomes. Accumulating evidence supports an extensive viral role in LGT, and it has recently been reported that most laterally transferred genes in bacterial genomes probably represent the constituent components of phages or other selfish genetic material (Daubin et al. 2003). Furthermore, it is known that viruses can transfer DNA between prokaryotes in different biomes (Sano et al. 2004). Several lines of evidence indicate that viruses may be the driving force behind LGT of thy genes. For instance, a number of thyX sequences in bacteria are annotated as prophage sequences, such as the thyX sequence of Mycobacterium leprae (Cole et al. 2001) and all the thyX sequences from the Bacillus cereus group. Other examples of putative viral-mediated LGT are the cases of thyX of Halobacteria (described in the section above) and thyA2 of Bacillales (described in the section below). We conjecture that the polarity of these transfers is from the phage to the bacterium, with the phage serving as a vehicle of thy transport from another unknown bacterium.

Bacteria with Genomes Encoding 2 thy Genes

ThyA and ThyX.—

Occupying widely divergent ecological niches, 20 bacterial species in our data set encode both thyA and thyX (online Supplementary Table S2). The evolutionary phenomenon whereby the same organism encodes 2 structurally distinct enzymes performing the same function was postulated to be the hallmark of a transition phase in the process of an LGT event and subsequent gene loss (Doolittle et al. 2003). However, actual data supporting this concept are limited (but see Shaul et al. 2006). Accordingly, the 20 bacterial species in our sample encoding thyA and thyX simultaneously provide support for the concept of a transition phase.

If the genomes of these organisms constitute a transitional phase, we would expect one of the genes to disappear in the fullness of time (i.e., become a pseudogene). However, we could not find any evidence for thy “pseudogenization” (i.e., genes that harbor internal stop codons and are thus shorter on average than other functional thy genes) in the 19 genomes harboring both types of enzymes. This may indicate that the acquisition of the second thy gene was a relatively recent event. Support of this hypothesis was found in 3 species (B. cereus, B. weihenstephanensis, and B. anthracis; online Supplementary Table S2), in which the G + C% content of the thyX gene was notably different from that of the remaining genome (see Materials and Methods section).

If encoding both enzymes confers a selective advantage to an organism, we expect that both will be preserved. Several alternatives come to mind: 1) for a subset of pathogens, joint expression of thyX and thyA may not affect their fitness when free living but could contribute to the virulence of their interaction with the host; 2) the availability of 2 distinct genes will ensure constitutive formation of thymidine when one of the enzymes cannot function properly due to the presence of inhibiting analogs (Santi and McHenry 1972; Costi et al. 2005); and 3) in environments with oxygen-limiting conditions, thyX and thyA are differentially expressed, thus enhancing survivability (Giladi et al. 2002). In this context, the question for which bacteria the encoding of both enzymes constitutes one of the selective benefits listed above is currently unknown.

Two thyA genes.—

Four bacterial genomes in our data set encode 2 thyA genes (online Supplementary Table S2). The existence of 2 thyA genes in the same genome was discovered in B. subtilis, and, due to their dissimilarity (the amino acid sequences share 30% identity), they were called thyA and thyB (Tam and Borriss 1998). To emphasize that both enzymes belong to the ThyA family, we will henceforth call the 2 genes thyA1 and thyA2 instead of thyB and thyA, respectively. ThyA1 of B. subtilis is similar to the enzyme encoded by the majority of bacteria (upper bacterial clade in Fig. 2), and it is distinguished by low specific activity and sensitivity to higher temperatures (Tam and Borriss 1998). ThyA2 provides 92–95% of the total cellular Thy activity of B. subtilis. Previous research has suggested that the bacillus phage Φ-3T is the source of thyA2 in this bacterium (Tam and Borriss 1998; Filee et al. 2003), a proposition supported by the ThyA gene tree (Fig. 2, boxed clade). The presence of both active thyA genes in B. subtilis apparently confers it a selective benefit in environments of temperature changes. Indeed, its endospores, tolerant of extreme environmental conditions, are equipped for accelerated DNA replication during germination (Fairhead et al. 1993). The other species found to encode 2 thyA genes, Aurantimonas sp., also dwells in environments of considerable temperature gradients; we surmise that similar to the studied case of B. subtilis, the availability of 2 types of ThyA enzymes may constitute an important advantage and enhance the capability of the organism to respond to such gradients.

DISCUSSION

In this work, extensive sets of ThyA and ThyX sequences were analyzed to study the evolution of de novo thymidylate synthesis. For this purpose, we developed a novel probability-based evolutionary model that accounts for nonhomologous LGT events. This model is one of the first evolutionary models built within a likelihood framework that assesses LGT (Hao and Golding 2006; but see Cohen et al. 2008). Applying the model to the Thy sequences, we revealed that LGT characterized the evolution of Thy enzymes. The model was used to determine the expectation of the number of LGT events that occurred along the phylogeny and to locate the lineages in which transitions between different Thy states most probably occurred. Simulation studies were performed to assess the validity of the results with regard to Thy evolution. Finally, for each inferred LGT event, a potential donor was searched for based on ThyA and ThyX gene trees.

How widespread is LGT in Thy genes? Dagan and Martin (2007) estimated an average of 1.1 LGT events (including both homologous and nonhomologous LGT events) per gene family over a phylogeny of a similar extent to the one used in this study. Hence, the inference of more than $\sim 20$ nonorthologous LGT events in Thy genes catalogs as extensive. Notably, in the approach used in this study, occurrences of homologous LGT (i.e., xenologous displacement, where one enzyme replaces its orthologous counterpart) are not accounted for. Hence, estimates of LGT given by the model are probably underestimates of the actual number of LGT events involving Thy.

Viral-Driven Evolution of Thy LGT

What causes such a high rate of LGT involving thy genes? The biosphere is permeated with viruses and phages, many encoding thy. Each such particle is a potential LGT vehicle. We propose that the reason for the abundance of LGT between the 2 types of enzymes is the high availability of these vehicles for thy transfer and not necessarily a selective advantage of one enzyme over the other. Let us consider the following scenario: bacteria coding for thyX are surrounded by viruses, some encoding for thyX and some for thyA. By chance, a virus encoding for thyA infects a bacterium, and the viral thyA is integrated into its genome. This bacterium now has 2 genes performing the same function, possibly even functioning similarly under the same conditions. A deleterious mutation to any of the genes will not disadvantage the organism because it has an alternative functional copy. A chance mutation at thyX could lead to what we infer today as a swap between thyX and thyA. According to this perspective, LGT involving thy does not necessarily stem from a clear-cut selective advantage for the host to switch between thy genes. Hence, we propose that thy LGT is viral driven: the driving force is the selective advantage to the virus (in the case of thy, increased thymidylate production), which explains the abundance of viruses coding for thy. Nevertheless, the alternative hypothesis, according to which viruses are mainly recipients of genes and cellular organisms also swap genes by other means, cannot be excluded. To fully resolve this issue, comparative data are required from other gene families where nonhomologous LGT occurs.

Several viral Thy sequences in this study display an intriguing pattern of evolution. The T4-like phages comprise a monophyletic group, which is located at a basal position in the ThyA gene tree (Fig. 2), in agreement with the study of Filee et al. (2003). This location of the T4-like phages implies an ancient origin for the T4-like ThyA enzyme and may have implications on theories regarding the origins of viral and cellular DNA (Forterre 2006b). Two eukaryal viruses that code for a Thy enzyme also display a puzzling pattern of evolution: Mimivirus and Paramecium bursaria chlorella virus 1 (PBCV-1). The former is located at the base of the eukaryal gene tree of ThyA (Fig. 2). This has been noted before (Raoult et al. 2004), and it has been suggested that Mimivirus represents a “fourth domain of life,” leading to an intense debate on the validity of this observation (Moreira and Lopez-Garcia 2005; Ogata et al. 2005). The PBCV-1 provides a more profound mystery: while the virus codes for thyX, its eukaryal host most likely encodes thyA (Graziani et al. 2004). Further complicating this story, the virus is believed to be an extant representative of a primordial viral group (Graziani et al. 2004; Iyer et al. 2006; Yamada et al., 2006). Evidently, more viral and cellular molecular data are required to shed light on the viral origins of Thy enzymes.

SUPPLEMENTARY MATERIAL

Supplementary material can be found at http://www.sysbio.oxfordjournals.org/.

FUNDING

A.S. was supported by a fellowship from the Edmond J. Safra Bioinformatics Program at Tel-Aviv University. I.M. is supported by a Killam postdoctoral fellowship. O.P. is a fellow of the Converging Technologies scholarship program. U.G. and T.P. are supported by the Research Networks Program in Bioinformatics of the Ministry of Science and Technology of the State of Israel, the Ministry of Foreign Affairs and the Ministry of National Education and Research of France. T.P. is supported by a grant from the Israel Science Foundation, number 1208/04, and by a grant from the Israeli Ministry of Science.

APPENDIX

Section 1: Computing Posterior Probabilities in a Nonreversible Model

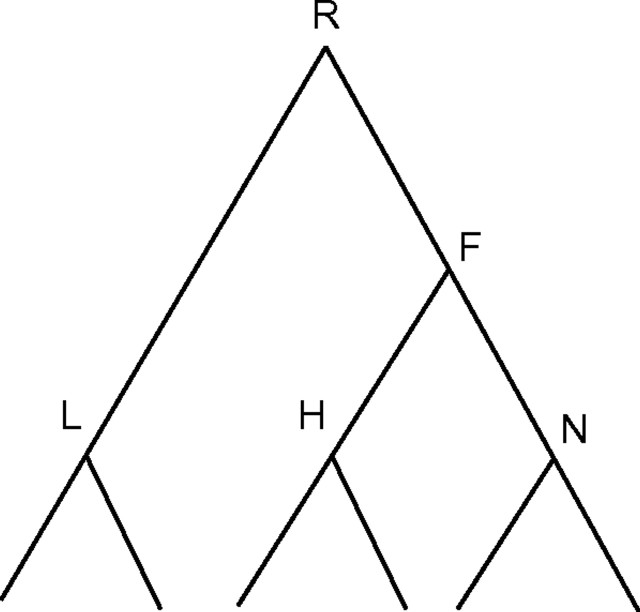
For each edge, we would like to calculate the posterior probability that a gain event (representing LGT) has occurred along this edge. Without loss of generality, we will henceforth refer to edge FN in the tree in Figure A1. Let W represent the event where a $u\to v$ transition has occurred (e.g., gain of ThyX) at least once along the edge FN. Then, the posterior probability of W is

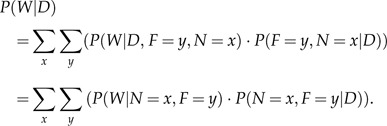(A.1)

FIGURE A1.

An example tree used to illustrate the computation of posterior probabilities.

The first term in the summation represents the probability of a $u\to v$ transition, given that we know the states at the terminals of the edge FN. This can be calculated via simulation studies (Nielsen 2002) and is described in Section 4 below. The second term of the summation is the joint probability of observing 2 particular states at the terminals of edge FN and can be calculated as described in Section 2. Note that in Equation (A.1), we take into account situations where the states at the edge terminals are equal (i.e., $x=y$). Nevertheless, in these cases, there is still some probability that a $u\to v$ transition occurred (possibly followed by a backward $v\to u$ transition).

Section 2: Computing Joint Probabilities along an Edge

The joint probability $P(F=y,N=x|D)$ is calculated using the following formula:

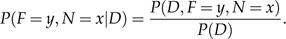(A.2)

In order to compute, let us define 2 terms representing partial likelihoods in the tree:

${\text{Up}}_n^y$ is computed using Felsenstein's (1981) pruning algorithm.

In a time-reversible model, ${\text{Down}}_N^y$ is computed similarly using the following recursion:

(A.3)

The initial condition for the son of the root is

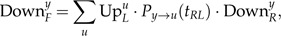where ${\text{Down}}_R^y=1\forall y$.

In a time-reversible model, rerooting the tree does not affect the likelihood. Hence, we can reroot the tree at node F, and the likelihood term $P(D,F=y,N=x)$ from Equation (A.2) is now

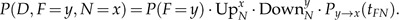(A.4)

The full likelihood of the tree can now be computed as follows:

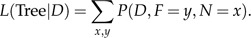(A.5)

However, in a nonreversible model, we cannot reroot the tree. Thus, the computation of $P(D,F=y,N=x)$ at each internal node is now dependent on the assignment at the root. We first note that

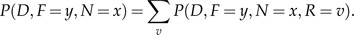(A.6)

To compute each such term, we use the following:

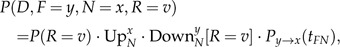(A.7)

where

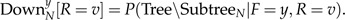The computation of ${\text{Down}}_F^y[R=v]$ follows the same recursion as in the time-reversible case described above. The only difference is in the computation of the Down term for the root

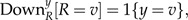(A.8)

where $1\{y=v\}$ is an indicator function. Furthermore, the full likelihood of the tree is now

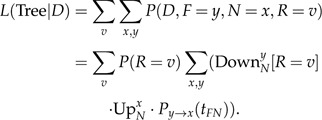(A.9)

Section 3: Computing the Expectation of the Number of Changes along an Edge

Apart from calculating the posterior probabilities of gains or losses along each edge, we would like to be able to compute the expectation of the number of changes from character u to character v along a certain edge (without loss of generality, we will refer to edge FN). We will denote this number by $N_{uv}\left(FN\right)$:

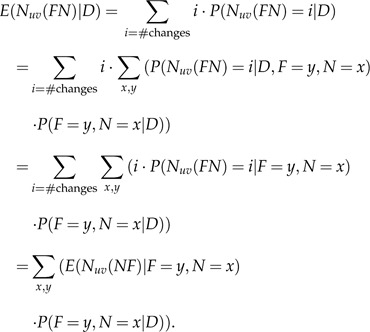(A.10)

The second term $P(F=y,N=x|D)$ is calculated as described in Section 2, whereas the first term is obtained via simulations as described in Section 4. The expectation of the number of changes from character u to character v throughout the whole phylogeny is now simply

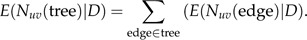(A.11)

Section 4: Calculating the Expectation and Probabilities of Events via Simulations

Our aim was to simulate a continuous-time Markov chain (Fig. A2). Each simulation is run with a different starting state. The simulation is performed based on a Markov process, defined by its instantaneous rate matrix Q. Waiting times between states are assumed to follow an exponential distribution. The λ parameter of the distribution is simply $-Q_{ii}$, where i is the state at the beginning of the transition. Given that a change has occurred, the probability that state j was obtained is $Q_{ij}/-Q_{ii}$.

We perform the simulations n times (where n is chosen so that the inferences based on the simulation have converged; usually $n=10,000$). For each edge length, we count the number of transitions of each type, given the state at the beginning of the edge and the state at the end of this edge. For example, for an edge of length $t_1+t_2+t_3+0.5t_4$, the state at the beginning is black (Fig. A2). Based on the simulation of the waiting times, the state at the end of such an edge is also black. In this case, we will count one black → red transition, one red → yellow transition, and one yellow → black transition. After n simulations, we can estimate probabilities and expectations of transition events, given an edge and the states at its tips.

FIGURE A2.

A schematic representation of a continuous-time Markov chain. Circles represent different states represented by different colors, and t₁–t₄ represent the waiting times.