Abstract
Purpose: To investigate the potential of the normalized probabilistic atlases and computer-aided medical image analysis to automatically segment and quantify livers and spleens for extracting imaging biomarkers (volume and height).
Methods: A clinical tool was developed to segment livers and spleen from 257 abdominal contrast-enhanced CT studies. There were 51 normal livers, 44 normal spleens, 128 splenomegaly, 59 hepatomegaly, and 23 partial hepatectomy cases. 20 more contrast-enhanced CT scans from a public site with manual segmentations of mainly pathological livers were used to test the method. Data were acquired on a variety of scanners from different manufacturers and at varying resolution. Probabilistic atlases of livers and spleens were created using manually segmented data from ten noncontrast CT scans (five male and five female). The organ locations were modeled in the physical space and normalized to the position of an anatomical landmark, the xiphoid. The construction and exploitation of liver and spleen atlases enabled the automated quantifications of liver∕spleen volumes and heights (midhepatic liver height and cephalocaudal spleen height) from abdominal CT data. The quantification was improved incrementally by a geodesic active contour, patient specific contrast-enhancement characteristics passed to an adaptive convolution, and correction for shape and location errors.
Results: The livers and spleens were robustly segmented from normal and pathological cases. For the liver, the Dice∕Tanimoto volume overlaps were 96.2%∕92.7%, the volume∕height errors were 2.2%∕2.8%, the root-mean-squared error (RMSE) was 2.3 mm, and the average surface distance (ASD) was 1.2 mm. The spleen quantification led to 95.2%∕91% Dice∕Tanimoto overlaps, 3.3%∕1.7% volume∕height errors, 1.1 mm RMSE, and 0.7 ASD. The correlations (R2) with clinical∕manual height measurements were 0.97 and 0.93 for the spleen and liver, respectively (p<0.0001). No significant difference (p>0.2) was found comparing interobserver and automatic-manual volume∕height errors for liver and spleen.
Conclusions: The algorithm is robust to segmenting normal and enlarged spleens and livers, and in the presence of tumors and large morphological changes due to partial hepatectomy. Imaging biomarkers of the liver and spleen from automated computer-assisted tools have the potential to assist the diagnosis of abdominal disorders from routine analysis of clinical data and guide clinical management.
Keywords: liver, spleen, imaging biomarkers, probabilistic atlas, segmentation
INTRODUCTION
The three-dimensional (3D) size and shape variability of liver and spleen can be essential image-based biomarkers of disorders.1, 2, 3, 4, 5, 6, 7 In addition to diagnosis, organ volume∕height measurements have also been found to be important in making surgical decisions involving organ transplantation.8, 9, 10 In traditional clinical practice, 3D organ analysis is performed via time-consuming manual measurements; alternatively, the evaluation is based on 2D projection images, which introduces bias.11 The implementation of a fully automated 3D segmentation technique would allow radiologists and other health professionals to have easy and convenient access to organ measurements. The proposed method for the automated segmentation of spleen and liver can be employed as an assisting diagnostic tool robust to morphological changes from normal and pathological anatomical variability.
In clinical practice, the liver size is estimated by height measurements at the midhepatic line (MHL);12, 13 similarly, the spleen size is approximated as the cephalocaudal (CC) height.11, 14, 15, 16 However, liver height does not fully characterize the morphology of the liver due to the wide variety of liver shapes,17 soft tissue deformations, and occasional enlarged left lobe. Spleen measurements suffer from similar shortcomings. Studies have shown that clinical volumetric measurements from ultrasound18 and∕or computed tomography (CT)19, 20 are highly relevant to diagnosing liver disorders; volumes were computed by multiplying the axial slice area of the organ from manual tracings by the slice thickness.21, 22
A variety of sophisticated methods to segment the liver has been proposed in recent years to support routine hepatic analysis. This methodological explosion reflects the difficulty of liver segmentation for clinical applications. The following paragraphs enumerate some of the most relevant published techniques.
One of the early statistical approaches to label the abdomen was presented in Ref. 23 using a stochastic method of abdominal geometry. In Ref. 24, statistical analysis and dimensionality reduction from sparse information models were used to segment the liver. The method was very fast, but suffered from the misrepresentation of the liver shape from a statistical model. A model-based segmentation was also employed in a supervised segmentation using graph representation in Ref. 25. In Ref. 26, a shape-guided deformable model was developed using an evolutionary algorithm, but unacceptable segmentations were omitted in the analysis. User interaction was requested for the iterative Bayesian approach proposed in Ref. 27. A fast hierarchical model using marginal space learning was introduced in Ref. 28, but segmentation outliers were also excluded from validation. A comprehensive technique for hepatic surgery was published in Ref. 29 using model fitting and liver functional information but was inaccurate in hepatectomy cases. Active contours using gradient vector flow were used to address both liver and hepatic tumor segmentation,30 while a multilevel statistical shape model and principal component analysis were used in Ref. 31 but required heavy manual initialization.
A comprehensive review of CT-based liver segmentation techniques was done by Campadelli et al.,32 describing additional methods that employed live wire,33, 34, 35, 36 gray-level analysis,32, 37, 38, 39, 40, 41, 42, 43, 44 neural networks,45, 46, 47, 48 model fitting,49, 50, 51 level sets,52 and probabilistic atlases.53, 54, 55, 56 Campadelli et al. highlighted respective advantages and drawbacks that limit the use of such techniques in the clinic.
In 2007, a liver segmentation competition from CT data was held.57, 58 A variety of techniques was presented and their performance evaluated through a combination of metrics, including volume overlap and error, root-mean square error (RMSE), and average surface distance (ASD). Among the ten automatic and six interactive methods for liver segmentation, the interactive methods achieved some of the best segmentation results.59, 60, 61 The automatic methods based on statistical shape models were found to perform similar to the semiautomatic techniques. Notably, a combination of shape-constrained statistical deformable models based on a heuristic intensity model had the best performance among automated methods62 with slight undersegmentation of the liver. Region growing was used in Ref. 63 with good results, but the technique was sensitive to liver abnormalities. A semantic formulation of knowledge and context was presented in Ref. 64, but the segmentation overlap was only 84%.
Unlike the abundance of research on automated and interactive liver segmentation, there are few similar studies involving the human spleen. A nondensity-based approach using edge detection to automatically segment the spleen was implemented in Ref. 65. Registration and edge detection were combined with the elimination of extraneously segmented regions via binarization of a frequency image of the spleen. The study required multiphase data acquisition and provided vague validation results. Price et al.66 used a 3D level sets method to segment the spleen of mice; a manual seed point was needed to begin the segmentation.
Combined spleen and liver segmentation has been addressed as a part of abdominal multiorgan analysis, but with limited accuracy. Park et al.54 used an atlas registered with thin plate splines to propagate the segmentation of liver, kidneys, and aorta. Using a similar principle, a priori data from probabilistic atlases were used to initialize the segmentation of abdominal organs in Refs. 55, 67. Both methods used measures of relationship and hierarchy between organs and manual landmarks. A group of organs, including the liver, was segmented using contrast-enhancement information in the abdomen in Ref. 68; parts of the heart were erroneously labeled as liver. Multidimensional CT data from four phases were employed in Refs. 69, 70. Hu et al.69 used independent component analysis in a variational Bayesian mixture, while Sakashita et al.70 combined expectation-maximization and principal component analysis to segment abdominal CT. Very recently, Seifert et al.71 proposed a semantic navigation for fast multiorgan segmentation from CT data. The liver and spleen were also segmented from magnetic resonance imaging data in Ref. 72.
Probabilistic atlases and their value to improve anatomical segmentation were mentioned in previous paragraphs. Most of the work has taken place on the construction of atlases of the brain73, 74, 75 and the heart.76, 77 However, recent work has been done on the construction of abdominal multiorgan atlases. Notably, in Ref. 54 a nonlinear registration based on thin plate splines was used for the generation of an atlas of the kidneys, liver, and spleen. On a different note, Okada et al.31, 78 developed a hierarchical statistical atlas of the liver normalized to the abdominal cavity as part of a process to automatically segment the liver. The construction and exploitation of these abdominal atlases required user interaction through manual landmarks.
This paper proposes the extraction of imaging biomarkers by the automated segmentation of the liver and spleen involving a combination of appearance∕enhancement, shape, and location statistics. Normalized probabilistic atlases of the liver and spleen were constructed from a patient population. The atlases are size invariant and normalized to the position of an anatomical landmark (the xiphoid). For the coarse estimation of organs, mean models from the liver and spleen were aligned to the patient contrast-enhanced CT image. This estimation was improved by a geodesic active contour (GAC). Subsequently, the patient specific enhancement characteristics in the liver and spleen were estimated and passed to an adaptive convolution. Only homogenous tissue areas that satisfied the enhancement constraints were labeled as liver∕spleen. Finally, shape and location corrections from the normalized probabilistic atlas were performed. The organ’s morphologies were characterized by their heights (midhepatic height for the liver and cephalocaudal height for the spleen) and volumes. The method was validated with manual volumetric segmentations and height measurements of normal and pathological livers and spleen.
MATERIALS AND METHODS
Data and manual measurements
The data used for this study were declared exempt for IRB review by the National Institutes of Health’s Office of Human Subjects Research. For the construction of the normalized probabilistic atlas and analysis of shape variability, ten abdominal noncontrast CT scans of patients with no abnormalities in the liver or spleen were used: Five male and five female (mean age of 59.9 yr: 60.6 for male and 59.2 for female). Data were collected with a LightSpeed Ultra scanner (GE Healthcare, Milwaukee, WI) and image resolution ranged from 0.54 to 0.77 mm in the axial plane with an interslice distance of 1 mm. Livers and spleens were manually segmented from the ten CT scans.
For the segmentation of spleens and livers, 257 abdominal CT scans of patients from a mixed population were used: 51 had normal livers, 44 had normal spleens, 128 had splenomegaly (enlarged spleen), 59 had hepatomegaly (enlarged liver), and 23 had partial hepatectomy (partial liver resection). As the common clinical practice for splenectomy requires the total removal of the spleen, we did not have access to partial splenectomy cases. Patients were injected with 130 ml of Isovue-300 and images acquired at portal venous phase using fixed delays or bolus tracking.80 Data were collected on LightSpeed Ultra and QX∕I (GE Healthcare), Brilliance64 and Mx8000 IDT 16 (Philips Healthcare, Cleveland, OH), Definition (SIEMENS Healthcare, Cary, NC), and Aquilion ONE (Toshiba Medical Systems, Irvine, CA) scanners. Image resolution ranged from 0.62 to 0.93 mm in the axial plane with a slice thickness from 1 to 5 mm. The livers and spleens were manually segmented in 14 low resolution (5 mm slice thickness) cases for training from random CT data without knowledge of organ size. 14 spleens (7 random normal spleens and 7 random enlarged spleens) and 19 livers (7 random normal livers, 7 random enlarged livers, and 5 random cases of partial hepatectomy) were manually segmented from low resolution (5 mm slice thickness) CT scans for testing. The test data were segmented manually by two observers to assess interobserver variability. Livers and spleens were also manually segmented from 20 high resolution (1 mm slice thickness) testing CT scans. The organ heights were manually measured in all data, excepting the hepatectomy cases, by two observers. The midhepatic liver height was traced on the computer screen at the approximate location of the MHL following the method in Ref. 13. The CC spleen height was measured by multiplying the number of slices between the estimated top and bottom of the spleen by the interslice distance.
The diagnoses were established by radiologists without following any single criterion. The patient cases were collected using search parameters in the Radiology Information System (RIS–Cerner Corporation, Kansas City, MO) and the Clinical Research Information System (CRIS–Eclipsys Corporation, Atlanta, GA). The radiological reports had to include keywords referring to hepatomegaly, splenomegaly, or hepatosplenomegaly. For hepatosplenomegaly cases, both liver and spleen were segmented. The control population was selected from kidney donors and had both liver and spleen were segmented, unless one of the organs had poor perfusion or imaging artifacts.
For additional comparative tests, we used 20 more contrast-enhanced CT scans with manual segmentations of the liver downloadable from www.sliver07.isi.uu.nl, addressed as MICCAI data in the paper. These CT data were used for the MICCAI 2007 liver segmentation competition and were acquired in transversal plane with pixel sizes between 0.55 and 0.8 mm and interslice distance between 1 and 5 mm.
Contrast-enhanced images corresponded to mainly pathological cases and were acquired on a variety of scanners from different manufacturers.
Atlas construction
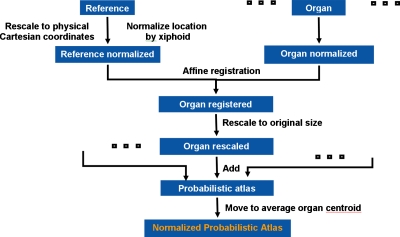
The normalized probabilistic models of the liver and spleen were generated using the algorithm presented in Fig. 1. A random image from the database was set as reference J, and all other subject data, addressed as image I, were registered to the reference. For all ten subjects, the manual segmentation of livers and spleens were used to generate organ masks. Then, each organ was registered individually to its corresponding mask in the reference set. Interpatient organ variability was retained by using a size-preserving affine registration modified from a 9-parameter affine transformation. First the volume of each organ is computed and then an anisotropic scaling of organs is allowed during registration. Then, organs are rescaled isotropically to their size before the transformation. Restricting the degrees of freedom in the transformation and imposing volume preservation, the organ shape∕size bias from the reference data was minimized. Spatial variability was reduced by normalizing the physical coordinates of the organ to the position of the xiphoid.
Figure 1.
A schematic of the construction of the normalized probabilistic atlases of liver and spleen.
The modified affine registration was based on normalized mutual information M,79 where p(I,J) is the joint entropy of images I and J, and p(I) and p(J) their marginal entropies, computed from the intensity distributions of I and J,
| (1) |
The transformation was size invariant and the physical coordinates of organs (image independent) were used, normalized by the xiphoid. Finally, registered livers and spleens were translated in the atlas to the location of the average normalized centroid and probabilistic organ atlases were computed. This spatial normalization also offers a mean model of liver and spleen shape and location in the abdomen.
Liver and spleen segmentation
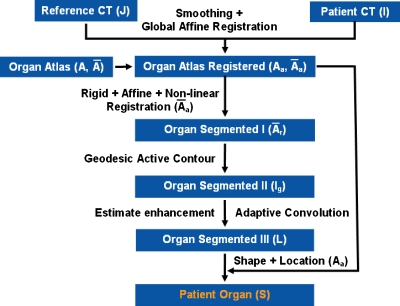
A diagram of the automated segmentation algorithm is shown in Fig. 2. The following sections describe the registration, active contour, adaptive convolution by enhancement estimation, and shape and location correction employed to segment the liver and spleen from CT data.
Figure 2.
A schematic of the automated liver and spleen segmentation algorithm.
Registration
From the construction of probabilistic atlas, two models are extracted for each organ: A conservative model A and a mean model . A can be seen as a binary image where a value of 1 refers to a nonzero probability (1%–100%) of an organ to be present at that location in the probabilistic atlas constructed in Sec. 2B. The mean model reflects in a binary way only probabilities higher than 50% in the probabilistic atlas. Then, the patient CT image (I) was smoothed with anisotropic diffusion,80 using five iterations, a conductance of 5, and a time step of 0.0625, and the result was Is. First, a global affine registration between J and I (CT scans) was performed, where J is the reference image from the construction of the atlas. The resulting spatial normalization was then applied to both A and , which became Aa and (Fig. 2). The affine registration was based on normalized mutual information M as in Sec. 2B.
A more flexible alignment of was required to compensate for the residual deformation, resulting in (Fig. 2). We used a succession of rigid, affine (12 degrees of freedom) and nonlinear transformations to register to I. The nonlinear registration algorithm used B-splines.81 B-splines allowed the local control of the deformation T to find a compromise between the similarity M and smoothing D,
| (2) |
Thus, we obtained an initial estimation of the target organs based solely on registration (organ segmented I in Fig. 2). An open source implementation of the B-spline algorithm can be found at http://www.doc.ic.ac.uk/~dr/software/. For this application, the registration used 64 intensity bins, linear interpolation, and three resolution levels starting with a control point spacing of 10 mm for the free-form deformation at the coarse level.
Geodesic active contour
Abdominal organs, especially the liver, exhibit significant shape and size variations, which may not be covered by the registered atlas . To account for possibly missing parts of spleen and liver, a GAC (Ref. 82) was implemented to correct the organ boundaries based on contrast-enhanced image intensities. To initialize the active contour, was input as zero level into a GAC Ig [Eq. 3 and Fig. 2]. The edge features Ie were computed from the sigmoid of the gradient of Is, where α relates to the minimum gradient on the organ boundaries, and β is a measure of the mean gradient values within the organ,
| (3) |
The weight wc controls the speed c of the contour, while k represents its curvature. In our experimental setup, wc was set after training to 0.2. Parameters α and β of the image sigmoid were 10 and 8, respectively. All parameters were trained empirically and a logic tree was used to find the best combination for the segmentation of liver and spleen.
Enhancement estimation and adaptive convolution
A common difficulty in processing contrast-enhanced CT data is the estimation of the optimal time for image acquisition. In practice, fixed delays or bolus-tracking techniques83 are used and can notoriously yield a different enhancement (darker or brighter) and appearance of organs at each acquisition. Hence, variations in an organ’s enhancement are common and, in the case of the commonly used portal venous phase, span between late-arterial and late-portal venous phases. The GAC was trained on a relatively small database and would not have captured wider appearance variations in the images. With the assumption (clinically based) that both the liver and spleen should enhance homogeneously at portal venous phase, we estimated the level of enhancement of the organs to reject volumes that were erroneously captured by GAC.
The segmentations of liver and spleen provided by the GAC were used to compute the mean (μj) and standard deviation (σj) of the organs intensities (j=1,2 for liver and spleen). Then outliers were rejected by computing and to account for organ enhancement. Using and an adaptive convolution was applied to Ig in the form of a heterogeneous erosion filter based on image characteristics. Thus only regions for which all the voxels in the erosion element E satisfy the homogeneous intensity criteria in Eq. 4 were labeled as organs of interest,
| (4) |
where L represents the labeled image and lj represents the labels (Fig. 2). L is then dilated to account for the convolution with E.
Shape and location correction
Finally, the normalized Aa was used to correct the shape and location of the liver∕spleen in L. S=L⋅Aa is the image of the segmented liver and spleen, where Aa resulted from applying an affine transformation to the probabilistic atlas constructed with restricted degrees of freedom (Fig. 2). Thus, extraneous regions at the organ boundaries, such as parts of the pancreas, heart, intestines, or muscles, with intensities similar to that of the target organs and not detected by the adaptive convolution got removed.
Data analysis
The volume overlap (VO) and Dice coefficient (DC) of the automatically segmented livers and spleen compared to the manual segmentations were calculated, where Vmanual and Vauto are binary 3D volumes (matrices of voxels) of the manually and automatically segmented organ,
| (5) |
To correlate with clinical evaluations of the liver and spleen performed by linear measurements of organ height, the MHL was approximated at the half-distance between the midpoint of the spine and the outer surface of the liver. Then the maximum liver height along the sagittal plane at the location of MHL was computed, as in Ref. 13. The spleen CC height was calculated as the Euclidean distance between the top and bottom sagittal slices containing the spleen. In addition, volume estimation error (VER), height estimation error (HER), RMSE, and ASD between automated and manual segmentations were also computed. The surface distance was computed from nearest neighbor estimates. VER and HER were computed as the percentage of absolute volume∕height difference between automated and manual measurements relative to the true (manual) measurement. Correlations (R2) for groups of data were performed and Bland–Altman agreements84 reported. If data were normally distributed, student’s t-tests were used to evaluate significance; otherwise, a nonparametric test (Mann–Whitney) was employed. Significance was assessed at 95% confidence level.
RESULTS
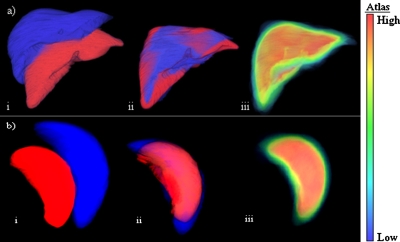
Figure 3 exemplifies the registration of livers and spleens used in the construction of the atlases along with probabilistic models of organs. An example of liver and spleen detection and segmentation at different stages of the method is presented in Fig. 4.
Figure 3.
Normalized probabilistic atlases of the liver (a) and spleen (b) were created using a modified affine transformation: (i) Image of two organs before registration, (ii) after the modified affine registration; and (iii) the probabilistic atlas with a probability color map. Each atlas voxel contains probabilities associated with the presence of the liver or spleen.
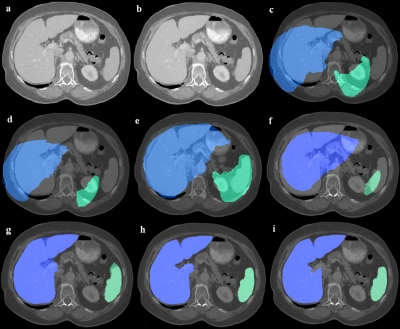
Figure 4.
An example of automated organ segmentation, liver, and spleen: (a) The patient image (I); (b) the smoothed data (Is); (c) the conservative model (A) of organs overlaid on the patient data; (d) the mean model of organs overlaid on the patient data; (e) the registered conservative model after the global affine registration (Aa) covering the patient liver∕spleen; (f) the registered mean model after the global affine registration; (g) the mean model after nonlinear registration ; (h) the segmentation after GAC and adaptive convolution (L); and (i) the final segmentation after shape and location corrections (S).
Liver segmentation
Quantitative incremental results from applying our method to the segmentation of the liver are presented in Table 1. We compared results on training data after nonlinear registration (step 1), adding GAC and adaptive convolution (step 2), and after incorporating shape and location correction (step 3). For test data, results are reported on the full segmentation method (step 3). As expected, results are more accurate on data with high spatial resolution. Table 1 also presents interobserver variability for the segmentation of liver. Table 2 indicates that there is a significant difference in all the metrics when comparing results after nonlinear registration (step 1) with those after the addition of GAC and adaptive convolution (step 2). However, even though the metrics improved with the shape and location correction (step 3), the only significant change occurred for VER. When results on test sets with low and high resolution were compared, a significant difference was found for most metrics, with the exception of VER and HER. These statistics suggest that the computation of liver volumes and heights using the proposed method is not significantly influenced by image resolution. Moreover, test data at low resolution were separated into normal and hepatomegaly cases to test the sensitivity of the method to pathology. There were no significant (p>0.2) differences in the method performance when tested on normal and abnormal cases. No significant difference (p>0.2) was found comparing interobserver and automatic-manual VER and HER.
Table 1.
Statistics for the liver segmentation results from training and test data. Incremental results are shown for the training set at step 1—after nonrigid registration, step 2—using GAC and adaptive convolution, and step 3—after incorporating shape and location correction. Columns present the DC, VO, VER, HER, RMSE, and ASD.
| Data set∕no. of cases | DC (%) | VO (%) | VER (%) | HER (%) | RMSE (mm) | ASD (mm) |
|---|---|---|---|---|---|---|
| Training liver step 1∕14 | 90.9±3.7 | 83.6±6 | 14.9±9.6 | 12.2±13.2 | 4.4±2.1 | 2.6±1.2 |
| Training liver step 2∕14 | 94.3±1.5 | 89.3±2.6 | 3.3±3.7 | 3.7±3.7 | 3.8±1.8 | 1.7±0.8 |
| Training liver step 3∕14 | 94.5±0.8 | 90±1 | 2±2.1 | 3.4±3.1 | 2.9±0.5 | 1.5±0.3 |
| Test liver (low resolution)∕14 | 94.8±1 | 90.4±1.1 | 2.8±1.9 | 3.4±3.1 | 2.8±0.6 | 1.5±0.4 |
| Normal∕7 | 94.1±1 | 89.9±1 | 2.6±1.8 | 3±3.5 | 1.9±0.5 | 1.2±0.2 |
| Hepatomegaly∕7 | 95.2±1.2 | 91.5±1.3 | 3.1±2 | 3.9±2.9 | 3.2±0.8 | 1.7±0.5 |
| Test liver (high resolution)∕10 | 96.2±0.6 | 92.7±1.1 | 2.2±2.1 | 2.8±3.3 | 2.3±0.5 | 1.2±0.2 |
| MICCAI liver∕20 | 95.9±0.9 | 92±1.8 | 2.6±2 | 4.3±4.6 | 2.9±1 | 1.4±0.5 |
| Hepatectomy cases∕5 | 93.9±1.3 | 88.5±2.3 | 4.1±2.8 | N∕A | 3.3±0.6 | 1.6±0.2 |
| Interobserver liver∕14 | 96.4±0.9 | 92.3±1.2 | 1.25±1.1 | 3.9±2.7 | 1.7±0.4 | 0.7±0.2 |
Table 2.
Comparative statistics (p values) between different steps in the liver segmentation from the training set and between test sets of low and high resolutions (see Table 1).
| Liver segmentation (p value) | DC | VO | VER | HER | RMSE | ASD |
|---|---|---|---|---|---|---|
| Step 1 vs step 2 | 0.0002 | 0.0002 | 0.0002 | 0.01 | 0.02 | 0.001 |
| Step 2 vs step 3 | 0.83 | 0.68 | 0.05 | 0.62 | 0.37 | 0.41 |
| Low vs high resolution | 0.0007 | <0.0001 | 0.48 | 0.58 | 0.04 | 0.04 |
The results from testing the automated liver segmentation algorithm on the MICCAI data are also provided in Table 1. The segmentation score was 69, close to that of 68 of the competition winner, as reported in Ref. 58. Although the same evaluation tools provided by the competition organizers57 were used, note that our score was obtained on the training cases provided by the organizers, as we did not have access to the test data used in Refs. 57, 58. Our algorithm was trained on an independent database.
Unsurprisingly, segmentation results on hepatectomy cases were inferior to those of normal or even pathological full livers, as the organ morphology is drastically changed after partial hepatic resection. Additional challenges came from the presence of abdominal fluid replacing removed liver segments, and the lack of visceral fat tissue, which compressed the abdominal organs against each other. Nevertheless, as seen in Table 1, the algorithm satisfactorily segmented and quantified a variety of pathological livers.
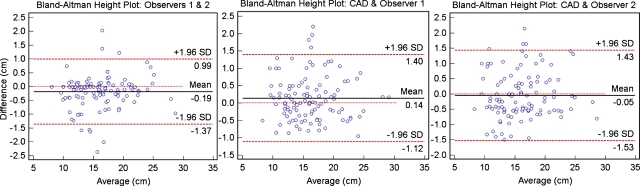
Finally, automated volumetric and linear 3D measurements were obtained for an additional 110 clinical cases with manual MHL height measurements: 51 had normal livers, while 59 cases had hepatomegaly. Figure 5 shows the Bland–Altman height measurement agreements between two different observers and between each observer and the automatic MHL heights. There were significant correlations (p<0.0001) between interobserver measurements (R2=0.97) and each observer and the automatic measurements (R2=0.95).
Figure 5.
Bland–Altman agreement plots for the linear estimations of liver height at MHL; from left to right we show the interobserver variability and the difference between manual (observers 1 and 2) and automatic (CAD) measurements.
Spleen segmentation
Table 3 shows quantitative incremental and comparative results from applying our method to the segmentation of the spleen. The different stages of the segmentation process are compared in Table 4; while the use of GAC and adaptive convolution significantly improved all the validation metrics, there were no significant changes after the shape and location correction with an improvement noted for VER and a worsening for ASD. When results on test sets with low and high resolutions were compared, a significant difference was found for most metrics, except DC and VER. The results suggest that the computation of spleen imaging biomarkers may be influenced by image resolution, although the small differences are probably not clinically meaningful. Test data at low resolution were separated into normal and splenomegaly cases to test the sensitivity of the method to pathology. There were no significant (p>0.1) differences in the method performance when tested on normal and abnormal cases. No significant difference (p>0.4) was found comparing interobserver and automatic-manual VER and HER.
Table 3.
Statistics for the spleen segmentation results from training and test data. Incremental results are shown for the training set at step 1—after nonrigid registration, step 2—using GAC and adaptive convolution, and step 3—after incorporating shape and location correction. Columns present the DC, VO, VER, HER, RMSE, and ASD.
| Data set∕no. of cases | DC (%) | VO (%) | VER (%) | HER (%) | RMSE (mm) | ASD (mm) |
|---|---|---|---|---|---|---|
| Training spleen step 1∕14 | 87.5±4.8 | 78±7.5 | 13.6±10.5 | 9.7±9.2 | 2.9±1.2 | 1.6±0.7 |
| Training spleen step 2∕14 | 91±2 | 83.5±3.3 | 6.6±5.3 | 3.5±3.4 | 2.1±0.5 | 1±0.2 |
| Training spleen step 3∕14 | 90.6±2.1 | 83±3.5 | 5.5±4.9 | 3.5±5.1 | 2.1±0.6 | 1.3±0.8 |
| Test spleen (low resolution)∕14 | 94±1.7 | 88.8±2.9 | 4.3±3.6 | 3.1±2.9 | 2.1±0.8 | 1±0.5 |
| Normal∕7 | 93.3±1.2 | 87.5±2.1 | 3.9±3.1 | 2.7±3.8 | 1.7±0.3 | 0.8±0.1 |
| Splenomegaly∕7 | 94.7±1.8 | 90±3.3 | 4.7±4.2 | 3.5±2.1 | 2.5±1 | 1.2±0.5 |
| Test spleen (high resolution)∕10 | 95.2±1.4 | 91±2.6 | 3.3±2.7 | 1.7±0.7 | 1.1±0.3 | 0.7±0.1 |
| Interobserver spleen∕14 | 95.1±0.8 | 90.6±1.5 | 2.9±3 | 1.28±3.5 | 0.9±0.2 | 0.4±0.1 |
Table 4.
Comparative statistics (p values) between different steps in the spleen segmentation from the training set and between test sets of low and high resolution (see Table 3).
| Spleen segmentation (p value) | DC | VO | VER | HER | RMSE | ASD |
|---|---|---|---|---|---|---|
| Step 1 vs step 2 | 0.0003 | 0.003 | 0.01 | 0.01 | 0.04 | 0.01 |
| Step 2 vs step 3 | 0.3 | 0.3 | 0.41 | 0.87 | 0.89 | 0.63 |
| Low vs high resolution | 0.07 | 0.0005 | 0.5 | 0.04 | 0.0004 | 0.01 |
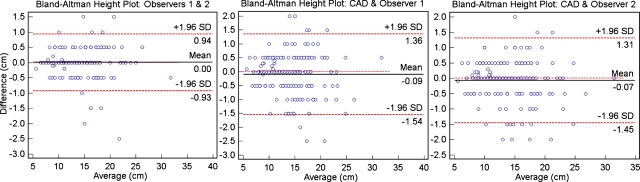
Figure 6 presents the Bland–Altman height measurement agreements between two different observers and between each observer and the automatic CC heights for an additional 172 clinical cases: 44 had normal spleens, while 128 cases had splenomegaly. There were significant correlations (p<0.0001) between interobserver measurements (R2=0.99) and each observer and the automatic measurements (R2=0.98).
Figure 6.
Bland–Altman agreement plots for the linear estimations of spleen CC height; from left to right we show the interobserver variability and the difference between manual (observers 1 and 2) and automatic (CAD) measurements. The discrete 5 mm spaced steps are related to the slice thickness of image data.
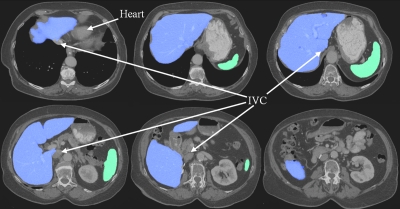
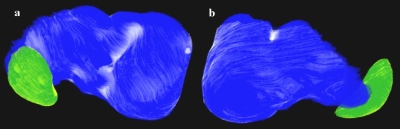
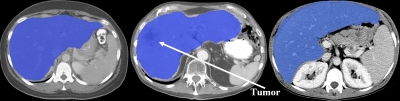
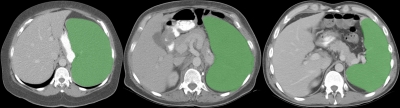
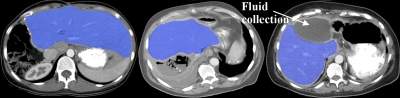
An example of liver and spleen segmentation from a normal data set is shown in Fig. 7. Note the good separation from the heart; parts of inferior vena cava (IVC) were incorporated in the liver in regions where the contrast enhancement was low. Figure 8 illustrates volume renderings of the 3D segmentation along with the segmentation errors between the manual and automated methods. Figure 9 presents automatic segmentations on three examples of enlarged livers with pathologies and unusual shapes. Similarly, Fig. 10 illustrates three examples of automatic spleen segmentations from cases with splenomegaly. A pathological liver from the MICCAI database was segmented in Fig. 11; note the robustness of the algorithm in the presence of tumors, and the good separation of the heart and IVC. Lastly, we present three examples of segmentations from cases with hepatectomy, which exhibit unusual liver shapes, locations, and sizes (see Fig. 12).
Figure 7.
An example of liver and spleen automatically segmented from a normal test case. 2D axial slices of the 3D CT data are shown.
Figure 8.
Volume renderings of the segmentation of liver and spleen; (a) is a posterior view and (b) an anterior view. The liver and spleen ground truths are shown in dark colors with automated segmentation errors overlaid in light shades.
Figure 9.
Three examples of segmentations of pathological, enlarged livers with unusual shapes from three different patients.
Figure 10.
Examples from three different patients of segmentations of abnormal, enlarged spleens.
Figure 11.
An example of pathological liver segmentation from the MICCAI data. 2D axial slices of the 3D CT data are shown.
Figure 12.
Three examples of segmentation of livers from cases with partial hepatectomy from three different patients.
DISCUSSION
We presented an automated technique to compute imaging biomarkers (volume and height) from the segmentation of normal and pathological livers and spleens from contrast-enhanced CT scans. Data were obtained from various institutions and scanners and probabilistic models of the liver and spleen were constructed. Organ’s locations were modeled in the physical space and normalized to the position of the xiphoid. The xiphoid is a point of symmetry in the abdomen, but also located close the dome of the liver.
Relating the locations of liver and spleen to an anatomical landmark, the atlases were normalized to a coordinate system with easily found correspondence in patient images. A line or plane would offer better constraints, as it would offer information about patient’s body orientation. However, the location normalization by the xiphoid is followed by further spatial normalization by registration, which accounts for body positioning. Furthermore, by restricting the degrees of freedom in the registration used to construct the atlases and preserving the size of organs, the bias from the reference data was minimized.
The segmentation method involved a combination of enhancement, shape, and location statistics of livers and spleens. For the segmentation of liver and spleen, the initialization of the models was simultaneous, but their segmentation sequential. The spatial constellation of organs was taken into account through the initial registration. The patient specific contrast-enhancement characteristics were estimated and input into an adaptive convolution that preserved only homogenous tissue areas that satisfied the enhancement constraints of the liver∕spleen. Additionally, the shape and location information from the normalized probabilistic atlases were utilized to improve the accuracy of the segmentation. The results demonstrated the ability of the technique to segment normal and abnormal livers and spleens with a precision comparable to the interobserver variability and errors close to the voxel size.
While nonlinear registration and geodesic active contours were used before for segmenting the liver, our paper proposed additional case-specific enhancement, shape, and location corrections. The improvement brought by the adaptive convolution using enhancement estimation was significant when compared to the atlas-based segmentation. We found that using shape information from a normalized probabilistic atlas in the training set improved significantly (p<0.05) only the liver volume estimations. This may be explained partly by the small sample of cases used to construct the atlas, which was used to initiate the segmentation and offered constraints to the model, but did not offer sufficient information for active shape∕appearance models. However, the robustness of the method is mainly owed to the adaptive enhancement estimation, which rejected segmentation outliers by adjusting the parameters to patient specific information. The technique performed robustly on 277 CT scans combining normal and pathological cases (enlarged livers and spleens, partial hepatectomy, and liver tumors) with large morphological changes acquired on a variety of CT scanners.
The global affine registration between the new CT and the reference CT was important to detect the position of the organs [Fig. 4a]. An alternative global nonlinear registration between the CTs was inaccurate due to the high interpatient abdominal variability. However, using a subsequent nonlinear registration between the mean organ models and the patient CT, a first stage of organ segmentation was achieved, as seen in Fig. 4b. However, the segmentation by registration struggled at faint boundaries between liver and adjacent organs, e.g., IVC, kidneys, pancreas, and heart. The organ segmentation was improved with the addition of enhancement and shape constraints [Figs. 4c, 4d].
During the first steps of the validation of the method, we conducted an analysis on the improvement obtained after the nonlinear registration step (see Fig. 2) by using a liver atlas over a single liver model, as well as by using contrast-enhanced CT over noncontrast CT. We found an improvement of 5%∕5.8% DC∕VO and 2 mm RMSE when contrast agent was used. Using a liver atlas over a single liver model improved the segmentation results by 4.4%∕4.5% DC∕VO and 2.3 mm RMSE.
A common difficulty for computer-aided liver segmentation is the erroneous inclusion of heart volumes, which our method robustly avoided. Additional challenges come from the partial enhancement of the IVC and its contact with the liver tissue. Although the IVC was not incorporated in the liver segmentation in the majority of cases, parts of the vein may be erroneously segmented in the midcephalocaudal hepatic region when contrast enhancement is low. This issue is apparent in many liver segmentation methods including recent publications.28, 31, 71
The outliers in Fig. 5 are attributed partially to undersegmentation by our method, but mainly to partial volume effects in images of low resolution, and the estimation of the position of MHL between observers. As expected, segmentation results were more accurate on data with high spatial resolution, although results suggest that the computation of liver imaging biomarkers using the proposed method are not significantly influenced by image resolution.
Table 5 presents a comparison to other studies for the automated liver segmentation that performed similar validations. Note that only certain metrics were available in other publications and different databases were used to generate results. While we report results on the entire test set, other authors preferred to exclude outliers, i.e., Refs. 26, 28, 29. In the case of Ref. 24, the results are approximated from boxplots.
Table 5.
Comparative results for the liver segmentation (in alphabetical order of authors). Columns present the DC, VO, VER, RMSE, and ASD.
| DC (%) | VO (%) | VER (%) | RMSE (mm) | ASD (mm) | |
|---|---|---|---|---|---|
| Our method | 96.2±0.6 | 92.7±1.1 | 2.2±2.1 | 2.3±0.5 | 1.2±0.2 |
| Campadelli et al.a | 95.2±1.2 | N∕A | N∕A | N∕A | N∕A |
| Florin et al.b | 91.6 | N∕A | >3 | >3.5 | 3 |
| Freiman et al.c | N∕A | 91.4 | 2.7 | 2.9 | 1.4 |
| Heimann et al.d | 94.9±1.4 | N∕A | N∕A | 3.3±1.2 | 1.6±0.5 |
| Kainmüller et al.e | N∕A | 93 | 3.6 | 2.3 | 1.1 |
| Ling et al.f | N∕A | N∕A | N∕A | N∕A | 1.5±0.5 |
| Massoptier and Casciarog | 94.2±1.1 | N∕A | N∕A | N∕A | 3.7±1.8 |
| Okada et al.h | N∕A | 89.2±1.4 | N∕A | N∕A | 1.3±0.2 |
| Rusko et al.i | N∕A | 89.3 | 4.3 | 3.8 | 1.8 |
| Schmidt et al.j | N∕A | 83.8 | 5 | 5.4 | 2.8 |
| Soler et al.k | N∕A | N∕A | N∕A | N∕A | 2 |
The most straightforward comparison would be with the methods from the MICCAI 2007 competition, although our method was trained on an independent database and tested on the MICCAI training set, while the papers in the competition were trained on the MICCAI training set and tested on a data set available to the participants to the competition. This makes our results indirectly comparable to those of the MICCAI competition, but this comparison provides a flavor of how well our technique performed. Comparative analyses on the results obtained by the 16 teams competing for the MICCAI 2007 Grand Challenge were published in Ref. 58. The best overall scores for automated methods on a combination of metrics including VO, ASD, RMSE, and VER at the on-site competition were achieved by Kainmüller et al.62 with 68 points, which was placed first in the competition, Rusko et al.63 with 57 points, and Schmidt et al.64 with 50 points. Our algorithm achieved a score of 69 on the MICCAI data using the validation tools provided by the organizers of the MICCAI competition. Three interactive segmentation methods had higher scores, but required different levels of user intervention: Dawant et al.60 (75 points), Beck and Aurich59 (73 points), and Lee et al.61 (70 points). We are not aware of any equivalent comparisons being performed for spleen segmentation methods.
The segmentation of the spleen has been seldom addressed in medical imaging. However, the morphological analysis of the spleen is as important as that of the liver for diagnosis. While the segmentation of the spleen may be less challenging than that of the liver, it can still suffer from errors induced by adjacent organs, partial volume effects and variations in contrast in-take during enhancement. The proposed method is robust in addressing the segmentation of both liver and spleen.
Indeed, there are very few metrics reported for the automated segmentation of the spleen. Seifert et al.71 obtained 2.1±0.5 ASD, Zhang et al.65 reported a coincidence ratio of 96% and an average error rate of 4.3%, while Sakashita et al.70 segmented the spleen with a recall ratio of 73.2%. Table 3 presents the validation metrics using our technique to segment the spleen. In our data, we noted that few cases of splenomegaly presented segmentation errors in the vicinity of intestines, as enlarged spleens pushed against the bowels. Besides oversegmentation, the outliers in Fig. 6 were mainly attributed to partial volume effects in images of low resolution and cases with partial enhancement of the spleen during image acquisition. The results suggest that the computation of spleen imaging biomarkers may be influenced by image resolution. However, differences were small and probably not clinically meaningful.
Over the course of the study, the livers and spleens were quantified as 3D objects to assess both their heights and volumes. In general, radiologists exclusively rely on liver and spleen 2D height measurements from projection images in their examination for abnormalities.12 Due to the lengthy time required for manual segmentations of abdominal organs, the volumes are disregarded and at most approximated. Thus, there is the risk to misrepresent organ sizes and shapes and misread spleen and liver examinations. Our automated technique has the potential to offer complementary imaging biomarkers to assist and improve the diagnosis.
With the development of probabilistic organ models, the analysis of abdominal atlases could provide information about anatomy and intersubject variability for computer-aided diagnosis and modeling of normal and abnormal soft tissue. For instance, the segmentation of liver lobes would provide hierarchical models of the organ and be extremely useful for liver interventions and diagnosis. However, large numbers of cases are required to cover population variability. Future work will also investigate the use of imaging biomarkers to establish diagnosis criteria for the detection of hepatomegaly and splenomegaly and will address additional challenges from a variety of abdominal pathologies. We anticipate having our method used in routine clinical investigations in the near future.
CONCLUSION
The normalized probabilistic atlases of the liver and spleen were constructed and used in the automated computation of imaging biomarkers from the segmentation of the liver and spleen from contrast-enhanced CT images. In addition to the mean organ model registration and use of a geodesic active contour, our method introduced important new steps: (i) The contrast enhancements of liver and spleen were estimated to adjust to patient image characteristics, and an adaptive convolution refined the segmentations, and (ii) the normalized probabilistic atlases corrected for organ shape and location. For the robust validation of the technique, data were acquired on a variety of scanners and consisted of a combination of normal and pathological cases. Automatically segmented livers∕spleens from testing data sets had an average Dice coefficient of 96.2%∕95.2% and volume overlap of 92.7%∕91%. The computed midhepatic liver height and cephalocaudal spleen height showed very high correlations (0.93∕0.97 for liver∕spleen) with manual measurements of organ’s heights from 277 clinical cases. Imaging biomarkers of the liver and spleen from automated computer-assisted tools have the potential to assist the diagnosis of abdominal disorders from routine analysis of clinical data.
ACKNOWLEDGMENTS
This work was supported by the Intramural Research Program of the National Institutes of Health, Clinical Center. The authors would like to thank See Chin and John A. Pura for helping with the manual segmentation.
References
- Ellert J. and Kreel L., “The role of computed tomography in the initial staging and subsequent management of the lymphomas,” J. Comput. Assist. Tomogr. 4(3), 368–391 (1980). 10.1097/00004728-198006000-00014 [DOI] [PubMed] [Google Scholar]
- Okamoto E. et al. , “Prediction of the safe limits of hepatectomy by combined volumetric and functional measurements in patients with impaired hepatic function,” Surgery (St. Louis) 95(5), 586–592 (1984). [PubMed] [Google Scholar]
- Zoli M. et al. , “Prognostic indicators in compensated cirrhosis,” Am. J. Gastroenterol. 86(10), 1508–1513 (1991). [PubMed] [Google Scholar]
- Soyer P. et al. , “Hepatic metastases from colorectal cancer: Influence of hepatic volumetric analysis on surgical decision making,” Radiology 184(3), 695–697 (1992). [DOI] [PubMed] [Google Scholar]
- Sekiyama K. et al. , “Prognostic value of hepatic volumetry in fulminant hepatic failure,” Dig. Dis. Sci. 39(2), 240–244 (1994). 10.1007/BF02090192 [DOI] [PubMed] [Google Scholar]
- Elstein D. et al. , “Accuracy of ultrasonography in assessing spleen and liver size in patients with Gaucher disease: Comparison to computed tomographic measurements,” J. Ultrasound Med. 16 (3), 209–211 (1997). [DOI] [PubMed] [Google Scholar]
- Tsushima Y. and Endo K., “Spleen enlargement in patients with nonalco-holic fatty liver: Correlation between degree of fatty infiltration in liver and size of spleen,” Dig. Dis. Sci. 45(1), 196–200 (2000). 10.1023/A:1005446418589 [DOI] [PubMed] [Google Scholar]
- Broering D. C., Sterneck M., and Rogiers X., “Living donor liver transplantation,” J. Hepatol. 38, 119–135 (2003). 10.1016/S0168-8278(03)00009-6 [DOI] [PubMed] [Google Scholar]
- Kawasaki S. et al. , “Preoperative measurement of segmental liver volume of donors for living related liver transplantation,” Hepatology 18(5), 1115–1120 (1993). 10.1002/hep.1840180516 [DOI] [PubMed] [Google Scholar]
- Sugarbaker P. H., “Surgical decision making for large bowel cancer metastatic to the liver,” Radiology 174(3), 621–626 (1990). [DOI] [PubMed] [Google Scholar]
- Cools L. et al. , “Prediction of splenic volume by a simple CT measurement: A statistical study,” J. Comput. Assist. Tomogr. 7(3), 426–430 (1983). 10.1097/00004728-198306000-00007 [DOI] [PubMed] [Google Scholar]
- Rosenfield A. T. and Schneider P. B., “Rapid evaluation of hepatic size on radioisotope scan,” J. Nucl. Med. 15(4), 237–240 (1974). [PubMed] [Google Scholar]
- Gosink B. B. and Leymaster C. E., “Ultrasonic determination of hepatomegaly,” J. Clin. Ultrasound 9(1), 37–41 (1981). 10.1002/jcu.1870090110 [DOI] [PubMed] [Google Scholar]
- Bezerra A. S. et al. , “Determination of splenomegaly by CT: Is there a place for a single measurement?,” AJR, Am. J. Roentgenol. 184(5), 1510–1513 (2005). [DOI] [PubMed] [Google Scholar]
- Koga T. and Morikawa Y., “Ultrasonographic determination of the splenic size and its clinical usefulness in various liver diseases,” Radiology 115(1), 157–161 (1975). [DOI] [PubMed] [Google Scholar]
- Niederau C. et al. , “Sonographic measurements of the normal liver, spleen, pancreas, and portal vein,” Radiology 149(2), 537–540 (1983). [DOI] [PubMed] [Google Scholar]
- McAfee J. G., Ause R. G., and H. N.Wagner, Jr., “Diagnostic value of scintillation scanning of the liver,” Arch. Intern Med. 116, 95–110 (1965). [DOI] [PubMed] [Google Scholar]
- Hausken T. et al. , “Estimation of the human liver volume and configuration using three-dimensional ultrasonography: Effect of a high-caloric liquid meal,” Ultrasound Med. Biol. 24(9), 1357–1367 (1998). 10.1016/S0301-5629(98)00120-3 [DOI] [PubMed] [Google Scholar]
- Andersen V. et al. , “The volume of the liver in patients correlates to body weight and alcohol consumption,” Alcohol Alcohol 35(5), 531–532 (2000). 10.1093/alcalc/35.5.531 [DOI] [PubMed] [Google Scholar]
- Sandrasegaran K. et al. , “Measurement of liver volume using spiral CT and the curved line and cubic spline algorithms: Reproducibility and interobserver variation,” Abdom. Imaging 24(1), 61–65 (1999). 10.1007/s002619900441 [DOI] [PubMed] [Google Scholar]
- Henderson J. M. et al. , “Measurement of liver and spleen volume by computed tomography. Assessment of reproducibility and changes found following a selective distal splenorenal shunt,” Radiology 141(2), 525–527 (1981). [DOI] [PubMed] [Google Scholar]
- Heymsfield S. B. et al. , “Accurate measurement of liver, kidney, and spleen volume and mass by computerized axial tomography,” Ann. Intern Med. 90(2), 185–187 (1979). [DOI] [PubMed] [Google Scholar]
- Karssemeijer N., “A statistical method for automatic labeling of tissues in medical images,” Mach. Vision Appl. 3(2), 75–86 (1990). 10.1007/BF01212192 [DOI] [Google Scholar]
- Florin C. et al. , “Liver segmentation using sparse 3D prior models with optimal data support,” Proc. Inf. Process. Med. Imaging 4584, 38–49 (2007). 10.1007/978-3-540-73273-0_4 [DOI] [PubMed] [Google Scholar]
- Seghers D. et al. , “Model-based segmentation using graph representations,” Proc. Med. Image Comput. Comput. Assist. Interv. 11, 393–400 (2008). [DOI] [PubMed] [Google Scholar]
- Heimann T. et al. , “A shape-guided deformable model with evolutionary algorithm initialization for 3D soft tissue segmentation,” Proc. Inf. Process. Med. Imaging 4584, 1–12 (2007). 10.1007/978-3-540-73273-0_1 [DOI] [PubMed] [Google Scholar]
- Freiman M. et al. , “A Bayesian approach for liver analysis: Algorithm and validation study,” Proc. Med. Image Comput. Comput. Assist. Interv. 11, 85–92 (2008). [DOI] [PubMed] [Google Scholar]
- Ling H.et al. , “Hierarchical, learning-based automatic liver segmentation,” Proceedings of the 26th IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Anchorage, AK, 2008, 1–8.
- Soler L. et al. , “Fully automatic anatomical, pathological, and functional segmentation from CT scans for hepatic surgery,” Comput. Aided Surg. 6(3), 131–142 (2001). 10.3109/10929080109145999 [DOI] [PubMed] [Google Scholar]
- Massoptier L. and Casciaro S., “A new fully automatic and robust algorithm for fast segmentation of liver tissue and tumors from CT scans,” Eur. Radiol. 18(8), 1658–1665 (2008). 10.1007/s00330-008-0924-y [DOI] [PubMed] [Google Scholar]
- Okada T. et al. , “Automated segmentation of the liver from 3D CT images using probabilistic atlas and multilevel statistical shape model,” Acad. Radiol. 15(11), 1390–1403 (2008). 10.1016/j.acra.2008.07.008 [DOI] [PubMed] [Google Scholar]
- Campadelli P., Casiraghi E., and Esposito A., “Liver segmentation from computed tomography scans: A survey and a new algorithm,” Artif. Intell. Med. 45(2), 185–196 (2009). 10.1016/j.artmed.2008.07.020 [DOI] [PubMed] [Google Scholar]
- Frericks B. B. et al. , “3D CT modeling of hepatic vessel architecture and volume calculation in living donated liver transplantation,” Eur. Radiol. 14(2), 326–333 (2004). 10.1007/s00330-003-2161-8 [DOI] [PubMed] [Google Scholar]
- Hermoye L. et al. , “Liver segmentation in living liver transplant donors: Comparison of semiautomatic and manual methods,” Radiology 234(1), 171–178 (2005). 10.1148/radiol.2341031801 [DOI] [PubMed] [Google Scholar]
- Schenk A., Prause G., and Peitgen H. O., “Efficient semiautomatic segmentation of 3D objects in medical images,” Proceedings of Med. Image. Comput. Comput. Assist. Interv., 2000, Vol. 1935, pp. 186–195.
- Schenk A., Prause G., and Peitgen H. O., “Local cost computation for efficient segmentation of 3D objects with live wire,” Proc. SPIE 4322, 1357–1364 (2001). 10.1117/12.431015 [DOI] [Google Scholar]
- Bae K. T. et al. , “Automatic segmentation of liver structure in CT images,” Med. Phys. 20(1), 71–78 (1993). 10.1118/1.597064 [DOI] [PubMed] [Google Scholar]
- Gao L. et al. , “Automatic liver segmentation technique for three-dimensional visualization of CT data,” Radiology 201(2), 359–364 (1996). [DOI] [PubMed] [Google Scholar]
- Fujimoto H., Gu L., and Kaneko T., “Recognition of abdominal organs using 3D mathematical morphology,” Syst. Comput. Japan 33(8), 75–83 (2002). 10.1002/scj.1148 [DOI] [Google Scholar]
- Kobashi M. and Shapiro L. G., “Knowledge-based organ identification from CT images,” Pattern Recogn. 28(4), 475–491 (1995). 10.1016/0031-3203(94)00124-5 [DOI] [Google Scholar]
- Lim S. J. et al. , “Automatic segmentation of the liver in CT images using the watershed algorithm based on morphological filtering,” Proc. SPIE 5370, 1658–1666 (2004). 10.1117/12.533586 [DOI] [Google Scholar]
- Lim S. J., Jeong Y. Y., and Ho Y. S., “Segmentation of the liver using the deformable contour method on CT images,” Lect. Notes Comput. Sci. 3767, 570–581 (2005). 10.1007/11581772_50 [DOI] [Google Scholar]
- Lim S. J., Jeong Y. Y., and Ho Y. S., “Automatic liver segmentation for volume measurement in CT images,” J. Visual Commun. Image Represent 17(4), 860–875 (2006). 10.1016/j.jvcir.2005.07.001 [DOI] [Google Scholar]
- Liu F. et al. , “Liver segmentation for CT images using GVF snake,” Med. Phys. 32(12), 3699–3706 (2005). 10.1118/1.2132573 [DOI] [PubMed] [Google Scholar]
- Koss J. E. et al. , “Abdominal organ segmentation using texture transforms and a Hopfield neural network,” IEEE Trans. Med. Imaging 18(7), 640–648 (1999). 10.1109/42.790463 [DOI] [PubMed] [Google Scholar]
- Lee C. C. and Chung P. C., “Recognizing abdominal organs in CT images using contextual neural network and fuzzy rules,” Proceedings of the 22th Annual EMBS International Conference, 2000, pp. 1745–1748.
- Lee C. C., Chung P. C., and Tsai H. M., “Identifying multiple abdominal organs from CT image series using a multimodule contextual neural network and spatial fuzzy rules,” IEEE Trans. Inf. Technol. Biomed. 7, 208–217 (2003). 10.1109/TITB.2003.813795 [DOI] [PubMed] [Google Scholar]
- Tsai D. -Y. and Tanahashi N., “Neural-network-based boundary detection of liver structure in CT images for 3-D visualization,” IEEE International Conference on Neural Networks—Conference Proceedings, 1994, Vol. 6, pp. 3484–3489.
- Gao L., Heath D. G., and Fishman E. K., “Abdominal image segmentation using three-dimensional deformable models,” Invest. Radiol. 33(6), 348–355 (1998). 10.1097/00004424-199806000-00006 [DOI] [PubMed] [Google Scholar]
- Lamecker H., Lange T., and Seebass M., “Segmentation of the liver using a 3D statistical shape model,” ZIB Report No. 04–09, April 2004, pp. 1–25.
- Montagnat J. and Delingette H., “Volumetric medical images segmentation using shape contrained deformable models,” Proceedings of CVRMed-MRCAS (Springer, 1996);; [ Lect. Notes Comput. Sci. 1205, 13–22 (1997)]. 10.1007/BFb0029220 [DOI] [Google Scholar]
- Pan S. and Dawant B. M., “Automatic 3D segmentation of the liver from abdominal CT images: A level-set approach,” Proc. SPIE 4322(1), 128–138 (2001). 10.1117/12.431019 [DOI] [Google Scholar]
- Boes J., Weymouth T., and Meyer C., “Multiple organ definition in CT using a Bayesian approach for 3D model fitting,” Proc. SPIE 2573, 244–251 (1995). 10.1117/12.216418 [DOI] [Google Scholar]
- Hyunjin P., Bland P. H., and Meyer C. R., “Construction of an abdominal probabilistic atlas and its application in segmentation,” IEEE Trans. Med. Imaging 22(4), 483–492 (2003). 10.1109/TMI.2003.809139 [DOI] [PubMed] [Google Scholar]
- Shimizu A. et al. , “Multi-organ segmentation in three dimensional abdominal CT images,” Int. J. Computer Assisted Radiology and Surgery 1, 76–78 (2006). [Google Scholar]
- Zhou X. et al. , “Construction of a probabilistic atlas for automated liver segmentation in non-contrast torso CT images,” Int. Congr. Ser. 1281, 1169–1174 (2005). 10.1016/j.ics.2005.03.079 [DOI] [Google Scholar]
- van Ginneken B., Heimann T., and Styner M., “MICCAI workshop on 3D Segmentation in the Clinic: A grand challenge,” MICCAI Workshop on 3D Segmentation in the Clinic: A Grand Challenge, 2007, 7–15.
- Heimann T. et al. , “Comparison and evaluation of methods for liver segmentation from CT datasets,” IEEE Trans. Med. Imaging 28(8), 1251–1265 (2009). 10.1109/TMI.2009.2013851 [DOI] [PubMed] [Google Scholar]
- Beck A. and Aurich V., “HepaTux—A semiautomatic liver segmentation system,” MICCAI Workshop on 3D Segmentation in the Clinic: A Grand Challenge, 2007, 225–233.
- Dawant B. M.et al. , “Semi-automatic segmentation of the liver and its evaluation on the MICCAI 2007 grand challenge data set,” MICCAI Workshop on 3D Segmentation in the Clinic: A Grand Challenge, 2007, 215–221.
- Lee J. et al. , “Efficient liver segmentation using a level-set method with optimal detection of the initial liver boundary from level-set speed images,” Comput. Methods Programs Biomed. 88, 26–38 (2007). 10.1016/j.cmpb.2007.07.005 [DOI] [PubMed] [Google Scholar]
- Kainmüller D., Lange T., and Lamecker H., “Shape constrained automatic segmentation of the liver based on a heuristic intensity model,” MICCAI Workshop on 3D Segmentation in the Clinic: A Grand Challenge, 2007, 109–116.
- Rusko L.et al. , “Fully automatic liver segmentation for contrast-enhanced CT images,” MICCAI Workshop on 3D Segmentation in the Clinic: A Grand Challenge, 2007, 143–150.
- Schmidt G.et al. , “Cognition network technology for a fully automated 3D segmentation of the liver,” MICCAI Workshop on 3D Segmentation in the Clinic: A Grand Challenge, 2007, 125–133.
- Zhang X.et al. , “A novel method for extraction of spleen by using thin-plate splines (TPS) deformation and edge detection from abdominal CT images,”Proceedings of BMEI, 2008, Vol. 1, 830–834.
- Price J. R., Aykac D., and Wall J., “A 3D level sets method for segmenting the mouse spleen and follicles in volumetric microCT images,” Conference Proceedings of IEEE Engineering in Medicine and Biology Society, 2006, Vol. 1, pp. 2332–2336. [DOI] [PubMed]
- Yao C. et al. , “Simultaneous location detection of multi-organ by atlas-guided eigen-organ method in volumetric medical images,” Int J CARS 1, 42–45 (2006). [Google Scholar]
- Linguraru M. G. and Summers R. M., “Multi-organ segmentation in 4D contrast-enhanced abdominal CT,” IEEE Symposium on Biomedical Imaging 2008 (ISBI), 2008, 45–48.
- Hu X. B.et al. , “Independent component analysis of four-phase abdominal CT images,” Medical Image Computing and Computer-Assisted Intervention—Proceedings of MICCAI, 2004, Vol. 3217, pp. 916–924.
- Sakashita M. et al. , “A method for extracting multi-organ from four-phase contrasted CT images based on CT value distribution estimation using EM-algorithm,” Proc. SPIE 6509, 65141C.1–65141C.12 (2007). 10.1117/12.709232 [DOI] [Google Scholar]
- Seifert S. et al. , “Hierarchical parsing and semantic navigation of full body CT data,” Proc. SPIE 7259, 725902-1–8 (2009). 10.1117/12.812214 [DOI] [Google Scholar]
- Farraher S. W. et al. , “Liver and spleen volumetry with quantitative MR imaging and dual-space clustering segmentation,” Radiology 237, 322–328 (2005). 10.1148/radiol.2371041416 [DOI] [PubMed] [Google Scholar]
- Joshi S. et al. , “Unbiased diffeomorphic atlas construction for computational anatomy,” Neuroimage 23, S151–S160 (2004). 10.1016/j.neuroimage.2004.07.068 [DOI] [PubMed] [Google Scholar]
- Mazziotta J. et al. , “A probabilistic atlas and reference system for the human brain: International consortium for brain mapping (ICBM),” Philos. Trans. R. Soc. London, Ser. B 356, 1293–1322 (2001). 10.1098/rstb.2001.0915 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson P. M. et al. , “Mathematical∕computational challenges in creating deformable and probabilistic atlases of the human brain,” Hum. Brain Mapp. 9, 81–92 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peyrat J. M. et al. , “A computational framework for the statistical analysis of cardiac diffusion tensors: Application to a small database of canine hearts,” IEEE Trans. Med. Imaging 26, 1500–1514 (2007). 10.1109/TMI.2007.907286 [DOI] [PubMed] [Google Scholar]
- Lorenzo-Valdés M. et al. , “Segmentation of 4D cardiac MR images using a probabilistic atlas and the EM algorithm,” Med. Image Anal. 8, 255–265 (2004). 10.1016/j.media.2004.06.005 [DOI] [PubMed] [Google Scholar]
- Okada T. et al. , “Construction of hierarchical multi-organ statistical atlases and their application to multi-organ segmentation from CT images,” Proc. Med. Image Comput. Comput. Assist. Interv. 5242, 502–509 (2008). [DOI] [PubMed] [Google Scholar]
- Studholme C., Hill D. L. G., and Hawkes D. J., “An overlap invariant entropy measure of 3D medical image alignment,” Pattern Recogn. 32, 71–86 (1999). 10.1016/S0031-3203(98)00091-0 [DOI] [Google Scholar]
- Perona P. and Malik J., “Scale-space and edge-detection using anisotropic diffusion,” IEEE Trans. Pattern Anal. Mach. Intell. 12, 629–639 (1990). 10.1109/34.56205 [DOI] [Google Scholar]
- Rueckert D. et al. , “Nonrigid registration using free-form deformations: Application to breast MR images,” IEEE Trans. Med. Imaging 18, 712–721 (1999). 10.1109/42.796284 [DOI] [PubMed] [Google Scholar]
- Caselles V., Kimmel R., and Sapiro G., “Geodesic active contours,” Int. J. Comput. Vis. 22, 61–79 (1997). 10.1023/A:1007979827043 [DOI] [Google Scholar]
- Goshima S. et al. , “Multi-detector row CT of the kidney: Optimizing scan delays for bolus tracking techniques of arterial, corticomedullary, and nephrographic phases,” Eur. J. Radiol. 63, 420–426 (2007). 10.1016/j.ejrad.2007.02.005 [DOI] [PubMed] [Google Scholar]
- Bland J. M. and Altman D. G., “Statistical methods for assessing agreement between two methods of clinical measurement,” Lancet 8476, 307–310 (1986). [PubMed] [Google Scholar]