Abstract
Purpose: Low wall shear stress (WSS) and high oscillatory shear index (OSI) influence plaque formation, yet little is known about their role in progression∕regression of established plaques because of lack of practical means to calculate them in individual patients. Our aim was to use computational fluid dynamics (CFD) models of patients with carotid plaque undergoing statin treatment to calculate WSS and OSI in a time-efficient manner, and determine their relationship to plaque thickness (PT), plaque composition (PC), and regression.
Methods: Eight patients (68±9 yr, one female) underwent multicontrast 3 T MRI at baseline and six-month post statin treatment. PT and PC were measured in carotid segments (common–CC, bifurcation–B, internal–IC) and circumferentially in nonoverlapping 60° angles and correlated with CFD models created from MRI, ultrasound, and blood pressure.
Results: PT was highest in B (2.42±0.98 versus CC: 1.60±0.47, IC: 1.62±0.52 mm, p<0.01). Circumferentially, plaque was greatest opposite the flow divider (p<0.01), where the lowest WSS and highest OSI were observed. In B and IC, PT was inversely related to WSS (R=−0.28 and −0.37, p<0.01) and directly related to OSI (R=0.22 and 0.52, p<0.05). The total plaque volume changed from 1140±437 to 974±587 mm3 at six months (p=0.1). Baseline WSS, but not OSI, correlated with changes in PT, necrotic tissue, and hemorrhage in B and IC, but not CC. CFD modeling took 49±18 h per patient.
Conclusions: PT and PC correspond to adverse WSS and OSI in B and IC, and WSS is modestly but significantly related to changes in PT after short-term statin treatment. Regional hemodynamics from CFD can feasibly augment routine clinical imaging for comprehensive plaque evaluation.
Keywords: stroke, MRI, hemodynamics, computational fluid dynamics, carotid atherosclerosis
INTRODUCTION
Extracranial carotid artery disease is a major risk factor for stroke, the third leading cause of death in the United States. Hemodynamic forces are important in the development of atherosclerosis. Specifically, low time-averaged wall shear stress (WSS), defined as the tangential force per unit area exerted on a blood vessel wall as a result of flowing blood, in the carotid bifurcation are thought to lead to atherogenesis.1 Atherogenesis is also thought to be promoted by high oscillatory shear index (OSI), an index of directional changes in WSS (low OSI indicates the WSS is oriented predominantly in the direction of blood flow, while a value of 0.5 is indicative of bidirectional WSS with a time-average value of zero throughout the cardiac cycle).1 Flow perturbations from plaque buildup subsequently increase WSS leading to endothelial injury, plaque rupture, or thrombogenesis.2, 3 Despite the suggested importance of WSS in atherosclerosis development and plaque rupture,4 no practical time-efficient means of measuring this variable exists in a clinical setting. Furthermore, we know little about the relationship of regional WSS and OSI in plaque regression in vessels with established plaque during statin treatment since plaque luminal protrusion and developing luminal stenosis can alter WSS distributions. Finally, the relationship between WSS and the change in specific plaque components, important in plaque vulnerability to rupture, is also not well known.
Computational fluid dynamics (CFD) is a tool to study hemodynamics by creating vascular representations (models) from imaging data. For CFD simulations to be useful, they should replicate blood flow, vascular geometry, blood pressure, and wall motion obtained clinically to provide WSS indices that attempt to closely approximate reality. The process must be time-efficient and should provide information beyond structural and flow data that can be obtained from conventional imaging. Although important advances have been made, many carotid artery CFD studies still contain potential limitations in these areas that may limit practical use including rigid walls,5, 6, 7, 8 boundary conditions that are physiologically limiting,9, 10 or idealized geometries.11, 12, 13 For example, resistance through the carotid arteries is not only determined by regional vascular disease dictating local geometry, but often to a greater extent by the resistance at the level of the downstream vasculature. Therefore, one desirable way to implement outlet boundary conditions is to couple the CFD model with a representation of the downstream vessels that is known from clinical measurements, and may therefore allow for predictive analysis as compared to methods that impose pressure or flow waveforms at the inlet and outlet of models. The carotid bifurcation is also one of the vascular regions most frequently studied using CFD. Previous bench-top studies of altered hemodynamics correlated indices of WSS with the localization of plaque at specified spatial locations. Although CFD generates temporal data at millions of precisely known locations throughout a computational representation of the carotid bifurcation, localized WSS indices are rarely reported, especially with respect to the severity and location of plaque as was previously performed using more laborious ex vivo approaches.1
The objectives of this investigation are to: (1) Create patient-specific CFD models from 3 T MRI data to quantify fluid dynamics in patients with mild to moderate carotid plaque; (2) spatially correlate plaque burden and plaque components with regional time-averaged WSS and OSI; (3) quantify changes in plaque burden after six months of statin treatment and relate the changes to fluid dynamics; and (4) conduct the analyses within a clinically reasonable timeframe.
METHODS
Study subjects
Eight consecutive volunteers (68±9 yr, one female) with previously known coronary or cerebrovascular disease and with ≥1.1 mm carotid plaque on Duplex ultrasound, computed tomography, or magnetic resonance imaging were enrolled. Seven of the subjects had <50% stenosis of the carotid arteries by ultrasound criteria,14 while one subject had 50%–70% stenosis by magnetic resonance angiography. Informed consent was obtained from all subjects after IRB approval. Subjects underwent carotid MRI at baseline and following six months of statin treatment. Five patients had initiation or intensification of their statin regimen (three atorvastatin 80 mg∕day, one simvastatin 80 mg∕day, one started atorvastatin 40 mg∕day), while three maintained their regimen (two simvastatin 20 mg∕day and one lovastatin 40 mg∕day).
MRI
Imaging was performed in a 3 T GE scanner (Waukesha, WI) using a four-channel carotid surface coil (Clinical MR Solutions, Brookfield, WI). An oblique sagittal spin echo sequence was obtained on the index carotid artery (the artery with the greater plaque burden) to determine the position of the flow divider, and used for planning of all pulse sequences. Only the index artery was used for analyses. Axial T1, T2, proton density (PD)-weighted spin echo, and time of flight gradient echo pulse sequences (spatial resolution 0.31–0.62×0.31–0.62×2 mm; fields of view chosen were smallest that subject neck size would accommodate without wrap artifact) were performed similar to previous protocols (courtesy of Dr. Chun Yuan and Dr. Vasily Yarnykh, University of Washington).15 Baseline and six-month MRI was performed.
Ultrasound
With ECG gating, the lumen diameter of the common carotid on long axis view during diastole and systole was measured using Philips iE33 ultrasound (L11–3 transducer). These data were utilized to determine parameters necessary to conduct the deformable wall CFD simulations described below.
Quantification of plaque burden and components
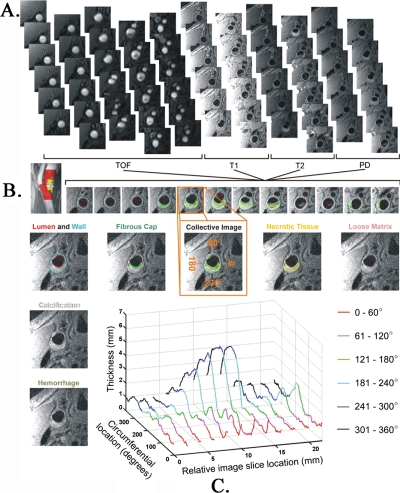
Carotid plaque and plaque components (necrotic tissue, hemorrhage, loose matrix, and calcification) were quantified using MR-PLAQUEVIEW software (VPDiagnostics, Seattle, WA).15 The images were analyzed in random order of subject enrollment as well as baseline or six-month status by an investigator blind to subject and order of scan information. Briefly, the software allows simultaneous viewing of all four multicontrast images of the same slice. Using a semiautomated method with occasional manual adjustment, the lumen and adventitial borders were traced [Fig. 1a]. The software calculated plaque area, thickness, and delineated plaque components based on contrast characteristics using an automatic classifier (morphology-enhanced probabilistic plaque segmentation algorithm).15, 16, 17 This algorithm has been validated at 1.5 T MRI to correlate with histology16 and results at 1.5 T correlated highly with 3 T imaging15, 17 [Fig. 1b]. Corresponding slices were compared between baseline and six months.
Figure 1.
Plaque analysis. (a) Representative TOF, T1, T2, and PD-weighted images. (b) Carotid lumen and wall segments traced (middle row) and plaque components delineated by the software. (c) Lumen thickness as a function of image slice and circumferential location.
The luminal, adventitial, and plaque component tracings were then imported into MATLAB [Fig. 1b]. The spatial location and thickness of the vessel wall and thickness of plaque components (in millimeters) were determined relative to the lumen center [Fig. 1c]. The convention used in the current investigation selected 0° as the most medial point of the carotid artery in a standard axial slice as demonstrated in Fig. 1. Circumferential locations then proceed anterolaterally [viewed caudo-cephalad direction, Figs. 1c, 5c]. Using this convention, an axially oriented line intersecting the carina is typically located at a circumferential location in the vicinity of 90°. For purpose of analyses, six equidistant circumferential regions were selected; the choice of six regions was arbitrary to demonstrate the spatial distribution of plaque, WSS, and OSI.
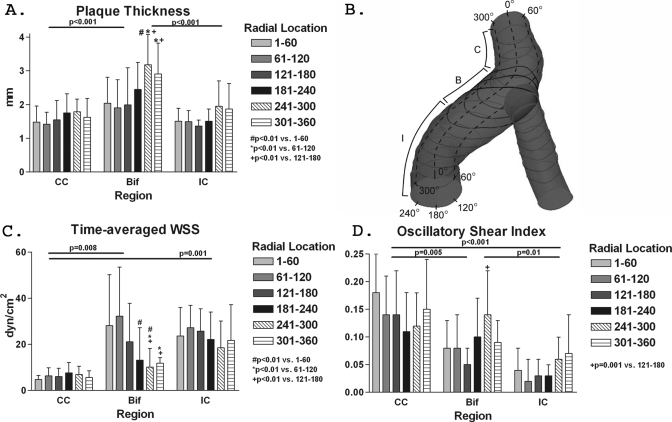
Figure 5.
Regional segmental and circumferential distribution of plaque, WSS, and OSI. There is regional segmental and circumferential variability in (a) plaque thickness, (c) time-averaged WSS, and (d) OSI. In the bifurcation region, the circumferential variability in WSS and OSI closely follows plaque distribution. The regional segmental and circumferential designations are depicted in (b).
Computational model construction
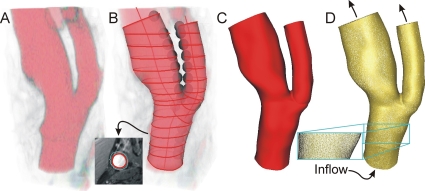
CFD models of the arteries (baseline∕six months) were created from MRI data using CVSIM (Mountain View, CA; Fig. 2), which is based on SIMVASCULAR open-source software.18 Centerline path and vessel segments were extracted from luminal boundaries (T1 images) using MR-PLAQUEVIEW so CFD model results are directly comparable to plaque data.
Figure 2.
CFD modeling. The process involves (a) finding the centerline path, (b) performing segmentation to delineate the wall, (c) connecting these segments to form a representative model, and (d) discretizing the model using an automatic mesh generation program.
Boundary conditions and simulation parameters
A representative inflow waveform from 17 subjects19 was selected and scaled to each subject’s body surface area (BSA) and imposed using a temporally varying Womersley velocity profile. The impact of this assumption was investigated by comparing resulting indices of WSS obtained with this idealized waveform with those obtained from a single patient in whom a patient-specific inflow waveform was available as discussed further in Sec. 3. To replicate the influence of vessels distal to CFD model outlets, three-element Windkessel representations (RcCRd) were imposed at each outlet by coupled multidomain method.20C was selected from the fraction of total arterial compliance accounted for by the carotid arteries21 and scaled to BSA. The Rc:Rd ratio for each outlet was adjusted to match blood pressure using the pulse pressure method.22 Blood flow was distributed between the internal and external carotid arteries (70:30) similar to previous studies.23 Vascular wall displacement was included by assigning physiologic material properties to luminal surface.24 Average wall thickness of each common carotid artery from MRI was implemented and a modulus of elasticity was calculated using the ratio of local wall stress to change in diameter determined from pulse pressure, average wall thickness of each common carotid artery, and change in lumen dimension delineated by ultrasound.
CFD Simulations
CFD simulations were performed with CVSIM, which uses a stabilized finite element method to solve the conservation of mass (continuity), balance of fluid momentum (Navier–Stokes), and vessel wall elastodynamics equations assuming a thin-walled approximation and using a linear membrane formulation enhanced with transverse shear modes as previously discussed by Figueroa et al.24 Meshes utilized adaptive capabilities within the software25, 26 with successively larger meshes until regional differences between WSS were <0.09 dyn∕cm2. Simulations were run on a computing cluster constructed from commercially available components including a Dell Quadcore Xeon 1.86 GHz desktop with 8 GB memory serving as the head node for computing, quantification, and visualization, connected to 12 HP dc7700 computer nodes with Pentium-D 3.4 GHz processors, gigabit Ethernet connections, and 2 GB memory. Simulations were run in succession using all processors and time to complete each step was logged.
Quantification of simulations
WSS and OSI were calculated as previously described.27 WSS and OSI results for the common∕bifurcation∕internal carotid arteries were isolated in the vicinity of each slice and plotted as a function of circumferential location consistent with spatial characterization of plaque components. Circumferential WSS, OSI, plaque thickness, and plaque component thickness results were grouped into six circumferential sections and isolated into common∕bifurcation∕internal carotid segments. The bifurcation segment was designated as the region superior to the common carotid in the vicinity of the carina where the lumen cross-sectional area increased >4% between successive image slices. This region was determined based on visual inspection of time of flight (TOF) volume data prior to CFD simulations and a technique similar to that employed by others,28 whereby the start of the bifurcation region is calculated relative to the distance from the carina and proximal common carotid segments. Slices inferior and superior to the bifurcation were denoted as common and internal carotid segments, respectively.
Statistical analyses
Data are presented as mean±standard deviation. WSS, OSI, and plaque thickness were compared by carotid segment and circumferential location from baseline images using repeated measures analysis of variance (SIGMASTAT 3.5, Systat Software, Richmond, CA). Correlation analyses were performed using Pearson’s (normally distributed data) or Spearman’s method (non-normally distributed data). Total plaque volume at baseline was compared to six months using paired t-test. Significant p-value was p<0.05. Bland–Altman analysis was used to compare regional WSS measured using idealized versus patient-specific carotid flow waveforms where possible.
RESULTS
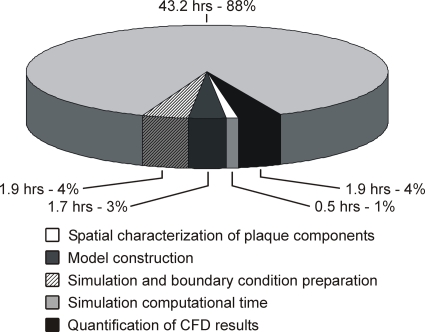
Computational fluid dynamic modeling was completed within 49±18 hr per patient (Fig. 3). Simulation computation was the most time-consuming, but model construction, simulation preparation, and results quantification were more user-intensive, collectively requiring ∼6 hr per patient.
Figure 3.
Simulation timing. Summary of the time required to complete each portion of the simulation process. Values represent averages from 16 simulations conducted on a computing cluster constructed from standard commercially available components.
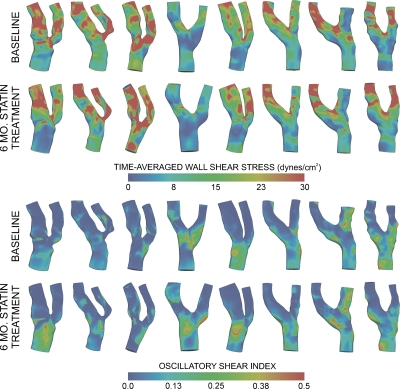
Computed blood flow and pressure values were within 1% of their aimed and clinical values, respectively (data not shown). WSS and OSI in each slice were quantified (Fig. 4). There was significant variation in WSS by segment: Greatest in the internal, least in the common carotid [p<0.01, Fig. 5c]. When all segments are included, WSS also varied by circumferential location: Lowest at 241°–300° and 301°–360° (p<0.01). Taken by segments, circumferential WSS variation was only significant at the bifurcation, but not the common or internal carotid. OSI also varied by segment: Lowest in the internal and highest in the common carotid artery [p<0.01, Fig. 5d]. OSI showed no significant variation by circumferential location overall (p=0.33), but at the bifurcation, OSI at 241°–300° was higher compared to 121°–180° (p=0.001).
Figure 4.
WSS and OSI. Time-averaged wall shear stress (top half) and oscillatory shear index distributions (bottom half) for each patient at baseline and after six months.
Similar to WSS, there was segmental variation in plaque thickness with highest values in the bifurcation [p<0.01, Fig. 5a]. There was regional variation in plaque thickness by circumferential location, with the greatest plaque burden at 241°–300° and 301°–360° (p<0.01). The circumferential variation in plaque thickness was only significant in the bifurcation, but not in the common or internal carotid arteries.
WSS was inversely related to plaque thickness in the bifurcation (R=−0.23, p=0.006) and internal carotid (R=−0.37, p<0.001), but not the common carotid. OSI correlated with plaque thickness in the bifurcation (R=0.22, p=0.04) and internal carotid (R=0.52, p<0.001), but this was not observed in the common carotid region.
At the bifurcation, there was an inverse relationship between WSS and amount (in millimeter thickness) of necrotic tissue, hemorrhage, and loose matrix (R=−0.24,−0.21,−0.33, respectively, all p<0.05), but not calcification. A significant relationship between OSI and amount of necrotic tissue and hemorrhage (R=0.25,0.22, respectively, both p<0.05) was also observed. In the internal carotid, there was an inverse relationship between WSS and necrotic tissue (R=−0.42, p<0.001) and a significant relationship between OSI and necrotic tissue (R=0.41, p<0.001). In the common carotid, there was no relationship between WSS or OSI and plaque components.
Following the six-month statin treatment, total plaque volume changed from 1140±437 (baseline) to 974±587 mm3. Although plaque volume reduced in seven of eight subjects, the difference was not significant (p=0.1). There was no change in WSS and OSI by segment or circumferential location from baseline to six months (Table 1). In the bifurcation and internal carotid, the change in plaque thickness (six-month value minus baseline) was inversely related to baseline WSS (R=−0.5, p<0.001), but not baseline OSI (R=0.13, p=0.24). Baseline WSS was also inversely related to the change in necrotic plaque (R=−0.49, p<0.001) and hemorrhage (R=−0.38, p<0.001) in the bifurcation and internal carotid. In the common carotid, there was no significant relationship between plaque thickness change and WSS (R=0.16, p=0.4) or OSI (R=0.02, p=0.93); similarly, baseline WSS or OSI was not related to the change in plaque components.
Table 1.
Change in plaque thickness, WSS, and OSI at six months.
| Segment | Circumferential location | Delta plaque thickness (mm)a | Delta WSS (dynes∕cm2) a | Delta OSIa | |||
|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | ||
| CC | Overall | 0.12 | 0.47 | 1.21 | 5.10 | 0.01 | 0.09 |
| 1–60 | 0.07 | 0.36 | 1.17 | 3.70 | 0.00 | 0.15 | |
| 61–120 | 0.05 | 0.37 | −0.82 | 4.54 | 0.03 | 0.09 | |
| 121–180 | 0.26 | 0.81 | 1.26 | 7.18 | 0.03 | 0.11 | |
| 181–240 | 0.07 | 0.42 | 1.81 | 7.00 | 0.01 | 0.07 | |
| 241–300 | 0.13 | 0.33 | 1.34 | 2.78 | 0.00 | 0.03 | |
| 301–360 | 0.15 | 0.52 | 2.66 | 4.96 | −0.02 | 0.10 | |
| Bif | Overall | −0.36 | 0.75 | −0.56 | 14.48 | 0.01 | 0.05 |
| 1–60 | −0.10 | 0.23 | −4.77 | 27.44 | −0.01 | 0.06 | |
| 61–120 | −0.37 | 0.95 | −0.96 | 13.50 | 0.01 | 0.05 | |
| 121–180 | −0.39 | 1.21 | −0.12 | 10.51 | 0.02 | 0.05 | |
| 181–240 | −0.25 | 0.70 | −0.61 | 2.65 | 0.02 | 0.06 | |
| 241–300 | −0.48 | 0.49 | 1.57 | 9.55 | 0.03 | 0.05 | |
| 301–360 | −0.55 | 0.72 | 1.50 | 15.26 | −0.01 | 0.05 | |
| IC | Overall | −0.03 | 0.53 | −0.43 | 7.54 | 0.00 | 0.03 |
| 1–60 | −0.09 | 0.34 | −1.73 | 5.38 | 0.00 | 0.03 | |
| 61–120 | −0.02 | 0.19 | −0.52 | 5.54 | −0.01 | 0.01 | |
| 121–180 | 0.07 | 0.34 | 0.43 | 7.36 | 0.00 | 0.02 | |
| 181–240 | −0.12 | 0.37 | 0.67 | 10.10 | 0.00 | 0.01 | |
| 241–300 | −0.03 | 0.81 | 1.41 | 7.34 | 0.00 | 0.04 | |
| 301–360 | 0.01 | 0.93 | −3.19 | 10.18 | 0.00 | 0.06 | |
| All regions | Overall | −0.09 | 0.63 | 0.40 | 10.65 | 0.01 | 0.06 |
| 1–60 | −0.05 | 0.32 | 0.44 | 18.81 | 0.00 | 0.09 | |
| 61–120 | −0.12 | 0.60 | −0.69 | 8.32 | 0.01 | 0.06 | |
| 121–180 | −0.11 | 0.78 | 0.40 | 8.25 | 0.01 | 0.07 | |
| 181–240 | −0.01 | 0.64 | 0.48 | 7.02 | 0.01 | 0.04 | |
| 241–300 | −0.13 | 0.62 | 0.91 | 6.63 | 0.01 | 0.05 | |
| 301–360 | −0.14 | 0.74 | 0.83 | 10.71 | −0.01 | 0.07 | |
Six-month value minus baseline value.
In one patient, carotid flow waveform contours were available from Doppler ultrasound, and regional WSS was calculated using the patient-specific waveforms and compared to WSS calculated using the idealized waveform. By Bland–Altman analysis, the differences in WSS between the two measurements were within 1.97 times the standard deviation of the mean difference at both baseline (96.1% of all observations) and six-month study (95.3% of all observations), signifying that the two methods of measuring WSS in this subject are comparable.
DISCUSSION
We report three novel findings. One, in established carotid atherosclerosis, there is segmental and circumferential regional variation in plaque thickness and plaque component distribution that relate to time-averaged WSS and OSI. Two, regional change in plaque thickness and composition following six months of statin therapy is related to baseline WSS. Further investigations with a larger patient base must be conducted in order to confirm these results. Finally, the construction, simulation, and quantification of vessel wall hemodynamics using image-based CFD models is made feasible within a timeframe useful for augmenting plaque morphology and flow information from routine clinical imaging. Specifically, the entire analysis for a given patient including model creation, establishing boundary conditions, running multiple simulations for four to five cardiac cycles to obtain results largely independent of mesh density, quantifying these results in a spatial manner, and correlating spatial results to local plaque thickness and morphology were all performed in an average of 49 h. It is likely that results could be obtained within a comparable duration by other groups with access to similar commercially available hardware and software as well as postprocessing scripts, highlighting the potential for wide applicability.
Low and oscillating WSS contribute to intima thickening and plaque progression.29 However, progressive lumen narrowing results in elevated WSS.9 The role of WSS in the progression∕regression of established plaque and its relationship to plaque composition is not well-established. Mechanical stresses (tensile and WSS) lead to fissuring and affect macrophage distribution leading to plaque destabilization and rupture.4 Elevated tensile stress exerted on plaque radially from vascular blood pressure or axially by high WSS may be responsible for rupture, but the spatial location of ruptures in the upstream lateral shoulder or midline of fibrous caps indicate that WSS plays an integral role in the process, perhaps through signal transduction pathways affecting plaque components.4
Previous carotid CFD studies describe the contribution of altered fluid dynamics to plaque onset and progression.30, 31, 32 Despite these landmark observations, however, there are limited data on the interplay between regional hemodynamic milieu, pharmacologic intervention, and plaque regression∕progression, pointing to the need for prospective studies utilizing clinical data as inputs to CFD studies.32 Recently, lumen delineated from MRI was used to analyze carotid blood flow with independent and uncoupled 2D structural analyses of stresses imposed on plaque components.9, 33 However, these processes should really be coupled spatiotemporally to assess effects on plaque formation∕rupture. Other studies have applied inlet∕outlet boundary conditions that are physiologically limiting.9, 10 Our technique allows for replication of aimed blood flow, pressure, and wall displacement to increase the likelihood of obtaining physiologic WSS.
Our observations are consistent with previous studies. In this cohort with established carotid disease, plaque thickness was highest in the bifurcation and internal carotid arteries; in these two segments, relative to the common carotid, WSS was higher and OSI was lower consistent with high WSS reported in regions with established plaque and∕or luminal stenosis.9, 27 In addition, our study demonstrated that in carotid segments with significant plaque burden (bifurcation and internal), there is circumferential variation in WSS and OSI with lowest WSS and highest OSI on the side opposite the flow divider where plaque thickness was greatest. As a novel finding, WSS in the bifurcation and internal carotid region at baseline were inversely related to change in plaque thickness (six–month value minus baseline value), necrotic plaque, and hemorrhagic plaque, albeit with modest correlations. These findings may provide some clarity to the current controversy as to whether the low WSS hypothesis may still apply in the progression of intermediate∕advanced plaques. One possible interpretation of our findings is that even when time-averaged WSS is increased in the bifurcation and internal carotid arteries as a result of plaque buildup, regions of relatively low WSS exist, where further plaque progression is more prominent. In addition, similar to findings in coronary arteries, regions in the bifurcation, and internal carotid arteries exposed to high WSS show plaque thickness regression. It is not clear, however, whether regions with low WSS in the bifurcation∕internal carotid that experience plaque progression and an increase in necrotic∕hemorrhagic components are more prone to plaque destabilization∕rupture, or whether areas with high WSS leading to plaque regression are more susceptible in light of the known regressive effect of high WSS on the thin-cap fibroatheroma.4 Moreover, we cannot definitively ascertain as to whether change in plaque burden alters vessel geometry sufficiently to modify WSS, or whether regional distribution WSS causes a modification of local plaque regression. In light of the overall low correlation coefficients, the results need to be validated in a larger series of subjects in order to have greater confidence that the direction of change (positive or negative slope) are really concordant between plaque burden and WSS and not merely due to nonspecific temporal change.
It is not clear why WSS and OSI were not related to plaque thickness and components in the common carotid segment, in contrast to the bifurcation and internal carotid segments. In the common carotid, the WSS circumferential distribution was more uniform whereas it was more heterogeneous in the bifurcation. Prior investigators pointed that maintenance of normal shear stress distribution is an early adaptive response by endothelial cells sensing shear stress, and in a feedback-control loop adapts arterial dimensions to blood flow.4, 34 In areas of bifurcation, this shear stress control is modified at eccentrically located sites to let it remain at low levels in order to maintain normal shear stress distribution. In so doing, in the presence of risk factors for atherosclerosis, these eccentric areas of low shear stress promote eccentric plaque buildup leading initially to outward vessel remodeling. Maintaining normal lumen (and as a result a normal shear stress distribution), therefore, has been implicated in worsening eccentric plaque growth.34 Our results in conjunction with other investigators, therefore, suggest, through mechanisms that are yet to be elucidated, that heterogeneity in WSS circumferential distribution, and not just absolute WSS values, may play a role in plaque development and regression. A significant relationship was also found between low WSS and high OSI with amount of necrotic tissue and hemorrhage in the bifurcation and necrotic tissue in the internal carotid. This is consistent with findings by other investigators that in plaque areas with low WSS, there is associated endothelial cell apoptosis, atherosclerosis progression, lipid oxidation, recruitment of monocytes∕macrophages, and reduction in tissue strength from metalloproteinases degrading collagen and matrix.4, 34, 35, 36, 37, 38 The balance between simultaneously occurring matrix degradation and matrix production by smooth muscle cells4 likely controls the amount of loose matrix, and the regional variation in the balance between these two opposing forces may be responsible for the lack of correlation between WSS∕OSI and loose matrix.
Our results demonstrate that baseline WSS is inversely related to regional change in plaque thickness following six months of statin therapy. This result contrasts with the findings of Wentzel and colleagues,39 wherein they showed that baseline WSS was not related to regional change in plaque thickness in atherosclerotic descending thoracic aorta following two years of statin treatment. The difference in findings may be related to differences in vascular bed studied (aorta versus carotid) or even differences in segment of vascular bed studied. In our study, we show no relationship in WSS and plaque thickness change in the relatively straight common carotid artery but demonstrate a relationship in the bifurcation and internal carotid arteries. Wentzel and colleagues only studied the relatively straight descending thoracic aorta and it is unknown whether similar findings would be found in the aortic arch. The previous study did not report the gradient of differences in circumferential WSS in each segment of the aorta, and it is possible that the WSS role in plaque regression is important only in segments with wide discrepancy in circumferential WSS (such as the bifurcation) and not in segments without much variation (such as the common carotid). In addition, our follow-up is shorter (six months) and the temporal difference may affect arterial and plaque remodeling. Differences relative to the current investigation may also be related to the near-wall distance utilized for WSS calculation as well as our assumptions regarding inflow, branch flow distributions. and uniform material properties.
There are several investigational limitations. We used a representative inflow waveform and branch blood flow distribution as well as a single elastic modulus and average thickness for each CFD model. Although recent reports indicate differences in mean flow introduced by idealized, as compared to measured, flow data have little impact on patterns of TAWSS and disparities introduced by differences in waveform contours are on the order of measurement uncertainty,40, 41, 42 our future work in this area will utilize phase-contrast MRI or Doppler ultrasound to measure flow directly. Future simulations will also work toward incorporating material properties based on regional plaque component variation. While computational time could be reduced substantially with rigid walls, the current work describes a process that has been established to ultimately determine potential mechanisms of a relationship between local mechanotransduction in response to spatiotemporal alterations in WSS indices and the onset and progression of atherosclerosis. Deformable walls, despite the assumptions here, provide a more realistic representation of the simulation and quantification timing that can be expected with this process. Previous studies using similar CFD methods have quantified the impact of geometric variability and reproducibility on subsequent WSS accuracy.31, 41, 43 The accuracy of plaque composition analysis was not assessed in the current investigation, but this method has been validated with histology and has excellent observer reliability.15, 17, 44 A longer duration of follow-up may be helpful in following plaque regression. The differences in field of view and spatial resolution among subjects due to different neck sizes can also potentially affect determination of smaller plaque components whose sizes are close to the limits of spatial resolution of the study. The technique employed for delineating the vascular regions relied on carina location and may therefore be sensitive to image acquisition and reconstruction artifacts. It is possible that region designations may vary by a fraction of the slice thickness employed here, or relative to techniques employed by others to designate vascular regions. The role of statin treatment vis-à-vis regional WSS in affecting change in plaque burden is not well-defined in this study. Because of guideline-based ubiquity of statin treatment in this population group, a placebo group is not feasible; future studies incorporating low and high intensive statin dosing while assessing change in regional WSS and local plaque burden may provide insight into the interactions among these three factors. Plaque measurements were determined for imaging planes that may not necessarily have been orthogonal to the vessel wall. Previous studies have demonstrated how plaque thickness can be overestimated by features including angulation between artery and slice orientation, slice thickness and in-plane resolution. One of these studies45 using voxel dimensions similar to those in the current investigation showed plaque thickness measurements are overestimated mostly due to partial volume errors, but the impact of vessel obliquity can be mitigated with correction by the cosine of the angulation between the vessel and slice. This correction was not performed in the current investigation since the severity of plaque components relative to local thickness was desired and an equivalent correction for plaque components is not trivial due to their often discontinuous nature.
SUMMARY
In summary, circumferential regional variation in WSS and OSI in the carotid bifurcation is associated with complementary variation in plaque burden and baseline WSS in the bifurcation and internal carotid regions are inversely, although modestly, related to the change in plaque thickness and composition. The current results demonstrate that patient-specific CFD models utilizing a commercially available computing hardware and software are feasible and may complement routine clinical imaging for carotid artery disease to better understand the forces leading to plaque rupture and vulnerability.
ACKNOWLEDGMENTS
Funding was provided by Advancing Healthier Wisconsin (Grant No. 5520053), National Institutes of Health MCW GCRC Grant No. M01-RR00058, and NIH T32 HL07702.
References
- Zarins C. K., Giddens D. P., Haradvaj B. K. B., Sottiurai V. S., Mabon R. F., and Glagov S., “Carotid bifurcation atherosclerosis. Quantitative correlation of plaque localization with flow velocity profiles and wall shear stress,” Circ. Res. 53, 502–514 (1983). [DOI] [PubMed] [Google Scholar]
- Holme P. A., Orvim U., Hamers M. J., Solum N. O., Brosstad F. R., Barstad R. M., and Sakariassen K. S., “Shear-induced platelet activation and platelet microparticle formation at blood flow conditions as in arteries with a severe stenosis,” Arterioscler., Thromb., Vasc. Biol. 17, 646–653 (1997). [DOI] [PubMed] [Google Scholar]
- Karino T. and Goldsmith H. L., “Role of blood cell-wall interactions in thrombogenesis and atherogenesis: A microrheological study,” Biorheology 21, 587–601 (1984). [DOI] [PubMed] [Google Scholar]
- Slager C. J., Wentzel J. J., Gijsen F. J., Thury A., van der Wal A. C., Schaar J. A., and Serruys P. W., “The role of shear stress in the destabilization of vulnerable plaques and related therapeutic implications,” Nat. Clin. Pract. Cardiovasc. Med. 2, 456–464 (2005). 10.1038/ncpcardio0298 [DOI] [PubMed] [Google Scholar]
- Birchall D., Zaman A., Hacker J., Davies G., and Mendelow D., “Analysis of haemodynamic disturbance in the atherosclerotic carotid artery using computational fluid dynamics,” Eur. Radiol. 16, 1074–1083 (2006). 10.1007/s00330-005-0048-6 [DOI] [PubMed] [Google Scholar]
- Marshall I., Zhao S., Papathanasopoulou P., Hoskins P., and Xu Y., “MRI and CFD studies of pulsatile flow in healthy and stenosed carotid bifurcation models,” J. Biomech. 37, 679–687 (2004). 10.1016/j.jbiomech.2003.09.032 [DOI] [PubMed] [Google Scholar]
- Ladak H. M., Milner J. S., and Steinman D. A., “Rapid three-dimensional segmentation of the carotid bifurcation from serial MR images,” J. Biomech. Eng. 122, 96–99 (2000). 10.1115/1.429646 [DOI] [PubMed] [Google Scholar]
- Xue Y., Gao P., Lin Y., and Dai C., “Preliminary study of hemodynamics in human carotid bifurcation by computational fluid dynamics combined with magnetic resonance angiography,” Acta Radiol. 48, 788–797 (2007). 10.1080/02841850701408236 [DOI] [PubMed] [Google Scholar]
- Tang D., Yang C., Mondal S., Liu F., Canton G., Hatsukami T. S., and Yuan C., “A negative correlation between human carotid atherosclerotic plaque progression and plaque wall stress: In vivo MRI-based 2D/3D FSI models,” J. Biomech. 41, 727–736 (2008). 10.1016/j.jbiomech.2007.11.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Augst A. D., Ariff B., Mc G. T. S. A., Xu X. Y., and Hughes A. D., “Analysis of complex flow and the relationship between blood pressure, wall shear stress, and intima-media thickness in the human carotid artery,” Am. J. Physiol. Heart Circ. Physiol. 293, H1031–H1037 (2007). 10.1152/ajpheart.00989.2006 [DOI] [PubMed] [Google Scholar]
- Younis H. F., Kaazempur-Mofrad M. R., Chung C., Chan R. C., and Kamm R. D., “Computational analysis of the effects of exercise on hemodynamics in the carotid bifurcation,” Ann. Biomed. Eng. 31, 995–1006 (2003). 10.1114/1.1590661 [DOI] [PubMed] [Google Scholar]
- Tambasco M. and Steinman D. A., “Path-dependent hemodynamics of the stenosed carotid bifurcation,” Ann. Biomed. Eng. 31, 1054–1065 (2003). 10.1114/1.1603257 [DOI] [PubMed] [Google Scholar]
- Zhao S. Z., Xu X. Y., Hughes A. D., Thom S. A., Stanton A. V., Ariff B., and Long Q., “Blood flow and vessel mechanics in a physiologically realistic model of a human carotid arterial bifurcation,” J. Biomech. 33, 975–984 (2000). 10.1016/S0021-9290(00)00043-9 [DOI] [PubMed] [Google Scholar]
- Chang Y. J., Golby A. J., and Albers G. W., “Detection of carotid stenosis. From NASCET results to clinical practice,” Stroke 26, 1325–1328 (1995). [DOI] [PubMed] [Google Scholar]
- Yarnykh V. L., Terashima M., Hayes C. E., Shimakawa A., Takaya N., Nguyen P. K., Brittain J. H., McConnell M. V., and Yuan C., “Multicontrast black-blood MRI of carotid arteries: Comparison between 1.5 and 3 tesla magnetic field strengths,” J. Magn. Reson Imaging 23, 691–698 (2006). 10.1002/jmri.20562 [DOI] [PubMed] [Google Scholar]
- Yuan C., Mitsumori L. M., Ferguson M. S., Polissar N. L., Echelard D., Ortiz G., Small R., Davies J. W., Kerwin W. S., and Hatsukami T. S., “In vivo accuracy of multispectral magnetic resonance imaging for identifying lipid-rich necrotic cores and intraplaque hemorrhage in advanced human carotid plaques,” Circulation 104, 2051–2056 (2001). 10.1161/hc4201.097839 [DOI] [PubMed] [Google Scholar]
- Kerwin W. S., Liu F., Yarnykh V., Underhill H., Oikawa M., Yu W., Hatsukami T. S., and Yuan C., “Signal features of the atherosclerotic plaque at 3.0 tesla versus 1.5 tesla: Impact on automatic classification,” J. Magn. Reson Imaging 28, 987–995 (2008). 10.1002/jmri.21529 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson N., Wang K., Dutton R., and Taylor C. A., “A software framework for creating patient specific geometric models from medical imaging data for simulation based medical planning of vascular surgery,” Lect. Notes Comput. Sci. 2208, 449–456 (2001). [Google Scholar]
- Holdsworth D. W., Norley C. J., Frayne R., Steinman D. A., and Rutt B. K., “Characterization of common carotid artery blood-flow waveforms in normal human subjects,” Physiol. Meas 20, 219–240 (1999). 10.1088/0967-3334/20/3/301 [DOI] [PubMed] [Google Scholar]
- Vignon-Clementel I. E., Figueroa C. A., Jansen K. E., and Taylor C. A., “Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries,” Comput. Methods Appl. Mech. Eng. 195, 3776–3796 (2006). 10.1016/j.cma.2005.04.014 [DOI] [Google Scholar]
- Westerhof N., Bosman F., De Vries C. J., and Noordergraaf A., “Analog studies of the human systemic arterial tree,” J. Biomech. 2, 121–143 (1969). 10.1016/0021-9290(69)90024-4 [DOI] [PubMed] [Google Scholar]
- Stergiopulos N., Segers P., and Westerhof N., “Use of pulse pressure method for estimating total arterial compliance in vivo,” Am. J. Physiol. 276, H424–H428 (1999). [DOI] [PubMed] [Google Scholar]
- Thomas J. B., Milner J. S., Rutt B. K., and Steinman D. A., “Reproducibility of image-based computational fluid dynamics models of the human carotid bifurcation,” Ann. Biomed. Eng. 31, 132–141 (2003). 10.1114/1.1540102 [DOI] [PubMed] [Google Scholar]
- Figueroa C. A., Vignon-Clementel I. E., Jansen K. E., Hughes T. J. R., and Taylor C. A., “A coupled momentum method for modeling blood flow in three-dimensional deformable arteries,” Comput. Methods Appl. Mech. Eng. 195, 5685–5706 (2006). 10.1016/j.cma.2005.11.011 [DOI] [Google Scholar]
- Müller J., Sahni O., Li X., Jansen K. E., Shephard M. S., and Taylor C. A., “Anisotropic adaptive finite element method for modeling blood flow,” Comput. Methods Biomech. Biomed. Eng. 8, 295–305 (2005). 10.1080/10255840500264742 [DOI] [PubMed] [Google Scholar]
- Sahni O., Muller J., Jansen K. E., Shephard M. S., and Taylor C. A., “Efficient anisotropic adaptive discretization of the cardiovascular system,” Comput. Methods Biomech. Biomed. Eng. 195, 5634–5655 (2006). [Google Scholar]
- Tang B. T., Cheng C. P., Draney M. T., Wilson N. M., Tsao P. S., Herfkens R. J., and Taylor C. A., “Abdominal aortic hemodynamics in young healthy adults at rest and during lower limb exercise: Quantification using image-based computer modeling,” Am. J. Physiol. Heart Circ. Physiol. 291, H668–676 (2006). 10.1152/ajpheart.01301.2005 [DOI] [PubMed] [Google Scholar]
- Long Q., Ariff B., Zhao S. Z., Thom S. A., Hughes A. D., and Xu X. Y., “Reproducibility study of 3D geometrical reconstruction of the human carotid bifurcation from magnetic resonance images,” Magn. Reson. Med. 49, 665–674 (2003). 10.1002/mrm.10401 [DOI] [PubMed] [Google Scholar]
- Ku D. N., Giddens D. P., Zarins C. K., and Glagov S., “Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low oscillating shear stress,” Arteriosclerosis (Dallas) 5, 293–302 (1985). [DOI] [PubMed] [Google Scholar]
- Lee S. W. and Steinman D. A., “On the relative importance of rheology for image-based CFD models of the carotid bifurcation,” J. Biomech. Eng. 129, 273–278 (2007). 10.1115/1.2540836 [DOI] [PubMed] [Google Scholar]
- Moyle K. R., Antiga L., and Steinman D. A., “Inlet conditions for image-based CFD models of the carotid bifurcation: Is it reasonable to assume fully developed flow?,” J. Biomech. Eng. 128, 371–379 (2006). 10.1115/1.2187035 [DOI] [PubMed] [Google Scholar]
- Steinman D. A., Thomas J. B., Ladak H. M., Milner J. S., Rutt B. K., and Spence J. D., “Reconstruction of carotid bifurcation hemodynamics and wall thickness using computational fluid dynamics and MRI,” Magn. Reson. Med. 47, 149–159 (2002). 10.1002/mrm.10025 [DOI] [PubMed] [Google Scholar]
- Kock S. A., Nygaard J. V., Eldrup N., Frund E. T., Klaerke A., Paaske W. P., Falk E., and Yong Kim W., “Mechanical stresses in carotid plaques using MRI-based fluid-structure interaction models,” J. Biomech. 41, 1651–1658 (2008). 10.1016/j.jbiomech.2008.03.019 [DOI] [PubMed] [Google Scholar]
- Slager C. J., Wentzel J. J., Gijsen F. J., Schuurbiers J. C., van der Wal A. C., van der Steen A. F., and Serruys P. W., “The role of shear stress in the generation of rupture-prone vulnerable plaques,” Nat. Clin. Pract. Cardiovasc. Med. 2, 401–407 (2005). 10.1038/ncpcardio0274 [DOI] [PubMed] [Google Scholar]
- Bjorkerud B. and Bjorkerud S., “Contrary effects of lightly and strongly oxidized LDL with potent promotion of growth versus apoptosis on arterial smooth muscle cells, macrophages, and fibroblasts,” Arterioscler., Thromb., Vasc. Biol. 16, 416–424 (1996). [DOI] [PubMed] [Google Scholar]
- Libby P., “Molecular bases of the acute coronary syndromes,” Circulation 91, 2844–2850 (1995). [DOI] [PubMed] [Google Scholar]
- Tricot O., Mallat Z., Heymes C., Belmin J., Leseche G., and Tedgui A., “Relation between endothelial cell apoptosis and blood flow direction in human atherosclerotic plaques,” Circulation 101, 2450–2453 (2000). [DOI] [PubMed] [Google Scholar]
- Williams B., “Mechanical influences on vascular smooth muscle cell function,” J. Hypertens. 16, 1921–1929 (1998). 10.1097/00004872-199816121-00011 [DOI] [PubMed] [Google Scholar]
- Wentzel J. J., Corti R., Fayad Z. A., Wisdom P., Macaluso F., Winkelman M. O., Fuster V., and Badimon J. J., “Does shear stress modulate both plaque progression and regression in the thoracic aorta? Human study using serial magnetic resonance imaging,” J. Am. Coll. Cardiol. 45, 846–854 (2005). 10.1016/j.jacc.2004.12.026 [DOI] [PubMed] [Google Scholar]
- Friedman M. H. and Giddens D. P., “Blood flow in major blood vessels-modeling and experiments,” Ann. Biomed. Eng. 33, 1710–1713 (2005). 10.1007/s10439-005-8773-1 [DOI] [PubMed] [Google Scholar]
- Lee S. W., Antiga L., Spence J. D., and Steinman D. A., “Geometry of the carotid bifurcation predicts its exposure to disturbed flow,” Stroke 39, 2341–2347 (2008). 10.1161/STROKEAHA.107.510644 [DOI] [PubMed] [Google Scholar]
- Wake A. K., Oshinski J. N., Tannenbaum A. R., and Giddens D. P., “Choice of in vivo versus idealized velocity boundary conditions influences physiologically relevant flow patterns in a subject-specific simulation of flow in the human carotid bifurcation,” J. Biomech. Eng. 131, 021013 (2009). 10.1115/1.3005157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glor F. P., Long Q., Hughes A. D., Augst A. D., Ariff B., Thom S. A., Verdonck P. R., and Xu X. Y., “Reproducibility study of magnetic resonance image-based computational fluid dynamics prediction of carotid bifurcation flow,” Ann. Biomed. Eng. 31, 142–151 (2003). 10.1114/1.1537694 [DOI] [PubMed] [Google Scholar]
- Kerwin W., Hooker A., Spilker M., Vicini P., Ferguson M., Hatsukami T., and Yuan C., “Quantitative magnetic resonance imaging analysis of neovasculature volume in carotid atherosclerotic plaque,” Circulation 107, 851–856 (2003). 10.1161/01.CIR.0000048145.52309.31 [DOI] [PubMed] [Google Scholar]
- Antiga L., Wasserman B. A., and Steinman D. A., “On the overestimation of early wall thickening at the carotid bulb by black blood MRI, with implications for coronary and vulnerable plaque imaging,” Magn. Reson. Med. 60, 1020–1028 (2008). 10.1002/mrm.21758 [DOI] [PubMed] [Google Scholar]