Abstract
Purpose: Scatter correction is a major challenge in x-ray imaging using large area detectors. Recently, the authors proposed a promising scatter correction method for x-ray computed tomography (CT) using primary modulation. Proof of concept was previously illustrated by Monte Carlo simulations and physical experiments on a small phantom with a simple geometry. In this work, the authors provide a quantitative evaluation of the primary modulation technique and demonstrate its performance in applications where scatter correction is more challenging.
Methods: The authors first analyze the potential errors of the estimated scatter in the primary modulation method. On two tabletop CT systems, the method is investigated using three phantoms: A Catphan©600 phantom, an anthropomorphic chest phantom, and the Catphan©600 phantom with two annuli. Two different primary modulators are also designed to show the impact of the modulator parameters on the scatter correction efficiency. The first is an aluminum modulator with a weak modulation and a low modulation frequency, and the second is a copper modulator with a strong modulation and a high modulation frequency.
Results: On the Catphan©600 phantom in the first study, the method reduces the error of the CT number in the selected regions of interest (ROIs) from 371.4 to 21.9 Hounsfield units (HU); the contrast to noise ratio also increases from 10.9 to 19.2. On the anthropomorphic chest phantom in the second study, which represents a more difficult case due to the high scatter signals and object heterogeneity, the method reduces the error of the CT number from 327 to 19 HU in the selected ROIs and from 31.4% to 5.7% on the overall average. The third study is to investigate the impact of object size on the efficiency of our method. The scatter-to-primary ratio estimation error on the Catphan©600 phantom without any annulus (20 cm in diameter) is at the level of 0.04, it rises to 0.07 and 0.1 on the phantom with an elliptical annulus (30 cm in the minor axis and 38 cm in the major axis) and with a circular annulus (38 cm in diameter).
Conclusions: On the three phantom studies, good scatter correction performance of the proposed method has been demonstrated using both image comparisons and quantitative analysis. The theory and experiments demonstrate that a strong primary modulation that possesses a low transmission factor and a high modulation frequency is preferred for high scatter correction accuracy.
Keywords: scatter correction, cone-beam CT, primary modulation
INTRODUCTION
An x-ray system with a large area detector, as commonly used for cone-beam computed tomography (CBCT), is more susceptible to scatter-related artifacts. To alleviate this problem, various correction methods which use software-based,1, 2, 3, 4, 5, 6, 7, 8 hardware-based,9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 or combined hybrid approaches22, 23, 24, 25 have been proposed in the literature. Significant image quality improvements have been shown by using these methods in some situations such as when the scatter-to-primary ratio (SPR) is low or the object has a simple geometry with a high homogeneity. However, the development of an effective scatter control technique without increasing the patient dose, scanning time, and computation complexity still remains a major challenge, especially when SPR is very high.
To achieve an improved scatter correction performance, we recently proposed a new method using primary modulation.26A calibration sheet with spatially variant attenuating materials is inserted between the x-ray source and the object. Part of the primary distribution is modulated by the attenuation pattern of the modulator, and it is strongly separated from the scatter in the Fourier domain. Subsequent image processing techniques of linear filtering and demodulation are implemented to effectively correct for the scatter. This method is computationally efficient, easy to implement, and provides scatter correction using a single scan acquisition without the loss of real-time imaging capabilities. The algorithm performance has been demonstrated using Monte Carlo (MC) simulations and preliminary experimental results on a simple evaluation phantom.26 Image resolution performance has also been investigated using image comparison26 and modulation transfer function (MTF) measurements.27 The results show that our method does not result in noticeable resolution loss even though filtering-based techniques are involved.
In this paper, we further evaluate the primary modulation method using phantom studies on two tabletop CBCT systems. Two different modulators are designed to investigate the impact of the modulator parameters on the scatter correction performance. The first is an aluminum modulator with a weak modulation and a low modulation frequency, and the second is a copper modulator with a strong modulation and a high modulation frequency. The copper modulator is expected to have a stronger scatter correction capability, while the aluminum modulator should cause less perturbation to the primary and scatter distributions and the resultant images should be less affected by the beam hardening effects of the modulator. Our first study is performed on the Catphan©600 phantom. The phantom has a simple geometry and a detailed quantitative analysis of the performance of the primary modulation method is carried out. To fully investigate our approach for imaging applications on a complex anatomy, we use an anthropomorphic chest phantom in the second study. This study represents one of the most challenging cases of scatter correction in practice, since the phantom is highly heterogeneous and results in high scatter signals due to its large volume. In the third study, the impact of object size on the efficiency of our method is investigated using the Catphan©600 phantom with and without an annulus.
THE PRIMARY MODULATION METHOD
The basic concept and implementation
The basic concept of the primary modulation method is to insert a high-frequency attenuation sheet—a “primary modulator”—between the scanned object and the x-ray source to apply a high-frequency modulation onto the primary signal. With such a modulator in the field of view (FOV), the measured x-ray image in the Fourier space can be expressed as26
| (1) |
where P and S denote the Fourier transforms of primary and scatter, respectively, and ω∊[−π,π]×[−π,π] is the 2D coordinate of (ωx,ωy) in the Fourier domain. Parameter α∊(0,1) is the transmission factor of the modulator blocker, whose value is determined by the material and thickness of the blocker in a given x-ray system. In Eq. 1, we do not distinguish between the scatter arising in the object and the scatter arising in the detector. Signals from veiling glare in the CsI converter material are included in our definition of detector scatter and are generally low frequency in nature.14, 25, 28, 29, 30 If we ignore quantum noise and Rayleigh scattering, then based on the key hypothesis that low-frequency components dominate the scatter distribution even if high-frequency components are present in the incident x-ray intensity distribution,26 scatter is immune to the high-frequency modulation and is mostly concentrated in the low-frequency region. This allows the modulated high-frequency primary distribution, [(1−α)∕2]P(ω−π), to bypass the contamination of the scatter, and separation of scatter and primary signals is possible using filtering techniques. The effects of the primary modulator are depicted in Fig. 1. Scatter alone has less high-frequency content than primary alone, however these two signals overlap in the Fourier domain and cannot be distinguished efficiently. However, when a primary modulator is used, a significant signal increase (enclosed by the ellipses) is seen around ±π (high-frequency region, far from the low-frequency region where scatter is predominantly located), which are the contributions from the modulated primary. As a result, the primary modulator strongly separates primary and scatter signals which are otherwise overlapped in the Fourier domain.
Figure 1.
The spatial form (left) and the Fourier form (right, semilog coordinates) of primary, scatter, primary plus scatter, and primary with a modulator plus scatter for a cylindrical object. Scatter alone has less high-frequency content than does primary alone (as shown in the first two rows). However, these two signals are overlapped in the Fourier domain (as shown in the third row). With a primary modulator, a significant signal increase (enclosed by the ellipses in the last row) is seen around ±π, which is the contribution from the modulated primary.
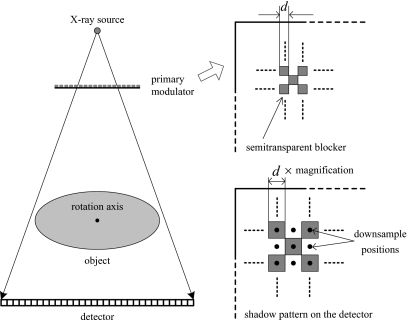
Figure 2 shows the system geometry with the insertion of the primary modulator. For ease in manufacturing, we use a primary modulator with a “checkerboard” pattern. The implementation of the primary modulation method is embedded in the conventional image processing stage of x-ray CT as the following steps:
Step 1. Do two calibration air scans with and without the primary modulator, estimate the blocker shadow position, and obtain the modulation function.
Step 2. Acquire transmission images of the object with the primary modulator in place.
Step 3. Estimate a scatter distribution from the transmission images by using the filtering and demodulation techniques.
Step 4. Subtract the scatter from the transmission images, divide the result by the flat field distribution measured in air scan with primary modulator, and take the negative logarithm operation to create projection data.
Step 5. Reconstruct CT images from the processed projection data.
Figure 2.
Geometric configuration of the x-ray system with the insertion of the primary modulator.
Among these data acquisition and processing steps, step 3 is the heart of our scatter correction algorithm. In this step, the projection images are first downsampled at the centers of the modulator blocker shadows, as illustrated in Fig. 2. To avoid the penumbra effect of the blocker edge, only the data at the centers of high and low intensity areas on the detector are averaged as a downsampled images. From the downsampled images, the scatter distribution is then estimated (details will be given in the following Secs. 2B, 2C). The obtained scatter estimation is finally upsampled to generate a whole-field scatter distribution using a conventional interpolation method. More details of these signal processing procedures can be found in Ref. 26, where a boundary detection auxiliary and a soft-cutoff function were introduced as extra effects to depress high frequencies in the object boundary and to guarantee that the estimated scatter is always less than the measured projection data.
The algorithm of scatter estimation
The scatter estimation algorithm (step 3) is reviewed here for the purpose of better understanding the primary modulation method. The goal of the scatter estimation algorithm is to separate the scatter signals, S(ω), from the measured transmission signals, P′(ω). Denote H(ω) as a low-pass filter with a bandwidth of ωmax. By shifting the frequency pass region by π, we obtain H(ω−π), a high-pass filter with the same bandwidth. Based on the hypothesis described earlier, the scatter distribution still has dominant low-frequency components while the primary signal contains high frequencies due to the modulation. With a proper choice of ωmax, we have the following approximations:
| (2) |
| (3) |
Furthermore, the transmission image of an object is always non-negative, with large low-frequency components (as shown in Fig. 1). It is reasonable to assume that the low-frequency primary components are much larger than the high-frequency components. Mathematically, we have
| (4) |
or
| (5) |
Multiplying both sides of Eq. 1 by H(ω) and using the approximation of Eqs. 2, 4, one obtains
| (6) |
Similarly, multiplying both sides of Eq. 1 by H(ω−π) and using the approximation of Eqs. 3, 5, we obtain
| (7) |
Demodulating Eq. 7 (change the variable from ω−π to ω) and subtracting it with a weighting factor of (1+α)∕(1−α) from Eq. 6, a scatter distribution can be estimated as
| (8) |
Errors of the scatter estimation
In the proposed method, we modulate the primary distribution such that the separation of the primary and the scatter is possible. This modulation is equivalent to a replication of signals from the low-frequency area to the high-frequency area, which requires a periodic alternating pattern for the modulation function, i.e., a uniform α over the whole image field. Although the designed modulator has a uniform blocker thickness, the effective blocker attenuation is nonuniform since incident beam angles and beam hardening effects are spatially different across the transmission image of an object. Such a variable modulation function causes errors in the scatter estimate in our algorithm.
When the variation in the modulation function is negligible, Eq. 1 is accurate. Substituting Eq. 1 into Eq. 8, we can see that the scatter estimate actually is
| (9) |
Therefore, subtracting Sest(ω) from S(ω), we obtain the scatter estimate error in the frequency domain, Es(ω), as
| (10) |
The first term in Eq. 10 is the high-frequency components of the scatter. The second term is the low-frequency components when the scatter frequency spectrum is shifted by π. For the errors from these two terms to be small, it is required that the frequencies of the dominant components of the scatter distribution are much lower than the modulation frequency. In other words, a high primary modulation frequency is preferred. It is worth mentioning that although the mean value of the scatter signals has a low-frequency behavior, the scatter statistical noise is high frequency. Our method is not able to correct for these high-frequency signals and the scatter noise is left in the corrected images. However, we want to emphasize that scatter noise is a general problem for all the postprocessing methods which perform scatter correction after the transmission image is contaminated by the scatter signal. More discussion on this issue will follow in a later section.
The third term in Eq. 10 is the low-frequency components when the primary frequency spectrum is shifted by π. Small errors from this term require that the unmodulated primary distribution has small high-frequency components. In general, this requirement cannot be fully satisfied, although the high-frequency signals in the primary distribution are partially suppressed using the boundary detection algorithm as described in Ref. 26. One approach to reduce this error is to enlarge the frequency space such that the modulated primary moves farther away from the low-frequency region. Therefore, when nonideal effects, such as beam hardening and finite focal spot size, are not considered, a modulator with a high modulation frequency is preferred. Furthermore, the third term in Eq. 10 has an additional weighting factor of 2α∕(1−α). To make this weighting small, a high attenuation for the modulator is preferred.
In summary, there are two types of scatter estimation errors using our algorithm. The first type is related to the variation in the modulation function or, equivalently, variation in α. The incident beam angle has a small effect on the variability. The variation and errors due to beam hardening are hard to analyze because of their nonlinear properties. The beam hardening effects therefore are not considered in the derivation of our method, and they may cause scatter estimation errors as well as introduce new artifacts due to the insertion of the modulator into the system. The correction for the beam hardening effects is another challenging topic in x-ray imaging, and it is beyond the scope of this paper. In this work, we ignore beam hardening effects in the scatter correction and investigate the influence of these effects by evaluating the final scatter corrected results. The second type of scatter estimation error is described in Eq. 10, and it is determined by the design of the primary modulator and the imaged object. Equation 10 predicts the scatter correction performance of a certain modulator and provides a useful guide for modulator design.
EXPERIMENTS AND RESULTS
The tabletop CBCT systems and the phantoms
The system parameters of the two tabletop CBCT systems used in this work are summarized in Table 1. These two systems had geometries that were conceptually equivalent to that of clinical CBCT systems, except that the phantom was rotated, which provided an ideal circular trajectory. System I in our laboratory consisted of a CPI Indico 100 100 kW programmable x-ray generator (CPI Communication & Medical Products Division, Georgetown, Ontario, Canada), a Varian G-1590SP x-ray tube (Varian X-ray Products, Salt Lake City, UT), a rotation stage, a Varian PaxScan 4030CB flat panel a-Si large area x-ray detector, and a workstation. The x-ray tube had an inherent filtration of 1.0 mm Al, 12° target angle, and operated with a 0.6 mm nominal focal spot size. No bow-tie filter or antiscatter grid was used on this system. We mounted the primary modulator on the outside surface of the collimator, with a nominal distance to the x-ray focal spot of 231 mm.
Table 1.
Imaging parameters of the physical experiments.
| Parameters | System I | System II |
|---|---|---|
| X-ray focal spot | 0.6 mm | 0.4 mm |
| X-ray energy | 120 kVp | 125 kVp |
| Detector size | 397.3×298.0 mm2 | 397.3×298.0 mm2 |
| 1024×768 pixels | 1024×768 pixels | |
| SIDa | 1423 mm | 1482 mm |
| SADb | 860 mm | 974 mm |
| SMDc | 231 mm | 400 mm |
| Circular rotation | 360° | 360° |
| No. of views | 800 | 625 |
| Antiscatter grid | No | 10:1 grid, 60 lp∕cm |
| Bow-tie filter | No | Al bow-tie |
Source-to-imager distance.
Source-to-axis distance.
Source-to-modulator distance.
System II at Ginzton Technology Center, Varian Medical Systems, Mountain View, CA, comprised of a Varian G242 X-ray tube with a 14° target angle and a 0.4 mm focal spot size, and the same type of detector as the first system. A half-fan mode was used, with the detector shifted laterally to increase the FOV. A bow-tie filter was inserted between the x-ray source and the detector to improve image statistics for a given dose and make the primary distribution on the detector more uniform. On this system, although an antiscatter grid (10:1 grid, 60 lp∕cm) has already been mounted onto the detector, severe and complicated scatter artifacts have been demonstrated under these conditions.31 These artifacts are mainly due to the large illuminated volume size and the asymmetry on the projection images caused by the use of offset detector. The system geometry and parameters were chosen to match those of the Varian Acuity CT simulator and the on-board imaging system, which are used for patient setup and treatment planning in radiation therapy.
To fully evaluate the proposed method, three phantoms were used in our studies. In the first study, we used the Catphan©600 phantom (The Phantom Laboratory, Salem, NY) on system I for both qualitative and quantitative assessments of the scatter correction performance of the primary modulation method. An anthropomorphic chest phantom was used in the second study, also on system I, to further demonstrate the scatter correction capability of the proposed method. The phantom was highly heterogeneous and results in high scatter signals due to its large volume. Because of the limited FOV, projection data of the chest phantom were truncated, leading to only the central region of the CT image free from noticeable truncation artifacts. It well represented the challenges of scatter correction during CBCT imaging of a human torso, and also demonstrated the capability of our scatter correction method in the presence of data truncation. Finally, the Catphan©600 phantom with and without annulus were scanned on system II to investigate the impacts of object size on the efficiency of our method.
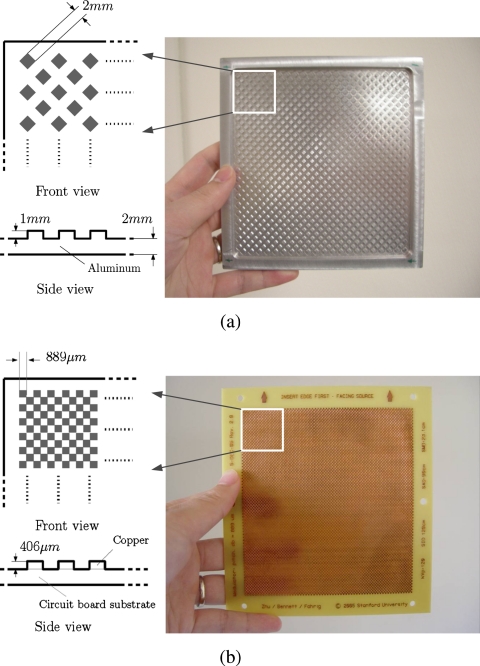
The aluminum and the copper primary modulators
Two different modulators, an aluminum modulator and a copper modulator, were designed to investigate the impact of modulator parameters on the scatter correction performance. The geometry of the aluminum modulator is shown in Fig. 3a. The blocker pattern is different from the ideal checkerboard pattern due to manufacturing considerations. However, all of the theories still apply since we process only the downsampled data and the shape of the blocker does not matter. The side length of the blocker square is 2 mm, its thickness is 1 mm, and the base thickness of the modulator is 2 mm. Therefore, the modulation period on the detector in the algorithm is times the magnification factor from the primary modulator to the detector, which is approximately 17 mm. The measured transmission of the blocker is approximately 90% when the x-ray source operates at 120 kVp on system I. Figure 3b shows the copper primary modulator. To lower the manufacturing cost, the modulator was built on a circuit board using a conventional etching method. The copper blocker on the modulator has a side length of 889 μm, and a thickness of 406 μm. The resulting modulation period on the detector is approximately 5.5 mm on system I and 3.3 mm on system II. The measured transmission of the blocker, α, is approximately 70% at 120 and 125 kVp.
Figure 3.
Two modulators used in the phantom studies: (a) An aluminum modulator with a large blocker spacing and (b) a copper modulator with a small blocker spacing.
The goal of the modulator design is to achieve an accurate scatter correction without introducing new artifacts. The theory of the proposed method shows that a strong primary modulation is preferred to achieve a superior scatter correction performance. However, a strong modulation leads to strong perturbation of the incident x-ray intensity distribution, which may cause additional artifacts due to the beam hardening effects of the modulator. The designs of the aluminum and the copper modulators trade off these aspects. The aluminum modulator results in less perturbation to the system, while the copper modulator provides a stronger primary modulation. The investigations of these two modulators provide guidance for optimal modulator designs in the future. An additional investigation, using downsampling of the copper modulator to match that of the aluminum modulator, is carried out to isolate the effect of modulator frequency from modulator transmission, as shown in Eq. 10.
Experiments and evaluations
Both aluminum and copper modulators were evaluated using the Catphan©600 phantom without any annulus on system I (the first study). The scatter correction for the anthropomorphic chest phantom on system I (the second study) and the Catphan©600 phantom with annuli on system II (the third study) were more challenging either due to the high SPR and object heterogeneity, or due to the large signal dynamic range and the non-negligible beam hardening effect. As a result, the aluminum modulator did not achieve an accurate scatter estimation, and only the copper modulator was used in these two studies. In the three phantom studies, fan-beam scans using a narrow collimator (10 mm of width on the detector) were carried out. Since the scatter signals in these scans were very low due to the small illumination volume, they were considered to be scatter-free and were used as ground-truth references in the comparisons. For the Catphan©600 phantom, the estimated scatter was also compared to the measured scatter, which was a 1D profile and was obtained by subtracting the fan-beam transmission image from the cone-beam transmission image in the illuminated area. The scatter estimation errors in the measured scatter and primary signals were analyzed using Eq. 10, as presented in Sec. 2C.
The details of the signal processing steps of the scatter correction using our method can be found in Ref. 26. In this work, we used a Hamming window with ωmax=π∕3 as the low-pass filter H(ω), the boundary detection, and soft-cutoff function were also applied in the same way as in Ref. 26. The standard FDK algorithm32 was used in the reconstructions. The reconstructed images were presented in Hounsfield units (HU), i.e., with a CT number of −1000 HU for air and a CT number of 0 HU for water-equivalent materials. A ring artifact correction was carried out after the image reconstruction to suppress the artifacts caused by the insertion of the primary modulator.33
Besides side-by-side image comparisons, the quality of the reconstructed images was also quantified using the contrast to noise ratio (CNR) and the error of CT number. The CNR was computed as
| (11) |
where mA, mB, σA, and σB are the mean and standard deviation of the CT numbers in the two neighboring regions of interest (ROIs). The error of the CT number in the ROIs was calculated as the square root of the mean square error (RMSE), defined as
| (12) |
where i is the index of the ROI, μi is the mean reconstructed value in HU inside the ROI, and is the corresponding value measured in the ground-truth image. In the study of the anthropomorphic chest phantom, the error of the CT number was also quantified as the average relative reconstruction error (RRE) in percentage in the ROI, defined as
| (13) |
where v is the reconstructed value in mm−1 and is the corresponding value of the fan-beam image. Parameters (x,y) are the coordinates of the reconstructed image. Since the z direction coverage was very small using a narrow collimator, only 2D slices were compared. The ROI was chosen as the nonair region, which was determined by thresholding.
First study: Catphan©600 phantom on system I
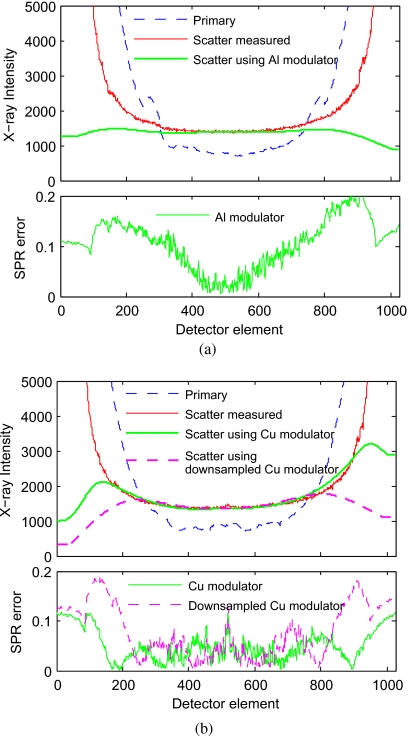
Figure 4 shows the measured primary profiles and the measured scatter profiles. The measured SPR is about 2 around the center of the object. Applying Eq. 10 on the measured profiles, we can predict the scatter estimation errors when the two different modulators are employed. Using the aluminum modulator, the average SPR estimation errors from the first two terms of Eq. 10 and from the last term are 1.95% and 4.96%, respectively. Using the copper modulator with a low blocker transmission and a high modulation frequency, these errors are reduced to 1.16% and 1.43%. This result is consistent with our previous argument that an accurate scatter estimation requires a strong modulation. The difference in scatter estimation accuracy using these two modulators is also seen in the comparisons of the scatter profiles and the errors in SPR, which is also included in Fig. 4. In this paper, the SPR error is calculated as the absolute difference between the measured SPR and the estimated SPR. Note that due to the logarithm operation in the calculation of line integral images, the reconstruction error is proportional to the SPR error, instead of the scatter estimation error. We can see that after scatter correction using the aluminum modulator and the copper modulator, the SPR errors are reduced to lower than 0.05 for central areas inside object boundary. Because of the boundary detection auxiliary and the modulation frequency limit, the SPR errors near and outside object boundary are higher (up to 0.2 for the aluminum modulator and 0.1 for the copper modulator).
Figure 4.
The 1D horizontal profiles of the measured and estimated scatter signals on the CatPhan©600 phantom: (a) Using the aluminum modulator and (b) using the copper modulator with and without frequency downgrading. The SPR error is obtained by calculating the absolute difference between the measured SPR and the estimated SPR.
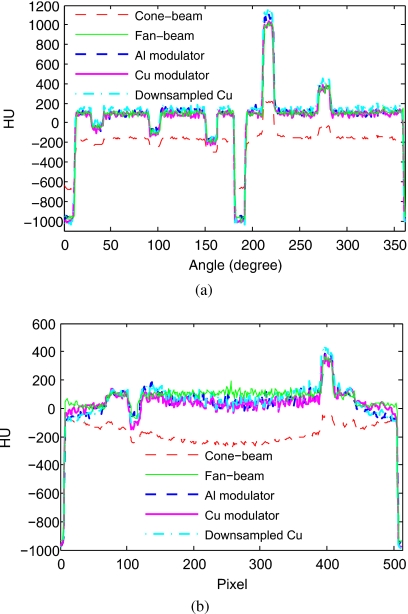
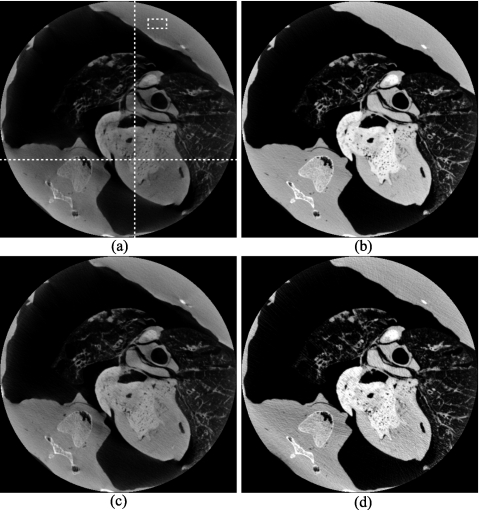
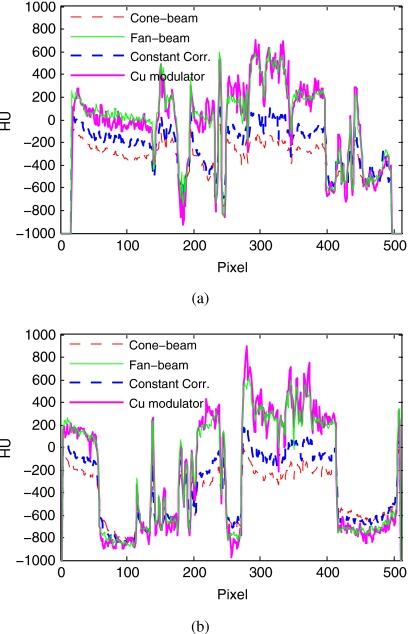
The scatter correction performances using the two modulators are more obvious in the comparison of the reconstructed images, as shown in Fig. 5. The reconstructions have a size of 512×512 pixels, with 0.4×0.4 mm2 for a pixel. The slice thickness in the z direction is 2 mm. Figure 6 shows the comparison of the 1D profiles of these reconstructed images, along the central vertical line and along the circular line passing through the centers of the contrast rods. The fan-beam reconstruction shown in Fig. 5b is used as the reference. Without scatter correction, the reconstructed cone-beam image has severe cupping artifacts. These artifacts are significantly suppressed when the proposed method is used with the aluminum modulator or the copper modula-tor. However, as also shown in Fig. 4, the scatter estimation using the aluminum modulator has relatively large errors due to the high blocker transmission and low modulation frequency of the modulator. Residual artifacts, such as streaks around the high-intensity objects, are present in the images after scatter correction. The copper modulator has a stronger scatter correction capability and effectively corrects for the scatter artifacts without introducing new ones. For a better illustration of the scatter correction performance for different modulation frequencies and transmission factors, we downsample the data during scatter correction using the copper modulator. The effective modulation frequency is reduced to that of the aluminum modulator. The results using the downsampled copper modulator are shown in Fig. 5e. It is seen that the scatter correction performance of the downsampled copper modulator is between that of the two modulators as expected, validating the conclusion in Eq. 10 that higher modulation frequency and lower transmission factor result in smaller errors and better scatter correction.
Figure 5.
Image reconstructions of the CatPhan©600 phantom from cone-beam scans with and without scatter correction. Reconstruction size: 512×512 pixels with 0.4×0.4 mm2 for a pixel. Display window: [−300,630] HU: (a) The cone-beam image without scatter correction; (b) the fan-beam image (reference); (c) the cone-beam image with scatter corrected using the aluminum modulator; (d) the cone-beam image with scatter corrected using the copper modulator; (e) the cone-beam image with scatter corrected using the downsampled copper modulator (its modulation frequency is reduced to the same as that of the aluminum), and (f) the six contrast rods selected as ROIs for the quantitative analysis shown in Table 2.
Figure 6.
Profiles of the reconstructed images in Fig. 5. The circular profiles are for a circle passing the centers of the rods shown in Fig. 5f: (a) Circular profiles and (b) central vertical profiles.
For a quantitative analysis of the reconstructed images, we measured the CT numbers, the noise [standard deviation (STD)], and the CNRs in the selected ROIs shown in Fig. 5f. The results are summarized in Table 2. Using the aluminum modulator, our approach reduces the RMSE [defined in Eq. 12] in the ROIs from 371.4 to 25.4 HU and enhances the CNR from 10.9 to 17.2. When the copper modulator is used, the RMSE in the ROIs is further reduced to 21.9 HU and the CNR is further increased to 19.2. For the downsampled copper modulator, almost the same CNR as that using the original copper modulator is obtained but the CT numbers are less accurate (the RMSE is 65.7 HU). Note that a relatively higher noise level is seen in the scatter corrected images, nearly twice the level in the fan-beam image. Such an increase in noise is an expected result for all postprocessing scatter correction algorithms.34 In our experiments, the reduction in x-ray intensity when using the modulator (20% for the aluminum modulator and 30% for the copper modulator) also contributed to this noise increase. More discussion on this issue is included below.
Table 2.
Mean, STD, and CNR in the selected ROIs of the CatPhan©600 phantom.
| ROIs | Air 1 | Air 2 | PMP | LDPE | Polysty. | Acrylic | Delrin™ | Teflon | ERMSE | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean (HU) | Cone-beam | −656.9 | −661.7 | −287.2 | −241.9 | −223.3 | −150.2 | −44.7 | 216.1 | 371.4 | ∕ |
| Fan-beam | −967.7 | −967.0 | −179.2 | −92.0 | −36.9 | 128.9 | 354.1 | 996.0 | ∕ | ∕ | |
| Al modulator | −963.4 | −951.5 | −169.6 | −61.2 | −38.9 | 109.9 | 371.6 | 1052.6 | 25.4 | ∕ | |
| Cu modulator | −1006.6 | −1004.6 | −196.7 | −104.8 | −53.6 | 116.6 | 350.8 | 1000.0 | 21.9 | ∕ | |
| Downsampled Cu | −1024.8 | −1024.1 | −160.7 | −66.1 | −2.9 | 178.2 | 424.6 | 1131.7 | 65.7 | ∕ | |
| STD (HU) | Cone-beam | 12.0 | 12.0 | 7.8 | 9.5 | 8.8 | 11.0 | 14.4 | 22.4 | ∕ | 12.2 |
| Fan-beam | 11.5 | 11.7 | 10.9 | 11.9 | 11.0 | 11.5 | 12.2 | 14.1 | ∕ | 11.2 | |
| Al modulator | 19.2 | 24.1 | 18.0 | 20.6 | 21.1 | 19.5 | 23.3 | 29.6 | ∕ | 20.9 | |
| Cu modulator | 18.9 | 21.2 | 22.2 | 21.7 | 22.9 | 23.8 | 24.8 | 28.6 | ∕ | 21.8 | |
| Downsampled Cu | 20.8 | 22.7 | 23.0 | 22.2 | 23.8 | 24.5 | 25.2 | 33.7 | ∕ | 23.4 | |
| CNR | Cone-beam | 25.5 | 23.9 | 9.1 | 5.8 | 3.4 | 0.0 | 5.3 | 13.9 | ∕ | 10.9 |
| Fan-beam | 53.8 | 54.5 | 13.2 | 9.0 | 6.4 | 1.4 | 12.0 | 37.0 | ∕ | 23.4 | |
| Al modulator | 36.1 | 31.5 | 10.3 | 5.9 | 4.6 | 0.8 | 8.2 | 25.6 | ∕ | 17.2a | |
| Cu modulator | 38.9 | 35.5 | 9.4 | 6.5 | 4.6 | 0.8 | 7.5 | 25 | ∕ | 19.2a | |
| Downsampled Cu | 37.1 | 36.0 | 9.7 | 6.6 | 4.6 | 1.2 | 8.2 | 24.6 | ∕ | 19.1a | |
To compensate for the attenuation of the modulator, the values are normalized to the same total patient dose.
Second study: Chest phantom on system I
To further demonstrate the scatter correction capability of the primary modulation method, we use an anthropomorphic chest phantom in the second study. The phantom has a maximum width of approximately 40 cm and contains the lung, heart, bone, and soft-tissue structures. Due to the limited FOV of the flat panel detector, projections in most views are truncated. Thus, we only reconstruct a central region of approximately 20 cm in diameter, where the truncation artifacts on the reconstructed images are negligible (shown in Fig. 7). The reconstructed images have a size of 512×512×384 voxels with an isotropic resolution of 0.4 mm.
Figure 7.
The whole chest phantom and the reconstructed size (circled area) in this study.
The measured SPR of the cone-beam projections in this study is highly nonuniform across the image and reaches up to 5 around the center of the object. Our proposed method using the copper modulator achieves excellent scatter correction for this challenging case, demonstrating that it works even with data truncation. As shown in the comparisons of the reconstructed images (Figs. 89) and 1D profiles (Fig. 10), the image shading and distortion artifacts due to scatter are effectively suppressed using our approach. The quality of the scatter corrected image is close to that of the fan-beam image, which is almost scatter-free. For a better comparison, an additional scatter correction result is also included, which uses a constant (the average of the measured scatter in the central region) to approximate the scatter distribution. The constant correction suppresses the scatter artifacts to some extent. In the selected ROI, as shown in Fig. 8a, the constant correction reduces the error from 327 to 210 HU; the overall RRE [defined in Eq. 13] is reduced from 31.4% to 22.0%. Using the proposed method with the copper modulator, these errors are further reduced to 19 HU and 5.7%. The noise levels for the cone-beam, fan-beam, and scatter corrected images using constant and our method are 33, 31, 36, and 47 HU, respectively.
Figure 8.
Image reconstructions of the chest phantom in the X-Y plane. Reconstruction size: 512×512 pixels with 0.4×0.4 mm2 for a pixel. Display window: [−770,630] HU: (a) The cone-beam image without scatter correction; (b) the fan-beam image (reference); (c) the cone-beam image with scatter corrected using a constant; and (d) the cone-beam image with scatter corrected using the proposed method with the copper modulator. The horizontal and vertical lines indicate the positions of the profiles in Fig. 10, which are also the positions of the X-Z slice and Y-Z slice in Fig. 9. The mean values of the CT number in the rectangle area [shown in image (a)] are −230 HU for (a), 97 HU for (b), −113 HU for (c), and 78 HU for (d). The corresponding standard deviations are 33, 31, 36, and 47 HU, respectively.
Figure 9.
Image reconstructions of the chest phantom in the X-Z plane (left column) and the Y-Z plane (right column), taken at the positions shown in Fig. 8a. Reconstruction size: 512×384 pixels with 0.4×0.4 mm2 for a pixel. Display window: [−770, 630] HU. (a) and (b) are the images without scatter correction; (c) and (d) are the images with scatter corrected using a constant; and (e) and (f) are the images with scatter corrected using the proposed method with the copper modulator.
Figure 10.
Profiles of reconstructed images in Fig. 8, taken at the lines shown in Fig. 8a: (a) Horizontal profiles at row 345 and (b) vertical profiles at column 292.
Third study: Catphan©600 phantom on system II
This study investigates the impact of the object size on the efficiency of our proposed method. Three different sizes of the Catphan©600 phantom were used: Catphan©600 phantom without an annulus (20 cm in diameter), the phantom with an elliptical body annulus (30 cm in the minor axis and 38 cm in the major axis), and the phantom with a circular body annulus (38 cm in diameter). The ranges of signal magnitudes for the three object sizes are roughly 1–80, 1–740, and 1–4300, respectively (we assume the linear attenuation coefficient is 0.22 cm−1). Half-fan mode was used when scanning the phantom with the annuli, with the detector laterally shifted 16 cm to increase the FOV.
The accuracy of scatter estimation for the three different object diameters is seen in Fig. 11, which shows the 1D profiles of primary, measured and estimated scatter, as well as the corresponding SPR errors. Significant scatter distributions are observed even though an antiscatter grid and a bow-tie filter that also reduce scatter35 are in place. The maximum SPRs for the Catphan©600 phantom without an annulus, with the elliptical annulus, and with the circular annulus are 0.5, 1.0, and 1.5, respectively. The estimated scatter using the copper modulator is quite close to the measured scatter. As shown in Fig. 11, the average SPR errors for the three objects are at the level of 0.04, 0.07, and 0.1, respectively.
Figure 11.
The 1D horizontal profiles of the measured and estimated scatter signals for the CatPhan©600 phantom with and without an annulus: (a) Without an annulus, (b) with the elliptical annulus, and (c) with the circular annulus.
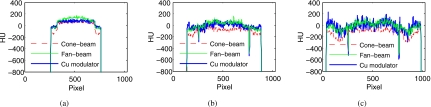
The reconstructions have a size of 1024×1024 pixels, with 0.4×0.4 mm2 for a pixel. From the reconstructed images shown in Fig. 12 and the corresponding 1D profiles in Fig. 13, we can see that our proposed method achieves good results on the phantom without an annulus. In the central area, CT numbers of the scatter corrected image are even more uniform than that of the fan-beam image. When the annuli are used, our method reduces scatter artifacts as well. Taking the fan-beam image in Fig. 12d as a reference, the RMSE of the CT number, the average CNR, and the noise in the same rod ROIs, as indicated in Fig. 5f, are listed in Table 3. For the phantom without an annulus, our proposed method reduces the RMSE from 116.0 to 26.1 HU and enhances the CNR from 16.9 to 18.5; for the phantom with the elliptical annulus, and with the circular annulus, the RMSEs are reduced from 298.7 and 355.1 HU to 91.0 and 103.3 HU. After scatter correction the CNRs for these two phantoms remain unchanged, although contrasts are improved. This is due to the relatively high noise level in the scatter corrected images because of scatter noise. More details on this issue can be found in Ref. 34.
Figure 12.
Image reconstructions of the Catphan©600 phantom with and without annulus. Reconstruction size: 1024×1024 pixels, with 0.4×0.4 mm2 for a pixel. Display window: [−700,300] HU. The first column is for the Catphan©600 phantom without annulus; the second column is for the phantom with the elliptical annulus; and the third column is for the phantom with the circular annuls. (a)–(c) are the cone-beam images without scatter correction; (d)–(f) are the fan-beam images; and (g)–(i) are the cone-beam image with scatter corrected using the copper modulator.
Figure 13.
Profiles of reconstructed images in Fig. 12: (a) Without annulus, (b) with the elliptical annulus, and (c) with the circular annulus.
Table 3.
The RMSE, averaged CNR, and noise in the rods in Fig. 12.
| Annulus | Scan | ERMSE (HU) | Noise (HU) | CNR |
|---|---|---|---|---|
| No | Cone-beam | 116.0 | 15.7 | 16.9 |
| Fan-beam | ∕ | 16.7 | 19.8 | |
| Cu modulator | 26.1 | 21.5 | 18.5a | |
| Elliptical | Cone-beam | 298.7 | 35.3 | 5.0 |
| Fan-beam | 79.9 | 47.8 | 6.4 | |
| Cu modulator | 91.0 | 74.8 | 5.0a | |
| Circular | Cone-beam | 355.1 | 40.8 | 3.3 |
| Fan-beam | 106.1 | 62.4 | 4.4 | |
| Cu modulator | 103.3 | 105.9 | 3.3a |
To compensate for the attenuation of the modulator, the values are normalized to the same total patient dose.
As demonstrated above, scatter correction becomes more challenging as the size of the scanned object increases. This is due to the increased scatter signals, the beam hardening effect, and the dynamic range of the signal. For the phantom with the elliptical annulus and with the circular annulus, the effect of beam hardening is non-negligible, which results in relatively high errors of the CT number even in the fan-beam images (the corresponding RMSEs are 79.9 and 106.1 HU). As discussed in Sec. 2C, beam hardening increases the nonuniformity of the transmission factor, α, and hence reduces the efficiency of scatter estimation. In addition, a larger object in the FOV leads to a larger signal dynamic range, indicating that a higher modulation frequency is required in order to obtain the same level of accuracy in scatter estimation as for a smaller object. It is worth noting that the absence of cupping artifact in Fig. 12a is due to the bow-tie filter. The geometry of the bow-tie filter happens to match that of the Catphan©600 phantom and makes the SPR nearly constant. Therefore, after reconstruction we do not see too much scatter artifact around the phantom center since the constant SPR is filtered out in the ramp filtering step. The doming in the central region of Fig. 12d and the annular swaths in CT images of the phantom with annuli are caused by the beam hardening of the bow-tie filter. The influence of the bow-tie filter on the CBCT image quality is beyond the scope of this paper and can be found in Ref. 35.
DISCUSSION AND CONCLUSIONS
As seen in the above three studies, the scatter corrected cone-beam images have a relatively higher noise level than the fan-beam images. The increase in noise level mainly stems from the scatter noise which is left in the scatter corrected projections using our method. We emphasize again that the issue of uncorrected scatter noise is a general problem for all postprocessing scatter algorithms which correct for scatter after the scatter photons reach the detector. Due to the randomness of the scattering event, the scatter noise cannot be suppressed using any of the postprocessing methods. Several noise reduction techniques are available36, 37, 38 and we have recently shown that the noise increase in scatter corrected images from a clinical system greatly degrades the image quality including the low-contrast detectability and a novel noise suppression scheme was suggested.34 It is worth noting that due to the reduction in x-ray intensity by the primary modulator itself, an increase in mA s is needed in practical applications to achieve the same noise level as that without a modulator. Consequently, the x-ray tube power requirements are somewhat higher. However, in general, the dose to the patient does not increase because the primary modulator is inserted between the x-ray tube and the patient.
The parameters of the modulator, the transmission factor and the modulation frequency, are critical to the scatter correction performance of the proposed method. The theory of primary modulation shows that a strong primary modulation (i.e., a low transmission factor and a high modulation frequency) is preferred for high scatter estimation accuracy. However, a primary modulator with a strong modulation has strong beam hardening effects and causes more perturbation to the incident x-ray intensity distribution. These effects are ignored in the proposed algorithm derivation, and may lead to scatter estimation errors as well as new artifacts in the reconstructed images. In this work, based on the MC simulations shown in Ref. 26, two modulators were designed and evaluated. The phantom studies indicated that the copper modulator with a higher modulation frequency and a lower transmission factor has a stronger scatter correction capability than the aluminum modulator.
In summary, three phantom studies are carried out in this paper to fully evaluate the previously developed primary modulation method. Good scatter correction performance of the proposed method has been demonstrated using both image comparisons and quantitative analysis. On the Catphan©600 phantom in the first study, the SPR estimation error for the scatter estimated by our proposed method is at the level of 0.05. Excellent scatter correction is also shown on the anthropomorphic chest phantom in the second study, which is more challenging due to the high SPR and the object heterogeneity. The impact of object diameter on the efficiency of our method is investigated in the third study. Accurate scatter correction is achieved on the Catphan©600 phantom without annulus (the SPR error is only 0.04); and scatter artifacts are also reduced on the phantom with the elliptical and the circular annuli (the corresponding SPR errors are 0.07 and 0.1). Scatter corrections on the phantom with the annulus are very challenging due to the non-negligible beam hardening effect and the large dynamic range of the signal.
The optimization of the modulator design and the improvement of the scatter estimation algorithm by taking noise and beam hardening effect into account are the subjects of future investigations. We will further evaluate the primary modulation method on clinical systems using various x-ray spectra. A comprehensive comparison with other scatter correction methods is also underway.
ACKNOWLEDGMENTS
This project was supported by the NIH under Grant Nos. R21 EB008186 and R01 EB003524 and by the Lucas Foundation. The authors would like to thank the editor and the anonymous reviewers for their valuable and insightful comments. Thanks also go to Jared Starman for his help with the tabletop system.
References
- Boone J. and Seibert J., “An analytical model of the scattered radiation distribution in diagnostic radiology,” Med. Phys. 15(5), 721–725 (1988). 10.1118/1.596186 [DOI] [PubMed] [Google Scholar]
- Seibert J. and Boone J., “X-ray scatter removal by deconvolution,” Med. Phys. 15(4), 567–575 (1988). 10.1118/1.596208 [DOI] [PubMed] [Google Scholar]
- Floyd C. E., Baydush A. H., Lo J. Y., Bowsher J. E., and Ravin C. E., “Scatter compensation for digital chest radiography using maximum likelihood expectation maximization,” Invest. Radiol. 28(5), 427–433 (1993). 10.1097/00004424-199305000-00009 [DOI] [PubMed] [Google Scholar]
- Honda M., Kikuchi K., and Komatsu K., “Method for estimating the intensity of scattered radiation using a scatter generation model,” Med. Phys. 18(2), 219–226 (1991). 10.1118/1.596710 [DOI] [PubMed] [Google Scholar]
- Wiegert J., Bertram M., Rose G., and Aach T., “Model-based scatter correction for cone-beam computed tomography,” Proc. SPIE 5745, 271–282 (2005). 10.1117/12.594520 [DOI] [Google Scholar]
- Kruger D. G., Zink F., Peppler W. W., Ergun D. L., and Mistretta C. A., “A regional convolution kernel algorithm for scatter correction in dual-energy images: Comparison to single-kernel algorithms,” Med. Phys. 21(2), 175–184 (1994). 10.1118/1.597297 [DOI] [PubMed] [Google Scholar]
- Bertram M., Wiegert J., and Rose G., “Potential of software-based scatter corrections in cone-beam volume CT,” Proc. SPIE 5745, 259–270 (2005). 10.1117/12.595032 [DOI] [Google Scholar]
- Zellerhoff M., Scholz B., Ruhrnschopf E. P., and Brunner T., “Low contrast 3D-reconstruction from C-arm data,” Proc. SPIE 5745, 646–655 (2005). 10.1117/12.593433 [DOI] [Google Scholar]
- Sorenson J. and Floch J., “Scatter rejection by air gap: An empirical model,” Med. Phys. 12(3), 308–316 (1985). 10.1118/1.595690 [DOI] [PubMed] [Google Scholar]
- Neitzel U., “Grids or air gaps for scatter reduction in digital radiography: A model calculation,” Med. Phys. 19(2), 475–481 (1992). 10.1118/1.596836 [DOI] [PubMed] [Google Scholar]
- Lo J. Y., Floyd C. E., Baker J. A., and Ravin C. E., “Scatter compensation in digital chest radiography using the posterior beam stop technique,” Med. Phys. 21(3), 435–443 (1994). 10.1118/1.597388 [DOI] [PubMed] [Google Scholar]
- Ning R., Tang X., and Conover D., “X-ray scatter correction algorithm for cone-beam CT imaging,” Med. Phys. 31(5), 1195–1202 (2004). 10.1118/1.1711475 [DOI] [PubMed] [Google Scholar]
- Ning R., Tang X., Yu R., and Conover D., “X-ray scatter suppression algorithm for cone beam volume CT,” Proc. SPIE 4682, 774–781 (2002). 10.1117/12.465628 [DOI] [Google Scholar]
- Molloi S., Zhou Y., and Wamsely G., “Scatter-glare estimation for digital radiographic systems: Comparison of digital filtration and sampling techniques,” IEEE Trans. Med. Imaging 17(6), 881–888 (1998). 10.1109/42.746621 [DOI] [PubMed] [Google Scholar]
- Zhu L., Strobel N., and Fahrig R., “X-ray scatter correction for cone-beam CT using moving blocker array,” Proc. SPIE 5745, 251–258 (2005). 10.1117/12.594699 [DOI] [Google Scholar]
- Boone J., Seibert J., Tang C., and Lane S., “Grid and slot scan scatter reduction in mammography: Comparison by using Monte Carlo techniques,” Radiology 222(2), 519–527 (2002). 10.1148/radiol.2222010491 [DOI] [PubMed] [Google Scholar]
- Samei E., Lo J. Y., Yoshizumi T. T., Jesneck J. L., J. T.DobbinsIII, C. E.Floyd, Jr., McAdams H. P., and Ravin C. E., “Comparative scatter and dose performance of slot-scan and full-field digital chest radiography systems,” Radiology 235(3), 940–949 (2005). 10.1148/radiol.2353040516 [DOI] [PubMed] [Google Scholar]
- Boone J., “Scatter correction algorithm for digitally acquired radiographs: Theory and results,” Med. Phys. 13(3), 319–328 (1986). 10.1118/1.595920 [DOI] [PubMed] [Google Scholar]
- Bani-Hashemi A., Blanz E., Maltz J., Hristov D., and Svatos M., “Cone beam x-ray scatter removal via image frequency modulation and filtering,” Med. Phys. 32(6), 2093 (2005). 10.1118/1.1998387 [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H., Daly M. J., Bakhtiar B., Moseley D. J., Richard S., Keller H., and Jaffray D. A., “A simple, direct method for x-ray scatter estimation and correction in digital radiography and cone-beam CT,” Med. Phys. 33(1), 187–197 (2006). 10.1118/1.2148916 [DOI] [PubMed] [Google Scholar]
- Zhu L., Xie Y., Wang J., and Xing L., “Scatter correction for cone-beam CT in radiation therapy,” Med. Phys. 36(6), 2258–2268 (2009). 10.1118/1.3130047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Love L. A. and Kruger R. A., “Scatter estimation for a digital radiographic system using convolution filtering,” Med. Phys. 14(2), 178–185 (1987). 10.1118/1.596126 [DOI] [PubMed] [Google Scholar]
- Kyriakou Y., Deak P., Riedel T., Smekal L. V., and Kalender W. A., “Combining deterministic and Monte-Carlo methods in the simulation of x-ray attenuation and scatter,” Eur. Radiol. 15 (Supp. 1), 306 (2005). [Google Scholar]
- Kyriakou Y., Riedel T., and Kalender W. A., “Combining deterministic and Monte Carlo calculations for fast estimation of scatter intensities in CT,” Phys. Med. Biol. 51, 4567–4586 (2006). 10.1088/0031-9155/51/18/008 [DOI] [PubMed] [Google Scholar]
- Close R. A., Shah K. C., and Whiting J. S., “Regularization method for scatter-glare correction in fluoroscopic images,” Med. Phys. 26(9), 1794–1801 (1999). 10.1118/1.598683 [DOI] [PubMed] [Google Scholar]
- Zhu L., Bennett N. R., and Fahrig R., “Scatter correction method for X-ray CT using primary modulation: Theory and preliminary results,” IEEE Trans. Med. Imaging 25(12), 1573–1587 (2006). 10.1109/TMI.2006.884636 [DOI] [PubMed] [Google Scholar]
- Zhu L., Starman J., Bennett N. R., and Fahrig R., “MTF measurement and a phantom study for scatter correction in CBCT using primary modulation,” IEEE Nuclear Science Symposium Conference Record 3, 1964–1968 (2006). [Google Scholar]
- Seibert J. A., Nalcioglu O., and Roeck W. W., “Characterization of the veiling glare PSF in x-ray image intensified fluoroscopy,” Med. Phys. 11(2), 172–179 (1984). 10.1118/1.595494 [DOI] [PubMed] [Google Scholar]
- Cai W., Ning R., and Conover D., “Simplified method of scatter correction using a beam-stop-array algorithm for cone-beam computed tomography breast imaging,” Opt. Eng. 47(9), 097003 (2008). 10.1117/1.2977527 [DOI] [Google Scholar]
- Carton A. K., Acciavatti R., Kuo J., and Maidment A. D. A., “The effect of scatter and glare on image quality in contrast-enhanced breast imaging using an a-Si∕CsI(Tl) full-field flat panel detector,” Med. Phys. 36(3), 920–928 (2009). 10.1118/1.3077922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Virshup G., Suri R., and Star-Lack J., “Scatter characterization in cone-beam CT systems with offset flat panel imagers,” Med. Phys. 33(6), 2288–2288 (2006). 10.1118/1.2241938 [DOI] [Google Scholar]
- Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A 1, 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]
- Star-Lack J., Starman J., Munro P., Jeung A., Richters J., Mostafavi H., and Pavkovich J., “A fast variable-intensity ring suppression algorithm,” Med. Phys. 33(6), 1997–1997 (2006). 10.1118/1.2240242 [DOI] [Google Scholar]
- Zhu L., Wang J., and Xing L., “Noise suppression in scatter correction for cone-beam CT,” Med. Phys. 36(3), 741–752 (2009). 10.1118/1.3063001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mail N., Moseley D. J., Siewerdsen J. H., and Jaffray D. A., “The influence of bowtie filtration on cone-beam CT image quality,” Med. Phys. 36(1), 22–32 (2009). 10.1118/1.3017470 [DOI] [PubMed] [Google Scholar]
- Lange K. and Carson R., “EM reconstruction algorithms for emission and transmission tomography,” J. Comput. Assist. Tomogr. 8(2), 306–316 (1984). [PubMed] [Google Scholar]
- La Rivière P. J., “Penalized-likelihood sinogram smoothing for low-dose CT,” Med. Phys. 32(6), 1676–1683 (2005). 10.1118/1.1915015 [DOI] [PubMed] [Google Scholar]
- Wang J., Li T., Lu H., and Liang Z., “Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose x-ray computed tomography,” IEEE Trans. Med. Imaging 25(10), 1272–1283 (2006). 10.1109/TMI.2006.882141 [DOI] [PMC free article] [PubMed] [Google Scholar]