Radiation damage effects at four specimen temperatures from 4 K to 100 K

Abstract

Radiation damage is the primary factor that limits resolution in electron cryo-microscopy (cryo-EM) of frozen-hydrated biological samples. Negative effects of radiation damage are attenuated by cooling specimens to cryogenic temperatures using liquid nitrogen or liquid helium. We have examined the relationship between specimen temperature and radiation damage across a broad spectrum of resolution by analyzing images of frozen-hydrated catalase crystal at four specimen temperatures: 4 K, 25 K, 42 K, and 100 K. For each temperature, “exposure series” were collected consisting of consecutive images of the same area of sample, each with 10 e⁻/Ų exposure per image. Radiation damage effects were evaluated by examining the correlation between cumulative exposure and normalized amplitudes or IQ values of Bragg peaks across a broad range of resolution (4.0–173.5 Å). Results indicate that for sub-nanometer resolution, liquid nitrogen specimen temperature (100 K) provides the most consistent high-quality data while yielding statistically equivalent protection from radiation damage compared to the three lower temperatures. At lower resolution, suitable for tomography, intermediate temperatures (25 or 42 K) may provide a modest improvement in cryoprotection without introducing deleterious effects evident at 4 K.

1. Introduction

Electron cryo-microscopy (cryo-EM) has become a powerful tool in structural biology for a broad range of target resolutions. Electron crystallography of 2-D membrane protein crystals has yielded maps with better than 2 Å resolution, [1] and single-particle methods in cryo-EM have recently achieved near-atomic resolution structures of viruses and chaperonins [2–5]. On the other end of the resolution spectrum, electron cryo-tomography (cryo-ET) has been useful in determining the structures of cells, organelles, and assemblies with non-uniform structures, without the use of heavy atom staining or plastic embedding, and typically at molecular resolutions (see [6], and references therein). Although both single-particle cryo-EM and cryo-ET have provided a vast amount of structural data unattainable by other methods, neither has been able to routinely reach the resolution of other atomic-resolution methods such as x-ray crystallography or NMR. The principal obstacle to achieving high resolution in electron microscopy is radiation damage resulting from the flux of high-energy electrons incident on the specimen. Inelastic scattering of these electrons on the specimen causes excitation of specimen valence electrons resulting in radiation damage, which includes bond rupture, free radical formation, and structural rearrangements [7].

It is well known that the effects of radiation damage in electron microscopy are reduced when the specimen is cooled to cryogenic temperatures with liquid nitrogen [8,9] or liquid helium [10,11]. Low temperatures protect specimens by reducing the magnitude and influence of secondary chemical reactions, and by the “cage effect,” which slows the displacement of molecular fragments liberated by ionizing radiation [7,12]. This improved protection against radiation damage allows for imaging at higher electron exposures, resulting in increased signal-to-noise ratios and thus improved resolution. Optimization of imaging conditions to reduce radiation damage is therefore necessary to maximize the efficiency and quality of cryo-EM data collection.

Results from studies in both x-ray crystallography [13,14] and electron crystallography [9,15,16] have indicated that liquid helium temperature may provide a modest increase in the exposure tolerance of organic specimens compared to liquid nitrogen temperature, and the early success in using a liquid helium microscope to record images of protein crystals at ~3.7 Å [17] suggested that such temperatures might be well-suited for studies pursuing high resolution. At present, both liquid helium and liquid nitrogen have been shown to be capable of reaching similarly high resolutions. Of the four recent near-atomic resolution single-particle cryo-EM structures, two used liquid helium [2–3] and two used liquid nitrogen specimen [4–5] temperatures. However, we have observed that the yield of high-resolution images is generally much lower using liquid helium compared to liquid nitrogen (data not shown), and others have recently noted reduced image contrast and increased charging effects at liquid helium temperature [18]. Additionally, recent evidence from cryo-ET has indicated that liquid helium temperatures introduce ice density changes, increased specimen movement, and exaggerated bubbling under the high cumulative exposures characteristic of tomographic studies [19,20]. It thus remains unclear whether any additional radiation damage protection afforded by liquid helium translates into improvements in actual data collection.

To study the effect of specimen temperature on radiation damage across a broad range of exposures and resolutions, we have performed a detailed analysis of radiation damage effects on ice-embedded catalase crystal using bright-field cryo-EM imaging. We have quantified radiation damage effects by using two separate measures of “data quality”: (1) normalized Fourier peak amplitude and (2) IQ value, which is a measure of signal-to-noise ratio and a predictor of the phase error of Bragg peaks. By both measures, we find all four specimen temperatures examined have statistically equivalent radiation damage effects at the low cumulative exposures typically used for high-resolution single-particle imaging. At higher exposures typical of cryo-ET, the intermediate temperatures (25 and 42 K) appear to generally provide the greatest cryo-protection, while specimens at 4 K exhibit significant structural rearrangements and/or beam-induced specimen movement not evident at intermediate or liquid nitrogen temperatures.

2. Materials and methods

2.1. Specimen preparation

Catalase (Boehringer Mannheim GmbH, Mannheim, Germany) was centrifuged to harvest the microcrystals. The precipitate was dissolved in 10% NaCl and centrifuged to remove undissolved catalase. The supernatant was dialyzed against 0.05 M phosphate buffer, pH 6.3, then stored at 4° C. Subsequently, the prepared thin catalase crystals were vitrified in liquid ethane on washed and glow-discharged Quantifoil 400 R1.2/1.3 holey carbon grids (Quantifoil Micro Tools GmbH, Jena, Germany). Grids were stored in liquid nitrogen until they were loaded into the electron cryo-microscope for imaging.

2.2. Electron cryo-microscopy

In order to accommodate a wide range of specimen temperatures, images were acquired on two separate microscopes, both operated at 300 kV. Imaging at specimen temperatures of ~4 K and ~42 K was performed on a JEM3000SFF electron microscope (JEOL Inc, Tokyo, Japan). Imaging at specimen temperatures of ~25 K and ~100 K was performed on a JEM3200FSC electron microscope (JEOL Inc, Tokyo, Japan), including an in-column energy filter with width 15 eV. Specimen exposure rates on both microscopes were previously calibrated with screen current using a Faraday cage. Exposure rates were estimated during imaging based on the current density on each microscope's viewing screen, and verified by examining detector counts on the CCD camera. All images were acquired on Gatan US4000 4k×4k CCD cameras (Gatan, Pleasanton, CA) at a detector magnification of ~115,000×.

2.3. Image collection

Under low-exposure conditions, areas of ice-embedded catalase crystal suitable for imaging were identified by visual inspection. All imaged crystals were over holes in the carbon support so that the images contain only ice-embedded crystal with no supporting carbon film. For each specimen area imaged, an “exposure series” was collected consisting of consecutive images of the same area, each with 10 e⁻/Ų total exposure over one second. Consecutive images in each exposure series were collected with less than three seconds between each image acquisition. All microscope and detector parameters were held constant throughout each exposure series. Defocus values were held constant within each exposure series, with an overall range from 0.3 to 1.3 underfocus across all exposure series collected. Each exposure series contained a total of between 4 and 11 images, corresponding to cumulative exposures in the final images of 40 to 110 e⁻/Ų.

2.4. Image processing

To eliminate possible bias due to stage drift into unexposed areas, each 4096×4096 CCD frame was cropped so that only the central 3888×3888 real-space pixels from each frame were used in image processing. Each CCD frame in each exposure series was processed individually using 2dx [21]. Initially, several parameters were manually set including magnification, pixel size, spherical aberration, accelerating voltage, and unit cell size, which was set to 69.0×173.5 Å (as previously determined by [22]). Next, the following 2dx “standard scripts” were run in order: Initialize, Calculate FFT, Get Defocus & Tilt, and Get Lattice & Tilt. Based upon the output from 2dx, the lattice parameters were manually adjusted as necessary to ensure accurate and consistent labeling of Bragg peaks (reciprocal lattice points) across all images in each exposure series. Additionally, the defocus value was manually set to zero to effectively ignore CTF correction. Finally, the following 2dx “standard scripts” were run in order: Refine Lattice, Set Sample Tilt, Get Spotlist for Unbending, Unbend I, Get Spotlist (complete), and Unbend II. After processing each CCD frame with 2dx, the Miller indices, amplitude, and IQ value of each Bragg peak were obtained from the corresponding APH/*.fou.nolimit.aph file.

2.5. Data analysis

The Fourier transform of the initial CCD frame in each exposure series was evaluated by visual inspection. Any exposure series containing less than eight images or with significantly non-isotropic or low-resolution initial diffraction patterns were discarded. Then, based on the isotropy and resolution of the visible Bragg peaks in the Fourier transform of each initial image, we selected the four best exposure series from each temperature for subsequent analysis. A computer program was implemented in Python to parse the 2dx output and calculate statistics.

Fourier space was arbitrarily divided into ten “resolution zones”: 4–5, 5–6, 6–8, 8–10, 10–15, 15–20, 20–30, 30–40, 40–60, 60–173.5 Å. For each zone, the mean and standard error of the normalized Fourier amplitudes and IQ values (defined in sections 2.6 and 2.7, respectively) of all “valid” Bragg peaks were calculated. A Bragg peak was determined to be “valid” if its background-subtracted amplitude was non-zero and its IQ value was less than seven in the initial image of the exposure series. Statistics were combined from all exposure series for each temperature and fit using least squares regression to appropriate parametric models (discussed below). Critical exposures were calculated based on the resulting regression models. The statistical significance of differences in critical exposures between specimen temperatures was evaluated using a two-sample T-test with a 0.05 significance level.

2.6. Normalized Fourier amplitude

The traditional measure for evaluating radiation damage has been the normalized Fourier amplitude of Bragg peaks [23], which generally fade with increasing cumulative exposure. Let i ∈ [0,1,2,…] be the index of the images in an exposure series, such that i = 0 is the initial image (with 10 e⁻/Ų cumulative exposure), i = 1 is the second image of the same area (resulting in 20 e⁻/Ų cumulative exposure), and so on. Then the normalized amplitude of the Bragg peak with Miller indices (h,k) having background-subtracted peak amplitude P is,

$$N{A}_{(h,k),i}=\frac{P_{(h,k),i}}{P_{(h,k),0}}$$

Thus, all Bragg peaks in the first image of an exposure series have normalized amplitudes of 1.0 by definition. Generally, as the cumulative exposure increases in subsequent exposure series images, radiation damage disrupts the crystallinity and thus reduces the signal at each Bragg peak, causing the normalized amplitudes to decrease. However, it is also possible that radiation-induced structural rearrangements and/or ice density reductions could cause normalized amplitudes to increase with exposure. Since this effect is rarely observed, we identify such cases of increasing amplitude as “abnormal.”

As with previous studies [10,23], we defined e⁻¹ as the threshold value for normalized amplitude. The cumulative exposure at which this threshold value is reached is called the critical exposure.

2.7. IQ value

IQ value is a measure of signal-to-noise ratio [25], which serves as a predictor of the phase error at each Bragg peak [7]. The IQ value of the Bragg peak with exposure series index i and Miller indices (h,k), having background-subtracted peak amplitude P and mean background amplitude B is,

$$I{Q}_{(h,k),i}=1+\text{min}\left(8,\text{floor}\left[7\frac{B_{(h,k),i}}{P_{(h,k),i}}\right]\right)$$

Low IQ values denote high signal-to-noise ratio and small expected phase error. Bragg peaks with IQ values less than or equal to 7 are generally considered useful for data analysis [25], since they have expected phase error less than 45° and probability of false signal less than 0.30 [7]. Therefore, we use the IQ value of 7 as the critical exposure threshold for our analysis.

3. Results

3.1. Qualitative analysis

Effects of radiation damage are most directly visible and quantified with crystalline specimens. The Fourier transform of such images reveals a pattern with well-defined, regularly spaced Bragg peaks corresponding to the repeating structures in the unit cells (for more information, see [7]). Radiation damage causes deviation from native structure by introducing disorder into crystalline specimens, affecting both the Fourier amplitude and phase of the Bragg peaks—first for high resolution peaks, and then with increasing damage, in lower resolution peaks. Fig. 1 provides an example of this loss of signal characteristic of radiation damage, exemplified by the fading of Bragg peak intensities as cumulative exposure increases. As expected, this general pattern of fading was visible in every exposure series at all four temperatures examined.

Figure 1.

An example of Fourier transforms of 300 kV images from an exposure series of a catalase crystal at 100 K. Only a quarter-plane of the Fourier-space is shown, with the origin of each Fourier transform in the bottom-right of each frame. Each image was collected with 10 e⁻/Ų exposure, thus exposing the sample to an incrementally higher cumulative exposure in each image (shown in the top left of each frame).

3.2. Regression models

In order to quantify the relationship between cumulative exposure and the behavior of Bragg peaks, we fit parametric models to the measured data (normalized amplitude or IQ value). Previous studies have modeled Fourier amplitude decay with respect to cumulative exposure as a simple exponential function [10,23]. Residuals from the simple exponential regression analysis of our data exhibited a clear relationship to cumulative exposure (data not shown), indicating that the functional form of this model did not completely explain the data. In general, the simple exponential model overestimated the data at low cumulative exposures and underestimated the data at high cumulative exposures. We improved the fit by adding a square-root term in the exponential function, resulting in models of the form,

$$M(D,R)\propto \text{exp}\left[-a_{R}D-b_R\sqrt{D}\right]$$

where M(D,R) is the mean normalized amplitude or IQ value in resolution zone R at total cumulative exposure D, and a_R and b_R are fit coefficients.

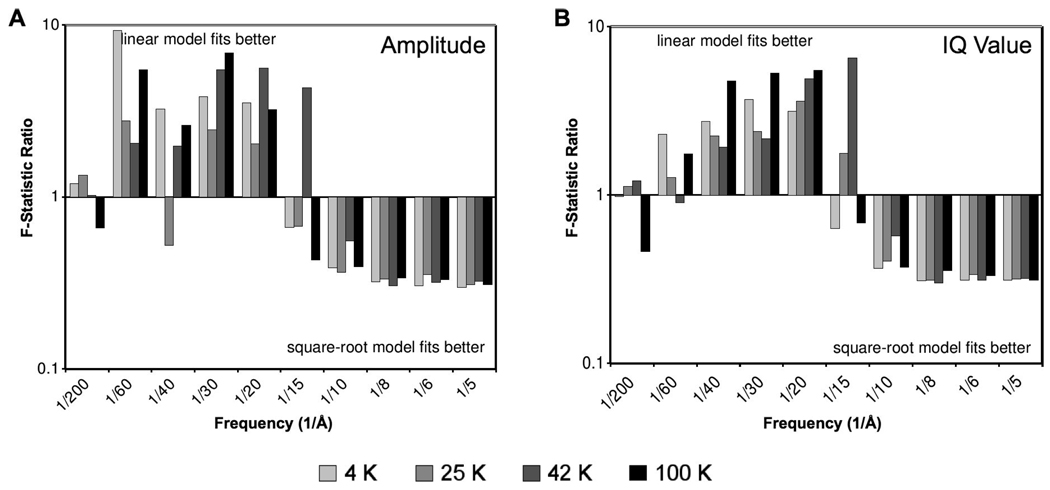
To evaluate the quality of our regression model, we compared the chi-squared values of three separate models: (1) the complete model with both linear and square-root terms, (2) a simple exponential model (by setting b_R = 0), and (3) an exponential square-root model (by setting a_R = 0). Pairwise comparisons were completed by calculating the F-statistic, which is a ratio of the quality of fit (chi-squared value) from each model. For all resolution zones, the F-statistics confirm that the complete model (1) improves the fit compared to either of the partial models (2 or 3). Moreover, pairwise comparison of the two partial models reveals a correlation with spatial frequency. Fig. 2 shows the F-statistics computed between the linear (2) and square-root (3) models. At high resolution, the square-root model (3) provides an improved fit compared to the linear model (2), while at lower resolution, the linear model (2) seems to fit better than the square-root model (3). Although this trend is observed in both measures of our data, the effect is more pronounced for normalized amplitude (Fig. 2A) compared to IQ value (Fig. 2B). Both measures exhibit a division between the two behaviors at about 15 Å.

Figure 2.

Plots of F-statistics (ratio of chi-squared values) comparing the quality of fit of two different parametric models of the data: exponential function of exposure (linear model), and exponential function of square-root of exposure (square-root model). Ratios greater than one indicate that the data is best fit by the linear model, and ratios less than one indicate that the data is best fit by the square-root model. The plots based on both normalized Fourier amplitude (A) and IQ value (B) reveals a clear correlation with resolution zone.

The improved fit of the square-root model (3) in high-resolution zones (<15 Å) implies that high-resolution Bragg peaks generally respond to irradiation by a steep initial decay. In contrast, the improved fit of the linear model (2) in low-resolution zones (>15 Å) implies that Bragg peaks at lower resolution tend to decay gradually, eventually approaching an asymptote. This differential behavior suggests that there may be two different mechanisms of radiation damage that affect high and low resolution information differently.

3.3. Fourier amplitude behavior

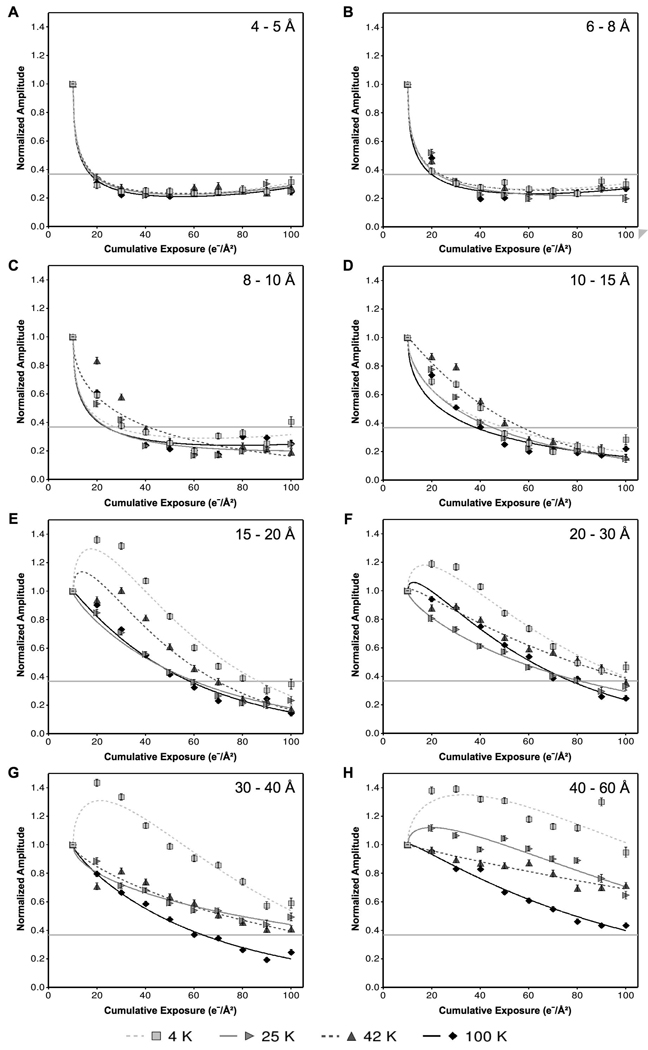
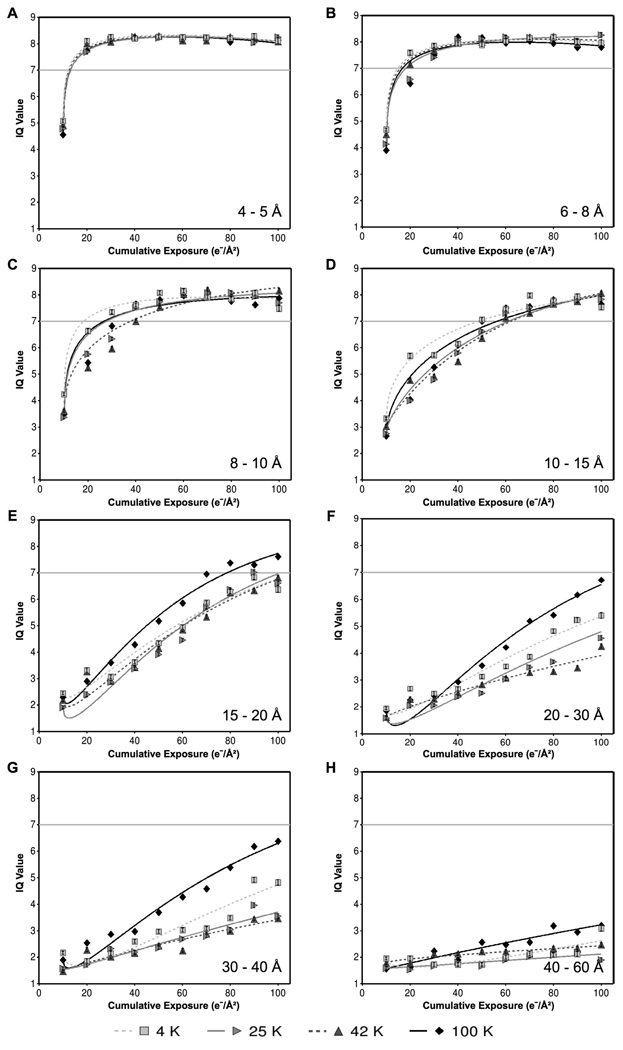
Fig. 3 shows the mean normalized amplitudes with respect to cumulative exposure for six different resolution zones, ranging from resolutions applicable to high-resolution single-particle studies (e.g., 4–5 Å) to resolutions applicable to electron tomography (e.g., 40–60 Å). At high resolution, such as 4–5 Å (Fig. 3A) and 6–8 Å (Fig. 3B), the specimen exhibits similar exposure tolerance in all four temperatures. In these resolution zones, the data points and regression model curves are nearly identical regardless of specimen temperature. Lower resolution zones from 15 to 60 Å (Fig. 3D–H) reveal discernable differences between the specimen temperatures, with liquid nitrogen temperature generally decaying faster than the three lower temperatures.

Figure 3.

Comparison of the effects of four different specimen temperatures on the radiation-induced decay of normalized Fourier amplitudes, grouped into resolution zones: (A) 4–5 Å, (B) 6–8 Å, (C) 8–10 Å, (D) 10–15 Å, (E) 15–20 Å, (F) 20–30 Å, (G) 30–40 Å, (H) 40–60 Å. Each data point represents the mean normalized amplitude of all Bragg peaks within the specified resolution zone at the specified cumulative exposure across all exposure series at the specified temperature. Curves were fit to the data by the method of least squares using an exponential model of exposure and square-root of exposure. Critical exposures were determined by the intersection of the fit models with the threshold value of e⁻¹ (shown as a horizontal gray line).

In these low resolution zones, the behavior at 4 K is particularly striking (Fig. 3E and Fig. 3F). While the other three specimen temperatures show the expected mean normalized amplitude decay, 4 K exhibits a significant initial increase between 10 and 20 e⁻/Ų. We observed this “abnormal” behavior at 4 K in all resolution zones between 15 and 60 Å.

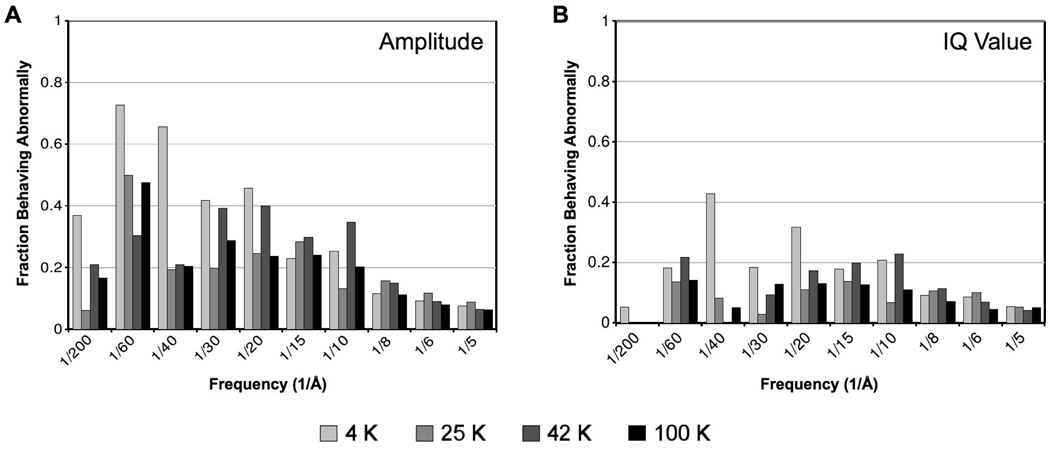
To further analyze this mean behavior, we examined the behavior of each individual Bragg peak from the first to second image in each exposure series. Results of this analysis are illustrated in Fig. 4A, which compares the effect of specimen temperature on the fraction of Bragg peaks behaving abnormally in each resolution zone. Consistent with the mean behavior illustrated in Fig. 3, the greatest frequency of abnormal behavior of individual peaks occurs at 4 K, and it correlates with resolution zone, with low-resolution Bragg peaks having a greater probability of abnormal behavior than high-resolution peaks across all temperatures. Specifically, from 30 to 60 Å resolution, more than half of the Bragg peaks at 4 K increase in amplitude in response to initial exposures. Therefore, the mean increase in normalized amplitude at 4 K is not due to behavior of outliers, but rather reflects the overall behavior of Bragg peaks at 4 K.

Figure 4.

Comparison of the effect of specimen temperature and spatial frequency on the fraction of Fourier peaks behaving “abnormally” in the second image of each exposure series. We define abnormal behavior as having either increasing normalized amplitude (A) or decreasing IQ value (B) between the first and second image in an exposure series (10 to 20 e⁻/Ų cumulative exposure). The plots show the fraction of peaks that initially behaved abnormally in each resolution zone across all exposure series examined at each temperature. Overall, normalized Fourier amplitudes in low-resolution zones at 4 K clearly show the most abnormal behavior.

Histograms of the behavior of individual Bragg peaks across all exposure series at each temperature follow the behavior of a stochastic process (data not shown), implying that radiation does not preferentially cause specific Bragg peaks to respond abnormally. Thus, the increased abnormal behavior at 4 K is probably not due to specific structural changes, but rather random occurrences from radiation damage.

Since the mean normalized amplitudes at 4 K initially increase in low-resolution zones, the critical exposures at these resolutions are biased towards higher values and do not reflect the entire impact of radiation damage at 4 K. Therefore, in the following comparisons, we ignore the critical exposure values at 4 K for resolution zones below 15 Å.

3.4. Normalized Fourier amplitude

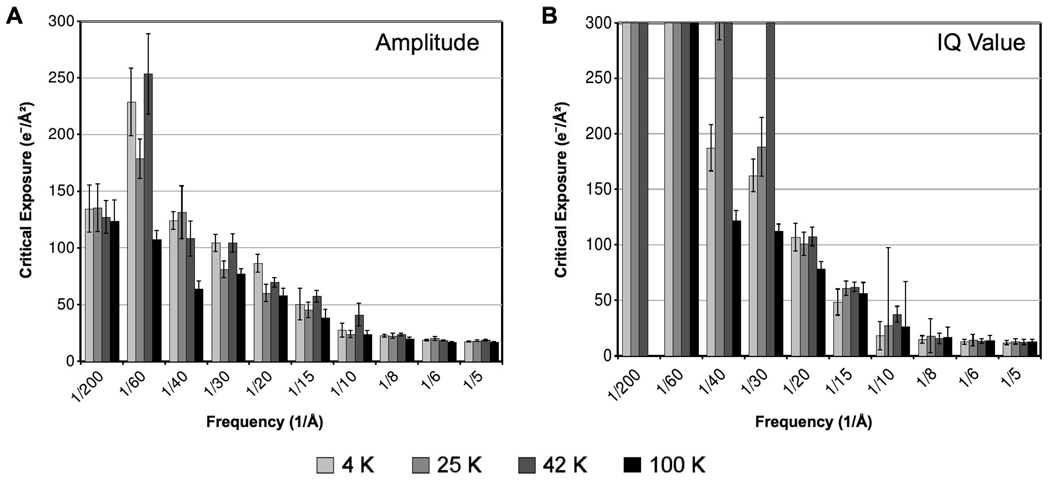
Quantitative comparisons of damage are visible in Fig. 5A, which shows the critical exposures based on normalized amplitudes at all four temperatures across all resolution zones examined. At high resolution, the Bragg peak amplitudes behave similarly with respect to exposure at all four specimen temperatures. Pairwise comparisons of critical exposures revealed no statistically significant differences within resolution zones higher than 15 Å (p>0.05). In particular, for resolution zones in the 4–8 Å range, the critical exposures are nearly identical across all four specimen temperatures. Within the 8–10 and 10–15 Å resolution zones, there is a moderate improvement at 42 K compared to the other temperatures (~1.6× and ~1.3×, respectively), but this improvement is uncertain since it is within the error interval for our significance level (p>0.05).

Figure 5.

Overall comparison of exposure tolerance at four specimen temperatures according to mean normalized Fourier amplitude decay (A) and mean IQ value decay (B) of Bragg peaks across a broad range of resolution. The critical exposure is the cumulative exposure at which the fitted model of the mean normalized amplitudes crosses e⁻¹, or the fitted model of the mean IQ values crosses 7.

As previously described, for resolution zones lower than 15 Å, we ignored the critical exposures at 4 K due to its abnormal behavior. At these lower resolutions, the intermediate temperatures (25 and 42 K) appear to provide a slight improvement compared to liquid nitrogen. We observed a statistically significant improvement at 42 K compared to 100 K in the 20–60 Å resolution range (~1.4–2.4×; p<0.02). 25 K specimen temperature also shows a statistically significant improvement compared to 100 K in the 30–60 Å resolution range (~1.7–2.1×; p<0.02). Overall, ignoring 4 K, our analysis indicates that 42 K may provide the greatest cryo-protection at low resolution (20–60 Å). However, the difference between the intermediate temperatures (25 and 42 K) in this resolution range is rarely significant based on the errors associated with each value, and thus these intermediate temperatures are often statistically indistinguishable (p>0.04). (Note that errors are large in these low-resolution zones because critical exposures above 100 e⁻/Ų were not directly observed and thus had to be extrapolated from the fit models at each temperature shown in Fig. 3.)

3.5. IQ value

Fig. 6 shows the mean IQ values with respect to cumulative exposure for six selected resolution zones, ranging from resolutions applicable in high-resolution single-particle studies (e.g. 4–5 Å) to resolutions applicable in electron tomography (e.g. 40–60 Å). As with our observations of normalized amplitude, we observed similar IQ value exposure response across all four specimen temperatures at high resolution, such as 4–5 Å (Fig. 6A) and 6–8 Å (Fig. 6B). At lower resolution, we observed the best overall performance at 42 K and the worst performance at either 4 K or 100 K (Fig. 6C–H). In contrast with the behavior of normalized amplitude, we did not observe significant “abnormal” behavior of IQ values at 4 K. Indeed, analysis of the behavior of individual Bragg peaks shows significantly less abnormal behavior of IQ values (Fig 4B) compared to normalized amplitudes (Fig. 4A). Still, as with normalized amplitude, we noted the most abnormal IQ value behavior in the Bragg peaks at low resolution (15–60 Å) at 4 K.

Figure 6.

Comparison of the effects of four different specimen temperatures on the radiation-induced decay of IQ values, grouped into resolution zones: (A) 4–5 Å, (B) 6–8 Å, (C) 8–10 Å, (D) 10–15 Å, (E) 15–20 Å, (F) 20–30 Å, (G) 30–40 Å, (H) 40–60 Å. Each data point represents the mean IQ value of all Bragg peaks within the specified resolution zone at the specified cumulative exposure across all exposure series at the specified temperature. Curves were fit to the data by the method of least squares using an exponential model of exposure and square-root of exposure. Critical exposures were determined by the intersection of the fit models with the threshold value of 7 (shown as a horizontal gray line).

Quantitative comparisons of critical exposures based on IQ values are illustrated in Fig. 5B. At high resolution (4–15 Å), all four temperatures deliver similar critical exposures (p>0.20). At lower resolution, we observed the worst critical exposures at 4 K and 100 K. In particular, critical exposures at 4 K and 100 K were significantly worse than at 42 K for 20–60 Å resolution (p<0.01), and significantly worse than at 25 K for 30–60 Å resolution (p<0.01). We observed the best low-resolution (20–60 Å) cryo-protection at 42 K, where critical exposures were ~3–4× greater than at 100 K.

We also found that the values of the critical exposures are often not equivalent between normalized amplitudes (Fig. 5A) and IQ value (Fig. 5B). The discrepancy is especially noticeable at low resolution, where the IQ value generally shows substantially higher critical exposures than the normalized amplitude. This difference is expected due to the threshold values used in our analysis. Bragg peaks at low resolution generally have low IQ value, corresponding to a high amplitude-to-background ratio. If the background remains approximately constant across the entire exposure series, then a reduction in the peak amplitude of e⁻¹ will not necessarily be enough to push the IQ value past its threshold value of 7. For example, assuming a constant background, a Bragg peak with IQ value of 2 must have normalized amplitude decay to ~e^−1.5 in order to reach the IQ value threshold of 7. Therefore, it is more meaningful to rely on the relative differences in critical exposures between temperatures, rather than the specific values of the critical exposures, for evaluating the relative merits of specimen temperatures for radiation damage protection.

4. Discussion

Radiation damage of various biological samples has been studied over the course of the past four decades [8–11,15,19,20,24,26,27]. With a few exceptions, most of these studies were directed at sub-nanometer resolution data. The successes of several structural studies at near-atomic resolution in both electron crystallography [1] and single particle analysis [2,3] have attracted considerable interest in using liquid helium as the cryogen in electron microscopy. However, increasing numbers of high-resolution structures have also been reported using liquid nitrogen temperature [4,5], and several studies have suggested specific undesirable effects at liquid helium specimen temperatures [19,20]. This study was aimed at thoroughly assessing radiation damage effects quantitatively, using multiple criteria, across a broad range of target resolutions.

4.1. Methods for assessing radiation damage

Conducting such a study of radiation damage is conceptually simple, yet practically challenging due to considerations of sample quality variation, specimen preservation method, exposure rate calibration, specimen stage stability, and method of assessment. We chose ice-embedded catalase crystal as the specimen of study. Crystalline specimens are advantageous for radiation damage studies because one can assess damage quantitatively at the Bragg peaks in reciprocal (Fourier) space. Since catalase crystal has a relatively large unit cell (69×173.5 Å), our data covers a broad range of resolutions, from resolution zones of interest in single particle analysis (e.g., 4–10 Å) to resolution zones of interest in tomography of whole cells (e.g., 40–60 Å).

In contrast to earlier studies that were often based on electron diffraction of crystalline specimens, we used bright-field imaging, which represents nearly all modern cryo-EM studies. Using imaging instead of diffraction allowed us to more closely match our study with the experimental conditions used in actual single-particle or tomographic data collection. Furthermore, it has been shown that electron diffraction and Fourier transforms of bright-field images can differ [28], possibly because imaging may be more sensitive than electron diffraction to certain radiation damage effects, such as specimen movement. Consequently, to quantitatively analyze crystal quality, we used Fourier transforms of bright field images to reveal Bragg peaks, corresponding to the crystal diffraction pattern (Fig. 1).

We analyzed the exposure response of Bragg peaks in Fourier transforms of images via normalized Fourier amplitude and IQ value. While these measures are related, they present two complementary perspectives regarding the data. Radiation damage impedes high-resolution data collection in cryo-EM by altering the specimen’s structure factor, which is comprised of both amplitude and phase information. Use of both normalized amplitude and IQ value (which is a predictor of phase error) allowed us to examine both components of the specimen’s structure factor, thus producing a more complete investigation of radiation damage effects.

4.2. Effects of specimen temperature on radiation damage at 4–20 Å

Results of our study show that, for high resolution (4–8 Å) typical of single particle work, none of the liquid helium cooled temperatures examined (4 K, 25 K, 42 K) provide significant improvement in cryo-protection compared to liquid nitrogen (100 K). Within these resolution zones, all four temperatures examined behave similarly, with less than 20% difference between the critical exposures of any two specimen temperatures, according to both normalized amplitude (Fig. 3A–B) and IQ value (Fig. 6A–B). By both measures, we observed the critical exposure for all four specimen temperatures in this resolution range to be 10–20 e⁻/Ų (Fig. 5), which is similar to the typical exposures of high-resolution single particle studies.

At slightly lower resolution (8–20 Å), we did not observe any significant improvements in exposure response at the three lower temperatures compared to 100 K, both in terms of normalized amplitude and IQ value decay. We conclude that, for target resolutions typical of single-particle cryo-EM (4–20 Å), there is no evidence that liquid helium cooling provides any advantage over liquid nitrogen with respect to cryo-protection from radiation damage.

Single particle electron microscopy at liquid helium temperature often has lower data yields compared to imaging at liquid nitrogen specimen temperature. For example, in the recent 4.5 Å structure of the bacteriophage ε15, only 40% of the ~3000 micrographs collected at ~4 K showed strong signal beyond 6 Å resolution and were thus included in the reconstruction [3]. We inspected the initial images (at 10 e⁻/Ų cumulative exposure) in each of our exposure series to assess the overall quality of images at each temperature with minimal radiation damage effects. Table 1 shows statistics of image quality based on visual inspection (isotropy and visible high-resolution spots). We observed the most consistent high-quality data with liquid nitrogen (100 K), where nearly all initial images produced Fourier transforms with isotropic, high-resolution diffraction patterns. 42 K provided the next most consistent high-quality data, and 25 K and 4 K had the lowest data yields. Therefore, since radiation damage effects between all four temperatures are statistically equivalent at high resolution (4–20 Å), and the quality of images appears most consistent at 100 K compared to lower temperatures, liquid nitrogen would appear to be the optimal cryogen for efficient high-resolution single particle imaging.

		Analysis of First Image in Each Exposure Series
Specimen Temperature	Exposure Series Collected	% with Isotropic FFT	% with Visible Spots <10 Å	% with Visible Spots <8 Å
4 K	7	57	100	71
25 K	16	50	69	56
42 K	26	77	96	77
100 K	9	89	100	89

4.3. Effects of temperature on radiation damage at 20–60 Å

For applications such as cryo-tomography, where lower resolution (20–60 Åand higher cumulative exposures (>40 e⁻/Ų) are typically used, the choice of the optimal specimen temperature is ostensibly more complex. Our results based on normalized amplitudes reveal a statistically significant improvement at 42 K (~1.4–2.4×) and 25 K (~1.7–2.1×) compared to liquid nitrogen temperature across the resolution range of 20–60 Å (Fig. 2; Fig. 5). Similar improvements were observed in our analysis of IQ value (Fig. 5; Fig. 6). Thus, by both measures of data quality, we find that specimen temperatures of 25 and 42 K appear to provide improved cryo-protection compared to 100 K.

4.4. Unusual radiation damage effects at 4 K

As previously noted, we were not able to directly evaluate critical exposures from normalized Fourier amplitudes at 4 K in low-resolution zones (>15 Å), due to the significant abnormal behavior of Bragg peaks at this temperature. The initial increase in normalized amplitudes at 4 K (Fig. 2E–H) causes misleading critical exposures at 4 K, because the values are inflated by the abnormal behavior. It is unlikely that this initial increase in some Fourier amplitudes signifies a radiation-induced “improvement” in the protein crystal, especially since IQ values decay as expected.

Similar to our observations, radiation induced amplitude increases of low-resolution Fourier peaks have also been observed near the transition temperature of lipid bilayers, likely due to large structure factor changes [24]. Such structure factor changes could result from radiation-induced bond rupture and rearrangement or effects of local specimen heating. In particular, significant structural rearrangements may be more frequent at 4 K due to the cage effect, which restricts the movement of damaged chemical bonds within the specimen [7,29]. Since liberated atoms are kept in close proximity, they may be more likely to engage in secondary chemical reactions, which would alter the specimen’s structure factor.

To further investigate the abnormal amplitude behavior at 4 K, we examined the individual Bragg peaks from the first and second images in each exposure series. Fig. 7 shows examples of individual Bragg peaks from two separate exposure series at 4 K. As illustrated by the examples, most of the Bragg peaks that initially increased in amplitude also increased in spot diameter. Such spreading of Bragg peaks implies deviation from perfect crystallinity, often due to beam-induced specimen movement [7].

Figure 7.

Examples from two different exposure series (separated horizontally by a gray line) of the initial behavior of low-resolution Fourier peaks at 4 K. The Miller index and corresponding resolution are shown below each example. The middle example (−1,4) shows the Fourier peak fading with increasing cumulative exposure as expected. However, many of the peaks at 4 K behaved abnormally, increasing in intensity in the second image. Many of these peaks that increased in intensity also appeared to expand in diameter.

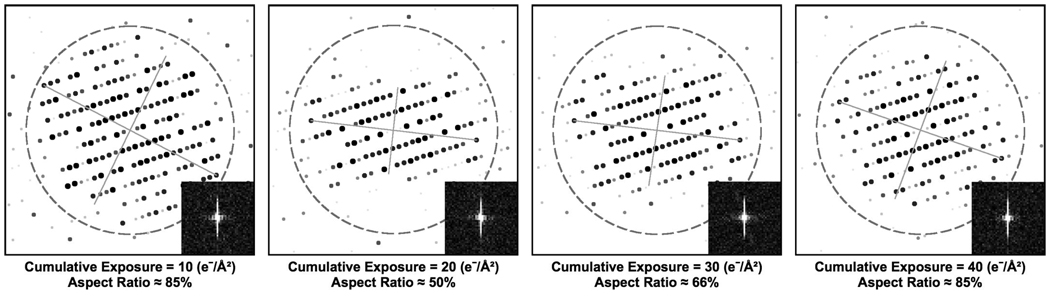
While comparing the behavior of the Fourier transforms at 4 K to other specimen temperatures, we also observed a second trend unique to 4 K. In three out of the four exposure series examined at 4 K, the second image in each exposure series (at 20 e⁻/Ų cumulative exposure) became significantly anisotropic compared to the first image in the exposure series (at 20 e⁻/Ų cumulative exposure). Fig. 8 shows IQ plots from one of these exposure series at 4 K. We only observed this sudden loss of isotropy in the second image of each exposure series at 4 K; none of the other three specimen temperatures exhibited similar behavior. This loss of high-resolution information in one direction is reminiscent of Fourier transforms of images acquired while the specimen stage is drifting. However, stage drift is unlikely since the stage was not seen to move between images in an exposure series and it appeared stable during all other images in each exposure series. Therefore, the transient loss of isotropy at 4 K is likely due to radiation-induced effects.

Figure 8.

Example of IQ plots from the first four images in an exposure series at 4 K. Each plot represents the Fourier transform of an image by showing the IQ values of each Fourier peak (with the largest dots representing an IQ value of 1, and smaller spots representing larger IQ values up to 6). The dashed circle shows the approximate location of the first CTF zero, and the inset in each frame shows the unscattered (central) peak in the respective Fourier transform. The gray cross on each IQ plot corresponds to the axes of ellipse enclosing all Fourier peaks with IQ values of 1 or 2. We quantify isotropy using the ratio of the lengths of these axes (aspect ratio), so that an aspect ratio of 100% corresponds to a perfectly isotropic pattern of Fourier peaks. In three out of the four exposure series examined at 4 K, the Fourier transform of the second image (20 e⁻/Ų cumulative exposure) suddenly loses isotropy, indicating either beam-induced specimen movement or charging. This effect was not observed at any other specimen temperature.

One possible explanation is specimen charging, which has been previously noted as a challenge of operating at 4 K [12,18]. However, we could not clearly discern other indicators of charging such as changes in the contrast transfer function (CTF) Thon rings or changes in the shape of the unscattered peak at the Fourier transform center [7] (Fig. 8). Alternatively, beam-induced translations or broad rotations of large specimen areas could cause temporary anisotropy similar to stage drift, and would be largely undetectable in electron diffraction experiments. Such broad translations may be caused by changes in the vitreous environment surrounding the specimen. It has been suggested that vitreous water collapses to a higher density state when irradiated at 4 K [30,31], and it is possible that these density changes could exert mechanical stresses on the protein crystal, causing some specimen movement. Analogous radiation-induced stresses have been noted as causing significant expansion from breaking covalent bonds [32] and contraction from mass loss [33]. These stresses could not only contribute to specimen movement, but also to broad structural rearrangements that would be reflected in erratic changes in the specimen’s structure factor at low resolutions.

Overall, we observed several radiation damage effects unique to 4 K, including abnormal amplitude increase with associated broadening of low-resolution Bragg peaks and transient loss of isotropy. So, while the reduced entropy at 4 K may improve cryo-protection by slowing down the movement of liberated protein fragments, this benefit is apparently negated by radiation-induced structural rearrangements and/or beam-induced specimen motion.

5. Conclusion

Because radiation damage limits the maximum attainable resolution in cryo-EM experiments, conditions must be optimized to reduce its effects. Investigators routinely use several strategies to reduce radiation damage on biological specimens, including use of high accelerating voltages, low exposure imaging, and cryogenic specimen temperatures.

We have examined radiation damage effects on protein crystals at four cryogenic specimen temperatures: 4 K, 25 K, 42 K, and 100 K. Analysis of the behavior of both normalized Fourier amplitudes and IQ values suggest that radiation damage effects are statistically equivalent across all four temperatures for the high resolution typical of single-particle cryo-EM imaging or electron crystallography (4–20 Å). Combined with the improved consistency of high-quality data obtained at 100 K, we conclude that liquid nitrogen specimen temperature is best suited for single-particle imaging.

At lower resolution (20–60 Å), the use of liquid helium temperature (4 K) in cryo-EM imaging apparently introduces or amplifies several radiation damage effects, which do not significantly affect specimens at higher temperatures. We observed beam-induced specimen movement and erratic radiation-induced structure factor changes at 4 K, which were not as pronounced at 25, 42, or 100 K, while others have observed increased specimen charging, changes in ice density [30,31], and increased local specimen movement and bubbling effects [19] at 4 K compared to liquid nitrogen temperature. Our analysis indicates that at these lower resolution zones, intermediate temperatures (25 and 42 K) may improve exposure tolerance (~2×) compared to liquid nitrogen temperature, without introducing the deleterious effects evident at 4 K. Therefore, these intermediate temperatures may be advantageous for “high-exposure” imaging applications such as electron cryo-tomography.