Abstract
Anti-cancer drugs targeted to specific oncogenic pathways have shown promising therapeutic results in the past few years; however, drug resistance remains an important obstacle for these therapies. Resistance to these drugs can emerge due to a variety of reasons including genetic or epigenetic changes which alter the binding site of the drug target, cellular metabolism or export mechanisms. Obtaining a better understanding of the evolution of resistant populations during therapy may enable the design of more effective therapeutic regimens which prevent or delay progression of disease due to resistance. In this paper, we use stochastic mathematical models to study the evolutionary dynamics of resistance under time-varying dosing schedules and pharmacokinetic effects. The populations of sensitive and resistant cells are modeled as multi-type non-homogeneous birth-death processes in which the drug concentration affects the birth and death rates of both the sensitive and resistant cell populations in continuous time. This flexible model allows us to consider the effects of generalized treatment strategies as well as detailed pharmacokinetic phenomena such as drug elimination and accumulation over multiple doses. We develop estimates for the probability of developing resistance and moments of the size of the resistant cell population. With these estimates, we optimize treatment schedules over a subspace of tolerated schedules to minimize the risk of disease progression due to resistance as well as locate ideal schedules for controlling the population size of resistant clones in situations where resistance is inevitable. Our methodology can be used to describe dynamics of resistance arising due to a single (epi)genetic alteration in any tumor type.
Keywords: targeted cancer therapy, resistance, evolution, stochastic models
1. Introduction
A new generation of anti-cancer drugs targeted to specific oncogenic pathways has emerged in recent years as a promising alternative to chemotherapy and radiation. Often referred to as ‘targeted therapeutics,’ these drugs inhibit specific protein targets which are essential for the continued viability and proliferation of cancer cells. Thus, they hold the potential to more effectively inhibit tumor growth with far less toxic effects than standard chemotherapeutic agents. Examples of targeted therapies include small-molecule inhibitors of the JAK2, FLT3 and BCR-ABL tyrosine kinases in leukemias (e.g. cep701, tg101348, imatinib (Gleevec)), and the EGFR pathway in lung, breast, and colorectal cancers (e.g. erlotinib (Tarceva), getinib (Iressa), and cetuximab (Erbitux)). Other targeted therapies include drugs blocking tumor invasion and metastasis, anti-angiogenesis agents, pro-apoptotic drugs and proteosome inhibitors.
Despite the success of targeted therapies in the past few years, drug resistance remains an important obstacle to the cure or prolonged control of tumors. Resistance may emerge due to a variety of reasons including changes in the binding site of the drug target, metabolism or export mechanisms via genetic or epigenetic alterations. For example, the tyrosine kinase inhibitors erlotinib and gefitinib initially elicit dramatic responses in non-small cell lung cancer patients with somatic gain-of-function mutations in the kinase domain of the epidermal growth factor receptor (EGFR) (Pao et al. (2004)). However, almost all patients eventually develop ‘acquired’ resistance which has been associated with a secondary point mutation (T790M) in the kinase domain of EGFR or amplification of MET (Pao et al. (2005); Engelmann et al. (2007)). Analogous mutations lead to acquired resistance to imatinib, a kinase inhibitor used in the treatment of chronic myeloid leukemia (CML) (Gorre et al. (2001)). Although second generation kinase inhibitors have been developed for CML, numerous point mutations have been identified which confer resistance to these drugs as well. These examples illustrate a significant weakness of targeted therapies: focused action on specific molecular targets renders these therapies vulnerable to alteration of the drug target by somatic mutations.
A better understanding of the evolution of resistant populations during therapy may enable the design of more effective therapeutic regimens using existing drugs which prevent or delay progression of disease due to resistance. Since mutations conferring resistance can arise as random events during the DNA replication phase of cell division, the emergence of resistant cells is described well by stochastic mathematical models wherein resistant cells arise during sensitive cell replication. Several stochastic models have been proposed to study the dynamics of resistance to chemotherapy and anti-cancer therapies. Coldman and co-authors pioneered the field by introducing stochastic models of resistance to chemotherapy (see e.g., Coldman and Goldie (1986); Coldman and Murray (2000) and references therein) to guide treatment schedules. In Coldman and Goldie (1986), a branching process model of tumor growth with a differentiation hierarchy was introduced to study the emergence of resistance to one or two equivalent chemotherapeutic drugs. In this study, the birth and death rates of cells were modeled as time-independent constants; cells were assumed to divide with a fixed and common interdivision time and each sensitive cell division gave rise to a resistant cell with a certain probability. The treatment was modeled as a series of fixed time points at which either of the drugs could be administered at a fixed dose and the effect of drug was modeled as an additional probabilistic cell kill law on the existing population. The goal of the model was to schedule the sequential administration of both drugs in order to maximize the probability of cure. A generalization of this approach was later studied by Day (1986), who relaxed the assumption of equivalence or ‘symmetry’ between the two drugs. This approach provided the basis of OncoTCap, a software developed by Day and colleagues (http://www.oncotcap.pitt.edu/2000/) that performs simulations of the treatment outcome of a single patient to assess the probability of cure. In a later study by Coldman and Murray (2000), toxic effects of chemotherapy on normal tissues were incorporated and an optimal control problem was formulated to maximize the probability of tumor cure times the probability of no toxicity. Later, Iwasa et al. (2003) used a multi-type branching process model to study the probability of resistance due to one or multiple mutations in populations under selection pressure. Komarova and Wodarz (2005) and Komarova (2006) developed a model for multi-drug resistance using a multi-type birth-death process in which the resistance to each drug was conferred by genetic alterations within a mutational network. In this model, birth and death rates of each cell type were constant over time and cells had an additional drug-induced death rate if they were sensitive to the drugs. The authors studied the evolution of resistant cells before and after the start of treatment and calculated the probability of treatment success under continuous drug treatment scenarios with varying numbers of drugs. More recently, Iwasa et al. (2006) and Haeno et al. (2007) studied the dynamics of resistance emerging due to one or two genetic alterations in a clonally expanding population of sensitive cells prior to the start of therapy; these scenarios were also modeled using a time-homogenous multi-type birth-death process.
In previous work we studied the dynamics of resistance during pulsed and continuous administration strategies of targeted drugs (Foo and Michor (2009)). In the present paper we build upon this framework to study the effect of time-varying dosing schedules and pharmacokinetic effects on the evolutionary dynamics of resistance. The populations of sensitive and resistant cells are modeled as multi-type non-homogeneous birth-death processes in which the drug concentration affects the birth and death rates of both the sensitive and resistant cell populations. Thus, the birth and death rate of each cell population is modeled as a general time-dependent function. This extension allows us to consider the effects of more generalized treatment strategies as well as detailed pharmacokinetic phenomena such as drug elimination and accumulation over multiple doses. We confine our analysis to the single-drug case where resistance is conferred by a single genetic alteration; however, the theory can easily be generalized to multiple drug/mutation scenarios. We develop estimates for the probability of developing resistance and moments of the resistant cell population size. With these estimates, we can optimize treatment schedules over a subspace of tolerated schedules to minimize the risk of disease progression due to resistance as well as locate ideal schedules for controlling the population size of resistant clones in situations where resistance is inevitable.
2. Model
We model the cancer cell population during treatment with a multi-type non-homogeneous continuous-time birth-death process. Here we consider only the sub-population of cancer cells that is capable of self-renewal to produce and maintain a resistant cell clone. This sub-population may be represented by cancer ‘stem’ cells since resistance mutations arising in more differentiated cell types may be lost from the population due to their limited self-renewal capacity. The number of sensitive cancer cells at any particular time t is given by X(t), and similarly the number of drug-resistant cancer cells is given by Y (t). The sensitive cancer cells proliferate and die with time-dependent rates λX (t) and μX (t), respectively, while the resistant stem cells proliferate and die with rates λY (t) and μY (t). These rates reflect the effect of the treatment on the cancer cells and thus depend on how the drug concentration varies in time. During each sensitive cell division a mutation may arise with probability u, giving rise to a new resistant cell.
The process X(t) ≡ (X(t), Y (t)) represents the state of the sensitive and resistant cell populations at time t. We assume that initially, the population consists of M sensitive cells: X(0) = (M, 0). The infinitesimal transition probabilities for this process are given by:
| (1) |
We aim to answer the following questions: 1) Under a specified dosing regimen (i.e. given λX (t), μX (t), λY (t), and μY (t)), what is the probability that there are resistant cells in the population at any given time? 2) What is the expected number of resistant cells as a function of time? Can we quantify the variance of this number? 3) How do pharmacokinetic effects such as drug accumulation and elimination modulate the risk of resistance? 4) Given a range of dosing regimens constrained by toxicity limitations, what is the optimal dosing regimen that minimizes the probability of resistance? In the following, we derive analytical approximations to the stochastic process to address these questions.
3. Analytical approximations
In this section we obtain analytical approximations for the probability of resistance as well as the mean and variance of the resistant cell number at any given time t. Since performing exact numerical simulations of the stochastic processes is computationally costly, such analytical approximations are vital for exploring parameter dependence of the model and for testing multiple dosing strategies.
It is useful to first review the properties of a single-type birth-death process Z(t), with time-dependent birth and death rates λ(t) and μ(t). The infinitesimal transition probabilities for this process are given by
The mean of this process at time t is given by
| (2) |
where Z0 = Z (0). The variance of this process at time t is given by
| (3) |
where
In following sections we will also use the generating function for this process G(s, t) =  [sZ(t)] (see, e.g. Parzen (1999))
[sZ(t)] (see, e.g. Parzen (1999))
| (4) |
where
We note from the generating function that the probability of extinction of the process at time t can be rewritten as
| (5) |
thus showing that the probability of eventual extinction PZ,ext = limt→∞G(0, t) is equal to one if and only if .
3.1. Expected number of resistant cells
To approximate the size of the resistant cell population, we first estimate the rate at which resistant cells are produced from the sensitive cell population X(t). To simplify our analysis, we approximate the birth rate of the sensitive cell process in the model, λX (1 − u), with λX in the following calculations. Since the mutation rate u per cell division is typically small for a specific mutation (much less than 10−2), this approximation leads to an insignificant difference. In section 4, the validity of this approximation is demonstrated via agreement of our formulae with exact stochastic simulations of the full multi-type process given in (1).
Thus, the rate of production of resistant cells from the sensitive cell population is
| (6) |
where M is the initial sensitive population size. Then the expected number of resistant cells as a function of time is approximated with the convolution
| (7) |
3.2. Probability of resistance
We are interested in finding the probability that there exists at least one resistant cell at a particular time, T. Consider a small time interval Δt ≪ 1 and a partition of the time period [0, T ] into N small intervals of size Δt: {t0, t1, t2, …, tN }, where ti = iΔt and Δt = T/N. The probability of a resistance mutation arising from the sensitive cell process within a given time interval [ti, ti + Δt] is approximately b(ti) Δt, where b(ti) is the rate of production of resistant cells from the sensitive cell population.
Since we exclude the possibility of back-mutation from resistant to sensitive cells, we consider the population size of a resistant cell clone originating from one resistant cell to be a single-type birth-death process. Using equation (5), we find that the probability that a clone originating from a single resistant cell produced at time t is extinct by time T is given by
| (8) |
where
| (9) |
Let us now calculate the probability that at time T, there are no resistant cells that have arisen from clones originating in the partition interval [ti, ti + Δt]. This quantity is estimated by summing the probability that no sensitive cell divisions give rise to a resistant cell in this interval and the probability that a resistant cell is produced but its clone becomes extinct by time T; thus it is approximated as
The probability that there are no resistant cells at time T is then the probability that there are no resistant cells at time T that have arisen from clones originating in any partition interval [ti, ti +Δt], i = 0…, N − 1. This quantity can be written as
We can simplify this expression by taking a logarithm and then exponentiating:
| (10) |
where a Taylor series approximation for the logarithm is used before the third line. Finally, the probability of resistance at time T then becomes
| (11) |
where b(t) and Pext(t, T) are given by equations (6) and (8), respectively.
3.3. Conditional expected number of resistant cells
In the previous two sections we have considered R(t), the average number of resistant cells at time t, and PR(t), the probability that at least one resistant cell is present at time t. Let us now calculate the expected number of resistant cells present at time t, averaged only over those patients who harbor resistant cells at this time. To find this conditional number of resistant cells, we simply note that
| (12) |
This quantity is of clinical interest since we may wish to find the expected resistant cell population size averaged only over the cohort of patients who develop resistance.
3.4. Variance of the resistant cell number
We are also interested in the variance of Y (T) to understand the variability in size of the resistant cell population. In estimating moments higher than the mean it is important to consider the stochasticity of the production of resistant cells from the sensitive cell process, as well as the stochasticity of the growth of each resistant clone.
Suppose a single resistant cell is produced at time t. Consider the random variable representing the population size of the resulting resistant clone at a later time T. Following equation (4), its generating function is given by
where ŵ is defined as in equation (9).
Next, consider once again the partition of the time period [0, T ] into N small intervals of size Δt: {t0, t1, t2, …, tN }. We note that the number of resistant cells produced in each time interval [ti, ti+1] is one with probability b(ti) Δt and zero with probability 1 − b(ti) Δt, where we have neglected higher order terms of Δt. Then, its generating function is approximately given by
Now, define Si to be the random variable representing the number of resistant cells present at time T which arose from a clone beginning in the time interval [ti, ti+1]. The generating function of Si is therefore given by
where
The variance of Si is thus given by
Since the total population of resistant cells at time T is the sum of independent random variables Si, i from 0…N − 1, the variance of Y (T) is given by . Thus, we find that
| (13) |
| (14) |
3.5. Extension to cases of pre-existing resistance
Suppose that at the start of therapy there exists a small population of resistant cells. If these cells are completely resistant to therapy, then by definition no dosing schedule will alter the growth of the resistant clone. However, in the case of partial resistance, we may adapt the theory to calculate the probability of resistance and expected size of the resistant clone under various dosing schedules. Let us consider the initial population as two separate populations: M (1 − s) sensitive cells and Ms resistant cells, where s is the initial fraction of resistant cells. Then the probability of having no resistant cells present at time T is calculated by
| (15) |
where is the probability that there are no resistant cells at time T originating from the initial population of sensitive cells, and is the probability that the clone arising from the initial population of Ms resistant cells becomes extinct before time T. The first term, , is calculated as in the last line of display (10) with an initial population of M (1 − s) sensitive cells. The second term, , is calculated as in equation (5) with an initial population of Ms resistant cells. Thus the probability of resistance at time T is given by
| (16) |
Then the expected number of resistant cells at time T is given by
| (17) |
where Rsens(T), calculated as in equation (7), is the expected number of resistant cells arising from the initial population of M (1 − s) cells. The term Rres(T) is simply the expected size of the clone arising from the initial population of Ms resistant cells, calculated as in equation (2). The variance of the resistant cell population size in the case of pre-existing resistance can also be easily found using analogous calculations.
4. Numerical examples
In this section, we use stochastic simulations to validate the theoretical formulae derived above, which will later be used for predictions of optimal dosing strategies. Since the birth and death rates of the process in our model (equation (1)) are time-dependent, standard Monte Carlo event-driven simulation techniques for Poisson processes with constant rates cannot be used. To perform exact simulations of our non-homogeneous birth-death process, we instead employ a slightly modified sampling technique called adaptive thinning (Lewis and Shedler (1978)). In this algorithm, the exponential waiting times between events are generated by first defining a stepwise constant rate function which majorizes the true instantaneous rate at any time t. After each event, an exponential waiting time is generated with the majorizing rate. This event is accepted if a uniform random variate generated on [0, 1] falls below the ratio of the true rate to the majorizing rate; otherwise, the event is rejected. More details on the use of this standard simulation technique for non-homogenous Poisson processes can be found in texts on stochastic simulation (see for example, page 60, example 4.2 of Asmussen and Glynn (2007)).
In these examples, the initial population is comprised of M sensitive cells unless stated otherwise.
4.1. Example: A single-type non-homogeneous birth-death process
Consider a process Z(t) representing a population of a single cell type with a sinusoidal birth rate, λ(t) = A sin(θt) + B, and a constant death rate, μ(t) = C. We require B ≥ A and C ≥ 0 so that the birth and death rates are always non-negative. For these simple birth and death rates, we calculate that for B ≤ C, the probability of extinction is one. This can be seen by noting that , so diverges as t → ∞ when B ≤ C. From equation (5), this implies that the probability of extinction is one.
Mean behavior of process
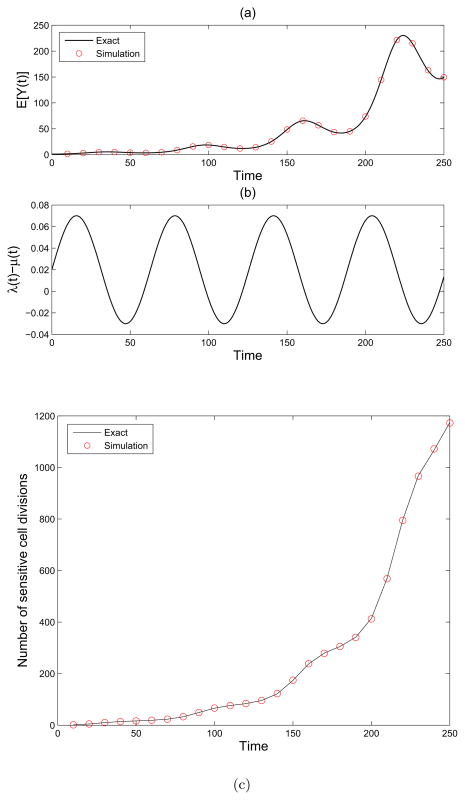
This process Z(t) with initial population size of 1 is simulated using the adaptive thinning algorithm described above. In Figure 1(a) we plot the simulation mean in red circles and the exact mean, given in (2), as a black line. Figure 1(b) shows the birth rate minus the death rate, λ(t) − μ(t), as a function of time.
Figure 1.
A single-type non-homogeneous birth-death process. (a): Simulation (red circles) and theoretical (black line) mean of the single-type birth and death process Z(t) with birth rate λ(t) = 0.05 sin(0.1t) + .1, death rate μ(t) = .08 and initial population size M = 1. (b) We plot the net growth minus death rate λ(t) − μ(t) as a function of time. (c) We show the number of sensitive cell divisions for the process Z(t) with birth rate λ(t) = 0.05 sin(0.1t) + .1, death rate μ(t) = .08 and initial population size M = 1. Simulation (red circles) and theory (black line) are shown.
Number of cell divisions
The rate of cell division in Z(t) is given by . Integrating this rate, we obtain the average number of cell divisions before time T as
Figure 1(c) shows the agreement between this formula and the simulation.
4.2. Example: Model population of sensitive and resistant cells
Next we consider an example of our model process, defined by equation (1), describing the evolution of sensitive and resistant cells during therapy. Let us define the birth and death rates as
Once again we require Bi ≥ Ai and Ci ≥ 0, for i = 1, 2 such that the birth and death rates are always non-negative.
Expected number of resistant cells
Recall that the expected size of the resistant cell population at time t is given by equation (7). Then we have
where the rate of production of resistant cells from the sensitive cell process, b(τ), is given by
| (18) |
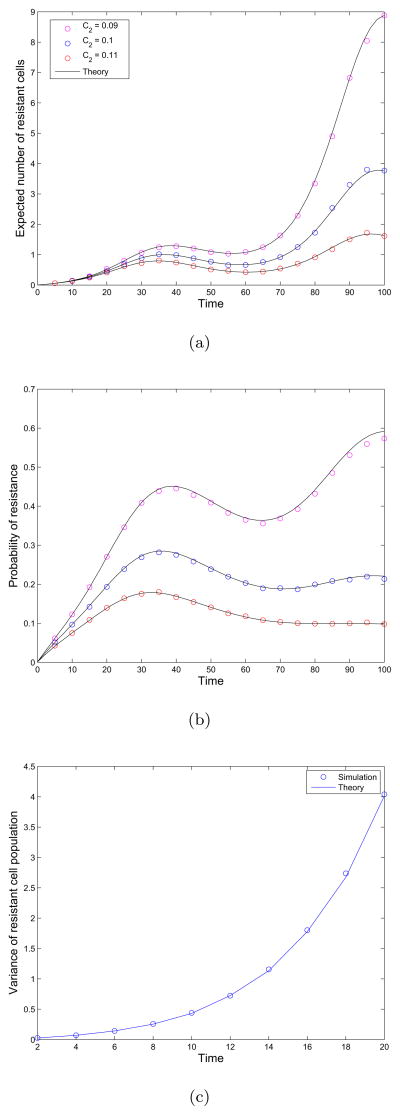
In Figure 2(a) we compare this formula with the results of simulating the full process for several choices of the parameter C2, the death rate of resistant cells. We observe that as the death rate of resistant cells increases, the average number of resistant cells decreases, as expected. Note the agreement between the simulation results and theoretical approximations derived above.
Figure 2.
Evolutionary dynamics of sensitive and resistant cells. (a) Average number of resistant cells 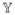 (t) as a function of time. The fixed parameters in this example are as follows: λX (t) = 0.05 sin(0.1t) + .1, μX (t) = 0.14, λY (t) = 0.05 sin(0.1t) + 0.12. The death rate of resistant cells is varied: μY (t) = 0.09, 0.1, 0.12. The initial population consists of M = 100 sensitive cells and the mutation rate u is 10−3 per cell division. Simulation results are plotted as circles and and theoretical formulas as black lines. (b) Probability of resistance as a function of time. The fixed parameters in this example are as follows: μX = 0.14, μY (t) = 0.1, λY (t) = 0.05 sin(0.1t) + 0.12. The birth rate of sensitive cells is varied: λX (t) = 0.05 sin(0.1t) + B1, where B1 takes values 0.1, 0.12, 0.14. The initial population consists of M = 100 sensitive cells and the mutation rate is 10−3 per cell division. Simulation results are plotted as circles and and theoretical formulas as black lines. (c) Variance of resistant cell population as a function of time. The parameters are as follows: μX = 0.14, μY (t) = 0.1, λY (t) = 0.05 sin(0.1t) + 0.12, and λX (t) = 0.05 sin(0.1t) + 0.1. The initial population consists of M = 100 sensitive cells and the mutation rate is 10−3 per cell division. Simulation results are plotted as circles and and theoretical formulas as lines.
(t) as a function of time. The fixed parameters in this example are as follows: λX (t) = 0.05 sin(0.1t) + .1, μX (t) = 0.14, λY (t) = 0.05 sin(0.1t) + 0.12. The death rate of resistant cells is varied: μY (t) = 0.09, 0.1, 0.12. The initial population consists of M = 100 sensitive cells and the mutation rate u is 10−3 per cell division. Simulation results are plotted as circles and and theoretical formulas as black lines. (b) Probability of resistance as a function of time. The fixed parameters in this example are as follows: μX = 0.14, μY (t) = 0.1, λY (t) = 0.05 sin(0.1t) + 0.12. The birth rate of sensitive cells is varied: λX (t) = 0.05 sin(0.1t) + B1, where B1 takes values 0.1, 0.12, 0.14. The initial population consists of M = 100 sensitive cells and the mutation rate is 10−3 per cell division. Simulation results are plotted as circles and and theoretical formulas as black lines. (c) Variance of resistant cell population as a function of time. The parameters are as follows: μX = 0.14, μY (t) = 0.1, λY (t) = 0.05 sin(0.1t) + 0.12, and λX (t) = 0.05 sin(0.1t) + 0.1. The initial population consists of M = 100 sensitive cells and the mutation rate is 10−3 per cell division. Simulation results are plotted as circles and and theoretical formulas as lines.
Probability of resistance
The probability of having at least one resistant cell at time T is approximated by equation (11), where b(t) is given as in equation (18). The probability of extinction of a single resistant clone beginning at time t is given (using equation (8)) as
where
In Figure 2(b) we validate our approximations with simulations. We observe that as the birth rate of sensitive cells increases with B1, the probability of resistance increases. If the sensitive cell population is driven to extinction, the probability of resistance reaches a steady value after the time of extinction since no additional resistant cell clones can be produced after this time. This effect can be seen in the results we have plotted for the case B1 = 0.1. Here, the sensitive cell population declines rapidly and the probability of extinction rapidly reaches a steady state.
Variance of resistant cell population
The variance of the resistant cell population as a function of time is given by equation (15). In Figure 2(c), we plot the predicted variance of the population size as a function of time as well as simulation results. We observe a good fit between simulation and predictions here as well.
4.3. Example: Pre-existing resistance
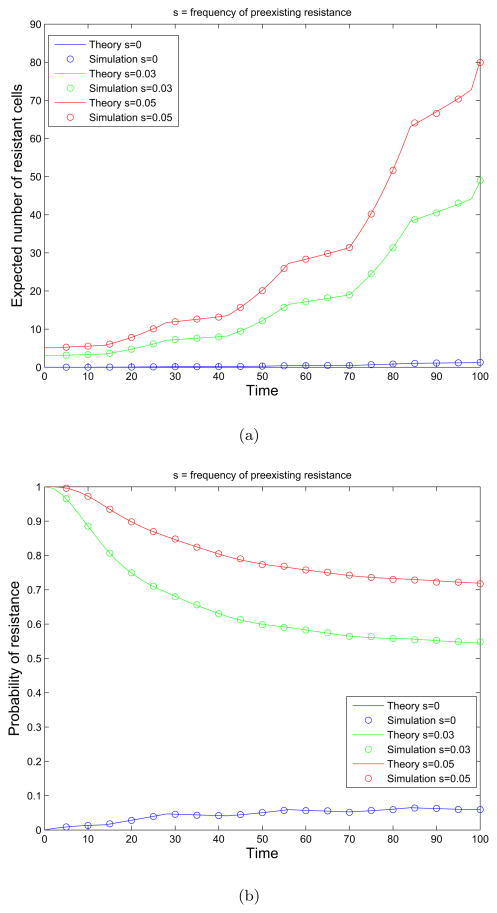
In this example we consider a pulsed therapy schedule on a population with initial frequency s of pre-existing resistant cells. More specifically, the initial population consists of M s resistant cells and M (1 − s) sensitive cells. We consider a pulsed 14-day on, 14-day off therapy schedule. The growth and death rates for the cells during and in the absence of therapy are as follows:
| (19) |
We next show the agreement of the theoretical predictions from equations (16) and (17) with simulation results. Figures 3(a) and 3(b) show the expected number of resistant cells and the probability of resistance, respectively, at varying pre-existing resistance fractions.
Figure 3.
The effects of pre-existing resistance on the dynamics of treatment response. (a) Expected number of resistant cells as a function of time. We show the expected number of resistant cells at varying pre-existing resistance fractions s = 0.0.03, 0.05 under 14-day on and 14-day off pulsed therapy schedule. The growth and death rates of the cells are given in equation (19). Simulation results are plotted as circles and and theoretical formulas as solid lines. (b) Probability of resistance as a function of time. We show the probability of resistance for varying pre-existing resistance fractions s = 0.0.03, 0.05 under 14-day on and 14-day off pulsed therapy schedule. The growth and death rates of the cells are given in equation (19). Simulation results are plotted as circles and and theoretical formulas as solid lines.
4.4. Effect of drug accumulation on the evolution of resistance
In this section we combine a simple pharmacokinetic model with our evolutionary model of resistance. We model the drug concentration after a single dose as an exponentially decaying function of time with a rate determined by the elimination half-life of the drug (see e.g. Towser and Rowland (2006)). When extending this approach to multiple dose regimes, we obtain a model for the accumulation of drug concentration over the course of treatment. For example, if the daily dose of drug is given by D units, then the concentration over time after one dose is
where κ is the rate of drug elimination. Suppose the dose D is administered every τ units of time. Then the maximum amount of drug in the patient after the N-th dose is given by
The drug concentration eventually reaches a steady state plateau wherein the amount of drug administered in each dose is equal to the amount lost through elimination during the τ units of time between doses. The maximum amount in the body at steady state is given by
In general, the amount of time it takes to reach the steady state is dependent upon the half-life of the drug and the dosing interval; however, it is possible to reach steady state levels more quickly by administering a loading dose. This term refers to an initial dose that is larger than the remaining maintenance doses which is often administered in order to hasten the approach to concentration levels within the therapeutic window.
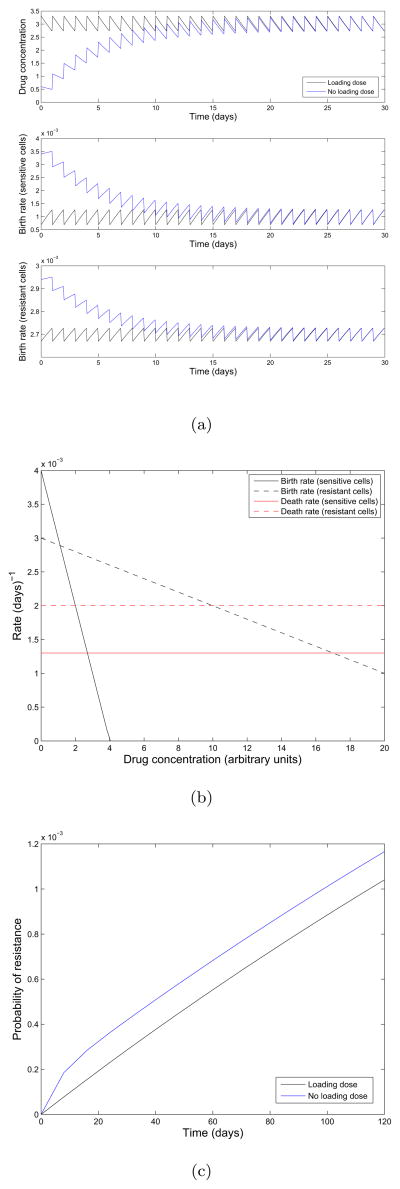
In the next example we investigate the effect of a delay in the accumulation to steady state on the evolution of resistance in an initially sensitive cell population. To do this we compare two scheduling regimes: in the first, a loading dose is used to bring the concentration immediately to steady state, and in the second no loading dose is used.
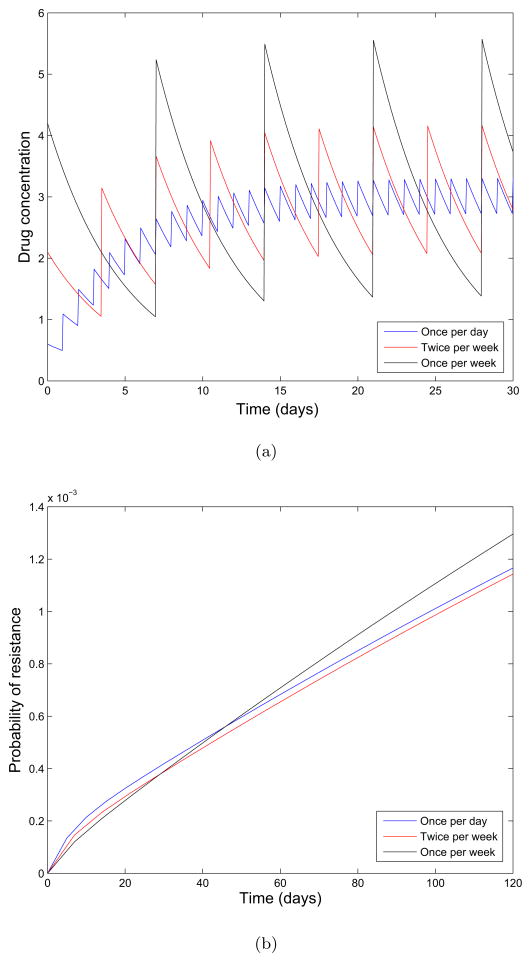
In the top panel of Figure 4(a), we show the concentration as a function of time for the schedules with and without the loading dose. In Figure 4(b), we show an example relationship between birth and death rates of sensitive cells and the current drug concentration. Resistant cells are assumed to be less fit than sensitive cells in the absence of drug, and only partial resistance is conferred to the drug. Only the birth rate of cells are affected by increasing drug concentration; the death rates remain constant. From these relationships we determine the growth and death rates over time λX (t), λY (t), μX (t), and μY (t) given in the lower two panels of 4(a). Using the theory from previous sections we plot the probability of resistance for the first 120 days of therapy in Figure 6(c). We note that the probability of resistance for the loaded dosing schedule is less than that of the normal dosing schedule, resulting in a lower probability of resistance. This effect results from the loading dose rapidly depleting the sensitive cancer cell population at the beginning of treatment when the sensitive population is the largest, thus inhibiting the initial production of resistant cells.
Figure 4.
Consideration of pharmacokinetic effects on the evolution of resistance. (a)Top: Concentration over time, for a schedule using the loading dose (black) and the normal accumulating schedule (blue). Middle: Birth rate of sensitive cells as a function of time. Bottom: Birth rate of resistant cells as a function of time. We use a maintenance dose of size D = 0.6, dose spacing interval of τ = 1, a decay rate of κ = 0.2 which corresponds to a half life of approximately 83 hours, and a loading dose of size of size . The initial population is comprised of 106 sensitive cells and we assume a mutation rate of u = 10−8 per cell division. (b) Birth and death rates of sensitive (solid black and red) and resistant cells (dashed black and red) as a function of drug concentration. (c) Probability of resistance for dosing schedules with and without a loading dose.
Figure 6.
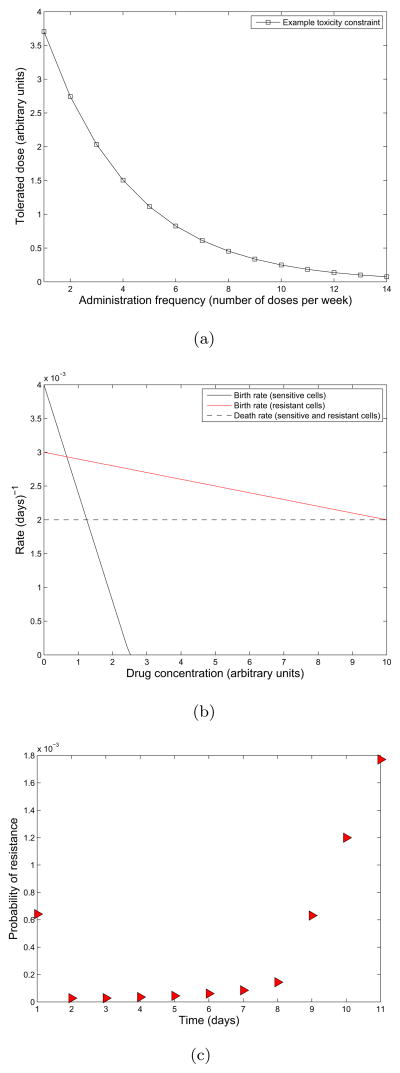
Optimum dosing frequency for an example toxicity constraint. (a)Toxicity constraint representing the maximum tolerated dose for each administration frequency. (b) Birth and death rates of sensitive (solid black and red) and resistant cells (dashed black and red) as a function of drug concentration. (c) Probability of resistance as a function of administration frequency. The rate of drug elimination is κ = 0.2 and all other parameters are the same as in the previous example.
4.5. Effect of varying dosing frequency subject to toxicity constraints
Let us now study the effect of varying the dosing frequency subject to toxicity constraints, using the same exponential model of drug elimination as described in the previous example.
4.5.1. Case 1: Constant area-under-the-curve (AUC)
In the first example, we assume that the concentration area-under-the-curve (AUC) per week at steady state is kept constant while the time interval between doses is varied. In Figure 5(a), three different dosing schedules are shown corresponding to daily, twice a week, and once per week dosing. Under these schedules we calculate the probability of resistance after 120 days of therapy (Figure 5(b)). We note that moving from daily to twice a week dosing slightly decreases the probability of resistance. However, for once per week dosing the tradeoff for attaining higher doses is offset by the 6-day treatment break and the probability of resistance rises above that of the other schedules by the 8th week of therapy. This scenario demonstrates how to compare the resistance dynamics of several dosing schedules with the same AUC.
Figure 5.
The effect of varying dosing frequency on the evolution of resistance. (a) Concentration over time for three dosing frequencies: once per day (blue), twice per week (red), and once per week (black). The dose is modified in each case so that area-under-the-curve (AUC) is constant over all three schedules. The rate of drug elimination is κ = 0.2 and the birth and death rates of sensitive and resistant cells are given as in Figure 4(b). All other parameters are the same as in the previous example. No loading dose is used. (b) Probability of resistance as a function of time for the once per day (blue), twice per week (red), and once per week (black) schedules.
4.5.2. Case 2: Optimization of dosing frequency under assumed clinical toxicity constraint
Next we consider a case in which the toxicity constraint is not governed by the AUC but instead given by data from clinical trials. Again using the pharmacokinetic model of drug elimination described earlier in this section, we investigate the variation of dose intensity and administration frequency and its effects on the dynamics of resistance. We are interested in finding the optimal dosing frequency that minimizes the probability of resistance.
To this end, let us first define 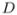 to be the space of all tolerated dosing schedules for a particular drug. For each particular dosing schedule ω ∈
to be the space of all tolerated dosing schedules for a particular drug. For each particular dosing schedule ω ∈ 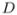 , let us denote the probability of resistance at time T to be PR(T; ω), which is calculated via equation (11) with time-varying birth and death rates corresponding to the dosing strategy ω. The general optimization problem we consider is: Find ωopt ∈
, let us denote the probability of resistance at time T to be PR(T; ω), which is calculated via equation (11) with time-varying birth and death rates corresponding to the dosing strategy ω. The general optimization problem we consider is: Find ωopt ∈ 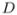 such that
such that
| (20) |
where PT (T; ω) is the objective function to be minimized. We note that the space 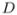 refers to only the subset of dosing schedules that satisfy the toxicity constraints for each particular drug.
refers to only the subset of dosing schedules that satisfy the toxicity constraints for each particular drug.
For the specific example considered here, the space of tolerated schedules 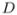 is constrained by an example toxicity constraint called g(x), plotted in Figure 6(a). This function represents the largest dose possible for each dosing frequency (assuming all doses are equally spaced). We have assumed here that the dosing frequency, x, varies in the range from 0 to 14 possible doses per week. The space of tolerated schedules
is constrained by an example toxicity constraint called g(x), plotted in Figure 6(a). This function represents the largest dose possible for each dosing frequency (assuming all doses are equally spaced). We have assumed here that the dosing frequency, x, varies in the range from 0 to 14 possible doses per week. The space of tolerated schedules 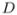 is defined to be the set of ordered pairs (x, y), where x represents the dosing frequency and y represents the dose, such that y ≤ g(x).
is defined to be the set of ordered pairs (x, y), where x represents the dosing frequency and y represents the dose, such that y ≤ g(x).
Figure 6(b) shows the relationship between sensitive and resistant cell birth and death rates and the drug concentration. Thus, for each dosing schedule (x, y) ∈ 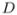 , the relationship plotted in Figure 6(b) defines the corresponding time-varying birth and death rates for the sensitive and resistant cells. The optimization problem for this specific example is: find (x, y)opt ∈ [0, 14] × ℝ such that
, the relationship plotted in Figure 6(b) defines the corresponding time-varying birth and death rates for the sensitive and resistant cells. The optimization problem for this specific example is: find (x, y)opt ∈ [0, 14] × ℝ such that
Since the birth rates of both the sensitive and resistant cells are both monotonically decreasing with increasing concentration, and since the death rates are constant (Fig. 6(b)), we can conclude immediately that the optimal schedule lies directly along the curve y = g(x). Thus, this example optimization problem reduces to a trivial one-dimensional problem: find xopt ∈ [0, 14] such that
Then the optimal dosing strategy is given by (xopt, g(xopt)).
We plot the probability of developing resistance after 120 days of therapy under each of the admissible dosing frequencies in Figure 6(c). Note that dosing frequencies higher that 11 times per week are not admissible since they do not cause a net decrease in the sensitive cell population, making resistance a secondary issue. We observe that the probability of resistance is lowest at the twice per week frequency under this toxicity constraint.
The simple example presented here for illustration reduces to a trivial one-dimensional optimization problem which can be solved graphically. However, realistic toxicity constraints derived from clinical data may include various types of adverse effects and therefore require the solution of more complex multidimensional constrained optimization problems. In such cases it will be necessary to utilize numerical optimization algorithms to solve equation (20); we refer the reader to texts on optimization (e.g. Fletcher (2000)) for more information on these methods.
5. Summary
In this paper, we have used the theory of non-homogenous multi-type birth-death processes to model the evolution of resistance to targeted cancer therapies under time-dependent dosing schedules. In this model, the birth and death rates of sensitive and resistant cells are dependent on a temporally varying drug concentration profile. This assumption represents a departure from previous stochastic models of resistance during therapy which represent the effect of drug as an additional probabilistic cell-kill, separate from the underlying simple birth and death process population model with constant rates. However, the effect of many targeted therapies is to reduce the proliferation rate of sensitive cells, which in turn leads to a decreased probability of resistant cell production. Normal apoptotic signals can also be affected by therapy, thus changing the intrinsic death rate of either sensitive or resistant cells. In addition, since cell kill was assumed to occur immediately upon drug application in previous models, drug half-life and prolonged concentration-dependent kill as the drug is metabolized could not be considered. By incorporating these effects into the underlying birth-death process and allowing the intrinsic rates to vary temporally, we obtain a more accurate description of the evolutionary dynamics of the system.
We have developed and validated analytical estimates of the probability of developing de novo resistance and moment statistics of the resistant cell population; these estimates have also been extended to address the case of pre-existing resistance populations at the start of therapy. These estimates make it possible to study the parameter dependence of the model and optimize dosing strategies without performing costly numerical simulations of the stochastic processes. For example, we have demonstrated how they can be used to study the evolution of resistance under dosing profiles which incorporate pharmacokinetic considerations such as drug elimination and accumulation. These models can be used to aid in clinical decisions regarding the frequency and dose intensity by analyzing the relative probability of resistance or the resistant cell burden under various schedules. We have demonstrated how these estimates can aid in locating the optimal dosing frequency that minimizes the probability of resistance subject to toxicity constraints. In situations where the probability of resistance is high regardless of the dosing regimen, we can alternatively use this model to locate optimal regimens that effectively control the expected size of the resistant cell population. With experimental investigation into the birth and death rates of these cell populations under various drug concentrations, the shape of the toxicity constraint curve and pharmacokinetic parameters, our mathematical framework may aid in the design of optimal administration strategies for targeted anti-cancer therapy.
Acknowledgments
We would like to thank William Pao, Juliann Chmielecki, Kevin Leder, Eric Keaveny and the Michor Lab for helpful discussions. We would also like to acknowledge funding support of NIH Grant R01CA138234.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Asmussen S, Glynn P. Stochastic Simulation. Springer; 2007. [Google Scholar]
- Coldman A, Goldie J. A stochastic model for the origin and treatment of tumors containing drug-resistant cells. Bull Math Biol. 1986;48(34):279–292. doi: 10.1007/BF02459682. [DOI] [PubMed] [Google Scholar]
- Coldman A, Murray J. Optimal control for a stochastic model of cancer chemotherapy. Math Biosciences. 2000;168:187–200. doi: 10.1016/s0025-5564(00)00045-6. [DOI] [PubMed] [Google Scholar]
- Day R. Treatment sequencing, asymmetry, and uncertainty: Protocol strategies for combination chemotherapy. Cancer Research. 1986;46:3876–3885. [PubMed] [Google Scholar]
- Engelmann J, Zejnullahu K, Mitsudomi T, Song Y, Hyland C, et al. Met amplification leads to gefitinib resistance in lung cancer by activating erbb3 signaling. Science. 2007;316 (5827):1039–1043. doi: 10.1126/science.1141478. [DOI] [PubMed] [Google Scholar]
- Fletcher R. Practical Methods of Optimization. Wiley; 2000. [Google Scholar]
- Foo J, Michor F. Evolution of resistance to targeted anti-cancer therapies during continuous and pulsed administration strategies. PLoS Computational Biology. 2009 doi: 10.1371/journal.pcbi.1000557. accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorre M, Mohammed M, Ellwood K, Hsu N, Paquette R, Rao P, Sawyers C. Clinical resistance to sti-571 cancer therapy caused by bcr-abl gene mutation or amplification. Science. 2001;293 (5531):876–880. doi: 10.1126/science.1062538. [DOI] [PubMed] [Google Scholar]
- Haeno H, YYI, Michor F. The evolution of two mutations during clonal expansion. Genetics. 2007;177:2209–2221. doi: 10.1534/genetics.107.078915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwasa Y, Michor F, Nowak M. Evolutionary dynamics of escape from biomedical intervention. Proc Roy Soc Lond B. 2003;270:2572–2578. doi: 10.1098/rspb.2003.2539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwasa Y, Nowak M, Michor F. Evolution of resistance during clonal expansion. Genetics. 2006;172:2557–2566. doi: 10.1534/genetics.105.049791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komarova N. Stochastic modeling of drug resistance in cancer. Journal of Theoretical Biology. 2006;239:351–366. doi: 10.1016/j.jtbi.2005.08.003. [DOI] [PubMed] [Google Scholar]
- Komarova N, Wodarz D. Drug resistance in cancer: Principles of emergence and prevention. PNAS. 2005;102:9714–9719. doi: 10.1073/pnas.0501870102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis P, Shedler G. Simulation of nonhomogeneous poisson processes by thinning. IBM Research Report. 1978 (RJ 2286) [Google Scholar]
- Pao W, Miller V, Politi K, GJGR, Somwar R, Zakowski M, MGMK, Varmus H. Acquired resistance of lung adenocarcinomas to gefitinib or erlotinib is associated with a second mutation in the egfr kinase domain. PLoS Medicine. 2005;2(73) doi: 10.1371/journal.pmed.0020073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pao W, Miller V, Zakowski V, JMD, et al. Egf receptor gene mutations are common in lung cancers from never smokers and are associated with sensitivity of tumors to gefitinib and erlotinib. Proc Natl Acad Sci USA. 2004;101:13306–13311. doi: 10.1073/pnas.0405220101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parzen E. Stochastic processes. SIAM; 1999. [Google Scholar]
- Towser T, Rowland M. Introduction to Pharmacokinetics and Pharmacodynamics: The Quantitative Basis of Drug Therapy. Lipincott Williams and Wilkins; 2006. [Google Scholar]