Photosynthesis in lightfleck areas of homobaric and heterobaric leaves

Abstract

Leaves within a canopy are exposed to a spatially and temporally fluctuating light environment which may cause lateral gradients in leaf internal CO₂ concentration and diffusion between shaded and illuminated areas. In previous studies it was hypothesized that lateral CO₂ diffusion may support leaf photosynthesis, but the magnitude of this effect is still not well understood. In the present study homobaric leaves of Vicia faba or heterobaric leaves of Glycine max were illuminated with lightflecks of different sizes, mimicking sunflecks. Photosynthetic properties of the lightfleck areas were assessed with combined gas exchange measurements and chlorophyll fluorescence imaging. Lateral diffusion in homobaric leaves with an interconnected intercellular air space stimulated photosynthesis and the effect was largest in small lightfleck areas, in particular when plants were under drought stress. Such effects were not observed in the heterobaric leaves with strongly compartmented intercellular gas spaces. It is concluded that lateral diffusion may significantly contribute to photosynthesis of lightfleck areas of homobaric leaves depending on lightfleck size, lateral diffusivity, and stomatal conductance. Since homobaric leaf structures have been reported for many plant species, it is hypothesized that leaf homobary may have an impact on overall plant performance under conditions with a highly heterogeneous light environment.

Introduction

Leaf photosynthesis is supplied with CO₂ mainly from ambient air (Hetherington and Woodward, 2003) or, to a minor degree, mitochondrial respiration (Loreto et al., 2001; Pinelli and Loreto, 2003), but illuminated parts of leaf blades may also benefit from CO₂ diffusing from nearby shaded areas through intercellular air spaces which may be effective over a distance of several millimetres (Pieruschka et al., 2006). The potential to use laterally diffusing CO₂ for photosynthesis depends on leaf anatomy. In heterobaric leaves, bundle sheath extensions provide internal barriers for gas diffusion, whereas homobaric leaves lack such extensions and have interconnected gas spaces open for lateral (peridermal) gas movement (Neger, 1918).

A lateral gradient in CO₂ concentration of homobaric leaves of Commelina communis was studied by using chlorophyll fluorescence imaging and was reported to affect photosynthetic CO₂ uptake over a distance of only 0.3 mm along the diffusion path (Morison et al., 2005). For homobaric leaves of Nicotiana tabacum and Vicia faba, however, lateral CO₂ diffusion from shaded to illuminated leaf parts affected photosynthesis over distances up to 3–4 mm when stomatal conductance was low, for example in drought-stressed plants; this impact of lateral CO₂ flux disappeared when stomata reopened after irrigation and ambient CO₂ became the main source of photosynthesis (Pieruschka et al., 2006).

The possible influence of lateral diffusion on photosynthesis was recently investigated by artificially closing stomata with grease and thus creating lateral CO₂ gradients inside leaves (Morison et al., 2007; Pieruschka et al., 2008). Both studies concluded that lateral diffusion may support photosynthesis, but with contrasting results considering heterobaric and homobaric leaves. On the one hand, lateral CO₂ flux rates were found to be effective over a range of no more than 1 mm and to be similar for both heterobaric and homobaric species (Morison et al., 2007). On the other hand, large differences in rates and distances of lateral CO₂ supply were reported (Pieruschka et al., 2008) and the authors concluded that the extent of lateral diffusion depends largely on the diffusivity of the intercellular air space. These studies were performed with artificially greased stomata which makes the estimation of the impact of lateral CO₂ diffusion on photosynthesis under sunfleck conditions in the field difficult. Here sunflecks were simulated by illuminating leaves of V. faba (homobaric) and Glycine max (heterobaric) consecutively with large or small lightflecks. Simultaneous measurement of gas exchange of the whole leaves and chlorophyll fluorescence imaging of the illuminated leaf areas were used to analyse net photosynthesis or quantum use efficiencies of lightfleck areas of plants exposed to progressive drought stress. The aim of the present work was to quantify the impact of lateral CO₂ diffusion (in addition to vertical gas diffusion through stomata) on photosynthetic carbon gain and light stress of lightfleck areas of homobaric and heterobaric leaves.

Materials and methods

Plant material and growth conditions

Plants of G. max (L.) Merr. cv. Williams (heterobaric leaves) and V. faba L. cv. Hangdown Grünkernig (homobaric) were grown from seeds in 1.0 l pots with soil (Einheitserde Typ ED; Balster Einheitserdewerk, Fröndenberg, Germany) in a greenhouse, periodically irrigated with tap water, and fertilized once a week. When the light intensity dropped below 110 μmol photons m⁻² s⁻¹, artificial light was added (SON-T Agro, 400 W, Philips, Germany) providing a photosynthetic photon flux density (PPFD) of 400–450 μmol m⁻² s⁻¹ at 30 cm above the pots.

Gas exchange system and chlorophyll fluorescence measurements

Gas exchange of leaves was measured by an open gas exchange system (Jahnke, 2001). A leaf chamber was constructed to enclose whole leaves with a maximal area of 140 cm² kept in position by two nets made from nylon; the chamber bottom and the removable lid were covered with highly light-translucent teflon films (Nowofol EFEP-RP 5000, Kunststoffprodukte, Siegsdorf, Germany). The air provided to the leaf chamber was generated either by mixing CO₂-free air with gaseous CO₂ or by mixing N₂, O₂, and CO₂ with mass-flow controllers (F201; Bronkhorst-Mättig, Kamen, Germany); the CO₂ concentration of the incoming air was 350 μmol mol⁻¹ in all experiments, whereas the O₂ concentration was 21% or 1%. The pressure difference between the atmosphere and the leaf chamber was kept at zero (Jahnke, 2001). Leaf temperature was 23–23.5 °C in darkness and 24–25 °C in the light. Net CO₂ exchange rates (NCERs; μmol CO₂ m⁻² s⁻¹) and transpiration rates (E; mmol m⁻² s⁻¹) were measured (Jahnke, 2001), and stomatal conductance for CO₂ (g_c) of the enclosed leaf was calculated (von Caemmerer and Farquhar, 1981). Chlorophyll fluorescence was detected with an Imaging-PAM Chlorophyll Fluorometer (Walz, Effeltrich, Germany). After plants were in darkness for 1 h, minimum (F₀) and maximum (F_m) fluorescence were recorded and used to calculate the quantum efficiency of dark-adapted leaves (F_v/F_m, with F_v=F_m–F₀). In actinic light (150 μmol photons m⁻² s⁻¹), maximal fluorescence (F_m′) and steady-state fluorescence prior to the flash (F) were measured while saturated light flashes were applied every 30 s. This was used to calculate the quantum efficiency of light-adapted leaves (ΔF/F_m′, with ΔF=F_m′–F). Electron transport rates (ETR = ΔF/F_m′×PPFD×0.85×0.5; with 0.85 as an estimate of absorbed light and 0.5 accounting for the partitioning of light between photosystem I and II) and non-photochemical quenching (NPQ=F_m/F′_m–1) were calculated according to Genty et al. (1989) and Bilger and Björkman (1990), respectively.

Experimental protocols

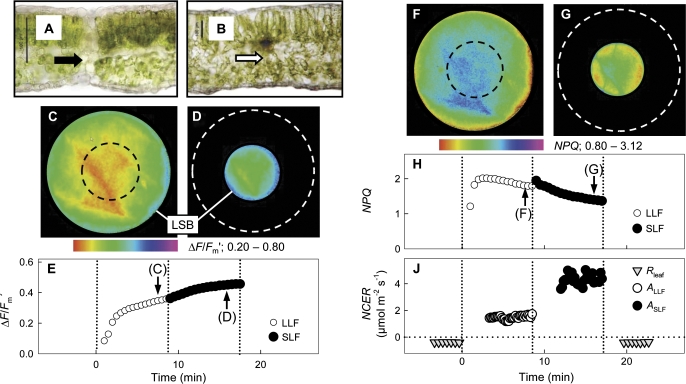
Gas exchange and chlorophyll fluorescence were measured simultaneously on 24 (photorespiratory conditions) and 23 (non-photorespiratory conditions) attached V. faba leaves, and 22 (photorespiratory conditions) and 22 (non-photorespiratory conditions) G. max leaves. The plants were exposed to different drought stress levels from 1 d to 5 d without irrigation. The leaves were shaded by a template with a circular opening; the illuminated leaf area underneath was denoted as a large lightfleck area (LLF; Fig. 1C), with a diameter of 23 mm, a projected surface area of 4.15 cm², a perimeter of 7.2 cm, and a perimeter to area ratio of 1.7 cm⁻¹. A second template could be moved over the larger opening providing a small lightfleck (SLF; Fig. 1D), with a diameter of 10 mm, an area of 0.79 cm², a perimeter of 3.1 cm, and an perimeter to area ratio of 4.0 cm⁻¹. The ratio between the perimeter to area ratios of the LLF and SLF areas was 0.43.

Fig. 1.

Transverse sections of (A) a heterobaric leaf of Glycine max where the bundle sheath extension (black arrow) completely separates the intercellular spaces of adjacent areoles and (B) a homobaric leaf of Vicia faba where no bundle sheath extensions are visible (white arrow; scale bars: 100 μm). Chlorophyll fluorescence and gas exchange of a V. faba leaf measured under photorespiratory conditions and illuminated either with a large (LLF with a diameter of 23 mm; C, F) or a small (SLF with a diameter of 10 mm; D, G) lightfleck. Images of ΔF/F_m′ when (C) the LLF area (black dashed line indicates the central area subsequently illuminated by the SLF) and (D) the SLF area (white dashed line indicates the previous LLF position) were illuminated. (C) The averaged ΔF/F_m′ values of the LLF area (open symbols) and the SLF area (closed symbols) versus time after illumination had started; the arrows denote the times the images (C, D) were taken. Images of NPQ when (F) the LLF area and (G) the SLF area were illuminated. (H) Averaged NPQ values of the LLF area and the SLF area; the arrows denote the times the images (F, G) were taken. (J) Net CO₂ exchange rates (NCER) of the leaf measured in the dark (R_leaf; PPFD ∼1–3 μmol photons m⁻² s⁻¹) and of the LLF (A_LLF) and SLF areas (A_SLF) in the light (150 μmol m⁻² s⁻¹). Due to applied drought stress, stomatal conductance (g_c) was low (16.1±1.1 mmol CO₂ m⁻² s⁻¹).

The experiment started with the measurement of leaf respiration in the dark (R_leaf=–NCER). Then the leaf was illuminated with an LLF (Fig. 1C, F), and gas exchange rates of the whole leaf and chlorophyll fluorescence parameters of the LLF were measured for 8 min. Thereafter, the LLF lightfleck area was reduced to the SLF (Fig. 1D, G) and gas exchange rates of the whole leaf and chlorophyll fluorescence parameters of the SLF were measured for another 8 min.

Data analysis

Chlorophyll fluorescence parameters and gas exchange rates were measured for LLF and SLF at approximately steady-state conditions. Quantum efficiency of light-adapted leaves (ΔF/F_m′), electron transport rate (ETR), and non-photochemical quenching (NPQ) were obtained for the LLF and SLF areas (Fig. 1). Gradients in ΔF/F_m′ were measured on the images of SLF and LLF by averaging six linear transects; starting with a vertical transect and moving the following transects by 30° clockwise. The analysis was performed by using the free software Image J (http://rsbweb.nih.gov/ij/).

Stomatal conductance for CO₂ of the LLF area was calculated as:

(1)

where g_leaf,D is leaf conductance in darkness, g_leaf,LLF is leaf conductance measured with illumination of LLF, LA_leaf is the area of the entire leaf, and LA_LLF is the LLF area. Illumination of the SLF area was obtained by shading the margin of the previously illuminated LLF area with a template as described before. Stomatal conductance of the SLF area (previously illuminated with the LLF) could not be measured so that conductance of the SLF was assumed to be similar to that of the LLF (g_LLF). Therefore, g_LLF was taken as an approximation of stomatal conductance for CO₂ (g_c) of the LLF and SLF areas.

Whole leaf NCER was denoted NCER_leaf, with negative values indicating dark respiration (R_leaf=–NCER) and positive values indicating the net CO₂ assimilation rate (A; Fig. 1J). NCER_leaf measured with LLF or SLF illumination was denoted NCER_leaf,LLF and NCER_leaf,SLF, respectively. The gross assimilation rate (A*) of the LLF leaf area was calculated as:

(2)

and for the SLF area as:

(3)

The assimilation rates of the LLF and SLF leaf areas were then calculated as A_LLF=A*_LLF+R_leaf and A_SLF=A*_SLF+R_leaf, respectively.

The electron requirement for assimilated CO₂ (ETR/A*) was calculated for the LLF (ETR_LLF/A*_LLF) and the SLF (ETR_SLF/A*_SLF). Regression analysis of the ETR/A* ratio (Fig. 5) and the data shown in Fig. 3E, F was performed with Table Curve (SPSS Inc.) by using least squares analysis. For linear and inverse linear regression analyses, the software SigmaPlot (SPSS Inc.) was used. T-tests were applied to analyse the data shown in Fig. 4 with the null hypothesis that the coefficient of the independent variable is zero with statistically significant differences for P <0.05 (Table 1). Further data analysis was performed with a simplified geometrical model which combines photosynthetic CO₂ uptake of the different lightflecks.

Fig. 5.

Electrons required for assimilated CO₂ (ETR/A*) of homobaric leaves of V. faba illuminated by (A) an LLF or (B) an SLF. The experiments were performed under photorespiratory (closed symbols, dashed regression lines) and non-photorespiratory conditions (open symbols, solid regression lines).

Fig. 3.

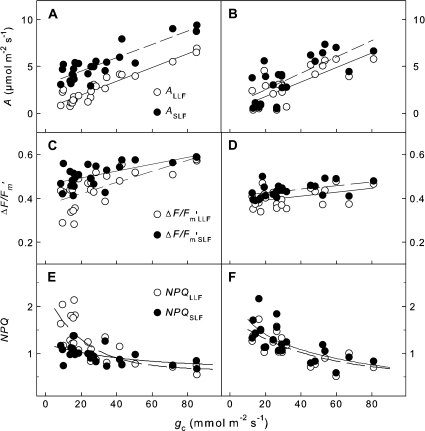
(A and B) Net CO₂ assimilation rates (A), (C and D) effective quantum yield of PSII (ΔF/F_m′), and (E and F) non-photochemical quenching (NPQ) as a function of stomatal conductance (g_c) of homobaric V. faba (A, C, E) and heterobaric G. max leaves (B, D, F) illuminated with an LLF and, subsequently, an SLF. The plants were exposed to different drought levels with 1–5 d without irrigation. The experiments were performed under photorespiratory conditions (21% [O₂]); regression analysis was performed by least squares analysis.

Fig. 4.

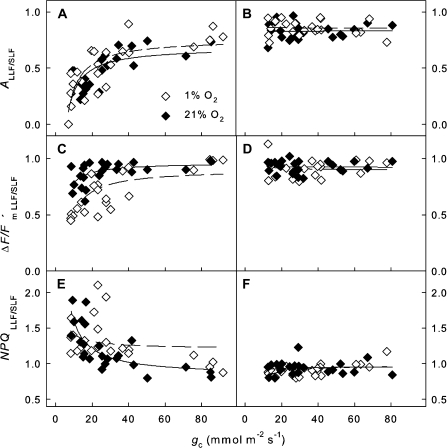
Ratios of the LLF to SLF areas versus stomatal conductance (g_c). (A and B) Ratios of assimilation rates (A_LLF/SLF), (C and D) effective quantum yield of PSII (ΔF/F_m′_LLF/LLF), and (E and F) non-photochemical quenching (NPQ_LLF/SLF) of V. faba (A, C, E) and G. max (B, D, F) leaves under photorespiratory (21% [O₂]) and non-photorespiratory (1% [O₂]) conditions. The data were fitted by using a simplified model considering lightfleck geometries (see Materials and methods), and the calculated parameters a’ and b’ are summarized in Table 1.

Table 1.

Estimated regression parameters a, b, a′, and b′ as function of stomatal CO₂ conductance (g_c) under photorespiratory and non-photorespiratory conditions

Regression equation	Physiological parameter	[O2] (%)	Vicia faba (homobaric)		Glycine max (heterobaric)
			a	b	a	b
f(gc)=agc+b	ALLF	21	0.07±0.01*	0.53±0.20*	0.08±0.01*	0.26±0.58
		1	0.11±0.01*	0.77±0.59	0.11±0.02*	–0.52±0.81
	ASLF	21	0.07±0.01*	3.09±0.31*	0.09±0.02*	0.79±0.71
		1	0.11±0.02*	3.74±0.70*	0.13±0.02*	–0.57±0.94

			a′	b′	a′	b′
f(gc)=a′gc−1+b′	ALLF/SLF	21	–4.53±0.78*	0.76±0.05*	–0.10±0.77	0.83±0.03*
		1	–3.99±0.85*	0.68±0.05*	0.02±0.70	0.86±0.03*
	ΔF/Fm′LLF/SLF	21	–4.02±0.73*	0.90±0.05*	0.10±0.58	0.92±0.03*
		1	–1.79±0.61*	0.96±0.03*	0.36±0.80	0.90±0.04*
	NPQLLF/SLF	21	7.68±1.47*	0.83±0.09*	–0.49±1.06	0.96±0.05*
		1	2.10±1.80	1.21±0.11*	–1.85±0.88*	0.98±0.04*

Mean values of the regression parameters (±SEM) were obtained from the denoted regression equations by fitting the respective data of Fig. 3 (parameter a and b; linear fit) and Fig. 4 (parameter a′ and b′; for a simplified geometric model see Materials and methods).

Asterisks indicate values significantly different from 0 (a, b, and a′) or 1 (b′) (P <0.05).

Simplified model of geometric dependence of CO₂ uptake of the lightflecks

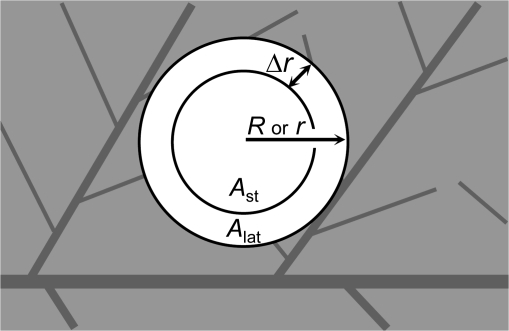
Lateral CO₂ diffusion from shaded areas may affect A, ΔF/F_m′, and NPQ of illuminated parts of homobaric leaves. For simplicity, only A is treated in the model. A_LLF and A_SLF denote the average assimilation rates of the LLF and SLF areas (Fig. 1), respectively. The geometrical dependency of assimilation can be quantified by the ratio A_LLF/A_SLF as a function of g_c. For both the LLF and SLF areas, assimilation rates can be considered to be composed of two regions: (i) the assimilation rate of an outer region (A_lat) which is adjacent to the shade and affected by lateral CO₂ supply from the shaded areas in addition to vertical CO₂ supply through the stomata; and (ii) the assimilation of an inner lightfleck region (A_st) only depending on CO₂ supply through the stomata (Figs. 6 and 2). This classification is sustainable as long as the lateral diffusion distance of CO₂ (Δr) across the light–shade border is small compared with the radius of the LLF or SLF (R or r). The average A_LLF of the LLF area with the radius R is given by:

(4)

Fig. 6.

Scheme of a lightfleck illustrating parameters used for the simplified model calculation (see Equation 6). R is the radius of the large light fleck (LLF) and r of the small light fleck (SLF). A_st is the averaged net CO₂ assimilation rate of the denoted inner area of the respective lightflecks (LLF or SLF) where CO₂ supply is only through stomata; A_lat is the averaged net CO₂ assimilation rate of the outer area of the respective lightflecks with an additional lateral CO₂ supply from adjacent areas. Δr designates the effective diffusion distance of CO₂ into the lightfleck.

Fig. 2.

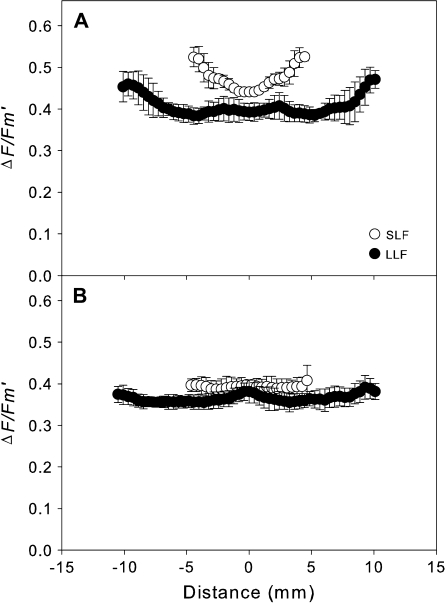
Radial gradients of ΔF/F_m′ values of SLF (open symbols) and LLF (closed symbols) areas of leaves of (A) Vicia faba measured at a stomatal conductance of (g_c) 16.1±1.1 mmol CO₂ m⁻² s⁻¹; (B) Glycine max measured at a g_c of 12.4±0.7 mmol CO₂ m⁻² s⁻¹. The error bars indicate the standard deviation obtained from six ΔF/F_m′ gradients on each lightfleck.

A short calculation renders:

(5)

Because Δr is small compared with R, we can approximate:

(6)

Thus, A_LLF can be approximated by the term:

(7)

A similar expression is found for the average assimilation rate of the small lightfleck, A_SLF (substitution of R by r). Thus, the LLF to SLF ratio is:

(8)

Moreover, because Δr is small compared with r, the geometric series can be used to approximate the ratio:

(9)

The functional dependence of Δr on g_c is not concrete in the sense that it depends on actual definition of Δr (diffusion is a continuous process). However, Δr becomes monotonically small, eventually zero for large g_c. Several empirical functions could therefore be used (exponential, rational, etc.). Here, a very simple function has been used:

(10)

where α is a positive constant. Finally, a possible model to fit the ratios is then:

(11)

where:

(12)

is a negative constant. Inspection of a’ reveals that it is composed of three parts: the first, α, contains the sensibility of Δr towards changes in g_c; the second, (A_lat–A_st)/A_st, describes implicitly the dependence on the lateral diffusivity of the leaf; the third, (2/r–2/R), models the geometric aspect. In general a’ is expected to approach 0 when there is no lateral CO₂ supply or to differ substantially from 0 when LLA and SLA are influenced by lateral CO₂ diffusion. The parameter b’ of Equation 11 is a saturation value which ideally has a value of 1 when g_c is high; that is, the stomata are fully open. The model was used to calculate the parameters a′ and b′ summarized in Table 1 by fitting the LLF/SLF ratios of various physiological parameters shown in Fig. 4.

Results

The maximum quantum yield (F_v/F_m) of dark-adapted leaves was 0.80±0.02 (n=44) for leaves of G. max (heterobaric leaf anatomy, Fig. 1A) and 0.78±0.02 (n=47) for V. faba (homobaric leaf anatomy, Fig. 1B), indicating that photosynthesis was not photoinhibited under the imposed drought stress. When homobaric V. faba leaves were illuminated by large (LLF) or small lightflecks (SLF), the quantum yield of light-adapted leaves (ΔF/F_m′) was highest near the light–shade borders (Fig. 1C, D) for plants under drought stress with low stomatal conductance (g_c) (16.1±1.1 mmol CO₂ m⁻² s⁻¹). For the LLF (Fig. 1C) the averaged ΔF/F_m′ value was lower when that area was illuminated by the SLF (Fig. 1D, E). The opposite was found for non-photochemical quenching (NPQ) as a measure of heat dissipation, with lowest values near the light–shade borders (Fig. 1F, G), while the averaged NPQ value of the LLF was higher than that of the SLF area (Fig. 1H). Simultaneous measurement of net CO₂ exchange rates (NCERs) showed respiration rates (R_leaf=–NCER_leaf) of 0.39±0.02 μmol m⁻² s⁻¹ when the leaf was in darkness, net CO₂ assimilation rates of the LLF area (A_LLF) of 1.48±0.13 μmol m⁻² s⁻¹, and 4.28±0.37 μmol m⁻² s⁻¹ for the SLF area (A_SLF; Fig. 1J). Comparing the perimeter to area ratios of the LLF and SLF resulted in a factor of 0.43, while the A_LLF to A_SLF ratios showed a factor of 0.34 (Fig. 1J). However, this can vary between 0.7 and 0.2 as shown in Fig. 4A.

Radial profiles of ΔF/F_m′ of the SLF and LLF areas showed large differences between V. faba and G. max (Fig. 2). The ΔF/F_m′ values for V. faba were higher at the edges than in the centre of the profiles and larger for the SLF than the LLF (Fig. 2A). For G. max, however, the ΔF/F_m′ profiles showed only small differences between the centres and the edges, and between SLF and LLF areas (Fig. 2B).

For homobaric V. faba leaves, A_SLF was larger than A_LLF at all g_c values (Fig. 3A), but this was not the case for heterobaric G. max leaves (Fig. 3B). Linear regression of A_LLF and A_SLF versus g_c of V. faba and G. max leaves resulted in similar slopes of 0.07–0.09 under photorespiratory conditions (21% [O₂]) and of 0.11–0.13 under non-photorespiratory conditions (1% [O₂]; Table 1). For V. faba, the axis intercepts of A_SLF were significantly larger than zero and substantially larger than A_LLF. For G. max, the intercepts were not significantly different from zero independently of LLF or SLF illumination (Table 1). For both homobaric and heterobaric leaves, the ΔF/F_m′ values declined with decreasing g_c values. The slope was smaller for the SLF than the LLF areas of homobaric V. faba leaves (Fig. 3C), whereas no differences between SLF and LLF were observed for heterobaric G. max leaves (Fig. 2D). In contrast, NPQ increased with decreasing g_c (Fig. 3E, F), with a smaller slope for the SLF than the LLF areas for V. faba (Fig. 3E) but no differences for G. max (Fig. 3F).

Differences between measured gas exchange and chlorophyll fluorescence parameters of the LLF and SLF areas were evaluated by analysing the dependence of the LLF/SLF ratios of net CO₂ assimilation rates, quantum yield, and non-photochemical quenching on g_c with inverse linear regression (ratio=b′+a′/g_c) (Fig. 4 and Table 1). The ratios denoted A_LLF/SLF, ΔF/F_m′_LLF/SLF, and NPQ_LLF/SLF showed substantial differences between homobaric and heterobaric leaves. For V. faba, the inverse linear regression parameters a′ were significantly different from zero for all ratios (except NPQ_LLF/SLF obtained under 1% [O₂]), whereas for G. max the a′ values were not different from zero apart from NPQ_LLF/SLF measured at 1% [O₂]. The saturation value b’ ranged between 0.68 and 1.21 for both species.

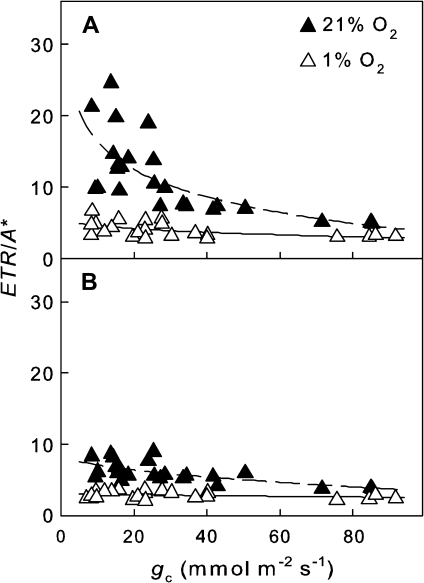
Ratios between the ETR and gross assimilation rate (A*) were calculated from data of combined gas exchange and chlorophyll fluorescence measurements. For LLF areas of V. faba leaves, ETR/A* values were up to 25 at low and ∼6 at high g_c under 21% [O₂], and ∼6 at low and 3 at high g_c under 1% [O₂] (Fig. 5A). For the SLF areas, ETR/A* was only slightly affected by g_c under both 21% and 1% [O₂] (Fig. 5B). For G. max leaves, the ETR/A* ratios were very similar for both the LLF and SLF areas, with values up to 20 at low (<30 mmol m⁻² s⁻¹) and ∼6 at high g_c under 21% [O₂] and up to 8 at low and 2–3 at high g_c with 1% [O₂] (data not shown).

Discussion

Photosynthesis is progressively impeded during drought stress mainly because of decreasing stomatal conductance, and the photosynthetic response can be understood as direct adjustment of the metabolism to low CO₂ availability (Flexas et al., 2004). Decreasing CO₂ availability due to stomatal closure was, in part, compensated in homobaric V. faba leaves by lateral CO₂ diffusion from shaded to illuminated leaf parts, as indicated by an increase in A and ΔF/F_m′ and a decrease in NPQ resulting in higher carbon gain and lower light stress in the small rather than the large lightfleck areas (LLF/SLF ratios <1; Fig. 4). In heterobaric G. max leaves, lateral CO₂ diffusion was not effective in either LLF or SLF areas.

Since lateral CO₂ diffusion increased CO₂ uptake while the rate of transpiration or stomatal conductance was not influenced (data not shown), the efficiency of water use also increased as previously reported (Morison et al., 2007; Pieruschka et al., 2008). However, the measurements of transpiration and stomatal conductance bear some uncertainties when measuring water fluxes of entire leaves which are partly shaded. Therefore, more detailed studies are necessary to quantify this effect.

Following illumination, thermal dissipation can be activated rapidly by de-epoxidation of xanthophylls, a mechanism very sensitive to changes in light intensity (Watling et al., 1997). The impact of CO₂ re-fixation is particularly large for drought-stressed plants with low g_c where lateral CO₂ flux may be the major source of CO₂, especially for SLF areas. For example, while A_LLF of V. faba reached values of ∼0 μmol CO₂ m⁻² s⁻¹ at low stomatal conductance, A_SLF was still substantially higher under these conditions (Fig. 3A). The ETR depends on c_i, and the rate of CO₂ assimilation and stomatal conductance may be driven by the ETR (Weis and Berry, 1987; Genty et al., 1989). An increase in ETR/A* (Fig. 5) is regarded as an indicator for stomatal limitations paralleled by an increase in alternative pathways of electron flow such as photorespiration (Cornic and Fresneau, 2002; Flexas and Medrano, 2002; Kitao et al., 2003; Bota et al., 2004). When heterobaric G. max leaves were illuminated with LLF or SLF, the ETR/A* ratios were not different (data not shown). For homobaric V. faba leaves, the ETR/A* values were substantially smaller in the SLF than the LLF areas due to CO₂ delivered from shaded leaf parts largely reducing stomatal limitations on photosynthesis (Fig. 5).

The LLF to SLF ratios as a function of stomatal conductance are described by a geometrical model which considers the dependency of a circular area on its radius (see Materials and methods). The ratio of the perimeter to area ratio of LLF (4 cm⁻¹) and SLF (1.7 cm⁻¹) is 0.43 and, when, for example, the ratios of the assimilation rates (A_LLF/SLF) would follow the lightfleck geometry the lower limit of A_LLF/SLF would approach 0.43. However, A_LLF/SLF was found to be substantially lower (Fig. 4A). If a lightfleck is influenced by lateral CO₂ then, as shown in Figs. 2 and 6, some portion of this lightfleck along the light–shade border (Δr) has a higher quantum yield and rate of assimilation (A_lat) then the centre of the lightfleck (A_st). The average assimilation of the LLF or SLF is therefore determined by the Δr, which is additionally affected by the non-linear response of photosynthesis to CO₂. The resulting A_LLF/SLF or ΔF/F_m′_LLF/SLF may differ from geometrical constraints.

Re-fixation of remotely supplied CO₂ additionally depends on a range of parameters and conditions. Leaves in different layers of a canopy are exposed to sunflecks with varying intensities, and duration ranging between seconds and minutes (Pfitsch and Pearcy, 1989; Pearcy et al., 1994). The differences in light intensity of the illuminated and shaded leaf areas as well as stomatal conductance may greatly influence lateral gradients in c_i. Additionally the shape, size, and interconnectivity of intercellular gas spaces can be very variable, for example between plant species or even leaves of the same plant (Neger, 1918; Wylie, 1952; Jahnke and Krewitt, 2002; Pieruschka et al., 2005), and affect lateral CO₂ diffusivity which can reach values up to 40% of diffusion in free air (Pieruschka et al., 2005). Stomatal conductance largely determines the ratio of the supply of photosynthesis by lateral CO₂ diffusion inside the leaf and ‘vertical’ CO₂ diffusion from the external air through the stomata (Pieruschka et al., 2008). Finally, a non-linear response of photosynthesis may additionally influence the re-fixation of laterally delivered CO₂ and under Rubisco-limited conditions the response may be larger than under RubP-limited conditions (von Caemmerer, 2000).

Stomatal response to rapidly fluctuating light conditions may be rather slow, in particular under drought stress, and leaf internal c_i gradients may be very variable in dynamically fluctuating conditions. For example, when a sunfleck emerges on a leaf with an activated photosynthetic apparatus, c_i is likely to decrease quickly, resulting in a large lateral Δc_i between shaded and illuminated areas. A gradual increase of stomatal conductance with the duration of the sunfleck exposure would then increase the vertical CO₂ supply from ambient air through the stomata, and the lateral Δc_i would decrease. Thus, leaf internal CO₂ concentration in sunfleck areas may be extremely variable, and detection of such fast and dynamic processes is very difficult with conventional measuring techniques. The response of stomatal conductance of drought-stressed plants may be slow and reduced as compared with well-watered plants. Thus, lateral CO₂ diffusion could support photosynthesis during transient opening of stomata more effectively, in particular in a dynamic light environment under drought stress. The present study confirms previous results with drought-stressed V. faba and N. tabacum plants where lateral CO₂ diffusion from shaded leaf parts affected ΔF/F_m′ and NPQ in adjacent illuminated areas up to 4 mm from a light–shade border, as measured with chlorophyll fluorescence imaging (Pieruschka et al., 2006). Studies in which stomata were closed with grease also came to the general conclusion that lateral CO₂ flux may support photosynthesis and, although greasing of stomata is an artificial treatment, it has proved to be very useful in estimating leaf internal diffusivities (Duarte et al., 2005; Morison et al., 2007; Pieruschka et al., 2008).

What the function is of homobaric leaves in natural ecosystems and whether lateral diffusion inside such leaves is effective in efficient carbon gain or water use is an intriguing question. Rainforest understorey and subcanopy species were reported to have homobaric leaves while light-exposed species are characterized by heterobaric leaves (Kenzo et al., 2007). This observation may correlate with the fact that only the upper layers of plant canopies are exposed to saturating light whereas leaves in the shaded layers obtain light mainly from sunflecks (up to 90% of daily photon flux; Pfitsch and Pearcy, 1989). Plants exposed to a fluctuating light environment as in forest understorey may thus benefit from having homobaric leaves which are capable of utilizing laterally supplied CO₂. This effect is obviously dependent on stomatal conductance and usually shade leaves open their stomata rather slowly after exposure to light when compared with sun leaves; however, once the stomata are fully open the closing mechanism is also very slow when the leaves are exposed to darkness again (Ooba and Takahashi, 2003). However, most of these experiments were performed by illuminating entire leaves or at least homogenously illuminated leaf areas inside leaf chambers. Whether stomata respond in the same way when only a small leaf area is illuminated or when a lightfleck is moving over the leaf blade while the other leaf part is exposed to shade is not known. This question is rather important to understand the productivity of understorey plants and their contribution to the overall carbon fluxes, and further studies and new methods to elucidate this effect are necessary.

In conclusion, lateral diffusion of CO₂ was found to contribute to photosynthesis of lightfleck areas of homobaric leaves and the contribution increases with smaller lightflecks. Additionally, lateral CO₂ diffusion reduces the light stress and most probably increases the water use efficiency. Stomatal conductance is the key player which determines the amount of lateral CO₂ supply to lightflecks. When stomatal conductance is high then the importance of lateral CO₂ diffusion for lightfleck photosynthesis is small, but it becomes substantial when stomata are closed.