Abstract
This study examines various optimization criteria as potential sources of constraints that eliminate (or at least reduce the degree of) mechanical redundancy in prehension. A model of nonvertical grasping mimicking the experimental conditions of Pataky et al. (current issue) was developed and numerically optimized. Several cost functions compared well with experimental data including energylike functions, entropylike functions, and a “motor command” function. A tissue deformation function failed to predict finger forces. In the prehension literature, the “safety margin” (SM) measure has been used to describe grasp quality. We demonstrate here that the SM is an inappropriate measure for nonvertical grasps. We introduce a new measure, the “generalized safety margin” (GSM), which reduces to the SM for vertical and two-digit grasps. It was found that a close-to-constant GSM accounts for many of the finger force patterns that are observed when grasping an object oriented arbitrarily with respect to the gravity field. It was hypothesized that, when determining finger forces, the CNS assumes that a grasped object is more slippery than it actually is. An “operative friction coefficient” of approximately 30% of the actual coefficient accounted for the offset between experimental and optimized data. The data suggest that the CNS utilizes an optimization strategy when coordinating finger forces during grasping.
1 Introduction
This paper is a sequel to Pataky et al. (2004a). Part I investigated digit forces while holding an object at various orientations with respect to the gravity field. The purposes of Part II are: (1) to elaborate on the mechanical peculiarities of nonvertical grasping and (2) to offer an explanation for the experimental results of Part I. The explanation is based on mechanical optimization of a model that describes the investigated task. In the interest of compactness, experimental results for only the four-finger task from Part I will be used to complement the current optimization discussion.
Despite its static indeterminacy, subjects perform multifinger grasping in a highly reproducible way (e.g., Li et al. 1998) when presented with a particular set of mechanical demands. While intertrial variability exists, this variability is smaller than the variability associated with changing the mechanical demands (e.g., Li et al. 1998). The fact that performance is repeatable across load magnitudes (Shim et al. 2003) indicates that similar mechanical demands beget similar CNS responses.
It is conceivable that the CNS produces digit forces according to some objective optimization criterion or criteria. The physiological basis for this contention is the fact that neuron activity level is related to mechanical variables that are manifested externally. That is, increasing alpha-motoneuron activity naturally increases muscle forces, while reducing this activity conserves energetic resources. Additionally, the strong coupling of afferents and alpha-motoneurons serving the hand (McNulty et al. 1999) implies that external mechanical variables may directly influence finger forces via spinal circuits without substantial supraspinal involvement and conscious perception. Regardless of the possible physiological mechanisms, optimization is attractive for addressing prehension’s static indeterminacy because it could constitute the constraint equations that would render the system solvable – thus leading to reproducible performance. Previous research on prehension has found qualitative agreement between experimental observations and optimization’s predictions (Hershkovitz et al. 1997; Zatsiorsky et al. 2002).
For a pinch grasp with vertical object orientation, the simplest optimization scheme would be to assign normal forces (Fn) the minimum value to prevent slip. However, it has been widely documented that the CNS does not employ this technique (e.g., Westling and Johansson 1984; Burstedt et al. 1999; Li 2002). Moreover, for more than two digits, this scheme does not provide a unique solution. The “safety margin” (SM) has been used in the literature to address this issue. Conceptually, the SM relates the observed Fn to the task-dependent minimum Fn. The SM was introduced for two-finger grasps (Westling and Johansson 1984) and was defined as the difference between the observed Fn and the Fn required forces to prevent slip. If the CNS specifies a constant SM, the pinch problem is solved (but only for vertical object orientation, i.e., when only tangential forces contribute to weight support). For more than two digits this scheme does not provide a unique solution. While the SM has been examined for more than two fingers (Burstedt et al. 1999), its relation to the corresponding static indeterminacy has not been addressed. Importantly, for nonvertical object orientations the SM, as it is defined in the literature, is ambiguous (Sect. 4.2). However, as will be discussed later, the SM concept can be extended to the general grasping task if, rather than specifying the Fn required to prevent slip, the “required” forces are defined on the basis of a mechanically optimum solution.
The current study thus examines various optimization criteria as potential sources for constraint equations that eliminate (or at least reduce the degree of) indeterminacy in prehension. New grasping control variables are proposed: generalized safety margin (GSM) and operative friction coefficient (μop). It was found that these optimization-based variables account for many of the finger force patterns that are observed during nonvertical grasping.
The paper is structured as follows. In Sect. 2 a mechanical model of nonvertical grasping is developed. The procedures and results of optimization in which five different cost functions were employed are described in Sect. 3. The mechanical peculiarities of nonvertical grasping are discussed in Sect. 4, and a summary discussion is provided in Sect. 5.
2 Model of nonvertical grasping
Consider the planar equilibrium of a grasped object with weight W. Two coordinate systems are defined as follows: normal (n) and tangential (t) object axes are coincident with the global horizontal (X) and vertical (Y) axes, respectively, for θ = 0, where θ is the angle between t and Y as defined by a right-handed coordinate system (see Fig. 1 for a description of all notation). The digit forces are denoted as: (Fq)i where q represents the axis of interest and the subscript i refers to any of the five digits – thumb (T), index (I), middle (M), ring (R), or little (L) – or to the “virtual finger” (VF). The VF is an imagined finger that produces a wrench equal to the wrenches produced by all of the fingers (Arbib et al. 1985; Iberall 1986). The point of application of FVF depends on the distribution of finger forces.
Fig. 1.
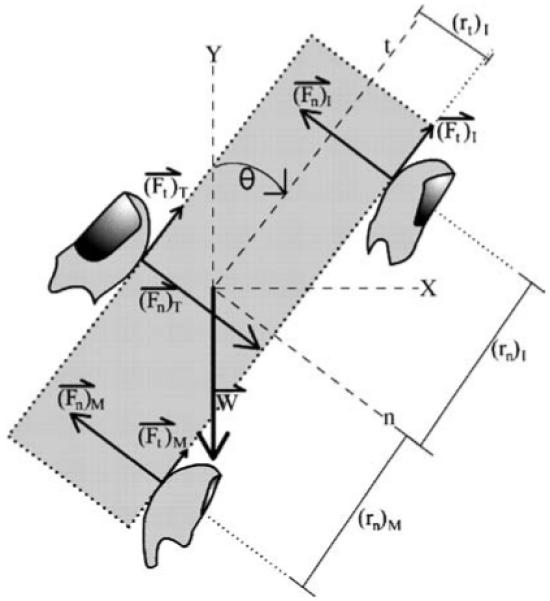
Coordinate systems and notation used. The local normal (n) and tangential (t) axes are coincident with global horizontal (X) and vertical (Y), respectively, for orientation θ = 0. The normal and tangential forces (Fn and Ft, respectively) are shown for the thumb and the index and middle fingers (T, I, and M, respectively). Moment arms (r) about the origin are shown for Fn and Ft separately, but not for all digit forces
To establish an algebraic basis for optimization, the constraints of object equilibrium must be considered. For planar static grasping there are three equilibrium equations to satisfy:
| (1) |
| (2) |
| (3) |
where N is the number of digits used (2 ≤ N ≤ 5), Mnt represents the moments exerted in the n–t plane, Mext is the negative of the external moment acting on the handle (or the resultant moment necessary to maintain equilibrium), and Wn and Wt are the projections of the object’s weight on the n and t axes, respectively:
| (4) |
| (5) |
Assuming hard finger–object contacts (i.e., point contact with friction and no contact couples) and Coulomb friction, the normal forces (Fn)i are also subject to the following no-slip constraint:
| (6) |
where μi is the coefficient of static friction between the ith finger and the grasped object. Equations (1-3) and (6) may be expressed as a set of linear constraints in matrix form as follows:
| (7) |
| (8) |
where (7) represents the no-slip constraints (6) and (8) represents the equilibrium constraints (2) and (3). Equations (7) and (8) collectively constitute a force closure (i.e., all solutions that simultaneously satisfy both equations represent static equilibrium). The vector F is the (2 N×1) vector of digit forces:
which implies that:
where i is the ith finger and F(i) is the ith element of F. Note that F is not the resultant force produced by the vector sum of Fn and Ft . The vector S is the (2 N × 1) zero vector that constitutes the no-slip inequality constraints and L is the (3×1) load vector that constitutes the right-hand side of the equilibrium constraints (1)-(3):
The matrix A is a (2N × 2N) square matrix, and the matrix Aeq is (3 × 2N). Both are best defined by example: if the T, I, and M digits are used to grasp the object shown in Fig. 1, the terms of (7) and (8) expand to:
where (rn)i and (rt)i are the moment arms of the normal and tangential forces, respectively. For compactness, moments are computed about the origin of the n–t coordinate system illustrated in Fig. 1 (i.e., such that W does not produce a moment). The moment arms (rn)i and (rt)i can be expressed as (1×N) vectors rn and rt. The coefficients μi were considered to be 1.4 for all digits [F. Gao (2002), unpublished M.S. thesis, The Pennsylvania State University]. Equations (7) and (8) constitute the full set of mechanical constraints to be submitted to an optimization routine.
3 Optimization procedure and results
3.1 Procedure
The optimization problem was formulated in terms of design variables F as follows:
where Ω = {F : gj (F) ≤ 0, hk(F) = 0}; j = 1, . . . , 2N; k = 1, 2, 3.
The function f is a cost function, and the gj’s and hk’s are the inequality and equality constraints, respectively, that are described by (7) and (8). The set Ω is the feasible solution region defined by the constraints. Geometrically Ω represents the intersection of the hk’s (which are 2N-dimensional hyperplanes) that is truncated by the gj’s. Importantly, the Ω described by (5) and (6) is a convex set. This is due to the fact that all gj’s are convex and all hk’s are linear (Burstedt et al. 1999). Thus, where f is a convex function, the optimization problem itself is convex and a local minimum is, in fact, the global minimum.
Five cost functions f(F) were selected on the basis of intuition or their previous use in the prehension literature (e.g., Hershkovitz et al. 1995, 1997). All were convex except one (Sect. 3.1.5). Each is addressed separately below in Sects. 3.1.1–3.1.5. All objective functions were tested for either all N digits or all fingers (i.e., N–1 digits excluding T). In all cases Mext = 0 and μi = μ = 1.4 for all digits.
All optimization problems were solved using the procedure fmincon from MATLAB’s optimization toolbox (The MathWorks Inc., Natick, MA, USA). The optimum (F*) results were unaffected by random variations in initial (F0) values submitted to the routines.
3.1.1 Energylike function over F
A measure that is proportional to the potential energy of deformation for a linear (i.e., Hookian) system has been used widely in the literature, for example, as a component of the human grasping quality sense (Hershkovitz et al. 1997):
where (Fr)i is the magnitude of the vector sum |(Fn)i + (Ft)i| and i0 is either 1 or 2 (i.e., summed over all digits or over only fingers). We are unaware of any earlier study that incorporates Ft into the objective function. Although f1 explicitly addresses only external contact forces, this function has been proposed to be related to minimization of muscular effort (Hershkovitz et al. 1995, 1997).
3.1.2 Energylike function over Fn
The energylike function can be expressed in terms of only Fn as:
This function was selected because it has been proposed that the Ft are “passive” consequences of external loading and of the selected Fn (Pataky et al. 2004b), i.e., that the CNS is concerned only with Fn coordination. Thus the inclusion of only Fn in a cost function is appropriate. This proposal is substantiated by the fact that Fn is constrained to a greater extent by (7) than Ft.
3.1.3 Entropylike function
Since it is conceivable that the CNS prefers to spread efforts as evenly as possible among redundant effectors, the entropy-motivated measure:
was introduced by Hershkovitz et al. (1995, 1997). The equation does not represent entropy as a physical variable but was rather derived from information theory to reflect the uniformity of the contact forces.
3.1.4 Motor command function
The procedure for computing motor commands (c) from observed Fn has been described elsewhere (Zatsiorsky et al. 2002; cf. Danion et al. 2003b). The N × 1 vector c represents the intended activation level of each finger (each ci ∊ [0, 1]) and the manifested Fn is the result of physiological interconnections among fingers. Thus, based on the neural network model of Zatsiorsky et al. (1998), an interconnection matrix (M) was constructed that linearly mapped c to Fn:
The c can be computed based on the observed Fn by inverting the square M matrix. Thus, the objective function:
represents a minimization of finger “activation”. This function was selected because of its physiological nature (Danion et al. 2003a) and because it has been demonstrated that f4 more closely predicts experimental data than do other objective functions (Zatsiorsky et al. 2002).
3.1.5 Tissue deformation function
Tissue displacement minimization is significant with respect to the robotics literature, which customarily formulates grasping optimization in terms of only Fn and assumes that the Ft are passive consequences of the mechanical properties of the effectors (e.g., Hershkovitz et al. 1995). Additionally, the neural sensitivity of finger pad afferents to small strains has been well documented (e.g., Bremner et al. 1991; McNulty et al. 1999). We are unaware of any earlier study that incorporates tissue strain in an objective function.
The only data available for which the mechanical properties of the finger pads were measured for all fingers are those of Pataky et al. (2004b). However, only shear strain was measured. The authors modeled tangential tissue displacement (δt) as:
where m and b are, respectively, the slope and intercept of linear regression of tangential stiffness on (Fn)i. A cost function could be formulated as:
However f0 suffers from nonconvexity (i.e., ▽2f0 is not positive semidefinite). In other words, increasing (Fn)i causes a decrease in f0. This can be avoided by including (Fn)i with a weighting coefficient (w) as a separate term in the function. The function thus becomes:
Note that optimization results obtained using f5 would approach those using f2 as w gets large. For small w, f5 approaches f0. A value of w = 1 was selected such that the (Fn)i were not more important than the (δt)i. Ideally, tissue strain could be assessed using a finite element model (e.g., Wu et al. 2002) and incorporated in a cost function. However, such a computationally intensive analysis is inconsistent with the purposes of this paper.
3.2 Results
Typical optimization results are presented in Fig. 2. All objective functions produced qualitatively similar results: experimental (Fn)i values paralleled (Fn)i* with a more or less constant offset. There were exceptions to this generalization, especially for f5 and in the vicinity of θ = 0°. In particular, while experimental results transitioned smoothly from θ < 0° to θ > 0°, the optimum results displayed nonsmooth transitions. The optimum thumb patterns appeared to be affected least by the cost function and also appeared to parallel experimental results most closely. This was confirmed statistically (Sect. 4.3.2).
Fig. 2.

Exemplary Fn* optimization results (gray) for the five objective functions (f – see text for a description of the functions). Each function incorporates different digits: i0 = 1 indicates that the T and all fingers were used, and i0 = 2 indicates that only the fingers were used. Different digits are presented in different columns. Experimental data are shown in black as a reference; error bars represent standard deviations. Note the different force scales for the T (left) and the fingers (right). All plots have θ > 0 to the left of the ordinate to be consistent with figures from Part I of this study
Because of the observed offset, the typically used root-mean-square (RMS) measure was inappropriate to quantify the correspondence of experimental and optimum results. We thus introduced a new measure, the (“GSM”), which is described later (Sect. 4.3). The use of the GSM measure is justified in Sect. 4, so it is not described here. The focus will be on three experimental measures whose patterns could not be readily explained in Part I: internal force, force sharing, and SM.
3.2.1 Internal force [(Fn)INT]
The [(Fn)INT] is defined as the normal force in excess of W sin θ. The experimental and optimum (Fn)INT results are presented in Fig. 3. These data are based on f2 with i0 = 2. As expected, optimization predicted zero (Fn)INT for θ = ±90°. This was not observed in the experimental results. Consistent with the experimental results, however, was the tendency for optimized (Fn)INT to be slightly larger in pronated postures. Also consistent with the experimental results was the curvilinear relation of (Fn)INT with sin θ, although the curve was “flatter” for the optimized results in the vicinity of θ = 0°. Note that a linear (Fn)INT vs. sin θ relation would imply that (Fn)INT is a trigonometric function of θ. Thus both the larger (Fn)INT in pronated postures and the curvilinear relation of (Fn)INT and sin θ have a purely mechanical explanation: both facts were predicted by optimization of a mechanical model.
Fig. 3.
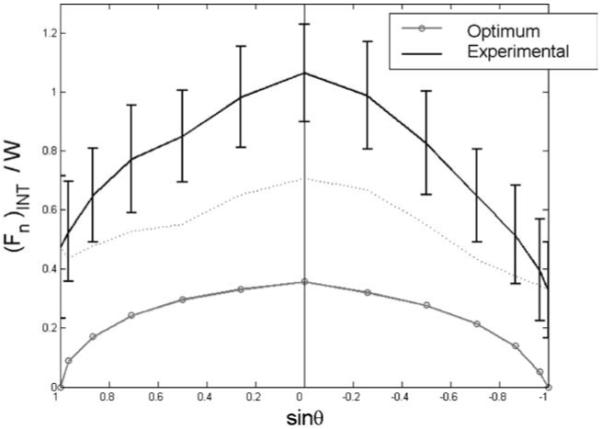
Internal normal force computed from experimental F data (black) and from F* (gray) for objective function f2 with i0 = 2 (i.e., fingers only without thumb). The dotted line represents the difference between the average experimental (Fn)INT and that calculated from F*. Data are presented, as in Part I of this study, as a function of sin θ
3.2.2 Force sharing
Normal force-sharing data are presented in Fig. 4. The data represent the percentage of the total normal force produced by all four fingers. The general shapes of the experimental and optimum (Fn)i-sharing vs. θ plots were quite similar. In particular, a finger’s normal force-sharing percentage tended to change across the θ = 0 line according to both its moment arm’s magnitude and direction. That is, an (Fn)i with a “pronation moment arm” [(rn)i > 0] tended to produce more than “even” sharing in pronation and vice versa for supination. The effect was more pronounced for larger (rn)i. Additionally, all fingers tended to return to near-constant sharing (i.e., 25%) for full supination, as predicted by optimization. Not observed in the experimental data was constant sharing for one side of the θ = 0° line (θ < 90°).
Fig. 4.
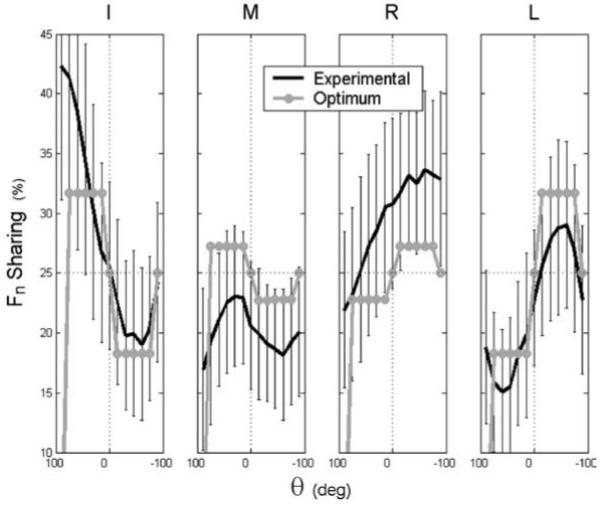
Force sharing computed from experimental F data (black) and from F* (gray) for objective function f2 with i0 = 2. The horizontal dotted lines indicate even sharing among the digits (i.e. 25%)
3.2.3 Safety margin
The SM has been defined (e.g., Burstedt et al. 1999) as:
| (9) |
The SM results derived from from F* are reported in Fig. 5. To interpret Fig. 5, it is useful to consider the concept of weight agonists (AG) and weight antagonists (ANT). That is, T may be considered an AG for θ > 0 (because [Fn]T acts to support W) and an ANT for θ < 0 (because [Fn]T “adds” to W), and vice versa for the fingers. Figure 5 reveals that optimization always predicted zero SM for the ANT digits. This is unsurprising due to the nature of the inequality constraints (7). However, for all functions f , the SM for AG digits increased monotonically for |θ| > 0 until its maximum value of 100% was reached at |θ| = 90°. This is counterintuitive: one imagines that the “safety” level should be zero for mechanically optimum results. It seems that when an object is held with the minimum possible forces – just so the object does not slip from the hand – the SM should be zero. However, all optimization results yield nonzero SM values. This problem is addressed in the next section.
Fig. 5.
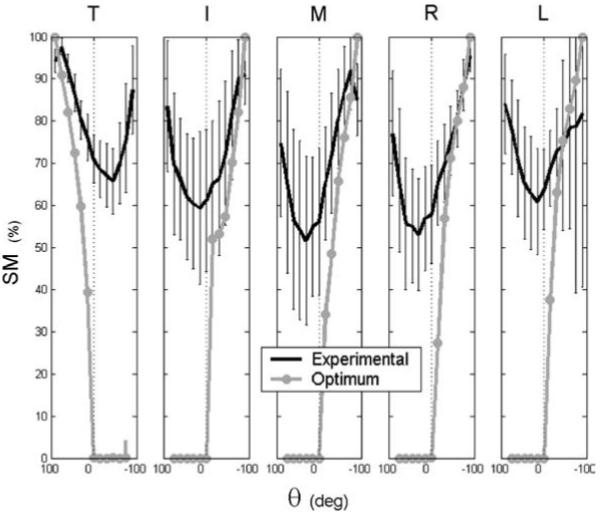
Safety margin computed from experimental F data (black) and from F* (gray) for objective function f2 with i0 = 2
Despite the conceptual problems with the SM, Fig. 5 reveals that, for the AG digit(s), optimization SM predictions were comparably close to experimental results. The decrease in the experimental SM between |θ| = 75° and 90° can be explained by the fact that individuals produce nonzero (Ft)i. En masse, the SM results indicate that slip prevention can explain the general behavior of the AG digit(s) only if a mechanically optimal solution is also considered. The SM was unable to account for the behavior of the ANT digit(s).
4 Mechanical peculiarities of nonvertical grasping
This section uses the concepts of AG and ANT (described above) to first describe the minimum normal forces required for pinch grasps and then to describe why (despite its common use in the literature) the SM is an inappropriate measure of prehension quality for nonvertical and/or multifinger grasps. In Sect. 4.2, a new measure, the GSM, is introduced. An alternative to the GSM measure, the operative friction coefficient (μop), is introduced in Sect. 4.3.3. The discussion that follows arises from a fundamental distinction: the equality constraints (8) explicitly depend on θ, while the no-slip (inequality) constraints (7) do not depend on θ.
4.1 Minimum normal forces for pinch grasp and nonvertical orientations
Consider the case of two-digit (pinch) grasp in which the T and I pinch the object shown in Fig. 1. Assume that the (Fn)T and (Fn)I are collinear such that no net moment is produced by the normal forces. In terms of the AG and ANT digits, (1)-(3) can be rewritten as follows:
| (10) |
| (11) |
| (12) |
where Wn and Wt are defined in (4) and (5). Recognizing that (rt)AG = (rt)ANT, rearranging (12) and substituting it into (11) yields:
| (13) |
Since the (Ft)ANT must be equal to half of the projection of W on the t axis, the minimum ANT normal force is given by:
| (14) |
because the ANT finger is subjected to the no-slip constraint (4). Note that in this situation of pinch grasp with no moments being produced by normal forces, the ANT finger must produce normal force, thereby adding to W. The same would be true for multifinger grasping if the VF could not change its point of force application by redistributing the normal forces among the fingers. The result of (14), when substituted into (10) yields:
| (15) |
Note that the AG force is indeed a minimum in (15) because Wn is always greater than zero. Since only (2μ)−1 Wt units of (Fn)AG are sufficient to prevent slip [see (14)], the AG finger would never slip (if the frictional conditions are identical at the two digits). This is because AG slip prevention is an inevitable consequence of equilibrium Eq. (1). A simple experiment could confirm this physical fact: during pinch grasp of an object held at θ ≠ 0, one cannot voluntarily slip the AG finger without first accelerating the object toward the AG finger [by virtue of (15)]. The SM thus seems ambiguous for the AG digit, despite the similarities between experimental and predicted SM values (Fig. 5) discussed in Sect. 3.2.3. The apparently dual roles of (Fn)AG for W support and for slip prevention are therefore actually physically inseparable in static pinch grasp. Defining a critical angle θ at which the role of the (Fn)AG changes from one of slip prevention to one of W support is thus superfluous.
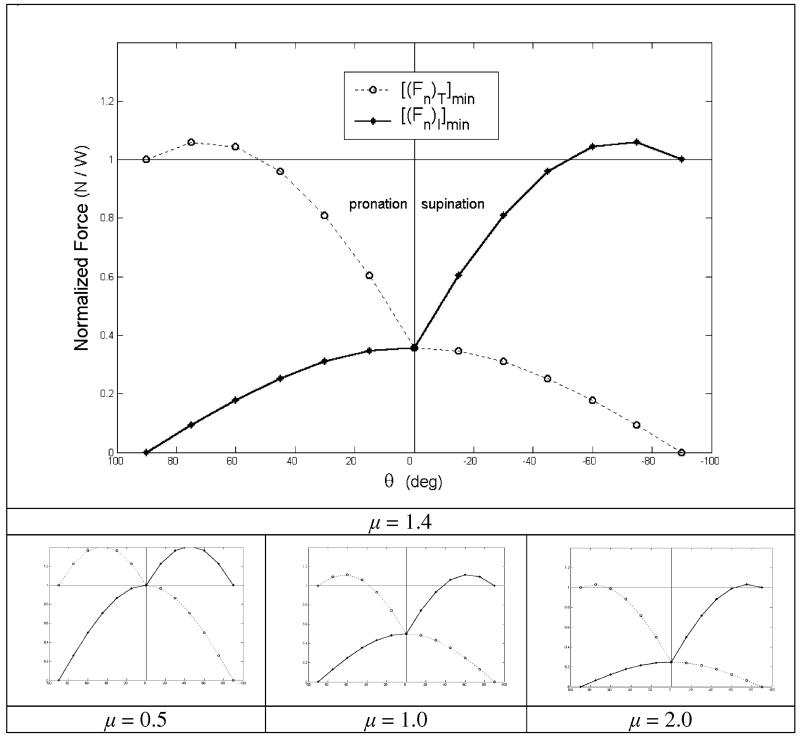
A graphical interpretation of (14) and (15) presented in Fig. 6 reveals the inherent nonlinearities of these equations. The minimum normal forces of individual fingers are nontrigonometric functions of θ, and μ obviously affects the shape of these functions. There is also a non-smooth transition in each digit’s behavior across the θ = 0 line.
Fig. 6.
Minimum normal forces of T and I fingers for a pinch grasp in which normal forces exert no net moment. The top panel shows the minimum finger forces for the coefficient of friction (μ) used in the experiment of Part I of this study (current issue). The bottom panels show the effect of μ on the minimum forces. Note that θ > 0 appears to the left of the ordinate
Figure 6 and (14) and (15) illustrate that the minimum (Fn)AG finger force clearly depends on many factors including W, θ, μ, and the selected (Fn)ANT – which must be at least [(Fn)ANT]min. Even this simple and idealized model has inherently highly complex mechanics.
4.2 Problems with the safety margin (SM) measure for nonvertical orientations
The literal interpretation of (9) – as stated in Sect. 2.4.2.2 of Part I of this study – is as follows: the SM is the proportion of a digit’s exerted normal force that is not functioning for slip prevention. This interpretation is valid for all θ. However, (9) has implicit meaning beyond this literal interpretation. An alternative interpretation arises because of the peculiarities of the task mechanics (7) and (8) and because of the literature’s original intended use of the SM for θ = 0 and for pinch grasp:
Alternative interpretation of the SM (as stated in Sect. 1): The SM is the proportion of a digit’s Fn that exceeds the task-dependent minimum Fn. This interpretation accounts for the inseparability of the finger forces’ dual roles of weight support and slip prevention when θ ≠ 0. We believe that this interpretation represents the essence of the original intended meaning of the SM. Note that the alternative interpretation is consistent with the literal interpretation for θ = 0. A mechanical analysis supports these ideas.
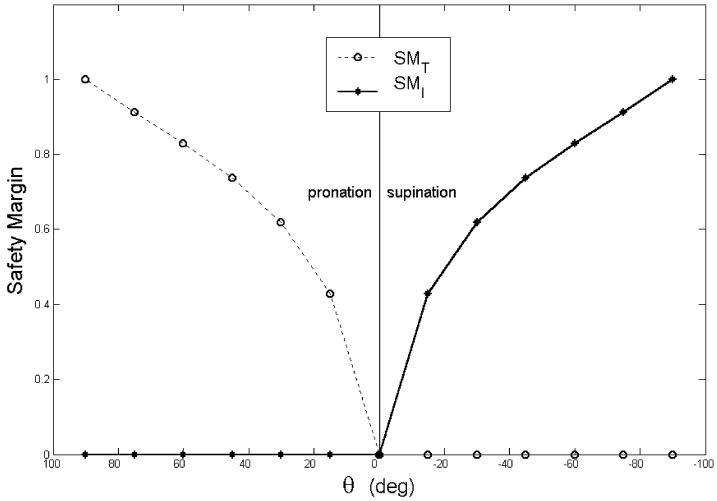
Assume that the CNS solves the two-digit pinch problem of Sect. 4.1 in exactly the way described in (14) and (15). If an experimenter were to quantify the SM as it appears in (9), the results would be as in Fig. 7 (for μ = 1.4). As in Fig. 5, when a digit acts as an ANT, the predicted SM is zero, as one would expect. However, when the finger is an AG, the SM is nonzero, and in fact reaches its maximum possible value of unity for θ = 90°.
Fig. 7.
Safety margin computed from the minimum force of Fig. 2 for μ = 1.4
This is paradoxical: the subject chooses the mechanically minimum normal force acting against the load, (Fn)AG, and yet his/her SM is nonzero. This paradox, we argue, is precisely the reason why (9) does not capture the essence of the SM. We thus propose a new measure that we believe does capture the intended meaning of the SM and that can be generalized to both nonvertical and multifinger grasping: the GSM.
4.3 Generalized safety margin
Because of the conceptual problems of the SM described above, we would like to introduce the generalized safety margin (GSM) as a means to quantify prehension quality. The GSM is calculated as:
| (16) |
where (Fq)i is the observed force of the ith finger along an arbitrary axis (q), and (Fq)i* is the optimum force determined by minimization of some objective function. The subscript i, q on GSM indicates that the GSM can be calculated for each digit and each axis separately. We use the term “scaling” in GSM because experimental data indicated that the GSM was never zero; rather experimental data seemed to have a constant offset from optimal data. The similarities between (16) and (9) are apparent; it can be shown that (16) reduces to (9) for θ = 0 and for pinch grasp. Importantly, if a subject selects the mechanically minimum forces prescribed by (14) and (15), the GSM would be zero. The GSM thus maintains the essence of the SM meaning while genera lizing the SM calculation to both θ ≠ 0 and multifingered grasping.
4.3.1 GSM results
To quantify the quality of fit between the predicted optimal and experimentally observed finger forces, the GSM measure was introduced (Sect. 3.1). A single GSM value was calculated for each i, q combination and for each θ. The mean normalized by W(Fq)i was computed for each θ.
As a demonstration of the GSM concept applied to experimental data, example optimization results appear in Fig. 8 for f2 and for i0 = 2 (refer to Fig. 2 for the Fn and Fn* data). No statistical tests were performed on the results presented in Fig. 8 – these data are simply intended to illustrate the concept of the GSM. It is apparent that the GSM is larger for θ = 0 vs. θ ≠ 0 for all digits except I. It is also apparent that T has the largest and most variable GSM for both axes; note that the (GSMn)T is equal to the (GSMn)VF.
Fig. 8.
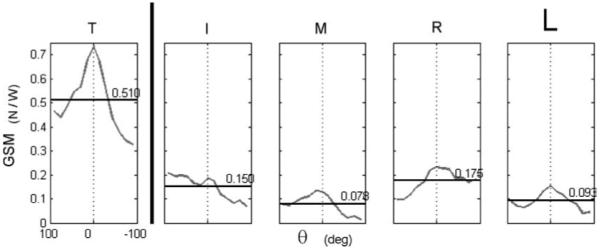
Exemplary GSM results. The objective function used here was f2 with i0 = 2. The average GSM is indicated by a horizontal line and its value is printed at the right side of each lower panel. The standard deviations of GSM across θ were: 0.137, 0.052, 0.043, 0.048, and 0.036 for the T, I, M, R, and L digits, respectively
4.3.2 “Best” objective function?
The quality of fit between optimum and experimental data was determined as follows: the average (GSMn)i was added to each to produce Fn* + GSM curves. The quality of fit for a given digit was then determined as the RMS between the experimental (Fn)i curve and the curve. This is analogous to quantifying the similarities in curve shapes across θ. Since GSMt values (not yet presented) were much lower than GSMn values, the RMS was computed between the unmodified Ft and Ft* curves.
The RMS data are presented in Table 1. The tissue displacement cost function f5 was not included in the analysis because of its dissimilar results (Fig. 2) and because a complete tissue strain measure could not be described parametrically (Sect. 3.1.5). All other functions produced very similar RMS values for a given digit and a given direction (i.e., n or t). Interestingly, the RMS values for (Fn)T were consistently the lowest. This might be due to the fact that there are no redundant effectors acting in parallel with (Fn)T. At a significance level α = 0.05, analysis of variance (ANOVA) confirmed that different functions did not affect the RMS values: p values were greater than 0.13 for all (Fn)i except for the I finger (p = 0.031), and p values were greater than 0.556 for all (Fti. Additionally, the RMS values were not affected by i0 for all (Fq)i(p > 0.130). Thus all cost functions yielded statistically similar results.
Table 1.
Root-mean-square (dimensionless units: N/W) between experimental F values and optimum F* results
| Cost function: | f1 | f1 | f2 | f2 | f3 | f3 | f4 |
|---|---|---|---|---|---|---|---|
| i0 | 1 | 2 | 1 | 2 | 1 | 2 | 2 |
| (Fn)T | 0.124 | 0.124 | 0.133 | 0.125 | 0.121 | 0.128 | 0.143 |
| (Fn)I | 0.536 | 0.539 | 0.537 | 0.538 | 0.536 | 0.537 | 0.547 |
| (Fn)M | 0.428 | 0.433 | 0.432 | 0.431 | 0.429 | 0.427 | 0.442 |
| (Fn)R | 0.665 | 0.661 | 0.668 | 0.662 | 0.662 | 0.667 | 0.663 |
| (Fn)L | 0.547 | 0.529 | 0.547 | 0.534 | 0.542 | 0.559 | 0.513 |
| (Ft)T | 0.086 | 0.078 | 0.102 | 0.074 | 0.079 | 0.106 | 0.097 |
| (Ft)I | 0.024 | 0.021 | 0.074 | 0.027 | 0.028 | 0.061 | 0.028 |
| (Ft)M | 0.037 | 0.027 | 0.048 | 0.031 | 0.035 | 0.043 | 0.019 |
| (Ft)R | 0.049 | 0.053 | 0.087 | 0.047 | 0.046 | 0.078 | 0.057 |
| (Ft)L | 0.027 | 0.013 | 0.047 | 0.014 | 0.018 | 0.053 | 0.021 |
The RMS for Fn was determined based on the Fn* plus the average OSF (see text). The cost functions fj are defined in Sect. 3.1. The index i0 indicates whether the cost functions incorporated all digits (i0 = 1) or only the fingers (i0 = 2). Function f5 was not included for reasons described in Sect. 4.3.2.
4.3.3 Alternative interpretation of GSM: operative friction coefficient
Rather than performing optimization and then scaling the results, as suggested above, the CNS could alternatively employ an operative friction coefficient (μop) that would describe the GSM. By assumption, the μop – which is different from the actual μ – is a coefficient that the CNS uses when it determines finger forces. That is, if the CNS assumes that there is a μ lower than the actual μ, then the Fn* solutions would be driven upward toward the experimental data. This μop thus reflects a SM of sorts. The intuitive appeal of the μop over either the SM or GSM measure is that the latter measures imply that the CNS stores some scaling number; the μop contrastingly reflects the fact that the CNS does not have explicit knowledge of the actual μ.
The μop that might be used by the CNS can be computed for each digit based on the relation between RMS and the μ that is submitted to an optimization routine. That is, the RMS of the difference between Fn and Fn* is computed as a function of μ (note that this RMS differs from the one used in Sect. 4.3.2). The μop is then the μ for which the RMS is a minimum.
Figure 9a illustrates the relation between RMS and μop. The figure indicates that the RMS reaches local minima for μop in the range 0.33 to 0.7. A μop value of 0.4 produces quite low RMS values for all digits. Therefore, if CNS assumes that the μ is 30% of its actual value, the experimental and optimal data have the closest agreement. The optimization results corresponding to μop = 0.4 are shown in Fig. 9b. While these Fn* results are certainly closer to the experimental data than the Fn* results shown in Fig. 2, there are still discrepancies. Note especially that for |θ| = 90°, optimization unsurprisingly still predicts zero ANT force.
Fig. 9a, b.
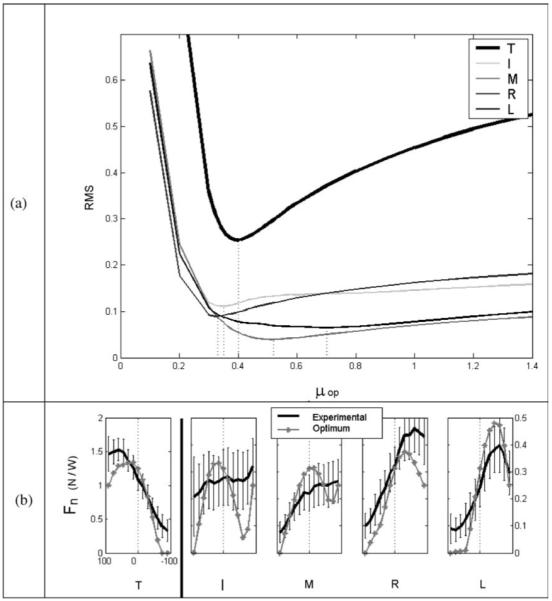
a RMS between experimental Fn and optimized Fn* as a function of the operative friction coefficient (μop – see text). The cost function used was f2 with i0 = 2. The dotted vertical lines show the μop values for which different digits have a minimum RMS. These minimum μop values range from 0.33 for the R finger to 0.7 for the L finger. b Optimization results for μop = 0.4 and experimental data
5 Discussion
The present study yielded three main findings:
The GSM, herein introduced, is a more broadly applicable measure than the typically used SM for quantifying prehension quality.
Various cost functions yield optimization results that are in good qualitative agreement with experimental force data obtained during nonvertical grasping.
Assuming that the CNS views an object as being more slippery than it is, in conjunction with optimization, can partially account for the offset between experimental and optimal data.
The first main finding, that the GSM is a better measure than the SM, is justified because the former can be generalized to nonvertical and multifinger grasps while preserving the meaning of the latter. Indeed the GSM reduces to the SM for vertical orientations and two-digit grasps. The remainder of the discussion addresses the second and third main findings.
Many of the human behaviors observed in Part I of this study (Pataky et al. 2004a) were explained by a purely mechanical analysis of nonvertical grasping. These behaviors included, among others, greater internal force for pronated postures, nonzero agonist SM, and the general patterns of force sharing among the redundant fingers. The difference in optimum forces between fingers emerged simply because of their different moment arms.
The finding that several cost functions worked equally well is consistent with a previous study that only found cost function differences for large external torques (Zatsiorsky et al. 2002). The finding that tissue displacement minimization did not produce good agreement with experimental data is significant because the grasp-planning algorithms proposed in the robotics literature are concerned primarily with normal forces; tangential forces are passive consequences of the structural properties of the effectors (e.g., Hershkovitz et al. 1995). Although tissue displacement minimization cannot explain the observed finger forces, perhaps more sophisticated models of the passive properties of the fingers could.
Of the experimental behaviors not explained by optimization, the most apparent was the more or less constant offset between experimental and optimum data (i.e., a constant GSM). The selective stabilization of the GSM, if real, suggests that at least two CNS processes may be responsible for the observed prehension synergies: (1) determining an optimal solution and (2) scaling the solution. The former does not imply that the CNS performs the mathematical operations described by optimization; it rather implies that finger forces map to some internal neural representation, and it is these variables that are fine-tuned by the system such that small changes in forces result in the increase of a perceivable signal. The process of force-to-neural mapping has physiological merit: forces are sensitively detected by mechanoreceptors in the finger pads and can be integrated by the CNS (McNulty et al. 1999). Additionally, it has been found that force is represented in the motor cortex (Asanuma 1973; Evarts 1973; Schieber et al. 2001).
The physiological basis for the GSM scaling process is more elusive. It is possible that the GSM arises from mechanisms similar to those that have been hypothesized to be responsible for the SM (Westling and Johansson 1984): psychological/mechanical factors including the desire for grasp stability, specifically the tendency to reduce the effects of potential external disturbances. If such a mechanism operates, it would be interesting to know whether grasping a vibrating object is associated with larger GSM. Explaining the cause of the GSM is certainly not trivial: even a more mathematically rigorous formulation of prehension optimization could not explain the scaling observed in human performance without incorporating a GSM-like measure (Hershkovitz et al. 1997).
Perhaps a more intuitively appealing account of the GSM is the following: if the CNS assumes that an object has some arbitrarily high slipperiness, then measures like the SM and GSM would naturally emerge, without explicit knowledge of either friction or the optimum solution. This idea is described herein by the operative friction coefficient. This new variable cannot, obviously, explain all the data: optimization still predicts zero normal forces for horizontal orientations. However, the present model is phenomenological and contains no anatomy or physiology (with the exception of the motor commands of Zatsiorsky et al. 1998); the fingers differ only in the moment arms with respect to the object’s axis of rotation. While a more sophisticated biomechanical model might explain the data more completely, the successes of the present model collectively represent a useful starting point.
The implications of the optimization-derived variables beget a plethora of empirical questions. In short, any experimental manipulation (e.g., changed friction, nonzero external moment, etc.) is expected to change the optimum forces. Whether the experimental forces follow the task-dependent optimum forces is unknown.
All optimization models suffer from the interdependence of the design variables. That is, slightly changing one finger force affects all other finger forces. Thus if a subject performs exactly optimally and then slightly changes one finger force, the quality of fit between experimental and optimum data balloons. It is precisely because of this interdependence problem that we were surprised to observe that all fingers closely paralleled the optimum results when no interfinger differences were incorporated into the model. Each finger has different geometry and hence different gross muscle architecture, and each finger also has different mechanical performance characteristics (e.g., Li et al. 1998). The parallel between experimental and optimal finger forces thus reflects a relation that transcends anatomy and follows mechanical principles. Solutions rendered by optimization of mechanically redundant models of prehension therefore appear to be promising resources for aiding interpretation of experimental human performance.
Acknowledgements
Supported in part by NIH grants AR-48563, AG-018751, and NS-35032.
References
- Arbib MA, Iberall T, Lyons D. Coordinated control programs for movements of the hand. Exp Brain Res Suppl. 1985;10:111–129. [Google Scholar]
- Asanuma H. Cerebral cortical control of movements. Physiologist. 1973;16:143–166. [PubMed] [Google Scholar]
- Belegundu AD, Chandrupatla TR. Optimization concepts and applications in engineering. Prentice-Hall; Englewood Cliffs, NJ: 1999. [Google Scholar]
- Bremner FD, Baker JR, Stephens JA. Correlation between the discharges of motor units recorded from the same and from different finger muscles in man. J Physiol. 1991;432:355–380. doi: 10.1113/jphysiol.1991.sp018389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burstedt MK, Flanagan JR, Johansson RS. Control of grasp stability in humans under different frictional conditions during multidigit manipulation. J Neurophysiol. 1999;82(5):2393–2405. doi: 10.1152/jn.1999.82.5.2393. [DOI] [PubMed] [Google Scholar]
- Danion F, Latash ML, Li S. Finger interactions studied with transcranial magnetic stimulation during multi-finger force production tasks. Clin Neurophysiol. 2003a;114:1445–1455. doi: 10.1016/s1388-2457(03)00105-6. [DOI] [PubMed] [Google Scholar]
- Danion F, Schoner G, Latash ML, Li S, Scholz JP, Zatsiorsky VM. A mode hypothesis for finger interaction during multi-finger force-production tasks. Biol Cybern. 2003b;88(2):91–98. doi: 10.1007/s00422-002-0336-z. [DOI] [PubMed] [Google Scholar]
- Evarts EV. Motor cortex reflexes associated with learned movement. Science. 1973;179:501–503. doi: 10.1126/science.179.4072.501. [DOI] [PubMed] [Google Scholar]
- Hershkovitz M, Tasch U, Teboulle M. Toward a formulation of the human grasping quality sense. J Robot Syst. 1995;12(4):249–256. [Google Scholar]
- Hershkovitz M, Tasch U, Teboulle M, Tzelgov J. Experimental validation of an optimization formulation of the human grasping quality sense. J Robot Syst. 1997;14(11):753–766. [Google Scholar]
- Iberall T. The representation of objects for grasping; Proceedings of the 8th Cognitive Society conference; 1986.pp. 547–561. [Google Scholar]
- Latash ML, Gelfand IM, Li ZM, Zatsiorsky VM. Changes in the force-sharing pattern induced by modifications of visual feedback during force production by a set of fingers. Exp Brain Res. 1998;123(3):255–262. doi: 10.1007/s002210050567. [DOI] [PubMed] [Google Scholar]
- Li ZM. Inter-digit co-ordination and object-digit interaction when holding an object with five digits. Ergonomics. 2002;45(6):425–440. doi: 10.1080/00140130210129673. [DOI] [PubMed] [Google Scholar]
- Li ZM, Latash ML, Newell KM, Zatsiorsky VM. Motor redundancy during maximal voluntary contraction in four-finger tasks. Exp Brain Res. 1998;122(1):71–78. doi: 10.1007/s002210050492. [DOI] [PubMed] [Google Scholar]
- Li ZM, Zatsiorsky VM, Latash ML. Contribution of the extrinsic and intrinsic hand muscles to the moments in finger joints. Clin Biomech. 2000;15(3):203–211. doi: 10.1016/s0268-0033(99)00058-3. [DOI] [PubMed] [Google Scholar]
- McNulty PA, Turker KS, Macefield VG. Evidence for strong synaptic coupling between single tactile afferents and motoneurones supplying the human hand. J Physiol. 1999;518(3):883–893. doi: 10.1111/j.1469-7793.1999.0883p.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pataky TC, Latash ML, Zatsiorsky VM. Prehension synergies during non-vertical grasping. I. Experimental observations. Biol Cybern. 2004a;91:148–158. doi: 10.1007/s00422-004-0505-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pataky TC, Latash ML, Zatsiorsky VM. Tangential load sharing among fingers during prehension. Ergonomics. 2004b;47(8):876–889. doi: 10.1080/00140130410001670381. [DOI] [PubMed] [Google Scholar]
- Pataky TC, Latash ML, Zatsiorsky VM. Viscoelastic response of the finger pad to incremental tangential displacements. J Biomech. 2004c doi: 10.1016/j.jbiomech.2004.07.004. in press. [DOI] [PubMed] [Google Scholar]
- Schieber MH. Constraints on somatotopic organization in the primary motor cortex. J Neurophysiol. 2001;86:2125–2143. doi: 10.1152/jn.2001.86.5.2125. [DOI] [PubMed] [Google Scholar]
- Shim JK, Latash ML, Zatsiorsky VM. Prehension synergies: trial-to-trial variability and hierarchical organization of stable performance. Exp Brain Res. 2003;152(2):173–184. doi: 10.1007/s00221-003-1527-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westling G, Johansson RS. Factors influencing the force control during precision grip. Exp Brain Res. 1984;53(2):277–284. doi: 10.1007/BF00238156. [DOI] [PubMed] [Google Scholar]
- Wu JZ, Dong RG, Rakheja S, Schopper AW. Simulation of mechanical responses of fingertip to dynamic loading. Med Eng Phys. 2002;24(4):253–264. doi: 10.1016/s1350-4533(02)00018-8. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gregory RW, Latash ML. Force and torque production in static multifinger prehension: biomechanics and control. II. Control. Biol Cybern. 2002;87(1):40–49. doi: 10.1007/s00422-002-0320-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Li ZM, Latash ML. Coordinated force production in multi-finger tasks: finger interaction and neural network modeling. Biol Cybern. 1998;79(2):139–150. doi: 10.1007/s004220050466. [DOI] [PubMed] [Google Scholar]