Finger coordination during moment production on a mechanically fixed object

Abstract

The moment production by several fingers on a mechanically fixed vertically oriented handle was studied under the systematic variations of task parameters such as (a) moment magnitude (1.0 Nm and 2.0 Nm) and (b) direction of moment production (into pronation and supination), as well as (c) vertical position of the handle from the moment axis, P (0, 2.0, 4.0, and 6.0 cm in both directions). The purpose of this study was twofold: to investigate the dependences between the task parameters and the performance variables and to test the mechanical advantage hypothesis. The performance variables changed symmetrically with P. In particular, magnitudes of the net horizontal and vertical forces both showed an S-shape change. The position of the point of zero free moment (PZFM) was determined. In the intermediate grasp locations (when 0<P magnitude <PZFM), the contribution of M_free (moment produced mainly by pronational or supinational effort) and the moment of the resultant force (moment generated mainly by pushing) into the total moment production scaled linearly with the P. The magnitudes of both agonist and antagonist moments (those acting in and against the direction of the required moment, respectively) of normal forces increased with P magnitudes while the magnitude of agonist moments of tangential forces decreased. For individual fingers, the ratio of finger force to its moment arm was not constant. The mechanical advantage hypothesis was successful in explaining some of the data but could not cope with other findings. We assume, therefore, that this hypothesis is limited in its applicability and may be task and effector specific.

Introduction

This study deals with the fingertip forces exerted during moment production on a handle affixed to an unmovable support. The task is analogous to turning a door handle and is quite common in everyday life. As compared to holding a free object—to date the most popular object for studying prehension (Augurelle et al. 2003; Shim et al. 2003; Zatsiorsky et al. 2003)—this task possesses one essential distinction. When a free object is held statically in the air, the forces and moments exerted on the object are constrained by the equilibrium equations. Specifically, to maintain the equilibrium the resultant horizontal force exerted on the object must equal zero, the resultant vertical force must equal the weight of the object, and the resultant moment should be equal to the external moment applied to the handle.

When a handle is affixed to an external support, the forces exerted on the handle can be of any magnitude. In this sense, the task is constraint-free and the finger forces are selected by the performer based on principles that are not dictated by the mechanics. In contrast, when the handle is mechanically free, the performer should exert only those forces and moments that satisfy the equilibrium requirements.

Moment production by the hand on a fixed handle has been studied in ergonomics to design better valves and tools or to discover optimal positions of operators (Dellinges and Tebrock 1993; Schulze et al. 1997; Shih and Wang 1997; Ciriello et al. 2002). Most of these studies were limited to the magnitude of the moment produced. The individual finger forces during moment production tasks have not attracted much attention among researchers.

It is known from mechanics that an arbitrary set of forces acting on a rigid body can be reduced to a wrench, a resultant force and a corresponding force couple, i.e. two equal and opposite forces that generate a moment (see, for instance, Zatsiorsky 2002). If a force does not cross an axis it produces a moment about this axis. A force couple generates a moment (free moment) about any axis that is not in the plane of the couple. When several fingers act on a hand-held object and produce a moment M about a fixed axis, the moment M is due both to the resultant force F acting on the handle and free moment M_free:M=M_free +d×F, where d is the moment arm of force F. In many practical situations, free moment M_free is generated by pronation/supination efforts of the hand, while the moment of force d×F is due to pushing the object in a certain direction.

Finger contact forces in multi-finger grasping can be presented as a sum of two orthogonal vectors: the first vector contributing to the resultant (net) force acting on the object and the second corresponding to the internal grasp force (Kerr and Roth 1986). The elements of the second vector cancel each other and, hence, do not contribute to the net force. To visualize the internal grasp force consider a task of maintaining a glass in the air at rest: the normal forces of the thumb and the fingers cancel each other—the horizontal net force is zero and the glass does not accelerate. When the object is in the air, the internal normal forces are necessary to prevent the glass from slipping (Flanagan et al. 1999), but if the object is fixed their role is less evident.

During moment production tasks while holding a free handle, the fingers located farther away from the axis of rotation generate larger forces than those fingers that are located closer to the axis (Zatsiorsky et al. 2002). Based on this observation, it has been speculated that the fingers are recruited according to their mechanical advantage, i.e. the moment arms with respect to the rotation axis (ibid). This axis of rotation was considered to be located at the level of thumb force application during prismatic grasping of a free object in a previous study (Shim et al. 2003), while the axis can be located farther away from the grasping hand during rotating a fixed object such as a door knob or a valve lever.

This suggestion is in line with a hypothesis that individual muscles are also activated in proportion to their mechanical advantage, i.e. the moment arm with respect to the joint rotation axis. For instance, during elbow flexion efforts biceps brachii is most active while brachioradialis and brachialis are less active (Buchanan et al. 1989); for a detailed discussion on the mechanical advantage hypothesis see Prilutsky (2000).

The goal of this study has been to investigate effects of the three task parameters—(1) the mechanical advantage of the fingers, (2) the magnitude, and (3) the direction of the produced moment—on the following outcome variables: (a) the net forces exerted on the object, (b) internal grasp force, (c) percentage contribution of the free moment (a force couple) and the net force to the total moment production, (d) agonist and antagonist moments, and (e) individual finger forces. We also tested the mechanical advantage hypothesis.

Methods

Equipment

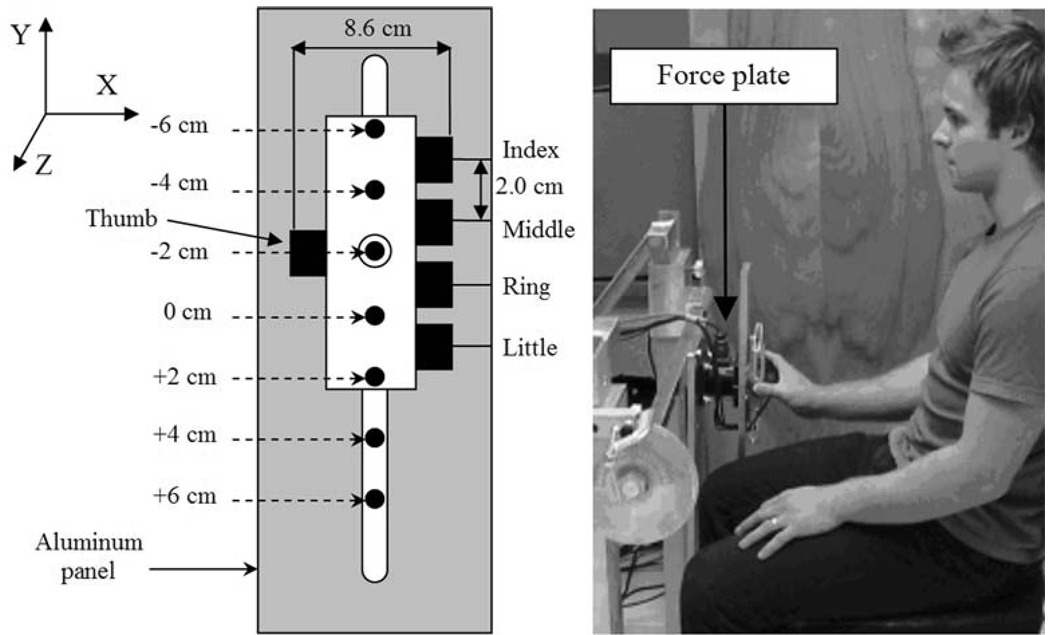
Five six-component (3 forces and 3 moments) transducers (four Nano-17’s and one Nano-25, ATI Industrial Automation, Garner, NC, USA) were fixed to an aluminum handle which was attached to an aluminum panel (Fig. 1). The panel was affixed to a small force plate (PY6, Bertec Co., Columbus, OH, USA) and the aluminum handle could be moved vertically along a slot in the panel while the orientation of the handle was kept constant. Sliding the handle along the panel changed the vertical position of the handle with respect to the moment axis, i.e. the axis which the subjects generate a moment. The position of the handle with respect to the moment axis, P (6.0 cm, 4.0 cm, 2.0 cm, 0 cm, −2.0 cm, −4.0 cm, and −6.0 cm), defined the finger force moment arms that varied in a systematic manner.

Fig. 1.

Experimental setup. Left panel A schematic representation of the handle (white rectangle) with the force sensors (black rectangles) and the panel (in gray). Seven positions of the axis of moment of the handle (black circular dots) were shown to subjects with a sticky marker. The circle around the black dot signifies center O with respect to which the free moments were computed (described later in the text). The position of the handle in the drawing is at −2.0 cm. Right panel A subject position

The vertical distance between adjacent finger sensors was 2.0 cm and the thumb sensor was placed midway between the middle and ring finger sensors. The horizontal distance between the contact surfaces of the thumb and finger sensors (grip width) was 8.6 cm. 100-grit sandpaper was affixed to the contact surface of each sensor to increase the friction between the digits and transducers. The static friction coefficient of the sandpaper was approximately 1.4–1.5 (previously measured; Zatsiorsky et al. 2002).

The total of 36 analog signals from the sensors (5 sensors × 6 components and 1 force plate × 6 components) were routed to a 12-bit analog-digital converter (PCI-6031, National Instrument, Austin, TX, USA) and processed by a microcomputer (Dell Dimension 8330, Austin, TX, USA).

Subjects

Thirteen right-handed young males served as subjects (age 25.3±2.2 years, weight 72.2±3.7 kg, height 176.6±4.3 cm, hand length 18.5±2.9 cm, hand width 9.1±1.1 cm). The hand length was measured between the middle fingertip and the distal crease of the wrist with the hand extended. The subjects had no previous history of neuropathy or trauma to the upper limbs. All subjects gave informed consent according to the procedures approved by the Office for Research Protections of The Pennsylvania State University.

Experimental procedure

Subjects washed their hands with soap and warm water to normalize the skin condition of the hands. The subjects were given a familiarization session to the experimental procedure to ensure that they were able to accomplish the experimental tasks.

The subjects sat on a chair and flexed the right elbow joint 90° in the sagittal plane. The forearm was in a neutral position between pronation and supination. A height-adjustable chair was used to keep the right-arm joint configurations of each subject constant. The height of the chair was adjusted when the vertical height of the handle was changed for different moment axis locations. The left hand rested naturally on the left thigh.

During data collection, hyperextended joint configurations were not allowed for any phalangeal joint of the right hand. The instruction to the subjects was to grasp the handle by placing the digit tip centers over the centers of the corresponding sensors and to produce a required moment about the moment axis as accurately as possible. The moments were generated in the counterclockwise (pronation, positive) and clockwise (supination, negative) direction, in total four moments: −2.0 Nm, −1.0 Nm, 1.0 Nm, and 2.0 Nm.

P varied for each moment magnitude and direction. For P of 6.0 cm and 4.0 cm, all digits were below the moment axis while at −4.0 cm and −6.0 cm they were all above the moment axis. At 0 cm, the moment axis was at the level of the center of the thumb sensor.

The subjects performed three trials for each combination of moment magnitude and P for the total of 84 trials (3 trials×4 moments×7 axis locations) in a randomized order of moment and P combinations. Signals from all channels were put to zero prior to each trial with the fingers off the sensors. When the subjects reported that they were holding the handle comfortably, data recording started. While performing a task, the subjects were watching a computer screen on which the moment they were producing was shown in real time. The task moment was presented as a horizontal line on the screen. The subjects were instructed to produce a prescribed task moment in 5 s and keep the moment constant for another 5 s. The data were collected at 100 Hz for 10 s. A minimum of a 20-s rest interval was given to the subjects between trials. A rest interval of 10 min was given between moment conditions to avoid fatigue effects. The order of the trial was randomized and balanced.

Data analysis

The analysis was limited to a frontal plane of the subject (X–Y plane in Fig. 1) and only forces along X- and Y-axes and moment about Z-axis were analyzed. The recorded force and moment data were averaged over 3-s periods between the 6th and 9th s for each trial separately. Further, data from the three trials performed with the same combination of moment and P were averaged. Positions of the points of digit force application along axis Y with respect to the sensor centers were found as y=−M_Z/F_X, where M_Z is the moment of force about axis Z and F_X is the normal force component.

Total moment and free moment

The digit forces exerted on the handle were reduced to one resultant force and a force couple that produced a free moment (for the theoretical background and method description see Zatsiorsky 2002). The resultant force was reduced to the center O with the following coordinates: in the vertical direction—at the center of the thumb sensor; in the horizontal direction—in the middle between the thumb and the finger sensors (see Fig. 1). Within this approach, the total moment about the axis was decomposed into the moment generated by the force acting at O (d×F) and the free moment. The force acting at O is due to the pushing efforts on the handle and the moment is due to the hand rotation efforts (supination or pronation). The relative contribution of the moment of (resultant) force and free moment into the total moment was computed.

The moments of the normal and tangential forces

The moments of normal (horizontal) digit forces and tangential (vertical) digit forces were computed according to Eq. 1

$$\begin{array}{cc}M\hfill & =\underset{\text{Moment}\text{of}\text{the}\text{normal}\text{forces}\equiv M^n}{\underbrace{F_i^n{d}_i^n+F_m^n{d}_m^n+F_r^n{d}_r^n+F_l^n{d}_l^n+F_{\mathit{\text{th}}}^n{d}_{\mathit{\text{th}}}^n}}\\ \hfill & +\underset{\text{Moment}\text{of}\text{the}\text{tangential}\text{forces}\equiv M^t}{\underbrace{F_i^t{d}^t+F_m^t{d}^t+F_r^t{d}^t+F_l^t{d}^t+F_{\mathit{\text{th}}}^t{d}^t}}\hfill \end{array}$$ (1)

where the subscripts th, i, m, r, and l refer to the thumb, index, middle, ring, and little finger, respectively, and n and t stand for the normal and tangential force components, dⁿ and d^t refer to the moment arms of the normal force and tangential force; d^t is a constant (grip width divided by two).

In particular, the moment of the normal finger forces Mⁿ about the moment axis was calculated using the following equation:

$$M^n=M_{\nu }^n+M_{\mathit{\text{th}}}^n=F_{\nu }^{n}D+F_{\mathit{\text{th}}}^n{d}_{\mathit{\text{th}}}={\displaystyle \sum _{f=1}^4{F}_f^n{d}_f+F_{\mathit{\text{th}}}^n{d}_{\mathit{\text{th}}}}$$ (2)

where f=i, m, r, and l, and ν symbolizes the virtual finger and D is the moment arm of the virtual normal force with respect to the moment axis. The virtual finger (VF) is an abstract representation of all four fingers that act as a functional unit. The VF normal force F_νⁿ and VF tangential force F_ν^t were computed as the sums of the normal and tangential forces of the four fingers, respectively. The location of D may vary due to (a) varied vertical position of the handle (the handle displacement changes individual finger moment arms d_f by a constant value), (b) changes in the sharing pattern among individual finger forces and (c) displacement of the points of finger force application with respect to the sensor centers.

Since the grip width was constant, the moment of the tangential forces M^t is proportional to the difference between the virtual tangential force and the thumb tangential force. Hence, the following equation is valid.

$$\begin{array}{cc}{M}^t\hfill & =M_{\nu }^t+M_{\mathit{\text{th}}}^t=F_{\nu }^t{d}^t-F_{\mathit{\text{th}}}^t{d}^t\\ \hfill & ={\displaystyle \sum _{f=1}^4\left(F_f^t{d}^t\right)-F_{\mathit{\text{th}}}^t{d}^t}\hfill \end{array}$$ (3)

The internal normal grasp forces

For each handle position P, the internal normal grasp force was determined as a smallest of the two forces, the thumb and the VF forces.

Agonist and antagonist moments

Agonist moments are created by finger forces, which produce a moment in the required direction, while antagonist moments are created by finger forces, which generate moments against the required task moment. The agonist moment can be calculated by summing up the moments produced by agonist normal and agonist tangential forces, and the antagonist moment can be calculated by summing up the moments of antagonist normal and tangential forces:

$$M^{\mathit{\text{ago}}}=M_{\mathit{\text{ago}}}^n+M_{\mathit{\text{ago}}}^t={\displaystyle \sum _{f=1}^{\mathit{\text{agon}}}{F}_f^n{d}_f+{\displaystyle \sum _{f=1}^{\mathit{\text{agot}}}{F}_f^{t}r}}$$ (4)

$$M_{\mathit{\text{ant}}}=M_{\mathit{\text{ant}}}^n+M_{\mathit{\text{ant}}}^t={\displaystyle \sum _{f=1}^{\mathit{\text{antn}}}{F}_f^n{d}_f+{\displaystyle \sum _{f=1}^{\mathit{\text{antt}}}{F}_f^{t}r}}$$ (5)

where ago and ant represent the agonist and antagonist, respectively; agon and agot designate the digits whose normal and tangential forces support the task moment, and antn and antt refer to the digits whose normal and tangential forces are against the task moment, respectively.

Individual finger forces and force sharing

The force sharing (S) among individual finger normal and tangential forces was calculated as:

$$S_f^n=\frac{F_f^n}{{\displaystyle \sum _{f=1}^4{F}_f^n}}\times 100\%$$ (6)

$$S_f^t=\frac{F_f^t}{{\displaystyle \sum _{f=1}^4{F}_f^t}}\times 100\%$$ (7)

Testing the mechanical advantage hypothesis: apparent stiffness of the fingers

The mechanical advantage hypothesis assumes that during the torque production tasks the fingers are activated in proportion to their moment arms with respect to the moment axis (Zatsiorsky et al. 2002). The hypothesis can be formalized as follows. During the torque production the hand/fingers system experiences a twist deformation θ. Hence, a fingertip displacement (with respect to the forearm) equals θr where r is the shortest distance from the fingertip to the moment axis (the moment arm). If the fingers possess a stiffness-like property and exert/resist force in proportion to the deformation, the finger force equals k′θr, or simply kr where k is the coefficient of apparent stiffness. According to the mechanical advantage hypothesis k should be equal for all the involved fingers. In such a case, the fingers with larger moment arms would exert proportionally larger forces.

Statistics

Data in the text are presented as averages and standard deviations. In figures, standard error bars are shown. Two-way repeated-measures ANOVAs were used with the factors POSITION (seven levels: 6.0 cm, 4.0 cm, 2.0 cm, 0 cm, −2.0 cm, −4.0 cm, and −6.0 cm) and MOMENT (four levels: 2.0 Nm, 1.0 Nm, −1.0 Nm, and −2.0 Nm). Three-way repeated-measures ANOVAs were used with MOMENT MAGNITUDE (two levels: 1.0 Nm and 2.0 Nm), MOMENT DIRECTION (two levels: clockwise and counterclockwise directions), and GRASP LOCATION (two levels: the hand below or above the moment axis). MANOVA with the factors of POSITION and MOMENT on finger force sharing and post hoc tests were performed with necessary comparisons. The correlation coefficients were computed to estimate the strength of linear relationships between the variables.

Results

The experimental data are presented below in a downward sequence of the control hierarchy (Shim et al. 2003), from resultant forces and moments acting on the handle to the virtual forces and then to the individual finger forces.

Net forces exerted on the handle

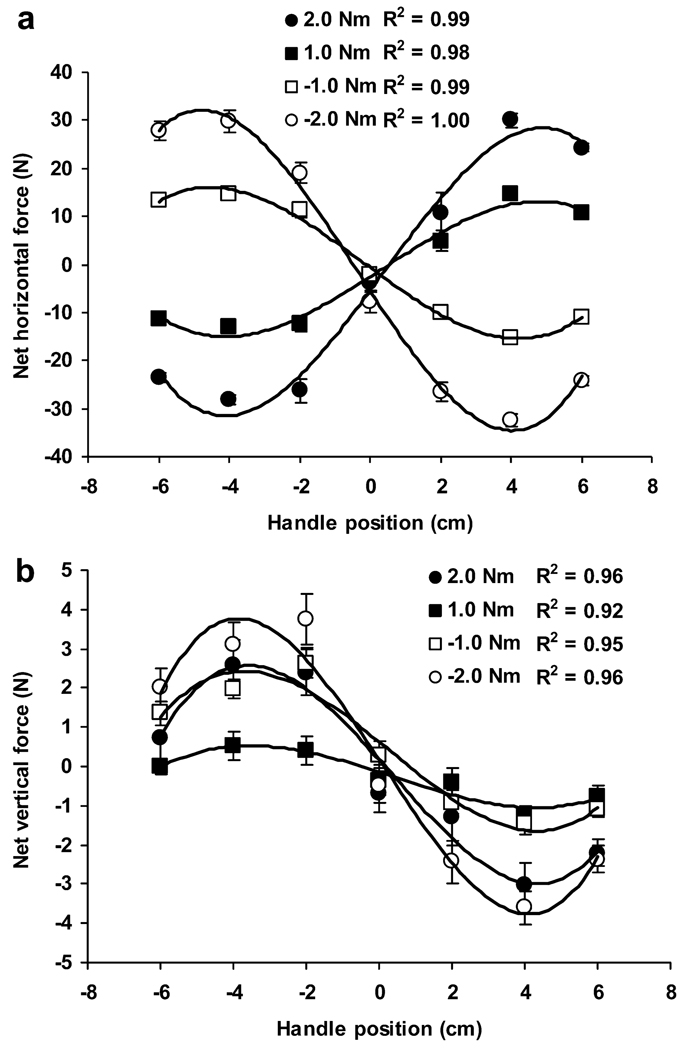
When a free object is held statically in the air, the net horizontal and vertical forces are prescribed; they represent mechanical constraints on the finger forces. In the present experiment—since the handle was fixed—these constraints were lifted. The constraint-free situation resulted in a systematic variation of both horizontal and vertical net forces exerted on the handle; Fig. 2. The subjects exerted a non-zero net horizontal force (at P≠0 cm) and non-constant vertical force while generating the desired moment. Such a force pattern cannot be used with a free object during static prehension.

Fig. 2.

The a horizontal and b vertical net forces exerted on the handle. Averaged across subject data are presented with standard error bars. Note the S-shape of the curves with low values for small P, larger values at P=2.0 and 4.0 cm, and slightly smaller values for P=6.0 cm. The relationships are approximated by the cubic parabolic equations. In this and other figures the positive values of the handle position correspond to the position of the handle below the moment axis. Averaged across subjects data are shown with standard error bars

A two-way repeated-measures ANOVA with factors of MOMENT and POSITION confirmed that there were significant effects of POSITION (F_(6,72)=8.93, p<0.001) and MOMENT × POSITION (F_(18,216)=201.379, p<0.001) on the horizontal net forces. MOMENT effect was slightly below the significance level (F_(3,36)=2.67, p<0.062). Pairwise comparisons showed that the horizontal net forces significantly increased when P expanded both to −4.0 cm and 4.0 cm (p<0.05 for all comparisons) and then stayed approximately constant (4.0 cm and 6.0 cm: P=0.19, −4.0 cm and −6.0 cm: P=0.87). The horizontal net forces were close to zero at 0 cm. The force-position curves could be described as S-shaped. The curves were satisfactorily approximated by the parabolic equations of the third power; the R² values were between 0.92 and 1.00.

A two-way repeated-measures ANOVA on vertical net forces showed significant POSITION (F_(6,72)=4.02, p<0.002), MOMENT (F_(3,36)=23.11, p<0.001), and MOMENT × POSITION (F_(18,216)=3.75, p<0.001) effects. The vertical forces at the task moments of 2.0 Nm and −2.0 Nm behaved in a similar manner with the largest force values observed when P were 4.0 cm. The vertical forces during the production of 1.0 Nm moments did not change much and were always below 1 N.

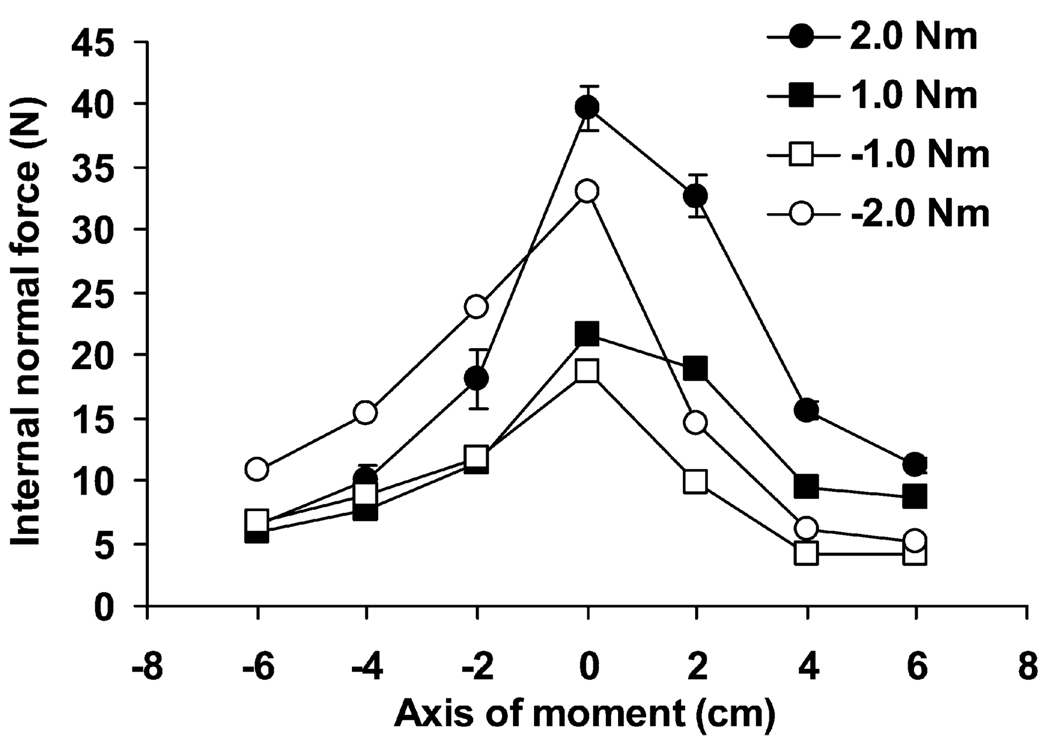
The internal grasp force

The internal grasp force varied as a function of the P being the maximal at P=0 (Fig. 3).

Fig. 3.

The internal normal grasp force at various handle locations with respect to the moment axes. Averaged across subjects data are shown with standard error bars

Free moment and the moment of the resultant force

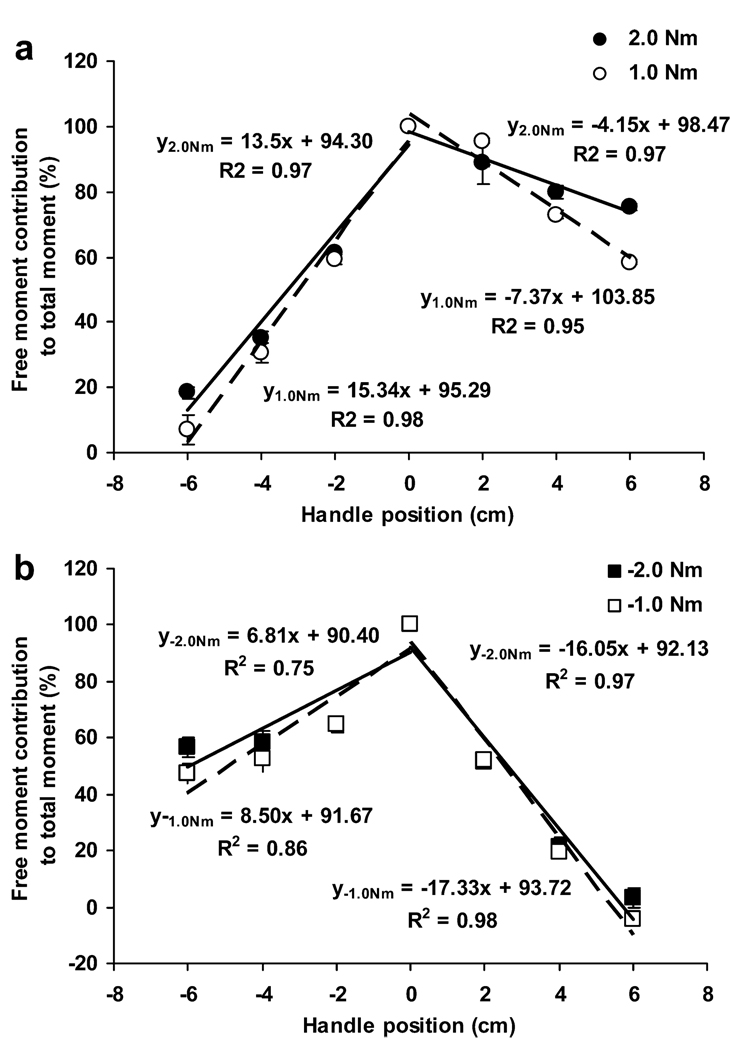
In the present experimental setup, the free moments M_free were generated by the pronation/supination efforts while pushing the handle generated the moment of the resultant force. The contribution of M_free into the total moment increased with P close to 0 cm and decreased with increasing P magnitude (Fig. 4). The contribution of the resultant force into the total moment production (not shown in Fig. 4) was larger for larger P.

Fig. 4.

a, b Free moment contribution to the total moment, %, as a function of the location of the moment axis. a Positive moment production (pronation efforts); b negative moment production (supination efforts). Averaged across subjects data are presented with standard error bars. To find the PZFMs, the regression lines were extrapolated to the level of the zero contribution of the free moment

At a certain P, the contribution of the free moment to the total moment was zero. At this P, the pronation/supination efforts do not contribute to the total moment production, and the moment is generated exclusively by the force exerted on the handle. The position of the point of zero free moment (PZFM) was computed by extrapolating the linear regression equations. The PZFM coordinates with respect to the moment axis in cm were equal to (−7.0, 23.7) at 2.0 Nm, (−6.2, 14.1) at 1.0 Nm, (−13.3, 5.7) at −1.0 Nm, and (−10.8, 5.4) at −2.0 Nm. A three-way repeated-measure ANOVA confirmed that the effects of MOMENT MAGNITUDE (F_(1,12)=11.09, p<0.005), MOMENT DIRECTION (F_(1,12)=29.14, p<0.001), and GRASP LOCATION were significant (F_(1,12)=829.89, p<0.001). The PZFM was smaller: (a) during pronation (positive) efforts—when the handle was above the moment axis and (b) during the supination (negative) efforts—when the handle was below the moment axis. In the both these conditions the fingers—rather than the thumb—were the main agonist moment producers.

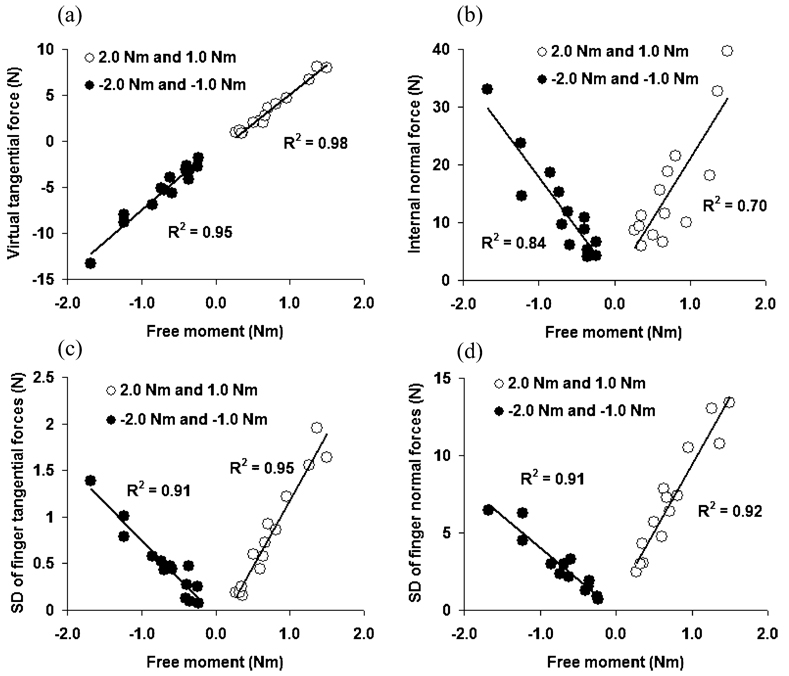
Figure 5 explains the mechanisms of generating the free moment (at the level of finger forces). As follows from the figure: (a) The free moment M_free is proportional to the virtual tangential force (the regression equation is M_free=6.28F_ν^t+1.10, r=0.99. (b) There is a V-like relationship between the M_free and the internal grasp force: M_free is close to zero when the internal force is minimal while its magnitude increases with the increase of the internal force. (c) and (d) The relationships between M_free and the standard deviation (SD) of the four finger respective normal and tangential forces consist of two opposite branches oriented similarly to the branches of letter V.

Fig. 5.

The scatterograms of the free moment M_free and a the virtual tangential force, b the virtual normal force, c the standard deviation of the normal finger forces (among the individual fingers in four-finger sets) and d the standard deviation of the tangential finger forces (among the individual fingers in four-finger sets). Averaged across subjects data are presented

Agonist and antagonist moments

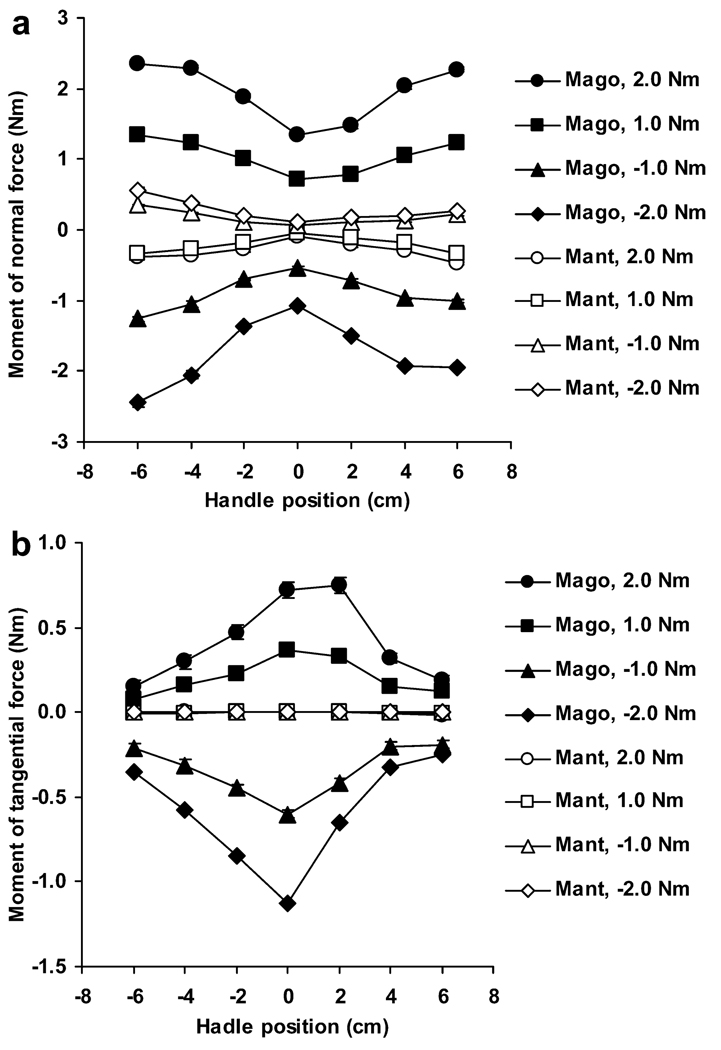
The magnitudes of both agonist and antagonist moments of the normal forces increased as the handle moved away from the axis of moment, while the magnitudes of agonist moments of the tangential forces decreased, Fig. 6. All antagonist moments of the tangential forces were close to zero. However, there existed considerable antagonist moments of normal forces throughout all P; the percentage of antagonist moment with respect to the agonist moment of normal forces ranged from 6.5% to 28.3%. Two-way repeated-measures ANOVAs on moment of normal forces showed that there were significant effects of POSITION (agonist: F_(6,72)=30.82, p<0.001; antagonist: F_(6,72)=17.58, p<0.001), MOMENT (agonist: F_(3,36) = 5,640.88, p<0.001; antagonist: F_(3,36) = 642.56, p<0.001), and POSITION × MOMENT (agonist: F_(18,216) = 378.39, p<0.001; antagonist: F_(18,216) = 40.41, p<0.001). Moments of tangential forces revealed significant effects of POSITION (agonist: F_(6,72) = 27.96, p<0.001; antagonist: F_(6,72) = 3.88, p<0.002), MOMENT (agonist: F_(3,36) = 20.13, p<0.001; antagonist: F_(3,36) = 642.56, p<0.001), and POSITION × MOMENT (agonist: F_(18,216) = 3.445, p<0.001; antagonist: F_(18,216) = 40.41, p<0.001) (Fig. 6).

Fig. 6.

a, b Moments of agonist (M_ago) and antagonist (M_ant) forces. a Moments of normal forces. b Moments of tangential forces. Averaged across subjects data are presented with standard error bars. All antagonist moments of tangential forces are zero

Individual finger forces and total force sharing

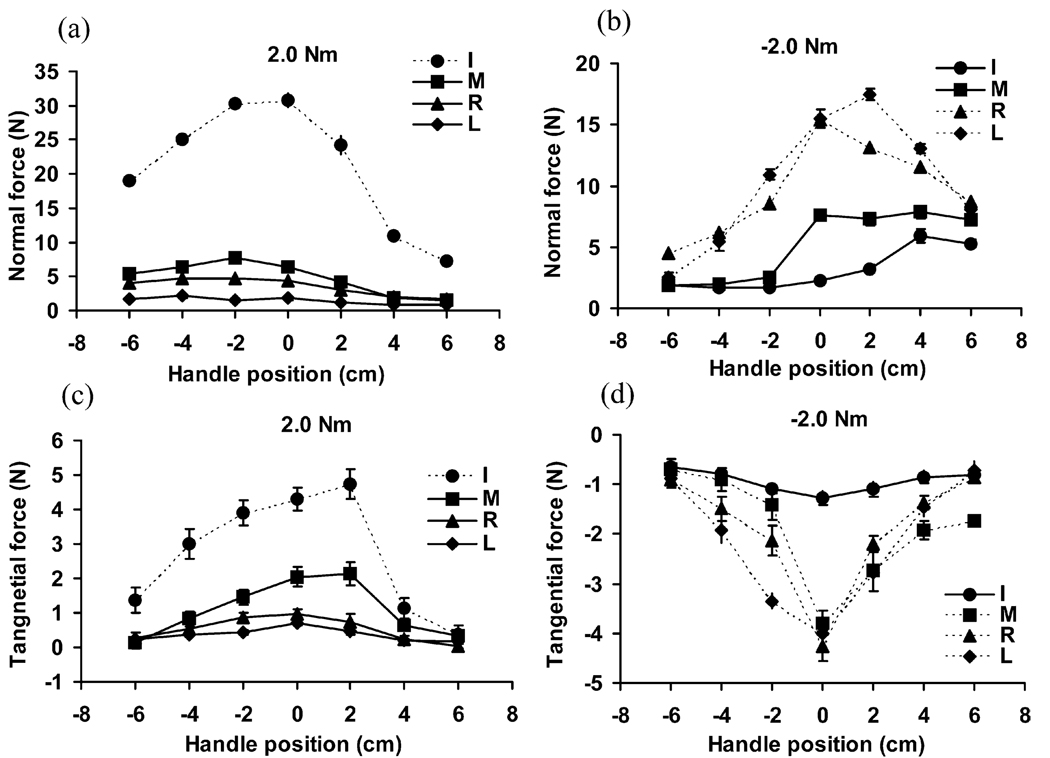
During the production of positive moments (into pronation), the index finger produced much of the total normal force. In contrast, during the production of negative moments (into supination), the ring and little fingers produced considerable normal forces, especially when the P was close to 0 cm. With respect to tangential forces, the index finger was used predominantly during the positive moment tasks while the middle, ring, and little fingers were used largely during the negative moment tasks. Figure 7 shows the forces produced by individual fingers for different external moments and different locations of the axis of moment production.

Fig. 7.

a–d Individual normal and tangential forces at 2.0 Nm and −2.0 Nm moment tasks. The fingers whose average forces across all P were greater than 25% of the average of the sum of finger forces across all P are shown with dotted lines. Averaged across subjects data are shown with standard error bars

The sharing of the total normal force among individual fingers remained relatively unchanged for the same direction of moment production over the seven P, regardless whether the fingers were agonists or antagonists with respect to the task (Table 1). A MANOVA with the factors of POSITION and MOMENT on finger force sharing and post hoc tests showed that the differences of normal or tangential finger force sharings between 2.0 Nm and 1.0 Nm or between −2.0 Nm and –1.0 Nm were not significant for the most of the combinations.

Table 1.

Sharing total normal and tangential force among individual fingers, %. Mean ± SD. Mean and SD values were calculated over all handle positions for all subjects

Task moment	Normal force (%)				Tangential force (%)
	I	M	R	L	I	M	R	L
2.0 Nm	68.4±4.3	14.9±2.4	11.8±2.1	4.9±1.2	50.0±16.1	19.0*±12.1	6.5±6.3	9.6±3.0
1.0 Nm	69.0±4.0	14.8±2.4	11.4±1.9	4.8±1.0	48.0±16.3	14.2±11.8	6.3±4.0	8.8±2.5
−1.0 Nm	14.1*±4.1	15.9*±2.5	36.1±1.8	34.0±1.0	18.3±17.7	23.3±12.0	27.0±4.4	28.2*±2.7
−2.0 Nm	12.2±4.3	17.3±2.4	35.4±2.0	35.0±1.0	15.3±18.2	26.6±11.7	26.5±4.3	31.1±2.7

^*Significant (p<0.05) differences of finger force sharing between 2.0 Nm and 1.0 Nm or between −2.0 Nm and −1.0 Nm

During the positive moment tasks the index finger produced 69% of the sum of normal finger forces while the ring and little fingers together generated 70% for the negative moment tasks. Note that the standard deviations (SD) of the normal forces sharing were much smaller than the SDs for the tangential forces. The sharing of tangential forces was subject specific (reflected in the relatively large standard deviations in Table 1) and depended on the P.

Mechanical advantage of finger position

The data on the apparent stiffness of the fingers that generate agonist moments are presented in Table 2. The columns of the table represent the apparent stiffness of the fingers at a given position of the handle. It is evident that, for a given task, the coefficients of the apparent stiffness differ across fingers. For instance, during pronation efforts of 1.0 Nm at P=−6.0 cm, the coefficients for the index finger (1.48) and the middle finger (0.70) differed by a factor of two.

Table 2.

Apparent stiffness of the agonist fingers

Moment (Nm)	1.0 (underlined upper left half) and −1.0 (lower right half)
Handle position (cm)	−6.0	−4.0	−2.0	0.0	2.0	4.0	6.0
I	1.48±0.10	1.86±0.24	3.13±0.27	5.04±0.44	10.85±2.36	1.94±0.73	1.70±0.43
M	0.70±0.19	0.75±0.25	1.47±0.42	5.94±1.44	5.03±1.25	1.44±0.32	1.33±0.23
R	0.89±0.23	0.91±0.31	2.37±0.67	10.47±1.09	3.94±0.58	1.57±0.13	1.20±0.12
L	1.06±0.30	1.11±0.31	7.19±1.11	4.41±0.79	3.19±0.30	1.39±0.15	0.86±0.12
Moment (Nm)	2.0 (underlined upper left half) and −2.0 (lower right half)
Handle position (cm)	−6.0	−4.0	−2.0	0.0	2.0	4.0	6.0
I	2.66±0.22	3.43±0.42	5.65±0.64	9.05±1.27	17.78±3.56	1.05±0.49	0.94±0.34
M	1.17±0.23	1.38±0.35	2.98±0.69	11.23±2.28	2.42±0.61	0.58±0.21	0.64±0.09
R	1.40±0.32	1.59±0.44	4.69±1.20	5.32±0.55	2.07±0.23	0.86±0.09	0.69±0.06
L	1.66±0.48	2.04±0.67	1.43±0.90	2.25±0.52	1.43±0.32	0.70±0.09	0.41±0.06

One-way repeated-measures ANOVAs with the factor of MOMENT on each finger stiffness coefficient confirmed that the effects of MOMENT were significant (F_(3,36)>75.48, p<0.001). The pairwise comparisons showed that the differences between the magnitudes of the coefficients for all tasks where the agonist moments were produced by three or four fingers were statistically significant (p<0.001 for all comparisons).

Discussion

Almost all previous research papers on the moment production by several fingers were performed on free objects that were either statically maintained or manipulated in the air. Imposing mechanical constraints on the object, as it was done in this study, and correspondingly relieving a performer from the task constraints changed noticeably the strategies used by the performer for generating the required moment. The most evident difference is that now the moment is generated mainly by the force exerted on the handle rather than by the force couple (with the exception of P=0 cm). This simply means that if performers have a choice they prefer to push or pull on the object rather than exert supination or pronation efforts on it. In the intermediate grasp locations, i.e. when 0<P magnitude<PZFM, the performers selected a mixture of the two above strategies such that the contribution of these strategies scaled linearly with the P. A note of the possible practical merit: to avoid the supination/pronation efforts completely—which may be important for injury prevention in repetitive job tasks—the handle length should be larger than the distance to the point of zero free moment.

When the P varies with respect to the moment axis, the recorded forces and moments change in a systematic way: the normal net force changes in an S-like manner, the free moment as well as the internal grasp force decrease in a linear fashion, agonist and antagonist moments also change, etc. Note that these relations are not direct consequences of mechanics. For example, when the axis of rotation was between the index and little fingers, the subjects were free to select how to share the total moment between the free moment and the moment of force; hence, the central segment of the mentioned S-shape relation reflects choice by the central nervous system. Such regular changes suggest that the central controller uses certain rules or optimization principles to select an appropriate finger force combination for any studied combination of the task parameters. Discovering such rules or optimization criteria is a challenging task. Due to the randomized orders of conditions and trials and the limited number of trials, potential improvements or adaptations of subject’s behaviors for optimization were not studied, which requires further investigation.

Stability of inter-digit synergies in prehension

Most of the everyday prehension tasks, such as drinking from a mug, using kitchen utensils, or writing with an implement are associated with maintaining equilibrium of the hand-held object. As such, patterns of forces exerted by the digits on the object need to satisfy equilibrium constraints that can be described, for static or pseudo-static (slow) tasks, with a set of equations of statics. For a planar case, these equations are presented in our previous publications (Zatsiorsky et al. 2002; Shim et al. 2003). Using combinations of such constrained force patterns may be expected to lead to the formation of stable synergies (relations among elemental variables such as digit forces and points of their application) that constrain patterns of these variables even when the equations of statics do not need to be satisfied. Earlier studies have shown that muscle and finger synergies tend to be very stable even in conditions when they are no longer optimal; such conditions were achieved by joint fixation or changes in the feedback on digit forces the subjects produced (Koshland and Hasan 1994; Latash et al. 1998).

Based on these considerations, we expected to see patterns of digit forces that do not violate the equilibrium equations in the present study when the object was fixed and the equations needed not be satisfied. However, the results did not confirm these expectations. In particular, the subjects used net forces in both horizontal and vertical directions that were significantly different from zero (Fig. 2) and would have led to movement of the handle, were it not fixed. The fact that forces in the current experiment did not obey equations of statics valid for a free object suggests that prehension tasks of the fixed object are characterized by significant flexibility and adaptability of associated inter-digit synergies.

Mechanical advantage and minimization of effort

Earlier studies have suggested that sharing a task among a set of effectors is commonly associated with patterns that are characterized by a larger involvement of effectors with larger mechanical advantage (Buchanan et al. 1989; Zatsiorsky et al. 2002). Such patterns may be viewed as reflecting minimization of the total effort by the controller: Effectors whose recruitment leads to larger changes in a required mechanical variable are preferentially involved as compared to effectors whose recruitment would be less effective.

The data on the individual fingers obtained in this study do not corroborate such a hypothesis—contrary to the findings obtained previously with free handles (Zatsiorsky et al. 2002). According to the hypothesis, finger involvement should change proportionally to the moment arms of individual fingers. By an assumption, during torque production the hand undergoes a torsion deformation such that the distant fingers deform to larger degrees than those fingers that are located closer to the axis of rotation. If each finger had spring-like properties it would produce force against such an externally imposed displacement in proportion to the magnitude of the displacement. This simple model produces force patterns that fit the mechanical advantage hypothesis only if the apparent stiffness of the fingers is similar across the fingers and does not depend on the location of the moment axis. Our results, however, have shown that the apparent stiffness varied substantially across the fingers and with changes in the handle location (Table 2). Hence, these results do not support the mechanical advantage hypothesis.

Patterns of force sharing across the four fingers (Table 1) suggest that during pronation moment generation, the index finger produced much of the normal force (up to 70%) and also a considerable proportion of the tangential force (about 50%). During supination moment production, the ring and little fingers produced much of the normal force (about 70%), while the tangential force was shared relatively uniformly among the four fingers. The mechanical advantage hypothesis supports the large involvement of the “most lateral” fingers (index and little) since these fingers have the largest moment arm with respect to the axis of moment production. However, changes in the location of the axis did not lead to changes in the proportion of the total force produced by these fingers, against predictions of the mechanical advantage hypothesis.

The mechanical advantage hypothesis can be considered, however, from a broader perspective. Not only the distribution of efforts among several effectors but also the patterns of force/moment production may be affected by the mechanical advantage associated with a given pattern. Within such an understanding of the mechanical advantage hypothesis, certain findings within this study support the hypothesis.

The total moment produced by the digits can be viewed as the sum of the free moment (M_free) and moment of the resultant force the digits produce (M_force). Changes inP led to changes in the moment arm for M_force. We found that an increase in d was associated with an increase in the relative proportion of the total moment produced by M_force. This result can be expected from the mechanical advantage hypothesis since an increase in d increases the contribution of the resultant force to the total moment.

Along similar lines, the total moment may be viewed as the sum of the moment produced by the tangential forces (M^t) and the moment produced by the normal forces (Mⁿ). The moment arm of the tangential forces did not change, while the moment arm of normal forces changed with shifts in P about which the total moment was produced. According to the mechanical advantage hypothesis, an increase in the moment arm of the normal forces may be expected to lead to an increase in the proportion of the total moment produced by the normal forces. This is exactly what was found in the experiments: at P=0 cm, M^t had higher magnitudes than other positions, while Mⁿ had lower values than others in agonist directions; at high P values in agonist directions, Mⁿ dominated. Note that an increase in Mⁿ with P was associated with both larger agonist and antagonist moments produced by the normal forces of individual digits (Fig. 6). The latter effect (larger antagonist moment) may be viewed as a consequence of the mechanical advantage hypothesis and the effects of finger enslaving (Zatsiorsky et al. 2000; Li et al. 2003).

Despite the support received by the mechanical advantage hypothesis in earlier studies (e.g., Prilutsky 2000), based on our current results, we can conclude that the range of applicability of this hypothesis is limited. Activation of the fingers according to their mechanical advantage reflects an intrinsic self-imposed tendency (in mathematical parlance—a cost function) to minimize the total amount of the finger forces, or a certain function of it, during standard tasks. This cost function works together with other criteria and constraints in defining patterns of effector involvement. Apparently, in some tasks, including those studied earlier, this cost function played a dominant role, while in the current experiments its effects could be concealed by a mixture of other criteria. Presently, the experimental data are available only for two extreme cases: (a) a free handle (mechanical constraints are absent) and (b) the handle is mechanically completely constrained. We are planning to perform experiments with a partially constrained handle (e.g. a handle that is free to move in only one direction, either vertically or horizontally). An idea is to test whether the mechanical advantage hypothesis is valid for such an experimental setup (this idea was inspired by the comments of the unknown reviewer on the first version of the manuscript; we are thankful to the reviewer for this inspiration).

Sharing patterns and enslaving

In all conditions, non-zero normal force was produced by fingers which acted against the required moment, i.e. non-zero antagonist moments were produced. In earlier studies (Zatsiorsky et al. 2002), antagonist moments were explained as effects of finger enslaving, i.e. unintended finger force production (Li et al. 1998; Zatsiorsky et al. 1998; Zatsiorsky et al. 2002). In the current study, however, shares of forces produced by the antagonist fingers were substantially higher as compared to what one could expect from earlier studies of enslaving in pressing tasks. For example, S. Li et al. (2002) reported that intentional force production by the index finger was accompanied by unintended force production by the ring and little fingers that was under 2% of the total force, while intended force production by the ring and little fingers together led to the index finger producing about 4% of the total force. These values are much lower than those observed in the current study (5%–10% and 14% respectively). Hence, one is forced to conclude that the subjects produced forces by the antagonist fingers that were significantly higher than those expected from the action of enslaving. Reasons for such excessive values of antagonist finger involvement are unclear and need to be explored in further studies.

Uniformity of finger forces

The SDs of individual finger forces signify the uniformity of the finger forces: if all the four fingers were producing equal forces the SD would be zero. Hence, when the SD increases, the individual fingers produce sharply different forces. According to Fig. 5, the smaller the SDs, i.e. the more equal are the finger forces to each other the closer is M_free to zero. While the relationship between the SDs for the normal forces and M_free follows from simple mechanics and is easy to explain, the relationship between the SDs of the tangential forces and M_free is not mechanically necessitated: the moment arms of the tangential finger forces are the same for all fingers, and there is no mechanical reason to increase the tangential force of some fingers while decreasing the force of other fingers to produce the desired total moment. Hence, the changed distribution of the tangential forces among the fingers represents the choice made by the central controller.

Are the relations necessitated by the task mechanics?

During manipulation of free objects, many observed relations are necessitated by the task mechanics: the task cannot be performed in another way (Shim et al. 2003). In contrast, in the present setup the task mechanics affect the relations among the variables but do not prescribe these relations completely. The task can be performed, albeit inefficiently and uneconomically, in different ways. For example, according to the experimental data the free moment scales with the internal normal force (the grasping force); however, this relation does not immediately follow from the task mechanics: A person, if he or she wishes, can grasp the handle more or less strongly without producing any torque on the object. The aforementioned relations between the SD of the normal forces and the free moment are also not prescribed by the mechanics: If large forces are exerted by the “peripheral” (the index and little) fingers, and small forces are produced by the “central” fingers (the middle and ring), the SD can be large while the free moment can be zero. Similarly, the moment of resultant force scales with the resultant horizontal force but only if the point of the force application does not displace. Even the observed values of the free moment close to zero at large values of P are not prescribed by the task mechanics. The performers could generate a non-zero free moment which would not contribute to the total moment. Such a pattern of force production would be inefficient but it is feasible.

Concluding comments

We would like to emphasize two main findings within the current study. First, we have shown that when working with mechanically constrained objects the performers exert forces and moments on the object quite differently from what they do when manipulate free objects (for the discussion on the force exertion on the constrained objects, see Zatsiorsky 2002.) Second, the mechanical advantage hypothesis was successful in explaining some of the data but could not handle other findings. We assume, therefore, that this hypothesis is limited in its applicability and may be task and effector specific. Besides, this is the first study to document patterns of elemental variables in a task when the central nervous system is free to select combinations of these variables in a relatively unconstrained way. Some of these patterns—which are regular and similar in different subjects—are not easy to interpret; they will wait for future studies.