Adjustments to Local Friction in Multifinger Prehension

Abstract

The authors studied the effects of surface friction at the digit–object interface on digit forces and moments when 12 participants statically held an object in a 5-digit grasp. The authors changed low-friction contact (LFC) with rayon and high-friction contact (HFC) with sandpaper independently for each digit in all 32 possible combinations. Normal forces of the thumb and virtual finger (VF), an imagined finger with a mechanical effect equal to that of the 4 fingers, increased with the thumb at LFC or with an increase in the number of fingers at LFC. When the thumb was at LFC, the thumb tangential force decreased. The VF tangential force decreased when the number of fingers at LFC increased. The interaction of the local responses to friction and the synergic responses necessary to maintain the equilibrium explain the coordination of individual digit forces.

When grasping an object, people adjust digit forces to the friction: More-slippery objects are grasped more strongly, resulting in a higher ratio of grip force (digit force normal to the grip surface) to load force (digit force tangential to the grip surface; Cadoret & Smith, 1996; Cole & Johansson, 1993; Johansson, 1996; Johansson & Westling, 1984b, 1987). Some researchers have examined participants' force adjustments when they used two or three digits to grasp objects that had a different friction for each digit (Burstedt, Edin, & Johansson, 1997; Burstedt, Flanagan, & Johansson, 1999; Edin, Westling, & Johansson, 1992; Quaney & Cole, 2004). The researchers found that a grip–load force ratio for individual digits was scaled on the basis of current local friction at those digits. Participants made the adjustments by modulating normal (grip force) and tangential (load force) digit forces. Similar force adjustments occur when two individuals do the grasping (Burstedt et al., 1997). It has therefore been concluded that coordination of individual digit-tip forces during human manipulation emerges from independent neural networks that control each engaged digit. That low level of control must be subordinate to a higher level of control related to other aspects of manipulative tasks. The investigators mentioned such aspects of the higher level control as (a) temporal synchronization of digit actions before substantial manipulative forces are applied to the object, (b) selecting grasp configurations, and (c) coping with various constraints imposed by the physical properties of the object, such as its weight and size.

Compared with the two-digit and tripod grasps, in grasps performed by all five digits, performers undoubtedly have greater freedom to select interdigit force sharing. During multifinger prehension, however, the forces and moments exerted on the object by individual digits always change in a highly coordinated manner (Baud-Bovy & Soechting, 2001; Iberall, 1987; Kinoshita, Kawai, & Ikuta, 1995; Santello & Soechting, 1997; Shim, Latash, & Zatsiorsky, 2003a, 2005; Zatsiorsky, Gao, & Latash, 2003). Such conjoint changes in mechanical variables produced by individual digits are usually referred to as prehension synergies (Zatsiorsky & Latash, 2004). The central nervous system (CNS) organizes the prehension synergies hierarchically, with at least two levels (Shim et al., 2003a, 2005; Zatsiorsky et al.; Zatsiorsky & Latash). At the higher level, force and torque constraints are distributed between the thumb and the virtual finger (VF)—an imagined finger that generates the same mechanical effect as do the four actual fingers (Arbib, Iberall, & Lyons, 1985; Baud-Bovy & Soechting; Iberall; Santello & Soechting). At the lower level, the force and torque of the VF are distributed among the individual fingers (IFs; that is, the IF level).

The concepts of independent finger control and prehension synergies do not agree well with each other. If the coordination of digit-tip forces emerges from independent neural networks controlling each engaged digit, then how can all the digit-tip forces change in such a precisely coordinated manner? How, then, is object equilibrium maintained? It has been recently suggested that two types of motor adjustments, local and synergic, define finger coordination in multifinger prehension (Aoki, Niu, Latash, & Zatsiorsky, 2006; Zatsiorsky, Gao, & Latash, 2006). In the present context, the term local designates adjustments that start and end at the same finger; for example, if the friction at a given digit changes, then the digit force also changes. The term synergic refers to adjustment of the force of a digit in response to friction alteration at other digits. Any local force change potentially perturbs the object's equilibrium. Therefore, one must use synergic action of other fingers to keep the object at rest (e.g., to prevent object rotation). So far, the interaction (and very existence) of the local and synergic motor adjustments has not been systematically addressed in the literature.

Recently, Aoki et al. (2006) investigated digit force coordination in five-digit prismatic grasp by arranging symmetrically and asymmetrically two surfaces with different friction for the thumb and VF. Several principles of force and moment adjustments to friction conditions were elucidated: (a) Whereas the forces normal to the surface were modulated by the friction condition, they were always equal in magnitude in the thumb and VF (that finding was expected from the equilibrium requirements); (b) although the thumb and VF tangential forces were similar in the symmetric friction conditions, the forces at the lower friction side were always smaller than those at the higher friction side in the asymmetric friction conditions; (c) the unequal tangential forces produced by the thumb and VF in the asymmetric conditions produced a moment of tangential forces; and (d) to maintain the rotational equilibrium, the central controller generated a moment of normal forces by changing the normal force sharing among the fingers.

In the just-mentioned experiment, the friction at all four finger contacts was similar, either high (sandpaper) or low (rayon). How the central controller tackles more complex tasks when the individual fingers touch surfaces with different friction remains unknown. If coordination of individual digit-tip forces emerges from independent neural networks controlling each engaged digit (Burstedt et al., 1997; Burstedt et al., 1999; Edin et al., 1992), then we should expect that in five-digit tasks, each digit would also adjust to its local friction condition (i.e., the tangential forces will be smaller and the normal forces will be larger at the low-friction contacts [LFCs]). That rule should not depend on the particular distribution of the high-friction contacts (HFCs) and LFCs among the digits.

Our concern in the present study was with the surface friction effects on normal and tangential force coordination of individual digits when humans hold an object statically with the five digits. In each single trial, the friction at each digit was constant, but it varied among the trials. We were interested in how normal and tangential forces of individual fingers adjust to a given surface friction—in particular, whether higher normal force and lower tangential force are exerted at the more slippery surface or surfaces than at the less slippery surface or surfaces, as predicted in the independent neural network hypothesis. An alternative hypothesis was that an interaction of two mechanisms, local and synergic, defines digit force adjustments.

Method

Participants

Twelve right-handed men volunteered to participate in this study (age = 29.7 ± 3.2 years [M ± SE]; height = 174.6 ± 2.2 cm; weight = 74.9 ± 5.1 kg). Their hand length was 19.0 ± 0.4 cm from the middle fingertip to the distal crease of the wrist, with the hand extended, and their hand width was 9.0 ± 0.3 cm. Participants had no previous history of neuropathies or trauma to the upper limbs. All participants were right-handed according to their preferential hand use during eating and writing. All participants gave informed consent according to the policies of the Office for Research Protections of The Pennsylvania State University.

Apparatus

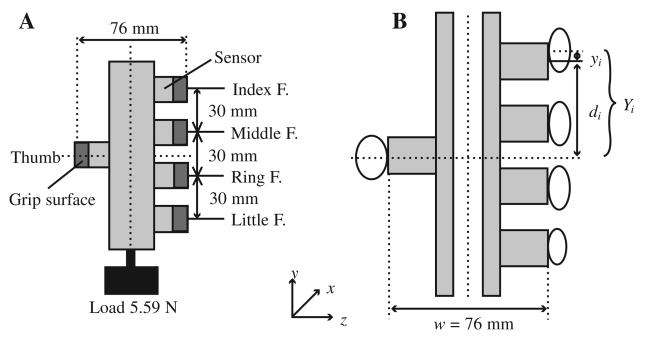
We mounted five six-component force–moment transducers (Nano-17; ATI Industrial Automation, Garner, NC) on an aluminum handle (21 mm × 130 mm × 31 mm; Figure 1). The center points of the index and middle fingers' sensors were located 45 mm and 15 mm above the midpoint of the handle, respectively. The center points of the ring and little fingers' sensors were located 15 mm and 45 mm below the midpoint, respectively. The thumb sensor was aligned with the midpoint. The grip width, which is the perpendicular distance between the surface of the thumb contact and those of the finger contacts, was 76 mm. We suspended a 5.59-N load from the bottom of the handle. For providing the participants with feedback on the handle orientation, we placed a level at the top of the handle. The total weight of the apparatus with the load was 9.81 N.

FIGURE 1.

Schematics of the instrumented handle (A) and the computation of the moment arms of the normal forces (B). In B, w is the handle width (w = 76 mm); y_i is the vertical coordinate of the index finger force application with respect to the sensor center; d_i is a projected vertical distance between the sensor centers of the index finger and thumb; and Y_i is the vertical coordinate of the point of the index finger force application. Note that the lowercase y_i designates the coordinate with respect to a sensor center, whereas the uppercase Y designates a coordinate in the handle-fixed reference system. F. = finger.

We achieved different friction conditions of the digit–object interface by exchanging the grip surfaces. Grip surfaces used for high and low friction were 100-grit sandpaper and rayon, respectively. To measure the static friction coefficient between the skin and those materials, we asked the participants to grasp the handle with only their thumb, middle finger, and ring finger and to then let the handle slip as slowly as possible. We detected slips as a sudden decrease in the tangential force at one of the digits. We determined the ratio between the normal force and the tangential force at slip (slip ratio; Johansson & Westling, 1984b). We used the inverse of the slip ratio as an estimate of the static friction coefficient (μ). The μ was 1.49 ± 0.05 for the sandpaper and 0.56 ± 0.05 for the rayon. Hence, the difference was almost threefold. Because the supported load in the present experiment and hence the tangential force were constant, it did not make much sense to compute the normal-force/tangential-force ratio and then compare that ratio with the slip ratio (as was done in some previous studies, e.g., Johansson & Westling, 1984b). Therefore, to determine the slipping conditions, we computed the relative safety margin. We evaluated the safety margin for each participant on the basis of the following equation (Pataky, Latash, & Zatsiorsky, 2004): Safety margin = (Fⁿ_i – |F^t_i|/μ)/Fⁿ_i, where i is an arbitrary digit, Fⁿ is the digit normal force, and F^t is the digit tangential force. For the safety margin of the VF, we used the overall friction coefficient for the calculation; we estimated the coefficient as mean friction for four fingers.

A 12-bit A/D converter (PCI-6033E, National Instruments, Austin, TX) digitized the force–moment signals from the sensors (6 signals × 5 sensors = 30) at 100 Hz, and a PC computer (Dell Dimension 8200) processed the result. The sampling frequency in tests used to determine the static friction coefficient was 300 Hz.

Experimental Procedure

Before the experiment, we asked participants to wash their right-hand digits with soap and warm water to normalize their skin condition. The fingertips were also wiped with alcohol. We gave participants an orientation session before testing to familiarize them with the experimental task and apparatus. The time from the finger cleaning to the main experimental session was not less than 15 min. That time should be sufficient to compensate for the immediate effects of the fingertip treatments and to make friction conditions stable (Johansson & Westling, 1984a).

Participants sat in a chair alongside a table; their right upper arm was positioned at approximately 45° abduction in the frontal plane and 45° flexion in the sagittal plane. The elbow joint was flexed approximately 45°. The forearm, but not the wrist and hand, was placed on the forearm brace affixed to the table. The forearm was pronated 90° so that the hand was in a natural grasping position. We paid special attention to digit placement on the sensors so that the center of each digit-tip coincided with the center of the corresponding sensor.

Participants were instructed to take the handle from the rack, place the forearm onto the brace, and hold the handle statically and vertically in the air. We also instructed them to hold the handle with minimal effort. When participants reported that they were holding the handle as instructed, we began data recording. Signals were recorded for 5 s. After the data collection stopped, the participants placed the handle back on the rack. We changed the two different surfaces independently for each digit. The experimental design included 32 friction conditions (Table 1), which we introduced to each participant in a balanced order. At each of the 32 experimental conditions, two trials in a row were performed. Hence, each participant performed 64 trials.

TABLE 1.

Surface Conditions in the Experimental Tasks

Friction at thumb contact	Slipperiness at VF contacts
	0	1	2	3	4
H	HHHHH	HLHHH	HLLHH	HLLLH	HLLLL
		HHLHH	HHLLH	HHLLL
		HHHLH	HHHLL	HLLHL
		HHHHL	HLHLH	HLHLL
			HHLHL
			HLHHL
L	LHHHH	LLHHH	LLLHH	LLLLH	LLLLL
		LHLHH	LHLLH	LHLLL
		LHHLH	LHHLL	LLLHL
		LHHHL	LLHLH	LLHLL
			LHLHL
			LLHHL

Note. The data of 32 surface conditions are categorized by the surface at the thumb contact (H = high-friction contact; L = low-friction contact) and by the number of fingers at low-friction contact (slipperiness = 0 to 4). The individual digits are listed in the following order: thumb, index, middle, ring, and little fingers. For example, the sequence HLLHH means that simultaneously the thumb was touching high-friction surface (sandpaper); the index and middle fingers were in contact with the low-friction surfaces (rayon); and the ring and little fingers were contacting high-friction surfaces (sandpaper).

We set the sensor signals to zero before each trial to remove the drift. After every 10th trial, we asked participants to wipe their right-hand digits with alcohol to maintain a constant skin condition. Breaks of at least 20-s were provided between trials, and we provided 5-min breaks after every 10th trial to avoid fatigue and stabilize the friction conditions (the friction becomes reasonably stable after 3–4 min; Johansson & Westling, 1984a). The total duration of each experiment was close to 1.5 hr.

Data Analysis and Statistics

We used data-acquisition software written in LabVIEW (National Instruments, Austin, TX) to convert digital signals into force and moment values. We performed data processing by using MATLAB (The MathWorks, Inc., Natick, MA). The raw force–moment data were not filtered because we considered only the mean signal over 2.9 s of the holding period (excluding 2.0 s at the beginning and 0.1 s at the end of the period). We used only the second-trial data for the analysis; the first trials were considered practice.

In the transducer-fixed reference system, forces normal to the transducer surface corresponded to the z direction, f^z. In this experiment, f^z was oriented horizontally with respect to the environment. Because the task was static, the tangential force always acted in the vertical direction. We modeled the digit contacts with the sensors as the soft finger contacts (Mason & Salisbury, 1985); in particular, we allowed the rolling of the fingers on the sensor surfaces.

The vertical coordinates (y) of the digit force application with respect to the sensor center were computed as y_i = m^x_i/f^z_i (i = 1, 2, 3, 4, 5), where m^x_i is the moment of the ith digit with respect to the x- (horizontal) axis and f^z_i is the normal force of the ith digit. We then used the obtained values to compute the moment arms of the normal forces in the handle reference frame. We determined the vertical coordinate of the point of VF normal force application Y_VF on the basis of the theorem of moments (the Varignon theorem; Zatsiorsky, 2002, p. 26) as Y_VF = ΣFⁿ_iY_i/Fⁿ_VF (i = 1, 2, 3, 4), where Y_i is the vertical coordinate of the force application point of finger i (Y_i = d_i + y_i, where d_i is a projected vertical distance between the sensor centers of finger i and the thumb). Fⁿ_VF is the sum of the normal forces produced by the four fingers. Note that we have used the uppercase Y to designate a coordinate in the handle-fixed reference system, whereas we have used the lowercase y_i to designate the coordinate with respect to the center of a sensor i.

At the VF level, we computed the moment of normal forces Mⁿ and the moment of the tangential forces M^t. We computed Mⁿ as

$$M^n={F^n}_{\mathit{VF}}(Y_{\mathit{VF}}-Y_{\mathit{TH}}),$$ (1)

and we computed M^t as

$$M^t=({F^t}_{\mathit{VF}}-{F^t}_{\mathit{TH}})w∕2,$$ (2)

where superscripts n and t represent the normal force and the tangential force, respectively; subscripts TH and VF represent the thumb and VF, respectively; and w stands for the width of the handle. The difference (Y_VF – Y_TH) is the moment arm of the couple of the normal forces. Mⁿ is the result of the normal forces of the thumb and the VF. Those forces are equal, opposite, and not collinear. Hence, they form a force couple. Because the moment of a couple is a free moment (i.e., it is the same for all moment centers and remains unchanged under parallel displacements; see, for instance, Zatsiorsky, 2002, p. 20), one can add Mⁿ to M^t to obtain the total moment exerted by the participant. We defined upward tangential forces and counterclockwise moments as positive.

We performed two-way repeated measures analyses of variance (ANOVAs) for normal forces, tangential forces, and safety margins for the thumb and VF; three-way ANOVAs for those variables for the individual digits; and two-way ANOVAs for Mⁿ and M^t to assess the effects of the following two factors—(a) surface at the thumb contact (two levels) and (b) number of the fingers in contact with rayon (five levels)—or the effects of the following three factors—(a) surface at the thumb contact (two levels), (b) surface at the finger contact (two levels), and (c) number of other fingers in contact with rayon (four levels)—on each individual variable. The two-way ANOVAs performed on the data obtained in 10 task conditions are presented in the individual cells of the right five columns of Table 1. For the three-way ANOVA, we used the data for 16 task conditions; those are presented in the individual cells of the right four columns of Table 2. Table 2 illustrates a particular case in which the index finger was in contact with either a high-friction or a low-friction surface. Similar categorization and similar three-way ANOVAs were performed for the middle, ring, and little fingers.

TABLE 2.

Example of the Categorization for the Index Finger

Friction at the index finger contact	No. of other fingers at low friction contact
	0	1	2	3
High friction at the thumb contact
H	HHHHH	HHLHH	HHLLH	HHLLL
		HHHLH	HHHLL
		HHHHL	HHLHL
L	HLHHH	HLLHH	HLLLH	HLLLL
		HLHLH	HLHLL
		HLHHL	HLLHL
Low friction at the thumb contact
H	LHHHH	LHLHH	LHLLH	LHLLL
		LHHLH	LHHLL
		LHHHL	LHLHL
L	LLHHH	LLLHH	LLLLH	LLLLL
		LLHLH	LLHLL
		LLHHL	LLLHL

Note. The data of 32 surface conditions for each finger were categorized by (a) surface at the thumb contact (high-friction contact [H] or low-friction contact [L]), (b) surface at the finger contact (H or L), and (c) number of other fingers at low-friction contact (from 0 to 3)—in total 16 groups. The groups are presented in the individual cells in the four right-hand columns of the table. For instance, the comparison was performed for the groups HHLHH, HHHLH, HHHHL and for the groups HLLHH, HLHLH, HLHHL. Similar categorizations and similar analyses were performed for the middle, ring, and little fingers.

To examine whether the individual participants adjusted their digit forces to local friction differently, we compared digit forces in pairs of trials in which one digit—for instance, the index finger (see Table 2)—was in contact with different surfaces, either high friction or low friction, while the other four digits were in contact with the same surface. We used the sign test for paired samples to compare the number of cases (pairs of trials) in which participants responded to local friction with the number of cases in which they did not. Examples of the pairs are HHHHH versus HLHHH conditions and HHLLH versus HLLLH conditions. There were 16 such pairs for each digit. In total, we performed 80 comparisons for a participant (16 pairs × 5 digits) and 960 comparisons for the group.

We performed a large number of planned statistical comparisons in the present study. Therefore, to lessen the probability of committing Type I errors, we accepted that the difference was significant at p < .01. We decided against using the alpha-level correction, for example, the Bonferroni correction, for two reasons. First, decreasing the alpha-level and, hence, decreasing the chances of making a Type I error (probability of making a false-positive statement) simultaneously increases the chances of making a Type II error (making a false-negative statement), that is, claiming that there is no effect of friction although, in fact, there is an effect. In the performed experiment those opposite conclusions were equally important, and there was no reason to decrease the probability of one error at the expense of increasing the probability of making the other error. Second, in the present study we addressed the effects of friction on the individual digits in different tasks. Hence, we evaluated more than one hypothesis, each one with a single test. There was no reason to expect that the effect of friction on the little finger force in the HHHH–HHHHL pair of tasks would depend on the effect of friction on the index finger force in the LLLLL–HLLLL task. That would be similar to performing several small studies that, for convenience of presentation, are combined into a larger study. The application of the Bonferroni correction in such a situation is a topic of active discussion among statisticians. A majority of experts are of the opinion that in such a situation each comparison should be done independently from other comparisons and that the Bonferroni correction should not be used (for a review, see Perneger, 1998). In the sign tests, we considered the differences significant at p < .05. For those tests, we needed to observe local adjustments in at least 13 of 16 pairs to claim statistical significance at p < .05, and we needed to observe local adjustments in 14 of 16 pairs to claim statistical significance at p < .01.

Results

Normal Forces

Thumb and VF

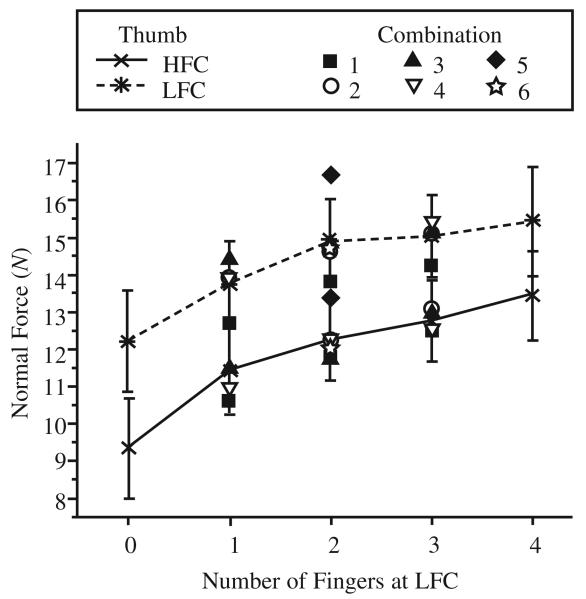
The normal forces generated by the thumb (Figure 2) and the VF (a) were approximately equal in magnitude and (b) were significantly larger when the thumb contacted a low-friction surface, Fs(1, 11) = 38.9 and 39.4, respectively, for the thumb and VF, both ps < .001. Those forces (c) increased with the slipperiness, that is, the number of fingers at LFC, Fs(4, 44) = 13.8 and 14.0, respectively, for the thumb and VF, both ps < .001. The thumb and VF normal forces were 21% larger on average when the thumb was at LFC than when the thumb was at HFC. The thumb and VF normal forces increased 35% on average when the number of fingers at LFC changed from zero to four. Whereas the thumb and VF normal forces depended on the number of fingers at LFC, one-way repeated measures ANOVAs revealed that the forces did not depend on how exactly the HFC and LFC were distributed among the fingers (p values varied from .021 to .520).

FIGURE 2.

Normal forces of the thumb: group averages and standard errors (bars). HFC = high-friction contact. LFC = low-friction contact. When one finger was at LFC, Combinations 1, 2, 3, and 4 corresponded to LHHH, HLHH, HHLH, and HHHL, respectively (the four-letter sequences here indicate high [H] and low [L] friction at the index, middle, ring, and little fingers, respectively). When two fingers were at LFC, Combinations 1, 2, 3, 4, 5, and 6 corresponded to LLHH, HLLH, HHLL, LHLH, HLHL, and LHHL, respectively. When three fingers were at LFC, combinations 1, 2, 3, and 4 corresponded to LLLH, HLLL, LLHL, and LHLL, respectively.

Individual Finger Forces

We first present the data on the local friction effects, that is, the effects of friction at a given finger on the force exerted by that finger. Then we present the data on the synergic friction effects, that is, the effects of friction at a given finger on the forces exerted by other digits.

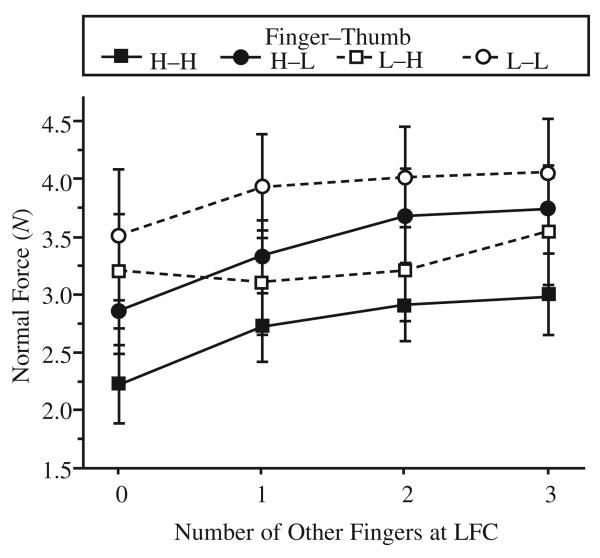
Statistically significant local friction effects were found only for the normal force of the middle finger, F(1, 11) = 10.3, p < .01 (Figure 3). The force was larger when the finger was at LFC. Normal force of the index finger also tended to be larger at LFC; the effect did not, however, reach the level of statistical significance, F(1, 11) = 5.9, p = .033.

FIGURE 3.

Normal forces of the middle finger: group averages and standard errors (bars). In the legends in this and the following figures, the first letter indicates surface friction of the finger of interest (in this figure, the middle finger), and the second letter indicates surface friction of the thumb. The solid line corresponds to the finger at high-friction contact (HFC), and the dotted line corresponds to the finger at low-friction contact (LFC). The squares correspond to the thumb at HFC, and the circles to the thumb at LFC.

When the number of fingers at LFC changed from zero to three (we did not include the finger of interest in that number), synergic friction effects were common: The finger normal forces depended on the thumb friction and the friction conditions for the other fingers. When the thumb was at LFC, finger normal forces except that of the index finger were on average larger (as compared with the thumb at HFC): For the middle finger, ring finger, and little finger, respectively, the differences were 22%, 34%, and 47%; Fs(1, 11) = 32.3, 20.7, 30.9, respectively, all ps < .001. The number of other fingers at LFC affected the index, F(3, 33) = 13.1, p < .001, and middle, F(3, 33) = 6.7, p < .01, finger forces. With the number of fingers at LFC increased from zero to three, the normal finger forces increased on average by 39%.

The results can be summarized as follows: Local effects were found only for the middle finger. Synergic effects were observed in all fingers, but to different degrees.

Sharing the Total Normal Force Among the Fingers

For the HHHHH condition, the normal forces of the index, middle, ring, and little fingers were 28.63%, 24.60%, 27.44%, and 19.33% of the total force, respectively. The corresponding values for the LLLLL condition were 26.14%, 27.09%, 26.33%, and 20.44%, respectively. The force distribution patterns in those two conditions did not differ significantly from each other—chi-square test, χ²(8, N = 3) = .287, p = .962. Therefore, the normal force-sharing pattern among the individual fingers when all fingers were at same-friction surfaces was similar, in agreement with previous studies (Aoki et al., 2006; Kinoshita et al., 1995).

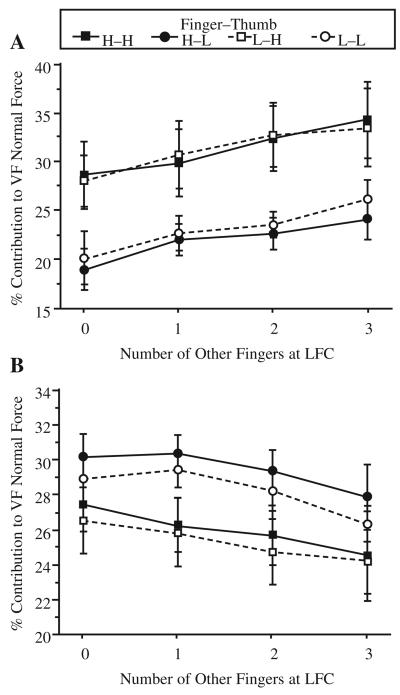
Statistically significant effects of the number of other fingers at LFC on the sharing percentage of a given finger were found for the index finger, F(3, 33) = 6.4, p < .01 (Figure 4A), ring finger, F(3, 33) = 8.4, p < .001 (Figure 4B), and little finger, F(3, 33) = 6.4, p < .01. When the number of other fingers at LFC increased, the percentage contribution of the index finger to the VF normal force increased, whereas those of the ring and little fingers decreased. Effects of the thumb surface friction were found for the index and little fingers, Fs(1, 11) = 20.9 and 18.0, respectively, both ps < .01. When the thumb was at LFC, the percentage contribution of the index finger decreased, whereas the contribution of the little finger increased. Note that an increase in the contribution of the index finger increased Mⁿ in the counterclockwise direction, whereas increased contribution of the ring and little fingers increased Mⁿ in the clockwise direction.

FIGURE 4.

Percentage contribution to the virtual finger (VF) normal force of (A) the index finger and (B) the ring finger: group averages and standard errors (bars). The symbols are similar to those used in Figure 3.

Tangential Forces

Thumb and VF

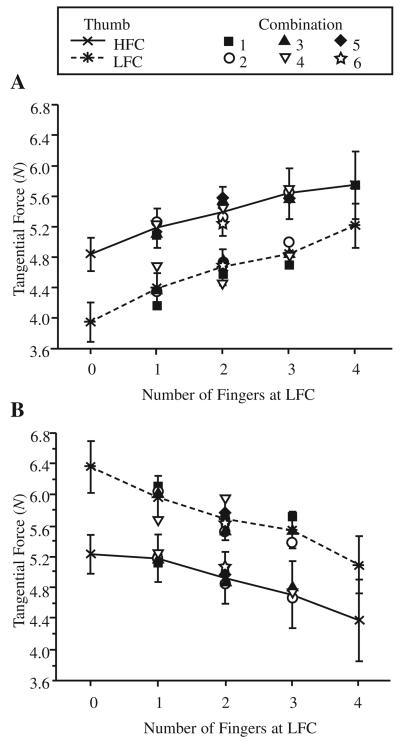
The tangential force of the thumb (a) was smaller when the thumb was at LFC (on average by 14%), F(1, 11) = 22.4, p < .001 (Figure 5A), and (b) increased with the slipperiness (on average by 25% when the number of fingers at LFC changed from zero to four), F(4, 44) = 17.0, p < .001. In contrast, the tangential force of the VF (a) was larger when the thumb was at LFC (on average by 17%), F(1, 11) = 30.5, p < .001 (Figure 5B), and (b) decreased with the slipperiness (on average by 18% when the number of fingers at LFC changed from zero to four), F(4, 44) = 10.4, p < .001. Those relationships did not depend significantly on the specific distribution of the surfaces with high and low friction among the fingers (p values were from .061 to .952). The tangential forces of the thumb and VF were expected to add up to the handle weight of 9.81 N. The total tangential force was 10.29 ± 0.11 N. The difference was most probably the result of the weight of the wires.

FIGURE 5.

Tangential forces of (A) the thumb and (B) the virtual finger: group averages and standard errors (bars). The solid line represents the thumb at high friction contact (HFC), and the dotted line represents the thumb at low friction contact (LFC). When one finger was at LFC, Combinations 1, 2, 3, and 4 corresponded to LHHH, HLHH, HHLH, and HHHL, respectively (the four-letter sequences here indicate friction at the index, middle, ring, and little fingers, respectively). When two fingers were at LFC, Combinations 1, 2, 3, 4, 5, and 6 corresponded to LLHH, HLLH, HHLL, LHLH, HLHL, and LHHL, respectively. When three fingers were at LFC, Combinations 1, 2, 3, and 4 corresponded to LLLH, HLLL, LLHL, and LHLL, respectively.

Individual Fingers

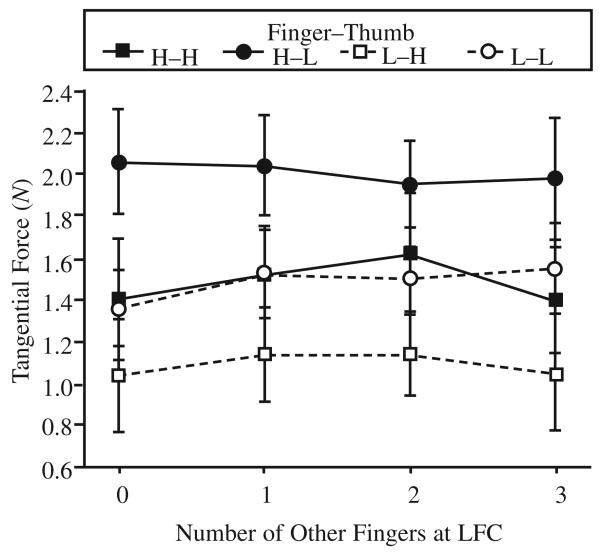
The local surface effects were significant in only the little finger, F(1, 11) = 17.0, p < .01 (Figure 6). The tangential force was smaller at LFC (on average by 26%). The tangential force of the index and middle fingers also tended to be smaller at LFC, on average, respectively, by 20%, F(1, 11) = 5.6, p = .038, and by 12%, F(1, 11) = 4.5, p = .058; however, the effect did not reach the level of statistical significance. The ring finger tangential force did not change with the friction.

FIGURE 6.

Tangential forces of the little finger: group averages and standard errors (bars). The symbols are similar to those used in Figure 3.

The synergic effects were found only for changes in the thumb friction conditions. Tangential force of the little finger was larger when the thumb was at LFC, F(1, 11) = 17.0, p < .01. Tangential forces of the middle and ring fingers also tended to increase when the thumb was at LFC. However, the effects did not reach the level of statistical significance, F(1, 11) = 8.0, p = .016, for the middle finger, and F(1, 11) = 9.0, p = .012, for the ring finger. A significant effect of the number of fingers at LFC—the number varied from zero to three—was not found in any fingers.

To explore whether the decrease of the tangential force produced by a particular finger was compensated by increases of the tangential forces of other fingers, we compared forces of the other fingers when a given finger was either at HFC or at LFC. The tangential force compensation was not found in any finger combination. Consequently, when a finger was at LFC and its tangential force decreased, the VF tangential force also decreased. The VF force decrease was significant when the middle finger or the little finger was at LFC, Fs(1, 11) = 18.6 and 11.0, respectively, both ps < .01; for both fingers, the difference was 5%. When the index finger was at LFC, the VF tangential force also tended to decrease (on average by 3%), F(1, 11) = 5.0, p = .047. As mentioned earlier, because the ring finger tangential force did not change with the local friction, the VF tangential force also did not change.

Those results can be summarized as follows. Local effects were found at the little finger. The synergic effects were observed in response to the thumb friction conditions only in the little finger. A decrease of the finger tangential force was not compensated by the other fingers and caused a VF tangential force decline.

Safety Margin

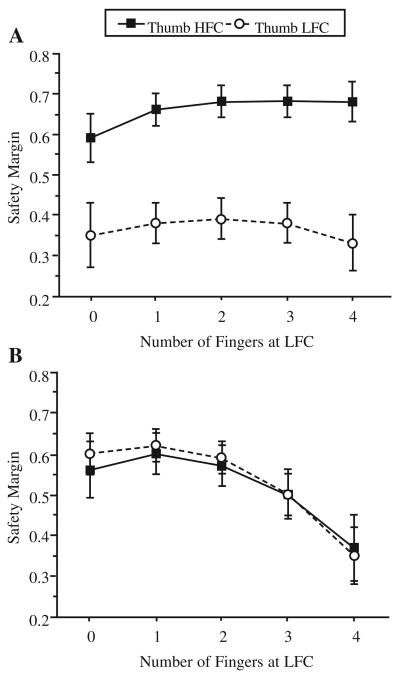
Thumb and VF

There was a general decline in the safety margin with a decrease in friction. The thumb safety margin was significantly smaller when the thumb was at LFC than when it was at HFC (on average by 44%), F(1, 11) = 104.5, p < .001 (Figure 7A). In addition, the VF safety margin decreased with the number of fingers at LFC (on average by 38% when the number of fingers at LFC changed from zero to four), F(4, 44) = 25.1, p < .001 (Figure 7B). Those data agreed with the previously reported finding that safety margins are lower at the more slippery surface (Aoki et al., 2006; Burstedt et al., 1999). The thumb safety margin did not depend on the number of fingers at LFC, and the VF safety margin did not depend on the thumb surface friction.

FIGURE 7.

Safety margins for (A) the thumb and (B) the virtual finger: group averages and standard errors (bars). The solid line represents the thumb at high-friction contact (HFC), and the dotted line represents the thumb at low-friction contact (LFC).

Individual Fingers

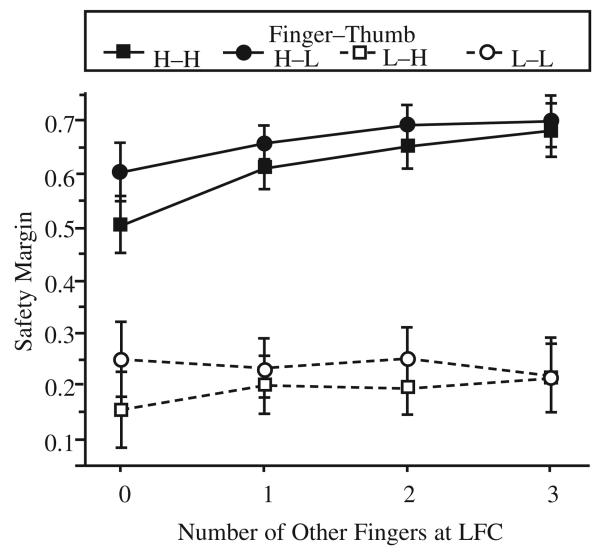
The local effects on safety margin were found in all fingers: Safety margins were significantly lower when the finger was at LFC than when it was at HFC, Fs(1, 11) = 42.4, 124.6, 186.0, and 78.3, respectively, all ps < .001, for the index, middle, little, and ring fingers (see Figure 8).

FIGURE 8.

Safety margins for the ring finger: group averages and standard errors (bars). The symbols are similar to those used in Figure 3.

The synergic effects were found only in the ring finger for the thumb friction, F(1, 11) = 11.7, p < .01, and for the number of other fingers at LFC, F(3, 33) = 6.1, p < .01. When the thumb was at LFC, the safety margin of the ring finger was significantly larger. To explore the synergic effects among individual fingers, we compared safety margins of the other fingers when a given finger was either at HFC or at LFC. However, we found no significant effects.

Safety margins averaged across the five digits decreased on average by 36% when the slipperiness increased, F(4, 44) = 21.9, p < .001. The averaged safety margins also tended to be smaller when the thumb was at LFC (by 6% on average), F(1, 11) = 8.2, p = .015.

Moments of Force

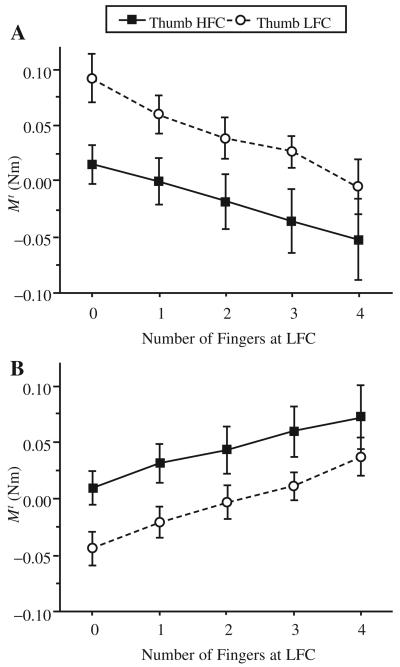
The difference in the tangential forces of the thumb and VF (see Figure 5A and B) resulted in the generation of an M^t. The M^t arising because of unequal friction conditions at the two sides of the handle has been defined in the literature as the friction-induced moment (Aoki et al., 2006). Note that not the friction itself, but the reaction of participants to it, resulted in the moment production. The M^t was significantly larger when the thumb was at LFC than when it was at HFC, F(1, 11) = 26.8, p < .001 (Figure 9A). When the thumb was at LFC, M^t was positive, except for the LLLLL condition. In contrast, when the thumb was at HFC, M^t was negative, except for the HHHHH condition. The effects of slipperiness were also significant, F(4, 44) = 13.8, p < .001. When the thumb was at LFC, the magnitude of M^t decreased with the slipperiness; the changes were the opposite when the thumb was at HFC.

FIGURE 9.

Moment of tangential forces, M^t (A), and moment of normal forces, Mⁿ (B), as the function of slipperiness: group averages and standard errors (bars). Solid lines represent the thumb at high-friction contact (HFC); dotted lines represent the thumb at low-friction contact (LFC).

Because the external torque on the handle was close to zero, the friction-induced moment had to be counteracted by Mⁿ. Indeed, Mⁿ was, as a rule, in the directions opposite to M^t (Figure 9B). Exceptions to that rule were seen in the HHHHH condition and in trials in which the thumb and three fingers were at LFC. The observed small positive total moments (0.031 ± 0.0001 Nm) were evidently the result of a slight deviation of the center of mass from the geometric center of the handle. Mⁿ (a) was significantly smaller when the thumb was at LFC, F(1, 11) = 20.0, p < .001, and (b) increased with the slipperiness, F(4, 44) = 16.6, p < .001. The Mⁿ increase means that it changed into more positive (less negative) values; that is, when the thumb was at HFC and Mⁿ was positive, its magnitude increased with the slipperiness, whereas when the thumb was at LFC and Mⁿ was negative, its magnitude decreased with the slipperiness.

Interparticipant Differences in the Local and Synergic Reactions

To examine whether the local or synergic reactions were predominantly used, we compared the data in the pairs of trials in which the friction under a given finger was either high or low while the friction at other digit contacts was the same. For instance, for the index finger (boldfaced) we performed the comparison, for example, in the pairs HHLHH–HLLHH and HHLLH–HLLLH (see Table 2 for the entire set). Then, we counted and used for the sign test the number of pairs in which local reactions were observed—that is, the normal force was larger at LFC than at HFC or the tangential force was smaller at LFC than at HFC. Similar analyses were performed for other fingers.

Table 3 shows the results of the sign tests: the number of participants who showed statistically significant adjustments of the digit forces in response to local friction (the normal force was larger at LFC than at HFC or the tangential force was smaller at LFC than at HFC). Note that in the present context for the sign test, the expression statistically significant refers not to the magnitude of the force changes but to the number of task pairs (out of 16) in which we observed local adjustments.

TABLE 3.

Number of Participants Who Adjusted the Digit Forces in Response to Local Friction (N = 12)

	Digit
Digit force	Thumb	Index	Middle	Ring	Little
Normal	10	1	4	2	2
Tangential	7	4	5	2	5

Note. For each participant, a paired sign test was used over the 16 pairs of trials in which a digit was at high-friction contact (HFC) or low-riction contact (LFC), whereas the other four digits were in contact with same surfaces. If normal forces were larger at LFC than at HFC or if tangential forces were smaller at LFC than at HFC in a statistically significant number of paired tasks (more than 12), then the participant was considered to have used local friction adjustments.

The normal forces of the thumb increased at the LFC in 10 out of 12 participants (.0001 < p < .05). In contrast, for the index finger, local effects in a statistically significant number of tasks were found in only 1 participant (p < .05). For the middle finger, significant local effects were found in 4 participants (.001 < p < .05). Significant local effects were found in 2 participants for the ring finger and in 2 participants for the little finger (both ps < .05). Hence, a majority of the participants showed no significant local force adjustments, which, according to the literature, should arise from independent neural networks (Burstedt et al., 1997). It seems natural to assume that those local adjustments were overridden by synergic reactions.

The tangential force of the thumb significantly decreased in response to the local LFC in 7 participants (.0001 < p < .05; Table 3). Local adjustments in a statistically significant number of tasks were seen for the index finger in 4 participants (.001 < p < .05), for the middle finger in 5 participants (.001 < p < .05), for the ring finger in 2 participants (p < .001), and for the little finger in 5 participants (.0001 < p < .01).

Discussion

The prehension tasks explored in the present study were rather unusual: It is not common in daily life to grasp objects with different friction beneath individual digits. However, the participants performed all the tasks successfully without any visible difficulties. It seems that the digit force adjustments were not deliberate but instead were subconscious. When some participants were asked to describe the friction conditions beneath the individual digits, they stated that the tasks were not always simple and that they usually required prolonged time delays, attempts to roll or move the fingertips on the sensor surface, and sequential shifts of attention from one digit to another. Large interindividual differences in the preferred patterns of digit coordination have been observed (cf. Zatsiorsky et al., 2003, who reported similar grasping patterns of the handle with different geometry but with uniform friction).

The main findings of the present study can be summarized as follows. At the thumb and VF level, the normal forces were higher at the LFCs and the tangential forces were lower at the side of lower friction. At the IF level, however, the force coordination was not always detected. Next, we discuss (a) force coordination between the thumb and VF, and among individual fingers, in response to varied surface friction conditions and (b) local and synergic responses to friction variation.

Force Adjustments to Different Surface Friction

The observed independence of the thumb and VF normal forces on the specific distribution of HFCs and LFCs among individual fingers supports the theory of a hierarchical control of prehension with two levels of control, the VF level and the IF level (Arbib et al., 1985; Baud-Bovy & Soechting, 2001; Iberall, 1987; Santello & Soechting, 1997; Zatsiorsky & Latash, 2004).

The VF level

At the VF level, the normal and tangential forces were adequately adjusted to a given surface friction: Higher normal forces and lower tangential forces at the more slippery surface or surfaces than at the less slippery surface or surfaces were observed. That is, the thumb and VF normal forces increased when the thumb was at LFC or when slipperiness, that is, the number of fingers at LFC, increased. When the thumb was at LFC, the thumb tangential force was smaller, whereas the VF tangential force was larger (the sum of the forces was always constant, as should be expected from the equilibrium requirements). When slipperiness increased, the changes were opposite: The VF tangential force went down while the thumb tangential force went up. Because the VF force did not depend on how exactly the HFCs and LFCs were distributed among the fingers, we may offer the hypothesis that the VF force adjusts to changes in the overall surface friction conditions for the four fingers. According to that hypothesis, individuals adjust both the magnitude of the thumb and VF normal forces and the sharing of the tangential forces between the thumb and VF to the different friction conditions. However, the relationships between the normal force and the slipperiness changes were nonlinear (see Figure 2). As a consequence, the VF safety margin changes were also nonlinear; the changes were much smaller when the number of fingers at LFC changed from one to two than when it changed from three to four (see Figure 7B).

In a previous study, Aoki et al. (2006) demonstrated that when surface friction was arranged asymmetrically for the thumb and VF, the tangential force at LFC decreased and the force at the other side increased. The difference between the tangential forces at the thumb and VF produced a friction-induced moment, that is, a moment resulting from unequal tangential forces exerted at the contacts with different friction (see Equation 2). When the thumb was at HFC and the VF was at LFC (the HLLLL condition), the friction-induced moment was in the clockwise direction. In contrast, in the reverse surface condition (the LHHHH condition), the moment was in the counterclockwise direction. When M^t changed, Mⁿ also changed so that the total moment (i.e., the sum M^t + Mⁿ) was kept constant. In the present study, the friction-induced moment scaled almost linearly with the slipperiness (see Figure 9A). When the thumb was at LFC, the magnitude of the friction-induced moment decreased with the decrease of friction at the VF. In contrast, when the thumb was at HFC, the magnitude of friction-induced moment increased with the decrease of friction at the VF. Therefore, the surface friction at the thumb and the slipperiness determined the magnitude and direction of friction-induced moment. Thus, the present study fills in the gap between the four extreme situations (LHHHH–LLLLL conditions and HHHHH–HLLLL conditions) investigated in Aoki et al. The difference is that in the present study, we changed the friction conditions at the VF in a step-like manner by varying the number of fingers at the LFC (slipperiness).

The changes of the thumb and VF forces in response to the friction variations were intercompensated in the sense that they did not violate the object equilibrium. Chain effects—that is, the cause–effect sequences or relations of particular local changes (Aoki et al., 2006; Shim et al., 2005; Zatsiorsky et al., 2003; Zatsiorsky & Latash, 2004)—can explain those changes. The sequences were thumb-friction dependent.

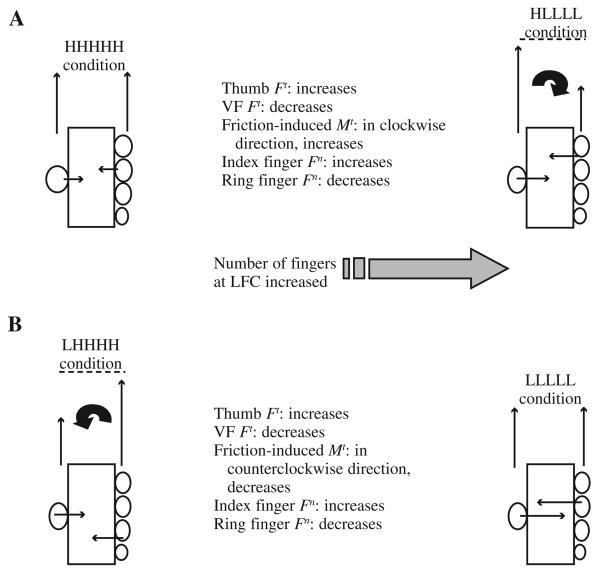
When the thumb was at HFC and the number of fingers at LFC increased (Figure 10, upper pictures), the following chain effects were observed: (a) The VF tangential force decreased while the thumb tangential force increased by an equal amount; (b) the difference between the tangential forces of the thumb and VF increased; (c) friction-induced moment in the clockwise direction was generated, and its magnitude increased with the slipperiness (see Figure 9A); (d) a counterclockwise Mⁿ to cancel out the friction-induced moment increased (see Figure 9B); and (e) the normal force of the index finger increased (see Figure 4A) so that the counterclockwise Mⁿ could be increased.

FIGURE 10.

Schematic graph showing the effects of increasing slipperiness on biomechanics of prehension. When the slipperiness increased, the virtual finger (VF) tangential force F^t decreased and the thumb F^t increased by equal amount. The effects of those changes on the friction-induced moments (M^t), however, depended on the thumb friction. (A) The thumb at high-friction contact (HFC). At zero slipperiness (all fingers are at the HFC), the thumb and VF F^t were equal and the friction-induced M^t was zero. With the increased slipperiness, the difference between the thumb and VF F^t—as well as the friction-induced M^t—emerged and built up. The friction-induced M^t in the clockwise direction was generated. (B) The thumb at low-friction contact (LFC). At zero slipperiness (all fingers were at the HFC), the thumb and VF F^t were not equal and the friction-induced M^t was in the counterclockwise direction. With the increased slipperiness, the difference between the thumb and VF F^t, as well the friction-induced M^t, decreased. Fⁿ is the normal force. See Figure 2 for explanation of conditions.

When the thumb was at LFC and the number of fingers at LFC increased (Figure 10, lower pictures), the following chain responses were found: (a) The VF tangential force decreased while the thumb tangential force increased by an equal amount; (b) the difference between the thumb and VF tangential forces decreased; (c) the friction-induced moment—it was in the counterclockwise direction—decreased (see Figure 9A); (d) a clockwise Mⁿ to cancel out the friction-induced moment decreased (see Figure 9B); and (e) the normal forces of the ring and little fingers decreased (see Figure 4B) so that the clockwise Mⁿ was decreased.

Thus, the results of the present study extend the findings of Aoki et al. (2006), who used only four extreme surface conditions (HHHHH, LLLLL, HLLLL, and LHHHH). Because similar digit force adjustments were also observed in two-digit and tripod grasps (Burstedt et al., 1997; Burstedt et al., 1999; Edin et al., 1992), it is likely that common principles govern force coordination in all cases of object grasping. Note, however, that conclusion is valid only for the VF level of control; at that level, the number of available degrees of freedom is limited and the equilibrium constraints must be satisfied.

The IF Level

The adjustments to the friction conditions observed at the VF level did not always apply to force coordination of individual fingers. Like the thumb and VF forces, the normal forces of the middle finger were larger at LFC than at HFC, and tangential forces of the little finger were smaller at LFC than at HFC. In other cases, however, such force adjustments were not observed. That finding is in an obvious disagreement with results of the just-cited studies, whose authors concluded that the adjustments of the individual digit forces in response to the local friction arise from the independent neural networks (Burstedt et al., 1997; Burstedt et al., 1999; Edin et al., 1992).

The forces of the individual fingers were adjusted not only to local surface friction but also to friction at other digits (synergic friction effects). Therefore, the present results do not exactly agree with the findings on two-digit and tripod grasps. In those studies, normal and tangential forces were adapted to friction of a given finger and effects of surface friction at other fingers were rather small (Burstedt et al., 1997; Burstedt et al., 1999; Edin et al., 1992). It seems reasonable to suppose that the discrepancy arose from the difference in the number of fingers involved in the tasks as well as from the difference in the grasping modes. In two-digit and tripod grasps, all finger contacts are necessary; that is, one cannot lift one of the fingers off its point of contact. In our task, participants could generally lift any one of the four fingers and still keep the handle at equilibrium. The interfinger force sharing was not completely defined by the task mechanics and to a certain degree depended on the participants' preference. That procedure allows for different local effects across fingers as well as for different adjustments seen in different participants. The basic requirements of grasp stability still had to be satisfied, however: The normal forces of the thumb and VF had to be equal in magnitude, the sum of the tangential forces of the five digits had to be equal to the object weight, and the sum of M^t and Mⁿ had to be zero. Moreover, object slipping should be prevented. Therefore, when friction at a digit changed, the participants had to make synergic force adjustments such that the just-mentioned requirements were satisfied. We discuss the local and synergic friction effects in more detail in the following section.

Local and Synergic Friction Effects

The local friction effects, that is, the effects of friction at a given digit on that digit's forces, were found in normal forces of the thumb and middle finger and tangential forces of the thumb and little finger. In those digits, normal forces were larger and tangential forces were smaller at the LFC. Such force changes, however, always perturb the object equilibrium. Therefore, participants needed a synergic action of other digits to keep the object at rest. Indeed, the synergic effects, that is, the effects of friction at a given digit on the forces exerted by other digits, were found in all digits.

The results of previous studies on friction effects (Aoki et al., 2006; Burstedt et al., 1997; Burstedt et al., 1999; Edin et al., 1992) all suggest that the digits tend to adjust to friction by increasing the normal force and decreasing the tangential force at the LFC. Such reactions were reported for two-digit pinch grasps (Edin et al.), object manipulation performed by two performers (each performer contacted the object with only one finger; Burstedt et al., 1997), tripod grasps (Burstedt et al., 1999), and for the thumb and VF for five-digit grasps when the friction was the same for all fingers (Aoki et al., 2006). Sensory information is obviously used for the scaling of normal and tangential forces in response to the surface friction. It is known that the friction information is conveyed mostly by the Meissner corpuscles in the glabrous skin (Johansson, 1996); their initial responses are strongly influenced by the surface material. In the present study, such local reactions were, however, observed in a limited number of cases.

We offer here the hypothesis that the coordination of the digit forces in multifinger prehension is determined by an interaction of two mechanisms, local and synergic. According to that hypothesis, local reactions always exist, but they are not always manifested; they often are masked by higher order synergic adjustments. Local reactions of individual digits disturb the object equilibrium. Hence, to maintain the equilibrium, the central controller has two options: to inhibit a local reaction or to let it emerge and then to correct its consequences.

In different individuals, either the first or the second mechanism prevails (see Table 3 and Interparticipant Differences in the Local and Synergic Reactions in the Results section). The data of this study reflected unpracticed behaviors that are not typical of daily life. That is precisely why the data are scientifically interesting; the redundant finger system is channeled toward several subsets of possible solutions, and the central controller selects one of them. Among our participants, 4 showed local reactions in all 16 paired task comparisons for the thumb at LFC or at HFC. In those participants, the normal thumb forces were always larger and the tangential thumb forces were always smaller at LFC. In 2 other participants, the corresponding number for the thumb normal force was only 12 of 16. Hence, the local reactions in those participants were inhibited in four pairs of conditions. The sign test does not allow us to claim that local reactions were preferred in those participants. For the individual fingers, the highest achievements were (a) for the index finger normal force, 13 local reactions (1 participant); (b) for the middle finger normal force, 15 local reactions (1 participant); (c) for the ring finger normal force, 13 local reactions (2 participants); and (d) for the little finger normal force, 13 local reactions (2 participants). Overall, however—with the exception of the thumb—the local reactions dominated in a statistically significant number of paired tasks (at least 13 of 16) only in a minority of the participants, for instance, for the ring finger in only 2 participants out of 12 (see Table 3).

If the local reactions are not inhibited and take place, then their perturbing effects on the object equilibrium have to be compensated. The compensation can theoretically be done either at the level of the finger forces or at the level of all five digit forces (at the level of prehension synergies). In the former case, the finger forces change but the thumb and VF forces stay put. For the tangential forces, that compensation could be easily achieved: When a finger is at LFC and its tangential force decreases, the force of another finger increases. Such an interfinger compensation, however, was never observed. As a result, when a finger tangential force decreased, the VF tangential force also decreased. The compensation of the normal force increase at LFC is also possible, but it requires a more complex coordination and the involvement of all three remaining fingers. Such a complex alteration is necessary because any change of a finger normal force breaks, at once, two equilibrium requirements: (a) the total force of the four fingers is not equal anymore to the thumb normal force, and (b) Mⁿ changes. One can discuss the issue of the interfinger force compensation mathematically by invoking the concept of null spaces. The null space of an m × n matrix G is the set of all vectors f in a state space Rⁿ such that Gf = 0 (for a more detailed discussion of the null spaces in multifinger prehension, see Gao, Latash, & Zatsiorsky, 2005). Let f be a 4 × 1 vector of normal finger forces, F be a 2 × 1 vector of the resultant consisting of the VF normal force and Mⁿ, and G be a 2 × 4 grasp matrix. The equation of interest is F = Gf. Because the rank of a 2 × 4 matrix is at most 2, the dimensionality of the null space of the grasp matrix (its nullity) is at least 2. Hence, there are such finger force combinations that the individual forces cancel each other and do not affect the VF normal force and Mⁿ. However, that potential opportunity was never realized; an increase in the slipperiness led to an increase in the VF normal force, F(4, 44) = 14.0, p < .001, for the VF, and Mⁿ changed (see Figures 9B and 10).

It is interesting that in four-finger pressing tasks, a pattern of covariation among finger forces that stabilizes both the total force and the total moment has been found (Scholz, Danion, Latash, & Schöner, 2002; Shim, Latash, & Zatsiorsky, 2003b; Shim, Lay, Zatsiorsky, & Latash, 2004). Hence, the central controller has the means to stabilize both the VF normal force and Mⁿ. It seems, however, that it does not use that option during prehension. Instead, the stabilization is performed at the level of prehension synergies (Zatsiorsky & Latash, 2004) and involves all five digits with the corresponding changes of the VF forces and moments. The old adage of Bernstein (1967)—a synergy never reacts to a small local change with another small local change but with changes in all its elemental variables—has once again been confirmed.

Biographies

Tomoko Aoki is a senior lecturer at the Prefecural University of Kumamoto, and she teaches, for example, “Lifespan Motor Development.” Her research interests include neurophysiological and biomechanical bases of motor and sensory functions in the human hand.

Mark L. Latash is a professor at The Pennsylvania State University. The courses he teaches include “Neurophysiological Basis of Movement.” His research is diverse in motor control and related neurophysiology, with strong interests in control and coordination of multielement systems participating in the production of voluntary movements.

Vladimir M. Zatsiorsky is a professor at the The Pennsylvania State University. He teaches, among other courses, “Advanced Biomechanics of Human Motion.” His research interests include biomechanical basis of motor control, with strong interests in biomechanics of hand and finger function and balance maintenance.