Effects of friction at the digit-object interface on the digit forces in multi-finger prehension

Abstract

The effects of surface friction at the digit-object interface on digit forces were studied when subjects (n = 8) statically held an object in a five-digit grasp. The friction conditions were SS (all surfaces are sandpaper), RR (all are rayon), SR (S for the thumb and R for the four fingers), and RS (the reverse of SR). The interaction effects of surface friction and external torque were also examined using five torques (−0.5, −0.25, 0, +0.25, +0.5 Nm). Forces and moments exerted by the digits on a handle were recorded. At zero torque conditions, in the SS and RR (symmetric) tasks the normal forces of the thumb and virtual finger (VF, an imagined finger with the mechanical effect equal to that of the four fingers) were larger for the RR than the SS conditions. In the SR and RS (asymmetric) tasks, the normal forces were between the RR and SS conditions. Tangential forces were smaller at the more slippery side than at the less slippery side. According to the mathematical optimization analysis decreasing the tangential forces at the more slippery sides decreases the cost function values. The difference between the thumb and VF tangential forces, ΔF^t, generated a moment of the tangential forces (friction-induced moment). At non-zero torque conditions the friction-induced moment and the moment counterbalancing the external torque (equilibrium-necessitated moment) could be in same or in opposite directions. When the two moments were in the same direction, the contribution of the moment of tangential forces to the total moment was large, and the normal forces were relatively low. In contrast, when the two moments were in opposite directions, the contribution of the moment of tangential forces to the total moment markedly decreased, which was compensated by an increase in the moment of normal forces. The apparently complicated results were explained as the result of summation of the friction-related (elemental) and torque-related (synergy) components of the central commands to the individual digits.

Introduction

Adjustment of the digit forces to different friction conditions during object manipulation has been a topic of study for the past two decades (Burstedt et al. 1997, 1999; Cadoret and Smith 1996; Cole and Johansson 1993; Edin et al. 1992; Johansson 1996; Johansson and Westling 1984, 1987; Kinoshita et al. 1995; Quaney and Cole 2004). Grip force becomes greater for an object with a more slippery surface, resulting in a higher grip force: load force ratio, while the safety margin (the percent difference between the grip force and the minimal normal force to prevent slippage) is kept relatively constant (Johansson and Westling 1984). This friction-related scaling effect is shown to be neither task-specific (Cole and Johansson 1993) nor grip configuration-specific (Burstedt et al. 1997, 1999; Kinoshita et al. 1995). Grip force also increases in response to the tangential torque, i.e. the torque in the tangential plane at the digit-surface interface (Goodwin et al. 1998; Kinoshita et al. 1997).

When subjects grasped objects with different surfaces for each digit, they scaled the grip-load force ratio independently based on the local friction condition at that digit (Burstedt et al. 1997, 1999; Edin et al. 1992; Quaney and Cole 2004). Apparently, tactile afferents from individual digits play a role in this force adjustment (Edin et al. 1992; Johansson and Westling 1987). It has been concluded that the coordination of digit-tip forces during human manipulation emerges from independent neural networks controlling each engaged digit (Burstedt et al. 1997). Under an asymmetric surface condition, when the friction at the thumb and index finger sites was different, the subjects tilted the handheld object toward the more slippery side (Edin et al. 1992).

The mentioned studies lay a foundation for understanding effects of surface friction on the pattern of digit forces selected by the central nervous system (CNS), but they still leave many questions unanswered. Three main delimitations of the above studies can be mentioned: (1) The subjects were not required to maintain a constant (vertical) orientation of the handle; as a result when the friction at opposing digits was different the subjects preferred to incline the handle, i.e. the rotational equilibrium of the object was not maintained. If the object were a cup filled with liquid, the liquid would be spilled. (2) The external torque exerted on the object was either zero or was applied in the tangential plane (Goodwin et al. 1998; Kinoshita et al. 1997); in the latter case the rotational equilibrium can be maintained by simply exerting larger grip force on the object. (3) In majority of studies a two-digit pinch grip was used.

There is only one study that examined the forces normal to the surface during five-digit prehension when all the digits were in touch with less or more slippery surfaces (Kinoshita et al. 1995). The friction conditions varied among the trials but in individual trials they were the same for each digit. Only the normal forces have been recorded. The authors reported that the normal force scaled with the friction condition and that the contribution of each of the four fingers was kept constant. When the contribution of individual fingers is constant while the total force changes, the moment generated by the force should change in proportion to the force magnitude—with the exception of the case when the moment is zero—and the rotational equilibrium of the object will not be maintained. Therefore the strategy found by Kinoshita et al. 1995 can only be used when the moment of the external force is zero.

During multi-digit prehension individual digit forces and moments change conjointly in relation to mechanical parameters such as object weight, width, torque balance, thumb placement, and object orientations with respect to vertical (Gao et al. 2005; Pataky et al. 2004a; Shim et al. 2003, 2005; Zatsiorsky and Latash 2004; Zatsiorsky et al. 2002b, 2003a, b). The authors have concluded that task-specific prehension synergies were used. Further analysis revealed that these synergies could be organized in the CNS hierarchically with at least two levels (Shim et al. 2003, 2005; Zatsiorsky and Latash 2004; Zatsiorsky et al. 2003b). At the higher level, force and torque constraints are distributed between the thumb and virtual finger (VF), an imagined finger that generates the same mechanical effect as the four actual fingers (Arbib et al. 1985; Baud-Bovy and Soechting 2001; Iberall 1987; Santello and Soechting 1997). At the lower level, the force and torque of the VF are distributed among the four fingers.

The present study is concerned with the effects of surface friction on normal-tangential force coordination of individual digits during statically holding an object using a prismatic five-digit grasp. Specifically, the aims of the present study were threefold. First, we investigated digit forces in response to slippery and non-slippery friction conditions. The friction conditions were arranged symmetrically and asymmetrically in the thumb and VF sides. Second, we investigated the interaction between the effects of the surface friction and external torque on digit forces. In addition to the above friction conditions, five levels of external torque in the normal plane were introduced for this purpose. Third, we addressed relations between the force coordination and rotational equilibrium of the object (preventing object tilting). These issues are important to be explored because people commonly manipulate objects with variations in surface friction under the fingers (e.g. due to partial wetness) and non-zero external torques, for example when the center of gravity is located outside the grasp.

Methods

Subjects

Eight right-handed males (age mean ± SE = 28.4 ± 2.2 years, weight 72.4 ± 3.4 kg, height 1.78 ± 0.02 m, hand length from middle fingertip to distal crease of the wrist with hand extended 19.8 ± 0.4 cm, hand width 9.4 ± 0.4 cm) volunteered to participate in this study. Subjects had no previous history of neuropathies or trauma to the upper limbs. All subjects gave informed consent according to the policies of the Office for Research Protections of the Pennsylvania State University.

Apparatus

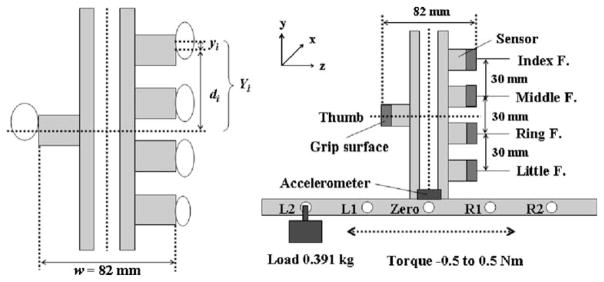
Five six-component force/moment transducers (Nano-17, ATI Industrial Automation, Garner, NC, USA) were mounted on an aluminum handle which was attached to the top edge of an aluminum beam (600 mm×25 mm×4 mm) at the midpoint of the beam in the mediolateral direction (Fig. 1). The center points of the index and middle finger sensors were located 45 and 15 mm above the midpoint of the handle, respectively. The center points of the ring and little finger sensors were located 15 and 45 mm below the midpoint, respectively. The thumb sensor was located at the midpoint. The grip width, which is the perpendicular distance between the surface of the thumb contact and those of the finger contacts, was 82 mm. A load of 0.391 kg was suspended from the beam at five different positions thus generating different levels of external torques. Total weight of the apparatus with the load was 1.178 kg.

Fig. 1.

Schematic of the point about which the moments are computed (left panel) and schematic of experimental handle/beam apparatus (right panel). In the left panel, w is the handle width (w = 82 mm); y_i is vertical coordinate of the index finger force application with respect to the sensor center; d_i is a projected vertical distance between the sensor centers of the index finger and the thumb; Y_i is vertical coordinate of the point of the index finger normal force application. Note that the lower case y_i designates the coordinate with respect to a sensor center i while the uppercase Y is used to designate a coordinate in the handle fixed reference system. In the right panel, for L1 and L2 torque conditions, the external torque was positive but the torque produced by the subjects was negative. In contrast, for R1 and R2 torque conditions, the external torque was negative but the torque produced by the subject was positive

Different friction conditions of digit-object interface were achieved by exchanging the grip surfaces. Grip surfaces used for high and low frictions were 100-grit sandpaper and rayon, respectively. To measure the static friction coefficient between the skin and these materials, the subjects were asked to grasp the handle using only the thumb and middle finger and then to let it slip as slowly as possible. Slips were detected by a sudden decrease in the tangential force at one of the digits. The ratio between the normal force and the tangential force at slip (slip ratio) was determined (Johansson and Westling 1984). The inverse of the slip ratio was used as an estimate of the friction coefficient (μ). The μ was 1.34 ± 0.05 for the sandpaper and 0.49 ± 0.05 for the rayon. The safety margin was evaluated for each subject based on the following equation (Pataky et al. 2004a): $\mathit{Safety}\mathit{margin}=(F_i^{\text{n}}-\mid F_i^{\text{t}}\mid /\mu )/F_i^{\text{n}}$, where i is an arbitrary digit, Fⁿ is the digit normal force, and F^t is the digit tangential force.

In ‘with-level tasks’, a level was attached onto the handle to visually guide the subjects to maintain the vertical orientation. Mediolateral tilting of the object was measured by an accelerometer (EGA 3, Entran, USA, range ± 5 g, weight 7 g) located at the bottom of the handle. The acceleration was recorded in the z direction (see Fig. 1 for the axes designation): if the handle is not being translated and is oriented vertically the acceleration should equal zero; if the handle is inclined 90° the recorded acceleration equals the acceleration due to gravity g = 9.81 m/s². Any intermediate recorded acceleration value corresponds to a sine of the inclination angle multiplied by g.

The force/moment signals from the sensors (6 signals ×5 sensors = 30) and a signal from the accelerometer were digitized by a 12-bit A/D converter (PCI-6033E, National Instruments, Austin, TX, USA) at 100 Hz and processed by a PC computer (Dell Dimension 8200, USA). The sampling frequency in tests used to determine the static friction coefficient was 300 Hz.

Experimental conditions

The experimental design included 4 frictions×5 torques×2 holding modes, resulting in the total of 40 different conditions that were introduced to each subject in a balanced order. The four friction conditions were: (1) sandpaper symmetric (SS: all surfaces are sandpaper), (2) rayon symmetric (RR: all are rayon), (3) sandpaper–rayon asymmetric (SR: sandpaper for the thumb and rayon for the four fingers), and (4) rayon–sandpaper asymmetric (RS: the reverse of SR). The five torques were −0.5 (L2), −0.25 (L1), 0 (zero), +0.25 (R1), and +0.5 (R2) Nm. The two holding modes were with and without visual feedback on the handle orientation provided by the level. Two trials were performed under each experimental condition.

Experimental procedure

Before the experiment, subjects washed their hands with soap and warm water to normalize skin condition. Subjects were given an orientation session before testing to become familiar with the experimental task and apparatus.

Subjects sat in a chair alongside a table, with the right upper arm positioned at approximately 45° abduction in the frontal plane and 45° flexion in the sagittal plane. The elbow joint was flexed approximately 45°. The forearm, but not the wrist and hand, was placed on the forearm brace affixed to the table. The forearm was pronated 90° so that the hand was in a natural grasping position. Special attention was paid to digit placement on the sensors such that the center of each digit-tip coincided with the center of the corresponding sensor.

Subjects were instructed to take the handle from the rack, place the forearm onto the brace, and hold the handle statically and vertically in the air. In the ‘with-level task’ subjects used the level for visual feedback while in the ‘without-level task’ the level was absent. In both tasks they were instructed to hold the handle with minimal force exertion. When the subjects reported that they were holding the handle as instructed, data recording started. Signals were recorded for 3 s. After the data collection stopped, the subjects placed the handle back on the rack.

Signals were set to zero before each trial. After every tenth trial, the subjects were asked to wipe their right-hand digits with alcohol in order to maintain constant skin condition. At least 20-s breaks were provided between trials and 5-min breaks were provided after every tenth trial in order to avoid fatigue. The total duration of each experiment was close to 2 h.

Data analysis and statistics

Data acquisition software written in LabVIEW (National Instrument, NC, USA) was used to convert digital signals into force, moment, and acceleration values. Data processing was performed using Matlab (Mathworks, Inc., Natric, MA, USA). The raw force/moment data were not filtered, because only the mean signal over 2.8 s of the holding period (excluding 0.1 s at the beginning and at the end of the period) was considered. We only used the second trial data in order to minimize the effect of adjustments to new friction and torque conditions.

In the transducer-fixed reference system, forces normal to the transducer surface corresponded to the z direction f^z. In this experiment, f^z was oriented horizontally with respect to the environment. Since the task was static, the tangential force always acted in the vertical direction. The digit-contacts with the sensors were modeled as the soft-finger-contacts (Mason and Salisbury 1985), in particular the rolling of the fingers on the sensor surfaces was allowed.

The vertical coordinates (y) of the digit force application with respect to the sensor center were computed as $y_i=m_i^x/f_i^z$ (i = 1, 2, 3, 4, 5) where $m_i^x$ is the moment of the ith digit with respect to x (horizontal) axis and $f_i^z$ is the normal force of the ith digit. The obtained values were then used to compute the moment arms of the normal forces in the handle reference frame. The vertical coordinate of the point of VF normal force application Y_vf was determined based on the theorem of moment (the Varignon theorem) as $Y_{\text{vf}}=\mathrm{\sum }{F}_i^{\text{n}}{Y}_i/F_{\text{vf}}^{\text{n}}$ (i = 1, 2, 3, 4), where Y_i is the vertical coordinate of the force application point of finger i (Y_i = d_i+ y_i, where d_i is a projected vertical distance between the sensor centers of finger i and the thumb). $F_{\text{vf}}^n$ is the sum of the normal forces produced by the four fingers. Note that the uppercase Y is used to designate a coordinate in the handle fixed reference system, while the lower case y_i designates the coordinate with respect to a sensor center i.

At the VF level, the moment of normal forces Mⁿ and the moment of the tangential forces M^t have been computed. The moment of normal forces was computed as

$$M^{\text{n}}=F_{\text{vf}}^{\text{n}}(Y_{\text{vf}}-Y_{\text{th}})$$ (1)

and the moment of tangential forces was computed as

$$M^{\text{t}}=(F_{\text{vf}}^{\text{t}}-F_{\text{th}}^{\text{t}})w/2,$$ (2)

where superscripts n and t represent the normal force and tangential force, respectively; subscripts th and vf represent the thumb and VF, respectively; and w stands for the width of the handle. The difference (Y_vf − Y_th) is the moment arm of the couple. The Mⁿ is due to the normal forces of the thumb and the VF. These forces are equal, opposite, and not collinear. Hence, they form a force couple. Because the moment of a couple is a free moment (i.e. it is the same for all moment centers and remained unchanged under parallel displacements, see for instance Zatsiorsky 2002, p 20), the Mⁿ can be added to the M^t to obtain the total moment exerted by the subject. Upward tangential forces and counterclockwise moments were defined as positive.

A three-way repeated measure MANOVA for normal forces, tangential forces, and safety margins for the thumb and VF, a three-way MANOVA for these variables for the individual digits, and a three-way MANOVA for Mⁿ, M^t, and Y_vf − Y_th were performed to assess the effects of three factors—Friction (four levels), Torque (five levels), and Holding mode (two levels) on each individual variable. Post-hoc analyses of the differences in the pairs of variables have been performed. The differences were considered significant if P < 0.05.

To explore whether the obtained results could be explained by a tendency of the CNS to minimize certain variables (e.g. digit forces), we performed optimization analysis (mathematical details are provided in the Appendix). Four cost functions (CF) that correspond to the following minimized variables have been used: (CF1) finger forces and, hence, the minimal potential energy of elastic deformation; (CF2) the same as CF1 but only for the normal finger forces; (CF3) equal distribution of the forces among the individual fingers (the more equal are digit forces the smaller the CF3); and (CF4) minimization of ‘neural commands’ (this approach takes into account the finger interdependence, also known as finger enslaving, see Pataky et al. 2004b; Zatsiorsky et al. 2002a, b).

Results

The MANOVA results confirmed that the main effects of Friction, Torque and Holding mode, and Friction × Torque interaction were statistically significant for the normal forces, tangential forces and safety margins for the thumb and VF level, as well as for the individual digit level (P < 0.001). It was also confirmed that the main effects of Friction (P < 0.001), Torque (P < 0.001), and Holding mode (P < 0.005) were statistically significant for the Mⁿ, M^t, and Y_vf − Y_th while all the interaction effects were not significant for these variables. Detailed MANOVA results of the main effects and interaction effects for each variable are not presented here due to space limitations. We used post-hoc analyses of the differences in the pairs of variables in the following parts of the results.

Effects of visual feedback

The tilting angle averaged for all torque conditions was only slightly larger for the without-level tasks in both SR (0.65° ± 0.78° toward right) and RS (0.41° ± 0.64° toward left) conditions than the with-level tasks (0.52° ± 0.44° toward left for the SR and 0.37° ± 0.33° toward left for the RS). When the level was not used for visual feedback, the subjects tilted the handle toward the low friction side in both SR and RS conditions. When the level was used and hence the object was kept more vertically oriented: (1) the normal forces of the thumb and VF were larger on average by 1.90 ± 0.89 N (F_[1,7] = 10.1, P < 0.05) and (2) tangential forces were similar to the without-level tasks. In the following parts of the paper the data for the with-level tasks will only be discussed.

Friction effects at zero torque

Symmetric surface tasks (SS and RR)

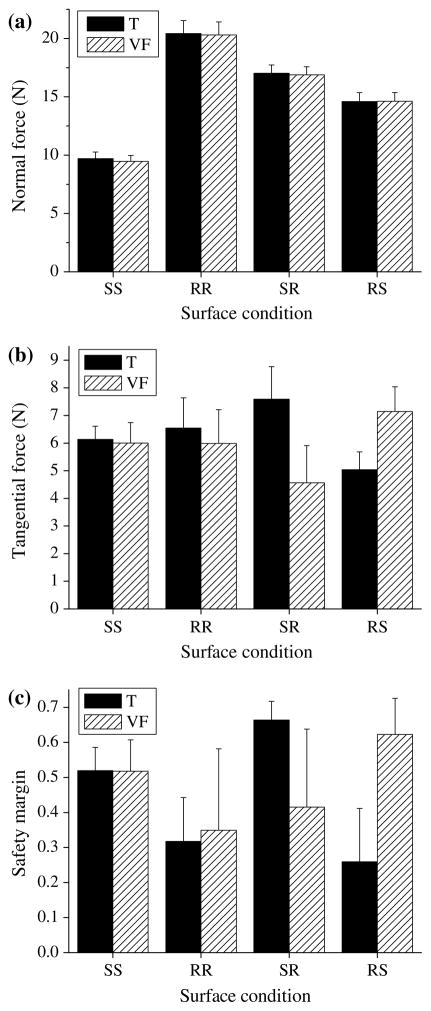
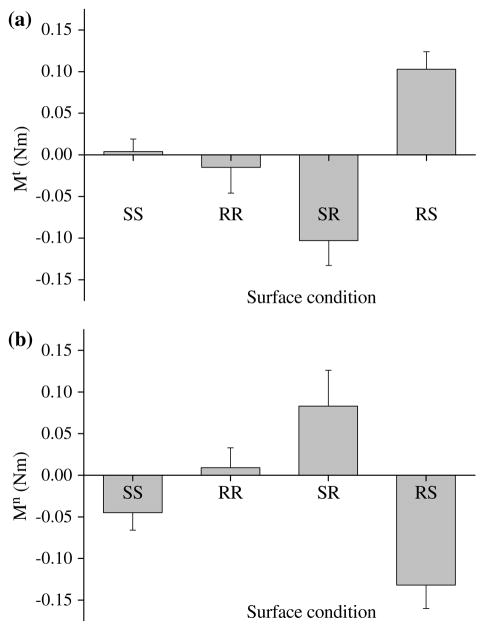
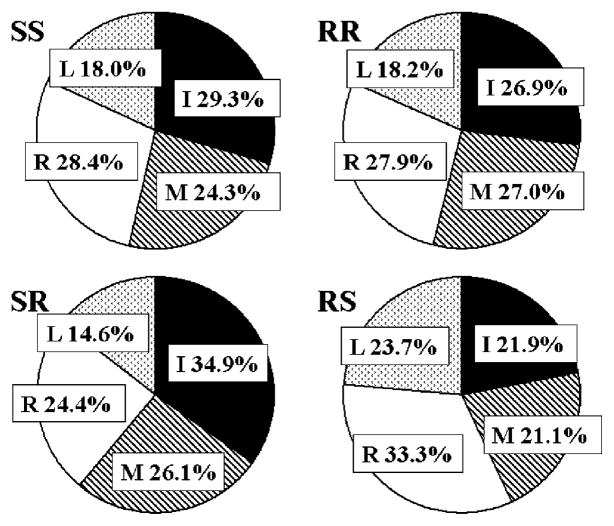
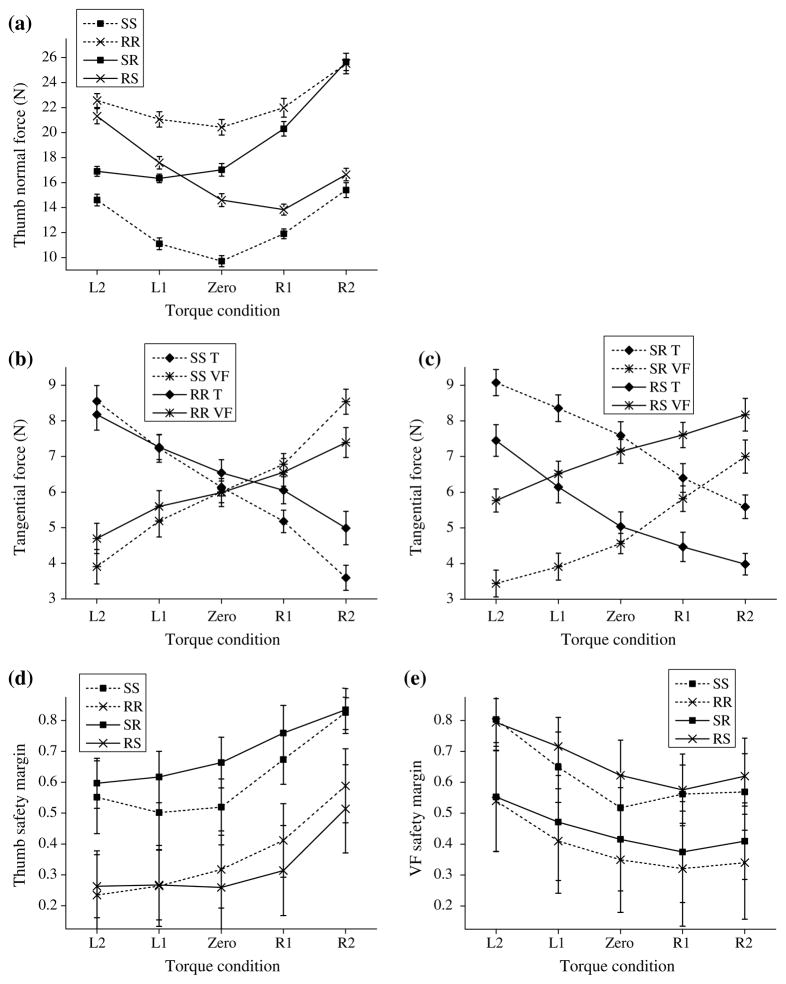
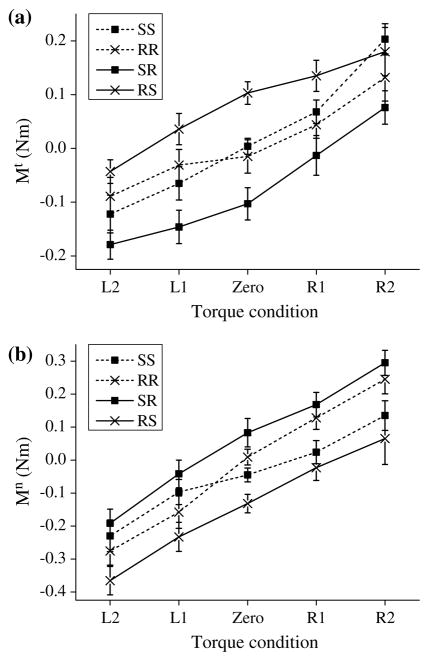
Normal forces generated by the thumb and VF were: (1) approximately equal (this finding was expected from the equilibrium requirements); and (2) larger in the RR than in the SS conditions (Fig. 2a, F_[1,7] = 55.2, P < 0.001 for the thumb and F_[1,7] = 62.2, P < 0.001 for VF). The latter fact was expected from the literature data (Kinoshita et al. 1995). The tangential components were similar for the thumb and VF, and for the SS and RR conditions (Fig. 2b). Safety margins for the SS condition were about 1.5 times larger than for the RR (Fig. 2c, F_[1,7] = 12.6, P < 0.01 for the thumb and F_[1,7] = 5.0, P = 0.06 for VF). The M^t (Fig. 3a) and Mⁿ (Fig. 3b) were small and similar for the SS and RR conditions. The total moments were close to zero (−0.006 ± 0.015 Nm for RR and −0.041 ± 0.011 Nm for SS). Normal force sharing pattern among the individual fingers was similar between SS and RR conditions (Fig. 4) which agrees with the previous study (Kinoshita et al. 1995).

Fig. 2.

Normal force (a), tangential force (b), and safety margin (c) for the thumb and VF at different friction conditions in the zero torque tasks. Group averages and standard errors

Fig. 3.

M^t (moment of tangential forces) (a) and Mⁿ (moment of normal forces) (b) at different friction conditions in the zero torque tasks. Group averages and standard errors

Fig. 4.

Normal forces by the individual fingers (% of the VF) at different friction conditions in the zero torque tasks. Group averages

Asymmetric surface tasks (SR and RS)

Normal forces by the thumb and VF were (1) approximately equal (this finding was expected from the equilibrium requirements); and (2) fell between those for the RR and SS conditions (Fig. 2a). Tangential forces were smaller at the more slippery side for both SR (F_[1,7] = 12.6, P<0.01) and RS (F_[1,7] = 16.3, P<0.01) conditions (Fig. 2b). The safety margins were always smaller at the more slippery side than at the less slippery side (Fig. 2c, F_[1,7] = 6.8, P<0.05 for SR and F_[1,7] = 41.3, P<0.001 for RS). Thus, the decrease in the tangential force did not compensate completely for the larger slipperiness at the R surface. Safety margins averaged between the thumb and VF were larger for the SR (0.54 ± 0.03, F_[1,7] = 34.5, P<0.001) and RS (0.44 ± 0.04, F_[1,7] = 7.8, P<0.05) conditions than at the RR condition (0.33 ± 0.05) and were similar to those in the SS condition.

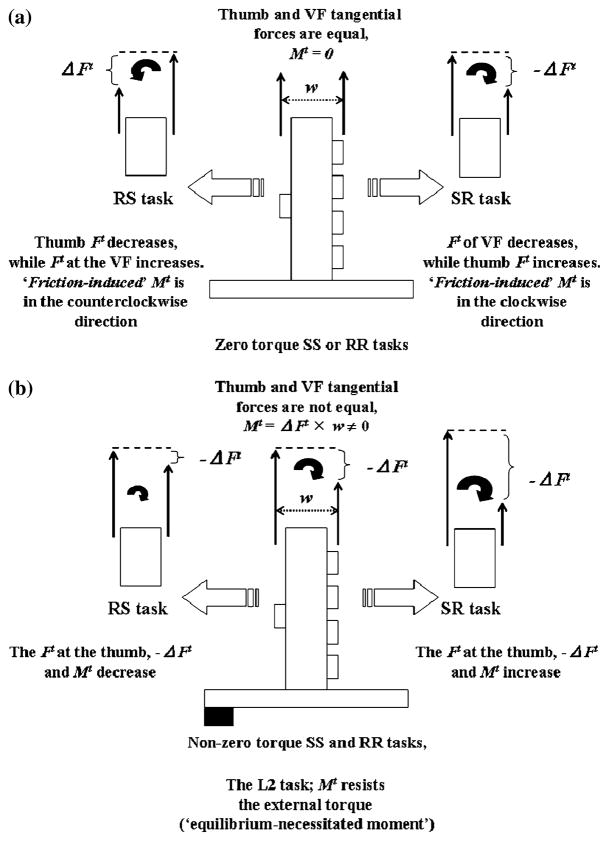
The difference in the tangential forces between the thumb and VF resulted in the generation of M^t (Fig. 3a). We will call the M^t arising due to unequal friction conditions on the two sides of the handle the ‘friction-induced moment’. The moment was in the clockwise direction (negative, supination) for the SR task and it was reversed in the RS task. Mⁿ for both the SR and RS conditions were in opposite directions to the M^t (Fig. 3b). As a result, the total moments were close to zero for both the SR (−0.020 ± 0.020 Nm) and RS (−0.029 ± 0.019 Nm) conditions, and were also similar to the symmetric tasks. The observed small total moments were due to the slight deviation of the center of mass from the geometrical center of the handle. Since normal forces of the thumb and VF were nearly the same in both surface conditions (Fig. 2a), the Mⁿ observed in asymmetric tasks were due to the different normal force sharing among the individual fingers in various tasks. Indeed, in the SR condition the index finger exerted the largest force, while in the RS condition the ring and little finger forces exerted larger forces than the index and middle fingers (Fig. 4).

Friction effects at non-zero torques

Symmetric surface tasks

The normal forces of the thumb and VF were equal at all torque levels (Fig. 5a). Thumb and VF normal forces for the RR condition were always larger than for the SS condition across all torques (F_[1,7] = 63.8, P < 0.001 for the thumb and F_[1,7] = 63.2, P < 0.001 for VF). The normal forces rose with increased mediolateral torque in both directions. The thumb and VF tangential forces for the SS conditions were similar to those for the RR (Fig. 5b).

Fig. 5.

Normal force for the thumb (a), thumb and VF tangential forces for symmetric (b) and asymmetric (c) tasks, and safety margin for the thumb (d) and VF (e) at different torque tasks. Group averages and standard errors

The safety margins were always larger for the SS conditions than for the RR conditions across all torques (F_[1,7] = 27.3, P < 0.01, Fig. 5d for the thumb and F_[1,7] = 12.5, P < 0.01, Fig. 5e for VF). Across the torques the smaller safety margins for the thumb were at L1, L2, and zero torque conditions while the smaller safety margins for the VF were at R1, R2, and zero torque conditions. The small safety margins at non-zero torque conditions were mainly attributed to the increase in the tangential force while those at zero torque conditions were due to the combined effect of the normal and tangential forces.

As expected from the tangential force data, M^t for both surface conditions increased when the external torque changed from L2 to R2 (Fig. 6a). The moments were similar between SS and RR conditions. When the external torque changed from L2 to R2, Mⁿ also increased in both surfaces (Fig. 6b). The moments were also similar in both surface conditions. Consequently, total moments were similar in both surface conditions, and the values were close to the external torque. In the SS conditions, contribution of M^t to the total moment ranged between 41 and 60%. In the RR conditions, the corresponding values were around 35%, except for the zero torque condition (59%). The contribution of M^t to the total moment did not undergo any systematic changes in response to surface and torque conditions. Since normal forces of the thumb and VF were nearly the same in both surface conditions, Mⁿ was mainly controlled by changing the sharing pattern. Indeed, for L1 and L2 conditions normal forces of the ring and little fingers increased to generate negative (clockwise) torque while for the R1 and R2 conditions the normal force of the index finger increased to generate positive (counterclockwise) torque. The moment arm for Mⁿ—i.e. the difference (Y_vf − Y_th), see Eq. 1—for both SS and RR conditions changed from negative to positive when the external torque changed from L2 to R2 (Fig. 7).

Fig. 6.

M^t (moment of tangential forces) (a) and Mⁿ (moment of normal forces) (b) at different friction conditions in the different torque tasks. Group averages and standard errors

Fig. 7.

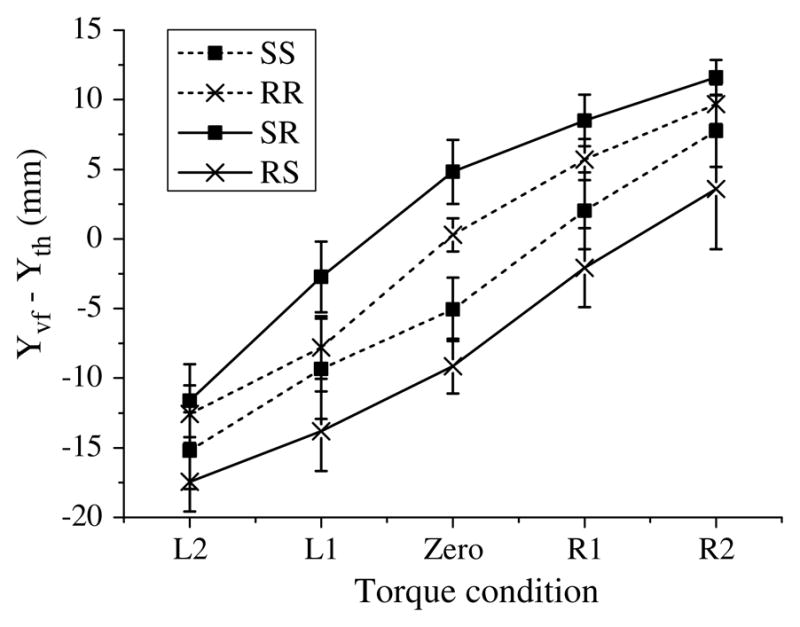
The difference between the position of the point of application of the VF normal force Y_vf and the position of the point of application of the thumb normal force Y_th in different tasks. The (Y_vf − Y_th) difference equals the moment arm of the force couple formed by the normal VF and thumb forces

Asymmetric surface tasks

Thumb and VF normal forces in both the SR and RS conditions increased to a larger degree when an external load was applied to the more slippery side (Fig. 5a). The tangential forces changed almost linearly in response to the changes in torque (Fig. 5c). To generate the M^t either the thumb or VF should produce a larger tangential force. At the same time, decreased friction requires decreasing the tangential force to increase the safety margin. Hence, at some friction–torque combination the requirement for the slip prevention can contradict the requirement for the moment production. This happens at the SR-pronation (R1, R2) and RS-supination (L1, L2) effort combinations. In such friction–torque combinations, the tangential forces were either similar at either sides or the force at more slippery side was larger than at the less slippery side. That is, the tangential force did not decrease at the more slippery side (the tendency to decrease the tangential force at the more slippery side was overridden by the requirement of the torque production).

The smaller safety margins for the thumb were observed at L1, L2, and zero torque conditions (Fig. 5d), while the VF had smaller values at R1, R2, and zero torque conditions (Fig. 5e). The safety margins averaged between the thumb and VF in the SR and RS conditions were larger than the RR conditions (F_[1,7] = 58.4, P<0.001 for the SR and F_[1,7] = 10.6, P<0.05 for the RS). The corresponding values in the RS conditions were smaller than the SS conditions (F_[1,7] = 24.6, P<0.01 for the RS), while significant difference was not found between the SR and SS conditions.

Compared with the M^t for the symmetric task of RR, those for the RS task were increased by 0.046–0.118 Nm (59–271%) across all torque levels (Fig. 6a), while the corresponding values for the SR task were decreased by 0.056–0.115 Nm (138–281%). In contrast, the Mⁿ for the RS task were decreased by 0.075–0.180 Nm (48–251%) across all torque levels (Fig. 6b), while the corresponding values for the SR task were increased by 0.040–0.116 Nm (36–101%). The total moments were similar in both surface conditions, and were also similar to symmetric tasks (as it should be to maintain the rotational equilibrium). Contribution of M^t to the total moment ranged from 16 to 57%. For both SR and RS conditions, the contribution of M^t to the total moment decreased when the external load was applied at more slippery side (i.e. in the SR conditions in the R1 and R2 tasks, and in the RS conditions in the L1 and L2 tasks). Mⁿ generation was due to changes in the normal force sharing among the fingers as is the symmetric tasks. For both SR and RS tasks, the moment arm of the normal forces, i.e. the (Y_vf − Y_th) difference, changed from negative to positive values when the external torque changed from L2 to R2 (Fig. 7). However, as compared with RR tasks, the values for the SR tasks were higher by 1.0–5.1 mm across all torque conditions. In contrast, for the RS tasks they were below those seen in the RR tasks by 4.9–9.4 mm across all torque conditions. Thus, the moment arm for Mⁿ changed compared to symmetric tasks to counteract the friction-induced moment.

Optimization results

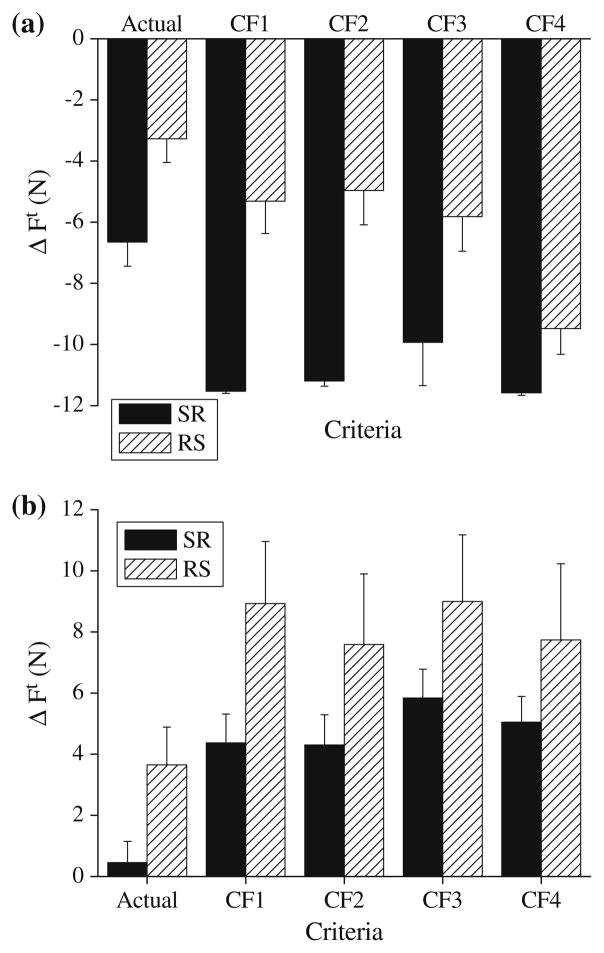
In the asymmetric zero torque tasks (Fig. 8), all the four cost functions predicted smaller tangential forces at the more slippery side (the R side). The ΔF^t in the RS tasks was positive and in the SR tasks it was negative. In other words, decreasing the tangential forces at the more slippery side decreased the cost function values. Hence, while the friction-induced moments (see Fig. 10a) arise due to local conditions at the fingertip-object interface, their existence is advantageous in a global sense; they assist in minimizing the objective function values. The motor command function (CF4) yielded a slightly more accurate prediction than the other three cost functions, which agrees with previously published results (Zatsiorsky et al. 2002a, b). The cost functions CF1 and CF2 yielded the ΔF^t values larger than the actual tangential force differences.

Fig. 8.

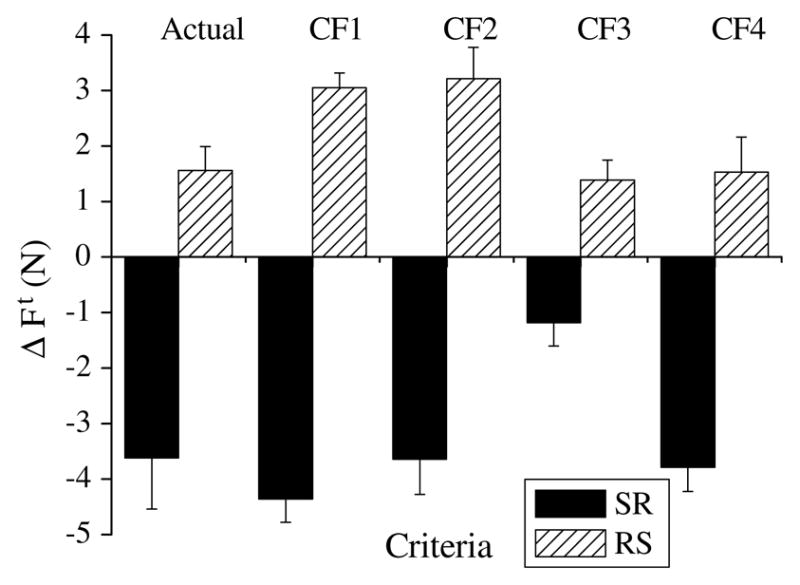
Actual and predicted from optimization differences between the tangential forces of the VF and thumb, ΔF^t, zero torque tasks. Group average data and standard errors. The optimization results are for the following cost functions: CF1—energy-like function over F^r; CF2—energy-like function over Fⁿ; CF3—entropy-like function; CF4—motor command function. The positive values of the ΔF^t signify the positive moment of the tangential forces (i.e. the friction-induced moment in the counterclockwise direction) while the negative values of the ΔF^t represent the moment of tangential forces in the negative (clockwise) direction. The figure illustrates generation of the friction-induced moments. See text for the further discussion

Fig. 10.

The friction-induced and equilibrium-necessitated moments and their interaction, a schematic. a The zero torque tasks. In the SS and RR tasks (the central picture), the tangential forces of the thumb and VF are equal and the moment of the tangential forces M^t is zero. In the RS and SR tasks, due to the opposite changes of the tangential forces F^t, the friction-induced moments arise. To prevent the object tilting, this moment must be compensated by an equal and opposite moment of the normal forces. b Non-zero (L2) torque tasks. In the SS and RR tasks, the moment resisting the external torque is generated (the equilibrium-necessitated moment). The moments seen in the RS and SR tasks are due to the blending of the friction-induced and equilibrium-necessitated moments

In the asymmetric non-zero torque tasks (Fig. 9), all the objective functions predicted well the M^t direction but not its magnitude. All the optimal (i.e. predicted mathematically) ΔF^t values were larger than the actual differences in the tangential forces. Hence, the central controller exerts smaller moments of the tangential forces (and hence larger moments of the normal forces) than it was expected from optimization procedures. Note, that in the asymmetric non-zero tasks the moments of the tangential forces are generated due to two reasons: (1) the necessity to counterbalance the external torque and (2) different friction conditions for the thumb and VF. This issue is deliberated in the ensuing Discussion section.

Fig. 9.

Actual and predicted from optimization differences between the tangential forces of the VF and thumb, ΔF^t, non-zero torque tasks. a L2 task, b R2 task. Group average data and standard errors. The figure illustrates the joint effects of the friction-induced moment and the equilibrium-necessitated moment on the VF and thumb tangential forces. All the four cost functions yielded the ΔF^t values that corresponded to the moments of the tangential forces in the same direction as the actual data while the moment magnitudes were different. See text for the further discussion

Discussion

The main finding of this study is that the subjects—task permitting—tend to decrease tangential forces at the contacts of lower friction. The other observed facts are either a consequence of this tendency, or in good agreement with it. The present discussion addresses; (1) force coordination for varied friction conditions, (2) interaction effects of surface friction and torque on the force coordination, and (3) chain effects.

Force coordination in response to different surface friction

In the symmetric surface conditions, the tangential forces exerted by the thumb and VF did not depend on the friction while greater normal forces were employed for more slippery surfaces. At the symmetric zero torque tasks, the safety margins for the thumb and VF were similar. This agrees with the earlier findings for the two- and three-digit pinch grasps (Burstedt et al. 1997, 1999; Edin et al. 1992; Johansson and Westling 1984).

In the asymmetric tasks, the subjects exerted a smaller tangential force at the more slippery side than at the less slippery side while the thumb and VF normal forces were equal. Because the tangential force did not change exactly in proportion to the surface friction, the safety margin differed between the thumb and VF; safety margin was always smaller at the more slippery side than at the less slippery side. In the SR and RS tasks, the magnitude of the normal force was larger than in the SS task but smaller than in the RR task. This was equally valid for the tasks without the handle orientation feedback and with the feedback (when the tilting was not allowed and the handle was oriented vertically during the trial). Similar results have been previously reported for two- and three-digit grasping tasks with allowable tilting (Burstedt et al. 1997, 1999; Edin et al. 1992). Thus, our findings have extended and generalized this rule—a smaller tangential force at the contacts of lower friction—to five-digit grasps performed under the conditions of rotational equilibrium control. It is likely that this rule governs force coordination in grasping of objects except for a pure horizontal two-digit grip situation where the normal forces are collinear and generation of counteracting moment Mⁿ is not possible.

Tilting of the object can be another possible strategy to cope with different surface friction in the asymmetric tasks. In agreement with previous studies (Burstedt et al. 1997, 1999; Edin et al. 1992), we found that without the level for visual feedback the subjects naturally tended to tilt the handle toward the lower friction side. However the angle of this tilt was small (<2.5°) even for the high external torque. Instead of tilting the object, the subjects preferred to generate the thumb and VF tangential forces of different magnitudes.

In asymmetric tasks, the adjustment to different friction conditions can be made by (1) changing normal forces and/or (2) redistributing tangential force among the thumb and VF such that the total force remains constant. In particular, subjects could have simply adjusted the thumb and VF normal forces to the more slippery surface without changing tangential forces. However, the subjects appear to prefer another strategy.

It has been previously conjectured that the strategy of normal force adjustment would require greater normal forces and, hence, is uneconomical (Burstedt et al. 1999). However, a mathematical proof of this hypothesis has not been provided. We applied optimization procedures to the obtained data and found that all the used cost functions yielded solutions that agreed well with the above hypothesis: They all showed a decrease in the tangential forces at the more slippery side with an equal increase in the tangential force at the less slippery side. As a result the total tangential force stays constant while the difference between the tangential forces ΔF^t changes. Note, that ΔF^t determines the M^t magnitude and direction, M^t = ΔF^tw/2 (see Eq. 2 above). In the zero torque tasks, the tangential forces were smaller at the R side. Therefore, the ΔF^t generates a friction-induced moment (the moment resulting from unequal tangential forces exerted at the contacts with different friction) in the clockwise direction for the SR task and in the counterclockwise direction for the RS task (see Figs. 8, 10a). Note that when the M^t changes Mⁿ should also change to maintain the total moment (i.e. the sum M^t + Mⁿ) constant. In the non-zero torque tasks, such as L2 and R2, the effect of the friction-induced moment depends on the direction of the background torque (Figs. 9, 10b). In particular, in L2 task where the subjects had to generate a clockwise moment to resist the external torque, the magnitudes of the ΔF^t (and hence the clockwise moments) were larger in the SR conditions than in the RS conditions, while in R2 task the effects were reversed (a more detailed discussion on the combined effects of friction and external torque on the digit forces is provided in the following section of this Discussion).

Some previous studies (Edin et al. 1992; Johansson and Westling 1984) reported that safety margin (described in percent of exerted grip force) was insensitive to surface friction, while others (Burstedt et al. 1999; Kinoshita et al. 1997) reported that it was smaller for digits touching a more slippery surface. The present results support the conclusions of the latter studies; percent safety margin values were always lower for the more slippery surface than for the less slippery surface in both symmetric and asymmetric tasks. This indicates that the subjects did not fully compensate for a decrease in the friction coefficient by an increase in the normal forces for symmetric tasks or by a decrease in the tangential forces for asymmetric tasks. In particular, for asymmetric zero torque tasks the differences between the tangential forces at the more and less slippery sides amounted to 199 ± 46% for the SR task and 146 ± 12% for the RS task (see Fig. 2b) which is much smaller than the roughly three-fold difference between the R and S friction. The absolute safety margins (expressed in N) were similar for the symmetric tasks but they were smaller at the more slippery side in the asymmetric tasks.

It is known that the friction information is conveyed mostly by the Meissner corpuscles in the glabrous skin (Johansson 1996); their initial responses are strongly influenced by the surface material. When the normal afferent inflow from the grasping digits had been blocked by local anesthesia, subjects commonly employed extremely large normal forces and equally partitioned tangential forces between the thumb and index finger even in the asymmetric tasks (Edin et al. 1992). Such a force pattern resulted in large and variable safety margins for engaged digits. The unequal tangential forces for the thumb and VF in the present asymmetric tasks also might have relied on afferent inputs from the cutaneous sensors. As a result the averaged safety margins for the thumb and VF were not excessive but sufficient (54% for SR and 44% for RS).

Combined effects of surface friction and torque on force coordination

In the asymmetric non-zero torque tasks, when the friction-induced moment and a moment counterbalancing the external torque (which we will call the ‘equilibrium-necessitated moment’) exerted by the subject were in the same directions (SR-supination and RS-pronation effort tasks) the normal forces were relatively low and the contribution of the M^t into the total moment was large (see Figs. 9, 10b). In contrast, when the friction-induced and equilibrium-necessitated moments were in opposite directions (SR-pronation and RS-supination effort tasks) the contribution of M^t to the total moment markedly decreased, which was compensated by the increased Mⁿ.

Although normal forces of the thumb and VF in the latter tasks were as large as those for the RR conditions, measured safety margin for the non-slippery side was not excessively large. Indeed, safety margin averaged between the thumb and VF in all asymmetric conditions were usually smaller those at the SS condition across all torques.

While tactile receptors play a decisive role in detecting friction condition between the skin and grip surface, maintenance of rotational equilibrium against external torque seems to be a consequence of control accomplished at the synergy level of the motor control system (Bernstein 1967). Proprioceptive information from muscle spindles, tendon organs, and joint receptors are known to play an important role in the latter control (Macefield and Johansson 1996; Proske 2005). In this regard, adjustments of digit forces to satisfy friction and external torque conditions might have been mediated by separate sensory information processing mechanisms, which could have made the control of force output efficient even when performing the hardest task (i.e. when surface friction and torque jointly demand tangential force adjustment in opposite directions).

Chain effects

The observed facts and relations between the experimental variables can be explained by the chain effects —i.e. the cause-effect sequences of particular local changes—triggered by the tendency of performers to maintain sufficiently high values of the safety margin (for discussion of the chain effects in other prehensile tasks see Shim et al. 2005; Zatsiorsky and Latash 2004; Zatsiorsky et al. 2003b). The term ‘sequence’ in the above definition does not imply a chronological order; it only refers to cause-effect relations. When the friction decreases, this tendency is manifested: (1) in symmetric tasks—via the increase of the normal thumb and VF forces and (2) in asymmetric tasks—via the decrease of the tangential forces at the more slippery side. The discussion below is limited to the asymmetric tasks.

For the zero torque data, it is possible to explain the observed digit force adjustments as follows: (1) the subjects decrease the tangential force of the thumb or VF that is in contact with lower friction; (2) to maintain the sum of the tangential forces constant they also increase the tangential force at the less slippery side; (3) these opposite tangential force changes generate the M^t; (4) the M^t is compensated by the opposite Mⁿ; and (5) to produce such a Mⁿ, normal forces of the individual fingers are rearranged.

For the non-zero torque data, the sequence was different depending on relations between surface friction and torque. When the friction-induced and equilibrium-necessitated moments were in the same directions: (1) tangential forces of the thumb and VF became greatly different, which generated a large moment; (2) contribution of the Mⁿ to total moment decreased; and (3) to decrease the Mⁿ, normal forces were also decreased. In contrast, when the friction-induced and equilibrium-necessitated moments were in the opposite directions, (1) the balance of tangential force between the thumb and VF could not produce sufficiently large M^t; (2) the deficiency was compensated by the Mⁿ; and (3) to increase the moment, normal forces increased. Thus, apparently complicated results can be explained as the sequence of responses to surface friction and torque conditions. The immediate friction-related adjustments in individual digit forces may come from independent digit-specific neural networks (Burstedt et al. 1999; Edin et al. 1992); they can be called local or elemental adjustments. The torque-related adjustments are due to the inter-digit interaction necessary to keep the handle vertical; they are synergetic ones.

When friction at all digit-tip interfaces is the same, large inter-trial correlations among the digit forces aimed at preserving the rotational equilibrium was observed (Shim et al. 2005; Zatsiorsky and Latash 2004). If digit forces reflect both friction-related components and torque-related components, variations in the friction at the individual interfaces may be expected to lead to a decrease in the above mentioned correlations because the trial-to-trial variations of the elemental components will bring about variability in digit forces affecting the synergy components of the commands. The following experiment can serve as a test of this hypothesis: the subjects are asked to hold at rest in the air an object using a five-digit grasp. In the first set of the trials the friction at all the digit-tips is the same while in the second set it is different. The expectation is that in the first set the inter-trial correlations among the digit forces will be larger (essentially close to 1.0) than in the second. We are going to perform this experiment in the near future.

Most of the observed events were determined by the task mechanics, but some of them represent a choice made by the CNS. For example, as mentioned above, the subjects could have simply used for the asymmetric conditions the same digit force pattern as the RR conditions. However, they employed distinctive force patterns depending on the surface and torque conditions. Because all employed cost functions predicted the observed reactions equally well we were not able to identify the ‘best’ cost function. It remains unknown whether the used cost functions yield similar results because (1) the functions are by themselves similar—i.e. the CNS uses a single cost function but the values of all functions decrease when one of them is minimized—or (2) the CNS uses all of them together. The explanation why the subjects prefer one solution over other feasible solutions is a challenge left to the future studies.

Our study has a number of limitations. The handle mass was 1.178 kg, which may be considered heavy for objects grasped by the fingers in daily activities. The instruction was to minimize the grip forces, which possibly biased the subjects toward optimizing force economy. These factors limit the ability to generalize the findings. A study manipulating the object weight and the instruction may resolve this issue.

Appendix

Optimization procedure

We used the methods of optimization and cost functions employed previously in our laboratory for studying finger forces in multi-finger tasks (Pataky et al. 2004b; Zatsiorsky et al. 2002a). The optimization problem was formulated in terms of design variables F as follows:

$$\begin{array}{l}\text{minimize}\{f(\mathbf{F}):\mathbf{F}\in \mathbf{\Omega }\}\\ \text{where}\mathbf{\Omega }=\{\mathbf{F}:g_j(\mathbf{F})\le 0,h_k(\mathbf{F})=0\};\\ j=1,\dots ,10;k=3.\end{array}$$

The function f is a cost function, the g_j’s and h_k’s are the inequality and equality constraints, respectively, and F is the vector of normal and tangential digit forces. The inequality constraints g_j are the no-slip constraint (five) and the constraints on non-negativity of normal digit forces (five); and the equality constraints h_k are the equilibrium constraints (totally three: for the horizontal forces, vertical forces, and the moment in the frontal plane). The set Ω is the feasible solution region defined by the constraints. Four convex cost functions f(F) were selected. The friction values for each subject were determined experimentally and the optimization was performed for each subject, friction condition, and task separately. The obtained data were averaged. Only the individual finger forces (n = 4) were subjected to optimization. The thumb and VF forces were not included explicitly in the cost functions.

(CF1) Energy-like function over F^r

The measure is proportional to the potential energy of deformation for a linear (i.e. Hookian) system

$$f_1=\sum _{i=1}^4{\left(F_i^r\right)}^2,$$

where ( $F_i^r$) is the sum of the vector magnitudes: $\mid F_i^{\text{n}}\mid +\mid F_i^{\text{t}}\mid$.

(CF2) Energy-like function over Fⁿ

The energy-like functional can be expressed in terms of only normal digit forces Fⁿ as:

$$f_2=\sum _{i=1}^4{\left(F_i^{\text{n}}\right)}^2.$$

(CF3) Entropy-like function

Since it is conceivable that the CNS prefers to spread efforts as evenly as possible among redundant effectors, an entropy-motivated measure:

$$f_3=\sum _{i=1}^4[F_i^{\text{n}}+1]log[F_i^{\text{n}}+1]-\sum _{i=1}^4{F}_i^{\text{n}}$$

was employed (Hershkovitz et al. 1995, 1997).

(CF4) Motor command function

The procedure for computing motor commands (c) from observed Fⁿ has been described elsewhere (Zatsiorsky et al. 2002a). The N×1 vector c represents the intended activation level of each finger (each c_i∈[0, 1]) and the manifested Fⁿ is the result of anatomical and physiological interconnections among fingers. Thus, based on the neural network model of Li et al. (2002) and Zatsiorsky et al. (1998), an interconnection matrix [M] was constructed that linearly mapped c to Fⁿ:

$$F^{\text{n}}=[\mathbf{M}]c.$$

The c can be computed based on the observed Fⁿ by inverting the square [M] matrix. Thus, the cost function:

$$f_4=\sum _{i=1}^4{c}_i^2$$

represents a minimization of finger activation.

All optimization problems were solved using the procedure: fmincon from MATLAB’s optimization toolbox (The MathWorks Inc., Natick, MA, USA). The optimum (F*) results were unaffected by random variations in initial (F⁰) values submitted to the routines.