Mechanism of Interaction between Single-Stranded DNA Binding Protein and DNA

Abstract

A single-stranded DNA binding protein (SSB), labeled with a fluorophore, interacts with single-stranded DNA (ssDNA), giving a 6-fold increase in fluorescence. The labeled protein is the adduct of the G26C mutant of the homotetrameric SSB from Escherichia coli and a diethylaminocoumarin {N-[2-(iodoacetamido)ethyl]-7-diethylaminocoumarin-3-carboxamide}. This adduct can be used to assay production of ssDNA during separation of double-stranded DNA by helicases. To use this probe effectively, as well as to investigate the interaction between ssDNA and SSB, the fluorescent SSB has been used to develop the kinetic mechanism by which the protein and ssDNA associate and dissociate. Under conditions where ∼70 base lengths of ssDNA wrap around the tetramer, initial association is relatively simple and rapid, possibly diffusion-controlled. The kinetics are similar for a 70-base length of ssDNA, which binds one tetramer, and poly(dT), which could bind several. Under some conditions (high SSB and/or low ionic strength), a second tetramer binds to each 70-base length, but at a rate 2 orders of magnitude slower than the rate of binding of the first tetramer. Dissociation kinetics are complex and greatly accelerated by the presence of free wild-type SSB. The main route of dissociation of the fluorescent SSB·ssDNA complex is via association first with an additional SSB and then dissociation. Comparison of binding data with different lengths of ssDNA gave no evidence of cooperativity between tetramers. Analytical ultracentrifugation was used to determine the dissociation constant for labeled SSB₂·dT₇₀ to be 1.1 μM at a high ionic strength (200 mM NaCl). Shorter lengths of ssDNA were tested for binding: only when the length is reduced to 20 bases is the affinity significantly reduced.

Within both eukaryotic and prokaryotic cells, there are proteins that bind specifically to single-stranded DNA (ssDNA),1 thereby stabilizing and controlling access to ssDNA, following separation of the duplex strands by helicases. Single-stranded DNA binding protein (SSB) from Escherichia coli is one such protein in which a number of features of its interaction with ssDNA have been clarified (1,2). In addition to its role in stabilizing ssDNA, SSB has also been implicated in several processes through interaction with DNA-handling enzymes. Examples include polymerases (3), helicases (4), and nucleases (5), although often the nature of interaction and the resulting regulation of the enzymes are not well understood. SSB is also likely to be important in the formation of RecA filaments on DNA (6). It seems likely that SSB forms stable interactions with ssDNA, ensuring that secondary structures, such as hairpins, are removed but also that SSB must rearrange along the DNA to enable DNA-processing enzymes to exert their functions.

Crystal structures of SSB from E. coli have been determined both in the absence and in the presence of DNA, and the latter shows a homotetramer wrapped with 65−70 bases of DNA (7,8). The DNA lies in a binding channel around the surface, and both nucleic acid backbone and bases interact with the protein. No significant conformational differences are revealed between monomers in the apo and DNA-bound structures. The SSB tetramer structure is formed by the interaction of two pairs of dimers, and there is a change in the relative orientation of these dimers on DNA binding (9). Crystal contacts in both the apo and DNA-bound forms show a second binding surface, which may reflect the interaction between tetramers when bound close to each other along a length of DNA.

Several studies have addressed the biophysical properties of SSB and the kinetics of interaction with ssDNA. Two major binding modes for the SSB−DNA interaction have been described. The complete filling of the binding channels is generally termed the “70-base” or “65-base” binding mode and is differentiated from a “35-base” binding mode, which is favored by low ionic strength and a high ratio of SSB to ssDNA (1,10). A variety of models are possible for changes in the SSB−ssDNA interaction but potentially include transitions between the 35- and 70-base binding modes, sliding, and cooperative binding due to interactions between tetramers. Studies that included the use of analytical ultracentrifugation have examined monomer−dimer−tetramer equilibria and suggest that wild-type SSB forms a stable tetramer (11,12). Kinetic measurements showed rapid binding of SSB to ssDNA, and this may be diffusion-controlled (13): this work also examined different lengths and different salt conditions. The same authors have also investigated transfer of SSB between different ssDNA molecules, measuring dissociation of fluorescently labeled oligonucleotides from SSB by displacement with the unlabeled oligonucleotide (14). Since intrinsic dissociation is very slow, the main pathway was shown to be a direct transfer mechanism including formation of a ternary complex of SSB, the labeled oligonucleotide, and the unlabeled displacer, before the labeled oligonucleotide dissociates (14). Laser T-jump measurements made it possible to access submillisecond times to measure wrapping of ssDNA around SSB tetramers following binding and thereby identified several intermediates on the pathway to the fully bound complex (15). Recent work has shown how SSB can diffuse along ssDNA and how its position can be redistributed, while it remains bound to the DNA (16).

SSB, labeled with a coumarin fluorophore, was developed as a probe for measuring the level of ssDNA formation in real-time assays (17), such as helicase activity (18). This reagentless biosensor is the G26C mutant of E. coli SSB, labeled with IDCC {N-[2-(iodoacetamido)ethyl]-7-diethylaminocoumarin-3-carboxamide}. The adduct, DCC-SSB, gives an ∼6-fold increase in fluorescence on binding to single-stranded DNA (ssDNA), and the kinetics of binding to dT₇₀, together with the effect of changing salt concentration, were measured using this fluorescence signal (17). DCC-SSB, when used in helicase assays, optimally requires conditions in which the binding to ssDNA is rapid, compared with dsDNA unwinding. Furthermore, the signal is most easily interpreted when DCC-SSB saturates the ssDNA.

We have exploited the fluorescence signal of DCC-SSB to investigate how SSB interacts with different lengths of DNA, the extent to which 35-base binding is important, and the kinetic mechanism of this interaction. The fluorescence of the coumarin gives excellent sensitivity for monitoring binding kinetics and is at a wavelength where other components do not interfere. The mechanistic data provide information about how SSB may rearrange along DNA, a process presumably important for its biological roles, outlined above. It also provides information about conditions that would ensure optimal use of this probe in ssDNA assays.

Experimental Procedures

DCC-SSB was prepared as described previously using G26C SSB from E. coli(17) with minor modifications (19), and wild-type SSB (wtSSB) was prepared using the equivalent expression plasmid. IDCC {N-[2-(iodoacetamido)ethyl]-7-diethylaminocoumarin-3-carboxamide} was a gift from J. E. T. Corrie (NIMR, London, U.K.). Oligonucleotides, both unlabeled and labeled with Cy3, were purchased from Eurogentec (Southampton, U.K.). Poly(dT) was from Sigma. For all lengths of oligo(dT) or poly(dT), an extinction coefficient of 8108.6 M⁻¹ cm⁻¹ per base at 260 nm was used for the calculation of concentrations.

Sedimentation Velocity Analytical Ultracentrifugation

Solutions were first dialyzed against the appropriate buffer for 2 h at room temperature and then run on a Beckman Optima XL-A ultracentrifuge at 20 °C. The wavelength was set to the maximum absorbance wavelength of the label (430 nm for diethylaminocoumarin or 555 nm for Cy3), and profiles were measured at 5 min time intervals, with the rotor at 40000 rpm. Data were fit to continuous sedimentation profiles, using Sedfit (version 11.71, National Institutes of Health, Bethesda, MD). The peak values in these distributions were used for further analysis. The variation in sedimentation coefficient with DCC-SSB concentration was fit using the following equation in Grafit version 6 (20), for which Sed₁ and Sed₂ are the sedimentation coefficients of DCC-SSB·Cy3-dT₇₀ and DCC-SSB₂·Cy3-dT₇₀, respectively, D is the total concentration of Cy3-dT₇₀, S is the concentration of DCC-SSB in excess of Cy3-dT₇₀, and K_d is the constant for dissociation of one tetramer from DCC-SSB₂·Cy3-dT₇₀. The observed sedimentation coefficient of the protein complex is then given by

Measurements were taken in a buffer consisting of 25 mM Tris-HCl (pH 7.5) and 200 mM NaCl, unless stated otherwise.

Absorbance and Fluorescence Measurements

Absorbance spectra were recorded on a Beckman DU640 spectrophotometer. Fluorescence measurements were taken on a Cary Eclipse fluorimeter with a xenon lamp. Stopped-flow experiments were conducted on a HiTech SF61MX apparatus (TgK Scientific Ltd., Bradford-on-Avon, U.K.) with a mercury−xenon lamp and HiTech IS-2 software. Data were recorded with a monochromator and 4 mm slits on the excitation light (436 nm) and a 455 nm cutoff filter on the emission. The stated concentrations of described experiments are those in the mixing chamber, unless shown otherwise. Traces, shown in the graphs, are from single acquisitions unless otherwise stated. Theoretical curves were fitted to the data using either the HiTech software, Modelmaker (ModelKinetix), or Grafit (20). Generally, fitting was performed on at least three acquisitions for each condition, and graphs of the concentration dependencies show the average of these under each condition.

All kinetic and titration measurements were taken at 20 °C in a buffer consisting of 25 mM Tris-HCl (pH 7.5) and 200 mM NaCl, containing 5 μM BSA, except as indicated.

Results

Measurements will first be described with dT₇₀, which in some ways provides the simplest model for SSB−DNA interaction, as the length of this oligonucleotide is similar to that of the tetramer binding site. Measurements will then be described using shorter lengths of DNA to obtain information about the minimum length of ssDNA that binds tightly and to define how kinetics, affinity, and stoichiometry change with DNA length. Measurements with poly(dT) probe how these parameters are affected by packing many SSB tetramers together on one DNA molecule. Data were collected at 20 °C in buffer containing 200 mM NaCl, but measurements at 20 mM NaCl will also be presented to show effects of ionic strength. Note that all SSB concentrations, given here, are those for the tetramer unless indicated otherwise, and data analysis assumes that this is the only SSB species.

Association Kinetics with Excess dT₇₀

Association kinetics were obtained at 20 °C by rapid mixing of DCC-SSB with a large excess of dT₇₀ under pseudo-first-order conditions (Figure 1). The concentration dependence of the main phase gave a second-order rate constant of 642 μM⁻¹ s⁻¹, but the intercept with the ordinate was too close to zero to obtain an accurate value for the dissociation rate constant. It seems likely that this represents association of one dT₇₀ with a tetramer with a rate that might be diffusion-controlled.

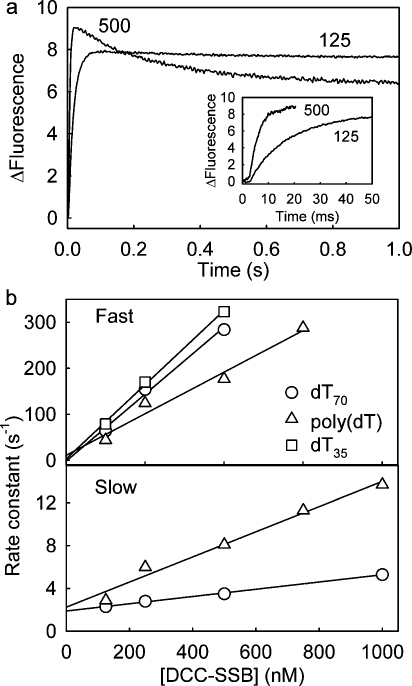
Figure 1.

Association kinetics for various lengths of DNA binding to DCC-SSB. DCC-SSB (5 nM) was rapidly mixed with various concentrations of DNA (concentrations in the mixing chamber). Solution conditions included 25 mM Tris-HCl (pH 7.5), 200 mM NaCl, and 5 μM BSA at 20 °C. The coumarin was excited at 436 nm, and emission was collected through a 455 nm cutoff filter. The fluorescence traces (not shown) were fit to double exponentials for dT₇₀, dT₃₅, and dT₂₇. In the case of dT₇₀, the slow phase was only ∼15% of the total signal at all concentrations, and this phase was not analyzed further. The traces for poly(dT) were well fit by single exponentials. For poly(dT), the DNA concentrations shown are based on the number of SSB binding sites, equivalent to 70-base sections (i.e., corresponding to the SSB binding length). The observed rate constants linearly increased with concentration, giving the following second-order association rate constants. The percentages in parentheses are the relative intensities of the fast and slow phases for double-exponential fits, taking into account the dead time; these were approximately constant as the concentration varied: 642 μM⁻¹ s⁻¹ (∼85%) for dT₇₀ (the slow phase is not shown), 377 μM⁻¹ s⁻¹ (30%) and 73 μM⁻¹ s⁻¹ (70%) for dT₃₅, 370 μM⁻¹ s⁻¹ (50%) and 126 μM⁻¹ s⁻¹ (50%) for dT₂₇, 121 μM⁻¹ s⁻¹ (single-exponential fit) for dT₂₀, and 322 μM⁻¹ s⁻¹ (single-exponential fit) for poly(dT).

Association Kinetics of dT₇₀ with Excess DCC-SSB

Measurements were also taken with a range of concentrations of DCC-SSB in excess over dT₇₀, and the data were fitted with a double exponential (Figure 2). In this case, the data showed a rapid increase in fluorescence, whose concentration dependence gives a second-order rate constant of 582 μM⁻¹ s⁻¹. This was followed by a slow decrease (3.4 μM⁻¹ s⁻¹ with a 1.9 s⁻¹ intercept). The rise seems likely to be due to formation of DCC-SSB·dT₇₀ with a rate constant similar to that found with excess dT₇₀. At high SSB concentrations, formation of (DCC-SSB)₂·dT₇₀ is possible and titration data, albeit at a low salt concentration (17), suggest that this would be accompanied by a decrease in fluorescence, as observed here in the second phase. The kinetics of this phase would then be those for formation of the 2:1 complex, leading to an estimate of 0.6 μM for the K_d from the ratio of rate constants (1.9/3.4). The relative amplitude of this second phase, taking into account the signal lost during the dead time of the stopped-flow instrument, increases with DCC-SSB concentration, from 3% at 125 nM to 25% at 1000 nM. This also suggests that the K_d for the dissociation of (DCC-SSB)₂·dT₇₀ is in the range of concentrations used or higher. Analytical ultracentrifugation (AUC) measurements, described below, were used to provide a measure of this K_d.

Figure 2.

Association kinetics for various lengths of DNA binding to excess DCC-SSB. In each case, the DNA concentration was maintained at 10% of that of DCC-SSB to approximate the pseudo-first-order conditions, while giving a reasonable signal. Solution conditions and wavelengths were as described in the legend of Figure 1. (a) Traces of binding of dT₇₀ to DCC-SSB at the nanomolar concentrations shown (concentrations in the mixing chamber). The inset shows the rapid phase on a short time scale; these data were used to fit a single exponential for this phase. (b) Dependence of rate constants of the fast and slow phases on DCC-SSB concentration. The linear fits gave association rate constants of 582 and 3.4 μM⁻¹ s⁻¹ for dT₇₀, 361 and 12 μM⁻¹ s⁻¹ for poly(dT), and 645 μM⁻¹ s⁻¹ for dT₃₅ (no slow phase). Intercepts of the slow phase with the ordinate are 1.9 s⁻¹ for dT₇₀ and 2.3 s⁻¹ for poly(dT).

Dissociation Kinetics of dT₇₀

We measured these by premixing dT₇₀ with DCC-SSB to make DCC-SSB·dT₇₀ and then rapidly mixing this complex with a large excess of wild-type SSB (wtSSB), which acts as a trap for free ssDNA. Previously, we showed that wtSSB binds dT₇₀ ∼30-fold tighter than DCC-SSB (17) and so should be effective as a trap at high concentrations. In the simplest model, spontaneous dissociation of DCC-SSB·dT₇₀ would be followed by rapid binding to the trap. The observed kinetics of the fluorescence change should reflect the dissociation rate constant and be independent of trap concentration. In practice, there was a decrease in fluorescence with a time course highly dependent on wtSSB concentration (Figure 3a). This is so even at micromolar concentrations of wtSSB, at which the association kinetics are very rapid relative to the dissociation traces here. The curves are biphasic and could well be described by a double exponential, whose rate constants are plotted in Figure 4a as a function of concentration. The linear dependencies suggest two steps in the dissociation mechanism that are both dependent on wtSSB concentration.

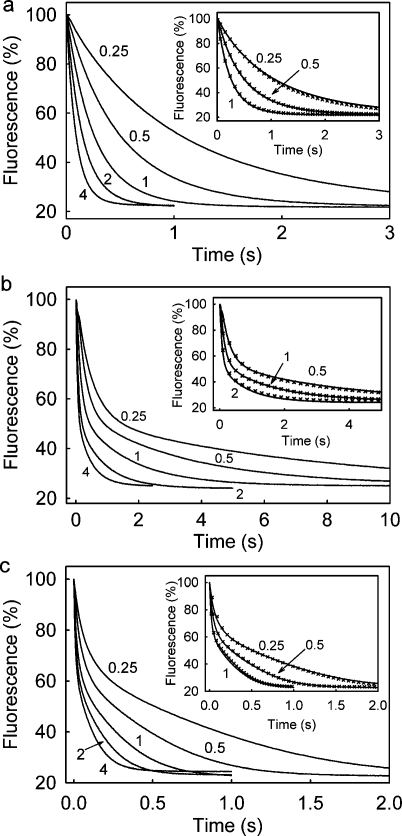
Figure 3.

Dissociation of DNA complexes with DCC-SSB, induced by excess wtSSB. Solution conditions and wavelengths were as described in the legend of Figure 1. Traces are shown with the micromolar concentrations of wtSSB. (a) For dT₇₀, 40 nM DCC-SSB was premixed with 50 nM dT₇₀ (syringe concentrations) and then mixed in the stopped-flow apparatus with wild-type SSB, to give the following mixing chamber concentrations: 0.25−4 μM wtSSB, 20 nM DCC-SSB, and 25 nM dT₇₀. For these conditions, the predominant initial complex should be DCC-SSB·dT₇₀. (b) For dT₃₅, as described for panel a, except 40 nM DCC-SSB was premixed with 100 nM dT₃₅ (syringe concentrations), so the predominant initial complex should be DCC-SSB·(dT₃₅)₂. (c) For poly(dT), as described for panel a, except 40 nM DCC-SSB was premixed with 2.8 μM poly(dT) in terms of bases (syringe concentrations), so that there is one DCC-SSB per 70 bases of poly(dT). Insets show the best fit to the kinetic models, as described in the text and Figure 5. In each case, the model was fitted to the data, measured at 0.5 μM wtSSB, and the other traces were then simulated, changing only the wtSSB concentration.

Figure 4.

Dependence of dissociation kinetics on wtSSB concentration. Data were obtained as described in the legend of Figure 3 and fitted to double exponentials for dT₇₀ and dT₃₅: the two rate constants from these fits were plotted (○ and △, respectively). When equimolar DCC-SSB and dT₃₅ were used, the predominant species should be DCC-SSB·dT₃₅. The fluorescence traces of this experiment are shown in Figure 2 of the Supporting Information. In this case, the rate constants for the predominant amplitude (80%) phase were plotted (◇). The lines are the best linear fits: (○) slope of 3.2 μM⁻¹ s⁻¹ and intercept of 0.9 s⁻¹ and (△) slope of 1.3 μM⁻¹ s⁻¹ and intercept of 0.3 s⁻¹ for DCC-SSB·dT₇₀, (○) slope of 5.6 μM⁻¹ s⁻¹ and intercept of 0.9 s⁻¹ and (△) slope of 0.51 μM⁻¹ s⁻¹ and intercept of 0.02 s⁻¹ for DCC-SSB·(dT₃₅)₂, and (◇) slope of 0.58 μM⁻¹ s⁻¹ and intercept of 0.03 s⁻¹ for DCC-SSB·dT₃₅ (line not shown).

A model was developed to accommodate these data (Figure 5a). The reaction starts with 70-base-bound DCC-SSB·dT₇₀. The addition of a high concentration of wtSSB favors the 35-base binding mode, so step 1 is binding of wtSSB to give DCC-SSB·wtSSB·dT₇₀. This binding is accompanied by a fluorescence decrease, consistent with the observations of the association kinetics with excess DCC-SSB, described above. To accommodate a second process that is dependent on wtSSB concentration, it is assumed that another wtSSB molecule binds (step 2) to give DCC-SSB·wtSSB₂·dT₇₀. Finally, either wtSSB (reverse of step 2) or DCC-SSB dissociates (step 3). This model assumes that both association steps 1 and 2 are much faster than dissociation of DCC-SSB from either DCC-SSB·dT₇₀ or DCC-SSB·wtSSB·dT₇₀, so those dissociations can be ignored at least in the concentration range studied. In practice, the intercepts at zero wtSSB in Figure 4a may indicate that such dissociation occurs at a very slow rate, which would be significant only at very low wtSSB concentrations.

Figure 5.

Schemes used to model the dissociation data with different lengths of ssDNA. Circles around the letter C represent DCC-SSB, empty circles wtSSB, and lines the DNA. Steps are numbered as shown: (a) dT₇₀, (b) dT₃₅, and (c) poly(dT), assuming dT₇₀₀.

The model was fit to the data at 0.5 μM wtSSB. The parameters that came from this best fit were then used to simulate traces at higher and lower concentrations, and these theoretical traces are shown in the insets of Figure 3a. The derived parameters are listed in Table 1, along with practical constraints on the modeling. In practice, the fit was not very dependent on the value of the dissociation rate constant for wtSSB, k₋₂, as long as it was low.

Table 1. Parameters Used To Model the Dissociation of DCC-SSB from Different Lengths of ssDNA, Induced by wtSSB^a.

	dT70	dT35	poly(dT)
fluorescence enhancementb
initial complex	4.5	4.0	4.3
other intermediates	1.6	2.0	2.6
k+1 (μM−1 s−1)	4.9	6.0	42
k+2 (μM−1 s−1)	3.4	0.61	33
k−2 (s−1)c	0.3	0.3	0.3
k+3 (s−1)c	9.7	9.7	9.7

^aThe models are shown in the schemes in Figure 5, and rate constants are defined such that step n has forward and reverse rate constants k_+n and k_−n, respectively.

^bThis ratio is the fluorescence of DNA-bound DCC-SSB relative to that of free DCC-SSB for either the initial complex, bound in the 70-base mode, or all other intermediates in the schemes, which may be in approximately the 35-base mode. The exception was the assumption that DCC-SSB·wtSSB·dT₃₅ had the same fluorescence as free DCC-SSB.

^cThe values for these two rate constants were optimized for the poly(dT) trace and those values fixed for other DNA lengths.

Analytical Ultracentrifugation with dT₇₀

To investigate the presence of different complexes and/or oligomers under different conditions, velocity analytical ultracentrifugation was conducted for various combinations of SSB and dT₇₀ (Figure 6). Except as indicated, the measurements were conducted under high-salt conditions. The sedimentation was followed with time using the absorbance wavelength of coumarin for DCC-SSB or of Cy3 for 5′-Cy3-dT₇₀; this simplifies interpretation because only complexes containing the labeled species were observed. The data were analyzed to give a continuous distribution of absorbance as a function of sedimentation coefficient, and one example of raw data, fit to give a continuous sedimentation coefficient profile, is given in Figure 1 of the Supporting Information. DCC-SSB was used throughout, so that the data would be comparable with that obtained by other techniques in this study.

Figure 6.

Velocity analytical ultracentrifugation of DCC-SSB with dT₇₀ or 5′-Cy3-dT₇₀. The protein distribution was measured, using the absorbance of the fluorophore (see Experimental Procedures and Figure 1 of the Supporting Information for details). The high-salt buffer was as described in the legend of Figure 1, but without BSA. (a) Distribution of sedimentation coefficients, obtained from the absorbance profiles, showing positions for the main species. 5′-Cy3-dT₇₀ was run at 1.5 μM. The other traces have 5 μM DCC-SSB in each run and the micromolar concentration of dT₇₀ as shown. DCC-SSB on its own is labeled -dT₇₀. The curves are normalized to a total intensity of 1 and offset vertically from each other. (b) Variation of sedimentation coefficients for different micromolar concentrations of DCC-SSB with 1.5 μM 5′-Cy3-dT₇₀. The absorbance of Cy3 was measured. The sedimentation coefficients were obtained from the peak maxima. The solid line shows a curve fit, as described in Experimental Procedures, giving a K_d of 1.1 ± 0.40 μM, defining binding of a second DCC-SSB tetramer to DCC-SSB·5′-Cy3-dT₇₀.

5′-Cy3-dT₇₀ on its own gives a peak at 2.2 S (Figure 6a). Interpretation in terms of molecular mass requires several assumptions, including shape and density, and so will be only approximate. In this case, the molecular mass, estimated from the sedimentation data, is 21 kDa, whereas the theoretical value is 22 kDa. DCC-SSB on its own, monitored by the coumarin absorbance, gave almost entirely a single peak with a maximum at 4.3 S (Figure 6a), which gives an estimated molecular mass of 61 kDa compared to the theoretical mass of 77 kDa for the tetramer. There was no sign of a smaller species, for example, monomer or dimer, but a small peak (∼3% of total) at a higher sedimentation coefficient that could be an octamer. In the presence of excess dT₇₀, the main peak was shifted to 5.2 S (estimated to be 91 kDa), consistent with it being the 1:1 complex, tetrameric DCC-SSB·dT₇₀ (theoretical mass of 99 kDa). When the dT₇₀ concentration was lower than the DCC-SSB concentration, generally multiple peaks were observed. At 1.5 μM dT₇₀ and 5 μM DCC-SSB, there were two main peaks, but well separated with maxima at 4.3 and 6.9 S. The second peak (estimated to be 160 kDa) is likely to be due mainly to (DCC-SSB)₂·dT₇₀ (176 kDa).

A series of measurements was taken with 1.5 μM 5′-Cy3-dT₇₀, varying the concentration of DCC-SSB and measuring the Cy3 absorbance. A single main peak was observed (see Figure 1 of the Supporting Information), if DCC-SSB was in excess, but also a second peak due to free DNA was seen, if DNA was in excess. With excess DCC-SSB, the position of the protein-dependent peak varied with concentration, as shown in Figure 6b. This suggests there is rapid exchange between DCC-SSB·5′-Cy3-dT₇₀ and (DCC-SSB)₂·5′-Cy3-dT₇₀, so that a single peak is observed, whose position is a weighted average of the two species (21,22). The variation in position with concentration (Figure 6b) can be fit to give the dissociation constant for a second tetramer bound to the DNA, as described in Experimental Procedures. The model for this fitting assumes that formation of DCC-SSB·5′-Cy3-dT₇₀ is very tight, so that DCC-SSB, at concentrations lower than that of the DNA, is all in the form of DCC-SSB·5′-Cy3-dT₇₀. This gives an estimate of 1.1 ± 0.4 μM for the second dissociation constant of (DCC-SSB)₂·5′-Cy3-dT₇₀.

Measurements with Shorter Oligonucleotides

Oligo(dT) of different lengths was titrated into a solution of DCC-SSB, and the fluorescence emission was measured. Similar titrations of dT₇₀ into a solution of DCC-SSB were reported previously (17). At a high concentration of DCC-SSB (∼250 nM tetramer), the titration showed a linear increase in fluorescence up to a 1:1 complex. At a low concentration (∼2.5 nM), the titration with dT₇₀ gave an approximate assessment of affinity (K_d ∼ 3 nM).

Titrations with dT₃₅ gave the plots in Figure 7a at high DCC-SSB concentrations and Figure 7b at low concentrations. Figure 7a shows two linear increases, with each stage spanning ssDNA addition approximately equimolar with the DCC-SSB. This would be consistent with two-stage tight binding. The first stage is likely to be formation of DCC-SSB·dT₃₅, having a fluorescence 2.1-fold greater than that of free DCC-SSB. The second stage [formation of DCC-SSB·(dT₃₅)₂] gave a fluorescence 5.1-fold greater than that of free DCC-SSB. The titration at 2.5 nM DCC-SSB gave a smaller total fluorescence change, as expected due to the background light scatter, described previously (17). These data at low DCC-SSB concentrations are also consistent with two-stage binding. The first stage could be described as a linear increase until added dT₃₅ was equimolar with DCC-SSB (Figure 7b, inset). The second stage was fitted to a hyperbola to give a K_d value of 29 nM. The total fluorescence change of the second stage [forming DCC-SSB·(dT₃₅)₂] is 2.4-fold greater than that of the first stage stage (forming DCC-SSB·dT₃₅), the same as that in the first titration at a high DCC-SSB concentration (5.1/2.1). Thus, the first dT₃₅ binds much tighter than the second but gives a smaller fluorescence change.

Figure 7.

Titrations of short oligonucleotides into DCC-SSB. (a) dT₃₅ was titrated into a solution of 250 nM DCC-SSB (tetramers) while fluorescence was measured. The data were fit assuming two-stage, tight binding (i.e., linear increases). (b) dT₃₅ was titrated into a solution of 2.5 nM DCC-SSB under the conditions described above. (c) dT₂₇ (◻) and dT₂₀ (○) were titrated into a solution of 2.5 nM DCC-SSB under the conditions described above. The data were fitted to binding equations: a quadratic (23) for the tighter-binding dT₃₅ (data from the breakpoint at 3 nM) to give a K_d of 28 nM and dT₂₇ to give a K_d of 43 nM and a hyperbola for dT₂₀ to give a K_d of 240 nM. All titrations were measured in 25 mM Tris-HCl (pH 7.5), 200 mM NaCl, and 5 μM BSA at 20 °C.

Titrations of dT₂₇ and dT₂₀ at low concentrations of DCC-SSB gave smaller fluorescence changes, and the data were fit to give single K_d values of 43 and 240 nM, respectively (Figure 7c). Titrations were also conducted with these short oligonucleotides at a high DCC-SSB concentration [0.25 μM (data not shown)]. The titration with dT₂₇ is similar to that with dT₃₅, suggesting two molecules can bind to the DCC-SSB tetramer, as might be expected from the similar length. The equivalent titration with dT₂₀ is curved, so it was not possible to determine the stoichiometry from those data. The data are consistent with the affinity of dT₂₇ being not much lower than that of dT₃₅, but dT₂₀ binding is significantly weaker.

Association kinetics were obtained with an excess of dT₃₅, dT₂₇, and dT₂₀. The fluorescence increases (data not shown) were fitted by double exponentials in the first two cases. The small fluorescence changes with dT₂₀ were fitted by single exponentials. The observed rate constants increase linearly with ssDNA concentration (Figure 1). With dT₇₀, described above, the amplitude of the rapid phase is much larger than that of the slow phase, consistent with the major process being the rapid formation of the 1:1 complex. The signals of dT₃₅, dT₂₇, and dT₂₀ presumably reflect the binding of more than one molecule of the oligonucleotides to each SSB tetramer. With dT₃₅, the rapid phase is smaller in amplitude than the slow, by 2.3-fold. This is similar to the relative fluorescence changes found from the titrations described above and is consistent with these kinetic phases representing the same processes as the two stages in the titration, namely, formation of DCC-SSB·dT₃₅ and then DCC-SSB·(dT₃₅)₂.

With all lengths except dT₂₀, the intercept of the concentration dependence of the observed rate constants with the ordinate was too close to zero to obtain a value for the dissociation rate constant. With dT₂₀, the intercept suggests a dissociation rate constant of 49 s⁻¹, producing a value of 396 nM for the equilibrium dissociation constant, 1.6-fold greater than that obtained from the equilibrium titration.

Association kinetics were also measured for dT₃₅ with DCC-SSB in excess (Figure 2). Unlike that with dT₇₀, only a single phase was observed, a rapid rise in fluorescence that is well fit by a single exponential. This would be consistent with formation of only the 1:1 complex under these conditions of excess DCC-SSB. The second-order rate constant is 645 μM⁻¹ s⁻¹, 1.7-fold greater than that obtained with excess dT₃₅.

Dissociation measurements with dT₃₅ were taken as described above for dT₇₀ but starting with an ∼2:1 ratio of DNA to tetramer, so DCC-SSB·(dT₃₅)₂ would be the main species initially. The data show a biphasic decrease in fluorescence with a time course dependent on wtSSB concentration (Figure 3b). The fluorescence traces showed a large rapid decrease in fluorescence followed by a smaller, slow phase and could be well fit by a double exponential. The amplitude of the rapid phase was a constant 1.8-fold greater than that of the slow phase. As observed with dT₇₀, both observed rate constants increased linearly with wtSSB concentration (Figure 4b). A model was used to describe the mechanism, equivalent to that for dT₇₀ (Figure 5b). It was assumed that, after a wtSSB binds to DCC-SSB·(dT₃₅)₂ to give DCC-SSB·wtSSB·(dT₃₅)₂ (step 1) this complex dissociates rapidly (k_+1a ≫ k₊₁[wtSSB]) to DCC-SSB·dT₃₅ and wtSSB·dT₃₅ (step 1a). This dissociation seems likely, both because it accommodates the data, described below, starting from DCC-SSB·dT₃₅, and because it reflects the fact that the 1:1 complex is likely to be the stable species at a high SSB:dT₃₅ ratio. Displacement of DCC-SSB from DCC-SSB·dT₃₅ is assumed to occur via the intermediate formation of DCC-SSB·wtSSB·dT₃₅ (step 2) and then dissociation of this complex (step 3), to explain the observed increase in the rate constant of the second phase with wtSSB concentration (Figure 4b). Although a complex of dT₃₅ with two SSB molecules, DCC-SSB·wtSSB·dT₃₅, is transiently formed in the dissociation experiments, the K_d for binding the second SSB is probably much lower than in the case of dT₇₀, and therefore, the 2:1 complex with dT₃₅, (DCC-SSB)₂·dT₃₅, is not observed in the stopped-flow experiments with excess DCC-SSB (see above). The parameters obtained by fitting the curves in Figure 3b (inset) are listed in Table 1.

To test this model further, equimolar DCC-SSB and dT₃₅ were premixed to form predominantly DCC-SSB·dT₃₅, which was then mixed with a large excess of wtSSB. The fluorescence traces (Figure 2 of the Supporting Information) were analyzed with double exponentials. The rapid phase was much smaller than in the measurement of DCC-SSB·(dT₃₅)₂ dissociation, as shown in Figure 4, 0.27-fold that of the slow phase. The rate constants of the major amplitude were very similar to the equivalent rate constants obtained with DCC-SSB·(dT₃₅)₂. This is consistent with the model in Figure 5b, but mainly starting from DCC-SSB·dT₃₅. The small rapid phase could be due to a small proportion of DCC-SSB·(dT₃₅)₂ at time zero, due to either inaccuracies in concentrations or simply equilibration of the complexes between different ratio species.

Measurements with Poly(dT)

Measurements with longer ssDNAs are potentially more complex to interpret, because there may not be discrete 70- and 35-base binding modes and, therefore, the number of tetramers of SSB, bound along a length of ssDNA, varies. To investigate this aspect, the kinetic measurements were conducted with poly(dT), which is typically >500 nucleotides long.

Association kinetics were obtained with excess poly(dT), in terms of 70-base binding sites, equivalent to those experiments described with excess dT₇₀. Only one phase was observed (data not shown), and the linear fit of the concentration dependence gave a second-order rate constant of 313 μM⁻¹ s⁻¹ (Figure 1). Association kinetics were also measured with DCC-SSB in excess. Two phases were observed, a rapid increase in fluorescence followed by a smaller decrease (Figure 3 of the Supporting Information). The two phases had approximately constant proportions as the concentration of DCC-SSB varied from 100 to 800 nM: the second phase was 35−40% of the first with only a slight increase with concentration, taking into account the fact that the initial part of the fast phase is lost in the dead time of the stopped-flow instrument. Linear fits of the concentration dependence of each phase gave second-order rate constants of 361 and 12 μM⁻¹ s⁻¹. The rapid second-order rate constant is similar to that obtained with excess poly(dT). The intercept of the linear fit to the slow phase at zero DCC-SSB is 2.3 s⁻¹, so that the K_d for the process, represented by this phase, is 0.2 μM. However, this represents a simplified analysis of the data, because each phase presumably represents binding of multiple tetramers along the DNA.

The dissociation kinetics with poly(dT) were measured with a ratio of one DCC-SSB to every 70 bases of poly(dT) and showed a decrease in fluorescence with a time course that was dependent on wtSSB concentration (Figure 3c). The curves showed a rapid, approximately exponential decrease followed by a second, slower decrease, which is reminiscent of a steady-state reaction with gradual depletion of substrate. The model mechanism assumes that dissociation occurs sequentially to replace DCC-SBB with a wtSSB one at a time (Figure 5c). The modeling was done for an ∼700-base length, so 10 DCC-SSB molecules were assumed to be bound in the premix complex. The initial binding of wtSSB to (DCC-SSB)₁₀·poly(dT) gives (DCC-SSB)₁₀·wtSSB₁₀·poly(dT). This was modeled as a single second-order reaction (step 1). This is clearly an oversimplification, so that the rate constant that was obtained is not meaningful per se and will be considered in the Discussion. Also, to keep the model as simple as possible, the next stage is simplified to random binding of one more wtSSB to give (DCC-SSB)₁₀·wtSSB₁₁·poly(dT) (step 2). The new complex can then lose either a single DCC-SSB (step 3) or wtSSB (reverse step 2). This process (steps 2 and 3) is repeated to achieve complete replacement of DCC-SSB with wtSSB. Because of the large excess of wtSSB in the experiment, wtSSB₁₀·poly(dT) is the final product. The parameters obtained by fitting a sequence of curves (Figure 3c inset) are listed in Table 1.

To test this model further, a salt-jump experiment was conducted. At a low salt concentration and a 2:1 ratio of DCC-SSB to 70-base binding sites, there should be a significant proportion of SSB bound in the 35-base binding mode. This ratio of DCC-SSB to poly(dT) was rapidly mixed with excess wtSSB, the latter in a very high salt concentration, so that the mixed solution had the same salt level (200 mM NaCl) as all the previous experiments. Fluorescence traces are shown in Figure 4 of the Supporting Information. The major feature is the absence of the rapid phase, seen in Figure 3c, supporting the idea that this phase represented binding of wtSSB to give 35-base binding. Qualitatively, the rest of the traces in Figure 4 of the Supporting Information are similar to Figure 3c, although the initial part of the time course appears to contain a minor, complex feature. The time scales are slightly different, and this may reflect the different details of the initial complex (all DCC-SSB) and experimental design.

Measurements at Low Salt Concentrations

Measurements were taken, particularly with dT₇₀, at 20 mM NaCl rather than 200 mM NaCl. Previous work has suggested that a low salt concentration favors formation of complexes with 35-base binding (1,10). In this case, formation of (DCC-SSB)₂·dT₇₀ is favored, but as described above, this complex has a lower fluorescence per SSB than DCC-SSB·dT₇₀.

Association kinetics with excess dT₇₀ (Figure 5a of the Supporting Information) were similar to those at high salt concentrations with a second-order rate constant of 880 μM⁻¹ s⁻¹. If there was excess DCC-SSB, the traces were qualitatively similar to those at high salt concentrations: a very rapid increase in fluorescence was followed by a slow decrease (Figure 5b of the Supporting Information). The rapid increase gave a high second-order rate constant of 1.1 nM⁻¹ s⁻¹. The rate constants of the slow phase are significantly higher than at high salt concentrations.

Dissociation kinetics were also measured and gave biphasic traces, qualitatively similar to those at high salt concentrations but with a much faster first phase (Figure 5c of the Supporting Information). In this case, a further test could be performed, by starting from a 2:1 DCC-SSB:dT₇₀ ratio, so the main species should be (DCC-SSB)₂·dT₇₀ under these low-salt conditions. These traces were monophasic and had rate constants similar to those of the slow phase of the dissociation of DCC-SSB·dT₇₀. This provides support for the model depicted in Figure 5a.

A series of analytical ultracentrifugation measurements were taken as described above but at low salt concentrations, and the data were analyzed to give continuous distributions. Cy3-dT₇₀ and DCC-SSB had very similar sedimentation coefficients as they did at high salt concentrations, but complexes at different DCC-SSB concentrations and a constant Cy3-dT₇₀ concentration of 1.5 μM showed separate, overlapping peaks for each species (data not shown). By an ∼2:1 DCC-SSB:Cy3-dT₇₀ ratio, almost all the Cy3 was giving a peak at 7.4 S, consistent with tight binding of the second tetramer with relatively slow exchange.

Association kinetics were also measured with poly(dT) at 20 mM NaCl. As described above for dT₇₀, the rates were somewhat higher than at high salt concentrations (Figure 5a,b of the Supporting Information).

Discussion

The data described in this work were aimed at providing a self-consistent kinetic mechanism and set of affinities for the interaction of ssDNA with SSB. To achieve this, DCC-SSB was used throughout and measurements were performed with different lengths of oligo(dT). Previous work showed that the labeling produced an ∼30-fold decrease in affinity at high salt concentrations (17).

The conditions used to measure association kinetics with excess DNA are likely to result in largely 70-base binding, whatever the length of DNA and whatever the salt conditions. However, results with dT₇₀ at high salt concentrations will be discussed first. The second-order rate constant for association suggests that the process may be diffusion-controlled (13). The first binding event is likely to be followed by rapid wrapping of the DNA within the binding channel as described previously (15).

At high SSB and low DNA concentrations, association of a second tetramer occurs to give the 35-base binding mode (DCC-SSB)₂·dT₇₀. This was demonstrated by measuring the fluorescence following mixing of dT₇₀ with excess DCC-SSB (Figure 2). After the rapid increase in fluorescence, probably representing formation of DCC-SSB·dT₇₀ and with a rate constant similar to that when DNA was in excess, there is a much slower decrease in fluorescence (3.4 μM⁻¹ s⁻¹), consistent with formation of (DCC-SSB)₂·dT₇₀. The rate constant for binding the second tetramer to DCC-SSB·dT₇₀ is 2 orders of magnitude slower than the binding of the first, as the second tetramer has partially to displace the first. This second binding event could occur via free ends of the dT₇₀, i.e., a few nucleotides at either end that remained unbound to the first tetramer. Alternatively, the second tetramer could bind to ends when they separate from the binding site. In the latter case, it might be supposed that the extent of separation is low, and if <1% of ends were sufficiently free at any time to bind a second tetramer, this would give rise to the observed slower association rate constant. A third possibility for binding the second tetramer is that interaction between tetramers plays a significant role. In any of these routes, the (DCC-SSB)₂·dT₇₀, formed initially, would then presumably rearrange to produce equal binding of each tetramer.

The AUC measurements gave direct support to this association measurement with excess DCC-SSB being due to formation of (DCC-SSB)₂·dT₇₀. The ratio of rate constants derived from the kinetic measurements gives a K_d (0.6 μM) similar to the value obtained from the AUC titration (1.1 μM) of formation of a complex with the correct molecular mass for (DCC-SSB)₂·dT₇₀.

The dissociation kinetics of DCC-SSB·dT₇₀ were measured by mixing this preformed complex with a large excess of wtSSB to act as a trap (Figure 3a). The main feature is that, even at several micromolar wtSSB concentrations, the observed rates increase with wtSSB concentration. In practice, the fluorescence traces are biphasic and need a relatively complex, association−association−dissociation model (Figure 5) to explain them for different lengths of ssDNA. In this model, the first phase of the fluorescence traces corresponds mainly to formation of DCC-SSB·wtSSB·dT₇₀ and has kinetics [4.9 μM⁻¹ s⁻¹ (Table 1)] similar to that for formation of (DCC-SSB)₂·dT₇₀, suggested in the slow phase of Figure 2a (3.4 μM⁻¹ s⁻¹). The intercept with the ordinate in Figure 4a suggests that the rate constant for spontaneous breakdown of DCC-SSB·dT₇₀ is at most 0.9 s⁻¹. The second phase, with a rate also dependent on wtSSB concentration, can be explained, if there is transient formation of DCC-SSB·wtSSB₂·dT₇₀ and this pathway is favored over direct breakdown of DCC-SSB·wtSSB·dT₇₀. The rate constant suggested for breakdown of (DCC-SSB)₂·dT₇₀ from the intercept in Figure 2b is 1.9 s⁻¹, so the rate constant for loss of one particular tetramer would be ∼1 s⁻¹. The observed rate constants of the slower phase for the proposed, favored pathway of dissociation (Figure 4a) increase from 0.3 s⁻¹, which is the intercept at zero wtSSB and is likely to represent the spontaneous breakdown of DCC-SSB·wtSSB·dT₇₀, if no further wtSSB binds. This difference in rate constants may simply be due to the effect of the wild type as opposed to the labeled mutant.

Simulations of the dissociation traces at extremes of concentrations were not used to fit to the model, as other mechanisms may become significant. At low wtSSB concentrations, spontaneous dissociation will contribute. At high SSB concentrations, a change in the dissociation mechanism, e.g., a change in the rate-limiting step, might be responsible for the deviation from the model. While the two rate constants of double-exponential fits exhibited a linear dependence on SSB in the concentration range shown in Figure 4, a hyperbolic behavior was observed at higher SSB concentrations (data not shown). This indicates that a unimolecular step is rate-limiting at higher concentrations. This step could be a conformational change or, more likely, a rearrangement of SSB on the DNA.

The interaction of DCC-SSB with shorter lengths of DNA was examined to obtain extra information about the general mechanism, but also to assess how the interaction with SSB varies with DNA length. On the basis of the titrations, binding remains tight as the length decreases and only becomes significantly weaker as the length decreases to dT₂₀. The association kinetics with excess DNA give a similar rate constant for the binding of the first dT₃₅ or dT₂₇. For these conditions, presumably a second molecule of DNA binds, corresponding to the slow phase (Figure 1). The rate constants obtained for these short lengths are similar to that obtained previously, for slightly different conditions (13).

The dissociation kinetics with dT₃₅ indicate that a mechanism occurs with two association steps, similar to that for dT₇₀. For measurements starting from DCC-SSB·(dT₃₅)₂, the first phase is binding a single wtSSB with kinetics similar to those observed with dT₇₀. This is consistent with the idea of “fraying ends” to the bound DNA providing a site for wtSSB to bind; albeit, there are four DNA ends in the initial complex DCC-SSB·(dT₃₅)₂. The extent of this fraying might be independent of DNA length. Once DCC-SSB·wtSSB·(dT₃₅)₂ is formed, it seems likely that it dissociates rapidly to DCC-SSB·dT₃₅ and wtSSB·dT₃₅ (step 1a of Figure 5b). The second phase of the dissociation fluorescence trace is 5-fold slower with dT₃₅ than with dT₇₀, presumably consistent with insufficient space on dT₃₅ for tight binding of two SSBs. An AUC measurement at 1.5 μM 5′-Cy3-dT₃₅ and 5 μM DCC-SSB showed no indication of formation of any DCC-SSB₂·Cy3-dT₃₅ (data not shown), suggesting that the complex with two SSBs may form only transiently during the dissociation. In a comparison of the situation with Cy3-dT₇₀, most DNA has two SSBs bound at these concentrations (Figure 6b).

We can now consider how to relate the measurements with dT₇₀ with those of poly(dT). The association measurements for the two lengths show rather little difference when the ssDNA is in excess. This might be expected as DCC-SSB would not be tightly packed along the poly(dT), so each tetramer could act independently. The association rate constants are similar (Figure 1) and may be diffusion-controlled. However, with DCC-SSB in excess, the DNA must be completely packed with tetramers. This is not reflected in any alteration in the first-phase kinetics: they are similar to those with DNA in excess and to those with dT₇₀ (Figure 2b). The second phase with excess DCC-SSB binding to poly(dT) is ∼3-fold faster than that phase with dT₇₀. This is a relatively small difference and might be simply due to the ability of multiple tetramers along a single DNA to rearrange and so provide new sites for extra DCC-SSB.

The fluorescence traces for dissociation of DCC-SSB from poly(dT) (Figure 3c) suggest a multistep process, and the model in Figure 5c tries to address that in a way analogous to the model for dT₇₀ (Figure 5a), i.e., an association−association−dissociation mechanism. The rate constants that come out of this model are very different from those for the short DNA (Table 1).

This model for dissociation from poly(dT) (Figure 5c) has been kept simple so that it can be tractable for data fitting. The data do not have the detail to help distinguish different, more complex models. In particular, step 1 [(DCC-SSB)₁₀·poly(dT) to (DCC-SSB)₁₀·wtSSB₁₀·poly(dT)] is considered as a single, second-order reaction with a fitted rate constant of 42 μM⁻¹ s⁻¹. In practice, this process must have multiple steps. Therefore, to mimic this initial step 1, a 10-step reaction was simulated with one wtSSB binding in each step and so causing one DCC-SSB to change to the 35-base binding mode with concomitant lower fluorescence. It was assumed that addition of each wtSSB became slower as the ssDNA became more packed. The first wtSSB bound at 400 μM⁻¹ s⁻¹, similar to the kinetics observed for association from Figures 1 and 2. There is an arbitrary 10% (i.e., 40 μM⁻¹ s⁻¹) linear decrease in rate constant for each subsequent binding step, so the 10th binding step is at 40 μM⁻¹ s⁻¹. Note that this final rate constant is similar to the rate constant for the binding of the 11th wtSSB (step 2 in Figure 5c) from fitting the whole model (Table 1). Simulating this model at each wtSSB concentration gave transient decreases in fluorescence that could be fit well by a single exponential with observed rate constants of 9.8 s⁻¹ at 250 nM wtSSB, 19.8 s⁻¹ at 500 nM wtSSB, and 39.7 s⁻¹ at 1000 nM wtSSB. The concentration dependence of these transient fits gave a second-order rate constant of 40 μM⁻¹ s⁻¹, similar to the value of 42 μM⁻¹ s⁻¹ from the modeling of the complete fluorescence traces (Table 1). In practice, step 1 of the model is closely associated with the initial fluorescence decrease observed experimentally during the dissociation (Figure 3c). Thus, this type of multistep mechanism could model this rapid decrease in fluorescence.

It is noticeable that there is a significant difference between the observed rate constant for the second phase of association with excess DCC-SSB [12 μM⁻¹ s⁻¹ (Figure 2b)] and the first phase of the dissociation [42 μM⁻¹ s⁻¹ (Figure 3c)]. Although these phases represent similar processes, packing in “extra” SSB molecules, the associating protein is DCC-SSB in one case and wtSSB in the other, and the rate constants may differ for the two forms of SSB. This possibility seems unlikely as the two equivalent rate constants with dT₇₀, discussed above, are similar (3.4 μM⁻¹ s⁻¹ from association kinetics with excess DCC-SSB and 4.9 μM⁻¹ s⁻¹ from dissociation kinetics using wtSSB as a trap). An alternate explanation is that, because any plausible model for this extra binding to poly(dT) includes multiple steps, differences in fluorescence change for each step between the two cases, DCC-SSB and wtSSB binding, may result in a significant difference between the apparent rate constant for the whole multistep process.

These data, taken together, demonstrate that the model in Figure 5c is feasible for long lengths of ssDNA. None of the data presented here require significant cooperativity to explain the data observed. Indeed, the association data are similar to those with dT₇₀, and modeling of the dissociation data, described above, includes the idea that packing extra SSB tetramers along ssDNA becomes slower as more molecules bind.

Some measurements were taken at low salt concentrations, at which 35-base binding is favored (1,10). Association kinetics are generally faster than at high salt concentrations. Rate constants are only slightly faster for formation of the 1:1 complex, but the association of a second SSB (wild type or DCC-labeled), to form a 2:1 complex, is greatly accelerated, evident from the second phase of association kinetics with excess DCC-SSB as well as dissociation kinetics with excess wtSSB. This is consistent with the AUC measurements, which also confirm that a low salt concentration favors 35-base binding mode and suggests that the higher affinity of the complex is at least in part due to faster association of the second SSB.

Estimates of the SSB concentration in bacterial cells range from 0.05 to 0.3 μM (2,13), although to determine the rate of processes involving SSB, the concentration of free SSB is the significant value. However, on the basis of the data presented here, this concentration in the cell spans the range over which there would be transition between 35-base and 70-base binding on ssDNA. In addition, the rate of binding free SSB might control the rate of SSB dissociation, and therefore rearrangement, along DNA. As outlined in the introductory section, SSB potentially interacts with a wide range of proteins that process DNA so the movement and rearrangement of SSB are likely to be complex. However, the sort of mechanism described here might aid the displacement, movement, and rearrangement of SSB by processing proteins that are binding to ssDNA itself or translocating on ssDNA.

Supporting Information Available

An example of analytical ultracentrifugation data and extra kinetic data. This material is available free of charge via the Internet at http://pubs.acs.org.