Adjusting O'Brien's Test to Control Type I Error for the Generalized Nonparametric Behrens–Fisher Problem

Summary

O'Brien (1984, Biometrics 40, 1079–1087) introduced a simple nonparametric test procedure for testing whether multiple outcomes in one treatment group have consistently larger values than outcomes in the other treatment group. We first explore the theoretical properties of O'Brien's test. We then extend it to the general nonparametric Behrens–Fisher hypothesis problem when no assumption is made regarding the shape of the distributions. We provide conditions when O'Brien's test controls its error probability asymptotically and when it fails. We also provide adjusted tests when the conditions do not hold. Throughout this article, we do not assume that all outcomes are continuous. Simulations are performed to compare the adjusted tests to O'Brien's test. The difference is also illustrated using data from a Parkinson's disease clinical trial.

1. Introduction

Parkinson's disease is one of the most common adult-onset neurodegenerative disorders. In recent years there has been an intensive search for neuroprotective therapies that can slow, stop, or reverse the degenerative process. A multicenter controlled clinical trial of Coenzyme Q₁₀ in early Parkinson's disease (QE2 trial) organized by the University of California, San Diego, in conjunction with the Parkinson Study Group was a study to determine whether Coenzyme Q₁₀ could slow the functional decline in Parkinson's disease (Shults et al., 2002). Multiple outcomes were collected to measure the disability. These included the mental (mentation), motor, and average daily living (ADL) subscales of the Unified Parkinson's Disease Rating Scale (UPDRS), and the Schwarb and England ADL (SEADL) score. The changes from baseline to the last visit in 16 months of these outcomes were used to compare the treatments.

Various multivariate tests have been proposed to compare two groups with multivariate outcomes. To list a few, there are the global statistical tests given by O'Brien (1984), Tang, Gnecco, and Geller (1989), Tang, Geller, and Pocock (1993), Tang and Lin (1997), Tang and Geller (1997), Lefkopoulou, Moore, and Ryan (1989), Lefkopoulou and Ryan (1993), and Pocock, Geller, and Tsiatis (1987), and nonparametric multivariate methods by Puri and Sen (1985). Most of these tests are derived under the null hypothesis that the outcome distributions from the two comparison groups are identical. Such a condition of identical distribution functions insures that the proposed test is distribution-free under the null hypothesis. This assumption is imposed for mathematical convenience because it allows the formulation of an exact significance level (α) critical region for the test. However, this assumption is not appropriate in the QE2 study. For example, a test of equal variance in mental score between the placebo group and the treatment group gives a p value of 0.002 (see details in Section 4). Ignoring unequal variance using conventional tests such as Hotelling's T² test or multivariate Wilcoxon test can result in a biased inference.

Pratt (1964) and Van der Vaart (1961) have studied how type I errors of Mann–Whitney–Wilcoxon and the normal scores tests are affected by the different distribution shapes or variances of the two treatment groups. Miller (1986) discussed how type I error of a t-test is affected by the unequal variance. A general nonparametric problem of comparing two groups without the assumption for the shapes of their distributions is called a nonparametric Behrens–Fisher problem that has been studied as early as 1963 by Potthoff. Fligner and Policello (1981) and Fligner and Rust (1982) provided nonparametric tests to compare medians. Recent work includes Troendle's (2002) numerical likelihood ratio test, Brunner, Munzel, and Puri's test (1999), and Munzel and Tamhane's test (2002) for a univariate outcome, and Brunner, Munzel, and Puri's (2002) test for multivariate outcomes. For multivariate outcomes, Brunner et al. (2002) proposed Wald-type and ANOVA-type tests for the general nonparametric Behrens–Fisher hypothesis problem with null hypothesis of the form

$${\mathrm{H}}_0:p_v=P(X_{iv}<Y_{jv})+\frac{1}{2}P(X_{iv}=Y_{jv})=\frac{1}{2},v=1,\dots ,k,$$ (1)

where X_iv and Y_jv are the vth outcome from the ith subject in group 1 and the jth subject in group 2, respectively (v = 1, …, k). Parameter p_v was called relative treatment effect for the vth outcome by Brunner et al. (2002).

In Parkinson's disease clinical trials, the goal is often to test whether one treatment is more effective than the other treatment on multiple outcomes. The null hypothesis is that the two treatments are equally effective. The alternative is that one treatment is preferred over the other treatment. Similar to Hotelling's T² test, Wald-type and ANOVA-type tests proposed by Brunner et al. (2002) assess whether two treatment groups differ. The null hypothesis can be rejected if a treatment greatly improves some outcomes and also greatly worsens some other outcomes at the same time. O'Brien (1984) proposed a simple rank-sum-type test to assess whether outcome measures from one group are consistently larger than outcome measures from the other group. Hence, O'Brien's test is appropriate to use under such a setting.

Adjusting for covariates in a nonparametric Behrens–Fisher problem is challenging, especially when covariates are continuous. When all covariates are categorical (or ordinal) with finite number of possible values, there are at most a finite number of covariate value combinations. If we introduce several dependent variables, one for each combination of the covariate values, then the original hypothesis testing problem can be reformulated as a multivariate hypothesis testing problem without any covariate. The split-plot factorial designs considered by Brunner et al. (1999) are one example of such a setting. Because O'Brien's test uses rank-sums, the multivariate problem is reduced to a univariate problem. When sample size is large, the correlation among rank-sums becomes small. Another advantage of O'Brien's test is that it is relatively easy to extend to cases with both continuous and categorical covariates and repeated measures. O'Brien (1984) also showed that the rank-sum-type test is robust when the sample size is smaller than the number of outcomes and when the distribution is skewed or there are outliers. Sankoh et al. (1999) also evaluated the performance of O'Brien's test under various covariance structures through simulation.

O'Brien's rank-sum-type test is being widely used in clinical research including studies in neurology, HIV, cancer, health services, psychiatry, and autoimmune disease. For example, it was used in a randomized clinical trial in dermatology (Kaufman et al., 1998); a randomized trial in multiple sclerosis (Li, Zhao, and Paty, 2001); an observational study comparing women with and without perimenstrual asthma (Shames et al., 1998); and for the secondary analyses of data from a series of rheumatoid arthritis clinical trials (Tilley et al., 2000). Irrespective of its numerous applications in medical research, the properties of O'Brien's rank-sum-type test have been investigated primarily through simulations. The theoretical justification for the test has not been established.

The major goal of this article is twofold: We first derive the theoretical properties of O'Brien's rank-sum-type test. This provides the necessary foundation to use O'Brien's rank-sum-type test and to understand its limitations. In Section 2, we demonstrate that the rank-sum-type test is neither distribution-free nor asymptotically distribution-free for testing the general Behrens–Fisher hypothesis problem (1). Simulations in Section 3 show that for both large and small samples, the actual significance level of O'Brien's rank-sum-type test can exceed the nominal level when the means are the same but the variances from both samples differ. We then provide an adjustment of O'Brien's test so that its use can be extended to the general Behrens–Fisher hypothesis problem. Although O'Brien (1984) considered only continuous distributions, the results presented in this article do not require all outcomes to be continuous. Section 2 gives the asymptotic properties of O'Brien's test. We provide conditions when O'Brien's test controls the type I error probability asymptotically and when it fails. Based on a consistent estimate for the variance of O'Brien's test, we propose a modified test that controls the significance level when the conditions do not hold. The new test reduces to O'Brien's test when the conditions hold. Section 3 compares the type I errors of O'Brien's test and our modified test numerically through simulation. In Section 4, we illustrate the difference of these tests using data from a Parkinson's disease clinical trial.

2. Notation and Asymptotic Distribution

Consider a randomized clinical trial, with m independent subjects randomized to treatment 1 (say, the placebo), and n independent subjects randomized to treatment 2 (say, the new treatment). Suppose there are k different outcomes of interest. Outcomes are coded such that larger (or smaller) values are preferred for all outcomes. Let X_i = (X_i1, …, X_ik) be the multiple outcomes from subject i in treatment group 1 (i = 1, …, m), and let Y_i = (Y_j1, …, Y_jk) be the multiple outcomes from subject j in treatment group 2 (j = 1, …, n). Suppose the X_i's are independent and identically distributed, with joint cumulative distribution function F(t₁, …, t_k) = P(X_i1 ≤ t₁, …, X_ik ≤ t_k), and the Y_j's are independent and identically distributed, with joint cumulative distribution function G(t₁, …, t_k) = P(Y_j1 ≤ t₁, …, Y_jk ≤ t_k). Denote θ_v = P(X_iv < Y_jv) − P(X_iv > Y_jv) for v = 1, …, k, and the middistribution functions $F_u^o\left(t\right)=P\left(X_u<t\right)+\frac{1}{2}P(X_u=t)$, and $G_u^o\left(t\right)=P\left(Y_u<t\right)+\frac{1}{2}P(Y_u=t)$ for u = 1, …, k. Throughout the article, we impose some regularity conditions on the outcomes to rule out degenerate distributions and redundant parameters: $\mathrm{Var}\left[G_v^o\left(X_v\right)\right]>0$ and $\mathrm{Var}\left[F_v^o\left(Y_v\right)\right]>0$ for all v = 1, …, k. An equivalent form of null hypothesis (1) is

$${\mathrm{H}}_0:{\theta }_1=\cdots ={\theta }_k=0.$$ (2)

Note, when all outcomes are continuous, (2) reduces to the simpler hypothesis form of ${\mathrm{H}}_0:P\left(X_{iv}<Y_{jv}\right)=\frac{1}{2}$, v = 1, …, k.

Let N = m + n be the total number of observations in the sample. For the vth outcome (v = 1, …, k), we rank the observations from all N subjects X_1v, …, X_mv, and Y_1v, …, Y_nv, regardless of treatment. Let R_x,iv = midrank (X_iv), and R_y,jv = midrank (Y_jv). The midrank of an observation is defined by either the regular rank when there is no tie on the observation or the average rank among the tied observations (Lehmann, 1975). The total rank from the ith individual in treatment group 1 is defined as the sum of the ranks over all k outcomes: $R_{xi}={\Sigma }_{v=1}^k{R}_{x,iv}$. Similarly, the total ranks from the jth individual in treatment group 2 is defined as $R_{yj}={\Sigma }_{v=1}^k{R}_{y,jv}$. O'Brien's (1984) rank-sum-type test ψ₁ is defined as the regular univariate two-sample t-test with pooled standard deviation for the two rank-sum samples: R_x1, R_x2, …, R_xm and R_y1, R_y2, …, R_yn. In particular, O'Brien's test statistic can be written as

$$T_1=\frac{{\stackrel{‒}{R}}_y-{\stackrel{‒}{R}}_x}{\widehat{\sigma }\sqrt{(1∕m+1∕n)}},$$ (3)

or, if there is concern about possible unequal variances of the ranks, Welch-modified two-sample t-test statistic can be used

$$T_2=\frac{{\stackrel{‒}{R}}_y-{\stackrel{‒}{R}}_x}{\sqrt{{\widehat{\sigma }}_x^2∕m+{\widehat{\sigma }}_y^2∕n}},$$ (4)

where ${\stackrel{‒}{R}}_x={\Sigma }_{i=1}^m{R}_{xi}∕m$, ${\stackrel{‒}{R}}_y={\Sigma }_{j=1}^n{R}_{yj}∕n$, ${\widehat{\sigma }}_x^2=(1∕m-1)\times {\Sigma }_{i=1}^m{(R_{xi}-{\stackrel{‒}{R}}_x)}^2$, ${\widehat{\sigma }}_y^2=(1∕n-1){\Sigma }_{j=1}^m{(R_{yj}-{\stackrel{‒}{R}}_y)}^2$, and ${\widehat{\sigma }}^2=(m-1){\widehat{\sigma }}_x^2+(n-1){\widehat{\sigma }}_y^2∕m+n-2$. O'Brien's test ψ_l rejects H₀ at significance level α whenever T_ℓ > t_df,α or T_ℓ < −t_df,α (ℓ = 1, 2) for two different one-sided alternatives, respectively; or it rejects H₀ whenever |T_ℓ| > t_df,α/2 for a two-sided alternative, where t_df,α is the (1 − α)th percentile of the t_df distribution with df degrees of freedom. Here, df = N − 2 when l = 1 and df = [ζ²/(m − 1) + (1 − ζ)²/(n − 1)]⁻¹ when l = 2, $\zeta =({\widehat{\sigma }}_x^2∕m)∕({\widehat{\sigma }}_x^2∕m+{\widehat{\sigma }}_y^2∕n)$. Theorem 1 gives the asymptotic distribution of statistics T₁ and T₂ under the null hypothesis (2):

Theorem 1

Suppose m/n → λ as N = (m + n) → ∞ for some finite constant 0 < λ < +∞. Then, under the null hypothesis (2), both statistics T₁ and T₂ defined by (3) and (4) converge in distribution to a normal distribution with mean 0 and variances h₁ and h₂, respectively, as N → ∞, where

$$\begin{array}{c}\hfill h_1=\frac{\sum _{u=1}^k\sum _{v=1}^k{(1+\lambda )}^2(a_{uv}+b_{uv}\lambda )}{\sum _{u=1}^k\sum _{v=1}^k\left[e_{uv}{\lambda }^3+(b_{uv}+2f_{uv}){\lambda }^2+(a_{uv}+2q_{uv})\lambda +p_{uv}\right]}\hfill \\ \hfill h_2=\frac{\sum _{u=1}^k\sum _{v=1}^k{(1+\lambda )}^2(a_{uv}+b_{uv}\lambda )}{\sum _{u=1}^k\sum _{v=1}^k\left[b_{uv}{\lambda }^3+(e_{uv}+2q_{uv}){\lambda }^2+(p_{uv}+2f_{uv})\lambda +a_{uv}\right]}\hfill \\ \hfill a_{uv}=\mathrm{cov}\left(G_u^o\left(X_u\right),G_v^o\left(X_v\right)\right),\hfill \\ \hfill b_{uv}=\mathrm{cov}\left(F_u^o\left(Y_u\right),F_v^o\left(Y_v\right)\right),\hfill \\ \hfill e_{uv}=\mathrm{cov}\left(F_u^o\left(X_u\right),F_v^o\left(X_v\right)\right),\hfill \\ \hfill f_{uv}=\mathrm{cov}\left(F_u^o\left(X_u\right),G_v^o\left(X_v\right)\right),\hfill \\ \hfill p_{uv}=\mathrm{cov}\left(G_u^o\left(Y_u\right),G_v^o\left(Y_v\right)\right),\mathrm{and}\hfill \\ \hfill q_{uv}=\mathrm{cov}\left(G_u^o\left(Y_u\right),F_v^o\left(Y_v\right)\right).\hfill \end{array}$$ (5)

Proof of Theorem 1 is given in the Appendix. Simple algebra shows that h₁ = h₂ = 1 when F = G. This establishes the asymptotic validity of O'Brien's rank-sum-type test for the null hypothesis of type H₀ : F = G In general, we have h₁ ≠ 1 and h₂ ≠ 1 when F ≠ G.

To extend the use of O'Brien's rank-sum-type test for the general Behrens–Fisher null hypothesis problem (1), we first note that the null hypothesis assumption of (2) may not imply F = G. There are families of distributions satisfying (2) but with quite different underlying distributions, e.g., equal medians, but unequal dispersion. If all outcomes have arbitrary nondegenerative symmetric distributions around zero: P(X_v ≤ −t) = P(X_v ≥ t), P(Y_v ≤ −t) = P(Y_v ≥ t) (v = 1, …, k), then the parameters θ_v = P(X_v < Y_v) − P(X_v > Y_v) = 0 for all v = 1, …, k. However, F and G can still be quite different in their shapes. Hence, O'Brien's rank-sum-type test ψ₁ or ψ₂ is neither distribution-free nor asymptotically distribution-free under the null hypothesis of the general Behrens–Fisher problem (1). The following simple example shows how h₁ and h₂ depend on the underlying distribution.

Example

Suppose X_i1, …, X_ik are independent, identically distributed with Uniform (−1, 1) distribution, and the Y_j1, …, Y_jk are independent but not identically distributed, Y_ju ~ Uniform(−r_u,r_u), (u = 1, …, k). Let m=n. Note that E(X_iu) = E(Y_ju) = θ_u = 0, but Var(X_iu) = 1/3 and $\mathrm{Var}\left(Y_{iu}\right)=r_u^2∕3$. Then, the h₁ and h₂ in Theorem 1 are

$$h_1=h_2=\frac{\sum _{u=1}^{k}4\left(r_u^2+\frac{1}{r_u^2}\right)}{\sum _{u=1}^k(1+r_u^2){\left(1+\frac{1}{r_u}\right)}^2}.$$

Thus, for uniform distributions, h₁ ≥ 1 and h₂ ≥ 1 for all r_u > 0 (u = 1, …, k), and h₁ = h₂ = 1 if and only if r₁ =…= r_k = 1 which is the same as F = G. O'Brien's (1984) simulations considered only a special case of F = G; under this condition, h₁ and h₂ are reduced to 1. Hence, his simulations demonstrated a proper control of the type I probabilities. Our simulation in Section 3 shows that significance levels of ψ₁ and ψ₂ may not be preserved both for small and large sample size when distributions from the treatment groups have different shapes.

It is seen that h₁ and h₂ are functions of the dependence of the k outcomes. Since the t distribution converges asymptotically to a standard normal distribution when N → ∞, the type I error of O'Brien's test ψ₁ converges to Φ(−z_α/[h₁]^1/2) for one-sided alternatives, and converges to 2Φ(−z_α/2/[h₁]^1/2) for two-sided alternatives, where Φ(·) is the cumulative distribution function of the standard normal distribution, and z_α is defined by Φ(z_α) = 1 − α. Similar results hold for test ψ₂. Theorem 1 shows that, for any 0 < α < 0.5, O'Brien's test ψ₁(or ψ₂) controls its type I error asymptotically if and only if h₁ = 1 (or h₂ = 1). Thus O'Brien's test inflates the type I error asymptotically when h₁ > 1 (or h₂ > 1), and is too conservative when h₁ < 1 (or h₂ < 1).

Based on Theorem 1, a direct adjustment to O'Brien's tests ψ₁ and ψ₂ is to modify their test statistics in (3) and (4) by using some consistent estimates of h₁ and h₂ in the denominators, i.e.,

$$T_{1a}=\frac{{\stackrel{‒}{R}}_y-{\stackrel{‒}{R}}_x}{\widehat{\sigma }\sqrt{{\widehat{h}}_1(1∕m+1∕n)}},T_{2a}=\frac{{\stackrel{‒}{R}}_y-{\stackrel{‒}{R}}_x}{\sqrt{{\widehat{h}}_2({\widehat{\sigma }}_x^2∕m+{\widehat{\sigma }}_y^2∕n)}},$$ (6)

respectively, where ${\widehat{h}}_{\ell }$ is a consistent estimate of h_ℓ under general distribution functions F and G; and let the adjusted statistic T_la take the same degrees of freedom as that of T_l (ℓ = 1, 2). The resulting adjusted tests are denoted as ψ_1a and ψ_2a. Consistent estimates of h₁ and h₂ can be obtained by using empirical estimates of F and G. Define the midranks R_y(x_iu) = the midrank of x_iu among {x_iu, y_1u, …, y_nu}; R_x0(x_iu) = the midrank of x_iu among {x_1u, …, x_mu}; R_x(y_iu) = the midrank of y_iu among {y_iu, x_1u, …, x_mu}; and R_y0(y_iu) = the midrank of y_iu among {y_1u, …, y_nu}. Let A₁ and A₂ be two m × k matrices with (i, u) elements $\{2R_y\left(x_{iu}\right)-2-n+n{\widehat{\theta }}_u\}$ and {2R_x0(x_iu) − 1 − m}, respectively; and let B₁ and B₂ be two n × k matrices with (i, u) elements $\{2R_x\left(y_{iu}\right)-2-m-m{\widehat{\theta }}_u\}$ and {2R_y0(y_iu) − 1 − n}, respectively, where ${\widehat{\theta }}_u={\Sigma }_{i=1}^m{\Sigma }_{j=1}^n\{I\left[\left(x_{iv}<y_{jv}\right)\right]-I\left[\left(x_{iv}>y_{jv}\right)\right]\}∕\left(mn\right)$ which is an unbiased estimate of θ_u. The indicator I[E] is defined by I[E] = 1 if event E is true, and I[E] = 0 otherwise. We define

$$\begin{array}{cc}\hfill & {\widehat{h}}_1=\left\{\frac{N^2}{mn}\right\}\times \frac{J^T(A_1^T{A}_1+B_1^T{B}_1)J}{J^T\{{(A_1+A_2)}^T(A_1+A_2)+{(B_1+B_2)}^T(B_1+B_2)\}J},\hfill \\ \hfill & {\widehat{h}}_2=\frac{N^2{J}^T(A_1^T{A}_1+B_1^T{B}_1)J}{J^T\{n^2{(A_1+A_2)}^T(A_1+A_2)+m^2{(B_1+B_2)}^T(B_1+B_2)\}J},\hfill \end{array}$$ (7)

where J is a vector of 1's. The asymptotic distribution of T_1a and T_2a can be established through the following theorem.

Theorem 2

Under the conditions of Theorem 1, random variables T_1a and T_2a with ${\widehat{h}}_1$ and ${\widehat{h}}_2$ given by (7) converge in distribution to a standard normal distribution as (m/n) → λ and (m + n) → ∞.

Proof of Theorem 2 is given in the Appendix. The adjusted test statistics T_1a and T_2a will have the same asymptotic distributions as T₁ and T₂, respectively, if the assumption F = G is true. They deviate from one another when the shapes of F and G differ.

3. Simulations

In this section, we explore how type I errors are affected when F and G have different shapes. Because a Parkinson's disease trial is used as our example, and many Parkinson's disease clinical outcomes are ordinal variables with five different levels (“normal,” “mild,” “moderate,” “severe,” and “most serious”), we generated ordinal data with five levels: −2, −1, 0, 1, and 2. Data are simulated under the null hypothesis θ₁ =…= θ_k = 0 but with F ≠ G. In particular, we generate samples from F and G with zero means but different variances. We evaluate the type I error rate of O'Brien's tests ψ₁, ψ₂ as well as our modified tests ψ_1a, ψ_2a. Simulations presented in Tables 1–3 quantify the type I errors of ψ₁, ψ₂, ψ_1a, and ψ_2a when h₁ ≠ 1 and h₂ ≠ 1. Recall, m is the sample size in treatment group 1, i.e., X_i = (X_i1, …, X_ik), (i = 1, …, m), and n is the sample size in treatment group 2, i.e., Y_j = (Y_j1, …, Y_jk), (j = 1, …, n). For chosen k = 2 and 10, the outcomes (X_i1, …, X_ik) are generated according to the following formula: $X_{iu}=-2\cdot I\left[\left(X_{iu}^{\prime }<r_{11}\right)\right]-I\left[(r_{11}\le X_{iu}^{\prime }<r_{12})\right]+I\left[(r_{13}\le X_{iu}^{\prime }<r_{14})\right]+2\cdot I\left[(X_{iu}^{\prime }\ge r_{14})\right]$, where $X_{iu}^{\prime }={\left(\rho \right)}^{1∕2}{X}_{i1}^{″}+{(1-\rho )}^{1∕2}{X}_{iu}^{″}\left(u>1\right)$, and $X_{i1}^{″},\dots ,X_{ik}^{″}~iid$ Uniform (−1, 1). (Y_i1, …, Y_ik) are generated similarly, but with r₁ = (r₁₁, r₁₂, r₁₃, r₁₄) replaced by r₂ = (r₂₁, r₂₂, r₂₃, r₂₄). For illustration purpose, r₁ = (−0.1, 0, 0, 0.1) and r₂ = (−0.9, −0.8, 0.8, 0.9) in all tables. Type I error rates are presented only for nominal level α = 0.05. Similar results were seen for nominal level α = 0.01. Three types of rejection rules are shown in each table: two-sided test when H₀ is rejected for large observed absolute values of test statistics; one-sided test 1 when H₀ is rejected for large observed test statistic values; and the one-sided test 2 when H₀ is rejected for small observed values.

Table 1.

Observed rejection rate (type I error) under the null hypothesis (2) with m = n. ψ₁ and ψ₂ are O'Brien's tests assuming equal and unequal variance, respectively. ψ_1a and ψ_2a are adjusted tests for ψ₁ and ψ₂, respectively (2,000 simulations).

α = 0.05			Two-sided test				One-sided test 1				One-sided test 2
ρ	k	m = n	ψ1	ψ2	ψ1a	ψ2a	ψ1	ψ2	ψ1a	ψ2a	ψ1	ψ2	ψ1a	ψ2a
0.0	2	20	0.114	0.110	0.059	0.058	0.090	0.088	0.057	0.054	0.089	0.086	0.055	0.054
0.0	2	200	0.108	0.107	0.053	0.053	0.091	0.091	0.052	0.052	0.090	0.089	0.050	0.050
0.0	10	20	0.117	0.109	0.056	0.053	0.116	0.113	0.065	0.061	0.083	0.080	0.046	0.045
0.0	10	200	0.108	0.107	0.050	0.050	0.086	0.086	0.047	0.047	0.091	0.091	0.051	0.051
0.9	2	20	0.104	0.096	0.047	0.044	0.094	0.091	0.057	0.055	0.085	0.082	0.046	0.045
0.9	2	200	0.099	0.098	0.046	0.046	0.090	0.090	0.046	0.046	0.077	0.077	0.042	0.042
0.9	10	20	0.106	0.100	0.056	0.053	0.090	0.087	0.054	0.053	0.085	0.080	0.046	0.043
0.9	10	200	0.116	0.115	0.053	0.053	0.102	0.101	0.055	0.054	0.088	0.088	0.049	0.049

Table 3.

Observed rejection rate (type I error) under the null hypothesis (2) with m = 2n. ψ₁ and ψ₂ are O'Brien's tests assuming equal and unequal variance, respectively. ψ_1a and ψ_2a are adjusted tests for ψ₁ and ψ₂, respectively (2,000 simulations).

α = 0.05, m = 2n			Two-sided test				One-sided test 1				One-sided test 2
ρ	k	n	ψ1	ψ2	ψ1a	ψ2a	ψ1	ψ2	ψ1a	ψ2a	ψ1	ψ2	ψ1a	ψ2a
0.0	2	20	0.050	0.121	0.046	0.045	0.044	0.091	0.043	0.043	0.052	0.102	0.050	0.050
0.0	2	200	0.061	0.148	0.055	0.055	0.056	0.109	0.052	0.052	0.063	0.113	0.059	0.060
0.0	10	20	0.055	0.139	0.050	0.050	0.043	0.105	0.041	0.040	0.060	0.110	0.056	0.056
0.0	10	200	0.058	0.133	0.055	0.055	0.053	0.096	0.051	0.051	0.053	0.110	0.051	0.051
0.9	2	20	0.048	0.129	0.050	0.050	0.047	0.094	0.048	0.048	0.053	0.107	0.055	0.055
0.9	2	200	0.050	0.130	0.049	0.049	0.043	0.102	0.043	0.044	0.052	0.108	0.051	0.051
0.9	10	20	0.058	0.155	0.063	0.062	0.056	0.111	0.056	0.056	0.063	0.123	0.066	0.067
0.9	10	200	0.047	0.133	0.049	0.049	0.046	0.090	0.048	0.048	0.045	0.114	0.047	0.047

Because sample sizes from different treatment groups may not be equal in medical applications, we consider three cases: m = n (Table 1); n = 2m (Table 2); and m = 2n (Table 3) in our simulation. Miller (1986) discussed how a t-test's type I error rate is affected by the unequal variances: Although it can tolerate large disparities in the variances (viz., ratios of 4 and up) without showing major ill effects on α, it can be seriously affected when the population with much larger variance has much smaller sample size. Similar results are seen in our simulation. Because Var(X_iv) > Var(Y_iv), ψ₁ is more seriously affected under m < n than the case under m > n. When m = n, Table 1 shows that tests ψ₁ and ψ₂ can inflate their type I errors by 100% (to 0.10). When n = 2m or m = 2n, either ψ₁ or ψ₂ is more seriously affected—it could inflate their type I errors by up to 400% (to 0.20). In all cases, our adjusted tests ψ_1a and ψ_2a have their type I errors close to the target nominal level α = 0.05.

Table 2.

Observed rejection rate (type I error) under the null hypothesis (2) with n = 2m. ψ₁ and ψ₂ are O'Brien's tests assuming equal and unequal variance, respectively. ψ_1a and ψ_2a are adjusted tests for ψ₁ and ψ₂, respectively (2,000 simulations).

α = 0.05, n = 2m			Two-sided test				One-sided test 1				One-sided test 2
ρ	k	m	ψ1	ψ2	ψ1a	ψ2a	ψ1	ψ2	ψ1a	ψ2a	ψ1	ψ2	ψ1a	ψ2a
0.0	2	20	0.192	0.091	0.067	0.056	0.141	0.085	0.067	0.062	0.133	0.073	0.051	0.046
0.0	2	200	0.179	0.090	0.053	0.053	0.132	0.079	0.056	0.055	0.130	0.077	0.049	0.049
0.0	10	20	0.193	0.097	0.071	0.060	0.126	0.079	0.060	0.056	0.138	0.085	0.062	0.056
0.0	10	200	0.185	0.076	0.046	0.044	0.132	0.074	0.047	0.046	0.129	0.076	0.045	0.044
0.9	2	20	0.184	0.075	0.056	0.048	0.118	0.063	0.048	0.041	0.144	0.078	0.061	0.055
0.9	2	200	0.194	0.098	0.064	0.062	0.127	0.075	0.054	0.053	0.149	0.091	0.060	0.060
0.9	10	20	0.202	0.087	0.067	0.055	0.132	0.075	0.059	0.052	0.152	0.081	0.065	0.058
0.9	10	200	0.195	0.081	0.051	0.051	0.138	0.078	0.054	0.053	0.130	0.072	0.045	0.044

4. An Example

To illustrate the difference between O'Brien's test and our adjusted test, we use data from the multicenter controlled clinical trial of Coenzyme Q₁₀ in early Parkinson's disease (QE2 trial). The trial was conducted in 1999–2001 to determine whether Coenzyme Q₁₀ could slow the functional decline in Parkinson's disease (Shults et al., 2002). There were 16, 21, 20, and 23 patients randomized to placebo or Coenzyme Q₁₀ at dosages of 300, 600, or 1200 mg/day, respectively. Patients were evaluated at the screening, baseline, and 1-, 4-, 8-, 12-, and 16-month visits. Subjects were followed for up to 16 months or until disability requiring treatment with levodopa had developed. Outcome measures for the treatment efficacy comparison include the mental (mentation), motor, and average daily living (ADL) subscales of the Unified Parkinson's Disease Rating Scale (UPDRS), and the Schwarb and England ADL (SEADL) score. The primary outcome was the change in the total score (the sum of mental, motor, and the ADL) on the UPDRS from baseline to the last visit at 16 months. Last observation carrying forward for missing data was used by the trial investigators. The primary analysis was a test for a trend between dosage and the mean change in the UPDRS score. A p-value of 0.09 (two-sided) was reported by the investigators (Shults et al., 2002).

As a secondary analysis, the trial investigators conducted a series of univariate tests for each single outcome, respectively. The goal is to assess whether Coenzyme Q₁₀, at any dose, is more effective than placebo with respect to changes in the mental, motor, and ADL of the UPDRS subscale, and the SEADL from the baseline visit to the last visit at 16 months. While we had performed both O'Brien's test and our adjusted test to contrast the placebo group to each of the three dose groups separately, for illustration purposes, here we combine all three Coenzyme Q₁₀ groups into a single Coenzyme Q₁₀ group. (We note parenthetically that the results of each pairwise comparison also provide evidence of differing p values when comparing O'Brien's test to the adjusted methods. These results are available from the authors.) With this simplification to a single combined Coenzyme group, the goal was to assess whether this combined Coenzyme group would perform better than the placebo. Five patients had missing observations at the final 16-month visit. Their 12-month visit measures were carried forward for these five patients. While the last-observation-carried forward approach is less than optimal, we used this approach in our example so that our results could be comparable to the previous reported trial results.

Figure 1 gives the density plot for all four outcomes. The variances in the two groups were not the same. For example, the placebo group had larger variance (=2.267) in the change of mental score compared to the variance (=0.729) in the treatment group. A test for equal variance gave a p value of 0.002. Since smaller values were considered as better functional disability measures for mental, motor, and ADL, while larger values of SEADL were considered poorer functional disability measures, we reversely coded the SEADL by multiplying (−1) so that smaller outcomes were preferred for all outcomes. All four outcomes were correlated. Table 4 gives the correlations and the corresponding p values among the four outcomes (combining all 80 patients). To compare the treatment versus placebo in these four outcomes, the p values from ψ₁ and ψ₂ were 0.0368 and 0.0493, respectively, ${\widehat{h}}_1=1.4717$, ${\widehat{h}}_2=1.4404$, and p values from the adjusted tests, ψ_1a and ψ_2a, were 0.0839 and 0.1014, respectively, that are 100% larger than the p values from tests ψ₁ and ψ₂. Hence, if the significance level were set to 0.05, O'Brien's test would reject the null hypothesis while the adjusted test would not.

Figure 1.

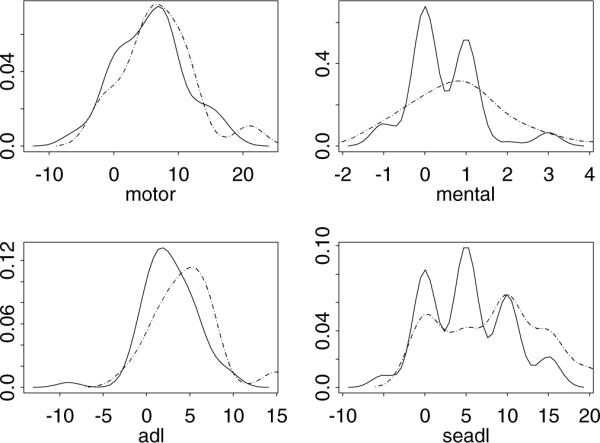
Densities of the outcome changes from the baseline to the last visit (N = 80 patients) in the QE2 trial. The solid line indicates the treatment group and the dashed line indicates the placebo group.

Table 4.

Correlation (p values) among motor, mental, ADL, and SEADL in the change from the baseline visit to the last visit at 16 months when combining all 80 patients. Last observation carrying forward. SEADL is reversely coded by multiplying (−1).

	Mental	ADL	SEADL
Motor	0.0797 (0.4823)	0.3840 (0.0004)	0.4715 (<0.0001)
Mental		0.3625 (0.0010)	0.1562 (0.1693)
ADL			0.4931 (<0.0001)

5. Discussion

O'Brien's rank-sum-type test provides a simple method to compare two groups with multiple outcomes. It is useful and appropriate to use when the rejection of the null hypothesis requires improvement in outcomes. When applying O'Brien's test to compare treatments, we need to specify clearly the definition of “no difference” between the two treatments. If it is specified that, under the null, the two distributions are identical, then O'Brien's test provides a simple valid test. Under this situation, ψ₁ = ψ_1a and ψ₂ = ψ_2a asymptotically, and all of them control type I errors asymptotically. We suggest the use of ψ₁ due to its simplicity. If the interest is to test whether the new treatment increases the outcome measures without assuming an identical covariance matrix or other features of the joint distribution that are not of interest to the clinicians, then this is a Behrens–Fisher problem and the adjusted tests ψ_1a or ψ_2a are recommended. Although ψ_1a and ψ_2a give similar results in our simulation, our experience suggests that ψ_1a gives slightly better results compared to ψ_2a.

The attractiveness of O'Brien's rank-sum-type test is its simplicity. Its statistical properties allow us to extend its use to more general settings. For example, we can use the asymptotic normality of mean rank-sums (such as ${\stackrel{‒}{R}}_x$ and ${\stackrel{‒}{R}}_y$ when there are only two groups) and similar methods used in the construction of the Kruskal–Wallis test to construct a test for multiple group (or dose-level) comparison. Depending on the question of interest, the test can be constructed based on a linear combination or a quadratic function of these mean rank-sums. When there are covariates or repeated measures of interest, conventional univariate response models for longitudinal data can be applied to the rank-sums with adjusted covariance matrices. Suppose y_ijk is the jth repeated measure of the kth outcome from the ith subject with covariate vector x_ij (i = 1, …, N; j = 1, …, T; k = 1, …, K). The treatment assignment is considered as a covariate. Let R_ijk be the rank of y_ijk among all observations from the kth outcome {y_ijk, i = 1, …, N; j = 1, …, T}. Compute rank-sums $R_{ij}={\Sigma }_{k=1}^K{R}_{ijk}$. For each j (j = 1, …, T), construct rank scores {a_j(R_ij), i = 1, …, N} using some nondecreasing function ϕ_j:a_j(i) = ϕ_j(i/(N + 1)). The test statistics can be constructed using a linear combination of rank statistics $T_j={\Sigma }_{i=1}^N(x_{ij}-{\stackrel{‒}{x}}_{\cdot j})a_j\left(R_{ij}\right)$, j = 1, … ,T. This form of test statistics has been used by many authors. For example, Hájek and Šidák (1967), Puri and Sen (1969, 1971, 1985), and Hettmansperger (1984). As discussed in this article, adjustment for the dependency among all R_ij's is needed to provide valid inference from the model. We are currently investigating extensions of the current methods to this problem. In particular, adjusted test statistics will be derived in which quantities similar to h₁ and h₂ must be estimated and applied to the covariance matrix. When there are missing observations, Domhof, Brunner, and Osgood (2002) considered rank procedures for univariate outcomes with missing observations. Their procedures can be easily extended to cases when there are discrete covariates with a finite number of levels. More-over, the use of regression model with the rank-sums allows adjustment for both continuous and categorical covariates. Some other multiple imputation methods or data augmentation method (Schafer, 1997) to the ranks of missing data may also be considered.

Appendix

Proof of Theorem 1

It is seen that ${\stackrel{‒}{R}}_y-{\stackrel{‒}{R}}_x=N^{1∕2}{J}^{T}W$ where W = (W₁, …, W_k)^T and $W_v=N^{1∕2}{\Sigma }_{i=1}^m{\Sigma }_{j=1}^n\{I\left[\left(x_{iv}<y_{jv}\right)\right]-I\left[\left(x_{iv}>y_{jv}\right)\right]\}∕\left(2mn\right)$. Since W is a U-statistic, it converges in distribution to a normal distribution with mean zero and variance Σ ≡ Var[W] when $\mathrm{Var}\left[G_v^o\left(X_v\right)\right]>0$ and $\mathrm{Var}\left[F_v^o\left(Y_v\right)\right]>0$ for all v = 1, …, k, and n/m + m/n = O(1) as N → ∞. We first compute (details are available from the first author) $E\left[{\widehat{\sigma }}_x^2\right]$, $E\left[{\widehat{\sigma }}_y^2\right]$, and $E\left[{\widehat{\sigma }}^2\right]$, then we obtain expressions $mn{J}^T\Sigma J∕E\left[{\widehat{\sigma }}^2\right]=h_1+O(1∕N)$ and $N{J}^T\Sigma J∕E[{\widehat{\sigma }}_x^2∕m+{\widehat{\sigma }}_y^2∕n]=h_2+O(1∕N)$. Based on Slutsky's Theorem, it suffices to show that ${\widehat{\sigma }}^2∕\left(mn\right)$ and $({\widehat{\sigma }}_x^2∕m+{\widehat{\sigma }}_y^2∕n)∕N$ converge in probability to J^T ΣJ/h₁ and J^T ΣJ/h₂, respectively, as N → ∞.

For convenience in notation, we denote R_i = R_xi if 1 ≤ i ≤ m, and R_i = R_y,i−m if m + 1 ≤ i ≤ N. Denote x_iv = y_i−m,v for m + 1 ≤ i ≤ N, v = 1, 2, …, k. For any l₁, l₂, l₃, l₄ ∈ {1, 2, …, N},

$$\begin{array}{cc}\hfill \mathrm{cov}& (R_{l_1}{R}_{l_2},R_{l_3}{R}_{l_4})\hfill \\ \hfill =& \sum _{i_1\ne l_1}\sum _{i_2\ne l_2}\sum _{i_3\ne l_3}\sum _{i_4\ne l_4}\sum _{u_1=1}^k\sum _{u_2=1}^k\sum _{u_3=1}^k\sum _{u_4=1}^k\times \hfill \\ \hfill & \mathrm{cov}[\left(I\left[(x_{i_1{u}_1}<x_{l_1{u}_1})\right]+\frac{1}{2}I\left[(x_{i_1{u}_1}=x_{l_1{u}_1})\right]+\frac{1}{N-1}\right)\phantom{]}\hfill \\ \hfill & \times \left(I\left[(x_{i_2{u}_2}<x_{l_2{u}_2})\right]+\frac{1}{2}I\left[(x_{i_2{u}_2}=x_{l_2{u}_2})\right]+\frac{1}{N-1}\right),\hfill \\ \hfill & \left(I\left[(x_{i_3{u}_3}<x_{l_3{u}_3})\right]+\frac{1}{2}I\left[(x_{i_3{u}_3}=x_{l_3{u}_3})\right]+\frac{1}{N-1}\right)\hfill \\ \hfill & \times \phantom{[}\left(I\left[(x_{i_4{u}_4}<x_{l_4{u}_4})\right]+\frac{1}{2}I\left[(x_{i_4{u}_4}=x_{l_4{u}_4})\right]+\frac{1}{N-1}\right)]\hfill \\ \hfill =& O\left(N^3\right).\hfill \end{array}$$ (A.1)

This is because all summands in (A.1) are uniformly bounded by one, and the summand is zero whenever {i₁, i₂} ∩ {i₃, i₄} is an empty set. The sums for i₁, i₂, i₃, i₄ in (A.1) are from 1 to N except i₁ = l₁, i₂ = l₂, i₃ = l₃, and i₄ = l₄, respectively. Rewrite $(N-2){\widehat{\sigma }}^2={\Sigma }_{i=1}^N{R}_i^2-m{\stackrel{‒}{R}}_x^2-n{\stackrel{‒}{R}}_y^2$. Applying (A.1), we have

$$\begin{array}{cc}\hfill & \mathrm{var}\left[R_i^2\right]=O\left(N^3\right),\hfill \\ \hfill & \mathrm{var}\left[{\stackrel{‒}{R}}_x^2\right]=\frac{1}{m^4}\sum _{l_1=1}^m\sum _{l_2=1}^m\sum _{l_3=1}^m\sum _{l_4=1}^m\times \mathrm{cov}\left(R_{l_1}{R}_{l_2},R_{l_3}{R}_{l_4}\right)=O\left(N^3\right),\hfill \\ \hfill & \mathrm{var}\left[{\stackrel{‒}{R}}_y^2\right]=\frac{1}{n^4}\sum _{l_1=m+1}^N\sum _{l_2=m+1}^N\sum _{l_3=m+1}^N\sum _{l_4=m+1}^N\times \mathrm{cov}\left(R_{l_1}{R}_{l_2},R_{l_3}{R}_{l_4}\right)=O\left(N^3\right).\hfill \end{array}$$

Thus

$$\begin{array}{cc}\hfill \mathrm{var}\left[(N-2){\widehat{\sigma }}^2\right]& \le {\left(2N\right)}^2\max \left\{\mathrm{var}\left[R_1^2\right],\dots ,\mathrm{Var}\left[R_N^2\right],\mathrm{var}\left[{\stackrel{‒}{R}}_x^2\right],\mathrm{var}\left[{\stackrel{‒}{R}}_y^2\right]\right\}\hfill \\ \hfill & ={\left(2N\right)}^2\cdot O\left(N^3\right)\hfill \\ \hfill \mathrm{var}[{\widehat{\sigma }}^2∕\left(mn\right)]& =O\left(\frac{1}{N}\right).\hfill \end{array}$$

For any constant ϵ > 0, applying Chebyshev's inequality, we have

$$\begin{array}{cc}\hfill P\left(\mid \frac{\widehat{\sigma }2}{mn}-\frac{J^T\Sigma J}{h_1}\mid >ϵ\right)& \le \frac{1}{{ϵ}^2}E{\left[\frac{\widehat{\sigma }2}{mn}-\frac{J^T\Sigma J}{h_1}\right]}^2\hfill \\ \hfill & =\frac{1}{{ϵ}^2}\left[\mathrm{var}\left(\frac{{\widehat{\sigma }}^2}{mn}\right)+O\left(\frac{1}{N^2}\right)\right]\hfill \\ \hfill & \to 0\mathrm{as}N\to \infty .\hfill \end{array}$$

Hence ${\widehat{\sigma }}^2∕\left(mn\right)$ converges in probability to J^T ΣJ/h₁ as N → ∞. Similarly we can show that $({\widehat{\sigma }}_x^2∕m+{\widehat{\sigma }}_y^2∕n)∕N$ converges in probability to J^T ΣJ/h₂ as N → ∞.

Proof of Theorem 2

It suffices to show that ${\widehat{h}}_{\ell }\to h_{\ell }(\ell =1,2)$ in probability as (m/n) → λ and (m + n) → ∞. The empirical estimates of $G_u^o\left(t\right)$ and $F_u^o\left(t\right)$ are ${\widehat{G}}_u^o\left(t\right)\equiv \frac{1}{n}{\Sigma }_{j=1}^n(I\left[\left(y_{ju}<t\right)\right]+\frac{1}{2}I\left[(y_{ju}=t)\right])$ and ${\widehat{F}}_u^o\left(t\right)\equiv \frac{1}{m}{\Sigma }_{i=1}^m\times (I\left[\left(x_{iu}<t\right)\right]+\frac{1}{2}I\left[(x_{iu}=t)\right])$. Note that ${\widehat{F}}_u^o\left(x_{iu}\right)=[R_{x0}\left(x_{iu}\right)-1∕2]∕m$; ${\widehat{G}}_u^o\left(y_{iu}\right)=[R_{y0}\left(y_{iu}\right)-1∕2]∕n$; ${\widehat{F}}_u^o\left(y_{iu}\right)=[R_x\left(y_{iu}\right)-1]∕m$; ${\widehat{G}}_u^o\left(x_{iu}\right)=[R_y\left(x_{iu}\right)-1]∕n$. The proof can be completed by using the consistent estimates of matrices $\left({\widehat{a}}_{uv}\right)=A_1^T{A}_1∕\left(4m{n}^2\right)$; $\left({\widehat{b}}_{uv}\right)=B_1^T{B}_1∕\left(4m^{2}n\right)$, $\left({\widehat{e}}_{uv}\right)=A_2^T{A}_2∕\left(4m^3\right)$, $\left({\widehat{f}}_{uv}\right)=A_2^T{A}_1∕\left(4m^{2}n\right)$, $\left({\widehat{p}}_{uv}\right)=B_2^T{B}_2∕\left(4n^2\right)$, $\left({\widehat{q}}_{uv}\right)=B_1^T{B}_2∕\left(4m{n}^2\right)$, and the Continuous Mapping Theorem 5.1 of Billingsley (1968, p. 30). Details are available from the first author.