Theoretical and experimental studies of the isomeric protonation in solution for a prototype aliphatic ring containing two nitrogens

Abstract

Theoretical calculations were carried out for studying the tautomeric protonation of N-methyl piperazine as a prototype six-member aliphatic ring containing a secondary and a tertiary nitrogen atom. The protonation was investigated in three solvents: water, acetonitrile, and dichloromethane. Calculations were performed up to the B3LYP/aug-cc-pvtz and QCISD(T)/CBS levels by applying the IEF-PCM polarizable continuum dielectric solvent model. Relative solvation free energies also were calculated upon explicit solvent models by utilizing the free-energy perturbation theory as implemented in Monte Carlo simulations.

The relative free energy for the N-methyl piperazine tautomer protonated at the secondary (NMps) rather than at the tertiary (NMpt) nitrogen was calculated at a ratio of 47/53 in infinitely dilute aqueous solution. The ratio further decreases in lower polarity solvents. In contrast, NMR experiments suggest that the protonation takes place primarily at the secondary nitrogen in 0.37 molar aqueous solution with NMps/NMpt = 80/20. The NMps tautomer is exclusive in dichloromethane at the same concentration. The discrepancy between theory and experiment was resolved by considering association equilibria in parallel with the protonation for the solute. As a result, the theoretically predicted tautomer ratios were obtained in close agreement with the experimental values. The NMps tautomer could form a preferable dimeric structure, where one or two chloride anion(s) is/are in hydrogen bonds with protons of the associating monomers.

The calculations suggest that the proton relocation may take place by solvent assistance in water or along an intramolecular proton jump in the twist-boat conformation. The predicted activation free energy was about 10 kcal/mol on the basis of variable temperature NMR experiments in DCM.

I. Introduction

Characterization of the interactions of ligand molecules with biopolymers is a central problem in theoretical drug-design. Such studies should discover the actual spatial fit for the ligand-receptor complex as well as the concomitant energy/free energy changes. The main stabilization factors for reversibly bound ligands include intermolecular hydrogen bonds, dispersion interactions and matching of nonpolar sites.

Many biologically active molecules contain basic and/or acidic sites. Amine derivatives also belong to this group of potential drugs. The protonation and deprotonation of the amine moiety, in order to optimize the electrostatic fit between the ligand and the receptor, alters the hydrogen bond donor/acceptor character of a ligand binding site. The binding cavity may be filled in by water molecules in the absence of the ligand. After the ligand binds to the receptor, nearby water molecules can mediate the protonation / deprotonation process. The feasibility for the change of protonation state of an amine strongly depends, however, on internal energy factors as well.

In a recent review, Morgenthaler et al.¹ emphasized the importance of the amine basicity in lead optimization. The authors’ conclusion was that no theoretical method is presently available for satisfactory estimation of amine basicities. However, considerable effort has been focused on developing theoretical methods having satisfactory predictive power in the past few years. Lu et al.^2a calculated the pK_a values for 24 amines, and their best theoretical approach determined an rmsd value of 1.30. Liu and Pedersen^2b found good correlation between pKa values and the molecular electrostatic potential for 154 amines. Klicic et al.^2c developed empirical parameters for their self-consistent reaction field method upon fitting the calculated and experimental pK_a values for a general training set. Using these parameters, the pK_a for a number of amines in the control group were predicted with deviations from the experimental values within 0.6 units.

Instead of estimating the absolute pK_a values, calculation of the relative pK_a may suffice in many cases. Upon a reliable estimation of the relative pK_a’s for a class of molecules, only one experimental value is required for estimating the absolute pK_a values for the series. Saturated heterocycles containing two nitrogen atoms in the ring represent an important example for such systems.

Several muscarinic agonists have been synthesized in our laboratory³ with some containing new heterocycles at the ends of a polyglycolic chain. Piperazine derivatives are being investigated as possible selective muscarinic agonists. Asymmetrically N-substituted piperazines (for the prototype see structure (1) in Scheme 1) have in common the possibility for tautomeric protonation. The favorable protonation of the secondary vs. the tertiary nitrogen atom in the piperazine ring may be a decisive factor in determining the actual conformation of the drug molecule. For example, the conformation of N-(methoxyethyl) piperazine (a substructure in our newly synthesized compounds) depends on the protonation site. If the molecule is protonated at the tertiary nitrogen, then formation of a five member ring becomes feasible due to the formation of an intramolecular O(ether)…H-N hydrogen bond. A recent study showed that ethers act as strong hydrogen-bond acceptors when located opposite to protonated donating sites.⁴ Formation of an intramolecular hydrogen bond maintains or at least internally favors the O-C-C-N gauche conformation. No such hydrogen bond can be formed if the secondary nitrogen atom is protonated, in which case the O-C-C-N chain may adopt the trans conformation easily.

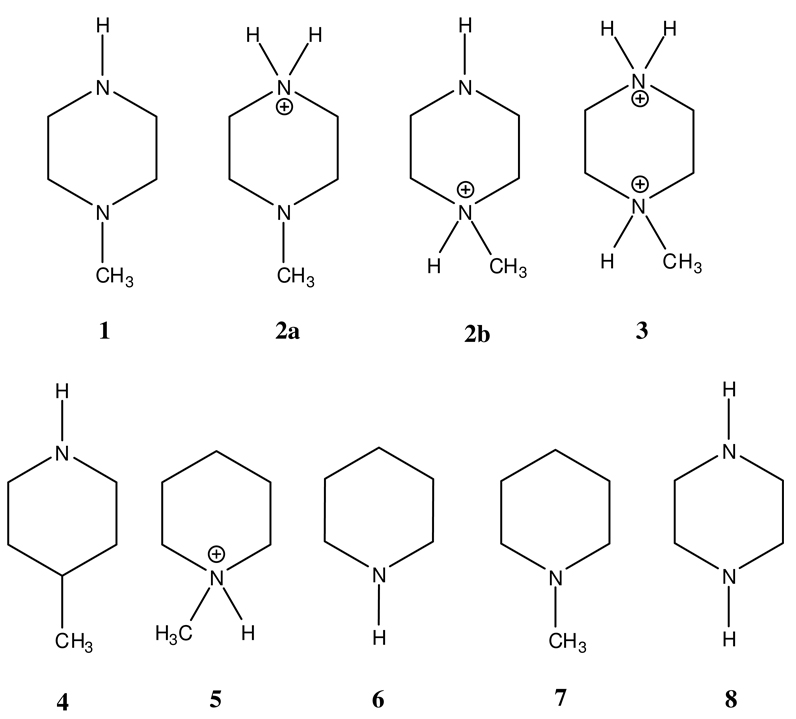
Scheme 1.

Structures studied: (1) N-methyl piperazine, (2a) N-methyl piperazine protonated at the secondary nitrogen (NMps, see text), (2b) N-methyl piperazine protonated at the tertiary nitrogen (NMpt, see text), (3) N-methyl piperazine diprotonated, (4) 4-methyl piperidine, (5) N-methyl piperidine protonated, (6) piperidine, (7) N-methyl piperidine, (8) piperazine. Asymmetrically substituted piperazines (see text) have the substituent in place of the methyl group of structure 1.

The O…H⁺(N) distance may be an important factor in determining the biological activity of the ligand. The problem is general for chemical systems having 1,2-disubstituted-ethane substructures containing substituents capable of forming hydrogen-bonds. Neurotransmitters such as norepinephrine and epinephrine are well-known examples for the gauche/trans conformational equilibrium modifying the actual O…N distance in the chain.5a,b The above problem emerges in our newly synthesized molecules, and the present paper aims to study the favorable protonation site for a prototype six-member ring with two nitrogen atoms held in a chemically non-equivalent environment. We considered only the ionic forms, so the difficulties related to the proper estimation of the (BH⁺ - B) free energy difference throughout the protonation process could be avoided. Since no experimental pK_a values were found in the literature for substituted piperazines, the predictive strength of the applied theoretical method was tested by comparing the calculated and the experimental relative pK_a values for the piperidine (6), N-methyl piperidine (7), and piperazine (8) bases.

II. Methods

Experimental

N-methyl piperazine was treated with 1 mole equivalent of hydrogen chloride to form the monosalt. Two similar reaction routes were used in the chemical preparation of compound 2a/2b to see whether the presence of water throughout the salt preparation would have an effect on the recorded NMR spectra for the monosalt product. Variable temperature NMR experiments (¹H NMR and COSY) were used to determine whether the monosalt obtained was protonated at the secondary (2a) or tertiary (2b) amine site. Compound 2a was found to be major product in about 85% reaction yields from both experiments. Full experimental details are provided as supplementary information.

In the NMR spectroscopy, temperature calibration was done using Varian 100% methanol sample (part number 968120-80). Due to supercooling, the sample remained in the liquid state significantly below the freezing point. This was verified by simultaneous temperature determination by NMR and with a copper constantan thermocouple in an NMR tube containing 100% methanol, inserted into the spectrometer. Recorded spectra and a table of chemical shifts are provided as supplementary information.

Models and Calculations

Gas phase and Continuum Solvent Calculations

The pK_a of a “B” base is defined for the dissociation process of BH⁺ ↔ B + H⁺ as

$${\text{pK}}_{\mathrm{a}}=(1/2.303\text{RT})({{\mathrm{G}}^{\mathrm{o}}}_{\mathrm{B}}+{{{\mathrm{G}}^{\mathrm{o}}}_{\mathrm{H}}}^{+}-{{{\mathrm{G}}^{\mathrm{o}}}_{\text{BH}}}^{+})$$ (1)

wherin G^o_x is the standard free energy for the species X. Experimental results are generally reported at T = 298 K. Recent theoretical calculations^2a,6a used −262.4 and −264.6 kcal/mol for the aqueous solvation of the proton. A value of −269.0 kcal/mol for the proton free energy in its standard state in aqueous solution allowed calculation of pK_a values in good agreement with the experiment for phenols,^6b,c imidazole and methanol.^6c

Even if a good estimate for G^o_H⁺ seems to have been reached, theoretical estimation of the (G^o_B − G^o_BH⁺) terms is still challenging. In several recent investigations, thermodynamic cycles considering both the gas-phase and the aqueous solution equilibria have been utilized for calculating these terms.^2,6 By performing only ΔpK_a calculations in-solution, we can avoid the application of such cycles and the acceptance of some value for G^o_H⁺.

In the present study, relative free energies of the neutral and protonated forms have been obtained directly in solution either by utilizing the IEF-PCM approach (integral-equation formalism for the polarizable continuum method)^7,8 or by performing MC simulations for the calculation of the relative solvation free energies. In both approaches, the total relative free energy is a sum of two terms:

$$\mathrm{\Delta }{\mathrm{G}}_{\text{tot}}=\mathrm{\Delta }{\mathrm{G}}_{\text{int}}+\mathrm{\Delta }{\mathrm{G}}_{\text{sol}}$$ (2)

where ΔG_int and ΔG_sol are the internal and solvation-related contributions to the change in the total free energy in infinitely dilute solution. In calculations of ΔG_tot by the IEF-PCM method, we applied the following partitioning:

$$\mathrm{\Delta }{\mathrm{G}}_{\text{tot}}=(\mathrm{\Delta }{{\mathrm{E}}^{\mathrm{s}}}_{\text{int}}+\mathrm{\Delta }{\mathrm{G}}_{\text{th}})+(\mathrm{\Delta }{\mathrm{E}}_{\text{elst}}+\mathrm{\Delta }{\mathrm{G}}_{\text{drc}})\equiv (\mathrm{\Delta }{{\mathrm{E}}^{\mathrm{s}}}_{\text{int}}+\mathrm{\Delta }{\mathrm{G}}_{\text{th}})+\mathrm{\Delta }{\mathrm{G}}_{\text{sol}}(\text{PCM})$$ (3)

$${{\mathrm{E}}^{\mathrm{s}}}_{\text{int}}=<\mathrm{\Psi }|\mathrm{H}|\mathrm{\Psi }>$$ (4a)

$${\mathrm{E}}_{\text{elst}}=<\mathrm{\Psi }|\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\mathrm{V}|\mathrm{\Psi }>$$ (4b)

wherein H is the solute’s Hamiltonian, V is the solvent reaction field generated by the fully polarized solute in solution, Ψ is the converged wave function of the solute obtained from the in-solution calculation. ΔG_drc is the relative dispersion-repulsion-cavitation free energy.

The relative thermal correction, ΔG_th was calculated as

$$\mathrm{\Delta }{\mathrm{G}}_{\text{th}}=\mathrm{\Delta }\text{ZPE}+\mathrm{\Delta }(\mathrm{H}(\mathrm{T})-\text{ZPE})-\mathrm{T}\mathrm{\Delta }\mathrm{S}(\mathrm{T})$$ (5)

where ZPE is the zero-point energy, H(T) and S(T) are the enthalpy and the entropy, respectively, at T = 298 K^o and p = 1 atm.

Molecular geometries were optimized at the DFT level using the B3LYP9a,b and B3P86^9a,c functionals and applying the 6-31G* and the 6-311++G** basis sets^10a. B3LYP/6-31G* optimizations predict correct gas-phase geometries for small molecules¹¹ and the IEF-PCM/B3LYP/6-31G* in-solution molecular electrostatic potential was successfully applied for deriving net atomic charges for Monte Carlo simulations.^5c,d,12a To study the effect of the basis set extension as well as the effect of the accepted DFT functional, both B3LYP/6-311++G** and B3P86/6-311++G** optimizations were considered in solution. The latter level was selected by Wiberg et al.¹³ who investigated the acidities of haloacetic acids. In the present study, the cavity in the solvent was defined by overlapping spheres around the atomic centers by utilizing the Bondi radii¹⁴ multiplied by a scaling factor of 1.2. The nitrogen and the polar hydrogen atoms acted as individual sphere centers, whereas the united atom model of the PCM was applied for the CH_n (n=2–3) units.^12a Local-energy-minimum structures were certified by all positive vibrational frequencies. Frequency dependent relative free-energy terms (eq. 5) were calculated in the rigid rotor – harmonic oscillator approach.^10b

Recent investigations¹² suggest that for a reasonable estimation of the relative free energy for isomers in solution, high-level relative internal energies are required. Accordingly, single-point relative energies at the DFT optimized geometries were calculated up the IEF-PCM/B3LYP/aug-cc-pvtz15a,b and the IEF-PCM/QCISD(T)/cc-pvtz^15c,16 levels.

Upon QCISD(T) calculations, the correlation-energy corrected ΔE^s_int was obtained as

$$\mathrm{\Delta }{{\mathrm{E}}^{\mathrm{s}}}_{\text{int}}=\mathrm{\Delta }<\mathrm{\Psi }|\mathrm{H}|\mathrm{\Psi }>+(\mathrm{\Delta }\mathrm{E}(\text{IEF}-\text{PCM}/\text{QCISD}(\mathrm{T}))-\mathrm{\Delta }<\mathrm{\Psi }|\mathrm{H}+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\mathrm{V}|\mathrm{\Psi }>)$$ (6)

Since the applied implementation of the IEF-PCM method in Gaussian 03 calculates the Eelst term at the Hartree-Fock level using the selected basis set even in QCISD(T) calculations, the ΔΨ|½V|Ψ term cancels out in eq. 6, and the difference of the last two terms provides the correlation correction for the relative internal energy. The QCISD(T) protonation internal energy differences were extrapolated to the complete basis set limit (CBS) using the formula by Hobza.¹⁷ In fact, we used the QCISD(T) rather than the CCSD(T) approach proposed in ref. 17. In our former studies of different tautomeric and conformational problems,^12a ΔE^s _int relative energies were in close agreement by the two approaches. The complete basis set limit for the ΔE_int = (E_B − E_BH⁺) internal energy difference, ΔE^QCISD(T)_CBS, was calculated as

$$\mathrm{\Delta }{{\mathrm{E}}^{\text{QCISD}(\mathrm{T})}}_{\text{CBS}}=\mathrm{\Delta }{{\mathrm{E}}^{\text{MP}2}}_{\text{CBS}}+(\mathrm{\Delta }{\mathrm{E}}^{\text{QCISD}(\mathrm{T})}-\mathrm{\Delta }{\mathrm{E}}^{\text{MP}2})$$ (7)

Molecular geometries were optimized at the MP2/aug-cc-pvdz level. The last term of eq. 7 was calculated using the aug-cc-pvdz basis set and the complete-basis-set MP2 energy, E^MP2_CBS, was obtained by using the formula^18a-c

$$\mathrm{E}(\mathrm{X})=\mathrm{E}(\text{CBS})+\mathrm{A}/{\mathrm{X}}^3$$ (8)

X in eq. 8 is the so-called cardinal number for the Dunning basis-set. The two parameters (E(CBS) and A) were calculated for selected pairs upon MP2/aug-cc-pvdz and single-point MP2/aug-cc-pvtz calculations with X values of 2 and 3, respectively.^18d,e

For validating the applied theoretical levels and exploring the smallest basis set providing converged results, gas-phase protonation energies and relative pK_a values were calculated for structures 6–8 (Scheme 1), for which experimental values are available.¹⁹ All quantum chemical calculations were performed with the Gaussian 03 software²⁰ running at the Ohio Supercomputer Center.

Monte Carlo Simulations

Monte Carlo (MC) simulations provide a useful theoretical approach for studying systems with a large number of interacting molecules in thermodynamic equilibrium at, e.g., some constant temperature and pressure value. Accepting the standard state of the solute as of c = 1 mol/dm³ (see appendix), change of the standard solvation free energy can be calculated upon the free energy perturbation method (FEP)²¹ as (μ_j^o_sol (c=1) − μ_i^o_sol (c=1)) = ΔG(FEP)_sol. At such concentration, however, solute-solute interactions may not be negligible.

A direct estimation of (μ_j^o_sol (c=1) − μ_i^o_sol (c=1)) is possible by means of the FEP method but would require very long calculations.^5d Instead, the equilibrium ratios for the tautomers at different solute concentrations were calculated by considering the relative free energy in infinitely dilute solution, and a correction was applied for the partial solute-solute association.

Infinitely dilute solutions may be modeled by means of moderate-size solvent boxes, if no solute-solute interaction is considered between the elements in the central and the replica boxes. Details of such calculations have been described in a number of former publications.^{5a,c,11,12,23,25–27} (For a short description of the MC technique applied in this paper, see the supporting information.) Using a solute-solvent cutoff of SCUT=12 Å is, however, too short in case of an ionic solute, thus we applied a reaction-field correction for considering the long-range electrostatic effects. IEF-PCM calculations were performed for the tautomeric solutes with cavity radii of 12 Å around all solute atoms. The resulting cavity was established upon overlapping spheres around all solute atoms with sphere radii = SCUT = 12 Å. For comparison, Ewald summation²² also was applied for the model when the protonated N-methyl piperazine and a chloride counterion were immersed in the solvent box. The N(tertiary)…Cl distance was fixed at 10 Å in a water box, whereas both fixed-distance ion-pair models and models with freely moving ions were considered in organic solvents.

Studying the (CH₃)₃C⁺..Cl⁻ ion-pair^30a and the (CH₃)₄N⁺..Cl⁻ ion-pair,^30b Jorgensen et al. found little ion association in aqueous solution. Our experimental results for dissolution features for the N-methyl piperazine HCl salt suggested that the salt dissolves in a dimeric form in DCM. Thus the possible association of the organic cation was followed by calculating the potential of mean-force (pmf) curve both in DCM and aqueous solutions (for computational details, see Supporting Information).

If solute molecules undergo partial dimerization, then the following relationships apply for the association constant, K_a³¹

$${\mathrm{K}}_{\mathrm{a}}=\mathrm{\alpha }/[2{(1-\mathrm{\alpha })}^{2}c]$$ 9a

$$-\mathit{\text{RT}}\text{ln}{\mathrm{K}}_{\mathrm{a}}={{\mathrm{\mu }}_{\mathrm{d}}}^{\mathrm{o}}-2{{\mathrm{\mu }}_{\mathrm{m}}}^{\mathrm{o}}$$ 9b

$${\mathrm{K}}_{\mathrm{a}}=2\pi {\mathrm{N}}_{\mathrm{A}}{10}^{-3}{\displaystyle \mathrm{\int }{\mathrm{r}}^2\text{exp}(-\mathrm{\Delta }\mathrm{G}(\mathrm{r})/\mathit{\text{RT}})\text{dr}}$$ 9c

For the symbols in eqs. 9a–c, c is the total solute concentration and a is the fraction of the solute involved in self-association. Subscript “d” and “m” refer to the dimer and the monomer, respectively, N_A is the Avogadro number. K_a is obtained in dm³/mole, if r is provided in Å. ΔG(r) stands for the pmf, and the integration goes from r=0 to an accepted r_max upper limit for the largest separation of the dimer reference atoms (the center of the rings in the present case).

Results and Discussion

Gas phase calculations

When in-solution free energy differences are to be calculated as a sum of internal and solvation-related terms (eq. 2), error cancellation may emerge in theoretical calculations. Good accord with the experimental values may be obtained despite possibly considerable errors in the calculated contributing terms. It is desirable then to study the capacity of the applied theoretical level by separate consideration of the internal energy and solvation related terms.

Comparison of the calculated proton affinities (PA) and gas-phase basicities with available experimental data may serve as a good test. The gas-phase protonation results for piperidine (6), N-Me-piperidine (7) and piperazine (8) are summarized in Table S3. The calculated ΔH(T) values are in good agreement with the experimental PA values¹⁹ upon B3LYP/6-311++G** geometry optimization and subsequent frequency calculation. Singly-point B3LYP/aug-cc-pvtz calculations increase the ΔE values only by 0.1 kcal/mol. ΔE^QCISD(T)_CBS values based on MP2/aug-cc-pvdz geometry optimization deviate from the B3LYP/6-311++G** energy differences by not more than 0.5 kcal/mol, corresponding to differences of less than 0.25% for the PA’s. Thus the protonation results on the basis of B3LYP/6-311++G** optimization and energy calculations are as acceptable as those from the much more time consuming QCISD(T)/CBS calculations for our structurally similar ring systems. It is noteworthy that ΔH(T) includes thermally excited vibrational energy contributions, as well, thus the ΔE + ΔZPE + Δ(H(T)_vibr − ZPE) terms together predicted correct values for proton affinities.

The role of the correctly predicted relative frequency- and entropy-related terms can be seen by the close agreement of the predicted gas-phase basicities, ΔG, and experimental values. Deviations from the experimental values were up to 1.1 kcal/mol, corresponding to 0.5% error at most. The experimental values have been published in Ref. 19 without an uncertainty range. Assuming that a ±2 kcal/mol experimental uncertainty published for haloacetic acids¹³ is typical, the present deviations are well within this limit.

Continuum solvent test calculations

For determining relative pK_a values, calculations of the in-solution deprotonation energies, ΔE^s_int = (E(B) − E(BH⁺)) and the related solvation free energies suffice (Table 1). Optimized geometric parameters show small dependence on the solvent environment. The individual internal energies optimized in-solution necessarily increase in comparison with their gas-phase counterparts, which were obtained without considering the polarization effect of the environment. In contrast, the ΔE^s_int energy may both increase and decrease upon solvation. The latter case (compare Tables S3 and 1) simply indicates that the internal energy of the protonated species increased more than that of the neutral form in solution. The larger polarization effect for the protonated species leads to more negative solute-solvent electrostatic interaction energy. Relative internal energies are compared on the basis of B3LYP/6-31G*, B3LYP/6-311++G**, B3P86/6-311++G**, and MP2/aug-cc-pvdz optimizations, frequencies and concomitant thermal corrections were calculated at each optimization level.

Table 1.

IEF-PCM calculated (B-BH⁺) energy and free energy differences in the aqueous solution^a

	ΔEsint	ΔG(T)th	ΔEelst	ΔGdrc	ΔGsol	ΔGtot
B3LYP/6-31G*
Piperidine	238.4	−9.7	54.1	−0.3	53.9	282.6
N-Me piperidine	241.6	−9.7	49.7	−0.3	49.4	281.3
Piperazineb	237.2	−9.1	53.7	−0.3	53.5	281.6
B3LYP/6-311++G**
Piperidine	235.4	−9.7	53.7	−0.2	53.5	279.2
N-Me piperidine	239.5	−9.8	49.3	−0.3	49.0	278.8
Piperazineb	233.7	−9.0	53.5	−0.2	53.3	278.0
B3P86/6-311++G**
Piperidine	236.3	−9.8	53.6	−0.2	53.4	279.9
N-Me piperidine	240.2	−9.8	49.2	−0.3	48.9	279.3
Piperazineb	234.6	−9.1	53.4	−0.2	53.2	278.7
	ΔEsint					ΔGsol
	MP2 aug-cc-pvdz	MP2 aug-cc-pvtz/SP	MP2CBS	QCISD(T) aug-cc-pvdz/SP	QCISD(T)c CBS
Piperidine	233.2	233.7	233.9	234.8	235.4	53.6
N-Me piperidine	237.6	237.9	238.1	239.4	239.8	49.2
Piperazine	231.3	231.8	232.0	232.9	233.5	53.7

^aEnergy terms in kcal/mol. By approximating ΔG^o_tot as ΔG_tot, ΔG_tot was calculated according to eq. 3.

^bEntropy decreased by 0.41 kcal/mol for the neutral piperazine due to a rotational symmetry number of 2 for a species with C_2h symmetry.

^cThe ΔE values were calculated as ΔE (QCISD(T)/CBS) = ΔE(MP2_CBS)+(ΔE(QCISDT(aug-cc-pvdz))-ΔE(MP2(aug-cc-pvdz))).The ΔE(MP2_CBS) values were estimated on the basis of aug-cc-pvdz optimization and aug-cc-pvtz single-point calculations. MP2 thermal corrections deviate from the B3LYP/6-311++G** values by up to −0.1 kcal/mol.

The relative internal energies were the most positive at the B3LYP/6-31G* level. Using the 6-311++G** basis set in DFT calculations, the ΔE^s_int values were higher by 0.7–0.9 kcal/mol when the B3P86 functional was applied as compared to the B3LYP functional. Differences in the thermal corrections and the ΔG_sol values were negligible for these calculations. The calculated IEF-PCM/ΔE^QCISD(T)_CBS values were very close to the IEF-PCM/B3LYP/6-311++G** ΔE^s_int energy differences.

Relative pK_a values (Table 2) at the B3LYP/6-31G* level did not follow the experimental trend. The trend was good in all other cases, but the ΔpK_a was too small for N-Me-piperazine by the ab initio method. The DFT methods also underestimated this pK_a difference by 0.3–0.4 units. A ΔpK_a of 0.65 for N-Me-piperazine compared to piperazine was, however, well predicted at the B3LYP/6-311++G** and the ab initio levels by providing ΔpK_a= 0.60 and 0.84, respectively. Overall we conclude that the computationally inexpensive B3LYP/6-311++G** level provided balanced results in calculating ΔpK_a values. Klicic et al.^2c calculated pK_a values at the B3LYP/cc-pvtz level. No remarkable change was calculated by us (see next section) when the cc-pvtz rather than the 6-311++G** basis set was applied for estimating internal energy differences through the tautomeric protonation.

Table 2.

Relative pK_a values from IEF-PCM calculations

	pKa (exp)a	ΔpKa	ΔpKa (calc)
			B3LYP 6-31G*	B3LYP 6-311++G**	B3P86 6-311++G**	QCISD(T) CBS
Piperidine	11.12	0.00	0.00	0.00	0.00	0.00
N-Me piperidine	10.38	−0.74	−0.93	−0.30	−0.45	−0.05
Piperazine	9.73	−1.39	−0.71	−0.90	−0.87	−0.89

^aRef. ¹⁹.

Continuum solvent calculations for monoprotonated N-Me piperazine

Variations of the relative internal energies and IEF-PCM solvation free energies calculated at different levels of theoretical approaches for the monoprotonated N-Me piperazine are summarized in Tables S4a and S4b. Hence codes NMps and NMpt will be used for the tautomer protonated at the secondary (2a) and the teriary nitrogen (2b), respectively. Unless otherwise noted, NMpt refers to the chair conformation of the ring.

On the basis of their strongly different dielectric constants, ε, the solvent effect of three solvents [water (ε = 78.39), acetonitrile (ε = 35.84) and dichloromethane (ε = 8.92)] were examined. Water can act both as a hydrogen-bond donor and acceptor. Acetonitrile is an acceptor, whereas DCM is practically not involved in any type of hydrogen bond.

Table S4a reports an extended study of the basis set effect and the effect of the geometry optimization on the calculated ΔE^s_int = E(NMps) − E(NMpt) values at the B3LYP level in solution, and the results are compared with QCISD(T)/CBS ΔE^s_int energy differences. The main conclusion is that except for the B3LYP/6-31G* calculations, ΔE^s_int values vary by about 0.1–0.2 kcal/mol with different basis sets at the IEF-PCM/B3LYP level. The QCISD(T)/cc-pvtz//B3LYP/6-31G* and the QCISD(T)/CBS// MP2/aug-cc-pvdz ΔE^s_int values differ by 0.02–0.05 kcal/mol in different solvents. The ΔE^s_int values decrease in the sequence of water, acetonitrile and DCM solvents according to any method. Thus the less polar solvent gradually stabilizes the internal energy for NMps relative to NMpt.

Table S4b summarizes the calculated ΔG_sol(PCM) values (see eq. 3). All terms are negative, indicating that the solvation is preferable for the NMps tautomer compared to the NMpt tautomer in any solvent. The terms change by only a few tenths of a kcal/mol if different basis sets are used in case of any given solvent. In contrast, the absolute values of the ΔG_sol terms decrease by up to 0.8 kcal/mol for the sequence of water, acetonitrile, DCM. Through B3LYP calculations, the reaction field was generated on the basis of the DFT wave function, thus the image charges were obtained by means of a wave function accounting partially for the electron correlation. In contrast, ΔG_sol was calculated at the HF level for QCISD(T) by the version of the IEF-PCM program as implemented in Gaussian 03. Nonetheless, the ΔG_sol values were close to each other whether calculated at the HF or the DFT level if the same basis set (cc-pvtz or aug-cc-pvtz) was applied.

All these values above refer to the chair conformation of the piperazine ring. The ring may flip over, however, for a limited time as suggested by NMR experiments (see below) and adopt a twist-boat (TB) conformation. For 1,4-dioxane, TB structures are higher in free energy than the chair form by 6.5–6.8 kcal/mol in aqueous solution³² with ΔE^s_int = 7.0–7.3 kcal/mol at the B3LYP/6-31G* level. In those conformations, two oxygen lone pairs get too close to each other, considerably raising the conformer energy. In the TB structure for protonated piperazine derivatives, an N-H bond faces the lone pair of the other nitrogen. The IEF-PCM/B3LYP/6-31G* optimized H…N distances are 2.35–2.48 Å in water and 2.34–2.45 Å in DCM, respectively. Such short N…H separations would considerably reduce the TB relative energy compared to that for 1,4-dioxane, and may facilitate an intramolecular proton relocation when solvent involvement is not expected throughout the tautomerization. The TB(t) relative energy in aqueous solution, thus the energy of the twist-boat structure relative to the chair form, was calculated at only 3.3–3.6 kcal/mol when the tertiary nitrogen was protonated. The TB(s) energy relative to that for the chair NMps structure is 3.5 kcal/mol at the IEF-PCM/B3LYP/6-311++G**//IEF-PCM/B3LYP/6-31G* level. The TB(s) – TB (t) energy values calculated with the 6-31G* and 6-311++G** basis sets inform about the proton tautomerization energy for the TB structures. The values of 4–5 kcal/mol are close to their counterparts calculated for the chair conformers both in water and in CH₂Cl₂.

It was assumed throughout our calculations that the chloride ion would be greatly separated from the protonated basis in aqueous solution, thus all IEF-PCM calculations were carried out for the pure cation. NMR results suggested, however, that the ion-pair may not be separated in DCM solvent, and a stable hydrogen-bonded structure could exist. Thus ion-pair calculations were carried out, as well, where the reference system is NMpt…Cl with an N-H…Cl hydrogen bond. For NMps, two isomeric systems were studied with NH_ax…Cl and NH_eq…Cl hydrogen bonds. Geometries of these systems were optimized both at the IEF-PCM/B3LYP/6-31G* and IEF-PCM/MP2/6-31G* levels. The calculated equilibrium H..Cl distances were similar: 1.94–1.97 Å and 1.97–1.98 Å at the B3LYP and MP2 level, respectively. The B3LYP/6-311++G**/SP values indicate a stability order of NMtH⁺…Cl⁻ > NMsH_eq⁺…Cl⁻ > NMsH_ax⁺…Cl⁺, without considering thermal corrections (Tables S4a,b).

The tautomerization preference depends on ΔG_tot (eq. 3). Total free energies for the chair conformer of the NMps cation relative to the chair NMpt cation in different solvents are compared Table 3. Common in Table 3 is that the ΔG_tot values become more positive in the series water, acetonitrile, and DCM. Thus the stability of the NMps cation relative to the NMpt cation decreases with decreasing polarity of the solvent. The sign of the ΔG_tot values is model dependent, and is most critical for the aqueous solution. The values were calculated in the range of −0.02 to 0.62 kcal/mol with basis sets larger than 6-31G*. The NMps/NMpt ratio is 47/53 based on the B3LYP/6-311++G** relative free energy in infinitely dilute solution. Consideration of the TB conformations in the equilibrium caused negligible shifts in the calculated ΔG_tot value. ΔG_tot was 0.52 kcal/mol in DCM at the same theoretical level, which corresponds to a tautomer ratio of NMpt:NMps = 71:29. However, the NMpt tautomer was not detected through ¹H NMR experiments in DCM and the NMR spectrum in D₂O was interpreted as showing predominantly the NMps tautomer.

Table 3.

IEF-PCM relative free energies in solution for N-Me piperazine in chair conformation and protonated at the secondary compared to the tertiary nitrogen^a

	B3LYP 6-31G*	B3LYP 6-311++G**	B3LYP cc-pvtz/SP	B3LYP aug-cc-pvtz/SP	QCISD(T) cc-pvtz/SP	QCISD(T) CBS
Water	−0.57	0.07	−0.02	0.16	0.62	0.43
CH3CN	−0.56	0.14	−0.03	0.16	0.67	0.52
CH2Cl2	−0.08	0.52	0.48	0.65	1.14	0.95

^aEnergies in kcal/mol. Single-point (SP) calculations were performed at the B3LYP/6-31G* optimized geometry. ΔG_th corrections based on B3LYP/6-31G* geometry optimizations were also considered in /SP values. ΔG_th calculated upon B3LYP/6-311++G** optimization was considered for calculating the corresponding QCISD(T)/CBS ΔG_tot value, as well. ΔG_th values utilized in the table are as follows: B3LYP/6-31G*: 0.10, −0.10, 0.00 kcal/mol; B3LYP/6-311++G**: −0.04, −0.17, −0.16 kcal/mol; MP2/aug-cc-pvdz: −0.08, −0.17, −0.16, in water, CH₃CN, and CH₂Cl₂, respectively.

NMR studies

Our original idea was that coupling of the methyl protons with the tertiary nitrogen proton would give rise to a doublet for the methyl protons in ¹H NMR. Indeed, such splitting for the H-C(4)-CH₃ moiety was observed for the 4-Me-piperidine (4) in DCM (Fig. S1.). For the N-Me-piperidine HCl salt (5), no splitting was detected for the methyl protons in the ¹H NMR spectrum at room temperature (Fig. S2). However, cross peaks correlating the N-CH₃ and (CH3-N)-H protons were observed in the 2D COSY experiment (Fig. S3).

Proton NMR spectra were recorded at 75 mg/1.5 ml and 1mg/1.5 ml concentration for the free base (1) (Figures S4 and S5), monosalt (2a/2b) (75 mg/1.5 ml, Figure S6), and for the N-Me-piperazine dication (3) (Figures S7 and S8) in D₂O at room temperature. The pK_a values for the first and second protonation were found experimentally as 9.1–9.3 and 4.9–5.2 at T=298 K.³⁴ Accordingly, solutions for both the free base and the dication are expected to include about 0.5% monoprotonated ion at pH = 7. No multiplet splittings were observed for the methyl group although the tertiary nitrogen in the N-Me-piperazine dication was protonated. The rapid hydrogen exchange in D₂O prevents the observation of a multiplet for the methyl hydrogens. The indication for the N(t) protonation comes from the observed reduction in shielding of the methyl protons causing the chemical shift to move from 2.21 ppm for the unprotonated species to 3.02 ppm for the diprotonated species.

The ¹H NMR spectrum for the N-Me-piperazine monosalt (2a/2b) indicated a chemical shift of 2.45 ppm for the methyl group in D₂O at the concentration of 75 mg/1.5 ml = 0.366 mol/dm³ (Fig. S6). There are two possible interpretations for this observed value. Either the N(s) protonation caused a 0.24 ppm shift for the methyl signal compared to its value in the free base, or an equilibrium emerged for the protonation at the N(s) and N(t) sites. In the latter case, the system may be considered as undergoing a rapid two-site exchange. On one site, the N(s) atom is protonated and the chemical shift of CH₃ protons is 2.21+0.12 ppm. The 0.12 ppm correction was applied on the basis of the in-DCM experiments (see below) and the related calculations are described in detail in the Supplementary information. In the other site, N(t) is protonated and the chemical shift of CH₃ protons is 3.02–0.12 ppm. Considering the system as a mixture of the two sites, a ratio of 80/20 was obtained for the NMps and NMpt tautomers.

Variable temperature ¹H NMR and COSY experiments were utilized for the assignment of the protonation site for the monoprotonated N-Me-piperazine ion in deuterated DCM solvent with solution concentration of 75mg/1.5 ml (Figures S9–S12). There was no difference in the spectra when the monosalt (2a/2b) was prepared either through experimental routes 1 or 2. Thus even if water was present in route 1, it was removed either by vaporization or did not enter the solution when the monosalt (2a/2b) was dissolved in dichloromethane. The similarity of the spectra and the reaction yields from both experiments suggests that no water assisted proton relocation might emerge in reaching the favored protonated tautomer.

Due to a rapid chair-chair ring inversion through some twist-boat conformation for the piperazine ring at room temperature, axial and equatorial CH₂ protons were non-distinguishable by ¹H NMR and the H-N-H peak also appeared as a broad singlet. Hence the temperature was gradually lowered in order to slow down the rate of conformational changes, which enabled the separation of axial and equatorial resonances for CH₂ and N-H atoms. The axial and equatorial protons attached to carbons became clearly distinguishable around 223 K, but an even lower temperature (166 K) was necessary for the observation of two distinct N-H peaks in the ¹H NMR (Figure S11). The difference for the chemical shifts of the equatorial and the axial proton was obtained at 166 K, just above the freezing point of the sample. A 2D COSY experiment at this temperature indicated cross peaks between both N-H protons and also with the protons attached to carbons in the ring closer to secondary amine (Fig. S12). The NMR lines were broad, so no multiplet patterns were observed. No cross peaks were observed for the N-methyl group with any N-H atoms. In contrast, a COSY cross peak was found for N-Me-piperidine (5), where only the methylated nitrogen could be protonated. Thus the NMR data support the protonation at N(s) in DCM solvent.

The free energy of activation at coalescence for an equally populated two-site system, with equatorial and axial sites undergoing exchange in our case, is given by^33c

$$\mathrm{\Delta }{\mathrm{G}}_{\mathrm{c}}=\text{aT}[9.972+\text{log}(\mathrm{T}/\mathrm{\Delta }\mathrm{\delta })]$$ (10)

where a = 4.575 × 10⁻³ kcal mol⁻¹ and T is the temperature where the NMR lines from axial and equatorial protons just coalesce. The overall uncertainty in the determination of the coalescence temperature is 2^o K. Since Δδ = |δ_axial − δ_equatorial | is more than 1 order of magnitude larger than the J couplings, the contribution of the latter term is relatively small and is not included in the computation of ΔG_c (Table 4).

Table 4.

Measured NMR characteristics for the protonated N-methyl piperazine in dichloromethane solvent

	1H shifts (ppm)	|δaxial − δequatorial |	Coalescence	ΔG
CH2 near N(t)	2.84 & 2.33	304.6 Hz	238.6K	10.69 kcal mol−1
CH2 near N(s)	3.33 & 2.98	206.2 Hz	236.5K	10.85 kcal mol−1
NH2	9.31 & 9.62	187.5 Hz	213.5K	9.79 kcal mol−1

The free energy of activation is dominated by the conformational change for the piperazine ring. Thus ΔG_c must be larger than ΔE^s_int + ΔG_sol(PCM) for the local energy minimum twist-boat structure compared to the chair form. Our calculated value is 5.6–6.2 kcal/mol at the 6-311++G**/SP level with reference to the NMpt structure (Tables S4a,b) and does not contradict an activation free energy of about 10 kcal/mol as determined by variable temperature NMR experiments. Overall, the NMR experiments concluded that there was no observable protonation at the N(t) atom of N-Me-piperazine in DCM, and the predominant tautomer was protonated at N(s) in aqueous solution. These findings are in contrast to the theoretically predicted preference for the tautomers (Table 3).

Monte Carlo simulations

Results obtained at different simulation conditions are compared in Table 5. The main point here is whether infinitely dilute systems or solutions of finite concentration should be studied in comparison with the experimental results. One solute molecule in a solvent box of edges a = 25Å corresponds to about 0.1 mol/dm³ concentration. Preliminary studies showed that in the absence of restrictions imposed on the cation-anion distance for an ion-pair and not applying the Ewald summation, the N(protonated)…Cl separation amounted to 10–15 Å after considering 20 M configurations in aqueous solution. Without Ewald summation the solution may be considered as infinitely dilute, because the BOSS program does not consider interactions between molecules in the central and image boxes. (Only the minimum image convention is applied by calculating the interaction for the closest cation-anion pair. The maximum distance of the reference atoms is (√3/2)a, corresponding to about 21.7 Å for the considered water box.) These studies suggest that the infinitely dilute model, considering a reaction field for the long-range electrostatic interactions, is applicable in order to calculate μ_j^o_sol − μ_i^o_sol. By application of the Ewald summation, an approximately 0.1 molar solution would be studied.

Table 5.

Comparison of the relative solvation free energies for the tautomeric protonation of N-Me piperazine in different solvents from Monte Carlo simulations and IEF-PCM calculations^a

	ΔG(FEP)sol	ΔG(PCM)solb
Water
Infinitely dilute, CHELPG	−3.22±0.11
Infinitely dilute, RESP	−3.79±0.11	−4.52, −4.50
Ewald + counterion (fix distance), CHELPG	−3.10±0.11
Ewald + counterion (fix distance), RESP	−2.90±0.11
CH3CN, CHELPG charges
Infinitely dilute,	−4.46±0.07	−4.25, −4.30
Ewald + counterion (fix distance)	−4.38±0.07
Ewald + counterion (freely moving)	−1.48±0.07
CH2Cl2, CHELPG charges
Infinitely dilute	−2.38±0.05	−3.74, −3.72
Ewald + counterion (fix distance)	−1.96±0.04
Ewald + counterion (freely moving)	−4.40±0.05

^aEnergies in kcal/mol. Values are for the free energy difference of G_sol(H⁺N(secondary)) − G_sol(H⁺N(tertiary)). Unless indicated, atomic charges were derived upon the CHELPG fit to the in-solution IEF-PCM/B3LYP/6-31G* molecular electrostatic potential for Monte Carlo calculations. Reaction field corrections applied in simulations with infinitely dilute solutions.

^bRelative solvation free energy values on the basis B3LYP/6-311++G** and QCISD(T)/CBS calculations from Table S4b.

Calculations for ion-pairs with fixed distances were performed by keeping the N(t)…Cl distance at 10 Å allowing for rotation of the cation about random axes through the N(t) atom. In case of water solvent, free movement of the ions led to large noise for the ΔG(FEP) terms at every intermediate step, preventing a reliable estimation of the solvation free energy difference for the two tautomeric cations. No such problems were noted with the organic solvents if the equilibration phase considered 7.5 – 22.5 M configurations. The standard deviations for the ΔG(FEP) increments were a few hundredths of a kcal/mol when 7.5 M configurations were considered for averaging.

Another central issue is the charge set to be utilized for simulations. Performance of the CHELG and RESP charges for different systems were studied previously. RESP charges were preferable considering the infinitely dilute aqueous solution model for the protonated amine serotonin^5c or for the isonicotinic acid zwitterion.^12a Use of the CHELPG charges rather than RESP charges provided better agreement with the experimental data in organic solvents.^12b

Table 5 shows that the calculated ΔG(FEP)_sol is not very sensitive to the applied modeling condition (infinitely dilute or Ewald summation with fixed ion separation) if the CHELPG charges are used. The deviations amounted up to 0.4 kcal/mol. Utilizing the RESP charges for aqueous solution simulations, ΔG_sol is less negative by 0.9 kcal/mol when the Ewald summation was considered. This feature of the RESP charges is in accord with the previous experience above.^12a

In organic solvents, ΔG_sol differs significantly whether the N…Cl distance is kept at a fixed value or the anion is allowed to freely move. ΔG(FEP)_sol is remarkably more negative in the latter case in DCM solvent. Nonetheless, combination of the IEF-PCM/6-311++G** relative internal free energies with ΔG(FEP)_sol values do not predict NMps/NMpt ratios in accord with the experimental values for any studied system.

The final configurations in case of a freely moving anion show that the chloride is hydrogen bonded to the protonated nitrogen site in DCM. This finding suggests that the anion may play a remarkable structure-building role in solutions of finite concentration, and this role may be revealed from calculations where at least two ion-pairs are considered in the model system.

In a 1 molar solution, the average volume per molecule is 1 dm³/N_A = 1661 ų, corresponding to a cube with an edge size of 11.84 Å. In a lattice-like arrangement of the solute in these cubes, the ring center…ring center separation is 11.84 Å. This separation was considered as the reference separation, thus the upper limit for two associated cations. Accordingly, the pmf values were calculated up to this center…center distance. For larger separations the relative free energy was accepted from the IEF-PCM/B3LYP/6-311++G** calculations.

The NMps/NMpt ratio at finite concentration was calculated according to the A8 formula in the Appendix. The formula shows a dependence on the total solute concentration. This dependence reflects that the protonation and association (dimerization) equilibria exist in parallel for each tautomer. The contribution of 1 mole solute to the Gibbs free energy of the system changes depending on the degree of association for the given tautomer. Both the monomer and the dimer have been considered of equal capacity for protonation, but the different degree of association for the two tautomers shifts the chemical potential. Formula A8 was derived on the basis that NMps/NMpt could be determined by means of the requirement for μ_NMps = μ_NMpt in equilibrium. The considered concentration was 0.366 moles N-methyl piperazine HCl / dm³ both in aqueous solution and in DCM, in accord with those in the NMR experiments.

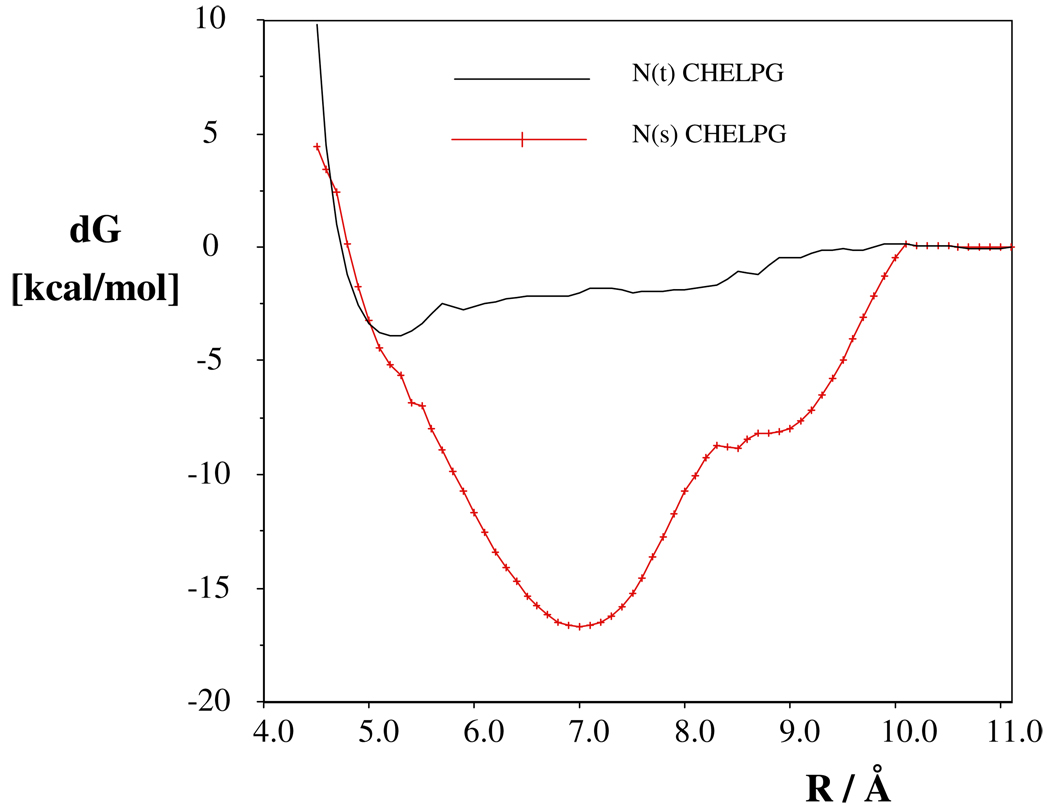
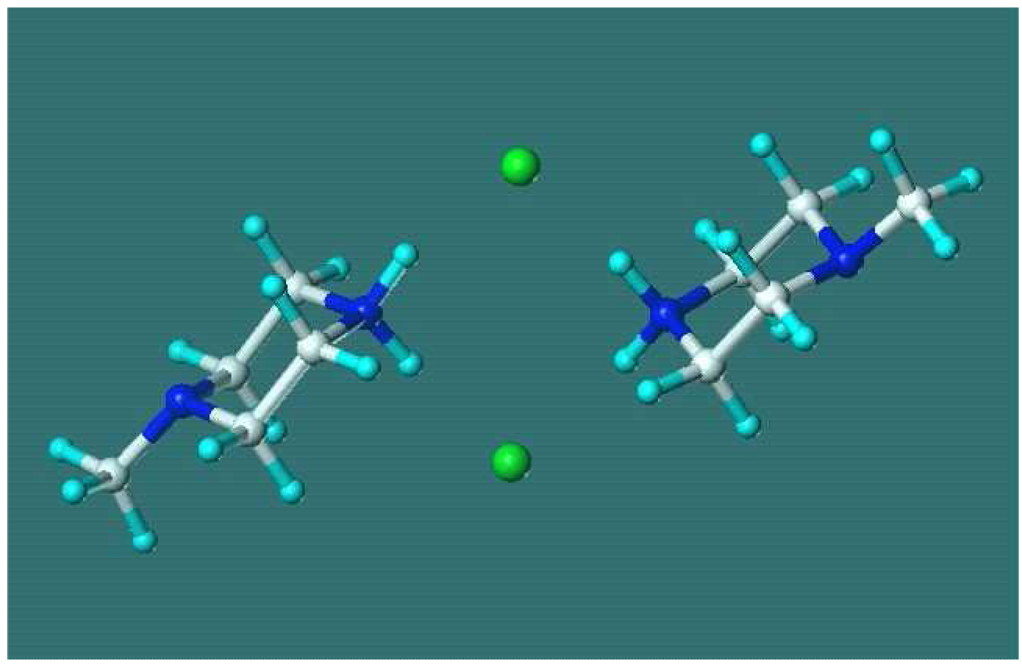
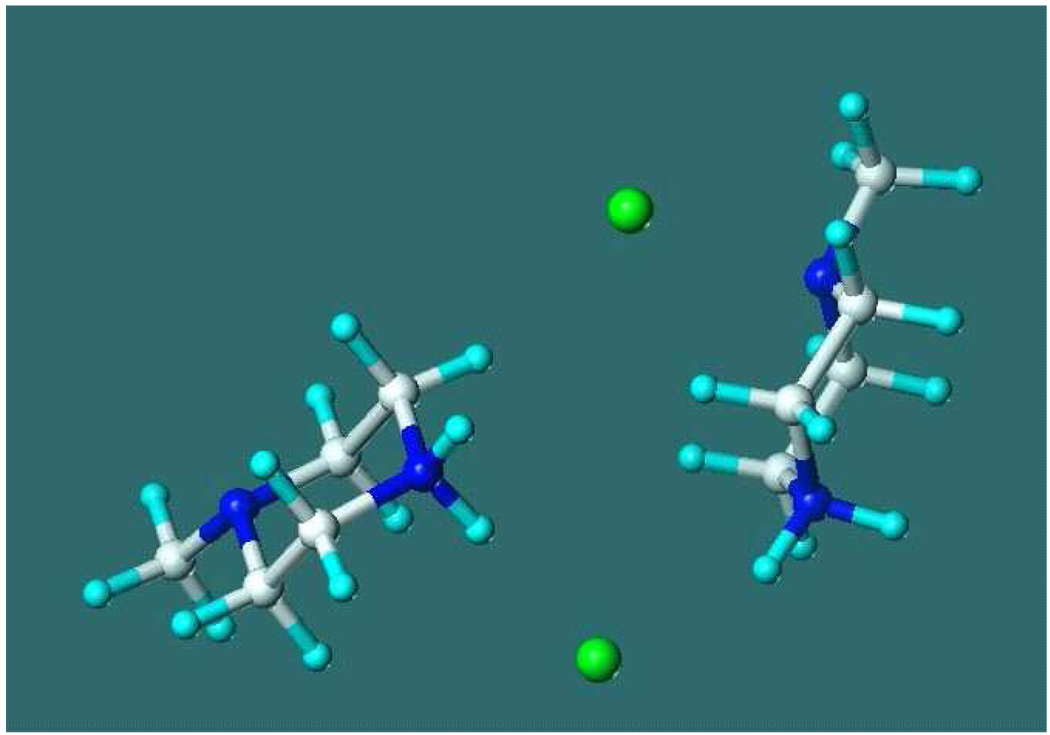
Potentials of mean-force curves were calculated in aqueous solution and in DCM by considering two moles of the salt in solvent boxes. With DCM solvent (Figure 1), the pmf values are nearly constant for r > 10 Å, and two, non-connecting hydrogen-bonded N-Me-piperazineH⁺…Cl− complexes were noticed for each tautomer at such separations. When the separations of the centers of the rings get shorter than 10.1 Å, the association dramatically stabilizes the NMps tautomer. In the most preferred arrangement of two NMps rings (separation of the centers is 7.0 Å, Figure 2), four H⁺…Cl hydrogen bonds came into existence upon the formation of an eight-member ring and were stably maintained throughout the averaging phase. In contrast, no such preferable structure, even at the minima of the pmf, 5.2 Å is possible for NMpt (see Figure S13). The determined K_a association constant was about nine orders of magnitude larger for NMps than for NMpt. This difference, as calculated from A8, accounts for the experimentally and exclusively observed NMps tautomer in DCM.

Fig. 1.

Potentials of mean-force for the different protonated tautomers of the N-methyl piperazine HCl salt in dichloromethane. For NMps and NMpt codes, see the text.

Fig. 2.

The structure of the N-methyl-piperazine HCl dimer from the last configuration of the Monte Carlo simulation in dichloromethane. CHELPG charges, protonation at the secondary nitrogen. Distance of the ring centers is 7.0 Å. N(s)H..Cl hydrogen-bond distances are 1.98, 2.11, 2.15, 2.31 Å.

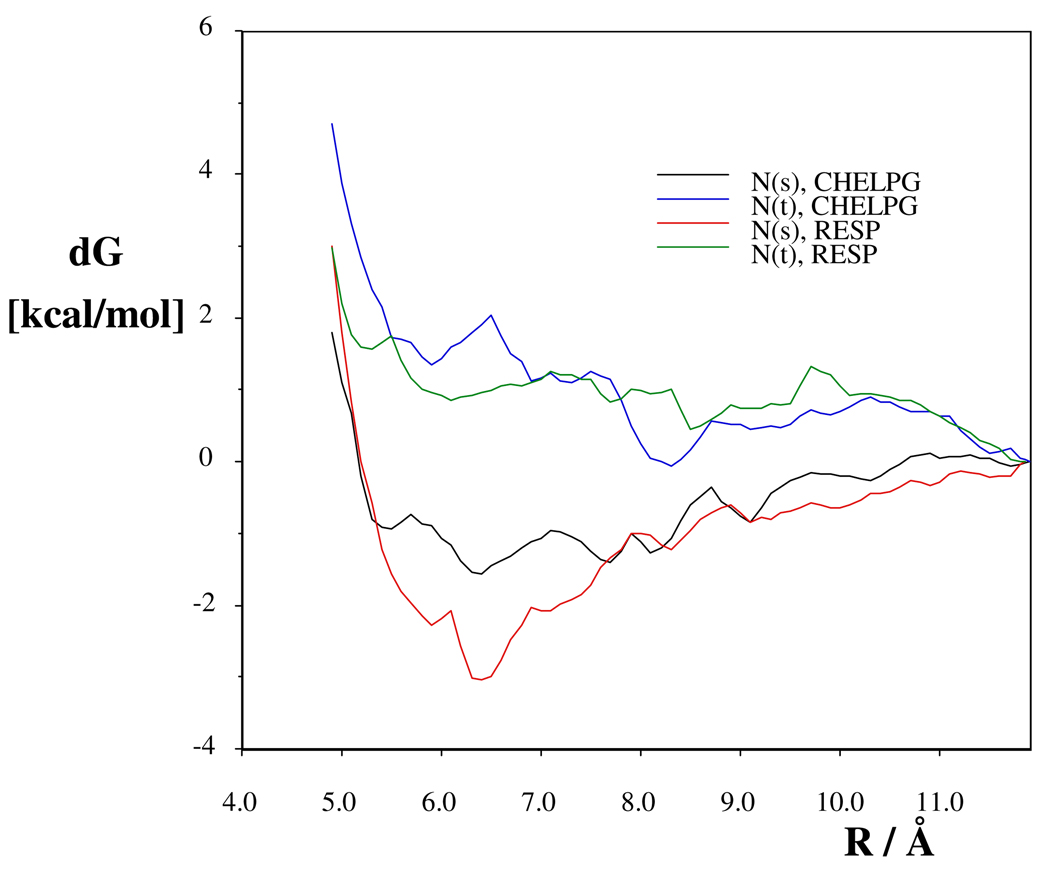
The pmfs with water solvent (Figure 3) also indicate that dimerization is preferable and stabilizes the NMps rather than the NMpt tautomer. The (NMps..Cl)₂ dimer structure shows, however, only two H⁺…Cl⁻ bonds in water (Figure 4) compared to four in DCM, and the (NMpt..Cl)₂ dimer has only one strong H⁺…Cl⁻ bond (Figure S14). Changes in the pmf values for r > 11.84 Å are comparable with the statistical uncertainties for dG(r) in aqueous solution. The derived NMps / NMpt ratios are subject to variations according to the applied CHELPG or RESP charges. The predicted values are 64/36 and 78/22 with the two charge sets, respectively. Both ratios show significant departures from the value of 47/53 obtained for the inifinitely dilute model by the IEF-PCM/B3LYP/6-311++G** method. Thus, consideration of the effect of association for the N-methyl-piperazine HCl is essential in order to predict ratios for the protonated tautomers in accord with the experimental values.

Fig. 3.

Potentials of mean-force for the different protonated tautomers of the N-methyl piperazine HCl salt in aqueous solution. For NMps and NMpt codes, see the text.

Fig. 4.

The structure of the N-methyl-piperazine HCl dimer from the last configuration of the Monte Carlo simulation in aqueous solution. CHELPG charges, protonation at the secondary nitrogen. Distance of the ring centers is 6.4 Å. N(s)H..Cl hydrogen-bond distances are 2.40, 2.48 Å.

The aqueous solution model found that the most stable form for the protonated N-methyl-piperazine was a NMps dimeric structure, when a chloride anion bridges two cations and forms a hydrogen bond with each. (Figure 4). This structure may be maintained for cyclic protonated amines when they penetrate in some protein pore. A tandem penetration of a pair of cationic acetylcholine molecules into the muscarinic receptor was hypothesized by Jakubik³⁵ in a new drug-protein interaction model. Our results suggest that the tandem may not be comprised of only two cations. Instead, a chloride anion, which is abundantly available in the extracellular aqueous phase in humans, can form a bridge between the penetrating pair of the protonated amine or acetylcholine molecules.

Solution structures

Radial distribution functions³⁶ (rdf) provide an insight in the structure of the solvation sphere for specific solute atoms. Coordination numbers are calculated by integrating the rdfs until their first minima (Table 6). Figure 5 and Figure 6 show rdf values for infinitely dilute solution models. Figs. S15 and S16 compare the solute-solvent pair-energy distribution functions (pedf).²³ The integral of the pedf until its first minimum provides the number of strongly bound solvent molecules per solute. In case of a possible solute-solvent hydrogen bond, this number may be considered as the approximate average number of these hydrogen bonds per solute molecule. Table 6 compares the calculated coordination numbers in the first solvation shell of the indicated atoms and the estimated number of the solute-solvent hydrogen bonds in the system.

Table 6.

Calculated coordination numbers and numbers of the solute-solvent hydrogen bonds

	(N)H+/Owat	(N)H/Owat	N/Hwat	(N)H+/Nacn	(N)H/Nacn	H+/ClDCM	nHBa
Water
NMpt	1.0	1.0b	0.7				0.9 (−9.5)
							2.9 (−6.5)d
NMps	1.3c	1.6b	0.1				2.4 (−9.0)
							4.2 (−6.0)d
CH3CN
NMpt				1.5	1.4b		1.1 (−12.0)
							8.9 (−5.0)d
NMps				1.1c	2.0b		3.0 (−10.5)
							7.7 (−5.5)d
CH2Cl2
NMpt						2.5	---
NMps						2.7c	---

Radial distributions were considered from infinitely solution models.

^aValues in parentheses indicate the upper limit for the integration of the solute-solvent pair energy distribution functions.

^bEquatorial hydrogen.

^cAxial hydrogen.

^dTotal number of strongly bound solvent molecules, as calculated by integration until the inflection point of the pedf.

Fig. 5.

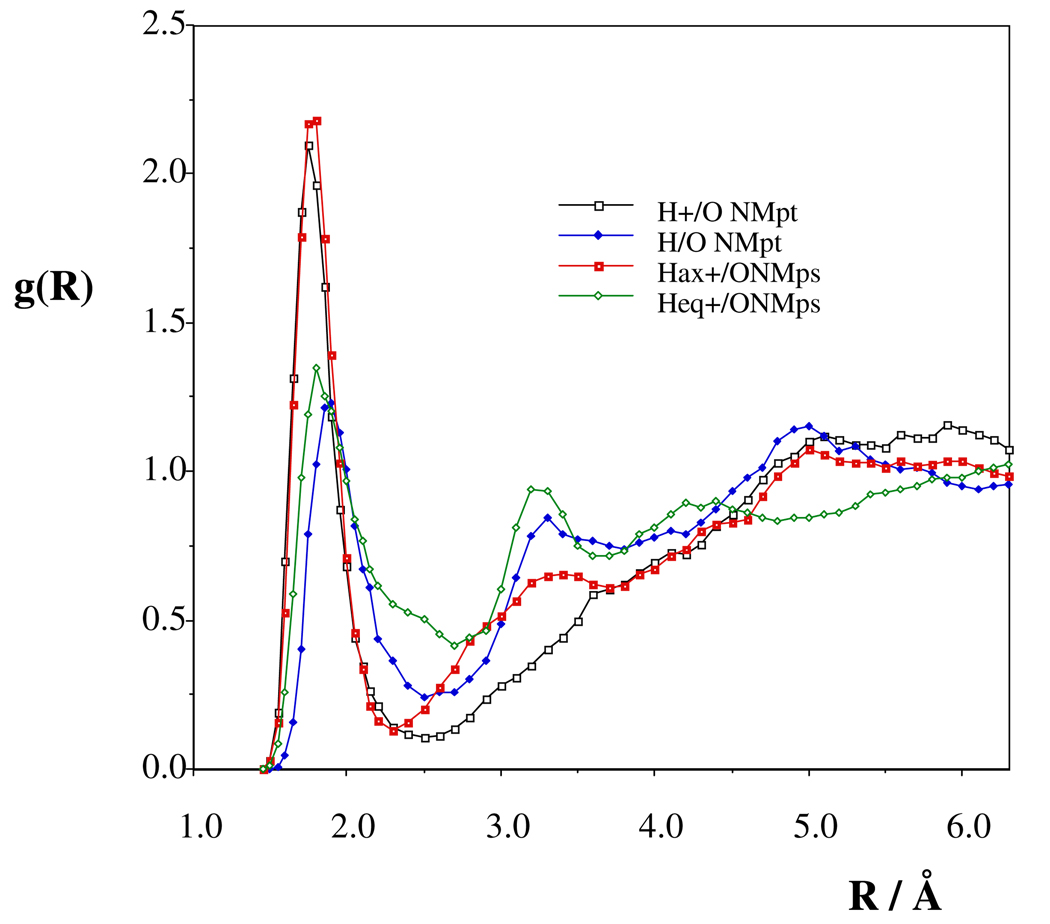
H_solute/O_water radial distribution functions for NMpt and NMps solutes.

Fig. 6.

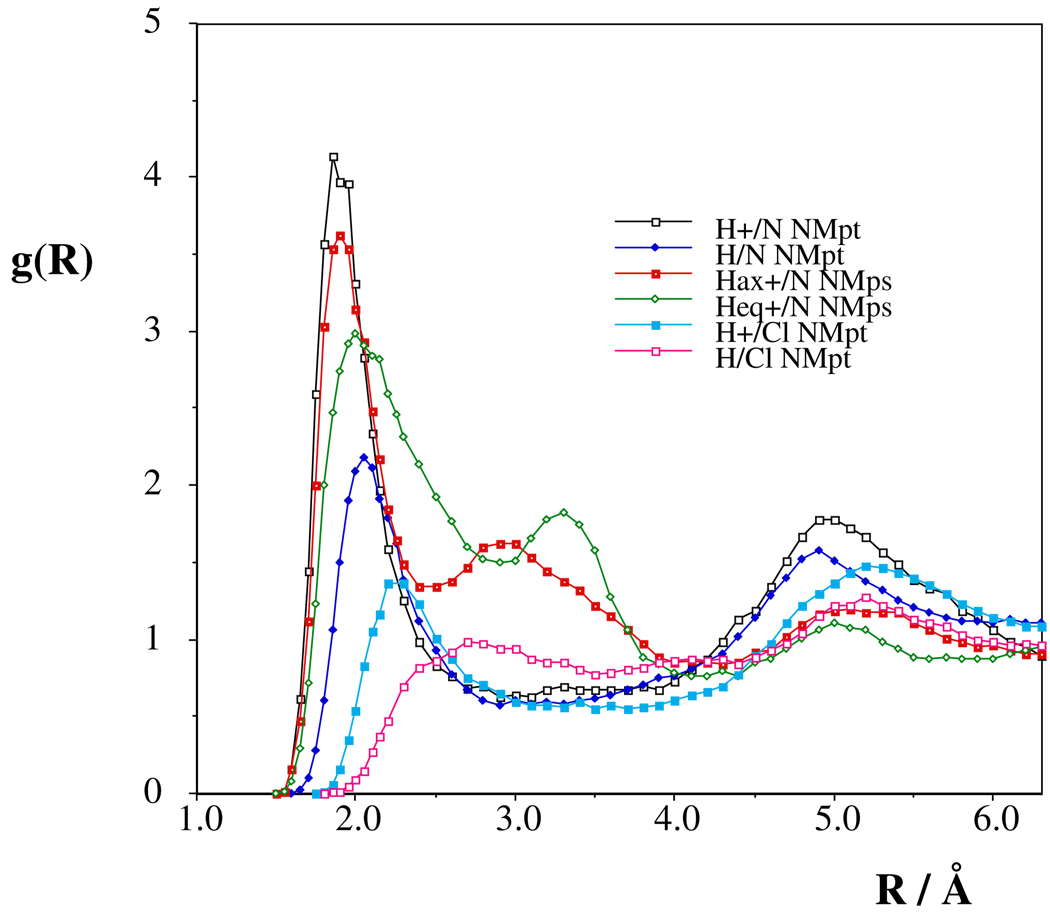
H_solute/N_acn and H⁺/Cl_DCM radial distribution functions for NMpt and NMps solutes in organic solvents.

The H_solute/O_water rdfs (Figure 5) suggest different strengths for the solvent localization around the specified solute atom. The H/O_wat minimum is at 2.35 Å for the axial NH proton in NMps compared to the rdf minimum at 2.75 Å for the equatorial proton on the secondary nitrogen. The more diffuse first solvation shell is reflected by the increased H/O coordination number from 1.3 to 1.6.

The in-water pedfs (Figure S15) show a local minimum at about −9 kcal/mol and an inflection point around −6 kcal/mol. The calculated number of strong hydrogen bonds are much different for the NMps and NMpt tautomers (Table 6). Only the N(t)H⁺…O_wat is strong for the NMpt tautomer, whereas at least two strong hydrogen bonds may be assigned to the N(s)H⁺…O_wat interactions. By integration of the NMpt pedf up to about − 6 kcal/mol, the N(s)..H_wat contribution would be also counted, but this possible hydrogen bond does not cause a resolved peak. It overlaps with contributions due to fairly strong N(t)H⁺…O_wat interactions, where O_wat atoms, beyond the hydrogen-bond distance but still within the first solvation shell, contribute to the pedf.

There are 1.4–1.5 acetonitrile nitrogens around any solute (N)H hydrogen atom in NMpt, providing altogether 1.2 strong N-H… N_acn hydrogen bonds (Figs. 6, S16). The difference of the location of the first minimum for the (N)H⁺/N_acn rdfs with axial and equatorial proton in NMps almost doubles the calculated coordination numbers. By considering the extended tails for the H⁺/N_acn rdfs, the acetonitrile nitrogens with a total H/N_acn coordination number of about 3 can create three hydrogen bonds with solute only if long hydrogen bonds are also counted in the total of 3 in Table 6.

The dichloromethane solvent does not form hydrogen bonds with the solute. Approximately 2.5–2.7 chlorine atoms are expected in the first solvation shell of the proton in infinitely dilute solution. It is worth mentioning, however, that the chloride counterion forms a stable N-H⁺…Cl⁻ hydrogen bond in solution of about 0.1 molar and a high level of association is expected even in very dilute solutions.

Interpretation of the ΔG_sol(FEP) values in combination with the explored solution structure characteristics suggests that the more negative ΔG_sol values for the NMps tautomer is mainly related to its better capacity for hydrogen-bond formation. The larger number of strongly bound acetonitrile than water molecules was attributed to the difference in the solvent dipole moments of 3.43 D and 2.18 D for the acetontirile and TIP4P water models, respectively.^26a,25 Furthermore, dispersion interactions with the solute are larger in case of acetonitrile rather than water solvent. Dispersion interactions are also important in the DCM solvent, where, however, the strongest interaction is of electrostatic origin between the cation and the chloride counterion at finite concentration. ΔG_sol(FEP) is considerably more negative in water and acetonitrile than in the DCM solvent for the infinitely dilute system. This difference for ΔG_sol was revealed only to a lesser extent from IEF-PCM calculations (see Table S4b).

Conclusions

B3LYP/6-311++G** and QCISD(T)/CBS calculations predicted proton affinities and gas-phase basicities in good agreement with the experimental values for six-member saturated heterocyles with one or two nitrogen atoms. Good estimates for the relative pK_a of piperazine and N-methyl piperidine upon IEF-PCM calculations were obtained at the B3LYP/6-311++G** level.

The calculated relative free energies for the protonated N-methyl piperazine tautomers differ by about 0.4 kcal/mol in calculations at the B3LYP/6-311++G** and QCISD(T)/CBS levels applied in the IEF-PCM continuum solvent model with three different solvents (ε = 8.92–78.39). Both methods predict the tertiary nitrogen as the favorable protonation site in infinitely dilute solution. The preference for the NMpt protonation increases when the solvent polarity decreases. NMR experiments, however, predict the secondary nitrogen as the exclusive protonation site in dichloromethane, and an NMps/NMpt ratio of 80/20 was derived for the protonated tautomers on the basis of NMR experiments in D₂O.

Calculation of the relative solvation free energy using explicit solvent models through Monte Carlo/FEP simulations do not provide results that, in combination with relative IEF-PCM internal free energies, would predict NMps/NMpt ratio in accord with the experiment. An accord was achieved only by assuming fractional association for the cations. A formula was derived that takes into consideration the parallel equilibria for the protonation and association. The NMps tautomer compared to the NMts tautomer could form a more preferred dimeric structure, where a chloride anion(s) is/are in hydrogen bonds with protons of the associating monomers. The calculated NMps fraction is about 100% in DCM, whereas the predicted NMps/NMpt ratio varies between 64/36 and 78/22, depending on the solute charge parameterization.

The calculations suggest that the proton relocation may take place by solvent assistance in water or along an intramolecular proton jump in the twist-boat conformation of the solute with relative free energy of about 6 kcal/mol. The predicted activation free energy is about 10 kcal/mol on the basis of variable temperature NMR experiments in DCM.

Appendix

Our model systems in Monte Carlo simulations were comprised of N_sv solvent molecules, and one molecule for each of the cation and the anion. The Gibbs free energies for the systems with cation “i” and “j” and anion “a” are

$$\mathrm{G}(\mathrm{i})={\mathrm{N}}_{\text{sv}}{\mathrm{\mu }}_{\text{sv}}+{\mathrm{\mu }}_{\mathrm{i}}+{\mathrm{\mu }}_{\mathrm{a}}$$ A1a

$$\mathrm{G}(\mathrm{j})={\mathrm{N}}_{\text{sv}}{\mathrm{\mu }}_{\text{sv}}+{\mathrm{\mu }}_{\mathrm{j}}+{\mathrm{\mu }}_{\mathrm{a}}$$ A1b

where “μ”s stand for the chemical potential of one mole of the respective components.

For the chemical equilibrium of species in structurally well-defined states (see below), the equilibrium constant is related to the change of the standard chemical potentials (μ^o) of the components as −RT ln K = Δμ^o. For obtaining the K = j/i value, characterizing the equilibrium ratio of two tautomeric species in the present case, the value of the (μ_j^o − μ_i^o) term is to be determined.

The chemical potential of one mole of species “k” in solution can be provided as

$${\mathrm{\mu }}_{\mathrm{k}}={{\mathrm{\mu }}_{\mathrm{k}}}^{\mathrm{o}}+\mathit{\text{RT}}\text{ln}{\mathrm{a}}_{\mathrm{k}}=({{{\mathrm{\mu }}_{\mathrm{k}}}^{\mathrm{o}}}_{\text{int}}+{{{\mathrm{\mu }}_{\mathrm{k}}}^{\mathrm{o}}}_{\text{sol}})+\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\mathrm{k}}{\mathrm{X}}_{\mathrm{k}}$$ A2

where a_k, γ_k, and x_k are the activity, activity coefficient, and the molar fraction for component “k”, respectively.

In case of similar cations and equal anions appearing in eqs. A1a and A1b, eq. A3 is a reasonable approximation for the difference of the solution free energies

$$\mathrm{G}(\mathrm{j})-\mathrm{G}(\mathrm{i})={\mathrm{\mu }}_{\mathrm{j}}-{\mathrm{\mu }}_{\mathrm{i}}={{{\mathrm{\mu }}_{\mathrm{j}}}^{\mathrm{o}}}_{\text{int}}-{{{\mathrm{\mu }}_{\mathrm{i}}}^{\mathrm{o}}}_{\text{int}}+{{{\mathrm{\mu }}_{\mathrm{j}}}^{\mathrm{o}}}_{\text{sol}}-{{{\mathrm{\mu }}_{\mathrm{i}}}^{\mathrm{o}}}_{\text{sol}}+\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\mathrm{j}}{\mathrm{X}}_{\mathrm{j}}/{\mathrm{\gamma }}_{\mathrm{i}}{\mathrm{\text{X}}}_{\mathrm{i}}$$ A3

In our dilute solutions, N_sv ≫ 1 applies with x_sv ≈ 1. Thus the solution is almost ideal from the point of view of the solvent and γ_sv is close to 1 in both systems. The molar fraction is constant for all components, and γ_a could be also nearly constant in cases of similar cations. Thus (N_sv μ_sv + μ_a) cancels out in eq. A3.

$$\mathrm{\Delta }\mathrm{G}=\mathrm{\Delta }{{\mathrm{\mu }}^{\mathrm{o}}}_{\text{int}}+({{{\mathrm{\mu }}_{\mathrm{j}}}^{\mathrm{o}}}_{\text{sol}}-{{{\mathrm{\mu }}_{\mathrm{i}}}^{\mathrm{o}}}_{\text{sol}}+\text{RT}\text{ln}{\mathrm{\gamma }}_{\mathrm{j}}/{\mathrm{\gamma }}_{\mathrm{i}}=(\mathrm{\Delta }{\mathrm{E}}_{\text{int}}+\mathrm{\Delta }{\mathrm{G}}_{\mathrm{t}\mathrm{h}})+\mathrm{\Delta }\mathrm{G}(\text{FEP}{)}_{\text{sol}}$$ A4

Δμ^o_int in eq. A4 corresponds to (ΔE_int+ΔG_th) for one mole of the cation and was obtained from IEF-PCM quantum chemical calculations in the present study. The solvation related free energy change, ΔG(FEP)_sol, could be obtained from MC simulations utilizing the free-energy perturbation (FEP) method.²¹

μ_k^o_sol in eq. A2 refers to a hypothetical state defined in terms as vapor pressure and the Henry constant, which makes its use inconvenient for computational chemistry calculations. A more pragmatic formulation of the chemical potential of one mole solute at concentration “c” mol/dm³ in the solution is:

$${\mathrm{\mu }}_{\mathrm{c}}={{\mathrm{\mu }}_{\mathrm{c}}}^{\mathrm{o}}+\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\mathrm{c}}\mathrm{c}/{\mathrm{c}}_{\mathrm{o}}=({{{\mathrm{\mu }}_{\mathrm{c}}}^{\mathrm{o}}}_{\text{int}}+{{{\mathrm{\mu }}_{\mathrm{c}}}^{\mathrm{o}}}_{\text{sol}})+\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\mathrm{c}}{\mathrm{c}/\mathrm{c}}_{\mathrm{o}}$$ A5a

where the μ_c^o standard chemical potential is comprised of internal and solvation related contributions at c_o = n_o mole solute / V_o dm³ concentration (n_o ≡ 1 mole, V_o ≡ 1dm³), and γ_c is the concentration dependent activity coefficient.

The (A2) and A5a expressions provide the same chemical potential value at any corresponding composition by setting

$$\begin{array}{c}\mathrm{x}={\mathrm{n}}_{\text{su},\mathrm{c}}/({\mathrm{n}}_{\text{su}}+{\mathrm{N}}_{\text{sv}}{)}_{\mathrm{c}}=({\mathrm{n}}_{\text{su},\mathrm{c}}/{\mathrm{n}}_{\mathrm{o}})\times {\mathrm{n}}_{\mathrm{o}}/({\mathrm{n}}_{\text{su}}+{\mathrm{N}}_{\text{sv}}{)}_{\mathrm{c}}=({\mathrm{n}}_{\text{su},\mathrm{c}}/{\mathrm{V}}_{\mathrm{o}}{\mathrm{c}}_{\mathrm{o}})\times {\mathrm{n}}_{\mathrm{o}}/({\mathrm{n}}_{\text{su}}+{\mathrm{N}}_{\text{sv}}{)}_{\mathrm{c}}=\hfill \\ \hfill =(\mathrm{c}/{\mathrm{c}}_{\mathrm{o}})\times {\mathrm{n}}_{\mathrm{o}}/({\mathrm{n}}_{\text{su}}+{\mathrm{N}}_{\text{sv}}{)}_{\mathrm{c}}\hfill \end{array}$$ A5b

$${{{\mathrm{\mu }}_{\mathrm{c}}}^{\mathrm{o}}}_{\text{sol}}={{{\mathrm{\mu }}_{\mathrm{x}}}^{\mathrm{o}}}_{\text{sol}}+\mathit{\text{RT}}\text{ln}{({\gamma }_{\mathrm{x},\text{co}}{\mathrm{n}}_{\mathrm{o}}{/(\mathrm{n}}_{\text{su}}{+\mathrm{N}}_{\text{sv}})}_{\text{co}}$$ A5c

$${\mathrm{\gamma }}_{\mathrm{c}}=({\mathrm{\gamma }}_{\mathrm{x},\mathrm{c}}/{\gamma }_{\mathrm{x},\text{co}})\times {({\mathrm{n}}_{\text{su}}+{\mathrm{N}}_{\text{sv}})}_{\text{co}}/{({\mathrm{n}}_{\text{su}}{+\mathrm{N}}_{\text{sv}})}_{\mathrm{c}}$$ A5d

N_sv and n_su refer to the number of moles of the solvent and solute components, respectively, at the concentration c_o or c, as indicated as subscript. Subscript “x” refer to the corresponding term in the molar-fraction-based definition of the chemical potential in eqs. A5c,d. Knowing the solution density, the molar composition can be calculated at any concentration in the V_o ≡ 1dm³ volume, and γ_x,c stands for γ_k (A2) at concentration “c”. From the A5d definition, γ_co = 1 at c = c_o, providing μ_co = μ_c^o_int + μ_c^o_sol from A5a.

If an α fraction of the solute with total concentration of c_k is involved in self-association forming (α/2)c_k mole dimer per dm³, the contribution of one mole of species “k” to the total free energy of the system (A1a,b) follows as

$$\begin{array}{cc}{\mathrm{\mu }}_{\mathrm{k}}={{{\mathrm{\mu }}_{\mathrm{k}}}^{\mathrm{o}}}_{\text{int}}\hfill & +(1-\mathrm{\alpha })({{{\mathrm{\mu }}_{\text{km}}}^{\mathrm{o}}}_{\text{sol}}+\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\mathrm{k}\mathrm{m}}(1-\mathrm{\alpha }){\mathrm{c}}_{\mathrm{k}}/{\mathrm{c}}_{\mathrm{o}})+\hfill \\ \hfill & +(\mathrm{\alpha }/2)({{{\mathrm{\mu }}_{\text{kd}}}^{\mathrm{o}}}_{\text{sol}}+\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\text{kd}}(\mathrm{\alpha }/2){\mathrm{c}}_{\mathrm{k}}/{\mathrm{c}}_{\mathrm{o}})\hfill \end{array}$$ A6a

where indices “m” and “d” refer to the monomeric and dimeric form, respectively. The internal free energy related term was accepted to remain unchanged throughout the dimerization process. The term α can be determined from eq. 9a, and by applying eq. 9b, μ_kd^o_sol can be expressed by means of the association constant:

$$\begin{array}{cc}{\mathrm{\mu }}_{\mathrm{k}}={{{\mathrm{\mu }}_{\mathrm{k}}}^{\mathrm{o}}}_{\text{int}}+{{{\mathrm{\mu }}_{\text{km}}}^{\mathrm{o}}}_{\text{sol}}-0.5\mathrm{\alpha }\mathit{\text{RT}}\text{ln}{\mathrm{K}}_{\mathrm{a}}\hfill & +(1-\mathrm{\alpha })\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\text{km}}(1-\mathrm{\alpha }){\mathrm{c}}_{\mathrm{k}}/{\mathrm{c}}_{\mathrm{o}}\hfill \\ \hfill & +(\mathrm{\alpha }/2)\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\text{kd}}(\mathrm{\alpha }/2){\mathrm{c}}_{\mathrm{k}}/{\mathrm{c}}_{\mathrm{o}}\hfill \end{array}$$ A6b

In the equilibrium mixture of the protonated N-methyl piperazine, c(NMps) + c(NMpt) = c_tot applies. By defining c(NMps) = βc_tot, c(NMpt) = (1-β)c_tot, then from A6b

$$\begin{array}{c}{\mathrm{\mu }}_{\mathrm{s}}(\mathrm{\beta }{\mathrm{c}}_{\mathrm{\text{tot}}})={{{\mathrm{\mu }}_{\mathrm{s}}}^{\mathrm{o}}}_{\text{int}}+{{{\mathrm{\mu }}_{\mathrm{s}}}^{\mathrm{o}}}_{\mathrm{\text{sol}}}-0.5{\mathrm{\alpha }}_{\mathrm{s}}\mathit{\text{RT}}\text{ln}{\mathrm{K}}_{\mathrm{a},\mathrm{s}}+(1-{\mathrm{\alpha }}_{\mathrm{s}})\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\text{sm}}(1-{\mathrm{\alpha }}_{\mathrm{s}})\mathrm{\beta }{\mathrm{c}}_{\mathrm{\text{tot}}}/{\mathrm{c}}_{\mathrm{o}}\hfill \\ \hfill +({\mathrm{\alpha }}_{\mathrm{s}}/2)\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\mathrm{s}\mathrm{d}}({\mathrm{\alpha }}_{\mathrm{s}}/2)\mathrm{\beta }{\mathrm{c}}_{\mathrm{\text{tot}}}/{\mathrm{c}}_{\mathrm{o}}\\ {\mathrm{\mu }}_{\mathrm{t}}((1-\mathrm{\beta }){\mathrm{c}}_{\mathrm{\text{tot}}})={{{\mathrm{\mu }}_{\mathrm{t}}}^{\mathrm{o}}}_{\text{int}}+{{{\mathrm{\mu }}_{\mathrm{t}}}^{\mathrm{o}}}_{\mathrm{\text{sol}}}-0.5{\mathrm{\alpha }}_{\mathrm{t}}RT\text{ln}{\mathrm{K}}_{\mathrm{a},\mathrm{t}}+(1-{\mathrm{\alpha }}_{\mathrm{t}})\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\mathrm{t}\mathrm{m}}(1-{\mathrm{\alpha }}_{\mathrm{t}})(1-\mathrm{\beta }){\mathrm{c}}_{\mathrm{\text{tot}}}/{\mathrm{c}}_{\mathrm{o}}\hfill \\ \hfill +({\mathrm{\alpha }}_{\mathrm{t}}/2)\mathit{\text{RT}}\text{ln}{\mathrm{\gamma }}_{\mathrm{t}\mathrm{d}}({\mathrm{\alpha }}_{\mathrm{t}}/2)(1-\mathrm{\beta }){\mathrm{c}}_{\mathrm{\text{tot}}}/{\mathrm{c}}_{\mathrm{o}}\end{array}$$ A7a,b

where indices “s” and “t” refer to NMps and NMpt, respectively.

In equilibrium, μ_s(βc_tot) = μ_t((1-β)c_tot). Upon the structural similarity, it is reasonable to assume that γ_sm ≈ γ_tm, and γ_sd ≈ γ_td. By taking some average γ_m value for γ_sm and γ_tm, and some γ_d for γ_sd and γ_td, A8 follows:

$$\begin{array}{c}({{{\mathrm{\mu }}_{\mathrm{s}}}^{\mathrm{o}}}_{\text{int}}+{{{\mathrm{\mu }}_{\mathrm{s}}}^{\mathrm{o}}}_{\mathrm{\text{sol}}}-{{{\mathrm{\mu }}_{\mathrm{t}}}^{\mathrm{o}}}_{\text{int}}-{{{\mathrm{\mu }}_{\mathrm{t}}}^{\mathrm{o}}}_{\mathrm{\text{sol}}})/\mathit{\text{RT}}-0.5({\mathrm{\alpha }}_{\mathrm{s}}\text{ln}{\mathrm{K}}_{\mathrm{a},\mathrm{s}}-{\mathrm{\alpha }}_{\mathrm{t}}\text{ln}{\mathrm{K}}_{\mathrm{a},\mathrm{t}})+(1-{\mathrm{\alpha }}_{\mathrm{s}})\text{ln}(1-{\mathrm{\alpha }}_{\mathrm{s}})-(1-{\mathrm{\alpha }}_{\mathrm{t}})\text{ln}(1-{\mathrm{\alpha }}_{\mathrm{t}})+\hfill \\ +({\mathrm{\alpha }}_{\mathrm{s}}/2)\text{ln}({\mathrm{\alpha }}_{\mathrm{s}}/2)-({\mathrm{\alpha }}_{\mathrm{t}}/2)\text{ln}({\mathrm{\alpha }}_{\mathrm{t}}/2)+0.5({\mathrm{\alpha }}_{\mathrm{t}}-{\mathrm{\alpha }}_{\mathrm{s}})\text{ln}{\mathrm{c}}_{\mathrm{\text{tot}}}/{\mathrm{c}}_{\mathrm{o}}+({\mathrm{\alpha }}_{\mathrm{t}}-{\mathrm{\alpha }}_{\mathrm{s}})\text{ln}{\mathrm{\gamma }}_{\mathrm{m}}-0.5({\mathrm{\alpha }}_{\mathrm{t}}-{\mathrm{\alpha }}_{\mathrm{s}})\text{ln}{\mathrm{\gamma }}_{\mathrm{d}}=\hfill \\ (1-{\mathrm{\alpha }}_{\mathrm{t}}/2)\text{ln}(1-\mathrm{\beta })-(1-{\mathrm{\alpha }}_{\mathrm{s}}/2)\text{ln}\mathrm{\beta }\hfill \end{array}$$ A8

The molar fraction, x, of a relatively small organic salt at 1 mol/dm³ concentration in aqueous solution is about 0.02. In the range of x = 0.00–0.02, the system may be considered as a dilute ideal solution, for which (γ_x,c / γ_x,co) (see eq. A5d) could be slightly larger or smaller than unity, considering that γ_x,c → 1, x → 0. The second factor in eq. A5d, (n_su + N_sv)_co/(n_su + N_sv)^c must be slightly smaller than unity, because the number of the total moles/dm³ should decrease with increasing organic component (larger concentration) in the solution, with the exception of extreme large volume contraction. Thus γ_c should have a value of about 1 for a 0.37 molar solution. This argument may apply both for the monomer or the dimer, because A5d does not distinguish explicitly the association feature. A single γ_c was accepted in A8 in the form of γ_m = γ_d = γ_c = 1 ± y, where y= 0.1, leading to a term of 0.5(α_t − α_s)ln (1± y) on the left-hand side of A8.

α_s and α_t depend on βc_tot and (1-β)c_tot, respectively; thus β can be obtained iteratively with a fast convergence from A8 at any c_tot. For aqueous solutions, 0.5(α_t − α_s) was estimated at about −(0.2–0.3), providing a contribution due to the activity term of about ±0.03 kcal/mol. If no association may be expected for NMpt in some solvents, α_t = 0 is to be implemented in A8. The limit for (α_t/2) ln (α_t/2) =0.