Time-frequency dynamics of resting-state brain connectivity measured with fMRI

Abstract

Most studies of resting-state functional connectivity using fMRI employ methods that assume temporal stationarity, such as correlation and data-driven decompositions computed across the duration of the scan. However, evidence from both task-based fMRI studies and animal electrophysiology suggests that functional connectivity may exhibit dynamic changes within time scales of seconds to minutes. In the present study, we investigated the dynamic behavior of resting-state connectivity across the course of a single scan, performing a time-frequency coherence analysis based on the wavelet transform. We focused on the connectivity of the posterior cingulate cortex (PCC), a primary node of the default-mode network, examining its relationship with both the “anticorrelated” (“task-positive”) network as well as other nodes of the default-mode network. It was observed that coherence and phase between the PCC and the anticorrelated network was variable in time and frequency, and statistical testing based on Monte Carlo simulations revealed the presence of significant scale-dependent temporal variability. In addition, a sliding-window correlation procedure identified other regions across the brain that exhibited variable connectivity with the PCC across the scan, which included areas previously implicated in attention and salience processing. Although it is unclear whether the observed coherence and phase variability can be attributed to residual noise or modulation of cognitive state, the present results illustrate that resting-state functional connectivity is not static, and it may therefore prove valuable to consider measures of variability, in addition to average quantities, when characterizing resting-state networks.

Introduction

Studies of the human brain using functional magnetic resonance imaging (fMRI) have revealed collections of distributed regions that exhibit low-frequency, temporally correlated BOLD signal fluctuations in the absence of an explicit task (resting state). Remarkably, these “resting-state networks” tend to comprise regions that are co-activated during tasks and are observed with consistency across subjects and scanning sessions (Damoiseaux et al., 2006; De Luca et al., 2006; Shehzad et al., 2009), suggesting a general principle of functional organization. In recent years, a large number of studies have emerged in an effort to understand the purpose of resting-state networks in subserving cognitive function or basic brain physiology (for reviews, see (Buckner and Vincent, 2007; Fox and Raichle, 2007)).

Currently, the analysis of resting-state networks across a single scanning session typically employs techniques that assume temporal stationarity: measures of linear dependence are computed over the entire scan and used to characterize the strength of connections across regions. Popular methods include seed-based region-of-interest (ROI) analysis, in which the time series of an ROI is used as a regressor to query regions of similar temporal behavior across the brain (Biswal et al., 1995; Greicius et al., 2003; Lowe et al., 1998), and independent component analysis (Beckmann et al., 2005; Kiviniemi et al., 2003; McKeown et al., 1998), which is a model-free approach for identifying spatial regions with temporally coordinated activity. Other methods for characterizing resting-state networks include partial correlation (Fransson and Marrelec, 2008), coherence and partial coherence (Salvador et al., 2005), phase relationships (Sun et al., 2005), clustering (Cordes et al., 2002; Mezer et al., 2009), and graph theory (Achard et al., 2006; Dosenbach et al., 2007).

Previous studies have demonstrated dynamic changes in network connectivity throughout development (Fair et al., 2008; Supekar et al., 2009), aging (Beason-Held et al., 2009), visual state (Bianciardi et al., 2009) and as a function of conscious awareness (Greicius et al., 2008; Horovitz et al., 2009; Martuzzi et al., 2009; Picchioni et al., 2008). Furthermore, there is evidence that inter-regional correlations can be modulated by cognitive processes that occur on time-scales of a typical (several-minute) scan. Task-based studies have revealed that attention (Esposito et al., 2006; Fransson, 2006), learning (Sun et al., 2007), and muscle fatigue (Deshpande et al., 2006) can effect changes in low-frequency dynamics and/or connectivity throughout the performance of the task and in subsequent resting-state scans (Barnes et al., 2009; Duff et al., 2008; Waites et al., 2005). Because the resting state is a condition of undirected wakefulness that may encompass varying levels of attention, mind-wandering, and arousal, one may hypothesize that the connectivity between and within networks may undergo substantial changes across the duration of a scan.

The aim of the present study was to investigate the temporal dynamics of connectivity between nodes of resting-state networks within the course of a 12- or 15-minute scanning session. Here, we focus specifically on the default-mode network (DMN) and regions with which it has negative correlations (the “anticorrelated” network, also referred to as the “task-positive” or “executive-control” network) (Fox et al., 2005; Fransson, 2005; Greicius et al., 2003). These networks, comprised of spatially distinct brain regions, have been shown to have negative correlations in the resting state, a finding that mirrors the opposing signal changes displayed by the two networks during controlled tasks (Toro et al., 2008) and which may emerge in simulated cortical networks (Deco et al., 2009). However, compared with the positive correlations exhibited between nodes within the same network, the magnitude of negative correlations between the two networks have been reported to be weaker and much less consistent (Shehzad et al., 2009), particularly without the controversial processing step of global signal removal (Chang and Glover, 2009; Fox et al., 2009; Murphy et al., 2009).

A possible explanation for the relative weakness of negative correlations is that the presence of common noise across the brain, such as that due to respiration and cardiac processes (Birn et al., 2006; Chang et al., 2009; Shmueli et al., 2007; Wise et al., 2004), biases inter-regional correlation coefficients in the positive direction. A second possibility is that the phase difference between the two networks is variable in time, driven perhaps by cognitive state. Using local field potentials recorded in the feline homologues of the DMN and its anticorrelated network, (Popa et al., 2009) found variable phase differences between gamma power fluctuations of the two networks wherein negative correlations were more frequent during waking and REM sleep compared to slow-wave sleep.

As previous fMRI studies of temporal relationships between the DMN and its anticorrelated network have computed correlation coefficients across all time points in the scan, the observed relative weakness of the negative correlations raises a number of interesting questions. For instance, to what extent, and at what frequencies, do the magnitude and the phase relationships between the networks fluctuate over time? Are negative correlations between the two networks consistently weak, or marked by transient periods of strong negative correlation?

In the current study, we apply a time-frequency analysis -- in particular, wavelet transform coherence -- to examine temporal variability in the relationship between nodes of the DMN and its anticorrelated network. Time-frequency methods are popular in the analysis of EEG, MEG, and electrophysiological data (e.g. see (Le Van Quyen and Bragin, 2007; Mitra and Pesaran, 1999; Roach and Mathalon, 2008)). Wavelet transform coherence has previously been applied to the analysis of neural signals using spike trains and EEG (e.g. (Klein et al., 2006; Li et al., 2007; Zhan et al., 2006) and to fMRI data to study the temporal variability in the phase relationships between different brain regions in a visual task (Muller et al., 2004), and to study resting-state network nodes throughout the course of a working-memory task (Almeida et al., 2007). In addition, to explore regions of the brain having potentially interesting dynamic connectivity with the default-mode network, a whole-brain sliding correlation analysis was applied and regions with large temporal variability in connectivity were identified.

Methods

Data acquisition and standard processing

Subjects

Participants included 12 healthy adults (6 female, aged 27.7 ± 12.4 yrs) recruited from the Stanford University community. All subjects provided written, informed consent, and all protocols were approved by the Stanford Institutional Review Board.

Imaging parameters

Magnetic resonance imaging was performed at 3.0 T using GE whole-body scanners (GE Healthcare Systems, Milwaukee, WI). Four of the 12 subjects (those henceforth labeled as Subjects 1–4) were scanned on a GE Signa HDX (rev. 12M5) using a custom quadrature birdcage head coil, while the remaining 8 subjects were scanned on a GE Signa 750 (rev. 20M3) using an 8-channel head coil. Head movement was minimized with a bite bar. Thirty oblique axial slices were obtained parallel to the AC-PC with 4-mm slice thickness, 1-mm skip. T2-weighted fast spin echo structural images (TR = 3000 ms, TE = 68 ms, ETL = 12, FOV = 22 cm, matrix 192 × 256) were acquired for anatomical reference. A T2*-sensitive gradient echo spiral-in/out pulse sequence (Glover and Lai, 1998; Glover and Law, 2001) was used for functional imaging (TR = 2000 ms, TE = 30 ms, flip angle = 77°, matrix 64 × 64, FOV = 22 cm, same slice prescription as the anatomic images). A high-order shimming procedure was used to reduce B0 heterogeneity prior to the functional scans (Kim et al., 2002). Importantly, a frequency navigation correction was employed during reconstruction of each image to eliminate blurring from breathing-induced changes in magnetic field; no bulk mis-registration occurs from off-resonance in spiral imaging (Pfeuffer et al., 2002).

Resting state scan

All subjects underwent a resting state scan, for which they were instructed only to keep their eyes closed and remain awake. For 5 of the subjects, the duration of the scan was 12 min; for 6 subjects, the total scan duration was 16 min, from which the latter 15 min were extracted for analysis. This is because subjects had been cued to perform a single 10s breath hold at the beginning of the scan as part of a separate study, and breath-holding has been shown to affect the BOLD signal for approximately 40 s (Birn et al., 2008). One subject was scanned for 16 min without performing the initial BH, but only 12 min was used for analysis due to excessive motion during the final minutes of the scan, despite the bite bar.

Physiological monitoring

Cardiac and respiratory processes were monitored using the scanner s built-in photoplethysmograph placed on a finger of the left hand and a pneumatic belt strapped around the upper abdomen, respectively. Cardiac and respiratory data were both sampled at 40 Hz on the Signa HDX, and at 100 Hz and 25 Hz, respectively, on the Signa 750. A file containing cardiac trigger times and respiratory waveforms was generated for each scan by the scanner’s software.

fMRI pre-processing and physiological noise reduction

Functional images were pre-processed using custom C and Matlab routines. The first 5 time frames were discarded to allow the MR signal to achieve T1 equilibration. Preprocessing included slice-timing correction using sinc interpolation, spatial smoothing with a 3D Gaussian kernel (FWHM=5 mm), and removal of linear and quadratic temporal trends. No additional temporal band-pass filtering was performed. Images were corrected for physiological noise by (1) applying RETROICOR (Glover et al., 2000) for the removal of time-locked cardiac and respiratory artifacts, and (2) filtering of low-frequency respiratory volume and heart rate effects using methods (“RVHRCOR”) described in (Chang and Glover, 2009). The time series of ROIs in the white matter and cerebrospinal fluid (CSF) and 6 affine motion parameters were also regressed out of the data. The white matter and CSF ROIs were 3mm-radius spheres centered at MNI coordinates (26,−12,35) and (19, −33, 18), reverse-normalized to each subject s brain (described below), and are identical to those used in (Chang and Glover, 2009). Importantly, global signal removal was not performed, as it is known to falsely increase anticorrelations between time series (Murphy et al., 2009). Motion parameters were calculated using methods described in (Friston et al., 1996).

Normalization and Group analysis

Unless otherwise mentioned, analyses were performed in native subject space. ROIs at specific standard coordinates were defined in MNI space using MarsBar (http://marsbar.sourceforge.net) and reverse-normalized to each subject s mean functional image using SPM5 (http://www.fil.ion.ucl.ac.uk/spm). To examine results at the group level, the relevant single-subject images were normalized to the SPM5 EPI template and entered into a group-level random-effects analysis using SPM5. A nuisance factor of “scanner” was included since subjects had been scanned on 1 of 2 different scanners. Single-subject correlation maps were converted to Fisher z-statistics prior to group analysis using the formula $z={\text{tanh}}^{-1}(r)·\sqrt{N-3}$, where r is the correlation coefficient and N is the number of time points. All coordinates are reported in MNI space, and all figures of group-level activation appear in neurological convention, superimposed on the ch2 template from the MRIcron software (http://www.mricron.com).

Defining network regions of interest

Default-mode and “anticorrelated” network

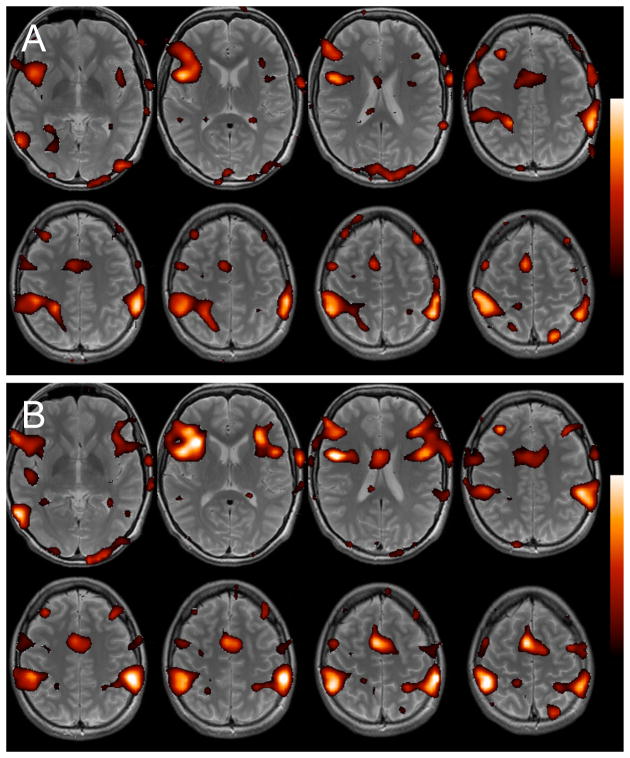
A region in the posterior cingulate (3mm-radius sphere, centered at (x = −6, y = −58, z = 28)) was selected as the primary ROI for the default-mode network. This region corresponds to a peak coordinate in a meta-analysis of task-based coactivation with DMN regions (Toro et al., 2008), and has been shown to display resting-state connectivity with other DMN regions with high test-retest reliability (Shehzad et al., 2009). To examine the set of voxels with similar temporal behavior across the entire duration of the scan, the Pearson correlation coefficient was computed between the full time series of the PCC ROI and that of every other voxel in the brain. It was verified that the PCC ROI exhibited strong correlations with high specificity, at both the individual and group level (Fig. 1), with other regions reported to be involved in the DMN.

Figure 1.

Group-level thresholded t-maps for positive (red) and negative (blue) correlations with the PCC. Clusters are labeled according to Table 1.

One objective of the current study is to examine the dynamic behavior of regions that are most strongly and consistently negatively correlated with the DMN. Because having a large magnitude of overall negative or positive correlation implies small variability of correlation across time, the degree of coupling between these regions and the DMN over time may be considered to yield an upper bound on the stationarity, or constant nature, of negative correlations within the current dataset. Accordingly, regions demonstrating strong negative correlations with the DMN were identified with the following approach. First, single-subject correlation maps with the PCC ROI (computed across all time points, as described above) were entered into a group-level analysis. The resulting (negative) contrast map was thresholded at p<0.01 uncorrected (t>2.76), and bilateral clusters in the supramarginal gyrus (SMG), dorso-lateral prefrontal cortex (DLPFC), and insula were extracted (Table 1). These 6 clusters were reverse-normalized to each subject, and – within each cluster – the voxel having the maximum negative correlation with the PCC across the entire scan was identified. Spheres of 3mm-radius were then drawn around each such voxel, yielding 6 subject-specific “anticorrelated” ROIs.

Table 1.

Clusters of positive and negative correlation with the PCC ROI selected for analysis.

				cluster centroid (mm)
	No.	Region	BA	x	y	z
	D1	MPFC	32/10	−2	50	17
Positive	D2	R. angular gyrus	39	50	−62	28
	D3	L. angular gyrus	39	−44	−69	34
	A1	L. insula	48	−39	8	5
	A2	L. DLPFC	46/45	−46	45	26
Negative	A3	L. SMG	40	−63	−36	41
	A4	R. insula	48	45	13	4
	A5	R. DLPFC	46	45	48	26
	A6	R. SMG	40	59	−36	46

The column ‘No.’ contains the label of the cluster within Fig. 1. BA, Brodmann area; L, left; R, right; MPFC, medial prefrontal cortex; DLPFC, dorsolateral prefrontal cortex; SMG, supramarginal gyrus.

The above procedure aims to maximize the sensitivity of selecting voxels having negative correlation with the PCC, while maintaining anatomical constraints such that results may be compared between subjects and across different brain regions. Two alternative approaches – selecting the peak coordinate of the group analysis to be the same ROI for all subjects, or using independent coordinates from the literature – were not found to yield the strongest negative correlations for all subjects.

For comparison, regions with the strongest positive correlation were defined in a similar manner. The most significant clusters (Table 1), occurring in the medial prefrontal cortex (MPFC) and the left and right angular gyri, were extracted by thresholding the positive contrast of the group-level analysis at t>8 (this threshold is more stringent than that used for negative clusters due to the very large cluster sizes). These 3 clusters were reverse-normalized to each subject, and voxels having maximum positive correlation with the PCC across the entire scan within each cluster were used to define 3 subject-specific 3mm-radius “default-mode” ROIs.

Detecting regions with variable default-mode connectivity

In addition to examining the dynamics of regions having the most consistent positive and negative correlations with the PCC, regions of the brain demonstrating variable correlations with the PCC were queried. For each subject, a whole-brain sliding-window correlation analysis (further described below) was performed against the time series of the PCC ROI. Window sizes of both 2 min and 4 min (60 and 120 time frames, respectively) were used. For each voxel, the standard deviation of its sequence of sliding-window correlation coefficients across the scan was computed. Maps were created to depict the standard deviation values across the brain for each subject, and a group analysis was performed by averaging the spatially-normalized single-subject maps.

Dynamic analysis methods

Wavelet transform coherence

Wavelet transform coherence (WTC) is a method for analyzing the coherence and phase lag between two time series as a function of both time and frequency (Torrence and Compo, 1998), and is therefore well-suited to investigating nonstationary changes in coupling between fMRI time series. WTC is based on the continuous wavelet transform, which decomposes a single time series into time-frequency space by successively convolving the time series with scaled and translated versions of a wavelet function ψ₀ (Mallat, 1999). The continuous wavelet transform of a time series x_n of length N, sampled from an underlying continuous waveform at equal time steps of size Δt, is defined as:

$$W^X(n,s)=\sqrt{\frac{\mathrm{\Delta }t}{s}}\sum _{n^{\prime }=1}^N{x}_n{\psi }_0^{\ast }[(n^{\prime }-n)(\frac{\mathrm{\Delta }t}{s})],$$ (1)

where n is a time index and s denotes the wavelet scale. The function ψ₀ is chosen to be the complex Morlet wavelet:

$${\psi }_0(\eta )={\pi }^{-1/4}{e}^{i{\omega }_0\eta }{e}^{-{\eta }^2/2},$$

where the parameter ω₀ governs the relative time and frequency resolution; here, ω₀= 6, which has been shown to provide a good trade-off between time and frequency localization (Grinsted et al., 2004; Muller et al., 2004). For the Morlet wavelet with ω₀= 6, the Fourier period (T) associated with scale s is approximately equal to the value of s (T = 1.03s). Note that ψ₀ is normalized to unit energy at each scale in Eq. 1, so that the wavelet transforms at each scale are directly comparable.

The wavelet transform W ^X (n,s) is a complex quantity whose modulus expresses the amount of power in x as a function of time and frequency (scale), and whose angle represents the local phase. Similarly, the cross-wavelet transform can be defined for two time series as:

$$W^{XY}(n,s)=W^X(n,s)W^{Y^{\ast }}(n,s),$$

whose modulus |W ^XY (n,s)|, known as the cross-wavelet power, expresses the amount of joint power between x and y as a function of time and frequency, and whose angle tan⁻¹(Im{ W ^XY (n,s)}/Re{W ^XY (n,s)) (cross-wavelet phase) describes their relative phase. Following (Torrence and Webster, 1999), the wavelet transform coherence is defined as

$$R^2(n,s)=\frac{{\left|\langle s^{-1}{W}^{XY}(n,s)\rangle \right|}^2}{{\left|\langle s^{-1}\left|W^X(n,s)\right|\rangle \right|}^2{\left|\langle s^{-1}\left|W^Y(n,s)\right|\rangle \right|}^2},$$ (2)

which reveals localized regions of phase-locked behavior. R² ranges between 0 and 1, and can be conceptualized as a localized correlation coefficient in time and frequency space (Grinsted et al., 2004). The brackets 〈·〉 indicate smoothing in both time and scale: the filter for temporal smoothing is a Gaussian function, which is matched to the Morlet wavelet; the scale smoothing is a boxcar filter (for further discussion, see (Torrence and Webster, 1999)). Implementation of the WTC and cross-wavelet transform was based on a library of MATLAB functions provided by Grinsted et al. (http://www.pol.ac.uk/home/research/waveletcoherence/).

Illustrative example

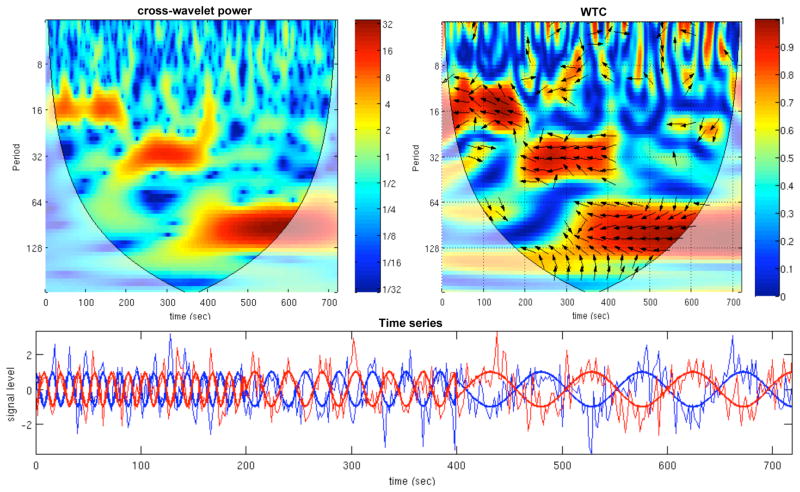
An example of the cross-wavelet power and WTC for simulated time series is shown in Fig. 2. The 2 simulated time series consist of negatively-correlated sinusoids with variable frequency (f=1/16 Hz for 0<t<200 sec, f=1/32 Hz for 200<t<400 sec, and f=1/96 Hz for 400<t<720 sec), embedded in additive independent Gaussian noise with a signal-to-noise ratio (SNR) of 1.25. Time is plotted on the x-axis, scale (which has been converted to its equivalent Fourier period) is on the y-axis. For the cross-wavelet power, the color scale represents the normalized log-spectrum ( ${log}_2\left|\frac{W^{XY}}{{\sigma }_x{\sigma }_y}\right|$) and in the CWT plot, the color scale represents the magnitude of coherence (R²; Eq. 2). The phase angle between the 2 time series at particular samples of the time-frequency plane is indicated by an arrow: a rightward-pointing arrow indicates that the time series are in phase, or positively correlated (φ = 0); a leftward-pointing arrow indicates anticorrelation (φ=π), and the downward- and upward-pointing arrows indicate phase angles of π/2 and −π/2, respectively. Areas inside the “cone of influence”, which are locations in the time-frequency plane where edge-effects give rise to lower confidence in the computed values, are shown in faded color outside of the conical contour. At longer Fourier periods, more time points are included in the cone of influence since wavelets at larger scales have substantial energy over a time window whose length approaches the total length of the data record. Note that due to the smoothing necessary for the WTC, there is poorer time and frequency resolution in the WTC relative to the cross-wavelet power.

Figure 2.

Example of the cross-wavelet power (above left) and wavelet transform coherence (above right) for simulated data (bottom). The simulated data consist of negatively-correlated sinusoids with piecewise frequency content (f = 1/16 Hz for 0<t<200 sec, f = 1/32 Hz for 200<t<400 sec, and f = 1/96 Hz for 400<t<720 sec; thick lines in figure), embedded in Gaussian white noise (SNR=1.25; thin lines in figure). For the WTC, the phase angle between the 2 time series at particular locations in the time-frequency plane is indicated by an arrow (see text for further detail). Regions inside the cone of influence appear in faded color.

Significance testing of wavelet transform coherence variability

It is of interest to know whether the observed pattern of coherence over time between brain regions exhibits significantly greater temporal variability than would be expected if the underlying relationship between the two signals were stationary (time-invariant). To this end, statistical testing of WTC temporal variability was performed using a Monte Carlo procedure based on time-series bootstrapping (Efron and Tibshirani, 1986), described as follows.

Let x and y represent the BOLD signal time series from 2 different ROIs. We first fit a (stationary) vector autoregressive (VAR) model to x and y:

$$\{\begin{array}{c}x(t)=\sum _{i=1}^p{a}_i^{x}x(t-i)+\sum _{i=1}^p{b}_i^{x}y(t-i)+u^x(t)\\ y(t)=\sum _{i=1}^p{a}_i^{y}x(t-i)+\sum _{i=1}^p{b}_i^{y}y(t-i)+u^y(t)\end{array},$$ (3)

where the optimal model order p is chosen according to the Bayesian information criterion (BIC) score, and t is a time index. Coefficients of the VAR model are estimated using least squares. Secondly, we generate 1000 bootstrap time series pairs having the same VAR coefficients (i.e. same stationary relationship) as Eq. 3; see Appendix A for further detail concerning the generation of bootstrap samples. For each bootstrap time series pair, the WTC is computed, yielding both a coherence magnitude (R²_b(n,s)) and phase (φ_b(n,s)) which can be represented together as the complex quantity ${\mathit{WTC}}_b(n,s)=R_b^2(n,s)·e^{i{\phi }_b(n,s)}$, where n denotes time, s denotes scale, and b denotes the bootstrap iteration. A measure of temporal variability at each scale s is computed on WTC_b(n,s) (i.e. for each row in the WTC matrix). Specifically, we define the variability at scale s to be σ_b²(s) = var(WTC_b(n,s)), where the function var(z) = <(z−μ_z)(z−μ_z)*> is the sample variance over a set of complex values (brackets <·> denote the sample mean, * denotes complex conjugate, and μ_z = <z>). By storing σ_b²(s) for each of the 1000 bootstrap samples, we obtain a null distribution for the complex variance at each scale of the WTC, which can be used to obtain confidence intervals and p-values for the WTC of real data (σ²(s)). We have treated each wavelet scale independently because the smoothness characteristics of the WTC are scale-dependent. Note that throughout this procedure, only WTC indices outside the cone of influence (i.e. those less susceptible to edge-effects) are considered.

Significance testing of wavelet transform coherence magnitude

Statistical significance of WTC magnitude (R²(n,s)) is estimated using a similar Monte Carlo approach. An autoregressive process of order p was fit to each input pair of time series (x and y), and a large number (here, 300) of bootstrapped time series pairs with the same AR coefficients and model order as x and y were generated. For each bootstrapped pair, one can calculate the WTC and estimate a null distribution for each scale, from which significance levels are derived. Unlike the above case, which involves testing for significant temporal variation in the WTC, here we are testing for significant coherence magnitude, and thus we do not model AR dependences between the surrogate time series pairs (as the null hypothesis is that a given coherence magnitude can arise between independently-generated processes). The model order for each time series was determined according to the BIC score.

Sliding window correlation analysis

The sliding-window correlation between two time series (x and y) is defined as $\rho (t)=\mathit{corr}(x_t^{t+w-1},y_t^{t+w-1})$, where w is the window size, $x_t^{t+w-1}$ and $y_t^{t+w-1}$ denote the portion of the time series from time t to t+w−1, and corr( ) denotes computation of the correlation coefficient. Sliding window correlation was performed to complement the wavelet coherence analysis and investigate the variability of correlations across the scan. Whole-brain sliding window calculations were implemented in C.

Analysis of potential confounds

Relationship between motion and variable connectivity

Although motion parameters are regressed out of the data as a pre-processing step, it is still possible that intermittent motion may contribute to any observed nonstationarity in the relationship between BOLD signal time series. We thus tested for relationships between motion and correlation variability on both an inter- and intra-subject basis.

Each subject s sequence of 6 rigid-body motion parameters across the scan was converted into two summary measures: (1) maximum drift (peak-to-peak excursion) and (2) maximum root-mean-square (RMS) fluctuation, where the maximum was taken across all 6 parameters. The Pearson correlation coefficient was used to compare, on an inter-subject basis, each of the two motion statistics with each of two different measures of connectivity variability between the PCC and anticorrelated ROIs: (1) the standard deviation of the 2-min sliding-window correlation coefficients and (2) the variance of the WTC at each wavelet scale (σ²(s), defined above). To examine the relationship between motion and connectivity variability on an intra-subject (intra-scan) basis, we partitioned the scan into non-overlapping time intervals of length 20 frames and calculated the fluctuation across motion parameters for each interval; more precisely, the motion fluctuation for the k^th interval (having time points t_k….t_k+20−1) was defined as $M_k={\displaystyle \sum _{j=1}^6}{\displaystyle \sum _{t=t_k}^{t_{k+20-1}}}{(m_j(t)-{\overline{m}}_{j,k})}^2$, where m_j is the j^th motion parameter and m̄_j,k is the mean of m_j within the k^th interval. We then calculated the fluctuation across the sliding-window correlation coefficients that were temporally aligned with the same non-overlapping intervals used in the calculation of M_k; i.e., connectivity fluctuation associated with the for the k^th interval was defined as $V_k={\displaystyle \sum _{r=1}^6}{\displaystyle \sum _{t=t_k}^{t_{k+20-1}}}{({\rho }_r(t)-{\overline{\rho }}_{r,k})}^2$, where ρ_r(t) is the sliding-window correlation coefficient (formula provided above) between the PCC and the r^th anticorrelated ROI (r ranges over A1,…A6 in Table 1), and ρ̄_r,k is the mean of ρ_r within the k^th interval. The resulting sequence M_k of motion-based deviations were then compared to the sequence V_k of connectivity-based deviations using Pearson correlation. Note that non-overlapping time intervals were used in order to minimize autocorrelations between the observations. Note also that V_k represents a longer effective time window than M_k, as each ρ(t) already integrates over a window of data in order to estimate a connectivity value, so this analysis in effect tests whether motion has an influence on the subsequent evolution of correlation variability. Sliding window sizes of both 40 s and 2 min were examined.

Effects of scanner and breath-holding

Inter-subject differences in connectivity variability across subjects may also relate to differences in the scanner used (Signa HDX vs. Signa 750) or the performance of the initial 10-s breath hold (BH) by a subset of subjects. We hypothesized that because the BOLD-signal response to a single deep breath is well-modeled by a function that decays to 0 after approximately 40 s (Birn et al., 2008), then discarding the first 1 min of data would largely remove the effects of the BH. However, the effect of a brief BH on longer-term correlation dynamics has not yet been studied, and it has been reported that more extreme challenges (e.g. (Kiviniemi et al., 2009), who used 2-min of hyperventilation) can alter the dynamic properties of individual BOLD time series. We compared connectivity variability between the 6 “non-BH” subjects and 6 “BH” subjects, where a measure of connectivity variability for each subject was obtained by taking the variance over the sequence of 2-min sliding-window correlation coefficients between the PCC and each of the 6 anticorrelated ROIs over 12 min of data, and summing the resulting variance across the 6 ROI pairs (similar to the above test for the influence of motion). Measures from the BH and non-BH groups were compared using a Wilcoxon rank-sum test, both with and without covarying for motion (maximum drift and RMS fluctuation) and scanner. Differences between subjects scanned at the Signa HDX and those scanned on the Signa 750 were queried using the same procedure.

Results

Default-mode network and anticorrelations

Figure 1 shows group-level t-maps of positive and negative correlation with the PCC ROI, where correlations for each subject were taken over all time points. The maps in Fig. 1 are displayed at a threshold identical to that used for obtaining the default-mode and anticorrelated clusters used as masks for deriving the subject-specific ROIs. Cluster locations (centroids and Brodmann areas) are provided in Table 1. The correlation coefficient (over all time points) between the PCC ROI and the subject-specific ROIs within the default-mode and anticorrelated clusters are provided in Table 2. Negative correlations with the anticorrelated network were weaker than positive correlations within the DMN, having across-subject mean values ranging from −0.26 (L. insula) to −0.40 (L. and R. SMG); those of the positive correlations ranged from 0.78 (R. angular gyrus) to 0.82 (MPFC).

Table 2.

Correlation coefficients (r) between the PCC ROI and subject-specific ROIs corresponding to the 6 anticorrelated and 3 default-mode clusters.

		Anticorrelated clusters (r)						Default-mode clusters (r)
subject	N	L SMG	R SMG	L DLPFC	R DLPFC	L insula	R insula	MPFC	L angular	R angular
1	355	−0.43	−0.41	−0.44	−0.35	−0.30	−0.40	0.83	0.83	0.82
2	355	−0.42	−0.28	−0.26	−0.33	−0.20	−0.22	0.80	0.78	0.80
3	355	−0.36	−0.38	−0.40	−0.41	−0.29	−0.39	0.88	0.83	0.83
4	355	−0.27	−0.30	−0.28	−0.22	−0.21	−0.27	0.69	0.74	0.76
5	355	−0.46	−0.42	−0.29	−0.40	−0.39	−0.39	0.83	0.80	0.77
6	355	−0.29	−0.39	−0.36	−0.36	−0.25	−0.26	0.76	0.80	0.75
7	451	−0.43	−0.47	−0.32	−0.26	−0.22	−0.38	0.83	0.75	0.70
8	451	−0.36	−0.40	−0.38	−0.29	−0.25	−0.32	0.85	0.88	0.80
9	451	−0.30	−0.37	−0.32	−0.38	−0.24	−0.19	0.79	0.68	0.73
10	451	−0.57	−0.59	−0.54	−0.47	−0.33	−0.40	0.85	0.77	0.78
11	451	−0.42	−0.43	−0.17	−0.25	−0.24	−0.40	0.84	0.84	0.74
12	451	−0.50	−0.42	−0.44	−0.47	−0.19	−0.40	0.83	0.86	0.82
mean		−0.40	−0.40	−0.35	−0.35	−0.26	−0.33	0.82	0.80	0.78
stdev		0.09	0.08	0.10	0.08	0.06	0.08	0.05	0.06	0.04

N, total number of time points analyzed in the scan; L, left; R, right; SMG, supramarginal gyrus; MPFC, medial prefrontal cortex; DLPFC, dorsolateral prefrontal cortex.

Wavelet coherence between default-mode and anticorrelated ROIs

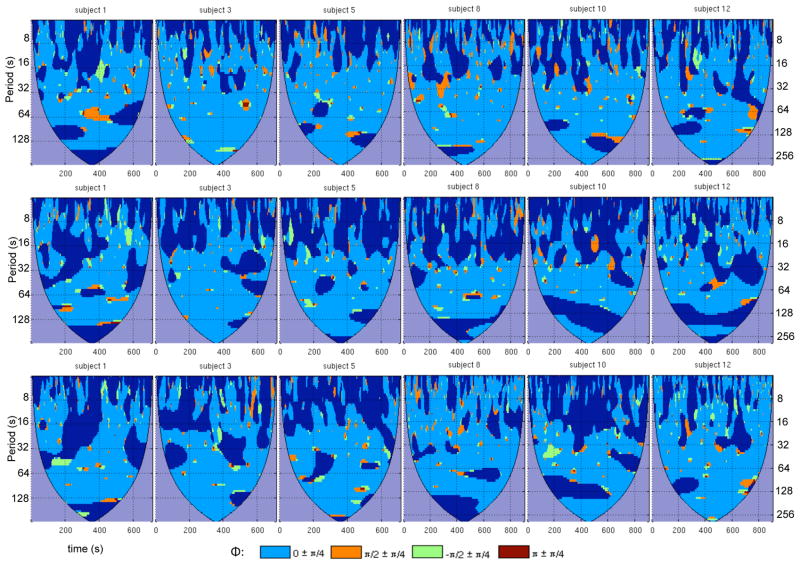
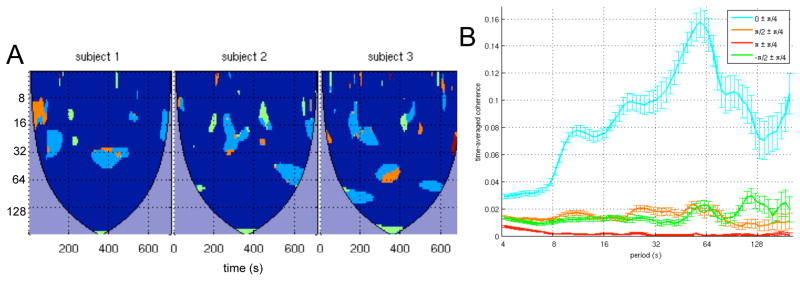
The wavelet transform coherence was computed between the PCC ROI and each of the 6 anti-correlated ROIs and 3 default-mode ROIs. Results of the WTC analysis for anticorrelated ROIs in the right SMG, right insula, and right DLPFC are shown in Fig. 3 for 6 subjects (see supplementary Fig. S1 for all subjects). Also shown are the WTC results between the PCC ROI and the 3 ROIs of the default-mode network (Fig. 4; see supplementary Fig. S2 for all subjects). The WTC maps of Figs. 3 and 4 are of a similar format as Fig. 2. however, for ease of visualization, only pixels whose coherence magnitude exceeds a 95% significance threshold are shown, and discrete ranges of the coherence phase are color-coded as indicated in the figure.

Figure 3.

Wavelet transform coherence between the PCC and 3 of its anticorrelated ROIs, shown for 6 subjects: (top row) right SMG, (middle row) right insula, and (bottom row) right DLPFC. For each WTC map, time is on the x-axis and scale (Fourier period) is on the y-axis. Maps have been thresholded to include only regions that were significant at 95% confidence based on Monte Carlo tests. Colors indicate ranges of the wavelet coherence phase. A phase difference of 0 indicates positive correlation; π indicates negative correlation; π/2 indicates that the PCC ROI leads the anticorrelated ROI; −π/2 indicates that the anticorrelated ROI leads the PCC ROI. Regions of insignificant coherence appear in dark blue, and areas inside the cone of influence are in purple.

Figure 4.

Wavelet transform coherence between the PCC and default-mode ROIs, shown for 6 subjects: (top row) MPFC, (middle row) right angular gyrus, (bottom row) left angular gyrus. For further detail, please refer to the caption of Fig. 3.

Figures 3 demonstrates that the anticorrelated ROIs exhibit considerable modulation of coherence across the time-frequency plane and that significant coherence was often focal in time, information that would be lost if performing a single (stationary) Fourier coherence analysis across the entire time series. The degree to which coherence varied over time was not uniform across subjects, as some subjects (e.g. Subject 8) showed more persistent significant negative correlations than others (e.g. Subject 12). On the other hand, positive correlations were more widespread for all subjects, as shown in Fig. 4. We note that using the peak (maximal negatively-correlated) voxel in each anticorrelated cluster, instead of spatially averaging voxels across the 3mm spheres, yielded very similar results (data not shown).

A statistical test based on Monte Carlo simulations was used to quantify the significance of variability in the wavelet transform coherence between the PCC and each of the anticorrelated ROIs. The results are summarized in Figure 5, which depicts the number of subjects having significantly nonstationary variation (as a function of scale) at both the 90% and 95% confidence levels. The identities of the subjects comprising the elements of each plot in Fig. 5 are indicated in Supplementary Figure S3. The BIC model order used for the significance testing is reported for each subject in Table 3A.

Figure 5.

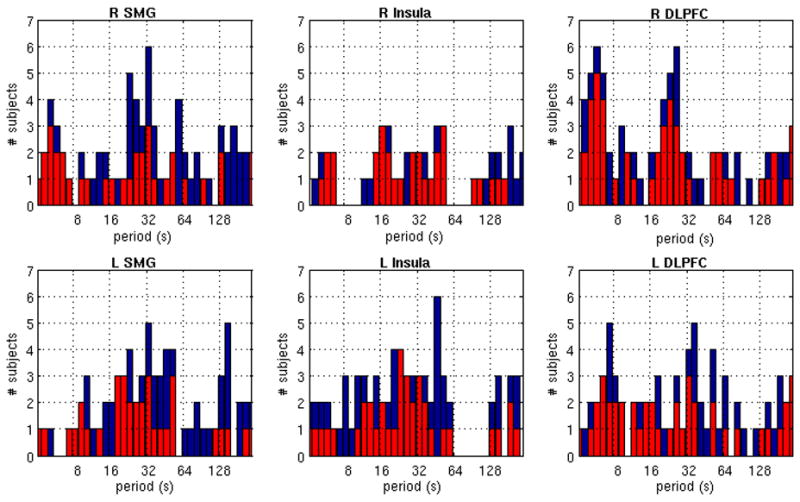
Significance of temporal variability in the wavelet transform coherence. Each plot shows the number of subjects for which the variance in the WTC between the PCC and the indicated ROI exceeded the 90% (blue) and 95% (red) confidence levels, for each wavelet scale (Fourier period).

Table 3.

Model order p (Eq. 3), as determined by the BIC score, for the vector autoregressive model fit between the PCC and (A) each anticorrelated ROI, and between the PCC and (B) each of the 5 ROIs indicated in Fig. 9A.

	A						B
subject	L SMG	R SMG	L DLPFC	R DLPFC	L insula	R insula	ROI1	ROI2	ROI3	ROI4	ROI5
1	2	2	2	2	2	2	2	2	2	2	2
2	1	1	1	1	1	1	2	1	1	1	1
3	1	1	1	1	1	1	1	1	1	1	1
4	2	2	2	4	3	4	2	2	1	1	3
5	2	2	2	2	2	1	2	1	1	1	2
6	3	2	2	3	3	3	2	2	2	2	2
7	3	3	3	3	3	3	3	4	3	3	4
8	1	2	1	1	1	1	2	1	1	2	1
9	2	2	2	2	2	2	2	3	2	2	2
10	1	1	1	1	2	1	1	1	1	2	1
11	1	1	1	2	3	3	2	1	1	1	1
12	2	2	2	2	2	2	4	3	2	2	3

L, left; R, right; SMG, supramarginal gyrus; DLPFC, dorsolateral prefrontal cortex.

To examine the distribution of phase values for which significant coherence was attained, we defined the time-averaged coherence as:

$$c(s,\phi )=\frac{1}{N_{\mathit{coi}}(s)}\sum _{t\notin \mathit{COI}(s)}{R}^2(t,s)·I\{R^2(t,s)>a_{95}\}·I\{arg(R^2(t,s))\in [\phi \pm \pi /4]\}$$ (4)

where N_coi is the number of pixels outside the cone of influence, I{·} is the indicator function (equal to 1 when its argument is true, and 0 otherwise), a₉₅ is the 95% significance level for coherence magnitude, R² is as defined in Eq. 2., arg(R²) is the coherence phase, and φ ∈ {0, π/2, π, −π/2}. Only scales that were common to all subjects were used (4<s<241.6, corresponding to 4.13<T<249.6 sec). The value of c(s,φ) is, in other words, the total significant coherence at scale s occurring within a phase range of φ±π/4, normalized by the maximum possible coherence at scale s (which is equal to N_coi(s), as maximum coherence would mean that R²=1 at each pixel outside the COI at scale s).

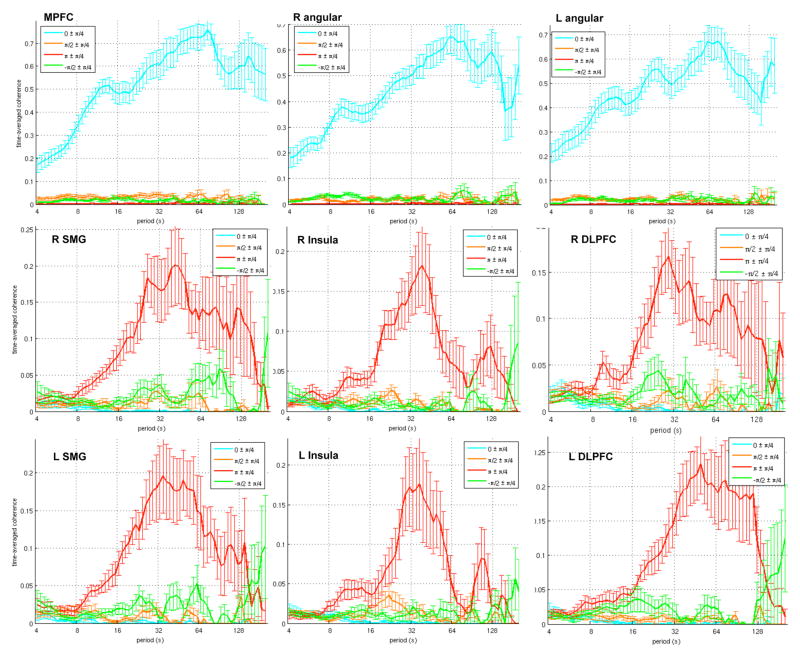
Figure 6 shows the time-averaged coherence across subjects (mean±SE, N=12). Because of disparities in time/frequency resolution across scales, c(s,φ) for a given φ does not strictly represent the “time” spent in significant coherence, and caution should be taken when comparing across scales for a given φ. However, the shape of the curve, and the relative magnitudes of different values of φ at a given scale, can be compared across distinct WTC analyses, indicating possible differences in the time-frequency relationships of different time series pairs. It can be seen that the anticorrelated ROIs have a distribution that is predominantly unimodal, peaking around a period of T = 32 sec (f ~ 0.03 Hz). Note that the time-averaged coherence differs from standard (stationary) cross-spectral analysis because the latter estimates a single magnitude and phase value for each frequency, while the former depicts the extent to which coherence can transition between different phase ranges (across time) at a given frequency.

Figure 6.

Time-averaged coherence (see Eq. 4), shown for default-mode (top row) and anticorrelated (middle and bottom rows) ROIs. Thick lines represent the mean across subjects (N=12), and error bars represent standard error.

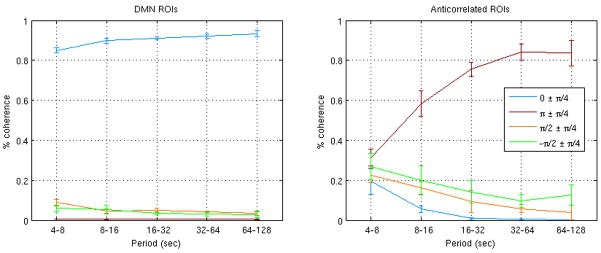
Figure 7 shows the percentage of the total coherence that occurred within each phase range (φ±π/4), quantified separately for 5 frequency bands: (1) 0.128–0.242 Hz (T ~ 4–8 sec), (2) 0.064–0.128 Hz (T ~ 8–16 sec), (3) 0.032–0.064 Hz (T ~ 16–32 sec), (4) 0.016–0.032 Hz (T ~ 32–64 sec), and (5) 0.008–0.016 Hz (T ~ 64–128 sec). Within a given frequency band, the anticorrelated ROIs were similar to one another with respect to phase content. The high frequency bands exhibited the greatest diversity of phase angles.

Figure 7.

Percentage of the total significant coherence occurring within each phase range (φ±π/4), within each of 5 different frequency bands. Lines and error bars represent the mean±SD, respectively, across the 3 DMN ROIs (left) and 6 anticorrelated ROIs (right).

Wavelet coherence: comparing positive and negative correlations

We also examined the coherence properties between the PCC and voxels having positive correlation coefficients of approximately the same magnitude as the negative correlation coefficients observed between the PCC and the anticorrelated ROIs. The motivation for this comparison was to see whether there is a symmetry between the coherence patterns of positive and negative correlation in the brain at an equivalent signal-to-noise ratio, wherein the source of the “noise” is embedded in the fMRI signal itself.

For each subject, a single voxel whose correlation with the PCC fell between 0.28 and 0.41 was identified for this comparison. To maintain a degree of spatial localization (and thus noise homogeneity), this voxel was constrained to lie within the MPFC cluster (Fig. 1, Table 1). A WTC analysis between the PCC and this voxel was computed (Fig. 8(A)), and the time-averaged coherence was obtained to summarize the WTC results over all 12 subjects. This procedure was repeated 50 times, each time with a different choice of voxels. The grand average over the 50 time-averaged coherence curves is displayed in Fig. 8(B). It can be seen that the primary peak of the time-averaged coherence occurs at a period slightly shorter than 64 sec (f ~ 0.016 Hz), a lower frequency than was observed for the anticorrelated ROIs in Fig. 6. The same procedure was repeated when constraining voxels to lie in the cluster of the right angular gyrus; the plot was similar to that of the MPFC cluster, though the peak occurred at an even lower frequency (96 sec; data not shown).

Figure 8.

(A) WTC analysis and (B) time-averaged coherence between the PCC ROI and voxels in the MPFC having an overall correlation coefficient with the same approximate SNR as the anticorrelated ROIs in the actual data (for the instance shown here, r = 0.35±0.03 (mean±SD across subjects)). For the time-averaged coherence, error bars indicate the standard error of the mean over 50 iterations.

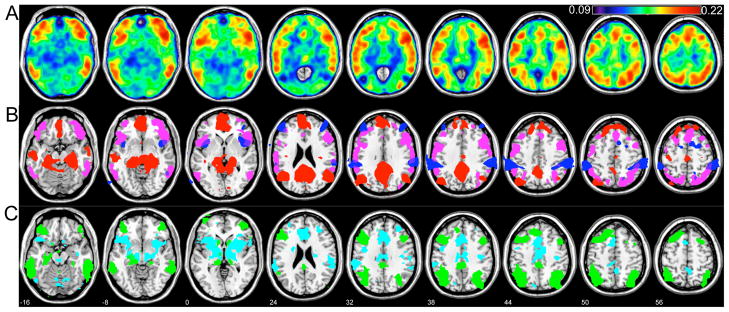
Brain regions of variable default-mode connectivity

A map of variability (standard deviation) over the sequence of 2-min sliding-window correlation coefficients is shown in Fig. 9(A), averaged across all 12 subjects. The map corresponding to 4-min sliding window was qualitatively similar, with identical maxima. Regions of highest variability included voxels in the supplementary motor area (SMA)/anterior cingulate cortex (ACC)/superior medial frontal cortex (BA 8, 24, 32); superior and inferior parietal cortex (BA 7, 40); precentral (BA 6) and frontal operculum (BA 44, 48); ventrolateral prefrontal cortex (VLPFC; BA 45) and middle/inferior orbitofrontal cortex (BA 47); and superior (BA 21, 22) and middle (BA 37) temporal cortex. Five foci corresponding to local maxima were defined as ROIs (Fig. 9A): these included regions in the right inferior parietal cortex (“ROI1”, x=34, y=−58, z=44), right inferior frontal operculum/BA44 (“ROI2”; x=50, y=18, z=32), right inferior temporal cortex (“ROI3”; x=58, y=−38, z=−16), right inferior orbitofrontal cortex (“ROI4”; x=50, y=26, z=−8), and ACC/BA24 (“ROI5”; x=−2, y=26, z=24). For comparison, the t-maps for the DMN and its anticorrelated network are shown in Fig. 9(B) along with a thresholded version of the map in Fig 9(A).

Figure 9.

(A) Variability (standard deviation) over the sequence of 2-min sliding-window correlation coefficients, averaged across all 12 subjects. Five ROIs chosen for further analysis are labeled. (B) t-maps of positive and negative correlations with the PCC (red and blue, respectively, and thresholded identically to Fig. 1), superimposed for anatomical comparison with regions of high variability (SD>0.18; magenta). (C) The intersection of group-level seeded correlation maps (computed across all time points in the scan) using ROIs 1, 2, and 3 as seed regions (green overlay), and using ROIs 4 and 5 as seed regions (cyan overlay). The slice location (z, mm) appears in white numerals and also applies to parts (A) and (B).

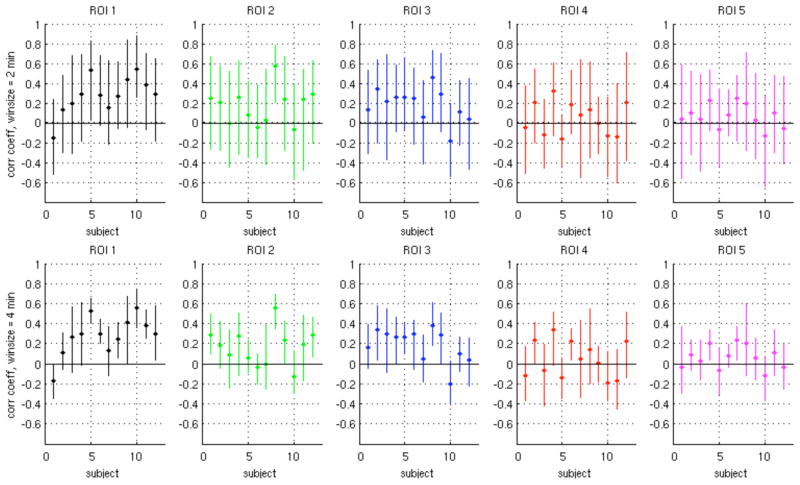
Ranges of sliding-window correlation coefficients for ROIs 1–5 and window lengths of 2 min and 4 min are described in Fig. 10 and Table 4. Due to the smoothing properties of longer sliding-window lengths, the range of variation within a given subject was smaller for a window length of 4 min compared to 2 min. As can be seen from Fig. 10, there are subjects and ROIs for which the correlation coefficients range from negative to positive over time. Across subjects, the range of sliding correlation values were centered more closely around zero for ROIs 4–5 compared to ROIs 1–3.

Figure 10.

Range of sliding-window correlation values for ROIs 1–5 (Fig. 9A), for window sizes of 2 min (top row) and 4 min (bottom row). Vertical lines indicate the minimum and maximum values of the windowed correlation coefficient across the scan, and the dot on each bar indicates the mean.

Table 4.

Summary of sliding-window correlation coefficients for 5 ROIs (Fig. 9A) having variable connectivity with the PCC.

	Window size = 2 min			Window size = 4 min
ROI	Mean	SD	% windows < 0	mean	SD	% windows < 0
1	0.28	0.19	0.16	0.28	0.12	0.13
2	0.17	0.22	0.32	0.17	0.13	0.28
3	0.18	0.21	0.24	0.19	0.13	0.19
4	0.04	0.22	0.44	0.04	0.15	0.42
5	0.07	0.20	0.39	0.06	0.12	0.35

The mean value, variability (standard deviation; SD), and percentage of sliding-window correlation coefficients that were less than 0 are shown for each of 5 ROIs, averaged across all 12 subjects.

To examine whether the locations of high variability exhibit temporal activity that is similar to one another, correlation coefficients between the raw time series of the 5 ROIs were computed (Fig. 11). In addition, each ROI was used as a seed to generate a correlation map for each subject, using all time-points in the scan. As expected by their high mutual correlation, a group analysis of the correlation map for each ROI revealed that ROIs 1, 2, and 3 generated highly overlapping networks, and that ROIs 4 and 5 generated overlapping networks that were primarily distinct from those of 1, 2, and 3 (Fig. 9(C)). The network formed by the intersection of seeded correlation maps from ROIs 1, 2, and 3 includes the ventro-lateral prefrontal cortex (BA 45, 47) extending into DLPFC (BA 46), superior/inferior parietal lobule (BA 7,40) and the middle/inferior temporal cortices (BA 21, 20, 37). The network formed by the intersection of seeded correlation maps from ROIs 4 and 5 includes the anterior cingulate cortex (BA 24, 32), supplementary motor area (BA 6), basal ganglia, and SMG extending into the superior temporal cortex (BA 40, 42). These resemble resting-state networks that have previously been reported in the literature (Damoiseaux et al., 2006; Seeley et al., 2007), and thus further analysis of the time-frequency dynamics of their seed ROIs relative to the PCC (default-mode) is of interest.

Figure 11.

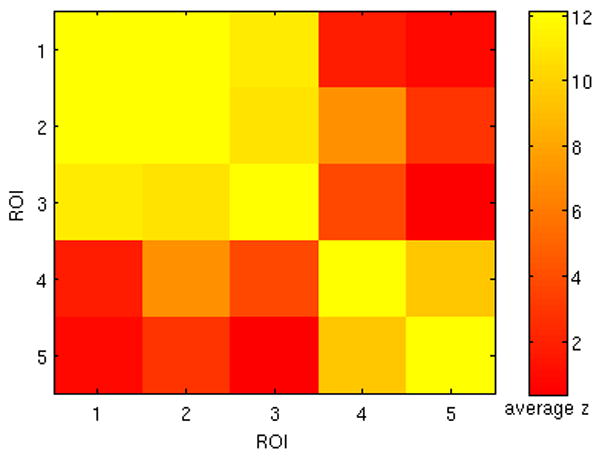
Group average (N=12) of Fisher z-transformed correlation coefficients between 5 ROIs (Fig. 9A) whose correlation with the PCC was highly variable over time. High mutual correlation was observed between ROIs 1–3, and between ROIs 4–5.

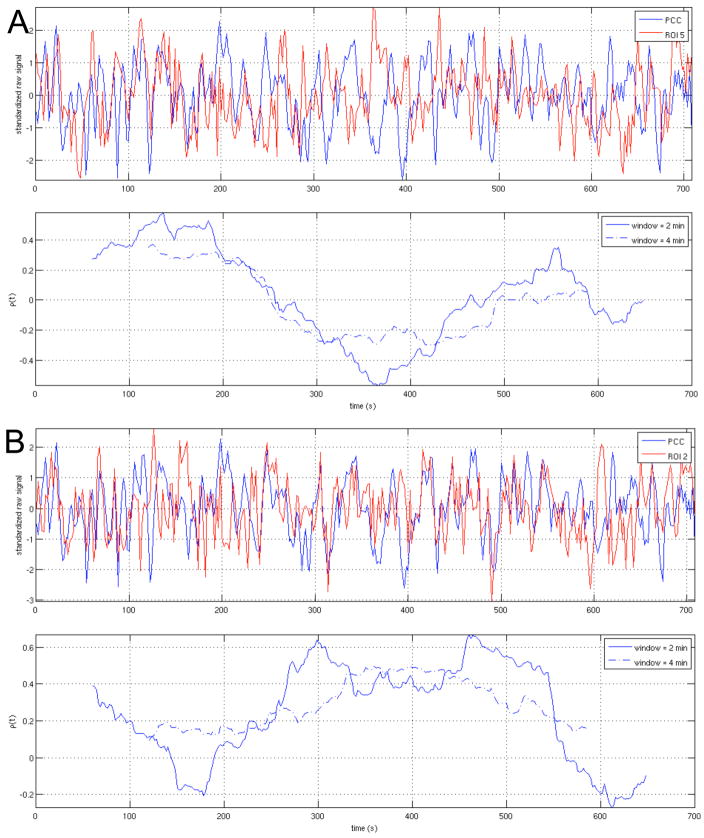
WTC analyses were performed between the PCC and each of the 5 ROIs; the resulting time-averaged coherence and scale-dependent significance in temporal variability are shown in Fig. 12. The BIC model order used for the significance testing is reported for each subject in Table 3B. WTC maps for two ROIs (ROI2 and ROI5) are provided in supplementary Fig. S4. Examples of raw time series from ROIs 2 and 5, along with their sliding-window correlation sequences for window lengths of 2 min and 4 min, are shown in Fig. 13 for one subject (Subject 1).

Figure 12.

(Top row) Time-averaged coherence for for the 5 ROIs indicated in Fig. 9A. Thick lines represent the mean across subjects (N=12), and error bars represent standard error. (Bottom row) Histograms of the number of subjects for which the variance in the WTC between the PCC and the indicated ROI exceeded the 90% (blue) and 95% (red) confidence levels, for each wavelet scale (Fourier period).

Figure 13.

Raw time series and sliding-window correlation coefficients between the PCC and (A) ROI5 and (B) ROI2, shown for one subject (Subject 1). Sliding-window correlation coefficients are plotted at the time point corresponding to the center of its associated window.

Effects of motion, scanner, and breath-holding on connectivity variability

Motion parameters for each subject are reported in Table 5, and were minimal (mean drift = 0.9 mm, mean RMS deviation = 0.12 mm). The inter-subject comparison between motion and connectivity variability yielded no significant relationships (p>0.05) with either the maximum drift or maximum RMS deviation. The inter-subject comparison between motion and scale-dependent variability in the WTC showed a significant (p<0.05) relationship at some scales for some ROIs (supplementary Table S1); however, this occurred only for very high frequencies (T<6.5s) and very low frequencies (T>112 s). Thus a large fraction of the spectrum does not appear to be related to motion, including frequencies in which high variability was observed (such as 16–64 s; see Fig 5). The intra-subject correlations between the sequence of motion-based deviations and the sequence of correlation-based deviations were not significant for any subject, for either of the 2 sliding-window lengths examined.

Table 5.

Summary of subject motion. Values are specified in mm, and refer to the maximum over all 6 motion parameters.

Subject	Drift	RMS
1	0.30	0.04
2	0.87	0.07
3	0.43	0.06
4	0.39	0.05
5	1.07	0.12
6	1.36	0.14
7	0.88	0.09
8	1.55	0.23
9	0.98	0.21
10	0.76	0.09
11	1.02	0.15
12	1.16	0.18
mean	0.90	0.12

Results of the comparison between BH and non-BH subjects were not significant (p=0.24), even after covarying for effects of motion and scanner (p=0.39). Results of the between-scanner comparison were also not significant (p=0.68). We further verified that none of these comparisons became significant when using 1- and 4-min sliding-window lengths, in addition to the 2-min sliding window, to compute the connectivity variability measure. Therefore, while scanner and BH do not appear to influence variability in the current dataset, the number of subjects in these between-group comparisons is small (N₁=N₂=6 for the BH comparison and N₁=4/N₂=8 for the scanner comparison) and thus further study with larger subject groups would be necessary to attain the power required for a more conclusive inference concerning these effects.

Discussion

This study presents a preliminary analysis of dynamic behavior between nodes of resting-state networks. We demonstrate the use of wavelet coherence analysis for analyzing time-varying interactions between brain regions in the resting state, focusing on the default-mode network and its negative correlations with regions of the “anticorrelated” network. In addition, regions of the brain with temporally-variable connectivity to the PCC, a major node of the default-mode network, were identified using sliding-window correlations. Results indicate that resting-state BOLD connectivity has dynamic properties that may be overlooked by stationary analyses, observations that complement recent studies of dynamic spontaneous activity in animal models (Majeed et al., 2009; Popa et al., 2009).

When considering all time points in the data, correlation coefficients between the PCC and its anticorrelated regions were found to be substantially weaker than those of the positive correlations within regions of the DMN, in agreement with previous literature. WTC analysis showed clear fluctuations in the magnitude of coherence for phase angles of π±π/4 within the course of a single scan, revealing the presence of temporally-localized periods of negative correlation. Significance tests indicated the existence of scale-dependent temporal variability beyond that which may be expected by a stationary VAR model. In addition, differences in the time-averaged coherence were observed between the anticorrelated and positively-correlated ROIs of approximately the same SNR, indicating either (a) functional differences in the way negatively- and positively-correlated regions couple to the PCC, and/or (b) differences in the noise characteristics of these anatomic regions.

A sliding-window correlation procedure was applied in order to detect areas across the whole brain whose linear relationship with the PCC had high relative variation across the duration of the scan. Interestingly, high variation was found in brain areas that have been implicated in higher-level cognitive function, such as attention and salience processing (Corbetta and Shulman, 2002; Seeley et al., 2007), and a seed-based ROI analysis suggested a general organization of these regions into two disjoint networks that resemble resting-state networks reported in previous studies (e.g. (Damoiseaux et al., 2006; Seeley et al., 2007). Further dynamic analysis of the associated seed ROIs revealed that for some subjects and ROIs, sliding-window correlation coefficients were ranged from positive to negative over time, particularly for ROIs in the ACC and right orbitofrontal cortex (ROIs 4 and 5; Table 4). For ROIs 1–3, WTC analyses revealed that the phase distribution associated with significant coherence magnitude was dominated by phase angles centered around 0 (positive correlation) at most scales; however, a suppression of positive correlations (and accompanying increase of negative correlations) was observed in the range of ~16–32 Hz, particularly for ROI 2. ROIs 4 and 5 exhibited a more uniform phase distribution (Fig. 12).

Further studies will be required to address the potential functional relevance of the observed temporal variability between these region and the default-mode networks in the resting state. In addition, because the map in Fig. 9 represents an average variability rather than a proper statistical measure, further analysis will be required to identify other regions of the brain that may have lower average variability and yet equal (or higher) statistical significance when accounting for autoregressive properties on a voxel-wise basis, as was done here for significance testing of the WTC.

One implication of the present findings is that the appearance of negative correlations, as calculated by seed-based correlation of ICA, may depend on the temporal segment of data considered for analysis. Thus, one is likely to observe inter-trial variability across scans of, e.g., 6 min in length, which is a typical acquisition time for a resting-state scan (Fig. 14). Furthermore, where weak and/or negative correlations are concerned, a single correlation coefficient computed across the duration of a longer scan may oversimplify the dynamic relationship between time series. Phase variability over time, such as observed in the ROIs identified by the sliding-window method, is also likely to confound measurements of causality computed across the entire scan. Therefore, quantifying the variability of interactions, in addition to averages across a scan, may be informative for characterizing the dynamics of resting-state networks.

Figure 14.

Negative correlations with the PCC across two successive 7-min segments of resting-state data, shown for one subject. (A) First 7 min, (B) second 7 min. Intensity values represent correlation coefficient (color scale is 0.08<r<0.4), and map is superimposed on the subject s T2-weighted anatomic image. Substantial differences between the two segments are apparent.

Yet, the wealth of information provided by a time-frequency analysis of connectivity (beyond than that of a conventional stationary analysis) presents additional challenges when studying multiple subjects and spatial locations. One way of handling this growth of information is to summarize the dynamic information (e.g. WTC maps) along several potentially-relevant dimensions such as those presented herein, e.g. time-averaged coherence, scale-dependent variability, and variance of the sliding-window correlations. Metrics that take into account even more “higher-order” aspects of variability, such as the rate at which correlations and phase are modulated in addition to the overall degree of change, may also prove important. Such metrics can be examined for variability within and between groups of subjects, yielding features that can complement those of static analyses when characterizing neural activity across subject groups and cognitive states. Future work will be required to determine the most informative metrics for a given hypothesis and subject population.

Given the design of this study, it is not possible to resolve the cause of the observed nonstationary relationships. As there are few constraints on a subject s cognitive processes during a resting-state scan, it is possible that changes in network dynamics may reflect changes in brain state or arousal. However, it is also possible that the apparent changes are driven simply by the noise (e.g. motion, physiological) at a given time, despite efforts to correct for known sources based on previous models and despite the lack of significant relationship between motion and variability using the tests described herein. Further experiments involving task manipulations or multiple modalities, such as combined fMRI-EEG or electrophysiology, will be required to better understand the sources of the time-varying dynamics between brain regions in the resting state.

Additional limitations pertaining to the methodology used herein suggest avenues of future work. For example, although we focus on connectivity with the PCC, previous studies have indicated the presence of heterogeneity across components of the DMN and their respective anticorrelations (Uddin et al., 2009), and thus greater insight may be obtained by examining the dynamics within subsets of networks. In addition, wavelet coherence was applied here to pairs of time series. In the future, it may be fruitful to apply multivariate analysis methods to resting-state data in a nonstationary sense, such as with sliding-window ICA (Karvanen and Theis, 2004) and adaptive multivariate autoregressive models (Deshpande et al., 2006; Sato et al., 2006).

Supplementary Material

01

Figure S1. Wavelet transform coherence between the PCC and 3 of its anticorrelated ROIs: (A) right SMG, (B) right insula, and (C) right DLPFC, for all subjects. For further detail, please refer to the caption of Fig. 3.

02

Figure S2. Wavelet transform coherence between the PCC and default-mode ROIs: (A) MPFC, (B) right angular gyrus, (C) left angular gyrus. For further detail, please refer to the caption of Fig. 3.

03

Figure S3. Subjects exhibiting significant variability between the PCC and anticorrelated ROIs at the 90% (gray) and 95% (black) levels, as a function of wavelet scale (Fourier period).

04

Figure S4. Wavelet transform coherence between the PCC and two ROIs with highly variable connectivity: (A) ROI 2, (B) ROI5. For further detail, please refer to the caption of Fig. 3.

05

Table S1. Wavelet scales having a significant (p<0.05) positive correlation with max RMS motion. (Results using drift as the motion parameter were similar.)

Appendix

Bootstrapping procedure

Given a VAR model of order p on the actual data (Eq. 3), each bootstrap time series pair ((x_b[n],y_b[n]), n = 1....N, b 1…1000) is generated as follows:

1. Select a time point n₀, 1≤ n₀ ≤ (N − p), uniformly at random.

2. Set (x_b[n],y_b[n]), n = 1…p to be equal to (x[m],y[m]), m n₀…(n₀ + p − 1). This step thus initializes the first p values of the bootstrap process to be a randomly-selected contiguous block of p observations from the actual data (Stine, 1987).

3. For each n = (p+1)…N, select a time index n̂ (1 ≤ n ≤ N) uniformly at random, and let û^x[n] = u^x[n̂] and û ^y[n] u^y[n̂]. In other words, the innovation term of the bootstrap process at the current time step consists of a randomly-sampled residual of the VAR fit to the original data.

   Then, let

   $$\{\begin{array}{c}{x}_b[n]=\sum _{i=1}^p{a}_i^x{x}_b[n-i]+\sum _{i=1}^p{b}_i^x{y}_b[n-i]+{\widehat{u}}^x[n]\\ y_b[n]=\sum _{i=1}^p{a}_i^y{x}_b[n-i]+\sum _{i=1}^p{b}_i^y{y}_b[n-i]+{\widehat{u}}^y[n]\end{array},$$

where the coefficients a^x_i, a^y_i, b^x_i, b^y_i had been estimated by least-squares fit of the pth-order VAR model to the original data.