Evaporation from microreservoirs

Abstract

As a result of very large surface area to volume ratios, evaporation is of significant importance when dealing with lab-on-a-chip devices that possess open air/liquid interfaces. For devices utilizing a reservoir as a fluid delivery method to a microfluidic network, excessive evaporation can quickly lead to reservoir dry out and overall device failure. Predicting the rates of evaporation from these reservoirs is difficult because the position of the air/liquid interface changes with time as the volume of liquid in the reservoir decreases. Here we present a two-step method to accurately predict the rates of evaporation of such an interface over time. First, a simple method is proposed to determine the shape of an air/liquid meniscus in a reservoir given a specific liquid volume. Second, computational fluid dynamics simulations are used to calculate the instantaneous rate of evaporation for that meniscus shape. It is shown that the rate of evaporation is strongly dependent on the overall geometry of the system, enhanced in expanding reservoirs while suppressed in contracting reservoirs, where the geometry can be easily controlled with simple experimental methods. Using no adjustable parameters, the model accurately predicts the position of the inner moving contact line as a function of time following meniscus rupture in poly(dimethylsiloxane) reservoirs, and predicts the overall time for the persistence of liquid in those reservoirs to within 0.5 minutes. The methods in this study can be used to design holding reservoirs for lab-on-a-chip devices that involve no external control of evaporation, such that evaporation rates can be adjusted as necessary by modification of the reservoir geometry.

Introduction

In the past decade, there has been an increasing amount of research dedicated to biological lab-on-a-chip (LOC) applications based on microfluidic unit operations.¹ The combined effect of these processes, including volume sampling and pretreatment, fluid pumping, mixing, reaction, separation, and chemical analysis, allow for the completion of biological assays in the span of seconds to minutes.² The rapid format combined with the small footprint of LOC devices facilitates development of accessible point-of-care diagnostics,³ as well as the simplification of traditional laboratory methods such as polymerase chain reaction (PCR),⁴ microarray technologies,⁵ DNA sequencing,⁶ and chemical analysis.⁷

Because of the high surface area to volume ratios in micro-fluidic systems, loss of fluid through evaporation and permeation becomes increasingly important.⁸ Evaporation may rapidly increase the local concentration of solutes in systems that include an open air/liquid interface, which can lead to detrimental effects in an analytical system. If not controlled, evaporation effects in systems containing sub-μL liquid volumes is of critical concern, as times required for the complete evaporation of a liquid sample can be less than a minute. In all microfluidic systems containing an open air/liquid interface, local evaporation rates and their dependence on local conditions and reservoir geometries must be taken into consideration.^9–11

In many open microfluidic systems, attempts are made to either mitigate or enhance evaporation effects. Reducing the evaporation rate is generally required to maintain analyte concentrations when performing chemical analysis on aqueous fluids introduced or extracted in microreservoirs. If no action is taken to replenish the reservoir solvents, sub-μL sized volumes can dry out within a few minutes,¹² requiring a sufficiently fast analytical procedure.¹³ Perhaps the easiest way to control evaporation from these reservoirs is via isolation of the air/liquid interface with either a solid lid¹⁴ or an immiscible liquid cap, such as mineral oil¹⁵ or another organic liquid.^16,17 Other direct approaches involve control of the relative humidity directly above the air/liquid interface, usually performed via sample placement near a water bath to keep the surrounding air saturated with water vapor.^9,18 More complicated approaches involve the fabrication of microreservoir arrays from agarose gel.¹⁹ These gel-based arrays consist of over 90% water, saturating the local environment above each reservoir and substantially reducing evaporation rates.

Evaporation enhancement in lab-on-a-chip applications is generally associated with passive microfluidic pumping applications. Based on evaporation effects or capillary forces, passive microfluidic pumping eliminates the need for moving parts or external power supplies and is a much sought after topic. Evaporation occurring at the outlet region of a microfluidic network (μFN) serves to drive fluid from an inlet reservoir through the system, usually at substantial volumetric flow rates. A simple and efficient approach to evaporation-based passive pumps can also be realized by exposing the outlet regions of a μFN to the atmosphere. Evaporation in these systems can then be enhanced by either forced convective air motion,²⁰ heating the outlet regions using microfabricated elements,²¹ or by increasing the air/liquid interface surface area at the μFN outlet with hydrophilic membranes²² or filter paper plugs.²³

There are many LOC designs where uncontrolled evaporation can lead to unwanted changes to the initial experimental conditions and, if given enough time, failure of the device. In the case of passive pumping methods based on capillary forces, either between two droplets of water^24,25 or liquid in an open faced micro-channel,²⁶ evaporation will continuously reduce the volume of water present in the system. This loss may lead to changes in the capillary forces driving liquid through the system, thus acting to increase (or decrease) the overall observed flow rate. In the case of μNFs used for the immobilization of immunoglobulins to a surface,²⁷ excessive evaporation from the inlet reservoir can lead to reservoir dry out and non-homogeneous deposition of material on to a surface. This behavior may affect the overall reliability of devices that depend on uniform surface coverage of capture ligands, such as those used in various micromosaic immunoassays.^28,29

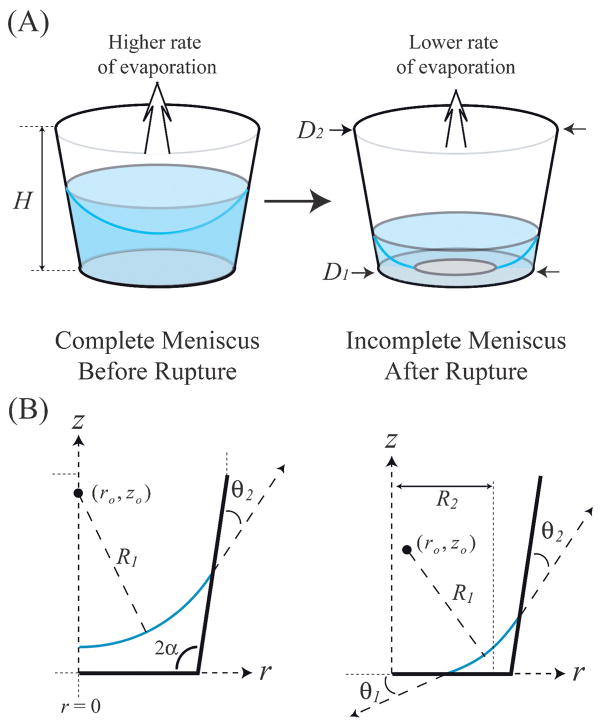
In many LOC devices it becomes important to calculate not only the dependence of device performance on the evaporation rate, but also the time at which that device might undergo failure. The rate of evaporation from an air/liquid interface (Q_e) is dependent on both the conditions of the environment above the meniscus as well as the geometry of the meniscus itself. Historically, the study of the evaporation rate and shape of a liquid meniscus from μL-sized volumes has focused on the role of evaporation of a sessile drop for deposition of solids onto a flat surface.^30–33 While the evaporation of sessile drops remains important for many LOC applications, there is little information regarding evaporation of a droplet of water confined to a micro-reservoir constructed from hydrophilic materials. Previously, this topic has been restricted to experimental studies concerning evaporation of droplets in shallow nanoliter wells, with the focus on solute deposition from the droplets,³⁴ evolution of the meniscus with time,^35,36 evaporation rate of the droplets,³⁷ or particle tracking studies of flow induced via evaporation.³⁸ In those studies meniscus shape evolution and the transient behavior of the droplet evaporation rate were not estimated or predicted. The absence of these data may very well be due to the complexity of the dynamics: as water in a microreservoir recedes to the point where the bottom of the meniscus reaches the reservoir floor, the meniscus will rupture due to the discontinuity of the surface energies between the initial air/liquid interface and the eventual solid/liquid interface along the reservoir floor (Fig. 1A). In the small geometry of the reservoir, it may be assumed that body forces have negligible impact on the interface shape such that, prior to rupture the meniscus is spherical. However, after rupture the meniscus takes on a more complicated shape.

Fig. 1.

(A) As a meniscus recedes towards the bottom of a reservoir, it will rupture into an incomplete state. (B) Geometric parameters describing a meniscus in a microreservoir in the r,z-plane.

In this study we examine the evaporation rate and shape evolution of an air/water meniscus situated in a cylindrical microreservoir modeled after those used in many LOC devices,^27–29 specifically, with a reservoir height (H), floor diameter (D₁), and upper diameter (D₂) all on the order of a millimeter. A simple geometric model is proposed to determine the shape of a meniscus representing a given volume of water in a reservoir having a circular, but not necessarily constant, cross-section. With the interface geometry known, the evaporation rate of the water in the well can then be determined utilizing computational fluid dynamics (CFD). The combined geometric/CFD model is shown to reliably predict the evolution of air/water menisci in experimental systems. It is demonstrated that evaporation of water from microreservoirs can be either enhanced or suppressed, depending on the geometry of the reservoir. The methods utilized within this study will prove useful in a wide array of applications such as the secondary measurement of the surface properties of a cylindrical shaped substrate, the concentration of solutes within a microreservoir, and the controlled deposition of solids onto the reservoir floor. Furthermore, knowledge of a meniscus geometry evolution over time can be utilized in the design of a passive microfluidic pumping device, where the capillary forces resulting from the curved meniscus would serve as a controlled driving force between two microreservoirs.

Numerical techniques

Evolution of a meniscus in a microreservoir

The geometries of the menisci and reservoirs used in this study are shown in Fig. 1(B). To predict the rate of evaporation from a microreservoir containing a given volume of liquid, one needs to know the shape of the air/liquid meniscus. Because the shape of the meniscus is dependent on the surface properties of the reservoir, a relationship is needed between those properties and the geometric parameters of the system. For systems in quasi-thermodynamic equilibrium, the relationship between the properties of the surface and the air/liquid interface can be described by Young’s equation,

$${\gamma }_{sv}={\gamma }_{lv}cos(\theta )+{\gamma }_{sl}$$ (1)

where θ is the apparent contact angle between the liquid andsurface and γ_sv, γ_lv, and γ_sl represent the surface and interfacial free energies of the solid–vapor, liquid–vapor, and solid–liquid interfaces, respectively. For reasonably dilute aqueous solutions θ can be assumed constant, and changes in θ will represent the relative hydrophilic/hydrophobic extent of the surface. In this study, θ₁ is defined as the contact angle between water and the reservoir floor and θ₂ as the contact angle between water and the reservoir sidewalls. The shape of the meniscus is then dependent on the geometry of the reservoir and surface conditions of the reservoir sidewalls and floor (D₁, D₂, H, θ₁, θ₂) as well as the given volume of water within the reservoir (V).

Determination of the shape of a free interface in mechanical equilibrium with a solid edge is not a straightforward process. Analytical solutions may only be found for a small number of cases, and numerical methods are usually required.³⁹ Furthermore, experimental measurements concerning the shape of menisci in microreservoirs via confocal³⁷ or interference-contrast microscopy³⁶ suffer from poor resolution near the reservoir walls. The problem can be simplified, however, by noting that the reservoirs will usually have a floor diameter of D₁ < 1 mm, such that for water with density ρ the Bond number can be calculated as B_o = ρgD₁²/4γ_lv ≤ 0.05; hence, surface tension forces will dominate gravitational forces. In this case it may be assumed that the two principal radii of curvature, R₁ and R₂, do not vary with respect to position along the interface. In Fig. 1(B), R₁ is defined as the radius of curvature of the meniscus in the r,z-plane, having a center of curvature based at the point (r_o, z_o). R₂ is defined (for incomplete menisci) as the radius of curvature in the r, θ-plane, extending from r = 0 to the average radial position of the meniscus. For a given reservoir liquid volume, the shape of the meniscus is then calculated from a curve that intersects the reservoir floor and sidewalls with intersection angles θ₁ and θ₂, respectively, and whose volume when integrated with respect to r, θ, and z is equivalent to the given volume of liquid in the reservoir. Because there is no explicit expression for r_o, z_o, and R₁ given H, D₁, D₂, θ₁, θ₂, and V, an iterative method must be utilized. The details of this process are given in Appendix I in the ESI.^†

Calculation of evaporation rates

An accurate relationship between the instantaneous evaporation rate Q_e and the liquid volume V(t) is needed to accurately predict the evolution of a meniscus over time. From Fig. 1, it may be seen that for a given reservoir geometry, Q_e will depend on the volume of water in the reservoir and cannot be assumed constant as in previous studies.^36–38 This transient behavior is primarily due to the increase in the average distance needed for water vapor diffusion as well as changes to the interfacial area as the meniscus recedes towards the reservoir floor. To proceed further with the development of the model it is necessary to make several additional, but physically justifiable assumptions.

The microreservoirs used in this study have an average diameter and height on the order of a millimeter. For these geometries it is reasonable to assume the gas (air) and liquid in the reservoir are essentially quiescient, and that water vapor is transported upward via diffusion. The mole fraction of water vapor just above the well (x_a2) is assumed constant, determined by the relative humidity (RH), pressure (p), and absolute temperature (T) of the system. The gas phase at the air/water meniscus reaches near-instantaneous equilibrium, and the mole fraction of water vapor at the interface (x_a1) may be determined using Raoult’s law. Because the meniscus recedes very slowly as evaporation proceeds the system is at pseudo steady-state, and also it can further be assumed that, due to the high surface-area to volume ratio, the system will be isothermal.

For dilute concentrations of water vapor at constant pressure, the volumetric evaporation rate from the meniscus can then be expressed as

$$Q_e=\frac{-p{M}_w\mathcal{D}}{\rho RT}\underset{A}{\int }\frac{\partial x_a}{\partial z}dA$$ (2)

where A is the cross-sectional area of the reservoir in the r,θ-plane, R is the gas constant, M_w is the molecular weight, ρ is the liquid density, and 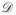is the diffusion coefficient of water vapor in air. Because of the curved geometry of the meniscus, exact solutions for x_a = x_a(r, z) in the gas phase cannot be derived and numerical methods must be applied to determine the evaporation rate from reservoirs with given parameters H, D₁, D₂, θ₁, θ₂, and V. Integration of eqn (2) is performed along a plane of constant z, where conservation of mass requires that the plane of integration must be situated at a z-position located higher than the top edge of the meniscus.

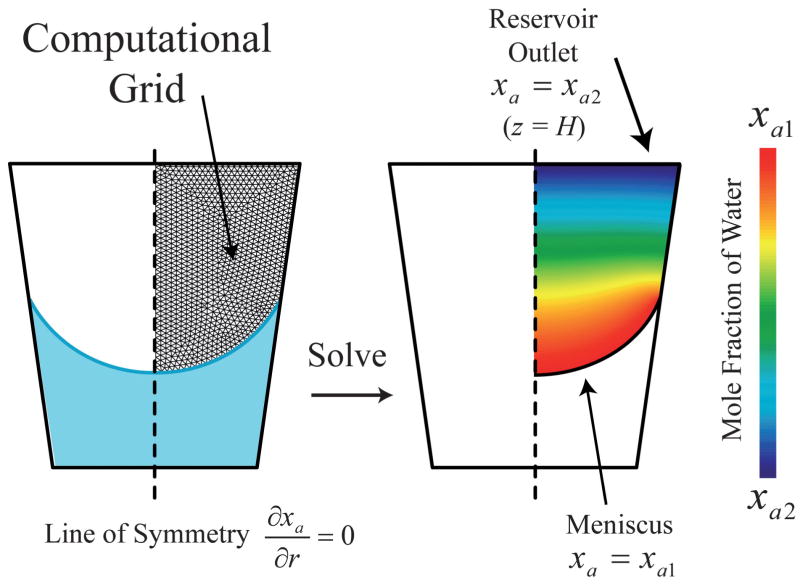
Fig. 2 illustrates the domain modeled in this study. Numerical calculations to determine the water vapor mole fraction distribution are performed using a 2-D axisymmetric CFD model. For each reservoir with given surface properties and external conditions a minimum of 25 simulations were performed, each pertaining to a specific reservoir liquid volume, where the shape of the meniscus was predetermined using the geometric model described above. The CFD preprocessing package Gambit^® was used to discretize the gas phase within the reservoir into 4-node elements, with typical element dimensions on the order of D₁/100. This discretization scheme has been pre-determined in this system to have sufficient resolution to ensure the predicted concentration field is independent of the mesh density. The finite volume CFD package FLUENT^® was then used to simulate the 2-D concentration distribution within the r,z-plane, where the mole fractions of water vapor along the meniscus and at the reservoir outlet were set to x_a1 and x_a2, respectively. The species conservation equation for water vapor was solved using a second-order accurate scheme, and the simulations were considered converged when the normalized residuals fell below 10⁻⁷. After the solution for x_a has converged the evaporation rate is calculated using eqn (2), where the integration is performed along the reservoir outlet plane at z = H.

Fig. 2.

Illustration of the axi-symmetric CFD model utilized in this study. The computational grid is for presentation purposes only.

Experimental techniques

The sidewalls of the microreservoirs were constructed from poly(dimethylsiloxane) (PDMS, Sylgard 184, Dow Corning), whereas the floors consisted of either PDMS or glass. After curing a flat PDMS mold (10 : 1 base : curing agent) on a polished silicon wafer at 95 °C for a minimum of 3 hours, high precision biopsy punches (Technical Innovations) were used to create the reservoir chamber, making sure the reservoir was as close to vertical as possible. The biopsy punch creates a conical cavity, which allows for an expanding (D₂ > D₁) or contracting (D₂ < D₁) reservoir, depending on which side of the substrate the reservoir floor is sealed. Prior to sealing, all PDMS substrates were treated via an extraction, which has been shown to stabilize the hydrophilic nature of an oxidized PDMS surface for up to 7 days.⁴⁰ The PDMS reservoir surfaces were rendered hydrophilic by exposure to air plasma (25 W, 900 mTorr, 20 s), after which the reservoirs were irreversibly sealed to either a glass or PDMS floor.

The reservoirs were typically used within 10 minutes after fabrication. A microliter pipette was used to inject solutions of 0.5 μm diameter rhodamine encapsulated polystyrene beads (Duke Scientific, 10⁶ beads/mL) in nanopure water into the reservoirs. Before filling, the bead solutions were agitated to ensure uniform distribution of the microspheres. Initial liquid volumes (V_o) ranged from 0.2 to 0.75 μL, depending on the reservoir geometry under consideration. The temperature, pressure, and relative humidity of the external environment was recorded at the onset of the experiment (Fluke 971 temperature humidity meter), and typically remained within 1 °C and 1.5% RH of the initial conditions for several hours. The diameters at the top and bottom of the reservoir were measured using a calibrated microscope, and the height of the reservoir was measured using a micrometer.

After filling (time t = 0), the reservoir was placed on an inverted microscope equipped with an epifluorescence attachment (Nikon TE-200U) and fitted with a CCD camera (Coolsnap fx). A series of images taken immediately after menisci rupture were then used to measure the diameter of the inner meniscus (D_cap) as a function of time. Figs. 3(A) and (B) show the diagram of the experimental setup and images displaying the meniscus before and after rupture. Fig. 3(C) displays D_cap as a function of time for an initial liquid volume of V_o = 0.65 μL in a reservoir with D₁ = 1.38 mm, D₂ = 0.77 mm, and H = 2.2 mm. The rupture event occurred at t_c = 42.9 min with an initial rupture diameter of D_cap(t_c) = 0.47 mm, and the reservoir was completely dry at t_end = 64.7 min.

Fig. 3.

(A) Illustration of the experimental techniques in this study. (B) Experimental images of a ruptured meniscus for a reservoir at T = 28 °C, RH = 31%, with geometry D₁ = 1.38 mm, D₂ = 0.77 mm, and H = 2.2 mm.

Discussion

Effect of reservoir geometries and surface properties on evaporation rate

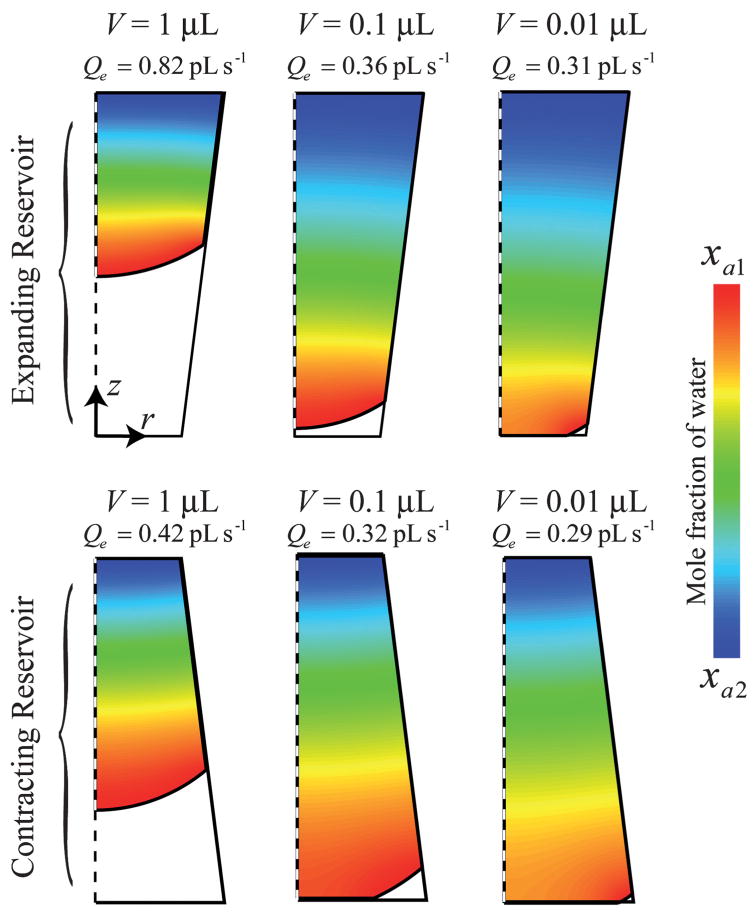
Experimentally observed evaporation rates of liquids contained in shallow reservoirs (D₁/H ≫ 1) have been shown to be proportional to the diameter of the reservoir and independent of time.^36–38 These functional relationships do not hold true for taller reservoirs such as those in this study (D₁/H ≈ 1). Fig. 4 displays mole fraction distributions and evaporation rates for water vapor within several reservoir geometries and reservoir liquid volumes. The difference in geometry between the expanding and contracting reservoirs would result from a reversed punch direction regarding a PDMS substrate. Several geometrical relationships affecting Q_e can be seen in Fig. 4. In general, a decrease in Q_e is seen with decreasing liquid volumes due to the increase in the average distance needed for diffusion as the meniscus recedes towards the reservoir floor. However, the evaporation rate is not only dependent on this diffusion distance, but also on the overall interfacial area as well as the geometry of the reservoir itself. The difference in evaporation rates for different reservoir geometries can be quite dramatic; for example, the evaporation rate for an expanding reservoir (for the conditions shown in Fig. 4) with V = 0.1 μL (Q_e = 0.36 pL s⁻¹) is only slightly lower than the case for a contracting reservoir with V = 1 μL (Q_e = 0.42 pL s⁻¹), even though there is clearly a difference in the interfacial area and diffusion length between the two cases. For a given volume of liquid, Q_e will be higher for an expanding reservoir than a contracting reservoir for several reasons: (1) the position of the meniscus will be higher in an expanding reservoir at a given volume, reducing the distance needed for diffusion and (2) evaporation rates are enhanced in expanding reservoirs due to the increase in the available area for diffusion area as z increases. The latter effect is made clear by examining one-dimensional diffusion in a well, and is examined in more detail in Appendix II, available within the ESI.^†

Fig. 4.

CFD simulations displaying the mole fraction of water vapor in several reservoirs with differing volumes. The simulations pertain to a reservoir with θ₁ = 25°, θ₂ = 50°, H = 2 mm, T = 28 °C, p = 686 Torr, and RH = 25%, with an expanding reservoir (D₁ = 1 mm, D₂ = 1.5 mm) and a contracting reservoir (D₁ = 1.5 mm, D₂ = 1 mm).

To determine a functional relationship between Q_e and V for a given reservoir with overall volume V_res, a minimum of 25 CFD simulations such as those shown in Fig. 4 were performed, with each simulation pertaining to a different reservoir liquid volume. The simulations are carried out such that a minimum of 10 simulations are evenly spaced along the range of V_c < V < V_o, corresponding to a complete meniscus, and a minimum of 15 simulations are evenly spaced along the range of −3 < log(V) < log(V_c) for an incomplete meniscus, where V_c is the critical volume at which the meniscus ruptures. Interpolation between the resulting data points is accomplished by fitting Q_e vs. V to the following relationships,

$$\text{complete}\text{meniscus}(V>V_c)Q_e=a_1{V}^2+a_{2}V+a_3$$ (3)

$$\text{incomplete}\text{meniscus}(V>V_c)Q_e=b_1\text{log}(V)+b_2\text{log}{\left(\frac{V}{V_{\mathit{res}}}\right)}^{b_3}$$ (4)

where the two distinct relationships are needed due to the discontinuous nature of the meniscus before and after rupture. The regression analysis within this study yielded R² coefficient values greater than 0.95 for systems that exhibit stable menisci (to be discussed later). There is little physical meaning associated with the fitting parameters in eqns. (3) and (4) and the parameters describing the system, and as such their values are not reported here.

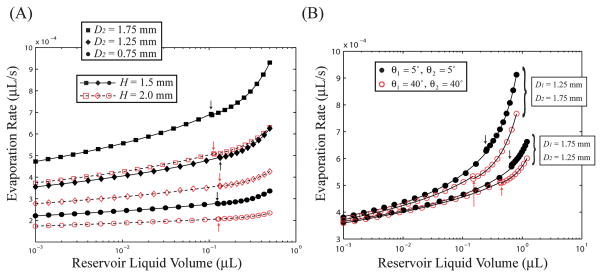
Fig. 5(a) displays Q_e vs. V for a variety of reservoir diameters and heights for a set value of D₁ = 1.25 mm and contact angles of θ₁ = 25° and θ₂ = 50°, representative of a typical reservoir in this study constructed from PDMS. Although the two curves for complete and incomplete menisci are discontinuous at V = V_c, the difference in Q_e between the two states at V = V_c is predicted to be small. For a given reservoir, the decrease in Q_e with decreasing V is clear in all reservoirs; for example, for the case of D₂ = 1.75 mm and H = 1.5 mm, there is a decrease in the evaporation rate by 49% from the liquid volume V = 0.5 μL (Q_e = 0.93 pL s⁻¹) to V = 10⁻³ μL (Q_e = 0.47 pL s⁻¹). Furthermore, the effect of the reservoir geometry is very significant, as evaporation rates in expanding reservoirs at a given liquid volume can be much greater than rates in contracting reservoirs: for the liquid volume V = 0.3 μL, the D₂ = 1.75 mm, H = 1.5 mm reservoir (Q_e = 0.80 pL s⁻¹) has an evaporation rate 260% greater than the D₂ = 0.75 mm reservoir of the same height (Q_e = 0.30 pL s⁻¹). The overall dependence on reservoir height is also important, as decreases in a reservoir height of H = 2.0 mm to H = 1.5 mm leads to increases in Q_e of 38% and 34% for the D₂ = 1.75 mm and D₂ = 0.75 mm reservoir (V = 0.1 μL), respectively.

Fig. 5.

(A) Effect of reservoir geometry on evaporation rate for constant contact angles of θ₁ = 25° and θ₂ = 50° and D₁ = 1.25 mm. (B) Effect of reservoir contact angles on evaporation rates from two reservoir geometries with H = 2.0 mm. Both figures pertain to a system with T = 28 °C, p = 686 Torr, and RH = 25%. The arrows indicate the critical volume at which the meniscus ruptures (V = V_c).

In addition to the effects of the reservoir geometry, the surface properties of the reservoir also have an effect on the evaporation rate, albeit to a lesser degree. Fig. 5(b) displays this effect, as decreases in both θ₁ and θ₂, that is, increased hydrophilicity, will serve to increase the evaporation rate from both expanding and contracting reservoirs. This effect is more pronounced at higher reservoir liquid volumes associated with complete menisci, where Q_e depends only on θ₂, and is mainly due to the increase in the interfacial area with decreasing liquid/reservoir contact angles. Fig. 5(b) also displays the dependence of θ₂ on V_c, as increases in θ₂ lead to decreases in V_c for all reservoir geometries.

For the reservoirs studied here, changes in temperature, pressure, and humidity on the evaporation rate are independent of the reservoir liquid volume and will not be discussed in detail. It should be noted that to ensure accuracy regarding the results in Fig. 5, the maximum reservoir liquid volume was limited so that the average distance from the meniscus to the top of the reservoir was less than H/2, and this will be discussed below.

Prediction of meniscus evolution during evaporation

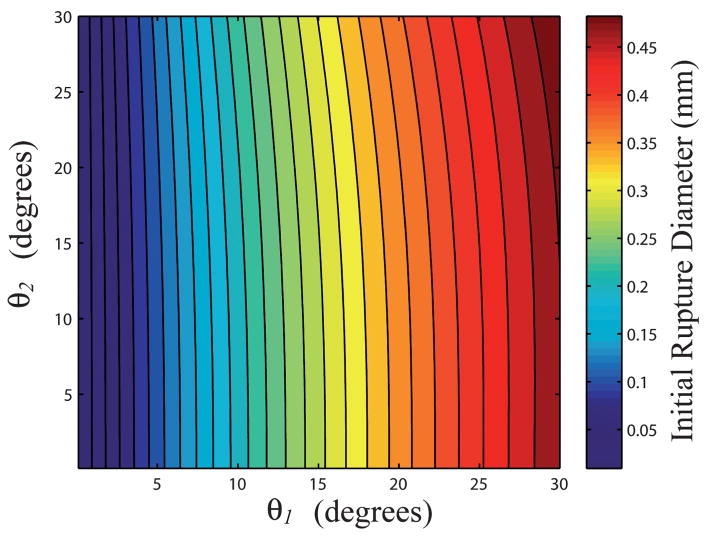
Given a specific reservoir geometry (D₁, D₂, H) and specific experimental conditions (T, p, RH, V_o), one only needs to know values of θ₁ and θ₂ to predict the evolution of an evaporating meniscus over time. Standard experimental methods cannot be used to measure the value of θ₂ due to the confined geometry of the reservoir sidewalls. However, because the critical volume of the reservoir depends only on θ₂, knowledge about the initial rupture diameter can be used to gain insight regarding predicted values of θ₁ and θ₂. Fig. 6 shows a contour plot of the predicted dependence of θ₁ and θ₂ on D_cap(t_c) for a reservoir with D₁ = 1.2 mm, D₂ = 1.6 mm, and H = 1.8 mm. A specific value of θ₂ determines V_c for a given reservoir geometry, which in turn establishes a relationship between θ₁ and D_cap(t_c). Using experimental values for D_cap(t_c), such as that shown in Fig. 3(c), a functional relationship for θ₁ in terms of θ₂ may then be determined. Thus, one needs only experimental values for D_cap(t_c) and an initial guess for θ₂ to predict the parameters V, r_o, z_o, R₁ and R₂ as a function of time.

Fig. 6.

Contour plot displaying the predicted initial rupture diameter D_cap(t_c) of a meniscus as a function of θ₁ and θ₂ for a reservoir with D₁ = 1.2 mm, D₂ = 1.6 mm, and H = 1.8 mm.

To predict the evolution of a meniscus during evaporation, the time rate of change for the volume within a reservoir is discretized using a first order forward difference

$$V^{n+1}=V^n-Q_e\mathrm{\Delta }t$$ (5)

where Vⁿ represents the volume of the liquid at time t = nΔt. The simulation is initialized with a liquid volume V_o, and values of Δt are adjusted such that Q_eΔt < 10⁻⁴ μL. An initial guess for θ₂ and the experimental value for D_cap(t_c) are used to determine a matching value for θ₁. These values are then used along with the experimental values of D₁, D₂, H, T, p, and RH as inputs to a series of CFD simulations to determine the parameters (a₁, a₂, a₃, b₁, b₂, b₃) associated with eqns (3) and (4). These parameters determine the relationship between Q_e and V, which in turn is used in eqn (5) to calculate V as a function of time. The predicted values of D_cap as a function of time (for t > t_c) can then be calculated using the geometric model (Appendix I in the ESI^†). Typically, several iterations involving a guess for θ₂ are required for a good fit to the experimental data, where each iteration involves calculation of the parameters associated with eqns (3) and (4).

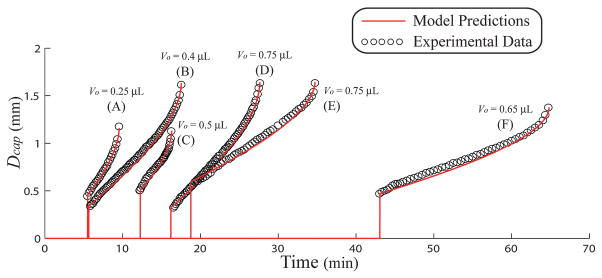
Fig. 7 compares experimental measurements to predicted values of D_cap as a function of time for several reservoir geometries and constructs (PDMS reservoir, glass or PDMS floor). The parameters associated with the results shown in Fig. 7 are displayed in Table 1. Aside from small scale differences in D_cap persisting for roughly 3 minutes after the meniscus rupture, the model does very well with respect to predicting experimental measurements. The geometric/CFD model predicts the time of meniscus rupture and overall time of the experiment (t_end) within 1.5 and 0.5 minutes, respectively, for all cases (16 total experiments). The effect of reservoir geometry on the overall evaporation rate may be seen from the results in Fig. 7. For example, the difference between an expanding and contracting reservoir can clearly be seen between the case (C) and (F), where times for reservoir dry out for a 0.5 μL droplet in an expanding reservoir was 16.2 min compared with 64.7 minutes for dry out of a 0.65 μL droplet in a smaller contracting reservoir. The reservoir in case (F) had 30% more liquid, yet took nearly 300% more time to dry out under roughly the same conditions. The initial slopes of D_cap shown in Fig. 7 are a complicated relationship between the reservoir geometries, surface conditions, and external conditions. This behavior is unlike the evaporation of water from shallow wells, where time derivatives of D_cap are independent of the reservoir geometry and volume.³⁵ The discrepancy between the two cases is most likely due to the pinning of the meniscus around the upper rim of a shallow reservoir while the lower meniscus edge recedes freely. Neither the upper or lower edge of menisci in the reservoirs in this study has been observed to be static. If either of the two contact lines of the meniscus were to be pinned in a microreservoir, the combined CFD/geometric model would likely not show the accuracy displayed in Fig. 7, since the geometric model assumes a contact line that can move freely along both the reservoir floor and sidewalls.

Fig. 7.

Experimental and predicted data showing the inner ruptured meniscus (D_cap) as a function of time. The parameters for the predictions are shown in Table 1.

Table 1.

Experimental and predicted parameters for the results shown in Fig. 7

	Type	D1 (mm)	D2 (mm)	H (mm)	Vo (μL)	T (°C)	RH (%)	θ1 (deg.)	θ2 (deg.)	Vc (μL)
(A)	PDMS/glass	1.17	1.65	2.1	0.25	27	23	21.5	48	0.095
(B)	PDMS/glass	1.65	1.15	2.0	0.4	28	31	9.5	54	0.259
(C)	PDMS/PDMS	1.14	1.65	1.7	0.5	26	20	28.5	42	0.102
(D)	PDMS/glass	1.65	1.15	1.9	0.75	28	26	9.8	50	0.280
(E)	PDMS/PDMS	1.65	1.13	2.0	0.75	25	38	23.8	50	0.306
(F)	PDMS/PDMS	1.38	0.77	2.2	0.65	28	31	28.5	43	0.192

A total of 16 experiments were fit to predictions such as those shown in Fig. 7 corresponding to a range of parameters from 0.77≤D₁,D₂ ≤ 2.2 mm, 1.0 ≤ H ≤ 3.5 mm, 9.8 ≤θ₁ ≤ 30°, and 41 ≤ θ₂ ≤ 58°. The predicted contact angle of water and a glass floor was θ_1,glass = 14 ± 5.6°, whereas the predicted value pertaining to a PDMS floor was θ_1,PDMS = 26 ± 3.4° (based on 8 experiments each). These values compare very well to experimental contact angle measurements of clean glass and PDMS oxidized with the conditions in this experiment (25 W, 900 mTorr air, 20 s).⁴¹ The predicted contact angle of water and the PDMS reservoir was θ_2,PDMS = 49 ± 4.7°, where there was no significant difference between θ_2,PDMS values pertaining to PDMS/PDMS and PDMS/glass reservoirs. The difference between θ_1,PDMS and θ_2,PDMS may be attributed to several factors, including the increase in surface roughness of the reservoir sidewalls as a result of the punching process⁴² and the lower efficiency of plasma penetration to the smaller diameter cavity. The small variance in the fitted parameters θ_1,PDMS, θ_{1, glass}, and θ_2,PDMS with respect to the large range of experimental parameters in this study highlight the effectiveness of the combined geometric/CFD model.

Regardless of the discrepancy between θ_1,PDMS and θ_2,PDMS, these averaged parameters may be used to predict the evolution of a meniscus with high accuracy. Table 2 displays the errors associated with t_c and t_end for the evolution of a meniscus in the reservoirs shown in Fig. 7 using the averaged parameters θ_1,PDMS, θ_1,glass, and θ_2,PDMS given above. As expected, the values of Δt_c and Δt_end are strongly dependent on Δθ₂, the difference between the averaged value θ_2,PDMS and the value θ₂ shown in Table 1. Because of the small dependence of Q_e on θ₁ and θ₂, as shown in Fig. 5(b), the error in Δt_end is much smaller than Δt_c, accurately predicting reservoir dry out within a minute for all cases.

Table 2.

Errors of prediction for the cases shown in Fig. 7 by utilizing the averaged parameters θ_1,glass = 14°, θ_1,PDMS = 26°, and θ_2,PDMS = 49°

	Experimental		Prediction				Error
	tc (min)	tend (min)	tc (min)	tend (min)	Δθ1(deg)	Δθ2 (deg)	Δtc (min)	Δtend (min)
(A)	5.5	9.5	5.52	9.47	−7.2	−0.4	0.02	0.03
(B)	5.8	17.5	4.23	18.2	3.5	−4.4	−1.57	0.7
(C)	12.2	16.2	12.95	16.4	3.8	6.6	0.75	0.02
(D)	16.5	27.6	16.0	27.4	3.7	−2.4	−0.5	−0.02
(E)	19.3	34.7	19.5	35.3	−0.1	1.6	0.02	0.6
(F)	43	64.7	44.2	65.1	1.0	4.6	1.2	0.4

Meniscus stability and model accuracy

It is hypothesized that there exists a stability criterion for a ruptured meniscus (as shown in Fig. 1) similar to that of a 2D meniscus lying on a solid edge with angle 2α. Following the example presented by Langbein,⁴³ it is expected that for values of 2α + θ₁ + θ₂ < π the ruptured meniscus will be stable in the concave form shown in Fig. 1. Beyond this stability criterion, for values of 2α + θ₁ + θ₂ > π, the ruptured meniscus is expected to exist in either a convex form or a shape not readily described mathematically. For experimental systems (PDMS/PDMS) made hydrophilic with a lower quality plasma (200 mTorr, 15 W, 20 s), the meniscus indeed ruptures to a state not defined by the geometric model proposed here; however, the boundary between the two states of stability has not been resolved. Animations of an unstable rupture can be viewed in the ESI.^†

Because of the dilute nature of the fluorescent bead solution used in this study, it is doubtful that θ₁ or θ₂ will change as a function of reservoir liquid volume. However, because the liquid within the reservoir reaches a point of infinite concentration as t → t_end, it is unlikely that solutions containing realistic solute concentrations would display constant apparent contact angles over the duration of the experiment. To model these systems, one would only need a relationship between θ₁ or θ₂ and the solute concentration, which in principle are obtainable through experiment. As long as solute precipitation does not interfere with the position of the mensiscus, or the stability criterion shown above is not violated, these systems could most likely be predicted with the same accuracy as the cases shown in Fig. 7.

In this study, care was taken to ensure that the average meniscus position was at a z-position lower than H/2 at the onset of the experiment. As the meniscus height approaches the top of the reservoir, or V →V_res, the evaporation rate calculated by eqn (2) increases in inverse proportion to the distance from the meniscus to the reservoir outlet. Under those conditions eqn (2) will over predict the evaporation rate from the meniscus, resulting in an under prediction of t_c and t_end. Because eqn (2) achieves significant accuracy as the liquid volume decreases, the model can be used for all systems with V ≤V_res to estimate the minimum time for reservoir dry out. To accurately describe the evolution of a meniscus in a microreservoir for conditions described above, one must (1) develop a model that accounts for the steady-state diffusion of water vapor into the space above the reservoir and (2) develop a function that gives a smooth transition between the two models as a function of the liquid volume in the reservoir.

Applications to lab-on-a-chip systems

When the situation arises for which long incubation times (> 10 min) are required for a continuous flow μFN based assay, it is important that analyte concentrations within the inlet reservoir remain relatively constant. For continuous flow assays, the volume of liquid in an inlet reservoir can be accurately determined using eqn (5) modified with a term to account for the loss of fluid via volumetric flow through a μFN,

$$V^{n+1}=V^n-(Q_e+Q_f)\mathrm{\Delta }t$$ (6)

where Q_f is the volumetric flow rate drawn from the inlet reservoir.

Rather than utilizing complex fabrication strategies or inclusion of unnecessary experimental protocols, the techniques in this study can be used to design inlet reservoirs such that the inlet concentration is within acceptable limits over a predetermined time. The simplicity of this approach is in significant contrast with some previous technologies; for example, the assay system developed by Zimmermann et al. requires an inlet reservoir to the μFN to be cooled to 2 °C above the dew point in order for a 0.6 μL water droplet to persist for over an hour.²¹ A reservoir such as that shown in Fig. 7, case (F), achieves the same result without the need to control the external environment. We have also fabricated reservoirs with D₁ = 1.1 mm, D₂ = 1.6 mm, and H = 3.5 mm that allow a 0.6 μL droplet to persist for over 90 minutes. For that case, it is predicted that (provided V_res/Q_f ≫t_end) at t = 20 min, V/V_o = 0.9, which is sufficient for most analytical measurements. This same approach may also be used to enhance evaporation in systems that require analyte pre-concentration for detection. An inlet reservoir designed with dimensions that produce higher evaporation rates used in microfluidic based assays would lead to systems with lower detection limits, as the reservoir solution could be concentrated by an order of magnitude within several minutes.

The predictive techniques used in this study can also be used for passive pumping applications based on capillary forces. The capillary pressure difference between a static air/liquid interface is described by the Young–Laplace equation

$$\mathrm{\Delta }p=p-p_1={\gamma }_{lv}\left(\frac{1}{R_1}+\frac{1}{R_2}\right)$$ (7)

where p_l represents the pressure in the liquid phase at the interface. Two reservoirs connected by a common μFN may be used to drive fluid between one another, provided that the two principal radii of curvature of liquid in the two reservoirs are different. This system would provide several advantages over the type of passive pump developed by Walker and Beebe,²⁵ namely (1) the air/liquid interface is located entirely within the reservoir, reducing the chance of unwanted contact with foreign materials and (2) the values of R₁ for reservoirs with low liquid volumes can be much smaller than the characteristic size of the reservoir, allowing for very high differential pressures. From the geometric model proposed here R₁ and R₂ can be calculated for a given reservoir liquid volume, thus the volumetric flow rate between two reservoirs can be accurately determined using eqn (7), while the volume of liquid in each reservoir can be determined using eqn (6). Initial studies show fluid velocities in a μFN between two reservoirs greater than 1 mm s⁻¹, corresponding to pressure drops Δp > 8600 Pa. The ease of fabrication and straightforward prediction of fluidic response may prove to be extremely valuable for lab-on-a-chip applications, and is the focus of future work.

Conclusion

There are many lab-on-a-chip designs that utilize a micro-reservoir either for direct chemical analysis or as a method for fluid introduction into a microfluidic network. Owing to both the small sample size and the likelihood that the liquid volume is open to the external environment, evaporation can quickly lead to detrimental results within the device. Knowledge of the rates of liquid evaporation within a microreservoir, and how that rate depends on the local conditions, is essential when considering the performance reliability of such a device.

To gain insight into the rate of evaporation in a given system, a simple geometric model is proposed that accounts for the shape of an air/liquid meniscus present in a cylindrical microreservoir with variable cross section. This model is utilized as a template for studying the rates of evaporation from the liquid volume via computational fluid dynamics. The combined geometric/CFD approach has been shown to quantitatively predict the evolution of a meniscus over time in experimental systems, and with high accuracy. This method can be used with any liquids as long as the geometry of the reservoir and solution properties obey the relation 2α + θ₁ + θ₂ < π. For liquid present in a microreservoir, simple methods to enhance or moderate evaporation have been discussed. Evaporation rates can be increased in microreservoirs by reducing the height of reservoir or increasing the overall diameter of the reservoir such that D₂ > D₁. Similarly, evaporation is readily decreased by increasing the height of the reservoir or decreasing the overall diameter such that D₁ > D₂.

The techniques used in this study may be used to optimize a variety of lab-on-a-chip applications that involve a holding reservoir open to the environment. Furthermore, the geometric model may be used to design passive pumping between multiple reservoirs, whose characteristics can be predicted over time as the meniscus in each reservoir evolves. The passive pumping mechanisms related to this study are the focus of future work.