HNCO-based measurement of one-bond amide ¹⁵N-¹H couplings with optimized precision

Abstract

A pair of 3D HNCO-based experiments have been developed with the aim of optimizing the precision of measurement of ¹J_NH couplings. Both pulse sequences record ¹J_NH coupling evolution during the entire constant time interval that ¹⁵N magnetization is dephasing or rephasing with respect to the directly bonded ¹³C′ nucleus, with ¹⁵N¹³C′ multiple quantum coherence maintained during the ¹³C′ evolution period. The first experiment, designed for smaller proteins, produces an apparent doubling of the ¹J_NH coupling without any accompanying increases in line width. The second experiment is a J-scaled TROSY-HNCO experiment in which the ¹J_NH coupling is measured by frequency difference between resonances offset symmetrically about the position of the downfield component of the ¹⁵N doublet (i.e. the TROSY resonance). This experiment delivers significant gains in precision of ¹J_NH coupling measurement compared to existing J-scaled TROSY-HNCO experiments. With the proper choice of acquisition parameters and sufficient sensitivity to acquire a 3D TROSY-HNCO experiment, it is shown that ¹J_NH couplings can be measured with a precision which approaches or exceeds the precision of measurement with which the frequency of the TROSY resonance itself can be determined.

Introduction

Residual dipolar couplings (RDCs) provide valuable restraints for 3D structure determination due to their sensitivity to bond vector orientations relative to a global coordinate frame (Bax et al. 2001; Blackledge 2005; Tolman and Ruan 2006). The use of RDC restraints is especially promising for high molecular weight systems in which fewer long range NOEs are available due to high levels of deuteration necessary to maintain adequate relaxation times. RDCs can also provide insight into protein dynamics over the full submillisecond timescale and thus are a useful complement to spin relaxation based studies (Briggman and Tolman 2003; Lange et al. 2008; Salmon et al. 2009). However, relative to structural determinants, motions affect the measured RDCs to second order, and thus high quality RDC data is especially important. As amide ¹⁵N-¹H RDCs are generally large and measurable even in highly perdeuterated proteins, it is desirable to have robust methods for the measurement of ¹J_NH splittings with high precision and accuracy over a wide range of protein molecular weights.

The major obstacles in systems of higher molecular weight are the accompanying increase in resonance overlap and decreasing transverse relaxation times, which diminish the number of RDCs that can reliably be measured. The use of 3D methods can effectively relieve overlap but come at a cost in sensitivity and precision relative to 2D methods. Nevertheless, experiments such as the ¹H-coupled HNCO experiment (de Alba et al. 2001) are well suited for measurement of one bond amide ¹⁵N-¹H RDCs in proteins of modest size. For amide ¹⁵N-¹H groups the TROSY technique (Pervushin et al. 1998; Salzmann et al. 1998), which exploits the fortuitous characteristics of the ¹⁵N-¹H dipole–dipole/¹⁵N chemical shift anisotropy cross correlation, can be employed to achieve dramatic improvements in sensitivity even for high molecular weight proteins. However, the desirable narrowing of the downfield component of the ¹⁵N doublet is accompanied by a corresponding broadening of the upfield component. When the aim is to measure ¹J_NH couplings in a large protein, the upfield component can become so broad that accurate measurement of ¹J_NH couplings is precluded.

These problems can be overcome by utilizing J-scaled TROSY-HNCO schemes (Yang et al. 1999; Kontaxis et al. 2000) in which the coupling is determined by difference between two distinct experiments. In the first experiment the normal TROSY spectrum is recorded. In a second experiment, the coupling is either partially decoupled or enhanced by introduction of an additional incremented coupling evolution period. All approaches require the interchange of fast and slow relaxing components of the ¹⁵N doublet (by means of application of a 180° ¹H pulse) and thus suffer some reduction in sensitivity and precision of measurement relative to that of the pure TROSY spectrum. Sensitivity considerations will therefore place a limit on the scaling factor that be employed and hence on the obtainable precision of coupling measurement. Successful application to high molecular weight systems requires a careful balance between additional relaxation losses and gains in precision associated with a given scaling factor.

We describe here two 3D HNCO-based experiments designed to optimize the precision of measurement of ¹J_NH couplings relative to the base sensitivity of the HNCO experiment. Both experiments feature a combined ¹⁵N chemical shift and coupling evolution period which stretches over both constant time ¹J_NC re/dephasing periods with ¹⁵N¹³C′ multiple quantum (MQ) coherence maintained during the ¹³C′ chemical shift evolution period. Use of such a ¹⁵N¹³C′ MQ approach has been used previously for increasing resolution in the TROSY-HNCA experiment (Salzmann et al. 1998) and very recently was proposed for increasing the precision of PRE measurements in the HNCO experiment (Hu et al. 2009). The present work is aimed at optimization of precision of RDC measurements. The first sequence, designed for small molecular weight proteins, acquires ¹H-coupled doublets in the ¹⁵N dimension which exhibit an apparent doubling of the coupling achieved by evolving the ¹J_NH coupling during the ¹J_NC′ dephasing period. This is accompanied by strategic inversion of the ¹H spin states in order to equalize the relaxation rates of both ¹⁵N doublet components, preventing losses in precision of measurement due to differential line broadening. The second implementation is a J-scaled TROSY experiment designed for larger proteins. During the first ¹J_NC′ dephasing period both the coupling and chemical shift are evolved but in the second ¹J_NC′ rephasing period ¹J_NH coupling evolves such that it either resumes or refocuses the J-evolution which occurred during the first period. A pair of experiments is acquired with the coupling scaled symmetrically about the TROSY line position, delivering at least sqrt(2) improved measurement precision compared to a corresponding measurement recorded relative to just the TROSY line. The approach is demonstrated with application to the 24 kDa protein Neisseria meningitides heme oxygenase (nmHO) and the B1 domain of protein G (GB1) and general guidelines are established for optimizing the precision of measurement of ¹J_NH couplings utilizing 3D HNCO-based methods.

Materials and methods

Preparation of NMR samples

¹⁵N, ¹³C, ²H-labeled nmHO was expressed and purified according to the procedure of (Zhu et al. 2000) modified according to the scheme of (Marley et al. 2001). Briefly, transformed E. coli (BL21) cells were grown in LB media to an OD₆₀₀ of at least 0.7 (typically 5–6 h) followed by resuspension in M9 minimal media containing 1 mg/L ¹⁵N-ammonium chloride, 4 mg/L ¹³C₆-glucose and 99% D₂O. After incubation for 1.5 h at 37°C, expression was induced with isopropyl-1-thiol-(d)-galactopyranodise (IPTG) and cell growth continued at 30°C for 40 h with reinduction with IPTG (1 mM) approximately every 12 h. After purification of apo-nmHO (Zhu et al. 2000), the protein solution was reduced to a volume of 0.5 ml and then titrated with a hemin solution containing a 10-fold Molar excess of KCN to a final 1:1 nmHO:hemin ratio. The solution was passed directly over a mini G-25 size exclusion column to remove any excess unbound heme and then the flow through solution was lyophilized. For NMR measurements, the lyophilized cyano-nmHO was resus-pended in a solution containing 20 mM Tris–HCl (pH 7.8), 50 mM NaCl, 10% D₂O, to a final concentration of 600 μM. ThWed into a Wilmad 541-PP-5 constricted NMR tube, evacuated and then flame sealed. ¹⁵N, ²H-labeled protein GB1 was expressed and purified as previously described (Ruan et al. 2008) with the exception that the M9 minimal media solution was prepared using 99% D₂O rather than H₂O. Cells were grown in LB media to an OD₆₀₀ of 0.75, resuspended in M9 minimal media, induced with IPTG and then incubated at 37°C for 7.5 h before harvesting. Final sample conditions were 1 mM protein GB1 in 10 mM phosphate (pH 6.6), 0.05% NaN₃ and 5% D₂O. The level of deuterium incorporation obtained when using the resuspension protocol (Marley et al. 2001) with protonated ¹³C₆-glucose and D₂O is typically 60–70% as determined by mass spectrometry.

Data acquisition

All NMR datasets were recorded at 20°C on a Varian Inova 800 MHz spectrometer equipped with a cryogenically cooled triple resonance (HCN) probehead and a Performa II actively shielded Z-axis gradient system. All datasets collected for the purpose of the measurement of ¹J_NH couplings were acquired in duplicate to allow estimation of precisions of measurement. Data processing was carried out using NMRpipe software (Delaglio et al. 1995) and peak positions determined by contour fitting using PIPP v.4.3.2 (Garrett et al. 1991) unless otherwise specified.

For the 3D J-doubled HNCO datasets on cyano-nmHO, 30, 64 and 830 complex points were acquired at spectral widths of 2,400, 2,431 and 12,775 Hz, which correspond to acquisition times of 12.1, 25.9 and 65 ms in the t₁, t₂ and t₃ time domains, respectively. The acquisition parameters for the 3D κnJ-scaled TROSY-HNCO datasets were 30, 61 and 1,040 complex points at spectral widths of 2,400, 2,148 and 16,000 Hz resulting in t₁, t₂ and t₃ acquisition times of 12.1, 27.9 and 65 ms. Eight transients were collected per stored FID corresponding to a total experimental duration of 20 h for each individual dataset. Complete 3D κnJ-scaled TROSY-HNCO datasets were acquired for scaling parameters κ = 1 and κ = 2, corresponding to a total of 80 h spectrometer time. For all datasets, time domain data were apodized with 90°-shifted squared sine-bell functions in all three dimensions prior to zero-filling and Fourier Transformation. The ¹³C′ t₁ time domain was doubled to 60 points using forward–backward linear prediction. Final data matrices were 196 × 512 × 2,048 points.

Transverse relaxation times for the upfield and down-field ¹⁵N doublet components of cyano-nmHO at 800 MHz were measured using a 2D [¹⁵N-¹H]-SE-TROSY-HSQC experiment (Palmer et al. 1991; Muhandiram and Kay 1994) modified by insertion of an ¹⁵N spin echoelement comprising the variable relaxation delay just prior to the indirect ¹⁵N evolution period. The ¹⁵N relaxation times T_2S and T_2F were measured by selecting for the TROSY and anti-TROSY line, respectively, with a ¹H 180° pulse applied just prior to the ¹⁵N evolution period in the case of the anti-TROSY experiment. Datasets were acquired with a recycle delay of 3.2 s, relaxation delays of 2, 10, 20 and 30 ms, and with 161 and 1,023 complex points at spectral widths of 2,301 and 16,000 Hz recorded in the t₁ and t₂ dimensions, respectively. Data were apodized with 90°-shifted squared sinebell function in both dimensions, zero-filled and then Fourier Transformed to constitute a final data matrix of 1,024 × 4,096 points. Spectra were peak picked and analyzed using the Sparky 3 software (Goddard and Kneller 2007). For all well resolved peaks in the 2D spectra, peak heights as a function of relaxation delay were fit to a mono-exponential decay function in order to extract relaxation times T_2S and T_2F.

A series of 2D [¹⁵N, ¹H] κnJ-scaled TROSY-HNCO spectra were recorded for protein GB1 for integral κ values ranging from 1 to 5 as well as a 2D [¹⁵N, ¹H] J-doubled HNCO experiment. Each dataset was recorded with 78 and 1,120 complex points at spectral widths of 2,755 and 16,000 Hz, which correspond to acquisition times of 28 and 70 ms in t₁ and t₂, respectively. Data were apodized with 90° and 72°-shifted squared sinebell functions in t₁ and t₂ domains, followed by zero filling and Fourier Transformation to produce 512 × 2,048 data matrices. Total experimental duration was 100 min per dataset. 2D [¹⁵N-¹H]-SE-IPAP-HSQC (Ottiger et al. 1998) data for protein GB1 was acquired with 193 and 819 complex points at spectral widths of 2,755 and 12,775 Hz in the t₁ and t₂ time domains, corresponding to acquisition times of 70 and 64 ms, respectively. Data were apodized with 90°-shifted squared sinebell functions in both dimensions, followed by zero filling and Fourier Transformation to produce 512 × 2,048 data matrices. Total experimental duration was 126 min. Peaks positions were determined by parabolic interpolation using the Sparky 3 software (Goddard and Kneller 2007) for all GB1 data.

Calculation of relative precision for TROSY-HNCO experiments

Comparisons of precision and sensitivity for different TROSY-HNCO experiments were carried out neglecting any differences other than the relaxation and frequency characteristics of the ¹⁵N evolution period (t₂), employing functions normalized to A at time t₂ = 0. As such, the TROSY-HNCO experiment of (Kontaxis et al. 2000) was modeled using the following function,

$$\begin{array}{cc}\hfill S\left(t_2\right)=& A\exp [-i{\Omega }_{15N}{t}_2+i\pi \alpha {\mathrm{J}}_{\mathrm{NH}}{t}_2]\exp \left[\frac{1}{2}(1+\alpha )R_{2\mathrm{S}}{t}_2\right]\hfill \\ \hfill & \times \exp [-(1+\alpha )R_{2\mathrm{F}}{t}_2]\hfill \end{array}$$ (1)

where the parameter α is set to a value between −1 and +1, corresponding to TROSY and anti-TROSY components respectively. R_2S and R_2F refer to the ¹⁵N transverse relaxation rates of the downfield and upfield components of the ¹⁵N doublet, respectively. Similarly, the TROSYHNCO experiment of (Yang et al. 1999) can be described as follows,

$$\begin{array}{cc}\hfill S\left(t_2\right)=& A\exp [-i{\Omega }_{15N}{t}_2+i\pi (1+\kappa ){\mathrm{J}}_{\mathrm{NH}}{t}_2]\hfill \\ \hfill & \times \exp \left[-\frac{\kappa }{2}{R}_{2\mathrm{S}}{t}_2\right]\exp \left[-\frac{\kappa }{2}{R}_{2\mathrm{F}}{t}_2\right]\hfill \end{array}$$ (2)

for which each integral increment of κ increases the apparent coupling by ½ J relative to the TROSY line.

Precision and sensitivity considerations

Precision of measurement of resonance frequencies

To a good approximation the experimental uncertainty of measurement of a resonance frequency, σ_ν, will scale proportionally to the linewidth, Δν_½, and inversely proportionally to the signal to noise ratio S measured in the frequency domain,

$${\sigma }_{\nu }\propto \frac{\Delta {\nu }_{1∕2}}{S}.$$ (3)

Although not useful for absolute calculations of precision, we will derive below a form of this expression to be utilized to compare the expected relative precision for different experiments acquired with similar acquisition parameters and the same total experimental duration.

Linewidth dependence

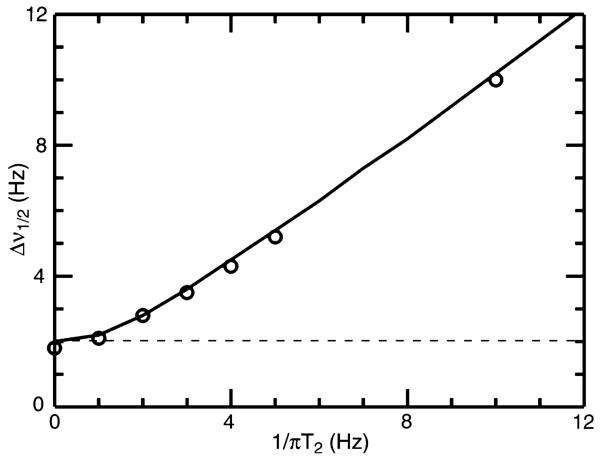
In 1D NMR spectroscopy it is inexpensive to acquire signals with sufficient duration such that their frequency domain linewidths are dependent only the corresponding transverse relaxation times $T_2^{\ast }$. However, for multi-dimensional experiments or cases in which decoupling limits acquisition time, the actual linewidth Δν_½ is very often dominated by the acquisition time, t_acq, in a manner which will be somewhat dependent on processing parameters. For example, shown in Fig. 1 is the actual measured linewidth as a function of inherent T₂ linebroadening (i.e. 1/πT₂) which resulted from analysis of noiseless synthetic data generated with t_acq = 500 ms and apodized using a cosine bell function prior to Fourier Transformation. While the observed linewidth is governed overall according to 1/πT₂, it is subject to a lower bound of ca. 1/t_acq, as indicated by the dashed line in Fig. 1. Clearly the T₂ and t_acq contributions are not simply additive. We propose the following approximate expression for Δν_½ which more closely models actual behavior, as indicated by the solid black line in Fig. 1,

$$\Delta {\nu }_{1∕2}\approx \sqrt{{\left(\frac{1}{t_{\mathrm{acq}}}\right)}^2+{\left(\frac{1}{\pi T_2}\right)}^2}.$$ (4)

Fig. 1.

Measured linewidth, Δν_½, as a function of T₂ relaxation time for synthetically generated data with an acquisition time, t_acq, of 500 ms. Synthetic data were generated for a single on-resonance signal for the applicable relaxation time, apodized with an unshifted cosine bell function, and then zero-filled four times prior to Fourier Transformation and subsequent measurement of the linewidth

These results are generally scalable to other T₂ and t_acq combinations when a cosine bell apodization function is used. Based purely on linewidth considerations, the optimal precision of measurement is obtained when the line-width is T₂ dominated, which can be achieved by setting t_acq greater than approximately 2πT₂. However, in order to optimize precision in an indirect dimension of a multidimensional experiment of fixed overall experimental duration, sensitivity considerations will favor shorter values of t_acq and so there will be an optimal compromise value for t_acq.

Sensitivity dependence

A relatively simple expression for the relative sensitivity as a function of t_acq can be obtained assuming that comparison is being made between 2D experiments with a constant total number of transients and overall experimental duration. Under these circumstances the relative noise for the two experiments being compared factors out and one can consider just the relative signal intensities. We will define the relative signal intensity as the summation over each of the recorded signals normalized to the recorded signal magnitude when t = 0. The discrete sum can conveniently be replaced with an integral, leading to the following expression for the relative loss in sensitivity as a function of t_acq (expressed relative to T₂) assuming a simple mono-exponential decay of signal intensity as a function of time,

$$S\left(\frac{t_{\mathrm{acq}}}{T_2}\right)=\frac{{\int }_0^{t_{\mathrm{acq}}}A\exp \left(-\frac{t}{T_2}\right)\mathrm{d}t}{{\int }_0^{t_{\mathrm{acq}}}A\mathrm{d}t}=\frac{T_2}{t_{\mathrm{acq}}}\left[1-\exp \left(-\frac{t_{\mathrm{acq}}}{T_2}\right)\right].$$ (5)

Combining this result with that of Eq. 4 leads to the desired working expression for the relative precision of measurement of the frequency of a single resonance,

$${\sigma }_{\nu }\propto \frac{\sqrt{{(1∕t_{\mathrm{acq}})}^2+{(1∕\pi T_2)}^2}}{\frac{T_2}{t_{\mathrm{acq}}}\left[1-\exp \left(-\frac{t_{\mathrm{acq}}}{T_2}\right)\right]}.$$ (6)

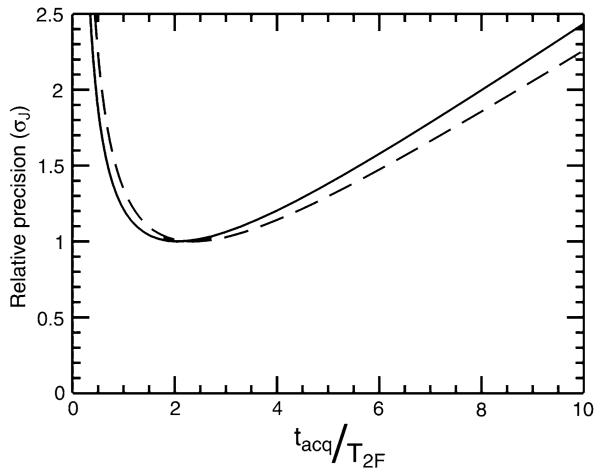
The relative precision, σ_ν, as a function of the ratio between the acquisition time t_acq and T₂ is illustrated by the solid line in Fig. 2. This relationship is equally valid for calculating the relative precision of measurement of splittings between lines of equal linewidth. While the expression of Eq. 6 predicts that optimal precision is achieved by setting t_acq ≈ 2T₂, the optimal range is rather broad with up to 50% errors in estimation of T₂ producing at most about a 10% loss in precision.

Fig. 2.

Calculated relative precision of measurement of the splitting between two lines (σ_J) with relative relaxation rates of 1 (solid line) and 5 (dashed line). Values were computed as discussed in the text and then scaled so that the best precision was equal to 1

In general, lines may exhibit unequal linewidths due to substantial cross-correlation effects between the ¹⁵N-¹H dipole–dipole (DD) and ¹⁵N chemical shift anisotropy (CSA) interactions as observed for amide ¹⁵N-{¹H^N} doublets in proteins. The uncertainty of measurement for the corresponding splitting, σ_J, must then take account of the respective uncertainties of measurement, σ_ν1 and σ_ν2, for the two lines of the doublet according to,

$${\sigma }_{\mathrm{J}}=\sqrt{{\sigma }_{\nu 1}^2+{\sigma }_{\nu 2}^2}.$$ (7)

The precision of measurement of couplings will therefore be largely dictated by the uncertainty in determination of the resonance frequency of the more rapidly relaxing line, as illustrated by the dashed line in Fig. 2 which corresponds to the case of fivefold differential line broadening. In this case, the optimal precision of measurement is obtained by setting t_acq ≈ 2.4 T_2F, where T_2F is the relaxation time of the broader line. If the acquisition time were set to optimize the precision of measurement of the narrower line, the overall loss in precision of coupling measurement (without changing overall experimental duration) would be a factor of 2.25. Achieving optimal precision of measurement should primarily be focused on optimizing the experiment for the relaxation rate of the broader line.

Relative sensitivity of 3D TROSY-HNCO experiments

The use of 3D methods to improve resonance dispersion invariably carries a cost in sensitivity relative to 2D HSQC-based methods. In addition to a loss in sensitivity of sqrt(2) when moving from a 2D to a 3D experiment, there are relaxation and magnetization transfer losses associated with the increased length of coherence transfer pathways as well as due to additional pulses and their associated imperfections. For example, the sensitivity of signals in the first acquired FID of a basic 3D TROSY-HNCO experiment (Salzmann et al. 1998; Loria et al. 1999; Yang and Kay 1999a, b) will be reduced by a factor ε_Tr–HNCO,

$${\epsilon }_{\mathrm{Tr}-\mathrm{HNCO}}={\sin }^2\left({\pi }^1{\mathrm{J}}_{{\mathrm{NC}}^{\prime }}2T_{\mathrm{N}}\right)\exp (-4R_{2\mathrm{S}}{T}_{\mathrm{N}})$$ (8)

relative to the first FID of a 2D [¹⁵N, ¹H]-TROSY-HSQC experiment acquired with the same number of transients and assuming that there are no differences in the ¹⁵N/¹H INEPT transfers. The two terms correspond to signal losses associated with coherence transfer from ¹⁵N to ¹³C′ and the relaxation rate, R_2S, of the slowly relaxing ¹⁵N doublet component during the two constant time periods each of duration 2T_N. Assuming that the ¹⁵N evolution period is fully constant time, the linewidth of the slowly relaxing TROSY line will be determined entirely by the acquisition time, which is approximately 2T_N. Utilizing the relationship of Eq. 6, the expected precision of measurement of the TROSY line frequency, σ_ν, for a 2D [¹⁵N, ¹H] plane of a TROSY-HNCO experiment relative to a 2D [¹⁵N, ¹H]-TROSY-HSQC experiment is,

$$\begin{array}{cc}\hfill {\sigma }_{\nu }& \left(\frac{\mathrm{TROSY}-\mathrm{HNCO}}{\mathrm{TROSY}-\mathrm{HSQC}}\right)\hfill \\ \hfill & \propto \frac{\frac{1}{2R_{2\mathrm{S}}{T}_{\mathrm{N}}}[1-\exp (-2R_{2\mathrm{S}}{T}_{\mathrm{N}})]}{{\sin }^2\left({\pi }^1{\mathrm{J}}_{{\mathrm{NC}}^{\prime }}2T_{\mathrm{N}}\right)\exp (-4R_{2\mathrm{S}}{T}_{\mathrm{N}})\sqrt{1+{\left(\frac{2R_{2\mathrm{S}}{T}_{\mathrm{N}}}{\pi }\right)}^2}}\hfill \end{array}$$ (9)

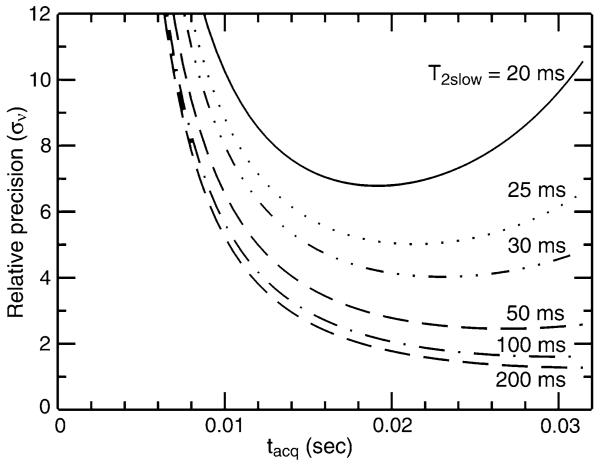
assuming that both experiments were acquired with the same ¹⁵N acquisition time (=2T_N) and the same total experiment time. As illustrated in Fig. 3, the success of the TROSY-HNCO experiment is governed primarily by the relaxation time of the slowly relaxing TROSY line, with optimization of T_N playing some role when relaxation times are very short. On the other hand, from the previous section we expect that the relaxation time of the rapidly relaxing anti-TROSY line will be the major factor which must be considered in optimizing precision of coupling measurements. Assuming that sample concentration, level of deuteration, experimental duration and field strength can be chosen such that recording of a TROSY-HNCO experiment is feasible, attention will be focused on how to optimize the precision of measurement of ¹J_NH couplings.

Fig. 3.

Relative precision of measurement of the TROSY resonance frequency (σ_ν) in a TROSY-HNCO experiment versus that in an [¹⁵N, ¹H]-TROSY-HSQC experiment. Relative precision is plotted as a function of ¹⁵N acquisition time, t_acq (=2T_N), and the relaxation time, T_2S, of the slowly relaxing downfield component (i.e. TROSY line) of the ¹⁵N doublet. For simplicity, the two experiments are compared based on acquisition of just the first [¹⁵N, ¹H] plane of the TROSYHNCO experiment and assuming the same total experimental duration

Results and discussion

Two novel HNCO-based pulse sequences have been developed which allow for improved precision of measurement of ¹J_NH couplings in proteins. The first is a J-doubled sequence designed for small proteins and the second is a TROSY-based version designed for medium to large sized proteins. The unifying principle between the two sequences is that they both maintain transverse ¹⁵N magnetization during the entire sequence aside from the ¹H/¹⁵N magnetization transfer elements. This maximizes ¹J_NH coupling evolution time allowing gains in corresponding precision of measurement to be realized. Such an approach requires that ¹⁵N¹³C′ multiple quantum coherence evolve during the ¹³C′ evolution period with ¹⁵N chemical shift refocused.

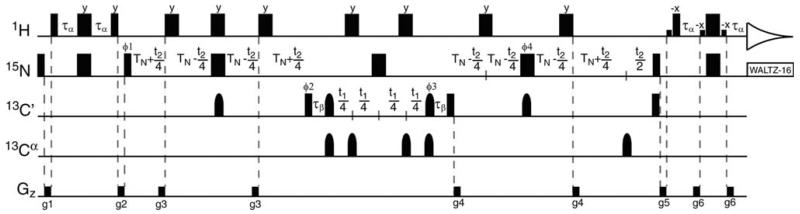
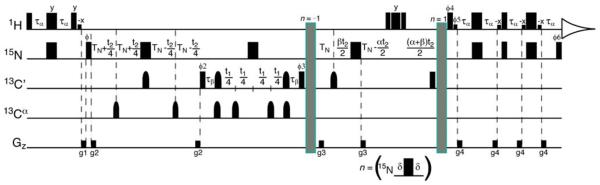
Shown in Fig. 4 is the pulse sequence for the 3D J-doubled HNCO experiment designed for use in smaller proteins. This experiment, which is closely based on a standard 3D HNCO experiment (Grzesiek and Bax 1992; Kay et al. 1994; Yang and Kay 1999a, b) can be summarized by the following flow of magnetization,

$$\begin{array}{cc}\hfill & {}^{1}H^N\stackrel{{}^{1}J_{\mathit{NH}}}{\to }{}^{15}N\underset{\left({\pi }^1{J}_{\mathit{NH}}{t}_2\right)}{\overset{{}^{1}J_{{\mathit{NC}}^{\prime }}}{\to }}{}^{15}N^{13}{C}^{\prime }\left({\Omega }_{C^{\prime }}{t}_1\right)\hfill \\ \hfill & \underset{\left({\Omega }_N{t}_2\pm {\pi }^1{J}_{\mathit{NH}}{t}_2\right)}{\overset{{}^{1}J_{{\mathit{NC}}^{\prime }}}{\to }}{}^{15}N\stackrel{{}^{1}J_{\mathit{NH}}}{\to }{}^{1}H^N\left({\Omega }_H{t}_3\right)\hfill \end{array}$$ (10)

in which the parenthesis denote terms that evolve during the incremented time domains. After polarization of the ¹⁵N nuclei by their attached protons, ¹⁵N magnetization evolves under ¹J_NH coupling during the first ¹J_NC′ dephasing period for a duration t₂. Application of a ¹³C′ 90° pulse creates ¹⁵N¹³C′ multiple quantum coherence, which then evolves only under ¹³C′ chemical shift during t₁. During the subsequent ¹J_NC′ rephasing period, ¹J_NH coupling continues to evolve for an additional duration t₂ along with ¹⁵N chemical shift. ¹H 180° pulses are applied over the entire course of ¹⁵N and ¹⁵N¹³C′ evolution periods in order to interchange the fast-relaxing upfield and slowly-relaxing downfield components of the ¹⁵N doublet such that they each decay at the average relaxation rate (R_2avg = ½(R_2F + R_2S)) over the full ¹⁵N constant time period 4T_N. This avoids large sensitivity losses for the broad upfield line, allowing both components of the ¹⁵N doublet to be recorded in a single experiment with optimal sensitivity. At the start of the ¹H acquisition period, the density operator may be described as,

$$\begin{array}{cc}\hfill \sigma (t_1,t_2)=& H_{\mathrm{x}}\cos \left({\Omega }_{C^{\prime }}{t}_1\right)\exp [-R_{\mathrm{MQ}}{t}_1]\exp [-4R_{2\mathrm{avg}}{T}_{\mathrm{N}}]\hfill \\ \hfill & \times \frac{1}{2}\{\cos \left({\Omega }_{\mathrm{N}}{t}_2-i\pi 2^1{\mathrm{J}}_{\mathrm{NH}}{t}_2\right)\exp \left[-\frac{1}{2}{R}_{2\mathrm{S}}{t}_2\right]\phantom{\}}\hfill \\ \hfill & \times \exp \left[\frac{1}{2}{R}_{2\mathrm{F}}{t}_2\right]+\cos \left({\Omega }_{\mathrm{N}}{t}_2+i\pi 2^1{\mathrm{J}}_{\mathrm{NH}}{t}_2\right)\hfill \\ \hfill & \times \phantom{\{}\exp \left[\frac{1}{2}{R}_{2\mathrm{S}}{t}_2\right]\exp \left[-\frac{1}{2}{R}_{2\mathrm{F}}{t}_2\right]\}\hfill \end{array}$$ (11)

in which R_MQ denotes the rate of relaxation of ¹⁵N¹³C′ MQ coherence. As the ¹⁵N¹³C′ autocorrelated dipole–dipole interaction is negligible (Pellecchia et al. 1999) and potential cross-correlations between ¹⁵N and ¹³C-centered interactions are refocused by the ¹⁵N 180° pulse applied at the midpoint of t₁, R_MQ can be well approximated as the sum of the single quantum ¹⁵N and ¹³C′ transverse relaxation rates. Signals in the resulting Fourier Transformed 3D spectrum will be centered at the corresponding ¹³C′, ¹⁵N, and ¹H^N chemical shifts with the ¹⁵N resonance split by 2 × ¹J_NH. As designed, both components of the ¹⁵N doublet decay at a fixed rate of R_2avg over the constant time period 4T_N. Yet the upfield and downfield components of the ¹⁵N doublet resume their natural rates of decay (R_2F and R_2S, respectively) as a function of t₂ evolution occurring during the second ¹J_NC′ rephasing period. This introduces an apparent decrease and increase in intensity for these two respective lines as a function of t₂, producing perceptible differences in linewidths in the frequency domain.

Fig. 4.

Pulse sequence for the 3D J-doubled HNCO experiment. All narrow (wide) pulses are applied with a flip angle of 90° (180°) with a phase of × unless otherwise indicated. ¹H, ¹⁵N and ¹³C carriers are centered at the water resonance, 119 and 175 ppm, respectively. Off-resonance ¹³C^α pulses were centered at 55 ppm. ¹H and ¹⁵N pulses are applied with a pulse width of 9.35 and 38 μs, respectively, except for the rectangular water selective pulses which have a pulse width of 1.12 ms. Rectangular ¹³C 90° pulses are applied with a pulse width of 14 μs, and shaped ¹³C inversion pulses are applied with a g3 profile (225 μs at 800 MHz) (Emsley and Bodenhausen 1990). The delays used are: τ_α = 2.5 ms, T_N = 13 ms, τ_β = 47.79 μs. The following eight step phase cycle is employed: ϕ₁ = x, −x; ϕ₂ = x; ϕ₃ = 4(x), 4(−x); ϕ₄ = 2(x), 2(−x); ϕ_rec = x, 2(−x), x, 2(−x), x, −x, 2(x), −x. Quadrature in F1 and F2 is achieved by the method of States-TPPI on ϕ2 and ϕ₁, respectively. The gradients were set as follows: g1 (0.5 ms, 17.25 G/cm), g2 (5 ms, 4.31 G/cm), g3 (0.2 ms, 4.31 G/cm), g4 (0.2 ms, 5.60 G/cm), g5 (0.5 ms, 4.31 G/cm) and g6 (0.25 ms, 3.24 G/mm)

The pulse sequence for the 3D κnJ-scaled TROSYHNCO experiment is shown in Fig. 5. The experiment is based on the TROSY-HNCO experiment (Salzmann et al. 1998; Loria et al. 1999; Yang and Kay 1999a, b), with the essential features and flow of magnetization summarized below,

$$\begin{array}{cc}\hfill & {}^{1}H^N\stackrel{{}^1\mathrm{J}_{\mathrm{NH}}}{\to }{}^{15}N\underset{\left({\Omega }_{\mathrm{N}}{t}_2+{\pi }^1{\mathrm{J}}_{\mathrm{NH}}{t}_2\right)}{\overset{{}^1\mathrm{J}_{{\mathrm{NC}}^{\prime }}}{\to }}{}^{15}N^{13}{C}^{\prime }\left({\Omega }_{{\mathrm{C}}^{\prime }}{t}_1\right)\hfill \\ \hfill & \underset{{\left(n\kappa {\pi }^1{\mathrm{J}}_{\mathrm{NH}}{t}_2\right)}_{n=-1,+1}}{\overset{{}^1\mathrm{J}_{{\mathrm{NC}}^{\prime }}}{\to }}{}^{15}N\stackrel{{}^1\mathrm{J}_{\mathrm{NH}}}{\to }{}^{1}H^N({\Omega }_{\mathrm{H}}{t}_3+{\pi }^1{\mathrm{J}}_{\mathrm{NH}}{t}_3).\hfill \end{array}$$ (12)

Fig. 5.

Pulse sequence for the 3D jnJ-scaled TROSY-HNCO experiment. Scheme n is inserted at the position labeled n = −1 for recording the upfield line and at the position labeled n = 1 for recording the downfield line. All narrow (wide) pulses are applied with a flip angle of 90° (180°) with a phase of × unless otherwise indicated. ¹H and ¹³C carriers are centered at the water resonance and 175 ppm, respectively, and off-resonance ¹³C^α pulses were centered at 55 ppm. The ¹⁵N carrier was adjusted for each scaling scheme and centered at 117.5, 118.5, 116.5 and 119.5 ppm for values of nj of −1, 1, −2 and 2 respectively. ¹H and ¹⁵N pulses are applied with a pulse width of 9.3 and 38 ls, respectively, except for the rectangular water selective pulses which have a pulse width of 1.16 ms. Rectangular ¹³C 90° pulses are applied with a pulse width of 14 μs, and shaped ¹³C inversion pulses are applied with a g3 profile (225 μs at 800 MHz) (Emsley and Bodenhausen 1990). The delays used are: τ_α = 2.5 ms, T_N = 14 ms, τ_β = 29.1 μs, δ = 3 μs. The parameter κ determines the extent of J scaling with apparent coupling J_app = κ × ¹J_NH. The parameters α and β are set such that α + β = κ with α = κ when κ ≤ 1 and α = 1 when κ > 1. The following eight step phase cycle is employed: ϕ₁ = y, −y, −x, x; ϕ₂ = x; ϕ₃ = 4(x), 4(−x); ϕ₄ = −y; ϕ₅ = y; ϕ₆ = y; ϕ_rec = x, −x, y, -y, −x, x, −y, y. Quadrature is achieved in F1 by the method of States-TPPI on ϕ₂ and in F2 by the echo-antiecho (enhanced sensitivity) (Rance et al. 1999) method whereby ϕ₄, ϕ₅, ϕ₆ and the latter two phases of ϕ₁ are incremented by 180° for each complex t₂ point. The initial duration of t₂ is set at 1/2SW, which requires a 180° first order phase correction during processing. The gradients employed are: g1 (0.5 ms, 2.16 G/cm), g2 (0.2 ms, 21.56 G/cm), g3 (0.2 ms, 15.1 G/cm), and g4 (0.3 ms, 32.35 G/cm)

During the first constant time ¹J_NC′ dephasing period, ¹⁵N chemical shift and ¹J_NH coupling are allowed to evolve as a function of t₂, while leaving the amide ¹H^N spin state unperturbed. This is a typical constant time TROSY ¹⁵N evolution period. At the end of this ¹J_C′N dephasing period, ¹⁵N¹³C′ MQ coherence is prepared and during the subsequent t₁ evolution period the carbonyl ¹³C′ chemical shift evolves while the ¹⁵N chemical shift is refocused. As the amide ¹H^N spin state remains unperturbed, the ¹⁵N contribution to the relaxation rate R_MQ is small and R_MQ will be dominated by the single quantum transverse relaxation rate of the ¹³C′ nucleus. During the subsequent constant time ¹J_NC′ rephasing period, the ¹J_NH coupling evolves for an additional duration of κt₂, where κ is the J-scaling factor. When scaling J by values of κ greater than 1, the ¹J_NC′ rephasing period is carried out in semi-constant time fashion to accommodate the additional coupling evolution. Evolution of ¹J_NH coupling alone requires that a ¹H 180° pulse be applied, interchanging the lines of the ¹⁵N doublet, which means that the magnetization relaxes as the broad upfield component of the ¹⁵N doublet for a duration of ½κt₂. Finally, a phase-cycled SE-TROSY element (Rance et al. 1999) is employed to transfer the ¹⁵N magnetization back to the upfield component of the ¹H^N doublet for observation. After summation over the first four steps of the phase cycle ϕ₁, the density operator just prior to ¹H acquisition is given by,

$$\begin{array}{cc}\hfill \sigma (t_1,t_2)=& \{2(H_{\mathrm{x}}+2H_{\mathrm{x}}{N}_{\mathrm{z}})\hfill \\ \hfill & \times \cos (-{\Omega }_{\mathrm{N}}{t}_2-i\pi (1+n\kappa ){\mathrm{J}}_{\mathrm{NH}}{t}_2)\hfill \\ \hfill & -2(H_{\mathrm{y}}+2H_{\mathrm{y}}{N}_{\mathrm{z}})\hfill \\ \hfill & \times \sin (-{\Omega }_{\mathrm{N}}{t}_2-i\pi (1+n\kappa ){\mathrm{J}}_{\mathrm{NH}}{t}_2)\}\hfill \\ \hfill & \times \cos \left({\Omega }_{\mathrm{C}}{t}_1\right)\exp [-R_{\mathrm{MQ}}{t}_1]\exp [-4R_{2\mathrm{S}}{T}_{\mathrm{N}}]\hfill \\ \hfill & \times \exp \left[\left(\frac{\kappa }{2}-\beta \right)R_{2\mathrm{S}}{t}_2\right]\exp \left[-\frac{\kappa }{2}{R}_{2\mathrm{F}}{t}_2\right]\hfill \end{array}$$ (13)

in which β = κ − 1 when κ > 1 and β = 0 otherwise. Importantly, the pure TROSY spectrum is never actually recorded in order to measure the ¹J_NH couplings. Instead, a pair of experiments is performed in which an ¹⁵N 180° pulse is inserted just prior to the ¹J_NC′ rephasing period (labeled n = −1) for the first experiment, and just after the ¹J_NC′ rephasing period (labeled n = 1) for the second experiment. The result is that the net t₂ evolution will, respectively, be equal to the difference and sum of the pure ¹J_NH coupling evolution of duration ½κt₂ and the evolution of the TROSY line itself which occurred during the first constant time ¹J_NC′ dephasing period. In the frequency domain, ¹⁵N resonances will be observed which are offset by ½κ¹J_NH downfield (n = 1) or upfield (n = −1) from the position of the TROSY line. Measurement of the difference in frequency between these two lines produces an apparent coupling J_app = κ × ¹J_NH. For a pair of experiments (i.e. n = ±1) acquired with κ = 1, the full unscaled value of the ¹J_NH coupling can be measured without lengthening the overall duration of the evolution period or recording the anti-TROSY line frequency. As such, this approach delivers clear gains in sensitivity and precision of measurement of ¹J_NH couplings relative to existing techniques (vide infra).

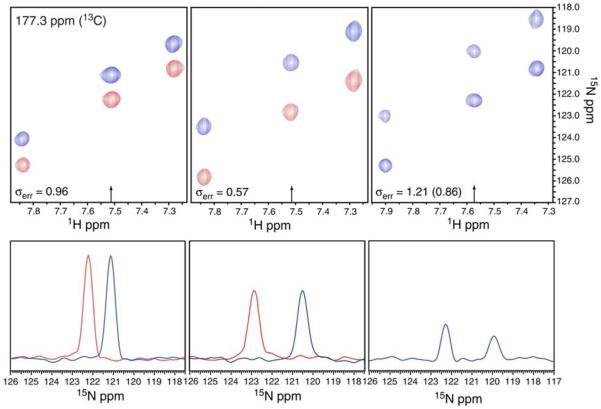
Both the J-doubled and κnJ-scaled TROSY-HNCO experiments were tested on a 600 μM ¹⁵N, ¹³C, ²H-labeled sample of cyano-nmHO at 20°C. At 20°C, the 24 kDa protein cyano-nmHO exhibits average ¹⁵N relaxation times T_2F and T_2S of 20 and 88 ms, respectively. Shown in Fig. 6 are expanded regions of 3D spectra acquired for cyano-nmHO using the J-doubled HNCO experiment and the κnJ-scaled TROSY-HNCO experiment collected with both κ = 1 and κ = 2. The precisions of measurement of the ¹J_NH couplings, estimated based on the RMSD between replicate experiments, are as indicated with the value in parenthesis for the J-doubled experiment representing the precision after scaling to correct for a shorter total experimental duration. Also shown are 1D slices taken at the ¹H frequencies indicated and scaled to have approximately the same noise amplitude. As expected, in the J-doubled experiment the upfield ¹⁵N line is slightly broader and weaker than the downfield component due to the differential relaxation rates of the two components as a function of the incremented time delay t₂. On the other hand, the two lines of the ¹⁵N doublet in the κnJ-scaled experiment have identical intensity and linewidth, differing only in frequency. The κ = 2 spectrum exhibits modest sensitivity loss and linebroadening relative to the κ = 1 spectrum but still delivers overall better precision of measurement (by 40%) due to the doubling of ¹J_NH. When corrected for the difference in total experimental duration, the J-doubled HNCO experiment delivers slightly better precision of measurement than the κ = 1 experiment, in spite of the somewhat unfavorable average ¹⁵N transverse relaxation time (T₂ = 33 ms) for cyano-nmHO at 20°C. These results underscore the significant gains in precision that can be achieved by J-scaling approaches.

Fig. 6.

Expanded plots of corresponding [¹⁵N,¹H] planes taken from 3D spectra acquired on cyano-nmHO using the J-doubled HNCO experiment (right), and the κnJ-scaled TROSY-HNCO experiment with κ = 1 (left) and κ = 2 (center). For the κnJ-scaled spectra the blue resonances correspond to the upfield shifted (n = −1) spectrum and the red resonances correspond to the downfield shifted (n = +1) spectrum. The lower panels are 1D ¹⁵N traces taken at the ¹H frequencies indicated with an arrow and scaled to approximately equal noise amplitude. The estimated experimental precisions (σ_err) are reported in Hz with the value in parenthesis for the J-doubled HNCO scaled to compensate for the longer total experimental duration of the knJ-scaled TROSY-HNCO datasets

Comparison of precision of measurement

A number of different pulse sequences for the measurement of ¹J_NH couplings in a TROSY-HNCO experiment (Yang et al. 1999; Kontaxis et al. 2000; Vijayan and Zweckstetter 2005) have been proposed. These experiments can be distinguished generally according to whether they scale the coupling out (i.e. downfield) by means of concatenation of an additional pure J-evolution element, or by scaling the coupling in (i.e. upfield) by means of decoupling or recording of the anti-TROSY component of the ¹⁵N doublet. The κnJ-scaled TROSY-HNCO experiment is a hybrid of these approaches in that the coupling is scaled both in and out, allowing full optimization of the precision of coupling measurements. To illustrate the advantages of this hybrid approach, it is useful to compare this approach to existing experiments. The first benchmark experiment was developed by Bax and coworkers (Kontaxis et al. 2000) and measures the ¹J_NH couplings by recording the TROSY line in one experiment, followed by recording of the decoupled or anti-TROSY line position in a second experiment. This experiment does not lengthen the pulse sequence as a function of t₂ but is limited to recording resonance frequencies which lie between the TROSY and anti-TROSY line positions. In the second experiment developed by Kay and coworkers (Yang et al. 1999) the apparent coupling is scaled to apparent values larger than its actual value but at the cost of increased duration of the pulse sequence.

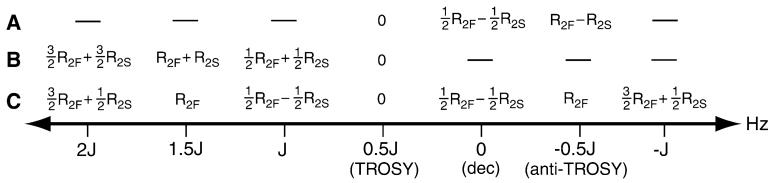
Summarized in Fig. 7 are the apparent relaxation rates which are operative during the ¹⁵N evolution period t₂ as a function of offset from the decoupled line position for the three TROSY-HNCO experiments under discussion. The κnJ-scaled TROSY-HNCO experiment has slightly lower relaxation costs relative to the Yang experiment when scaling out the coupling. On the other hand, it has slightly higher relaxation costs relative to the Kontaxis experiment when recording the anti-TROSY line as a result of an increase in the overall duration of the κnJ-scaled pulse sequence in that case. More significantly, recalling that the precision of coupling measurement is strongly dominated by the broader line, the results of Fig. 7 suggest an improved strategy for coupling measurement. By recording lines symmetrically about the TROSY line position, an effective doubling of the coupling can be achieved relative to a measurement made with respect to the TROSY line without increases in effective relaxation rates. For example, in the Kontaxis experiment an unscaled measurement of ¹J_NH corresponds to recording of the TROSY and anti-TROSY lines with effective relaxation rates (as a function of t₂) of 0 and (R_2F–R_2S). In the κnJ-scaled TROSY-HNCO experiment, a measurement of ¹J_NH is accomplished by recording lines which are offset from the TROSY line by ±½J and which each have associated relaxation rates of ½(R_2F–R_2S) during t₂. Even neglecting sensitivity considerations and the linewidth dependence on acquisition time, gains in precision of measurement of sqrt(2) can be anticipated when relaxation rates are rapid.

Fig. 7.

Effective relaxation rates for three different J-scaled TROSYHNCO experiments as a function of the scaled line position. Effective relaxation rates describe the decay of signal during the ¹⁵N evolution period (t₂) according to S(t₂) = S(0)exp[−R_efft₂], where the rates R_2F and R_2S refer to the rate of relaxation of the fast (upfield) and slow (downfield) relaxing components of the ¹⁵N doublet. The three experiments considered are: a The J-scaled TROSY-HNCO experiment of (Kontaxis et al. 2000) b The J-scaled TROSY-HNCO experiment of (Yang et al. 1999) and c The κnJ-scaled TROSYHNCO experiment described herein

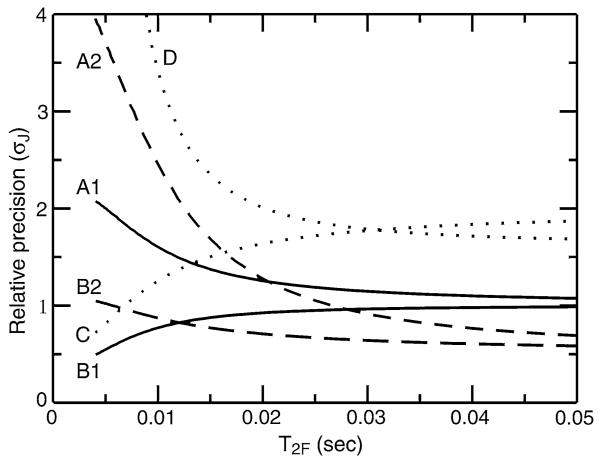
Shown in Fig. 8 is a comparison of the relative precision of measurement for these three experiments (calculated using Eqs. 1, 2, and 13) along with a half J measurement taken by difference between ¹⁵N frequencies observed in cpd-decoupled and TROSY-HNCO experiments. A reference precision of 1 is assigned to the Kontaxis experiment in which ¹J_NH is measured directly by recording the TROSY and anti-TROSY components of the ¹⁵N doublet. As expected, for long T_2F relaxation times and a specific scaling factor all experiments perform similarly for measurement of ¹J_NH. However, differences become notable for shorter relaxation times, with the κnJ-scaled TROSYHNCO experiment delivering better precision of measurement over the whole range of relaxation times. Somewhat surprisingly, the κnJ-scaled TROSY-HNCO experiment run with κ = 2 is expected to deliver superior precision to the κ = 1 version for relaxation times T_2F longer than ca. 12 ms. Furthermore, the measurement of ½J by difference between TROSY and cpd-decoupled HNCO experiments suffers significant losses in precision due to unfavorable scaling of the coupling and relaxation losses during the fixed ¹⁵N evolution periods in the cpd-decoupled HNCO. These results underscore the importance of using scaling parameters κ that are optimized for the operative relaxation times.

Fig. 8.

Calculated relative precision of ¹J_NH measurement (σ_J) for J-scaled HNCO experiments as a function of the relaxation time of the broad upfield component of the ¹⁵N doublet, T_2F. Relaxation parameters are chosen to correspond to that of a perdeuterated protein, with a narrow line relaxation time of T_2S = 5T_2F and a negligible contribution from ¹H spin flips (R_H ≈ 0). The calculated precision for direct measurement of ¹J_NH (i.e. from recording of TROSY and anti-TROSY lines) using the experiment of (Kontaxis et al. 2000) is assigned a reference precision of 1. Different lines denote a different extent of J-scaling: unscaled couplings (J_app = ¹J_NH; solid lines), halved couplings (J_app = ½ × ¹J_NH; dotted lines) and doubled couplings (J_app = 2 × ¹J_NH; dashed lines). The relative precisions are calculated for the TROSY-HNCO experiment of (Yang et al. 1999) (labeled A1 and A2), the κnJ-scaled TROSY-HNCO experiment (labeled B1 and B2), the TROSY-HNCO experiment of Kontaxis et al. (2000) (labeled C), and by difference in ¹⁵N frequency between cpd-decoupled HNCO and TROSY-HNCO experiments (labeled D)

Optimizing precision of ¹J_NH coupling measurements

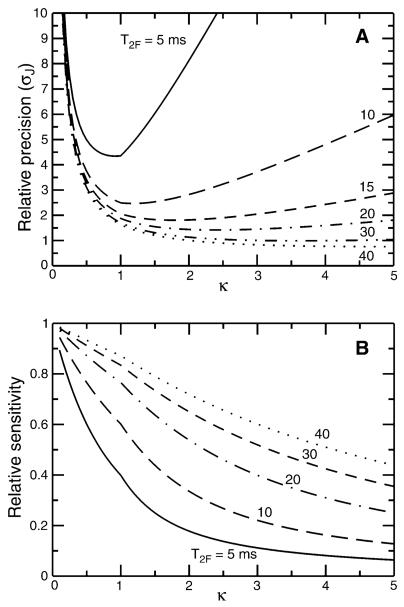
Recording of resonances symmetrically about the TROSY line frequency delivers optimal precision of measurement for a given scaling parameter, but how does precision depend on the scaling parameter? Clearly, a scaling parameter which is too large makes apparent relaxation rates too fast which in turn causes undesirable sensitivity losses. On the other hand, a scaling parameter which is too small produces linewidths governed by the acquisition time (i.e. 2T_N, the duration of the constant time element) in addition to forgoing the advantages of scaling up the apparent coupling. Shown in Fig. 9a is the expected relative precision of the κnJ-scaled TROSY-HNCO experiment as a function of T_2F and κ. For reference, the precision of coupling measurement (σ_J) is calculated relative to the precision with which the position of the TROSY line can be measured in a 3D TROSY-HNCO spectrum recorded with the same acquisition parameters. Notably, for relaxation times T_2F > ca. 30 ms it is possible to measure ¹J_NH with a precision (σ_J) that exceeds the precision of measurement of the TROSY line position (in a 3D TROSY-HNCO) due to the precision enhancement arising from J-scaling. For relaxation times T_2F = 10 ms, the optimal value of κ is approximately 1 with an expected factor of 2.5 loss of precision relative to the corresponding uncertainty in the position of the TROSY line. Referring back to the results for nmHO, for a T_2F = 20 ms it is predicted that the κ = 2 experiment will deliver a 25% improvement in precision relative to the κ = 1 experiment, which is somewhat less improvement than actually observed (40% from Fig. 6).

Fig. 9.

Plot of a relative precision of ¹J_NH measurement (σ_J) and b relative sensitivity as a function of κ for the κnJ-scaled TROSY-HNCO experiment. Results are shown for different values of the relaxation time of the broad upfield component of the ¹⁵N doublet, T_2F (with the slow relaxation time T_2S = 5T_2F). In both a and b, a value of 1 corresponds to the precision or sensitivity, respectively, if one were to record the TROSY line using the same experiment (e.g. by setting κ = 0)

Based on the results in Fig. 9a, it appears that even for very short T_2F (e.g. T_2F = 5 ms) the use of values of κ < 1 does not deliver improved precision, implying that values of κ < 1 may never be warranted. This is somewhat misleading as it rests on the assumption that sensitivity is not limiting, which is clearly a potential problem for very short T_2F. In such cases it may be desirable to trade some precision of measurement in order to increase sensitivity. Of course, at some point relaxation times become altogether too unfavorable for successful acquisition of a TROSY-HNCO experiment (Fig. 3). Figure 9b illustrates the sensitivity cost as a function of κ relative to the pure TROSY line for specific values of T_2F. Generally speaking, for values of κ which optimize precision, sensitivity losses relative to the pure TROSY-HNCO experiment are less than a factor of 2. An exception is the T_2F = 5 ms case, in which 60% sensitivity is lost when running with κ = 1. However, setting κ = 0.5 restores almost half of the lost sensitivity with only a minor reduction in precision of coupling measurement. This would clearly be the more desirable option when sensitivity is limiting. Taken together, these results suggest that if a TROSY-HNCO experiment can be acquired with good sensitivity, then one can be confident that ¹J_NH couplings can also be successfully measured with a sensitivity and precision comparable to that with which the TROSY line position itself can be measured.

A disadvantage of TROSY-based approaches to the measurement of ¹J_NH couplings is that two experiments must be acquired in order to obtain the desired splittings. This will carry a sqrt(2) cost in sensitivity relative to experiments such as the J-doubled HNCO in which both components of the doublet are recorded simultaneously. However, this cost is mitigated by Boltzman enhancement of the TROSY signal (Pervushin et al. 1998; Kontaxis et al. 2000) and overwhelmed by relaxation considerations when studying larger proteins. Absent considerations due to differences in ¹H/¹⁵N transfer elements, water saturation, or number of pulses, the relative sensitivity of the J-doubled HNCO vs. κnJ-scaled TROSY-HNCO experiments is,

$$\begin{array}{cc}\hfill S\left(\frac{\mathrm{J}-\text{doubled}}{\kappa \mathrm{nJ}-\text{scaled}}\right)& =\frac{\sqrt{2}\exp [-4R_{2\mathrm{avg}}{T}_{\mathrm{N}}]}{{\epsilon }_{\mathrm{TROSY}}\exp [-4R_{2\mathrm{S}}{T}_{\mathrm{N}}]}\hfill \\ \hfill & =\frac{\sqrt{2}}{{\epsilon }_{\mathrm{TROSY}}}\exp [-2(R_{2\mathrm{F}}-R_{2\mathrm{S}})T_{\mathrm{N}}]\hfill \end{array}$$ (14)

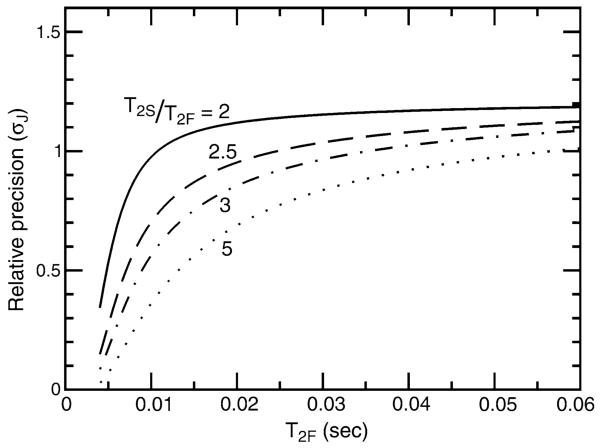
in which ε_TROSY (≈0.58) is the sensitivity of the Boltzman enhanced TROSY line relative to that of the decoupled doublet (Pervushin et al. 1998; Kontaxis et al. 2000). The relative precision of coupling measurement between the J-doubled and the κnJ-scaled (κ = 2) experiments based on Eqs. 6, 11, 13, and 14 is plotted in Fig. 10 as a function of ¹⁵N transverse relaxation times for T_2S/T_2F ratios ranging from 2 to 5. Higher T_2S/T_2F ratios are expected for perdeuterated proteins (Kontaxis et al. 2000) and under these circumstances the κnJ-scaled TROSY-HNCO experiment is more favorable from the standpoint of measurement precision. After factoring in additional benefits from TROSY narrowing of the detected amide ¹H^N signal, far fewer 180° ¹H pulses and the ability to scale to larger values of κ in smaller proteins, the κnJ-scaled TROSY-HNCO is likely the optimal choice of experiment for perdeuterated proteins regardless of molecular weight. In the application to cyano-nmHO, the κnJ-scaled (κ = 2) experiment delivered 33% better precision than the J-doubled experiment. This is close to the theoretical prediction (0.71) in Fig. 10 in spite of the neglect of differences in the reverse INEPT transfer and dephasing of the water in the J-doubled experiment.

Fig. 10.

Relative precision of ¹J_NH measurement (σ_J) for the J-doubled HNCO versus the κnJ-scaled TROSY-HNCO experiments as a function of the relaxation time of the broad upfield component of the ¹⁵N doublet, T_2F. Each of the lines corresponds to different ratios of downfield (T_2S) to upfield (T_2F) relaxation times: T_2S/T_2F = 2 (solid), 2.5 (dashed), 3 (dot-dashed), 5 (dotted)

The J-doubled HNCO experiment is expected to have the advantage for small protonated proteins (ca. <15 kDa) at lower magnetic field strengths (i.e. 11 T), where lower T_2S/T_2F ratios will be operative. Under these circumstances it may be desirable to employ a sensitivity enhanced reverse INEPT element (Palmer et al. 1991) rather than the watergated reverse INEPT utilized herein. Notably, the additional coupling evolution in the J-doubled HNCO experiment comes at the cost of removal of ¹H cpd decoupling, which is applied during the ¹J_C′N dephasing period in the 3D ¹H-coupled HNCO experiment (de Alba et al. 2001). This causes an increase in the ¹⁵N transverse relaxation by a rate R_H due to ¹H spin flips. A comparison of the expected relative precision of the J-doubled versus the ¹H-coupled HNCO experiment leads to,

$${\sigma }_{\mathrm{J}}\left(\frac{\mathrm{J}-\text{doubled}}{{}^1\mathrm{H}-\text{coupled}}\right)=\left(\frac{1}{2}\right)\exp \left[R_{\mathrm{H}}(2T_{\mathrm{N}}-\delta )\right]$$ (15)

in which 2T_N ≈ 1/2J_C′N and δ = 1/2J_NH. From the above expression, one finds that the ¹H spin flip contribution R_H must be ca. 30 Hz before the removal of cpd decoupling offsets the twofold gain in precision realized due to J-doubling.

Sensitivity to systematic errors

It is well recognized that cross-correlation effects operative within the unresolved fine multiplet structure of a peak can produce systematic errors which are undetectable to the eye (Tjandra and Bax 1997; de Alba and Tjandra 2006; Yao et al. 2009). For real time frequency domain measurements of ¹J_NH couplings, the most common source of error is due to a small splitting of the ¹⁵N resonance by a second proton H^k in conjunction with a non-negligible cross-correlation between NH^N and NH^k dipolar interactions (NH^N/NH^k). This NH^N/NH^k cross-correlation produces differential broadening of the outer and inner lines of this doublet of doublets, which in turn imperceptibly moves the two lines of the ¹⁵N-{¹H^N} doublet together or apart, respectively (Yao et al. 2009). Utilization of a constant time evolution period does not alleviate the problem as in that case it manifests in the form of differential line intensities rather than differential line broadening. In the absence of selective ¹H pulses or extensive perdeuteration, it can be expected that NH^N/NH^k cross-correlations and small couplings J_NHk will co-evolve to detrimental effect on ¹J_NH coupling measurements. Fortunately these effects are usually small and will largely cancel when RDCs are measured by difference between isotropic and anisotropic measurements of ¹J_NH (Yao et al. 2009).

In the J-doubled HNCO experiment, NH^N/NH^k cross-correlation mediated errors enter in as described above for a constant time frequency domain measurement. In the case of the κnJ-scaled TROSY-HNCO experiment, it can be shown that in the presence of a coupling J_NHk and nonnegligible NH^N/NH^k cross-correlation the following signal results at the end of the t₂ evolution period just prior to the SE-TROSY readout element,

$$\begin{array}{cc}\hfill & \sigma \left(t_2\right)\propto (2N_{\mathrm{x}}{H}_{\mathrm{z}}+N_{\mathrm{x}})\{\left(1-{\lambda }_{{\mathrm{NH}}^{\mathrm{N}}∕{\mathrm{NH}}^{\mathrm{k}}}\right)\phantom{\}}\hfill \\ \hfill & \times \cos [{\Omega }_{\mathrm{N}}{t}_2-\pi (1+n\kappa )({\mathrm{J}}_{{\mathrm{NH}}^{\mathrm{N}}}+{\mathrm{J}}_{{\mathrm{NH}}^{\mathrm{k}}})t_2]\hfill \\ \hfill & +\phantom{\{}\left(1+{\lambda }_{{\mathrm{NH}}^{\mathrm{N}}∕{\mathrm{NH}}^{\mathrm{k}}}\right)\cos [{\Omega }_{\mathrm{N}}{t}_2-\pi (1+n\kappa )({\mathrm{J}}_{{\mathrm{NH}}^{\mathrm{N}}}-{\mathrm{J}}_{{\mathrm{NH}}^{\mathrm{k}}})t_2]\}\hfill \end{array}$$ (16)

in which λ_NHN/NHk is a coefficient describing the extent of NH^N/NH^k cross-correlation mediated interconversion of density matrix elements which occur during evolution of ¹⁵N magnetization for a duration (4T_N + βt₂) (de Alba and Tjandra 2006). The effect is to cause both intensity (due to evolution for time 4T_N) and linewidth (due to evolution for time βt₂) differences between the lines of the unresolved ¹⁵N-{¹H^k} doublet depending on the sign of λ_NHN/NHk. This can potentially lead to κ-dependent differences in contributions to the measured ¹J_NH couplings due to the mixed constant time versus real time nature of the κnJ-scaled TROSY HNCO experiment, resulting from unequal impact of differential intensity versus broadening effects on the measured line position. Furthermore, these effects vanish when measuring the decoupled line position as in the case of the κ = 1 experiment.

In order to characterize the extent of these effects and any other systematic deviations, ¹J_NH couplings were measured on a 1 mM sample of ¹⁵N, ²H-labeled protein GB1 using a 2D [¹⁵N, ¹H] SE-IPAP-HSQC experiment, a 2D [¹⁵N, ¹H] plane of the J-doubled HNCO experiment, and 2D [¹⁵N, ¹H] planes of the κnJ-scaled TROSY-HNCO experiment for κ values ranging from 1 to 5. The results are summarized in Table 1. On average, the ¹J_NH couplings measured in the J-doubled or κnJ-scaled experiments show no systematic deviations from the IPAP results. However, the RMSD between the IPAP-HSQC and κnJ-scaled TROSY HNCO measurements shows a greater discrepancy (RMSD = 0.31) for the κ = 1 experiment while the others are very close to experimental precision. This is consistent with the presence of residual NH^N/NH^k cross-correlation-mediated lineshape distortions due to incomplete (ca. 70%) perdeuteration. In the absence of high level perdeuteration, errors can be minimized by using the same κ value for isotropic and anisotropic measurements to maximize cancelation and by limiting alignment strength such that ¹D_NH couplings are no larger than 15–20 Hz (Yao et al. 2009). Otherwise, ¹J_NH measurements from both the J-doubled HNCO and κnJ-scaled TROSY-HNCO experiments agree with the IPAP-HSQC couplings according to expectations based on estimated experimental precision. After correcting for total experimental duration, the IPAP-HSQC delivers slightly better precision while the J-doubled HNCO delivers slightly lower precision of measurement (σ_err = 0.18) relative to the κnJ-scaled data (σ_err = 0.12–0.14). This is consistent with the expectation that κnJ-scaled TROSY-HNCO experiment is better suited for application to perdeuterated proteins regardless of molecular weight. The estimated precisions of measurement for the κnJ-scaled data as a function of κ are nearly constant, which likely results from proximity to the high sensitivity limit where other experimental imperfections and instabilities become the dominant source of random errors.

Table 1.

¹J_NH measurement statistics for protein GB1

κ	κnJ-scaled TROSY-HNCO					J-doubled HNCO	SE- IPAP HSQC
	1	2	3	4	5
σ err a	0.13	0.12	0.13	0.14	0.13	0.25 (0.18d)	0.11 (0.09d)
RMSDb	0.31	0.20	0.16	0.17	0.18	0.33	NA
〈J〉c	93.23	93.25	93.23	93.22	93.21	93.27	93.24

^aTaken to be [1/sqrt(2)]*RMSD between replicate ¹J_NH measurements

^bRMSD from the IPAP ¹J_NH measurements

^cAverage over all measured values of ¹J_NH

^dScaled to correspond to the total measurement time of the κnJ-scaled TROSY-HNCO datasets

The κnJ-scaled TROSY HNCO experiment utilizes an SE-TROSY readout (Rance et al. 1999) which increases sensitivity according to the PEP principle (Cavanagh and Rance 1990). A question which arises, therefore, is whether this element could cause undesirable distortions when the operative ¹J_NH coupling departs significantly from the value to which the SE-TROSY element is tuned. A particularly undesirable outcome would be the admixture of absorptive and dispersive magnetization from the ¹⁵N evolution period, leading to slight shifts in line position. Generalizing the results of Eq. 13 to account for J mismatch during the SETROSY readout element leads to the following expression for the density operator just prior to acquisition,

$$\begin{array}{cc}\hfill \sigma (t_1,t_2)=& 2[{\delta }^{+}(2H_{\mathrm{x}}{N}_{\mathrm{z}}+H_{\mathrm{x}})+{\delta }^{-}(2H_{\mathrm{x}}{N}_{\mathrm{z}}-H_{\mathrm{x}})]\hfill \\ \hfill & \times [{\delta }^{-}\cos \alpha +{\delta }^{+}\cos \beta ]\hfill \\ \hfill & -2[{\delta }^{+}(2H_{\mathrm{y}}{N}_{\mathrm{z}}+H_{\mathrm{y}})+{\delta }^{-}(2H_{\mathrm{y}}{N}_{\mathrm{z}}-H_{\mathrm{y}})]\hfill \\ \hfill & \times [{\delta }^{-}\sin \alpha +{\delta }^{+}\sin \beta ]\hfill \end{array}$$ (17)

with

$$\begin{array}{cc}\hfill & \alpha =-{\Omega }_{\mathrm{N}}{t}_2+i\pi (1+n\kappa ){\mathrm{J}}_{\mathrm{NH}}{t}_2\hfill \\ \hfill & \beta =-{\Omega }_{\mathrm{N}}{t}_2-i\pi (1+n\kappa ){\mathrm{J}}_{\mathrm{NH}}{t}_2\hfill \\ \hfill & {\delta }^{-}=\frac{1}{2}(1-\cos \pi \Delta J2\tau )\hfill \\ \hfill & {\delta }^{+}=\frac{1}{2}(1+\cos \pi \Delta J2\tau )\hfill \\ \hfill & \Delta J={\mathrm{J}}_{\mathrm{NH}}-\frac{1}{4\tau }.\hfill \end{array}$$ (18)

The effect of a mismatch, ΔJ, is to differentially attenuate four elements of the density operator which are transformed by the SE-TROSY element. This preserves the pure phase characteristics of resonances but leads to the appearance of new resonances at (ω_15N, ω_1H) frequencies of (Ω_N−½J_NH, Ω_H−½J_NH) and (Ω_N + ½J_NH, Ω_H + ½J_NH) to first order (δ⁺δ⁻) and (Ω_N−½J_NH, Ω_H + ½J_NH) to second order (δ⁻²). These effects are nearly analogous to the expected consequences of differential relaxation of the four different magnetization pathways which pass through the SE-TROSY readout element (Rance et al. 1999). Nevertheless these artifacts can lead to errors in coupling measurements due to unfavorable overlap with the desired TROSY-narrowed resonances, a problem which is greatly minimized by separation of the (ω_15N, ω_1H) resonance into a third ¹³C′ dimension.

Conclusion

A pair of 3D HNCO-based pulse sequences have been proposed which optimize precision of measurement by utilizing both ¹J_NC′ dephasing/rephasing delays to record ¹J_NH coupling evolution. In the J-doubled HNCO experiment, this allows apparent ¹J_NH splittings to be doubled without any increases in apparent line width. But, in order to minimize precision losses, the 3D J-doubled HNCO experiment averages the relaxation rates of the upfield and downfield components of the ¹⁵N doublet over the course of the full constant time period, thus limiting its application to smaller proteins. The proposed κnJ-scaled TROSY-HNCO experiment is designed for application to larger proteins and measures the coupling by difference between a pair of experiments in which the impact of the broad line relaxation time T_2F on ¹J_NH measurement is minimized by measuring the difference in frequency between lines which are symmetrically displaced from the position of the TROSY line. With optimal choice of J-scaling parameter κ based on the operative relaxation time T_2F, precisions of ¹J_NH measurement can be achieved which are similar to that of the measurement of the frequency of the TROSY line itself with losses in sensitivity that are normally less than a factor of two. The experiments also provide accurate ¹J_NH couplings, as demonstrated by comparison of couplings measured for protein GB1 against those obtained using the [¹⁵N, ¹H]-IPAP-HSQC experiment. Additional desired improvements to precision are most fruitfully aimed at increasing the base sensitivity of the 3D TROSYHNCO experiment by means of increases in sample concentration, temperature, experimental acquisition time or the level of perdeuteration.