High Temperature Potentiometry: Modulated Response of Ion-Selective Electrodes During Heat Pulses

Abstract

The concept of locally heated polymeric membrane potentiometric sensors is introduced here for the first time. This is accomplished in an all solid state sensor configuration, utilizing poly(3-octylthiophene) as intermediate layer between the ion-selective membrane and underlying substrate that integrates the heating circuitry. Temperature pulse potentiometry (TPP) gives convenient peak-shaped analytical signals and affords an additional dimension with these sensors. Numerous advances are envisioned that will benefit the field. The heating step is shown to give an increase in the slope of the copper-selective electrode from 31 mV to 43 mV per 10-fold activity change, with a reproducibility of the heated potential pulses of 1% at 10 µM copper levels and a potential drift of 0.2 mV/h. Importantly, the magnitude of the potential pulse upon heating the electrode changes as a function of the copper activity, suggesting an attractive way for differential measurement of these devices. The heat pulse is also shown to decrease the detection limit by half an order of magnitude.

Potentiometry with ion-selective electrodes affords the direct translation of chemical information into an electrical signal, and is today widely used as an effective sensing principle in a variety of applications. Polymeric membrane electrodes, in particular, may be tuned in terms of sensor selectivity by selective interactions with molecular host molecules (ionophores) embedded within the membrane matrix. In recent years, these sensing systems have undergone a quiet revolution, with knowledge of the underlying membrane processes allowing researchers to demonstrate that ultra-low detection limits are today possible. This has been achieved by understanding and minimizing undesired ion fluxes across the ion-selective membrane.

While the simplicity of direct potentiometry is attractive, it results in passive sensing systems that cannot easily be tuned or triggered. In recent years, multipulse protocols have been developed to place potentiometry closer to voltammetric detection techniques by allowing for an electrochemical excitation before a potentiometric measurement step. This makes it possible to better control ion fluxes across such polymeric membranes and hence devise new, reliable sensing protocols based also on kinetic characteristics of these materials.

In this paper, we propose for the first time a thermal excitation pulse to modulate the behavior of polymeric membrane based potentiometric sensors. Potentials recorded at different local temperatures should provide an additional dimensionality in the measurement. The electrode slope is known to be temperature dependent, and it is also expected that some membrane formulations may exhibit temperature dependent sensing selectivities. Additionally, convective and diffusive mass transfer properties are temperature dependent, giving an additional tool in performing optimal potentiometric measurements.

Heated electrodes have been chiefly developed for electroanalysis (voltammetric techniques), and shown to provide a fast and convenient control of the temperature of the electrode surface and hence to enhance the performance of these devices.^{1, 2} Such improvements have been attributed to a) thermal convection within a thin solution layer adjacent to the surface, b) acceleration of the electron transfer reaction kinetics, c) thermal discrimination of analyte and interferent substances, as well as d) thermal regeneration of both nobel metal electrode surfaces (after biofouling) and biosensor recognition layers. A wide range of electroanalytical applications have thus benefited from the use of heated electrodes, including detection of dissolved oxygen,² amperometric monitoring of flowing streams,³ trace metal stripping analysis,^{1, 4} voltammetry above boiling point⁵ or biolectronic detection of DNA hybridization.⁶ Open circuit potentiometry of ferro/ferricyanide was employed only for temperature calibrations of many types of heated metal and carbon electrodes (based on the temperature coefficient of the standard electrode potential of this redox couple).^{2, 7} Indeed, this is the first time that the distinct advantages of hot-wire electrochemistry are applied to direct potentiometric measurements at modern ion-selective electrodes (ISEs).

Experimental

The ionophore N-N,N’,N’-tetracyclohexyl-3-thiaglutaric diamide (Copper (II) ionophore (IV)), lipophilic cation exchanger sodium tetrakis[3,5-bis(trifluoromethyl) phenyl]borate (Na-TFPB) and the lipophilic salt tetradodecyl ammonium tetrakis(4-chlorophenyl)borate (ETH 500) were purchased in Selectophore^® or Puriss grades from Fluka (Milwaukee, WI). Methylene chloride was obtained from Fisher (Pittsburgh, PA). Poly(3-octylthiophene) (POT) was synthesized following the procedure of Jarvinen et al.⁸ and was purified according to the patent application.⁹ The synthesis of methyl methacrylate-decyl methacrylate (MMA-DMA) copolymer matrix was based on Qin et al.¹⁰ Copper nitrate was obtained from sigma (St. Louis, MO) and all the solutions were prepared with deionized water from Milli-Q system.

Apparatus

Potentiometric measurements were performed with a multifunctional data acquisition board (779026-01 USB-6009 14 Bit, National Instruments, Austin, TX) connected to a six-channel high Z interface (WPI, Sarasota, FL). An E 3645A DC power supply (Agilent, USA) was used as to provide a direct current needed to vary the temperature of the indirectly heated working electrode. A spin coater machine was used for the membrane deposition. Indirectly heated gold disk electrodes (2 mm diam.) basing on a low temperature co-fired ceramic (LTCC) substrate were delivered by Tetekera GmbH (Ilmenau, Germany).

Potentiometric measurements

Potentiometric measurements were carried out in a 100 mL sample using the solid-contact Cu ISE and a commercial double junction reference electrode (Ag/AgCl|3M KCl, Type 6.0729.100, Metrohm AG, 9101 Herisau, Switzerland). The heat pulse experiments were performed by applying different electrode temperatures for exactly 20 s each, followed a 50 s cooling interval, and allow 2 additional min to reach the potential baseline.

A modified heated LTCC gold electrode (see below) was used as the ion-selective working electrode. The construction of this type of heated electrode has been described in detail previously.¹¹

All these electrodes were temperature calibrated in separate experiments (see below) leaving the bulk electrolyte at room temperature. Activity coefficients of copper were calculated according to the Debye-Huckel approximation and the potential values were corrected for liquid-junction potentials with the Henderson equation. Selectivity measurements were performed using separate calibration curves for hydrogen and copper ions, allowing one to obtain unbiased selectivity coefficients.¹² For this purpose, the electrode was conditioned in a 1 mM nitrate solution of the most discriminated ion, Ca²⁺, and a calibration curve for hydrogen ion was performed by incremental addition of nitric acid to this background (final concentrations: 1.0 × 10⁻⁵, 5.0 × 10⁻⁵, 1.0 × 10⁻⁴, 5.0 × 10⁻⁴, and 1.0 × 10⁻³ M). Subsequently, a calibration curve for copper was obtained in the same concentration range. The selectivity coefficient was calculated as established.¹³

Preparation of the copper ion-selective electrode

The Cu²⁺-ISE membrane contains the copper (II) ionophore (IV) (0.52 wt.%, 12 mmol kg⁻¹), NaTFPB (0.45 wt.%, 5 mmol kg⁻¹), ETH 500 (1.13 wt.%, 10 mmol kg⁻¹), and the copolymer MMA-DMA (97.85 wt.%). These membrane components (60 mg total) were dissolved in CH₂Cl₂ (0.8 mL). The resulting mixture was degassed by purging it with N₂ before casting it onto the POT-coated LTCC gold electrode. The solid-contact Cu²⁺-ISE was prepared on the ceramic substrate, first the gold disc on the ceramic substrate was cleaned by polishing it with alumina powder (0.5 µm) and washed with water and ethanol under ultrasond. Conducting polymer 3-octylthiophene was casted on it allowing to form a thin layer on the top. Then the cocktail (10 µL) was deposited using the spin coater at 10 RPM. Finally the resulting ISE was conditioned first in 10⁻³ M Cu(NO₃)₂ (1 day) and subsequently in a 10⁻⁷ M Cu(NO₃)₂ and 10⁻³ M Ca(NO₃)₂ mixture (overnight).

Temperature calibration

The stationary temperature of the unmodified heated electrodes was measured by using open circuit potentiometry in 0.1 M KCl solution containing 5 mM ferro-/ferricyanide. The temperature coefficient (−1.56 mV K⁻¹) of the standard electrode potential was used to calculate the temperature difference. The temperature calibration curve was obtained by regulating various heating voltages and plotting the temperature difference (data not shown). We assume that the heat insulating effect of the thin coatings can be neglected, and that the temperature drop across the polymer films is small.

Results and Discussion

The development of potentiometric sensors with localized heating capability was chiefly hampered by their traditional design, in which the membrane is back side contacted with an aqueous inner solution. In recent years, reliable all solid state configurations of ISEs have emerged, either based on conducting polymers^14–17 or high surface area capacitive materials such as nanostructured carbon surfaces.^{18, 19} A previously reported heated electrode design for electroanalysis, based on an Au electrode,¹¹ was modified here with the conducting polymer, poly(3-octyl thiophene) overlaid with an ion-selective plasticizer free membrane copolymer.^{10, 15} This conducting polymer has been shown to be very attractive in the fabrication of all solid state electrodes with ultra-low detection limits.^{16, 20} In particular, it was also shown by reflectometry experiments that such an ion to electron transducing material effectively suppresses the occurrence of a thin water layer between the ion-selective membrane and the internal redox element.²¹ Consequently, reversible and well behaved thin layer electrochemistry has been demonstrated with sandwich materials composed of this conducting polymer overlaid with an ion-selective polymeric membrane.^{22, 23}

Pulsed heating was achieved by applying voltage pulses of defined time duration across a heating meander embedded in the electrode substrate, see Scheme 1. The propagation of the temperature gradient from the gold electrode surface to the surrounding aqueous solution has been studied earlier.²⁴ While this may be used to approximate the behavior of the solid state ISE fabricated here, the heat capacity of the involved materials and the resulting temperature profiles are quite certainly different.

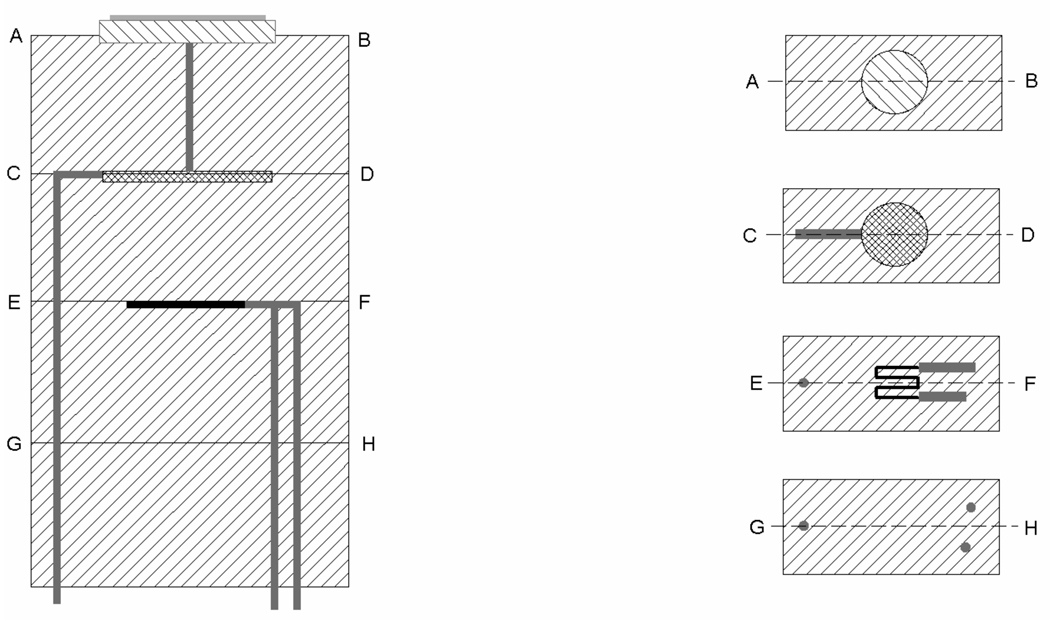
Scheme 1.

Design of the indirectly heated Au-LTCC sensor with cross sections showing Au working electrode (A–B), WORK contact with Ag heat distribution layer (C–D), through contact for WORK and heating meander (E–F), lower LTCC layer (G–H) with three through contacts for both WORK (left) and heating voltage (right). Modified from the reference.²⁶

A heat pulse is expected to most increase the temperature in the immediate vicinity of the underlying gold electrode. The all solid state configuration of the ISE may be understood as a series of distinct phases and associated temperature dependent boundary potentials, including that between the gold electrode and the conducting polymer, the conducting polymer and the ion-selective membrane, and between the membrane and the sample solution.

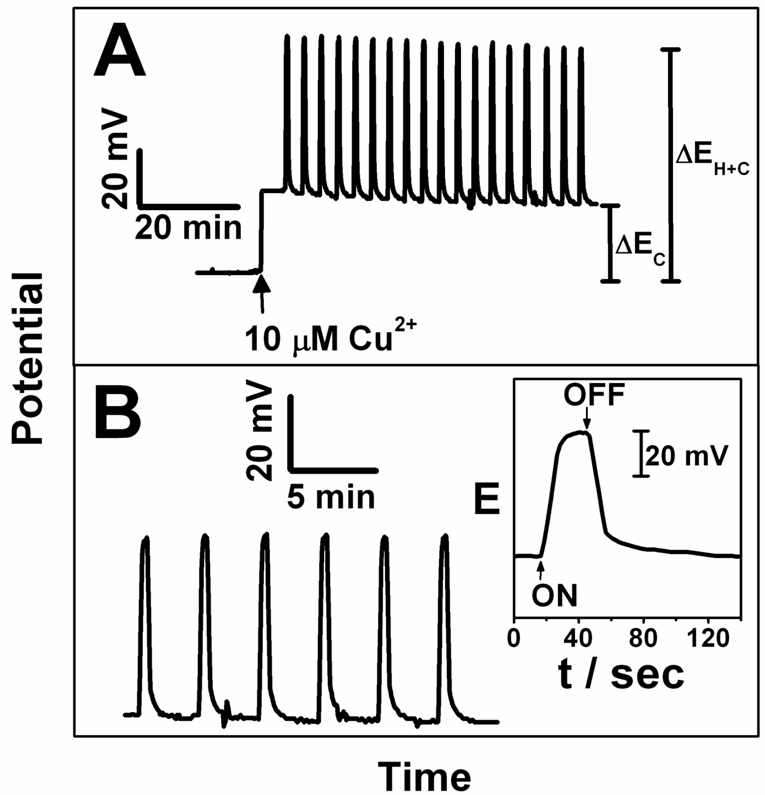
A copper selective electrode was fabricated and evaluated in the heated potentiometry configuration. Figure 1 demonstrates the observed electrode potentials in contact with 10 µM copper(II) upon repeatedly applying a heating pulse of 2.5 V (estimated temperature pulse of 50 °C). Rapid potential increases of about 54 mV were observed, which started to level off after about 10 s. The heat pulses were applied for 20 s, after which time the potentials were observed to return to baseline, suggesting efficient cooling of the device by the contacting aqueous solution. Note that the potential pulses shown in Figure 1A may be used to compensate for electrode drift, since the potentials for the baseline and the heat pulses are observed to drift similarly. Figure 1B demonstrates the same effect for 1 µM copper(II), for which a smaller potential change of about 48 mV is observed. Heated electrode potentiometry is chiefly useful, however, if the observed potential change primarily is due to heating at the sample–membrane interface. For permselective membranes exhibiting Nernstian response slopes, one expects only the potential at this interface to be sample dependent. All other, buried interfaces should behave independently of the sample solution composition. Figure 2 displays a calibration experiment with the copper-selective electrode heated to max. 60 °C while keeping the bulk solution at room temperature. The potential changes between cold and hot electrode conditions are indeed dependent on the sample composition, suggesting that the approach introduced here is analytically useful.

Figure 1.

Stability of Temperature Pulse Potentiometric signals. A) for 10 µM Cu²⁺ and B) for 1 µM Cu²⁺; Inset: Single peak showing the temperature effect and indicating the rate for heating and cooling of the working electrode. 20 s heat pulses with max. 50 °C (heating voltage 2.5 V).

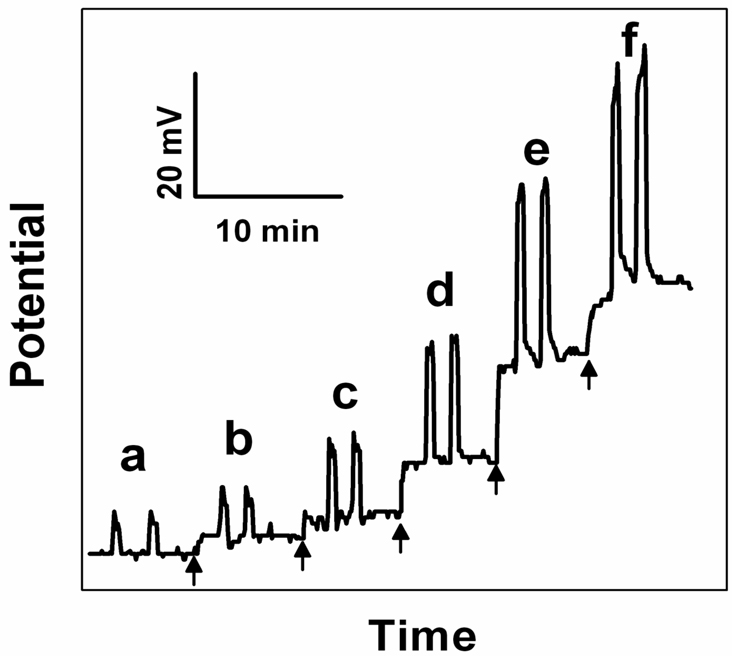
Figure 2.

Potentiometric response of the pulse-heated Cu²⁺ selective electrode inside a bulk solution kept at room temperature for: a) 0, b) 1, c) 5, d) 10, e) 50 and f) 100 nM of Cu²⁺, while applying 20 s heat pulses at 60 °C (heating voltage 3 V). The arrows indicate addition of Cu²⁺ ions to the bulk solution.

The electrode slopes at selected heat pulse amplitudes are expected to scale with the absolute temperature at the sample–membrane interface on the basis of the Nernst equation. While the temperature will also influence the ion activities to some extent, this effect is expected to be negligibly small in most cases, especially where sample complexation is not relevant. Note that activity changes in the membrane phase will only alter the potential offset, not the slope, in the Nernstian response region. The observed slope increased from 30.9 ± 0.9 mV to 43.5 ± 0.8 mV (n=3 different electrodes) per 10-fold activity change, which suggests a temperature of ca. 160 °C at the sample–membrane interface. This is larger than expected for gold electrodes in contact with water (60 °C) and indicates that additional effects besides the apparent Nernst equation may be temperature dependent, including partitioning equilibria at the sample–membrane interface. This will require further investigation to more fully rationalize this result. Note that in Figure 2 for higher concentrations the potential did not return fully to the baseline after the heating pulse, in which case a longer time (> 1min) was required to reach the baseline potential. Nevertheless, this was not detrimental to the electrode performance.

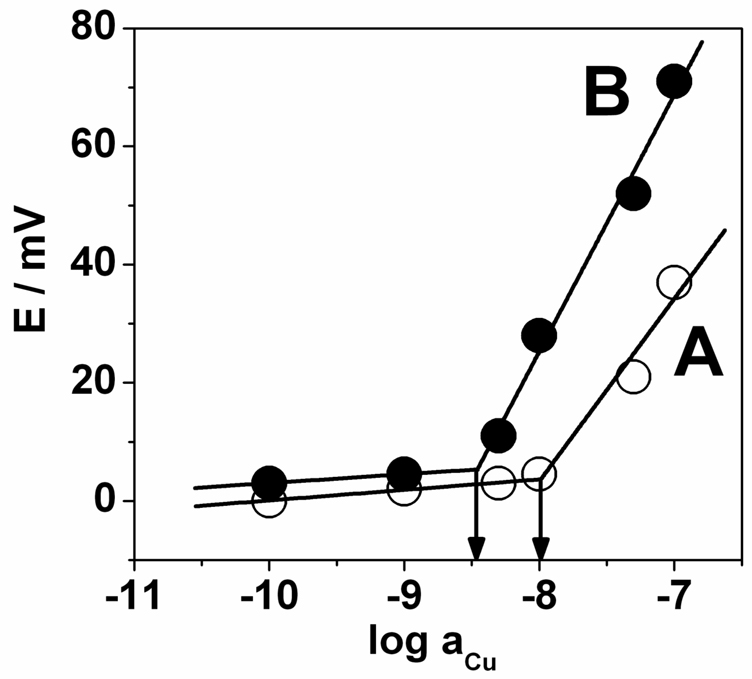
While heated electrode potentiometry will likely find numerous applications, we initially focused on evaluating whether a heating step may help achieve a lower detection limit. Figure 3 indeed demonstrates an improvement of half an order of magnitude for the heated membrane electrode. On the basis of the determined selectivity coefficient of the membrane (logK_Cu,H^pot = −1.3), which compares reasonably well to the literature value of −0.4 with a PVC–oNPOE membrane,²⁵ the detection limit in the absence of ion fluxes is estimated as 10^−13.3 M at pH 6. The detection limit observed in Figure 3 is, therefore, in all likelihood dictated by transmembrane ion fluxes. The diffusion coefficients are expected to increase both in the membrane and aqueous phase, and hence have a small effect on the resulting steady-state situation. The most convincing explanation, therefore, is improved convective mass transport in the aqueous phase by the temperature pulse. This is analogous to earlier work on heated metal electrodes for flow-through electroanalysis.³

Figure 3.

Cu²⁺ calibration plots for A) room temperature (25 °C) and B) elevated temperature (ca. 60 °C) with arrows indicating the limit of detection. Other conditions were the same as in Fig. 2.

Conclusions

Potentiometric sensors have traditionally been operated under isothermal conditions. A localized heat step is shown here to be an attractive expansion of the available potentiometric sensor toolbox, which has become possible with the advent of reliable all-solid state potentiometric sensor designs. We demonstrate here that temperature pulse potentiometry (TPP) offers an attractive peak-shaped signal whose magnitude is a function of the sample activity. This behavior may help eliminate undesired electrode drifts and will allow one to reduce the importance of the reference electrode stability to the measurement. More generally, such a localized heating step is anticipated to offer localized convective mass transport enhancement, and the copper selective electrodes studied here gave significantly lower detection limits. It is anticipated that a heat pulse control may be highly attractive for systems where mass transport processes become important, such as in ultra-trace level potentiometry and more modern concepts that make use of zero current ion fluxes. Heat pulses may ultimately also help one to design potentiometric sensors with tunable selectivity characteristics. This may be particularly attractive in the design of enantioselective sensors or sensors based on receptors with varying, temperature dependent complex stoichiometries.