Abstract
Background and objectives: Observational studies relating epoetin alfa (EPO) dose and mortality frequently use analytic methods that do not control time-dependent confounding by indication (CBI). The relationship between EPO dose and 1-year mortality, adjusting for the effects of time-dependent CBI, was examined using a marginal structural model.
Design, setting, participants, & measurements: This retrospective cohort study included 27,791 hemodialysis patients between July 2000 and June 2002. Patients were grouped at successive 2-wk intervals into a zero-dose category or four nonzero-dose categories. Ordinal regression was used to calculate inverse probability of treatment weights of patients receiving their own dose level given their covariate and treatment history. Three treatment models with an increasing number of treatment predictors were evaluated to assess the effect of model specification. A small number of excessively large patient weights were truncated. Relative hazards for higher-dose groups compared with the lowest nonzero-dose group varied by treatment model specification and by level of weight truncation.
Results: Results differed appreciably between the simplest treatment model, which incorporated only hemoglobin and EPO dosing history with 2% weight truncation (hazard ratio: 1.51; 95% confidence interval: 1.09, 1.89 for highest-dose patients), and the most comprehensive treatment model with 1% weight truncation (hazard ratio: 0.98; 95% confidence interval: 0.76, 1.74).
Conclusions: There is appreciable CBI at higher EPO doses, and EPO dose was not associated with increased mortality in marginal structural model analyses that more completely addressed this confounding.
Observational studies using the United States Renal Data System (USRDS) show that patients requiring higher doses of epoetin alfa (EPO) are at greater mortality risk (1,2). However, these patients have a higher prevalence of comorbid conditions and other characteristics associated with poorer prognosis (3–5). Subsequent analyses suggest that the observed association between EPO dose and mortality (1,2) may be due mostly to inadequate control of confounding factors (3).
The dynamic dosing in anemia management of hemodialysis (HD) patients also creates time-dependent confounding. Such confounding occurs when prognostic factors are markers for therapy and affected by therapy (6,7). EPO dose is titrated in response to hemoglobin concentration, which reflects previous dose and is a prognostic factor (8,9). This time-dependent confounding cannot be controlled by conventional survival analysis methods (10,11).
Marginal structural modeling (MSM) can control for time-dependent confounders affected by prior treatment (12). This method weights subjects proportionally to the inverse probability of receiving their observed treatment. This weighting balances confounding factors across treatment groups. Given specific assumptions, the treatment estimate from a MSM may have the same causal interpretation as an estimate from a randomized clinical trial (7,13).
We demonstrated previously (3) that adjustment for confounding variables available in dialysis provider data but unavailable in USRDS attenuated the EPO dose-mortality association (1,2). Here, we use an MSM to examine the association between EPO dose and mortality, adjusting for time-dependent confounding. We also present several models to illustrate the implications of decisions made during model development.
Materials and Methods
Data Source
We conducted a retrospective cohort study using data from a large U.S. dialysis organization. The data were deidentified and Health Insurance Portability and Accountability Act compliant. This dataset captures patient information, including demographics, routine dialysis care, vascular access type, laboratory parameters, medications (including injected medications), hospitalizations, and mortality. Most laboratory parameters were collected monthly; hemoglobin values were collected approximately twice a month. Each administered dose of EPO and iron is available. Hospitalization data are collected, including admission and discharge dates and diagnoses on the basis of International Classification of Disease, 9th Revision (ICD-9) codes. Medical history at dialysis initiation, similar to that collected on the Centers for Medicare & Medicaid Services Medical Evidence Form (2728), is not available.
Study Population
Our study population included approximately 60,000 HD patients who were at least 18 yr of age, had no history of peritoneal dialysis, and received in-center HD for at least 1 mo between July 2000 and June 2002. We focused on patients in the database before January 2001 who had 6 or more months of data (n = 27,791). The first 6 mo (entry period) provided baseline characteristics for patients. The first day after the 6-mo entry period was the index date for each patient.
EPO Exposure
Our primary exposure was EPO dose. We calculated the total outpatient dose within successive 2-wk intervals. Two-week EPO doses were grouped into a zero-dose category and four other categories. These categories were set on the basis of quartiles of the nonzero doses averaged over the baseline period (first quartile: ≤14,000 IU per 2 wk; second quartile: 14,001 to 27,000 IU per 2 wk; third quartile: 27,001 to 49,000 IU per 2 wk; fourth quartile: >49,000 IU per 2 wk). We kept the zero-dose group separate because it comprised less than 1% of patients, and these patients may have atypical laboratory values or clinical characteristics (8).
Study Outcome
Our primary outcome was mortality over the 12-mo follow-up period. Patients were followed until the first to occur among: date of death, loss to follow-up for reasons including transplantation and transfer out of the facility, or 365 d.
Covariates
Covariates of interest during the baseline period included age, sex, race (white, nonwhite), body mass index (kg/m2), diabetes as the primary cause of end-stage renal disease (yes versus no), and time on dialysis (dialysis vintage). Time-varying covariates, coded over successive 2-wk intervals, included laboratory values (albumin [g/dl], calcium [mg/dl], ferritin [ng/ml], hemoglobin [g/dl], parathyroid hormone [PTH; pg/ml], phosphorus [mg/dl], transferrin saturation [TSAT, %]); dialysis adequacy (urea reduction ratio); vascular access type (catheter, arteriovenous fistula, arteriovenous graft); hypertension (yes versus no) defined as a systolic BP > 140 mmHg and a diastolic BP > 90 mmHg on the basis of the last predialysis BP measurements in each month; and concomitant injectable medications (cumulative iron dose [mg]; vitamin D [yes versus no]). We identified all hospitalization events and classified them according to the primary diagnosis using ICD-9 codes.
Statistical Analysis
We created patient-specific inverse probability of treatment weights (IPTWs) on the basis of the inverse of the predicted probability of a patient receiving the treatment that he or she actually received, given his or her baseline (static) and time-dependent covariates. Patients who received doses that varied from prediction were up-weighted, increasing their contribution to the analysis (Table 1). Patients who received doses close to that predicted were relatively unchanged in their weightings, reducing their contribution to the analysis. This weighting creates a “pseudopopulation” in which there is no association between the confounders and EPO dose, effectively controlling for those confounders.
Table 1.
Illustrative example of the effect of weighting in changing a subject’s contribution to an analysis
| Future Dose |
||
|---|---|---|
| 12,000 Units per 2 wk (Dose Category 1) | 40,000 Units per 2 wk (Dose Category 3) | |
| Patient factors | ||
| current dose, units per 2 wk | 20,000 (dose category 2) | 30,000 (dose category 3) |
| current hemoglobin, g/dl | 10.4 | 10.4 |
| albumin, g/dl | 3.6 | 3.6 |
| TSAT, % | 19.2 | 19.2 |
| no. of recent hospitalizations | 1 | 1 |
| Predicted probability of future dose given patient factors, % | 10 | 80 |
| Weight calculation | 1 divided by the probability of (dose given patient factors) | 1 divided by the probability of (dose given patient factors) |
| Contribution to analysis | Increased by 10 | Increased by 1.25 |
IPTWs can result in excessively large weights when there is an unconventional treatment decision or, perhaps, a data error. Stabilized IPTWs have been advocated to reduce the potential for extreme IPTWs. In the stabilized weight, a numerator representing the calculated probability of the observed treatment given only static patient characteristics is added to the IPTW. The denominator remains the estimated probability given both the static and time-dependent patient characteristics.
We used ordinal logistic regression to calculate stabilized IPTWs (11) at baseline and for each 2-wk interval during follow-up (“treatment model”). For the numerator of our stabilized weight, we included all baseline static covariates to predict the expected dose. For the denominator, we included all static baseline variables in addition to varying levels of covariate history. We then examined the influence of increasing covariate history on weight estimation using three models for the IPTW denominator: 1) a “simple” model with hemoglobin and dose in the previous four 2-wk time intervals (we chose four intervals on the basis of the clinical guidance that treatment decisions are largely unrelated to hemoglobin concentrations and EPO doses more than 8 wk earlier); 2) a “case-mix” model, augmenting the simple model with time-varying assessments of dialysis care, laboratory measurements, iron use, and comorbidity information in the most recent 2-wk time interval; and 3) an “expanded” model that added the product term between hemoglobin and dose to the case-mix model. The case-mix and expanded models include variables that are not available within the USRDS database. See the Supplemental Information for a description of the variables included in each model. To impute missing variables in each time window, we used the “last observation carried forward” method.
To reduce the disproportional effect of few patients with extremely large weights when fitting the structural model, we calculated the aggregated weights on the basis of only the previous four time intervals (instead of all previous time points) and truncated the highest weights to either the 98th or 99th percentile values (14), which were 82 and 471, respectively, in the expanded treatment model.
To account for informative censoring, we fitted logistic regression models to calculate inverse probability of censoring weights at each time interval. As with our IPTW, we used the same models for the numerator and denominator of the stabilized inverse probability of censoring weights. We did not observe large censoring weights; thus, we did not truncate. The final stabilized weights used in our MSMs were calculated as the product of the treatment and censoring weights.
Last, to estimate the association between EPO dose and mortality, we estimated the hazard ratio (HR) using a stabilized weighted MSM (11). We obtained 95% confidence intervals (CIs) using a percentile-based nonparametric bootstrap (15) on the basis of 200 samples (with replacement). We used a generalized estimating equation that included dose and the weights on the basis of the EPO category predicted by the treatment model (described above) (Figure 1), plus all baseline covariates. EPO doses were categorized over successive 2-wk intervals, with the lowest nonzero-dose category as the referent group. EPO dose category was lagged by 8 wk (four time intervals) to allow for the fact that severely ill patients are often hospitalized during the weeks immediately preceding death (3). This terminal hospitalization can lead to a spurious protective effect of high EPO doses because unavailability of in-hospital dosing information would lead to artificially low dose estimates during the final weeks of life for decedents (16). For patients with missed EPO doses or who did not receive a dose during a dialysis session, a zero dose was recorded. In-hospital EPO doses were imputed using the most recent dose before hospitalization. There was no imputation for missing covariate data. All analyses were conducted using SAS V9.1 (SAS Institute Inc., Cary, NC).
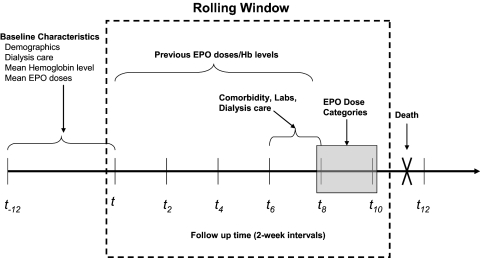
Figure 1.
Marginal structural outcome model. Figure is adapted from Brunelli et al. (24). Time is depicted on the x-axis in 2-wk intervals (t, t2, t4…t12). The period from t−12 to t represents the 6-mo entry period during which baseline patient characteristics were assessed. The shaded box represents the 2-wk interval during which cumulative EPO doses were assessed and categorized. Time-varying patient characteristics, including comorbidities, laboratory parameters, and dialysis care characteristics, were assessed in the interval immediately preceding the exposure assessment window. Previous EPO doses and hemoglobin levels were evaluated during the four 2-wk intervals preceding the exposure assessment window. Death events were identified during the 2-wk interval after exposure assessment. Windows were then rolled forward by 2-wk intervals to generate the next observation period.
Results
There were 34,468 potentially eligible patients. A total of 6677 (19.3%) were excluded for having less than 6 mo of baseline data (attributable to death, censor, or loss to follow-up) or because they were missing critical data (e.g., EPO dose, hemoglobin). Of the resulting 27,791 patients, 304 (1.1%) were not receiving EPO at baseline. On the basis of their dose during the last biweekly baseline period, 5544 (19.9%), 7904 (28.4%), 8336 (30.0%), and 5703 (20.5%) were included in the first, second, third, and fourth dose categories, respectively (Table 2). The average age of patients included in the analyses was 60.4 yr (SD: 14.7); 48% of the patients were women, 42% were black, and 51% had diabetes as the primary cause of ESRD. The mean hemoglobin at baseline was 11.7 g/dl.
Table 2.
Characteristics of the study population
| Patient Characteristic at Baseline | Dose Group Based on Epoetin alfa Dose (IU per 2 wk) at Baseline |
|||||
|---|---|---|---|---|---|---|
| Zero Dose | Category 1, ≤14,000 | Category 2, 14,001 to 27,000 | Category 3, 27,001 to 49,000 | Category 4 > 49000 | All | |
| n | 304 | 5544 | 7904 | 8336 | 5703 | 27,791 |
| Age, yr (SD) | 54.8 (14.0) | 61.0 (15.0) | 61.8 (15.1) | 60.5 (14.7) | 58.1 (14.7) | 60.4 (14.7) |
| Female gender, n (%) | 83 (27.3) | 2252 (40.6) | 3835 (48.5) | 4197 (50.3) | 2908 (51.0) | 13275 (47.8) |
| Black race, n (%) | 128 (42.1) | 2060 (37.2) | 3030 (38.3) | 3548 (42.6) | 2778 (48.7) | 11544 (41.5) |
| Region, n (%) | ||||||
| Midwest | 39 (12.8) | 488 (8.8) | 758 (9.6) | 841 (10.1) | 568 (10.0) | 2694 (9.7) |
| Northeast | 50 (16.4) | 927 (16.7) | 1277 (16.2) | 1450 (17.4) | 1111 (19.5) | 4815 (17.3) |
| South | 184 (60.5) | 3226 (58.2) | 4847 (61.3) | 5265 (63.2) | 3595 (63.0) | 17117 (61.6) |
| West | 31 (10.2) | 903 (16.3) | 1022 (12.9) | 780 (9.4) | 429 (7.5) | 3165 (11.4) |
| Primary Cause of ESRD, n (%) | ||||||
| Diabetes | 116 (38.2) | 2630 (47.4) | 4087 (51.7) | 4446 (53.3) | 2875 (50.4) | 14154 (50.9) |
| Hypertension | 42 (13.8) | 729 (13.1) | 1170 (14.8) | 1343 (16.1) | 997 (17.5) | 4281 (15.4) |
| Dialysis vintage, yr (SD) | 5.0 (4.8) | 3.4 (3.8) | 2.7 (3.3) | 2.5 (3.4) | 2.8 (3.6) | 2.8 (3.6) |
| Body mass index, kg/m2, mean (SD) | 28.0 (8.1) | 26.2 (6.7) | 26.4 (6.7) | 27.2 (7.2) | 28.3 (7.9) | 27.0 (7.9) |
| Ferritin, ng/ml, mean (SD) | 500.8 (322.9) | 591.8 (360.7) | 527.4 (341.5) | 478.7 (343.6) | 473.3 (351.8) | 514.2 (351.8) |
| Hemoglobin, g/dl, mean (SD) | 12.9 (1.3) | 12.1 (0.8) | 11.9 (0.8) | 11.6 (0.9) | 11.0 (1.1) | 11.7 (1.1) |
| TSAT, %, mean (SD) | 31.5 (10.4) | 32.1 (9.7) | 29.1 (9.2) | 26.5 (8.9) | 24.3 (9.3) | 28.0 (9.3) |
| Albumin, g/dl, mean (SD) | 3.9 (0.3) | 3.9 (0.3) | 3.8 (0.3) | 3.8 (0.3) | 3.7 (0.4) | 3.8 (0.4) |
The most influential predictors of EPO dose were previous dose, previous hemoglobin, and the hemoglobin-dose product. Other important predictors were vascular access type and hospitalization. Stabilized probability of treatment weights had a maximum value of 3095 at individual time points and were in the millions when multiplied over four time periods. We examined the distribution of the weights in the three models and at 1% and 2% truncation levels across the biweekly time intervals (Table 3). The mean weight was approximately 1 in all three models (1.00, 0.99, and 1.10 in the simple, case-mix, and expanded models respectively); values far from 1 indicate model misspecification (14). The only material differences observed in the weight distributions across the three models were at the upper end. Specifically, in the expanded model, weights were twice as large as observed in the other two models (Table 3). For models that take into account more confounding variables, such as our expanded model, a broader range of weights is expected. Such weighting compensates more accurately for factors that affect treatment. Therefore, the expanded model should best control for time-dependent confounding.
Table 3.
Weight distribution (average and extreme values) across biweekly time intervals
| Percentile | Treatment Model |
||
|---|---|---|---|
| Simple, Mean (Min to Max) | Case-Mix, Mean (Min to Max) | Expanded, Mean (Min to Max) | |
| 0 (minimum) | 0.00 (0.00 to 0.01) | 0.01 (0.00 to 0.01) | 0.00 (0.00 to 0.01) |
| First | 0.09 (0.09 to 0.10) | 0.10 (0.09 to 0.11) | 0.08 (0.08 to 0.09) |
| Second | 0.14 (0.13 to 0.15) | 0.15 (0.14 to 0.16) | 0.13 (0.12 to 0.14) |
| 25th | 0.59 (0.58 to 0.61) | 0.61 (0.59 to 0.62) | 0.60 (0.58 to 0.62) |
| 50th (median) | 0.81 (0.80 to 0.82) | 0.82 (0.80 to 0.82) | 0.82 (0.80 to 0.82) |
| 75th | 1.00 (0.99 to 1.00) | 1.00 (1.00 to 1.00) | 1.00 (1.00 to 1.00) |
| 98th | 3.26 (3.05 to 3.60) | 3.17 (3.00 to 3.50) | 3.45 (3.21 to 3.94) |
| 99th | 5.00 (4.66 to 5.91) | 4.83 (4.44 to 6.04) | 5.66 (4.91 to 7.51) |
| 100 (maximum) | 112.21 (105.01 to 133.37) | 104.09 (99.04 to 118.25) | 250.32 (183.25 to 471.49) |
| Mean | 1.00 (0.97 to 1.03) | 0.99 (0.97 to 1.03) | 1.10 (1.03 to 1.17) |
Table displays values from the “expanded” model with 1% truncation. Values are the mean of the indicated percentile weight across studied biweekly time intervals. Minimum (Min) and maximum (Max) values are the lowest and highest weights for the given percentile in any of the biweekly time intervals.
Table 4presents our MSM results from the different treatment models incorporating 1% and 2% weight truncation. The mortality HR estimates comparing EPO dose groups 2, 3, and 4 to the lowest nonzero dose varied noticeably across model and truncation levels. HR estimates generally were attenuated as the models included increasing covariate history and as weight truncation was reduced. For example, in the simple treatment model with 2% truncation, the mortality HR increased monotonically with increasing dose. Patients in the highest category had an HR of 1.51 (95% CI: 1.08, 1.89). At 2% truncation in the expanded treatment model, the HR estimate for the highest-dose category was 1.39 (95% CI: 1.08, 1.91). In the expanded model with 1% truncation, the mortality HR estimates across the dose categories were near null; for patients in the highest-dose category, the HR was 0.98 (95% CI: 0.76, 1.74).
Table 4.
Effect of model specification on mortality hazard ratio estimates
| Treatment Modela | Weight Truncation Level, % | Maximum Weight | Zero Dose HR (95% CI) | Epoetin alfa Dose Group |
|||
|---|---|---|---|---|---|---|---|
| Category 1 | Category 2, HR (95% CI) | Category 3, HR (95% CI) | Category 4, HR (95% CI) | ||||
| Simple | 2 | 32 | 1.69 (1.06, 2.39) | Referent | 1.09 (0.92, 1.31) | 1.27 (1.02, 1.60) | 1.51 (1.08, 1.89) |
| Case-mix | 2 | 28 | 1.62 (1.16, 2.09) | Referent | 1.09 (0.94, 1.35) | 1.24 (1.05, 1.56) | 1.49 (1.22, 1.91) |
| Expanded | 2 | 82 | 1.56 (0.98, 2.02) | Referent | 1.07 (0.91, 1.33) | 1.21 (1.00, 1.53) | 1.39 (1.08, 1.91) |
| Simple | 1 | 133 | 1.71 (1.00, 2.55) | Referent | 1.01 (0.83, 1.26) | 1.07 (0.89, 1.42) | 1.15 (0.94, 1.68) |
| Case-mix | 1 | 117 | 1.81 (0.87, 2.51) | Referent | 1.02 (0.82, 1.29) | 1.11 (0.85, 1.41) | 1.21 (0.90, 1.70) |
| Expanded | 1 | 471 | 1.72 (0.84, 2.59) | Referent | 0.97 (0.79, 1.33) | 1.00 (0.81, 1.45) | 0.98 (0.76, 1.74) |
Treatment models include baseline covariates and the following time-dependent covariates:
Simple = hemoglobin level and epoetin alfa dose 2, 4, 6, and 8 wk before exposure.
Expanded = covariates in simple model plus days in hospital, number of epoetin alfa doses administered outside the hospital, albumin, ferritin, TSAT, vascular access type, hypertension, and dialysis adequacy 2 wk before exposure.
Full = covariates in expanded model plus an interaction term between hemoglobin level and epoetin alfa dose 2 wk before exposure.
Patients in the zero-dose category consistently had a greater mortality hazard than those receiving EPO. However, the CIs were wider with increasing adjustment and less truncation. In the expanded model with 1% truncation, the HR estimate was 1.72 (95% CI: 0.84, 2.59).
Discussion
We used an MSM to examine the relationship between EPO dose and mortality among HD patients. IPTWs were developed from a robust set of clinical and treatment history variables. Increasing the extent of EPO dose predictors in our treatment models attenuated HR estimates and likely represented greater control of important confounders. The difference between HRs across treatment models and by level of weight truncation was greatest in the highest-dose category, where CBI and time-dependent confounding might be the strongest.
CBI and time-dependent confounding by hemoglobin complicate estimating the causal relationship between EPO dosing and mortality. Patients who require higher doses have a higher prevalence of comorbid conditions and other characteristics that are associated with poor outcomes (3–5,17). Analyses are further complicated because hemoglobin concentrations are the consequence of previous EPO doses and influence the next EPO dose. Adjusting for bias associated with hemoglobin as a predictor of EPO dose in conventional survival analyses may inappropriately adjust for the effect of past EPO dose on current hemoglobin concentration. Thus, conventional analyses cannot control this time-dependent confounding and will yield biased estimates of the effect of EPO dose on survival (10,11,18). We used MSMs to achieve a balance of baseline and time-dependent confounders to control for time-dependent confounding by indication (12) and observed HR estimates at or below the null. Our results are consistent with those recently reported by Zhang et al. (19), who also used an MSM approach to evaluate the EPO dose and mortality association using USRDS data.
A fundamental assumption in marginal structural modeling is “positivity” (14), or the experimental treatment assumption (20). Positivity requires that patients at any given hemoglobin level should have a nonzero probability of receiving a biweekly dose that would place them in any of the dose categories. To the extent that this assumption is not satisfied, for example, if patients with high hemoglobin levels have a zero probability of receiving a high EPO dose, the analysis may be dominated by patients who have very large weights resulting from unconventional treatment decisions. We did observe a small percentage of excessively large weights. This observation, coupled with the observed effect on results of varying weight truncation levels on our HR estimates and the knowledge that certain EPO doses are extremely unlikely for HD patients with clinical characteristics (e.g., receiving a dose increase after a high hemoglobin level), raises questions regarding the ability of MSMs to completely remove all confounding by measured factors.
Our study has several limitations. First, the validity of our analysis depends upon the assumption that we have adjusted for all important confounding variables. Although our database contained information on a variety of patient demographic characteristics, routine dialysis care, vascular access type, laboratory parameters, medications, and hospitalization events, other factors that influence EPO dose, for example, chronic or acute inflammation, may not have been accounted for adequately. In our treatment models, we did include both time-varying albumin levels and vascular access type to account for the effects of inflammation, but we did not have access to other inflammatory markers, such as C-reactive protein or lymphocyte count (part of the malnutrition and inflammation complex), which have been shown to predict EPO dose requirements (17,21). As part of our treatment history, we also included EPO dose during the previous 8 wk. Recent studies have shown that previous EPO dose is the strongest predictor of future dose (19,22), and thus may serve as a proxy for other time-varying changes in underlying clinical status, including episodes of inflammation. Second, valid estimation of the parameters of our MSM requires that the treatment, censoring, and structural models were correctly specified. For example, we used ordinal regression to predict dose category. If, in fact, the relationship between dose category and relevant predictors is not monotonic, alternative model structures, e.g., nominal logistic regression, may have been more appropriate. We have some evidence to support the view that our treatment model was reasonably well specified, because the mean of the stabilized weights (e.g., in the expanded model) was very close to one, a necessary condition for correct specification (23). It may be that our models could have been improved if factors more reflective of clinical practice beyond what we considered were included. Third, the results of our MSMs are affected by level of weight truncation, a phenomenon that reflects the tradeoff between control of confounding and precision of our effect estimates (14). Fourth, the wide CIs surrounding our HR estimates reflect the potential dominance of a few data points in the application of MSMs. We attempted to balance bias reduction and variance inflation in our treatment models by truncating weights at the extremes (resulting in variance reduction) (14). Furthermore, comparison of our three treatment models indicates that the more complete treatment model removes considerable residual confounding. Last, for missing in-hospital dosing information, we imputed EPO doses assuming thrice-weekly dosing using the prehospitalization dose, which attempts to reflect the doses the patient would have received in the outpatient setting. Nevertheless, this approach may not reflect actual in-hospital EPO dosing, so we also evaluated an alternative approach, which involved imputing at 80% of the expected dose. The resulting HR estimates were similar in magnitude and direction to the results using the full prehospitalization dose (data not shown). Only when we assumed doses 50% or lower than prehospital doses did the results change appreciably, resulting in markedly reduced HR estimates for patients in the upper EPO dose categories.
In summary, estimating the independent relationship between EPO dose and mortality in the HD patient population is difficult owing to patient comorbidity, the strong correlation between patient health status and EPO dose requirements, and the dynamic dosing paradigm for EPO in clinical practice. Using MSMs to control for time-dependent confounding, we observed, in our most detailed model with 1% weight truncation, a mortality HR for patients receiving the highest EPO doses relative to the lowest doses of 0.98 (95% CI: 0.76, 1.74). The relatively wide CIs likely reflect a more appropriate level of uncertainty (a consequence of the reweighting of each patient’s contribution) compared with more conventional time-dependent analyses (3), which likely have residual bias. We conclude that there is appreciable CBI at higher EPO doses and that EPO dose was not associated with increased mortality in MSM analyses that more completely addressed this confounding.
Disclosures
Ouhong Wang, Ryan D. Kilpatrick, Brian D. Bradbury, Cathy W. Critchlow, and John F. Acquavella are employees of Amgen Inc. Xiang Ling is a previous employee of Amgen Inc.; David T. Gilbertson has received consulting fees from Amgen Inc.; Allan J. Collins has received consulting fees from Amgen Inc., Merck, NxStage, AMAG Pharma, and Roche. Both David T. Gilbertson and Allan J. Collins are employed by Chronic Disease Research Group, an organization that receives research support from Amgen Inc. Kenneth J. Rothman is an employee of RTI Health Solutions. RTI is an independent nonprofit research organization that does work for government agencies and pharmaceutical companies.
Supplementary Material
Acknowledgments
This research was sponsored by Amgen Inc. The results of this analysis were presented at the American Society of Nephrology Annual Meeting; San Francisco, CA; October 31 through November 5, 2007. We thank Yeshi Mikyas for editorial assistance in the preparation of this manuscript.
Footnotes
Published online ahead of print. Publication date available at www.cjasn.org.
Supplemental information for this article is available online at http://www.cjasn.org/.
References
- 1.Cotter DJ, Stefanik K, Zhang Y, Thamer M, Scharfstein D, Kaufman J: Hematocrit was not validated as a surrogate end point for survival among epoetin-treated hemodialysis patients. J Clin Epidemiol 57: 1086–1095, 2004 [DOI] [PubMed] [Google Scholar]
- 2.Zhang Y, Thamer M, Stefanik K, Kaufman J, Cotter DJ: Epoetin requirements predict mortality in hemodialysis patients. Am J Kidney Dis 44: 866–876, 2004 [PubMed] [Google Scholar]
- 3.Bradbury BD, Wang O, Critchlow CW, Rothman KJ, Heagerty P, Keen M, Acquavella JF: Exploring relative mortality and epoetin alfa dose among hemodialysis patients. Am J Kidney Dis 51: 62–70, 2008 [DOI] [PubMed] [Google Scholar]
- 4.Roberts TL, Obrador GT, St Peter WL, Pereira BJ, Collins AJ: Relationship among catheter insertions, vascular access infections, and anemia management in hemodialysis patients. Kidney Int 66: 2429–2436, 2004 [DOI] [PubMed] [Google Scholar]
- 5.Teruel JL, Marcen R, Ocana J, Fernandez-Lucas M, Rivera M, Tabernero G, Ortuno J: Clinical significance of C-reactive protein in patients on hemodialysis: A longitudinal study. Nephron Clin Pract 100: c140–c145, 2005 [DOI] [PubMed] [Google Scholar]
- 6.Bodnar LM, Davidian M, Siega-Riz AM, Tsiatis AA: Marginal structural models for analyzing causal effects of time-dependent treatments: an application in perinatal epidemiology. Am J Epidemiol 159: 926–934, 2004 [DOI] [PubMed] [Google Scholar]
- 7.Hernan MA, Brumback BA, Robins JM: Estimating the causal effect of zidovudine on CD4 count with a marginal structural model for repeated measures. Stat Med 21: 1689–1709, 2002 [DOI] [PubMed] [Google Scholar]
- 8.Regidor DL, Kopple JD, Kovesdy CP, Kilpatrick RD, McAllister CJ, Aronovitz J, Greenland S, Kalantar-Zadeh K: Associations between changes in hemoglobin and administered erythropoiesis-stimulating agent and survival in hemodialysis patients. J Am Soc Nephrol 17: 1181–1191, 2006 [DOI] [PubMed] [Google Scholar]
- 9.Volkova N, Arab L: Evidence-based systematic literature review of hemoglobin/hematocrit and all-cause mortality in dialysis patients. Am J Kidney Dis 47: 24–36, 2006 [DOI] [PubMed] [Google Scholar]
- 10.Hernan MA, Brumback B, Robins JM: Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology 11: 561–570, 2000 [DOI] [PubMed] [Google Scholar]
- 11.Robins JM, Hernan MA, Brumback B: Marginal structural models and causal inference in epidemiology. Epidemiology 11: 550–560, 2000 [DOI] [PubMed] [Google Scholar]
- 12.Robins JM: Correction for non-compliance in equivalence trials. Stat Med 17: 269–302; 1998discussion 387-269 [DOI] [PubMed] [Google Scholar]
- 13.Cole SR, Hernan MA, Robins JM, Anastos K, Chmiel J, Detels R, Ervin C, Feldman J, Greenblatt R, Kingsley L, Lai S, Young M, Cohen M, Munoz A: Effect of highly active antiretroviral therapy on time to acquired immunodeficiency syndrome or death using marginal structural models. Am J Epidemiol 158: 687–694, 2003 [DOI] [PubMed] [Google Scholar]
- 14.Cole SR, Hernan MA: Constructing inverse probability weights for marginal structural models. Am J Epidemiol 168: 656–664, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Efron B, Taibshirani R: Confidence intervals based on bottstrap percentiles. In: An Introduction to the Bootstrap, New York, Chapman & Hall, pp 168–177, 1993 [Google Scholar]
- 16.Suissa S: Immortal time bias in pharmacoepidemiology. Am J Epidemiol 167: 492–499, 2008 [DOI] [PubMed] [Google Scholar]
- 17.Bradbury BD, Critchlow CW, Weir MR, Stewart R, Krishnan M, Hakim RH: Impact of elevated C-reactive protein levels on erythropoiesis-stimulating agent (ESA) dose and responsiveness in hemodialysis patients. Nephrol Dial Transplant 24: 919–925, 2009 [DOI] [PubMed] [Google Scholar]
- 18.Cook NR, Cole SR, Hennekens CH: Use of a marginal structural model to determine the effect of aspirin on cardiovascular mortality in the Physicians’ Health Study. Am J Epidemiol 155: 1045–1053, 2002 [DOI] [PubMed] [Google Scholar]
- 19.Zhang Y, Thamer M, Cotter D, Kaufman J, Hernan M: Estimated effect of Epoetin dosage on survival among elderly hemodialysis patients in the United States. Clin J Am Soc Nephrol 4: 638–644, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mortimer KM, Neugebauer R, van der Laan M, Tager IB: An application of model-fitting procedures for marginal structural models. Am J Epidemiol 162: 382–388, 2005 [DOI] [PubMed] [Google Scholar]
- 21.Kalantar-Zadeh K, Lee GH, Miller JE, Streja E, Jing J, Robertson JA, Kovesdy CP: Predictors of hyporesponsiveness to erythropoiesis-stimulating agents in hemodialysis patients. Am J Kidney Dis 53: 823–834, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bradbury BD, Danese M, Gleeson M, Critchlow CW: Effect of Epoetin alfa (EPO) dose changes on hemoglobin and mortality among hemodialysis patients with hemoglobin levels persistently below 11 g/dL. Clin J Am Soc Nephrol 4: 630–637, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hernan MA, Robins JM: Estimating causal effects from epidemiological data. J Epidemiol Community Health 578–586, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Brunelli SM, Joffe MM, Israni RK, Yang W, Fishbane S, Berns JS, Feldman HI: History-adjusted marginal structural analysis of the association between hemoglobin variability and mortality among chronic hemodialysis patients. Clin J Am Soc Nephrol 3: 777–782, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.