Interpreting the effect of vaccination on steady state infection in animals challenged with Simian Immunodeficiency Virus

Abstract

A representative vaccinated macaque challenged with SIVmac251 establishes a persistent infection with a lower virus load, higher CTL frequencies, and much higher helper cell frequencies, than a representative control animal. The reasons for the difference are not fully understood. Here we interpret this effect using a mathematical model we developed recently to explain results of various experiments on virus and CTL dynamics in SIV-infected macaques and HIV-infected humans. The model includes two types of cytotoxic lymphocytes (CTLs) regulated by antigen-activated helper cells and directly by infected cells, respectively, and predicts the existence of two steady states with different viremia, helper cell and CTL levels. Depending on the initial level of CTL memory cells and helper cells, a representative animal ends up in either the high-virus state or the low-virus state, which accounts for the observed differences between the two animal groups. However, the model does not explain why viremia in the “low-virus state” is surprisingly high and broadly distributed among challenged animals. We conclude that the model needs an update explaining extremely low sensitivity of uninfected helper cells to antigen in vaccinated animals.

1. Introduction

The failure of vaccine trials signifies poor understanding of the mechanisms of interaction between HIV and a host and stresses the need for more fundamental research. Given the complexity of the virus-host interaction and the inescapable number of variable factors, such research cannot be limited to experimental approaches, but also calls for development of detailed mechanistic models to support and guide the experiments.

An important and well-studied experimental model for HIV vaccines is rhesus macaques treated with a vaccine designed to elicit a strong CTL response and then challenged with a simian-human immunodeficiency virus hybrid

(SHIV). These animals do not clear the challenge virus, but persistent infection is established at very low levels (three to four orders of magnitude lower than in control animals) (Barouch et al., 2000). At steady state, the CTL frequency in such animals is an order of magnitude higher, and the T helper cell frequency is orders of magnitude higher than in control animals. Challenge of vaccinated animals with SIVmac251, a strain whose pathogenic properties and tropism are more representative of HIV-1, showed less impressive results (Letvin et al., 2006). Although the increase in helper cell and CTL response due to vaccination was as strong as in SHIV-infected animals, the effect on the steady state viremia was much smaller, on average, by a factor of 30 (Letvin et al., 2006). Higher viremia correlated with earlier onset of AIDS. Although it is clear that a representative vaccinated animal is in a different steady state from a representative control animal, the nature of this state, the methods of its control, and the reasons for the difference remain unclear.

Recently, De Boer (De Boer, 2007) attributed the vaccine failure to a low exponential rate of CTL expansion, as compared to the expansion rate of viremia, which results in small effector to target cell ratios. He used a simple model of helper-cell independent response to explain why the expansion and contraction rates of viremia are the same in vaccinated and control animals. The effect of vaccination is to decrease the viremia peak, an effect which, due to a small CTL expansion rate, requires very high initial levels of memory cells. The cited model predicts that vaccinated animals end up in the same steady state with a high viremia as control animals.

The aim of the present work is to understand the differences between the properties of a steady state in vaccinated animals and control animals. The basic idea is that a representative individual can have more than one stable steady state. Which state actually takes place depends on initial conditions, for example, on the vaccination status. A broad range of models predicts more than one steady state (Adams et al., 2007; Althaus and De Boer, 2008; Korthals Altes et al., 2003). Predictions of these models have not been applied systematically to vaccination trials, nor tested against a sufficiently broad range of other experimental observations.

In the present work, we address the vaccination trials using a model developed earlier (Rouzine et al., 2006; Sergeev et al., 2009) based on a range of observations on SIV and HIV dynamics and immunology, including acute infection and ART (Barouch et al., 2000; Cavert et al., 1997; Chun et al., 1997; De Boer et al., 2003; De Boer et al., 2001; Ho et al., 1995; Homann et al., 2001; Janssen et al., 2003; Jin et al., 1999; Kaech et al., 2003; Kalams and Walker, 1998; Kalams et al., 1999; Lau et al., 1994; Letvin et al., 2006; Li et al., 2005; Murali-Krishna et al., 1999; Murali-Krishna et al., 1998; Nowak et al., 1997; Ogg et al., 1999; Ogg et al., 1998; Ortiz et al., 1999; Ou et al., 2001; Oxenius et al., 2002; Schmitz et al., 1999; Shedlock and Shen, 2003; Wei et al., 1995; Wherry et al., 2003; Zhang et al., 1999). While the model is rather flexible and under construction, a relatively broad experimental range is the key: The dynamical factors important in these experiments are also potentially important for vaccination trials.

The model (Fig. 1) includes two types of effector cells regulated either by infected cells (direct effector cells) or by cytokines secreted by helper cells (indirect effector cells), respectively. The hypothesis of two distinct CTL types does not follow directly from data and has been introduced to explain some important experimental facts, as discussed in detail in our previous work (Sergeev et al., 2009). The model predicts two steady states per individual: One state with a high virus load, a modest level of helper-independent CTLs, and no detectable helper cells, and another state with a low virus load, a higher CTL level, and abundant helper cells maintaining the CTL response. Stability of the high-virus state is explained by infection and killing of helper cells. Qualitatively, these features are shared with a simpler model developed earlier by Wodarz and Nowak (Wodarz, 2001; Wodarz and Nowak, 1999; Wodarz et al., 1998), but the two models also differ in several important aspects (Sergeev et al., 2009). According to our model, a representative unvaccinated control animal is in the high-virus state. If the initial level of CTLs is sufficiently high, a representative vaccinated animal ends up in the low-virus state. We calculate the minimal frequency of the initial memory cells required for this effect to occur, at different values of the model parameters.

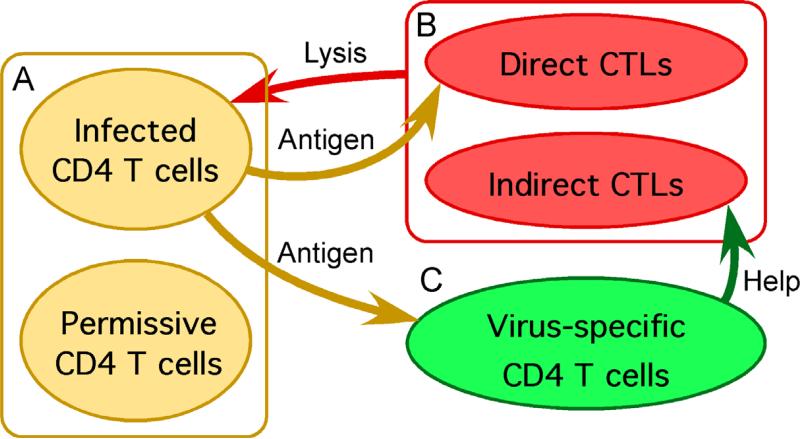
Figure 1.

Three blocks of a model of interaction between HIV/SIV and the immune system. The detailed structure of each block is shown in Fig. 2. “Direct” and “indirect” CTLs refer to helper-independent and helper cell-dependent CTLs, respectively.

We find that the model, although supported by many observations, fails to explain an important experimental fact not considered previously: A high, variable virus load in vaccinated animals challenged with SIVmac251. This observation indicates that sensitivity of helper cells to virus in vaccinated animals is surprisingly low and highly variable, relative to vaccinated animals challenged with SHIV. Therefore, the model has to be modified. In the future work, we need to locate, justify biologically, and explain in detail a new factor explaining this effect.

2. Model and parameter values

The model shown in Fig. 2, including infected cells and cells permissive for virus replication, a CTL block, and a helper cell block, was developed earlier (Rouzine et al., 2006; Sergeev et al., 2009) where we explained the model and discussed how different assumptions are linked to various observations. Specifically, the CTL block and the related experiments was addressed in Ref. (Sergeev et al., 2009). Model equations are given in Appendix A. We define various cell compartments and parameters in Fig. 2 and the legend. Values of model parameters were estimated previously (Sergeev et al., 2009). Of 30 parameter values, six were estimated from data obtained from individual unvaccinated animals from Ref. (Letvin et al., 2006) (Table 1). The other 24 parameters are fixed and are given in Appendix B.

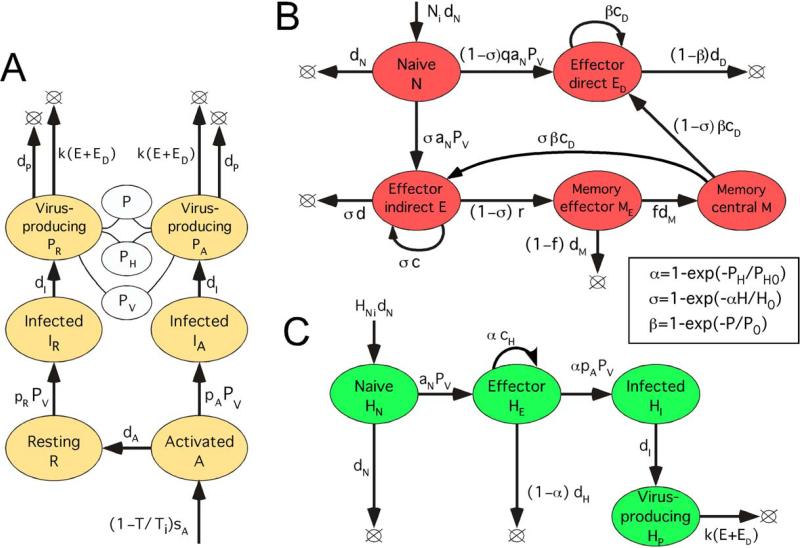
Figure 2. Detailed model diagram.

(A) Model block with non-HIV specific CD4 T cells, including infected cells and cells permissive for virus replication. R and A: Resting and activated uninfected CD4 T cells permissive for virus replication, respectively. I_R and I_A: Corresponding infected cells in the eclipse phase of replication cycle. P_R and P_A: Corresponding infected cells in the virus-producing phase. White oval: Linear combination of compartments, P = P_R+P_A, P_V = P_R+xP_A, P_H = P_R+x³P_A. Here x > 1 is the virion productivity ratio for activated versus resting infected cells, P is the total number of virus-producing cells, P_V is the effective number of virus-producing cells for free virus, and P_H is the effective number of virus-producing cells detected by helper cells. Virus load, V = v P_V (not shown). (B) Model block with HIV-specific CD8 T helper cells (CTLs). E and E_D: helper-dependent (“indirect”) and helper-independent (“direct”) effector CD8 T cells. (C) Model block with HIV-specific CD4 T cells. Inset: Control functions for the control of helper cells by antigen (α), direct effector cells by virus (β), and indirect effector cells by helper cells and antigen (σ), derived in Appendix B of Ref. (Sergeev et al., 2009). H = H_E+H_I+H_P is the total number of helper cells secreting cytokines, P₀ and P_H0 are antigen-sensitivity thresholds for direct CTL and helper cells, respectively, and H₀ is the characteristic threshold for indirect CTL in terms of helper cell percentage. (A-C) Colored oval: A cell compartment characterized by the number of cells in it. Arrow: Flux of cells from one compartment to another, or from a source to a compartment, or the proliferation or death of cells. Lower-case Roman letters and notation N_i, H_Ni, P₀, P_H0, and T_i: Model parameters (values in Table 1 and Appendix B). Expression at an arrow: Exponential rate of the process. The total CD4 count, T = A+R+I_A+I_R+P_A+P_R. Long-lived latently infected cells (not shown) are simulated by introducing several infected cells at random times.

Table 1.

Variable parameters for seven unvaccinated animals infected with SIVmac251 estimated in Ref. (Sergeev et al., 2009). First row: Animal p88 from Ref. (Kuroda et al., 1999). Second to seventh row: Six control animals from vaccination trials associated with Ref. (Letvin et al., 2006).

Animal ID	v	pR	c-d	P0	IR(0)/Pcut	Ti/sA
	107 copy/ml/%CD4	1/day/%CD4	1/day	10−3 %CD4	cell	day
p88, Ref. (Kuroda et al., 1999)	0.48	1.40	0.96	130	10	36
M-575	0.11	0.65	0.47	200	400	24
M-588	0.17	0.50	0.42	10	800	31
AC-04	1.86	0.55	0.45	17	200	33
AV-7G	0.62	0.60	0.47	12	200	67
44-I	1.00	0.75	0.45	17	200	40
64-I	2.71	0.50	0.47	50	120	33

3. Predicted effect of vaccination

To illustrate the predicted effect of preventive vaccination, we consider a set of model parameters corresponding to unvaccinated animal AC-04 from Ref. (Letvin et al., 2006) (Table 1). The effect of vaccination is described by introducing finite initial numbers of central memory CTLs, M(0), and effector helper cells, H_E(0).

The main reason why we cannot fit data for an individual vaccinated animal directly is that they are not inbred and, therefore, not genetically identical to any unvaccinated animal. A vaccinated animal has different model parameters than any unvaccinated animal. Another reason is that we do not know the initial levels of memory cells and helper cells in the cited study. Therefore, we would have to re-fit all these parameters for vaccinated animals. The related changes in the predicted dynamics would obscure the predicted effect of vaccination. To resolve this difficulty, we will simulate dynamics predicted for a hypothetical vaccinated animal with the same model parameters as unvaccinated animal AC-04.

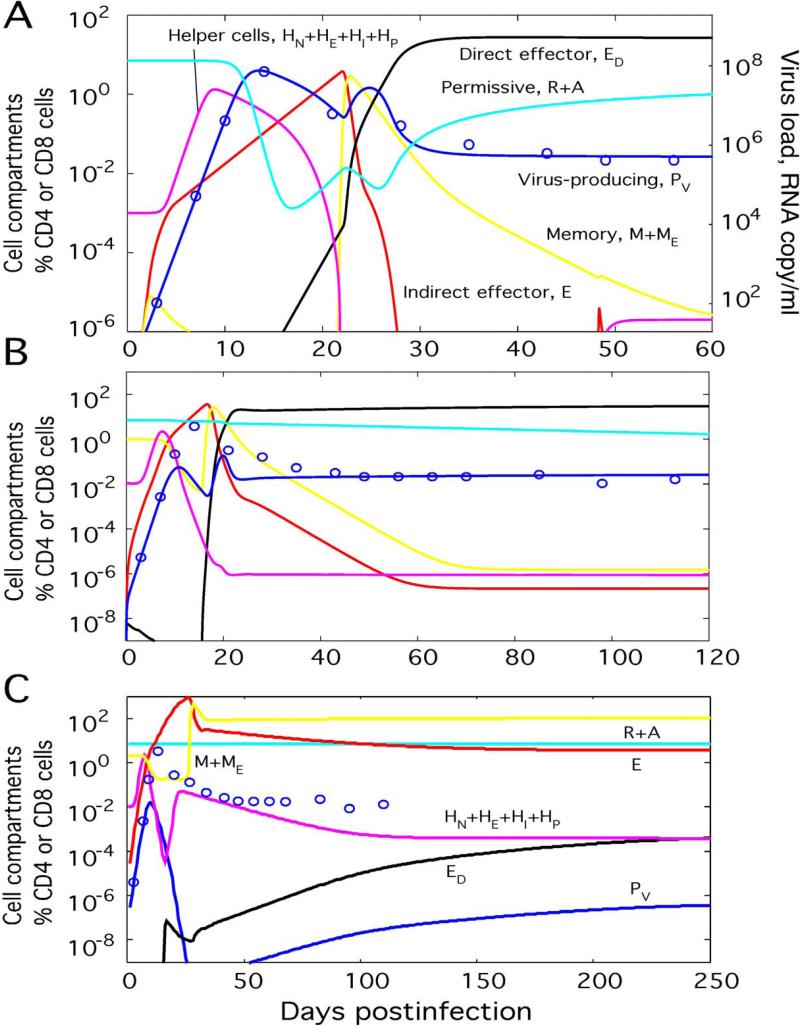
Simulation in the absence of vaccine (M(0) = H_E(0) = 0) and data points for animal AC-04 are shown in Fig. 3A. Parameters (Table 1) are found from matching data points with simulation results ((Sergeev et al., 2009), Fig. 5B). We observe accurate match between data points and simulation. Simulation in the presence of vaccine at two different values of M(0) is shown in Fig. 3B and C. We illustrate the predicted effect of vaccination by the difference between predicted dynamics and data points from unvaccinated animal AC-04. The model predicts three qualitatively different outcomes, depending on M(0) and H_E(0): a high-virus steady state, a low-virus steady state, and oscillatory state.

Figure 3. Predicted effect of vaccination.

(A) Simulated and observed virus dynamics for animal AC-04 used as an unvaccinated control in Ref. (Letvin et al., 2006). Model parameters (Table 1 and Appendix B; p_A/p_R = 2500) are estimated previously (Sergeev et al., 2009). Circles: Data points from Ref. (Letvin et al., 2006). Lines: Simulated cell compartments (Fig. 2) shown as percentage of CD4 T or CD8 T cell count in an average uninfected animal. (B and C) Two outcomes of vaccination depending on the initial level of memory cells. Simulated virus dynamics is shown for a vaccinated animal with the same parameter set as unvaccinated animal AC-04: (B) M(0) = 1% CD8 count (ends in the high-virus state), and (C) M(0) = 2% (ends in the low-virus state). Initial helper cell percentage, H_E(0) = 0.01% CD4 count.

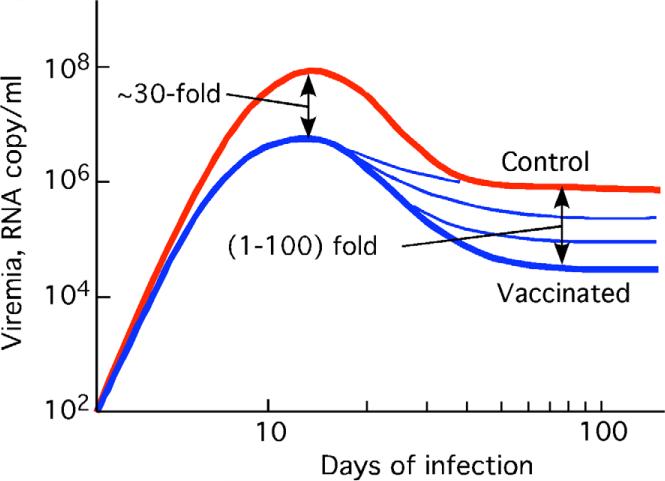
Figure 5.

Sketch of the effect of vaccination on virus dynamics, based on Fig. 2 in Ref. (Letvin et al., 2006).

In unvaccinated animals, M(0) = H_E(0) = 0, or at a modest initial level of memory cells M(0), the system ends up in the high-virus steady state, characterized by very low levels of helper cells and indirect effector cells E (Fig. 3A and B). Resting cells R are strongly depleted. The total number (measured as percentage of total CD4 T cell count in an average uninfected animal) of virus-producing cells and the virus load are both dominated by activated virus-producing cells, as given by P ≈ P_A, P_V ≈ xP_A (see definition of variables and parameters in Fig. 2 and the legend). The steady-state value is P = P^HVS = P₀ ln(1+ d_D / c_D), which ensures equilibrium for the direct effector cell population, dE_D/dt = 0 (Appendix A, second Eq. 3 neglecting terms with naïve and memory cells). Direct effector cells control virus replication. Their steady state number is given by $E_{\mathrm{D}}=E_{\mathrm{D}}^{\mathrm{HVS}}=s_{\mathrm{A}}∕k{P}^{\mathrm{HVS}})$ (Appendix A, Eqs. 1 with strong inequalities T << T_i, p_AP_V >> d_A, d_P << kE_D, E << E_D).

The mechanism behind the transition to the high-virus steady state can be understood from the model diagram in Fig. 2. Initial expansion of virus (or the effective number of infected cells P_V, Fig. 2A) initiates expansion of helper cells (H_E, Fig. 2C) and consequently of indirect effector cells (E, Fig. 2B) causing a decrease in viremia. Infection of helper cells (H_E→H_I→H_P) and their consequent killing by effector cells turns off the first wave of CTL expansion. The population of indirect effector cells (E) contracts by many orders of magnitude, causing a new virus expansion. A fraction of these cells survive to become memory cells (E→M_E→M), which are then reactivated by virus into direct effector cells (E_D, Fig. 2B). New effector cells expand until they bring virus down to the high-virus state level and assume the level at which they compensate de novo infection.

At larger M(0) exceeding a threshold value, the system ends up in the low-virus state characterized by high levels of helper cells and indirect effector cells and depleted direct effector cells (Fig. 3C). Resting cells are now close to their homeostatic level, R ≈ T_i. The total number of virus-producing cells and the virus load are now dominated by resting virus-producing cells, as given by P ≈ P_R, P_V ≈ P_R. Their steady-state level is P = P^HLS = P_H0 ln(1+ d_H / c_H), which follows from the equilibrium condition for helper cells, dH_E/dt = 0 (Appendix A, the second Eq. 2 neglecting naïve cells and infection). The virus load is controlled by indirect cells with the steady state number E = E^LVS = p_RT_i/k (Appendix A, Eq. 1 with R ≈ T_i, d_P << kE, E_D << E, and neglecting infection of activated cells).

The two reasons for the different outcome from the case of unvaccinated animals or small initial number of memory cells are, as follows: (i) Effector cell population reaches a greater number before it stops expanding, which gives it enough time to deplete virus to very low levels. (ii) Due to a lower virus peak, the (small) fraction of uninfected helper cells becomes larger (Fig. 3C). The lack of virus allows the small remaining fraction of uninfected helper cells (H_E) to re-expand and establish the steady state with abundant indirect effector cells. Direct effector cells (E_D) never have a chance to come up, and virus is stabilized at the low sensitivity threshold of helper cells (α ~ 1, inset in Fig. 2).

Thus, the outcome of the competition between virus, which tries to disable the helper-dependent response, and the helper-dependent response, which tries to clear virus, is sensitive to the initial level of memory CTLs.

At even larger M(0) (for the chosen parameter set, more than 8% of CD8 cell count), the predicted number of infected cells can fall below one cell, which corresponds to full clearance of virus. In a real HIV infection, small amounts of virus always remain hidden in latently infected cells, which are activated at rare random times. To simulate this effect, we introduce several infected cells at random times. Such a virus pulse initiates a virus rebound, resulting in activation of memory CTLs and quasiperiodic oscillations (results not shown). In most vaccinated SIV-infected animals, viremia is relatively high and the oscillatory behavior is not observed. The oscillatory effect may be important in vaccinated animals challenged with SHIV or patients treated with replication inhibitors.

As is clear from the above discussion, the outcome of an infection in a vaccinated animal also depends on the efficiency of infection of activated CD4 T cells, p_A. While p_R is estimated from the initial slope of virus expansion (previous work), we cannot estimate p_A from fitting any data, because its variation changes only the steady state number of uninfected activated CD4 cells, A, not measured in any experiment. (The definition of “activated cell” in our case is a cell in the interval of the cell cycle, possibly S-G2-M, where it is most infectable.) We are able only to estimate the lower bound for p_A. At sufficiently small p_A, the high-virus state is not stable in the long term even in the absence of vaccine, because helper cells are not infected at a sufficiently high rate to stay depleted and can expand. Therefore, the system spontaneously falls into the low-virus state, as is sometimes observed for some unvaccinated animals, especially those expressing the MAMU-A*01 MHC-I allele. When p_A increases, the minimum initial number of memory cells corresponding to the low-virus state (or the oscillating state), M_min(0), increases as well.

Previously (Sergeev et al., 2009), we matched predicted virus dynamics to data on five more unvaccinated animals from Ref. (Letvin et al., 2006) and estimated their parameters (Table 1). In the present work, we also tested the effect of vaccination on these animals. The predicted dynamics (not shown) is generally similar to that for animal AC-04 (Fig. 3), except, sometimes, a high level of memory cells results in an oscillatory state directly after the high-virus steady state, without the low-virus steady state in between.

We calculated the critical value of M_min(0) as a function of H_E(0) for parameter sets corresponding to three of the five unvaccinated animals, over a broad range of p_A/p_R (Fig. 4A). We also calculated the peak virus load at the critical point normalized to the corresponding value in an unvaccinated animal with the same model parameters (Fig. 4B). Interestingly, the virus peak at the critical point becomes lower at fewer initial helper cells, contrary to what is expected intuitively. At fixed M(0), the virus peak is, indeed, higher at lower H_E(0), because the delay of CTL expansion is larger. However, we also predict higher critical level of initial memory cells at lower H_E(0) (Fig. 4A), which decreases the virus peak and overcomes the previous effect.

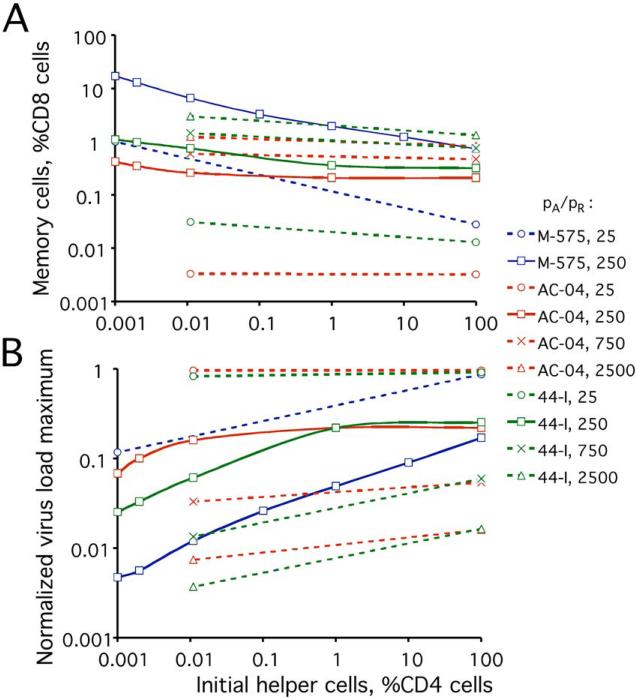
Figure 4. Critical condition of the transition to the low-virus steady state (or the oscillating state) after acute infection.

(A) Critical initial level of memory CTLs, M_c(0), required for the switch to the low-virus state or oscillating state, as a function of the initial helper cell level, H_N(0)+H_E(0). Cell levels are shown as percentage of CD4 T or CD8 T cell count in an average uninfected animal. (B) Decrease of the maximum virus load at the critical point, as compared to its value in a non-vaccinated animal. (A and B) The infectivity parameter ratio, p_A/p_R and identifiers of three unvaccinated animals from Ref. (Letvin et al., 2006), M-575 (blue), AC-04 (red), and 44-I (green), whose parameter sets were used for simulation (Table 1 and Appendix B), are shown in the legend. Solid lines with open squares: p_A/p_R=250. Dotted lines with other symbols: Other values of p_A/p_R, as shown.

The critical level of memory cells increases, and the critical viremia peak height decreases with p_A (Fig. 4). Indeed, as virus-specific helper cells become more infectable, the low-virus state becomes more difficult to reach, and a stronger suppression of virus peak is required. When ratio p_A/p_R, whose value is not known, is varied between 25 and 2500, the predicted critical level of memory cells varies within a very broad range, 0.003% to 10%. The normalized virus peak at the critical point varies between 0.003 and 1. Therefore, we cannot really predict the value of M_min(0) or the virus peak at the critical point. Instead, we can estimate p_A/p_R from the level of memory cells and virus peak (see below).

4. Observed effect of vaccination

We now compare these predictions with experimental observations in 24 vaccinated animals challenged with SIV (Letvin et al., 2006; Sun et al., 2006). A sketch of the dynamics of viremia based on actual data [Fig. 2 in Ref. (Letvin et al., 2006)] is shown in Fig. 5. The maximum virus load is decreased by an average factor of ~30 in vaccinated animals relative to control animals. At the steady state, viremia varies among vaccinated animals by several orders of magnitude. The log-average value is, again, roughly 30-fold lower than in unvaccinated, asymptomatic animals. Importantly, the number of helper cells in unvaccinated animals, as measured by IL-2 assay, is much higher than in control animals, in which helper cells are typically below detection. The CTL numbers measured by IFN-gamma ELISPOT at the steady state are also higher in vaccinated animals (Letvin et al., 2006). AIDS symptoms in vaccinated animals ensue, on average, in two years, compared to one year in unvaccinated animals.

We can roughly estimate the ratio p_A/p_R from available data on memory cells. Prior to infection, the maximum level of CTLs measured by multi-peptide IFN-gamma ELISPOT was in the range M(0) = 0.1%-0.2%, which corresponds to p_A/p_R ~ 250, if M(0) is close to the critical level, or less if M(0) exceeds that level (AC-04, 44-I in Fig. 4A). The typical peak suppression, ~ 0.03, corresponds to p_A/p_R ~ 250-750 or less. Unfortunately, the helper cell numbers prior to infection are not available. We also have to keep in mind that an assay using target cells sensitized with multiple peptides may underestimate the CTL level due to changes in cell-surface presentation of individual peptides, which is less symmetric in vivo.

Thus, the steady state in vaccinated animals infected with SIV has different properties than in control animals. Our model predicting bistability due to the assumption of two types of CTL regulation explains the increase in the CTL and helper response, as well as the decrease in viremia. At the same time, on the quantitative level, these properties do not exactly match any of the three predicted stationary states (including the oscillatory process). Because the numbers of CTLs and, most importantly, of helper cells are greatly increased due to vaccination, we cannot place vaccinated animals in the predicted high-virus state (Fig. 3B). The high number of CTLs and helper cells are consistent with the low-virus state (Fig. 3C). However, the log-average virus load in vaccinated animals does not show oscillation and is too high for the low-virus state (Fig. 3C), if we use vaccinated SHIV-infected animals [< 300 copies RNA/ml (Barouch et al., 2000)] as the reference system.

As already mentioned, the steady state level of total virus-producing cells in the low-virus state is given by P = P^LVS = P_H0ln(1+d_H/c_H), where P_H0 is the characteristic activation threshold for helper cells. It is expected to be much lower than the high-virus state level P^HVS = P₀ln(1+d_D/c_D), where P₀ is the characteristic activation threshold for direct effector cells, because P₀ should be larger than P_H0 by orders of magnitude. Indeed, soluble antigen produced by infected cells is internalized by APC, which travel far from infected cells and present it to helper cells elsewhere in the body (which send signals to indirect effector cells, E). In contrast, an effector cell has to encounter an infected cell on contact to get activated and divide. Therefore, the helper response can expand the detection volume of antigen from direct vicinity of a cell to the entire body. The strong difference in steady-state viremia between vaccinated and control animals challenged with SHIV (Barouch et al., 2000) confirms this general expectation.

We conclude that an important factor responsible for the “intermediate” behavior of chronic infection in vaccinated animals is missing from the model. The most important question is why, in the majority of vaccinated monkeys, helper cells are so weakly sensitive to antigen that rather large virus loads are required to maintain their equilibrium. The same question applies to human patients with viremia between 10 and 1000 RNA/ml and stable, detectable helper-dependent CTL response (Kalams et al., 1999). Possible reasons for this effect will be addressed elsewhere.

Appendix

A. Model equations

The model (Rouzine et al., 2006; Sergeev et al., 2009) consists of three interacting blocks: Infected cells and CD4 T cells permissive for virus replication, virus-specific helper cells, and virus-specific CTLs (Fig. 1). Detailed diagrams of three blocks are shown in Fig. 2, where we define all variables and constant model parameters. Each cell compartment is measured as percentage of the total CD4 or CD8 T cell count in an average uninfected animal. Below, we use “number” and “percentage” interchangeably. Equations for the block of permissive and infected CD4 T cells (Fig. 2A) have the form

$$\begin{array}{cc}\hfill & dA∕dt=(1-T∕T_{\mathrm{i}})s_{\mathrm{A}}-(d_{\mathrm{A}}+p_{\mathrm{A}}{P}_{\mathrm{V}})A\hfill \\ \hfill & dR∕dt=d_{\mathrm{A}}A-p_{\mathrm{R}}{P}_{\mathrm{V}}R\hfill \\ \hfill & d{I}_{\mathrm{A}}∕dt=p_{\mathrm{A}}{P}_{\mathrm{V}}A-d_{\mathrm{I}}{I}_{\mathrm{A}}\hfill \\ \hfill & d{I}_{\mathrm{R}}∕dt=p_{\mathrm{R}}{P}_{\mathrm{V}}R-d_{\mathrm{I}}{I}_{\mathrm{R}}\hfill \\ \hfill & d{P}_{\mathrm{A}}∕dt=d_{\mathrm{I}}{I}_{\mathrm{A}}-k(E+E_{\mathrm{D}})P_{\mathrm{A}}-d_{\mathrm{P}}{P}_A\hfill \\ \hfill & d{P}_{\mathrm{R}}∕dt=d_{\mathrm{I}}{I}_{\mathrm{R}}-k(E+E_{\mathrm{D}})P_{\mathrm{R}}-d_{\mathrm{P}}{P}_{\mathrm{R}}\hfill \end{array}$$ (1)

Here T = A + R + I_A + I_R + P_A + P_R is the total number of permissive or infected CD4 T cells, P_V = P_R + x P_A is the effective number of virus-producing cells with respect to free virus, and x is the ratio of virus productivity for activated versus resting cells. Virus load is given by V = vP_v, where v is a variable parameter reflecting productivity of infected cells. The block of antigen-specific helper cells (Fig. 2C) is described by a system of equations, as follows

$$\begin{array}{cc}\hfill & d{H}_{\mathrm{N}}∕dt=d_{\mathrm{N}}{H}_{\mathrm{Ni}}-[a_{\mathrm{N}}{P}_{\mathrm{V}}+d_{\mathrm{N}}]H_{\mathrm{N}}\hfill \\ \hfill & d{H}_{\mathrm{E}}∕dt=a_{\mathrm{N}}{P}_{\mathrm{V}}{H}_{\mathrm{N}}+[\alpha c_{\mathrm{H}}(1-H∕100)-(1-\alpha )d_{\mathrm{H}}-\alpha p_{\mathrm{A}}{P}_{\mathrm{V}}]H_{\mathrm{E}}\hfill \\ \hfill & d{H}_{\mathrm{I}}∕dt=\alpha p_{\mathrm{A}}{P}_{\mathrm{V}}{H}_{\mathrm{E}}-d_{\mathrm{I}}{H}_{\mathrm{I}}\hfill \\ \hfill & d{H}_{\mathrm{P}}∕dt=d_{\mathrm{I}}{H}_{\mathrm{I}}-k(E+E_{\mathrm{D}})H_{\mathrm{P}}\hfill \end{array}$$ (2)

Here H = H_E + H_I + H_P is the total number of primed helper cells, regardless of their infection status. Control function α is the fraction of helper cells detecting virus, α = 1 – exp(– P_H/P_H0), where P_H = P_R + x³P_A is the effective number of virus-producing cells with respect to the antigen activation of helper cells, and P_H0 is the antigen sensitivity threshold for helper cells. The cubic law x³ follows from a submodel assuming diffusion of soluble antigen from an infected cell in the tissue (Appendix B and Fig. 2B in Ref. (Sergeev et al., 2009)).

Equations for antigen-specific CD8 T cells (CTLs) (Fig. 2B):

$$\begin{array}{cc}\hfill & dN∕dt=d_{\mathrm{N}}{N}_{\mathrm{i}}-\{d_{\mathrm{N}}+[\sigma +q(1-\sigma )]a_{\mathrm{N}}{P}_{\mathrm{V}}\}N\hfill \\ \hfill & d{E}_{\mathrm{D}}∕dt=q(1-\sigma )a_{\mathrm{N}}{P}_{\mathrm{V}}N+(1-\sigma )\beta c_{\mathrm{D}}M+[\beta c_{\mathrm{D}}-(1-\beta )d_{\mathrm{D}}]E_{\mathrm{D}}\hfill \\ \hfill & dE∕dt=\sigma a_{\mathrm{N}}{P}_{\mathrm{V}}N+\sigma \beta c_{\mathrm{D}}M+[\sigma (1-E∕E_{\mathrm{m}})(c-d)-(1-\sigma )r]E\hfill \\ \hfill & d{M}_{\mathrm{E}}∕dt=(1-\sigma )rE-d_{\mathrm{M}}{M}_{\mathrm{E}}\hfill \\ \hfill & dM∕dt=f{d}_{\mathrm{M}}{M}_{\mathrm{E}}-\beta c_{\mathrm{D}}M\hfill \end{array}$$ (3)

Here β is the fraction of direct effector cells in contact with virus-producing cells, given by β = 1 – exp(– P/P₀), where P = P_R + P_A is the total number of virus-producing cells, and P₀ is the antigen sensitivity threshold for direct effector cells. Control function σ = 1 – exp(–αH/H₀) is the fraction of indirect effector CTLs receiving a cytokine signal from helper cells, where α is a control function defined above, and H₀ is the sensitivity threshold for indirect effector cells in terms of helper cell number. Control functions α, β, and σ are explained in Appendix B of Ref. (Sergeev et al., 2009).

The system of differential equations was solved numerically using the standard software ODE15S.M in MATLAB. The non-zero initial values for unvaccinated animals R(0) = T_i, N(0) = N_i, H_N(0) = H_Ni are fixed model parameters (below). To describe the effect of vaccination with different intensity, we used variable initial numbers of memory CTL and effector helper cells, M(0) and H_E(0) (legend to Fig. 3).

B. Parameter values and animals

We use parameter values estimated previously from various experiments as described in Ref. (Sergeev et al., 2009). 30 model parameters defined in Fig. 2 and the legend, and Eqs. 1-3 in Appendix A, include six variable parameters (Table 1) adjusted to match viremia data on individual unvaccinated SIVmac251-infected animals [Fig. 2 in Ref. (Letvin et al., 2006) and unpublished data provided by Norman Letvin]. 24 fixed parameters are, as follows: T_i = 7%CD4, d_A = 1/day, d_I = 1.3/day, d_P = 0.25/day, x = 5, k = 1/day/%CD8, H_Ni = 10⁻³ %CD4, d_N = 10⁻³/day, a_N = (3 10⁻³ v)/day/%CD4, c_H = 1.7/day, d_H = 0.07/day, P_H0 = (8.1 10¹⁶/v³)%CD4, N_i = 10⁻³ %CD4, q = 10⁻⁴, c_D = 1/day, d_D = 0.4/day, d = 2.4/day, E_m=1000%CD8, r = 6/day, d_M = 0.8/day, f = 0.06, vu = 7 10⁶ RNA copy/p27 ng, P_cut = 10⁻⁹ %CD4. Here vu is the ratio of units of viremia measured as RNA copies/ml blood and as p27 ng/ml blood, P_cut corresponds to a single cell in the body, and E_m is the theoretical maximum to which CTLs are allowed to expand in the lymphoid tissue. We set E_m at 1000% to allow for tissue expansion. We remind the reader that cell compartments are measured as percentage of the total CD4 T or CD8 T cell count in an average uninfected animal. The evidence for such a high tissue capacity is provided by acute LCMV Armstrong infection, in which the peak CTL number is much larger than the total CD8 count in uninfected animals (Murali-Krishna et al., 1998).