Model with Two Types of CTL regulation and Experiments on CTL Dynamics

Abstract

Recently, we developed a mathematical model of interaction between HIV and the immune system to match various dynamic experiments carried out in HIV-infected humans and SIV-infected macaques. The model includes helper cell-dependent and helper cell-independent cytotoxic lymphocytes (CTLs) and predicts two stable steady states, a state with a high virus load and few helper cells, and another state with a low virus load and many helper cells. Here we upgrade the model to take into account recent reports on the link between the activation status of infected cells and their ability to produce virus, the effect of helper cells at the time of priming on CTL differentiation, and virus dynamics in unvaccinated macaques with a broad genetic background acutely infected with SIVmac251. We also discuss in detail the experimental justification of the CTL block and the robustness of model predictions with respect to the hypothesis of two CTL subtypes.

1. Introduction

We continue a series of projects (Rouzine et al., 2005; Rouzine and Coffin, 1999; Rouzine et al., 2006) aimed at gradual development of a model of HIV-host interaction with a broad experimental application. The last version of the model agrees with a range of experimental facts [see (Rouzine et al., 2006) and references therein]. The model consists of three blocks, the block of infected cells and CD4 T cells permissive for virus replication, the block of virus-specific cytotoxic lymphocytes, and the block of helper cells. Most model elements are borrowed directly from the immunological literature; assumptions are made regarding the choice and connection of these elements. An important hypothesis of the model, which does not follow directly from data but is a hypothesis, and helps to explain important experiments, is the existence of two separate CTL subtypes with different mechanism of regulation.

The present work has two aims. Firstly, it offers a new update of the model. We incorporate results from additional experiments, such as the effect of the CD4 T cell activation status on the rate of virus production per cell (Cavert et al., 1997; Zhang et al., 1999) and the dependence of the differentiation pathway of CTLs on helper cells (Janssen et al., 2003; Shedlock and Shen, 2003). We apply the upgraded model to virus dynamics in unvaccinated monkeys with a broad genetic background challenged with SIVmac251 (Letvin et al., 2006). We explain the choice of parameter values and demonstrate that they agree with the estimates in the literature.

The second aim of the present work is to consider in detail the hypothesis that the model with two CTL subtypes can explain the dynamics of the CTL number and the virus load in two experiments with frequent sampling: In MAMU-A*01 expressing macaques acutely infected with SIVmac251 (Kuroda et al., 1999) and humans after the onset of drug therapy (Ogg et al., 1999).

The work is organized, as follows. In Section 2, we describe the model and specify the updated elements. The experimental evidence for and the model prediction of the existence of more than one steady state in an individual are discussed in Section 3. In Section 4, we consider the experimental support of the CTL model block, including dynamics in acute SIV infection and HIV-infected individuals following the onset of ART. We also examine the hypothesis of two CTL subtypes and show how the predictions change when the hypothesis is simplified. In Section 5, we discuss other models in the literature and propose some experimental tests. Mathematical equations, numeric simulation of different experiments, and the explanation of parameter values are given in Appendices A through E. The block of infected and CD4 T cells permissive for virus replication will be discussed elsewhere, in the context of vaccination trials.

2. Model

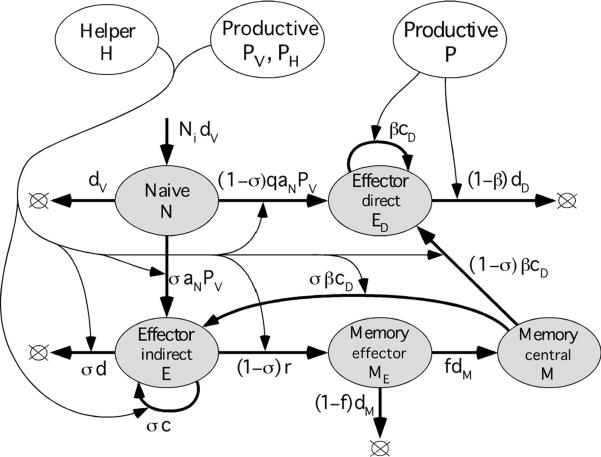
A model of interaction between HIV (SIV) and the immune system comprises three blocks (Figure 1), according to cell types: (i) Free virus, infected cells, and non-specific uninfected CD4 T cells permissive for virus replication, (ii) HIV-specific helper CD4 T cells, and (ii) HIV-specific CD8 T cells (CTLs). The three blocks interact with each other, as follows. Virus activates CTLs and helper cells and infects helper cells. CTLs kill infected (virus-specific and non-specific) CD4 T cells. Helper cells and virus control CTL differentiation.

Figure 1. Three blocks of a model of interaction between HIV and the immune system of a host.

In this Section, we describe each block. For the most part, the model was developed in our previous publications (Rouzine et al., 2005; Rouzine et al., 2006) based on experiments on SIV and HIV dynamics and immunology (Barouch et al., 2000; Chun et al., 1997; De Boer et al., 2003; De Boer et al., 2001; Ho et al., 1995; Homann et al., 2001; Jin et al., 1999; Kaech et al., 2003; Kalams and Walker, 1998; Kalams et al., 1999b; Lau et al., 1994; Letvin et al., 2006; Li et al., 2005; Murali-Krishna et al., 1999; Murali-Krishna et al., 1998; Nowak et al., 1997; Ogg et al., 1999; Ogg et al., 1998; Ortiz et al., 1999; Ou et al., 2001; Oxenius et al., 2002; Schmitz et al., 1999; Wei et al., 1995; Wherry et al., 2003b). Below we introduce and explain modifications of the model. The CTL block and the supporting experiments are discussed in more detail below in Section 4. The model is formalized by a system of first-order ordinary differential equations, one equation per cell compartment (Appendix A). Control functions determine how a controlled cell type reacts to the controlling compartment number (Appendix B). To describe extremely low virus loads, we introduce latently infected cells, not as a compartment but as an external factor. (Appendix C). We specify how we simulate various experiments (Appendix D) and estimate the parameter values (Appendix E).

2.1. HIV-specific helper CD4 T cells

We postulate that naïve helper CD4 T cells (H_N) are replenished at a constant, slow linear rate H_Nid_N (from thymus) and die at a slow, exponential rate d_N, where H_Ni is the equilibrium level in the absence of antigen (Figure 2a). In the presence of a virus, naive cells are primed with efficiency a_N at a rate a_NP_V, where P_V = P_R+xP_A is the virus level measured in terms of effective cell number, P_R and P_A are the numbers of infected cells among resting CD4 T cells and activated CD4 T cells, respectively, and x > 1 is the ratio of virion production for the two infected cells subtypes (Subsection 2.3 and Figure 4 below). Effector helper cells (H_E) expand, in response to antigen, with rate αc_H depending on antigen concentration (see below). In the absence of virus, effector cells die out at a rate d_H. They can be infected by the virus to become infected cells in the eclipse phase (H_I) and then virus-producing cells (H_P), which are killed by effector CTLs.

Figure 2. The model block with HIV-specific CD4 T helper cells.

(a) Diagram of the model block. Shaded oval: Cell compartment characterized by the number of cells in it. Thick arrow: Flux of cells from one compartment to another, or from a source to a compartment, or the death of cells. Thin arrow: Dependence of a cell flux on a third compartment shown by an expression at the thick arrow. Arrow loop: Cell proliferation. Lower-case Roman letters: model parameters (Table 1). Non-linear control function, α = 1−exp(−P_H/P_H0), where P_H = P_R+x³P_A (Figure 4), is the fraction of effector helper cells detecting antigen. (b) Schematic illustration of the control of effector helper cells (H_E) by the virus in the infected tissue. Blue diamonds: Infected cells. Red small circles: Effector helper cells detecting antigen. White small circles: Helper cells not detecting antigen. Large circles: Regions where the antigen concentration exceeds a sensitivity threshold for helper cells (more accurately, for antigen-presenting cells, macrophages and dendritic cells not shown in the panel). These regions occupy fraction α of the tissue.

Figure 4. The model block with non-HIV specific CD4 T cells, including infected cells and cells permissive for virus replication.

Notation is, as in Figure 2. White oval: Linear combination of compartments, P = P_R+P_A, P_V = P_R+xP_A, P_H = P_R+x³P_A. The total CD4 count, T = A+R+I_A+I_R+P_A+P_R. Virus load, V = vP_V (not shown). Long-lived latently infected cells are simulated by random pulses of infected cells not included in the diagram (Appendix C).

We characterize the effective antigen level detected by effector helper cells H_E by the effective number of virus-producing cells, P_H = P_R+x³P_A (Subsection 2.3 below and Figure 4). We assume that the proliferation rate of effector helper cells, αc_H, depends on P_H according to a “soft threshold” formula, α = 1−exp(−P_H/P_H0), where P_H0 is a constant determined by the sensitivity of helper cells to antigen. The formula is explained in Appendix B. Control function α denotes the fraction of effector helper cells, currently detecting antigen. These cells proliferate, secrete cytokines controlling CTL expansion (such as IL-2), and can be infected with high efficiency p_A. The remaining fraction of effector cells, 1−α, dies out at a small retirement rate, d_H. Thus, the proliferation rate varies between 0 and maximum value c_H, depending on the number of virus-producing cells.

As compared to the previous work (Rouzine et al., 2006), three modifications are introduced into the block: (i) We assume that these cells are primed at a rate linearly proportional to virus load (see the discussion for CD8 cells in the next subsection); (ii) the activation-induced death of activated cells (H_A) is now included in the total proliferation rate, αc_H; (iii) As it is known from LCMV studies (De Boer et al., 2003; Homann et al., 2001), the decay of helper cell population following the clearance of antigen actually occurs in three phases: Rapid decay due to the activation-induced death, a slower decay, and a long-lived memory phase (which starts very late and is low in number, as compared to CTL memory phase). Because quantitative data on dynamics of helper cells in HIV/SIV infection are lacking, we simplify differentiation of helper cells by combining the first two decay phases into one and neglect the memory phase.

2.2. HIV-specific CD8 T cells

The experimental support for the model block described below has been previously discussed (Rouzine et al., 2006). In this subsection, we explain new modifications. The assumption of two distinct subtypes of CTLs is addressed in Section 4.

We assume that naïve CTLs (N) arrive from thymus at a small fixed linear rate N_id_N and die out at an exponential rate d_N, where N_i is their normal homeostatic level. In the presence of antigen, naïve cells are primed to become either helper-dependent (indirect) effector cells (E) or helper-independent (direct) effector cells (E_D). The fate of primed CTLs depends on the presence of helper cells, as follows. In the presence of large numbers of helper cells, virus activates naïve cells with efficiency a_N to become helper-dependent (“indirect”) effector cells. In the absence of helper cells, virus activates naïve cells, with a much smaller efficiency qa_N, q << 1, into helper-independent (“direct”) effector cells. When direct effectors (E_D) encounter virus-producing cells, they proliferate; otherwise, they die out. Helper-dependent effectors (E) proliferate and die with rates depending on the concentration of antigen-detecting helper cells, as specified below. In the absence of helper cells, indirect effectors differentiate with rate r into effector memory cells (M_E), which either die with rate d_M or, a small fraction f, become long-lived central memory cells (M). In the presence of antigen, similar to naïve cells, central memory cells (M) are activated into either indirect or direct effector cells, depending on the presence or the absence of helper cells detecting virus.

Control of effector cells by virus and helper cells differs for the two effector cell compartments, E and E_D. Briefly, helper-dependent effector cells (E) proliferate in response to cytokines secreted by helper cells that currently detect antigen, whose concentration is αH, where H = H_E + H_I + H_P is the total number of helper cells capable of secreting cytokines, α is the fraction of helper cells detecting antigen (see previous subsection and Appendix B). Because cytokines act at a short distance, an effector cell E has to be sufficiently close to a helper cell to receive a cytokine signal. The fraction of such E cells is given by σ = 1−exp(−αH/H₀), where H₀ is a characteristic helper cell number depending on the CTL cytokine sensitivity (Appendix B). Hence, the average rate of CTL proliferation is given by cσ, where c is the maximum division rate. The activation-induced apoptosis rate of indirect effector cells is also proportional to σ and has maximum value d. The net expansion rate is (c–d)σ. In contrast, direct effector CTLs (E_D) proliferate only upon contact with virus-producing cells, so that their proliferation rate depends only on the total number of virus-producing cells, P_R + P_A, and is given by βc_D, where β = 1−exp[−(P_R+P_A)/P₀], and c_D is the maximum possible proliferation rate. Characteristic threshold P₀ is assumed to be much higher than the threshold for helper cells, P_H0. We assume that direct effector CTLs (E_D) have a constant death rate, d_D, even in the absence of activation.

As compared to the previous version (Rouzine et al., 2006), we improved the description of activation of naïve and memory CD8 T cells into effector cells. Although primary CTL response, generally, does not require the presence of helper cells, even a transient depletion of helper cells at the time of priming impairs formation of memory cells (M) (Janssen et al., 2003; Shedlock and Shen, 2003). Our model accounts for this fact postulating that formation of memory cells is associated with the helper-dependent pathway, N → E → M_E → M (Figure 3). Modifications are, as follows. (i) Earlier, we assumed that the priming of naive cells (N) and the proliferation of indirect effector cells (E) occur at the same rate, cσ. In fact, priming requires a direct contact of a CTL with an antigen-presenting cell (APC) to verify that a naïve cell is antigen-specific. In contrast, proliferation of a primed cell (E) is caused by a cytokine signal. The new version takes into account the difference, assuming a priming rate linear in antigen with coefficient a_N (Figure 3). (ii) Earlier, we did not specify how a naive cell decides between differentiation into indirect (E) and direct effector cells (E_D). We now introduce a helper-dependent fork: Naïve CTLs are programmed to become helper-dependent (E) or direct effector cells (E_D) with the rates proportional to σ and 1− σ, respectively (Figure 3). Also, it is known that a helper cell can upregulate MHC-I expression by macrophages. Therefore, priming of direct effector cells may be less effective than priming of indirect cells, which is now accounted for by factor q << 1 in the rate N-> E_D (Figure 3). Small q (Table 1) is required to explain a relatively late emergence of direct CTL response in SIVmac251 infection (Section 4.1). (iii) We also introduce a helper-dependent fork for memory cells (M), but without the asymmetry factor, q. The upgraded model predicts the initial dominance of either direct or indirect CTL response, depending on the initial amount of virus and helper cells. The price of the upgrade is two additional parameters, a_N and q; only their order of magnitude, which determines the time delay of effector cell expansion, is important for final results.

Figure 3. The model block with HIV-specific CD8 T cells (CTLs).

Notation is, as in Figure 2. Control function for direct effector cells: β = 1−exp(−P/P₀), where P = P_R+P_A is the total number of virus-producing cells (Figure 4). Control function for indirect effector cells: σ = 1−exp(−αH/H₀), where H = H_E+H_I+H_P is the total number of helper cells capable of sending signals to CTLs, and a is their current fraction detecting antigen (Figure 2, caption).

Table 1. Model parameters used in Figures 2 to 4 and Equations 1 to 3 (Appendix D).

Parameter	Description	Units	Biological range	Assumed value
pR	Efficiency of resting CD4 T cell infection	1/(day %CD4)		0.5–1.5
pA	Efficiency of activated CD4 T cell infection	1/(day %CD4)		>250pR
SA	Intensity of homeostatic replenishment of CD4 T cells	%CD4/day	Ti/(20–80)	Ti/(20–70)
Ti	Homeostatic number of permissive CD4 T cells	%CD4	~7	7
dA	Inverse duration of the activated CD4 T cell phase	1/day	>1	1
d1	Inverse latent period of an infected CD4 T cell	1/day	0.8–1.5	1.3
dP	Virus-induced death rate of virus-producing cells	1/day	0.25–0.5	0.25
x	Virus production ratio of activated and resting cells	1	~5	5
k	Efficiency of virus-producing cell killing by CTL	1/(day %CD8)		1
v	Virus load per percent resting virus-producing cell	RNA/ml/%CD4	106–108	(0.1–2.7)·107
HNi	Homeostatic number of naive helper cells	%CD4	10−4−3·10−3	10−3
dN	Death rate of naive helper cells and CTLs	1/day	~10−3	10−3
aN	Maximal efficiency of naive cell activation by virus	1/(day %CD4)		(3·10−3)v
cH	Maximum expansion rate of effector helper cells	1/day	1.07–1.59	1.7
dH	Death rate of effector helper cells in the absence of virus	1/day	0.12–0.82	0.07
PH0	Characteristic virus-producing cell number for expansion of helper cells	%CD4		8.1·1016/v3
Ni	Homeostatic number of naive CTLs	%CD8	10−4−3·10−3	10−3
q	Priming asymmetry for direct vs. indirect CTLs	1		10−4
cD	Maximum division rate of direct effector CTLs	1/day	0.98–2.21	1
dD	Maximum death rate of direct effector CTLs	1/day	0.34–0.47	0.4
P0	Characteristic virus-producing cell percent for direct effector CTLs	%CD4		0.01–0.2
c	Maximum division rate of indirect effector CTLs	1/day	<3.5	2.8–3.4
d	Maximum death rate of indirect effector CTLs	1/day	0.1–2	2.4
H0	Characteristic helper cell number for indirect effector CTLs	%CD4		(4–8)· 10−6
Em	Maximum number of effector CTLs	%CD8	<102	102
r	Indirect effector CTL retirement rate	1/day		6
dM	Effector memory CTL retirement rate	1/day		0.8
f	Fraction of effector memory CTLs becoming central memory	1	~0.05	0.06
vu	Virus unit relation, RNA/ml to p27 ng/ml	RNA/p27 ng	106−3·107	7·106
Pcut	Lower cutoff of infected cells in macaques	%CD4	~10−9	10−9

2.3. Infected cells and cells permissive for virus replication

We consider two types of cells permissive for virus replication (Figure 4). Resting CD4 T cells, whose number is denoted R, represent long-lived memory cells generated by previous unrelated infections. Their activated precursors (A) with a short phase period, d_A⁻¹, are replenished from a linear homeostatic source with maximum intensity s_A, which turns off gradually when the total CD4 count reaches a normal homeostatic value, T_i. Both resting (R) and activated cells (A) can be infected to become eclipse-phase cells (I_R and I_A), which, in average time d_I⁻¹, start producing free virus, which infects new permissive cells. Resting cells are infected with a much smaller efficiency than activated cells, as given by p_R << p_A. Virus-producing cells (P_R and P_A) are either killed by CTLs with efficiency k or die due to the pathogenic effect of accumulating virus products, in average time d_P⁻¹. Free virus is not included in the model as a separate compartment, because it is short-lived [half-life of 30–100 min in plasma (Ramratnam et al., 1999)] and, therefore, should remain proportional to the virus-producing cell number as it varies in time. The total virus load (number of free virus particles) is given by V = vP_V, where v is free virus per resting virus-producing cell. P_V = P_R + xP_A is the effective number of virus-producing cells with respect to the virus load, and x is the relative difference in free virus per cell between activated and resting cells. The values or ranges of model parameters relevant for this block are given in Table 1 (rows 1 to 10). The choice of parameter values is explained in Appendix E.

As compared to the previous version of the model (Rouzine et al., 2006), we introduced three modifications: (i) We now classify infected cells according to their activation status at the moment of virus entry, i.e., now we differentiate between I_A and I_R, and P_A and P_R. Indeed, infected cells expressing activation marker Ki67 were shown to produce about 5-fold more virus (Cavert et al., 1997; Zhang et al., 1999). (ii) To explain variation in the peak virus load during acute infection between individual patients and animals, we introduce a new parameter, the amount of free virus particles per infected cell, v. (iii) In addition to the death of virus-producing cells caused by CTLs, we include the death rate d_P due to the cytopathic viral effect, given by d_P⁻¹ = 2–4 days.

The model would predict full clearance of virus when less than one infected cell is left in a body, as given by P_A+P_R+I_R+I_A < 1 cell. In fact, the virus is never fully cleared even after years of highly active therapy and, following cessation of therapy, rebounds to the pre-drug level. The compartment that seeds virus are latently infected cells activated at random rare moments (Chun et al., 1997). To simulate this process, we introduce several infected cells (I_A and I_R) at random moments of time (Appendix C).

3. Two steady states

3.1 Experimental evidence

Several experiments imply the possibility of more than one steady state with non-zero viremia in the same individual:

(i) Some humans with initially high viremia, after irregular adherence to ART, are able to maintain stable, low viremia after the treatment has stopped (Ortiz et al., 1999). In these individuals, (helper-dependent) CTL response is maintained during ART, contributing to control of viremia at a low level. Once treatment stops, the steady state with low viremia continues, after adjustment of the CTL level.

(ii) Vaccination trials in rhesus macaques challenged with SIVmac251 (Letvin et al., 2006) and SHIV (Barouch et al., 2000) reveal that a persistent infection in vaccinated groups has different characteristic virus loads, CTL numbers, and helper cell numbers than a persistent infection in control animals. In SHIV vaccination trials (Barouch et al., 2000), a steady-state has viremia orders of magnitude lower than in control animals. In animals vaccinated against and challenged with SIV, the difference in viremia is less pronounced, ~30 fold (Letvin et al., 2006). In both cases, in vaccinated animals, the steady-state CTL level is ~10-fold higher, and the helper cell number orders of magnitude higher than in control animals, in which helper cells are generally undetectable.

Interpretation of these experiments is based on understanding that vaccination does not change intrinsic properties of an animal, but only the initial state (numbers of memory cells). Because animals in the two groups are selected from the same genetically diverse pool, and their final steady states are different, we must conclude that there is more than one possible steady state in an animal. Indeed, a steady state level of each variable (e.g. virus load) does not depend on the initial conditions, but is determined by the condition of the balance between the production rate and the death rate of the controlled cell subtype (in the above example, CTL). Which state actually takes place, however, depends on the initial conditions: A representative vaccinated animal ends up in a different steady state than a representative control animal.

Our simple model assumes that all CTL subsets have identical properties. In principle, variation in parameters among CTL subsets recognizing different epitopes could affect the predicted dynamics of these experiments. The main conclusion about two steady states, however, does not change. Let us assume for a moment that there is only one steady state per animal. If vaccine selectively amplifies the CTL subsets with low sensitivity to antigen, viremia is predicted to be transiently higher in vaccinated animals to keep these CTL subsets at a constant level. In a short time, the more sensitive CTL subsets will arise from low levels and bring viremia down to the same set point as in unvaccinated animals. The prediction disagrees with the cited experiments. If vaccine, in contrast, amplifies highly sensitive CTLs, then viremia would, again, reach the same level as in unvaccinated animals (where the sensitive CTL subset is expected to arise first), only even faster. Again, we have a disagreement. Finally, introduction of the helper-cell dependent CTL subsets and variable sensitivity of CTL to helper cells return us to essentially a more complex version of our model.

(iii) Additional evidence is offered by correlation across untreated unvaccinated patients between the virus load, the HIV-specific CTL frequency, and the helper cell response (Kalams et al., 1999b; Ogg et al., 1998). In patients selected for expression of A*0201 HLA allele, the diagram of gag-pol CTL frequency versus log viremia has a characteristic comet-like appearance [Figure 2B in (Ogg et al., 1998)]. Most infected individuals are restricted to the core region located at high virus loads, 10⁴−3·10⁵ RNA copies per ml blood, and relatively low CTL frequencies, 0.1–0.4% CD8 T cells. Others form a broad tail sweeping the area between 0.5% and 2% CD8 cells and below 10⁴ RNA copies/ml, respectively. A detectable helper cell response is associated with the tail region (Kalams et al., 1999b).

We note that the form of the distribution of viremia across untreated patients alone neither supports nor refutes the existence of two steady states. The high-viremia core overlaps the broad low-viremia tail, so that the full distribution is not bimodal but continuous. Only bringing into consideration other quantities (CTLs and helper cells) and the above mentioned facts, it becomes evident that the distribution actually consists of two overlapping components with fundamentally different properties. In vaccinated animals challenged with SIV, the low-viremia tail becomes more pronounced at the expense of the high-viremia core (Letvin et al., 2006). The reason for a broad distribution of the activation threshold of helper cells, P_H0, which we predict is responsible for the broad low-virus tail, is beyond the scope of the present work.

3.2. Model prediction

In keeping with these findings, our model predicts two stable steady states. One steady state, which identifies with a typical HIV infection in vivo, is characterized by high viremia, very low helper cells, and a modest CTL frequency. Direct effector cells (E_D) control the virus, while the helper-dependent CTL response is off, because helper cells are infected and depleted. The steady state values are given by P_V^HSS = xP₀ ln(1+d_D/c_D) (second Equation 3 in Appendix, M and N are small, P_V • xP_A) and E_D^HSS = s_Ax/(kP_V^HSS) (Equations 1, p_AP_V >> d_A, d_P << kE_D, E << E_D). The high-virus state can be stable in the long term, only if a virus infects helper cells with a high efficiency, as given by p_A > c_H/P_V^HSS (dH_E /dt < 0 in Equation 2, α • 1, small H_N, H << 100). Otherwise, helper cells and, hence, helper cell-dependent CTLs will expand and deplete the virus.

The second steady state has low viremia, high numbers of helper cells, and elevated frequencies of CTLs. The dominant CTLs are helper-dependent. The direct CTL response is low, because the virus load is too low to maintain it. The reason why the effector cell level is elevated is compared to the high steady state is that permissive cells are not depleted, and it takes more CTLs to balance virus replication. The steady state values are given by P_V^LSS = P_H0ln(1+d_H/c_H) and E^LSS = p_RT_i/k (Equations 3 and 1, P_V • P • P_H • P_R, H_N and p_AP_V are small).

In addition, the system may experience stationary oscillations, with the virus expanding transiently from “latent cells” simulated by random pulses of infected cells, and the CTL response being turned on and off (simulation results not shown).

To avoid possible confusion, a typical patient undergoing ART is not in the low-virus steady state: In this case the virus is depleted below the activation threshold of helper cells response, so the CTL response is turned off. A very low level of viremia is maintained due to replication inhibitors alone. After the treatment has been interrupted, a rebound to the high steady-state level occurs. In contrast, in the low-virus steady state, virus is sufficiently high to keep CTL response active. We interpret the rare maintenance of low viremia after cessation of intermittent ART (Ortiz et al., 1999) as a transition to the low-virus state. Reproducing the effect intentionally is very difficult, hence, the failure of empiric attempts at Structured Therapy Interruption. In fact, as our model predicts, it would require fine tuning of drug concentration based on individual patient parameters measured in advance, so that several critical variables (virus load, CTLs, helper cells) are brought in the close vicinity of their low-virus state values, all at the same time (Rouzine et al., 2006).

Other models predict multiple steady states as well (Adams et al., 2007; Korthals Altes et al., 2003; Wodarz, 2001) (see Section 5 below). Bi-stability predicted by our model is connected specifically to interesting experiments on CTL dynamics considered in the next section.

4. CTL block and supporting experiments

In Subsections 4.1 and 4.3, we discuss application of our model to two experiments on CTL dynamics (acute SIV infection of MAMU*01 macaques and ART in HIV infected humans), which, in our opinion, did not receive sufficient attention in the modeling literature. In other subsections, we will match our model predictions to more recent data on acute SIV infection in macaques with broad genetic background, list additional facts our CTL block helps to understand, and test what happens when the assumption of two different CTL subtypes is modified.

4.1 Acute SIV infection of MAMU*A01 animals: frequent sampling

Kuroda et al (Kuroda et al., 1999) studied CTL dynamics and virus during the first four weeks of SIVmac251 infection in six MAMU*A01 animals. As compared to other analogous papers, the authors provided rather frequent sampling and simultaneous measurement of three quantities: The CTL number (dominant epitope p11c by tetramer assay), the virus load (p27 assay), and the fraction of dying CTLs (Annexin V assay). Samples were taken frequently while the time variation of both quantities was relatively fast, on days 7, 9, 13, 15, and 17, and then on days 21 and 27, when it had slowed down (Figure 5 of the cited work). (In analogous experiments, viremia is measured every no more frequently than every 4 to 7 days.) The viremia assay, based on antibodies against SIV precursor protein p27, has a very high detection threshold, cannot measure virus load in a broad range of values, and is no longer in use. At the same time, it revealed some fine features of the near the viremia peak not addressed in RNA assay experiments (which also have less frequent sampling). The cell ligand of Annexin V is an early marker of both apoptosis and necrosis, whose expression correlates well with late markers of cell death detecting degradation of cellular DNA and membrane (Aubry et al., 1999; Dillon et al., 2000; Prochazkova et al., 2003; van Engeland et al., 1998). The delay between Annexin V and the late markers is 4 to 6 hours. Because Annexin V ligands are expressed a fixed time before cell death, the frequency of Annexin V positive cells is proportional to the exponential cell death rate, in arbitrary units.

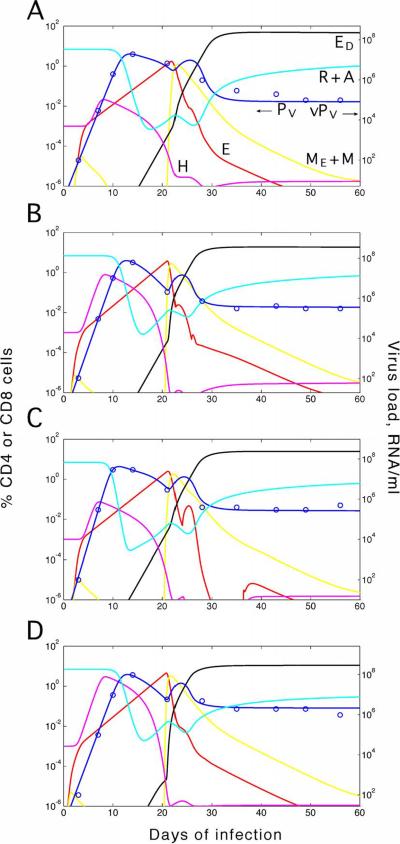
Figure 5. Data and the predictions for three unvaccinated rhesus macaques.

(a) MAMU-A*01-positive animal M-575 (Letvin et al., 2006). (b) A01-negative animal AC-04 (Letvin et al., 2006). (c) A01-positive animal p88 (Kuroda et al., 1999). Variable and fixed parameter values are given in Tables 2 and 1, respectively. Curves: Predicted dynamics for different cell compartments. Circles: Data points from Refs. (Kuroda et al., 1999; Letvin et al., 2006). Red: Indirect effector CTLs, E. Black: Direct effector cells, E_D. Yellow: Central and effector memory cells, M_E+M. Magenta: Total helper cells, H_N+H_E+H_I+H_P. Cyan: Total uninfected CD4 T cells, R+A. Blue: Virus shown as the effective virus-producing cell number P_V = P_R+xP_A in percentile of the total CD4 count (a and b, left axis), and as the free virus load in units RNA/ml blood (a, b, and c, right axis) and p27 ng/ml (c, left axis). Brown: Average CTL death rate in arbitrary units. Green: Total CTL number, N+E_D+E+M_E+M.

In five animals out of six studied, the cited work revealed a complex dynamics of viremia (Figure 5 in Kuroda et al). Data for animal p88 are shown in Figure 5c. In all six animals, virus is still below detection on day 7. Data are consistent with exponential increase between days 7 and 9 (observed by RNA assay and predicted by all published models), although the shape of increase cannot be seen directly due to a high detection threshold and the lack of intermediate points. The values taken on days 9, 11, 13, 15, and 17 show the existence of a double viremia peak. The first peak is either around day 9 (animals 87, 88, 191) or between days 9 and 11 (animals 253, 348, 575). The second, lower peak is evident in four animals out of six either around day 15 (animals 87, 88) or between days 15 and 17 (animals 191, 253). In the remaining two animals, 575 and 348, the data also allow a second peak, but do not show it directly, because there was no sampling on day 15.

CTL frequency also displays complex dynamics, which strongly correlates in time with the virus dynamics. In all animals, at the time of the first virus expansion, CTLs are still below detection. The following virus decrease is coincident with detectable CTL expansion until day 13. After that, in five animals out of six (except 87), CTL population contracts by a factor of two or larger, which is coincident with a second virus expansion (observable in animals 88, 191, and 153; in animals 575 and 348, as we already said, the point at day 15 is missing and the second virus expansion is not resolved). Finally, in animals 88, 191, 87, and 253, the second virus decrease after day 15 is accompanied by a second, slow CTL expansion; in remaining animals 575 and 348, CTLs stay very low.

In animals 88, 87, 191, 53, the cited authors also measured the frequency of cells scheduled for apoptosis by Annexin V assay (Figure 6B in (Kuroda et al., 1999)). Surprisingly, the initial CTL expansion and the following contraction are coincident with a high and low frequency of dying cells, respectively, and not vice versa, as one would intuitively expect. Annexin V+ population stays small until the end of experiment in 4 weeks. The drop in percentile of Annexin V+ cells is most pronounced in animals 87 and 88: From 70% at day 11 to < 10% at day 15. We elect animal 88, which displays all these characteristic features, to be our “representative animal” (Figure 5c). Note that the peak of CTLs, the local virus minimum, and the half-drop in Annexin V+ cells occur within the same time interval.

Figure 6. Data and predictions for four unvaccinated macaques (Letvin et al., 2006).

(a) MAMU-A*01-positive animal M-588. (b, c, d) MAMU-A*01-negative animals: AY-7G, 44-I, and 64-I, respectively. Variable and fixed parameter values are given in Tables 1 and 2, respectively. Notation is, as in Figure 5.

The CTL model block in Figure 3 was developed to match, among other observations, the tri-phasic pattern. The three phases are interpreted as E →M_E →M →E_D transition. In more detail [Figure 6b in Ref. (Rouzine et al., 2006)], when growing virus load crosses a low threshold ~ P_H0, helper cells (H_E) and, after a while, helper-dependent effector cells (E) start to proliferate. Effector cells both divide and become programmed for activation-induced apoptosis (Phase I). Expanding effector cells kill infected cells at increasing rate, eventually causing the first fall of viremia. Virus-specific helper cells are also infected and killed and, soon after viremia peak, fall below the activation threshold of CTLs (H₀). Not receiving sufficient signals from helper cells, E cells cease expansion and quickly retire to the effector memory phenotype (M_E). These cells cannot be reactivated by antigen and die out at a relatively slow rate; hence, the rapid decrease in the Annexin V+ cell number (Phase II). In the absence of armed effector cells, due to continued supply of activated permissive cells from the source (Figure 4), the virus load rises again. A small fraction of effector memory cells (f) survive, become central memory cells (M), and are reactivated into direct effector cells (E_D). As E_D cells expand in the presence of antigen, they gradually deplete infected cells to the steady state level (Phase III).

The reader may wonder whether a simpler model can equally well explain the observations in the cited experiments. The key support of our model is the tight correlation between ups and downs of CTLs and those of the virus. The sharp change in the frequency of dying cells is another important cue. In Subsection 4.5, we attempt several simplifications of the model and compare the predictions. In addition, the model is supported indirectly with other experimental facts (see the following Subsections). The model succeeds in explaining a set of facts not previously incorporated in any mechanistic model comprised of known biological elements. In the end, the question will be answered only once comparison with other models of similar scope is possible.

Staprans et al (Staprans et al., 1999), who also sampled viremia in primary SIVmac251 infection frequently, used cross-verified QC-PCR and bDNA assays. They also observed a second viremia peak in some animals [Fig. 2 in Ref. (Staprans et al., 1999)]. The first and second peaks were observed somewhat later than in (Kuroda et al., 1999), around day 11 instead of days 9–10, and on days 18–21 instead of days 15–16. The relative magnitude of the second peak varied significantly between animals. The sampling frequency in other experiments on primary SIV infection in the literature is not as high, so we cannot draw any conclusions. As these experiments are very important for understanding the mechanism of CTL differentiation, they are worth verification with an RNA assay, a high sampling frequency, and concurrent measurements of CTL frequencies and markers of CTL death.

4.2. Acute SIV infection in macaques with broad genetic background

The above experiment considered MAMU*A01 animals and the region of a viremia peak. To test whether the model can also explain virus dynamics measured by RNA assay in a broad range of values and its variation among individual animals with a broad genetic background, we now compare its prediction with data on unvaccinated SIVmac251-infected rhesus macaques (Letvin et al., 2006). We found out that variation of five model parameters and the effective infecting dose can account for the differences between individual animals (Table 2). These parameters were identified and adjusted by adjusting the model prediction to data points from early times to late times. The remaining 25 parameters were fixed (Appendix E). We did not use formal fitting or estimate the confidence intervals. Given that the model is under construction, and we compare it to more experiments in each publication, our aim is to keep parameter values in the previously estimated range, by an order of magnitude. Hence, approximate match and approximate estimates of parameters is what is realistic and appropriate at the present stage.

Table 2. Variable parameters for seven unvaccinated animals infected with SIVmac251.

First row: Animal p88 from Ref. (Kuroda et al., 1999). Second to seventh row: Six control animals from vaccination trials (Letvin et al., 2006). Parameters are defined in Figures 2 to 4 and Table 1. Dynamic plots are shown in Figures 5 and 6. In addition to the parameter values shown in the table, we assumed p_A/p_R > 250, H₀ = 8 10⁻⁶ %CD4 for animal p88, and H₀ = 4 10⁻⁶ %CD4 for the six control animals from Ref. (Letvin et al., 2006). Other parameter values are fixed (Table 1).

	V	pR	c–d	P0	IR(0)/Pcut	Ti/SA
Animal ID	107 copies/ml/%CD4	RNA (days %CD4)−1	1/day	10−3 %CD4	cells	days
p88, Ref. (Kuroda et al., 1999)	0.48	1.40	0.96	130	10	36
M-575	0.11	0.65	0.47	200	400	24
M-588	0.17	0.50	0.42	10	800	31
AC-04	1.86	0.55	0.45	17	200	33
AV-7G	0.62	0.60	0.47	12	200	67
44-I	1.00	0.75	0.45	17	200	40
64-I	2.71	0.50	0.47	50	120	33

The level of viremia was measured, on the average, every sixth day, i.e., three times less frequently than by Kuroda et al (Kuroda et al., 1999). The animals included two groups, two animals expressing MAMU-A*01 allele and four MAMU-A*01-negative animals. Data and model prediction for one representative animal from each group (M-575 and AC-04) are shown in Figure 5A, B. Results for the other four animals (M-588, AV-7G, 44-I and 64-I) are shown in Figure 6. We observe that predicted dynamics of the normalized virus load, calculated as the effective virus-producing cell number P_R+xP_A, is rather similar for the two groups of animals. The maximum virus load, proportional to the virus load per virus-producing cell, v, tends to be smaller for MAMU-A*01 animals by an order of magnitude (cf. right Y-axes in Figure 5A and B), in agreement with results of Newberg et al (Newberg et al., 2006).

Sparse data points show neither the presence nor the absence of a double peak of viremia. Model parameters can be adjusted to predict the second viremia maximum between two adjacent data points (Figures 5 and 6). A consistent difference between the two cited works is a slower dynamics of the virus load in the more recent work, for which we predict a lower virus infectivity (higher p_R and p_A) and a higher effective virus dose I(0)/P_cut (at the same census dose) (Table 2). A possible explanation of the difference in infectivity is that, before infection, virus is expanded in culture accumulating mutations and becoming genetically diverse. A few best-fit virus variants from the infecting mixture could dominate kinetics and the effective dose in animals (Dutta et al., 2008). A higher infectivity and a lower effective initial dose for the earlier SIVmac251 isolate (Kuroda et al., 1999) imply a broader fitness distribution of inoculum. Experiments with more frequent sampling and simultaneous measurements of CTL numbers can help to resolve this issue.

4.3. CTL dynamics in ART

In the previous two subsections, we interpreted the CTL dynamics in an acute SIV infection as a switch of the dominant effector cells from indirect to direct effector cells. The opposite switch is predicted after the onset of ART in chronically infected patients, which fact is relevant for another interesting experiment (Ogg et al., 1999). Using the tetramer assay, these authors monitored the frequency of CTLs recognizing two epitopes, p17^Gag 77–85 and Pol 476–484, during the first several weeks ART in HIV infected individuals expressing HLA allele A*0201. The drug cocktail consisting of protease and reverse transcriptase inhibitors depletes viremia below detection level of RNA assay. Samples for six patients with a base level CTL frequency below 0.5% CD8 T cell count were taken, on the average, weekly during the first 4–6 weeks and, in one patient (panel B), daily during the first week. Then, the study continued for 200 days with less frequent sampling. Patients showed reproducible non-monotonic CTL dynamics for both epitopes (Figure 1 in (Ogg et al., 1999), panels A to F), as follows: The CTL frequency dropped 2 to 5 fold from the base level within five to seven days of therapy, increased back within 2 to 6 weeks, decreased more slowly (median lifetime 45 days, Figure 2 in (Ogg et al., 1999)), and saturated at a level, 2 to 7-fold lower than the base level.

The error of tetramer assay is 20–30% or less, as it is shown from comparison with results of a functional assay, intracellular cytokine staining of CD8 T cells stimulated with single-peptide stimulated target cells (Casazza et al., 2001; Goulder et al., 2000; Murali-Krishna et al., 1998). The detection limit of tetramer assay is 0.02% CD8 T cells (Ogg et al., 1998). Further, Ogg et al (Ogg et al., 1999) measured epitope-specific CTLs as percentile of CD8 cells rather than as the absolute number. In fact, in an average patient, the total CD8 cell count in blood increases within ~2 weeks of ART and saturates (Carr et al., 1996; Pakker et al., 1998), so that the absolute CTL number may have slightly different time variation than the CTL frequency. However, the increase is usually less than 50%, much less than the 2 to 5-fold variation observed for the CTL clone size, so that the difference is, indeed, small.

Comparison of the above experiment with analogous experiments in the literature is difficult, because they use either low-accuracy assays (multi-epitope assays, limiting dilution, direct lysis) or low-frequency sampling, or both. For example, Ortiz et al (Ortiz et al., 1999) used the limiting dilution assay to monitor the CTL precursor frequency. This assay is known to have the efficiency of 1–10% and a high noise level (Casazza et al., 2001; Goulder et al., 2000; Murali-Krishna et al., 1998). Gray et al (Gray et al., 1999; Murali-Krishna et al., 1998) used the same two tetramers as Ogg et al (Ogg et al., 1999), but less frequent sampling (2 weeks or more sparse) to monitor the long-term behavior; they did not observe any consistent pattern. Sampling in Casazza et al (Casazza et al., 2001), who used single-peptide intracellular cytokine staining, was even less frequent: once per 5 to 10 weeks, for 600 days. Observed was predominantly monotonic decay. Kalams et al (Kalams et al., 1999a) also considered 600 days of ART in two patients; during first 200 days, they sampled CTLs every 2 to 3 weeks. Direct lysis, limiting dilution, with target cells prepulsed with single peptides or transfected with a vector expressing whole HIV proteins, and tetramer assay we used. CTL dynamics during the first month of ART does not resolve well in plots, although a sharp increase in direct lysis around day 13 is reported in one of two patients. Another patient demonstrated a steady decay of lysis over 200 days. The tetramer assay showed little change over that period.

As with any immunological measurements carried out in peripheral blood, redistribution of lymphocytes between blood and lymphoid tissue may affect these observations.

Our interpretation of the experiment (Ogg et al., 1999) is, as follows. Due to rapid exponential decay of antigen level under ART, direct effector cell population decays with rate d_D. At the same time, helper cells are no longer infected and expand causing expansion of helper-dependent CTLs. When the virus load drops to a very low level, as given by P_HH/P_H0H₀ << 1, so that σ << 1, and helper cells no longer detect antigen, CTLs retire to M_E cells which die out with rate d_M, producing the right slope of the observed CTL peak. Memory cells, M, are left. [As observed by (Kalams et al., 1999a), some memory cells preserve residual cytotoxic activity for several months. Our simple model does not account for this effect.]

4.4. Other relevant experiments and facts

The model does not hinge on two experiments. It can also explain other important findings:

(i) The ability of CTLs to leave memory cells capable of a secondary response (M) requires the presence of helper cells during priming (Janssen et al., 2003; Shedlock and Shen, 2003). The model explains this effect assuming helper-dependent priming of naïve cells into two distinct CTL types and the lack of E_D →M process (Figure 2).

(ii) Immediately after the virus peak, CTLs cannot be reactivated by antigen (Badovinac et al., 2005). This fact is accounted for by effector memory cells, M_E., which are progenitors of effector cells and cannot be reactivated.

(iii) A very important general observation is that almost any virus is cleared, although viruses vary broadly in their replication ability and the intrinsic clearance rate (limited, e.g., by the eclipse phase of virus production).

The CTL peak height correlates positively with the replication rate of a virus. For example, LCMV Armstrong replicates very rapidly expanding by orders of magnitude in three days of infection (De Boer et al., 2001; Lau et al., 1994). Accordingly, the peak CTL frequency greatly exceeds the total CD8 count in uninfected mice (up to 1000%) breaking the brain-blood barrier and killing a half of mice. [For persisting LCMV strains, C13 and Docile, the situation is more complex (Moskophidis et al., 1994; Ou et al., 2001; Wherry et al., 2003a; Zajac et al., 1998). The exponential replication rate is approximately the same as in LCMV Armstrong infection, but the initial replication delay related to the innate interferon response is absent. CTLs are functionally impaired and undergo anergy, which effects are not observed for Armstrong and HIV/SIV. As a result, the peak CTL level is lower than in LCMV Armstrong infection.] Initial expansion of HIV/SIV is much slower, and the maximum CTL frequency is down to (1–20)%. For slowly replicating vaccinia virus, the peak frequency is even smaller. Thus, the maximum level of CTL response is optimized between the level required to deplete a virus and the danger of immunopathology. Any model, which assumes that CTL response keeps expanding until virus is depleted to very low levels, predicts such a behavior. This includes our model (in the absence of helper-cell infection, H_E -> H_I). The direct and indirect parts of CTL response are efficient at high and low antigen concentrations, respectively.

Further, different viruses can have very different maximum clearance rates limited, in particular, by the eclipse phase of effective antigen recognition. To clear a broad range of viruses, CTLs cannot decay in a standard time after virus peak but must wait until a virus falls to extremely low levels. The presence of the helper-dependent component of the response with a very low activation threshold in antigen can explain this observation. For example, for LCMV Armstrong, the average eclipse phase is short, < 8 hours [data in (Lau et al., 1994)], respectively. For HIV, it is much longer: ~1 day for short-lived infected cells, ~14 days for longer-lived infected cells [the first and second phase of decay under ART (Perelson et al., 1997)], and even longer for latently infected cells. In LCMV Armstrong infection, which clears very fast, effector CTLs decay by two orders of magnitude within a week after the steep virus fall (Murali-Krishna et al., 1998). By comparison, in HIV-infected patients undergoing ART (when new infection of helper cells is suppressed by drug), high levels of direct lysis are preserved for 6 months (Kalams et al., 1999a). During most of this period, residual viremia (from latently infected, rarely reactivated cells) is already in the range 1 to 100 RNA/ml, i.e., 5 to 7 logs lower than the peak level.

(iv) HIV persists in infected individuals. To explain persistence, the model includes a virus-specific impairment mechanism of CTL response, infection of helper cells (Wodarz, 2001; Wodarz, 2005; Wodarz and Nowak, 1999b; Wodarz et al., 1998). If infection is not sufficiently effective, the high-virus state is unstable in the long term (Section 3). Another important feature of HIV is relatively long eclipse phase, which slows down virus clearance and gives time for the steady state to be established.

The same impairment mechanism exists for a small group of CD4 T cell-tropic viruses, including LCMV Armstrong. However, because that virus has a very short eclipse phase (~8 hours) and does not establish latent infection in cells, the model predicts full and rapid virus clearance before the system reaches near the steady state (results not shown). Persisting LCMV strains (Docile, C13) have an additional impairment mechanism causing CTL anergy (Ou et al., 2001) not observed for HIV/SIV (Goulder et al., 2000). This factor will be addressed elsewhere.

(v) The existence of more than one steady state in each individual (Section 3).

4.5. Hypothesis of two pathways of CTL differentiation

While effector cell activation by helper cells and on contact with infected cells is well described, there is no direct evidence the two mechanisms are associated with two distinct CTL subsets. This is the only element of our model not borrowed from the literature. It represents a hypothesis. Other assumptions are related either to the choice of well-known elements, which we include in the model, or the order of their interaction. In the absence of direct proof, we used reverse inference, i.e., show that once we make this simple assumption, several important observations discussed in previous Subsections become clear. Now we discuss briefly what happens with the predictions if we try to simplify the model and change this hypothesis. Because our focus is on the CTL model block, below we use only arguments based on the effect of virus on CTLs, but not the opposite effect, as it may depend on details of the virus-permissive cell block.

Model 1: Direct effector cells only. The model represents one differentiation pathway from our model (Figure 3), N → E_D. The division and the death of E_D are regulated by a smeared-threshold function of the virus, β(P/P₀) and 1−β(P/P₀), respectively (legend to Figure 3). A more developed model version includes memory cells, as given by process E_D → M → E_D. De Boer et al (De Boer et al., 2001) used this model only in the context of LCMV Armstrong infection. Application of the model to the experiments we discussed encounters problems, as follows: (i) It predicts a single steady state, which corresponds to the high-virus state in our model. (ii) It predicts that CTL will keep expanding while the virus is above the steady state level. Experiments on acute SIV/HIV/SHIV infection prove otherwise [Figure 5 and (Barouch et al., 2000; Newberg et al., 2006)]. (iii) In ART dynamics (Ogg et al., 1999), the model does not explain the second CTL expansion. Either a monotonous decay (first model version), or decay followed by saturation (second version) are predicted. (iv) More generally, the model predicts that viruses with long eclipse phase d_I⁻¹ will not be cleared from a host. Indeed, the CTL response turns off when the virus is still at a high threshold P₀, so that the virus has time to rebound to the steady state level. Finally, it predicts that formation of memory cells either does not occur at all (first model version) or occurs even if helper cells are absent at priming (second version), in contrast to experiment (Janssen et al., 2003; Shedlock and Shen, 2003). Only combining both versions and adding a helper-dependent fork can resolve this specific problem.

Model 2: The same model, but the CTL expansion and retirement are programmed at the moment of priming (Antia et al., 2005; De Boer et al., 2001). The discrepancies are, as follows. (i) It does not predict a steady state with finite frequency of effector cell (no stable point where CTL expansion is balanced by death). Hence, persistent HIV/SIV infection cannot be described. (ii) Dynamics of ART cannot be described. (iii) The second CTL expansion in acute SIV/HIV infection is not explained (Figure 5c). (iv) General: Because the process of priming detects virus peptides rather than parameters of virus replication, programmed CTL peak will be fairly standard: Either it will always be extremely high or not sufficient to check replication of fast-replicating viruses. Even if replication is stopped, viruses with a long eclipse phase (slowly-clearing viruses) will not be cleared, because CTL response turns off at a predetermined time, regardless of virus level.

Model 3: Helper-dependent CTLs only. The model represents one differentiation pathway from Figure 3, N → E → M → E. A more developed version includes effector memory cells, N → E → M_E → M → E. Control of the expansion and the retirement of effector cells and the reactivation of memory cells are described by a smeared-threshold function, σ[α(P_H/P_H0)H/H₀] (Figure 3 and the legend). Problems with the model: (i) It predicts only the low-virus steady state with a high frequency of helper cells (not detectable in most untreated HIV infected individuals). (ii) It does not predict the observed initial CTL drop after the onset of ART (Ogg et al., 1999). (iii) It does not predict the observed second CTL expansion (Kuroda et al., 1999). (iv) General: It does not explain why primary response in some viruses (e.g. LCMV Armstrong) is helper cell-independent.

Model 4: One type of CTL with two mechanisms of regulation. The model has a single pathway, N → E_comb → M_E →M, where effector cells E_comb are regulated as shown in Figure 3 for E cells, except the control function σ now depends on the combined effect of helper cells and the virus, σ[α(P_H/P_H0)H/H₀+P/P₀]. The model is the closest to the model we used. It predicts bi-stabilty if helper cells can be infected, agrees with CTL dynamics in ART, and predict clearance of various viruses for unimpaired CTL response. Still, it has two important defects: (i) Just as Model 1, it predicts only continuous expansion of CTLs in acute infection. The drop in the CTL number and the drop in their death rate are not explained. (ii) General: It predicts that formation of memory cells does not require the presence of helper cells at priming.

We emphasize that any arguments in favor or against a model based on experiments apply only at a chosen level of model complexity. Generally, simpler is better. For example, everywhere we assumed that effector cells are dividing precursors of memory cells. Some researchers believe it is the other way around, and the issue is still open. Our choice allows for a simplest interpretation of experiment by Kuroda et al (Kuroda et al., 1999). Ganusov et al (Antia et al., 2005; Ganusov, 2007) arrived at the same conclusion by comparing data on CTL dynamics in LCMV Armstrong infection (Murali-Krishna et al., 1998) with predictions of two simple models: N → E → M and N → M → E, where only effector cells and only memory cells are dividing, respectively. Taking into account that the division rate of cells is limited (< 5/day), they showed that the second model disagrees with the data: It does not explain the tall CTL peak. However, one cannot guarantee that the conclusion will hold when the model complexity is raised. For example, one can assume that CTLs keep dividing, for several rounds, already after the change from memory precursor cells to effector cells. Then, the E/M ratio will increase, and the tall CTL peak may be explained. The same consideration applies to our model as well.

5. Discussion

We have thus updated the previous model to incorporate important facts on CTL priming and memory cell formation, the presence of cells with different virus production rates, and account for variation of virus load kinetics among animals with a broad genetic background used as controls in vaccination trials. We also discussed in detail the connection between the CTL model block and important facts of CTL dynamics and tested the robustness of our predictions to the central hypothesis of two CTL subtypes.

Other models that predict multiple steady states have been published. A relatively simple model by Wodarz (Wodarz, 2001) developed from previous models by Wodarz and Nowak (Wodarz and Nowak, 1999a; Wodarz and Nowak, 1999b; Wodarz et al., 1998) also includes both helper-dependent and helper-independent CTL response and assumes that memory cells are associated only with helper-dependent response. As our model, the cited model predicts two steady states, with high virus and low helper cells, and vice versa, a possible switch between the two states via drug regiment, and non-monotonous CTL kinetics in acute infection and in ART. In addition to similarities, there are differences between the two models in assumptions and, consequently, predictions. In the cited work: (i) All helper cell and CTL expansion rates can be arbitrarily large. Actually, eukaryotic cells cannot divide more than five times a day. This assumption has various implications that disagree with experiment. For example, after the onset of ART when virus is in the high steady state, a peak of CTLs due to increase helper-dependent response is predicted, but immediately after drug starts, not in 2 to 3 weeks as is predicted by our model with threshold dependencies and is observed in experiment (Ogg et al., 1998). (ii) The block of infected and infectable cells is simplified: There is no distinction between virus-specific and non-specific CD4 helper cells. (iii) The opposite order of CTL differentiation, M → E, is assumed, so that memory cells dominate CTLs during the initial expansion in acute infection. As we discussed above, at the simplest level, the assumption creates a number of issues. (iv) The pioneering work (Wodarz, 2001) offers qualitative examples, without direct comparison with data. It is not clear whether parameters considered in these examples would agree with independent estimates.

Adams et al (Adams et al., 2007) proposed a model with direct effector cells. To obtain two stable steady states, the authors assumed that effector cells are replenished from a weak constant source and that large amounts of virus kill effector cells for an unspecified reason. Other models incorporate multiple-epitope responses in the interaction of the virus with the immune system (Althaus and De Boer, 2008; Korthals Altes et al., 2003). Taking into account multiple epitopes involves making assumptions of the degree to which clones compete for target cells, the determinants and rates of immune escape, and other factors of virus evolution. Models where clones compete and a finite number can coexist (Althaus and De Boer, 2008) or where competition is limited (Korthals Altes et al., 2003) lead to very different predictions for the effect on the overall virus load. Escape mutations occur throughout asymptomatic infection. It has been observed that escape mutations often coincide with progression to AIDS (Goulder et al., 1997; Kelleher et al., 2001) and has been conjectured to be a cause of disease progression (Feeney et al., 2004; Phillips et al., 1991). Using analytic methods and computation, we will address models including escape mutants and polyclonality of CTL response elsewhere.

The current model makes many testable predictions. Here is a small sample:

• 1)Virus load decay rate under ART will decrease in the presence of artificial CD8 cell depletion. Explanation: The producing phase in a steady state is limited by CTLs.
• 2)When two different highly efficacious HAART cocktails are compared, with and without integrase inhibitor, the viremia decay rate in the first case is predicted to be larger. Explanation: Suppose virus replication cycle in a cell consists of several time intervals, each distributed among cells according to Poisson formula, one can make a general statement: After an initial shoulder depending on all interval lengths, the exponential decay rate will be determined by the longest interval between the latest point in the virus replication cycle affected by the drug and the point of virion production. Suppose, the time interval between provirus integration and the onset of virus production starts is very short and can be neglected (Sedaghat et al., 2008). Then, in our two-stage model, when two different HAART cocktails are compared, with and without integrase inhibitor, the decay rate in the two cases is given, respectively, by the inverse of the eclipse phase and the virus-producing phase. The first phase is longer. [Unfortunately, existing experiments compare different monoinhibitors, for which the decay rate is affected by low efficacy of the drug (Hazuda et al., 2004; Murray et al., 2007).]
• 3)Gradually increasing the concentration of multi-drug ART in animals chronically infected with SIV will have a double-threshold effect on the average steady state virus load, as follows. Below a certain concentration, after initial decrease, average viremia will return to the high steady-state base level, and above that concentration, in some patients, it will switch to a low steady state. At highest concentrations, ART will clear short-lived infected cells below the threshold necessary to maintain immune response. Explanation: The existence of two steady states. (Note that the number of drugs in a cocktail has to be large (at least three) to prevent drug-resistant mutations influencing the experiment. Under certain parameter value sets, a stable low-virus state is not predicted, and only oscillatory pattern is possible, see above.)
• 4)In an interval of drug concentrations, where low steady state is observed (see previous experiment), viremia will remain stable and low even after ART is interrupted. Explanation: Once a switch to the low-virus state occurs, the steady state remains stable in the absence of drug. Note that, depending on the individual system parameters, this may not be achievable in all hosts, because several critical variables (CTL, virus, helper cells), all at the same time, must be brought into the narrow vicinity of their steady state. (In most patients, modern ART causes suppression of the virus far below the activation threshold of helper cells. In this state, the CTL response is off, and virus levels remain low only because of continued treatment. Upon ART interruption, the return of virus to pre-treatment levels is observed. This is not the predicted low-virus state controlled by CTLs.) Fine tuning of drug regiment and, possibly, the use of other control parameters is required to attain the low-virus state [see an example in (Rouzine et al., 2006)].
• 5)In mice acutely infected with LCMV Armstrong (non-persisting strain), an increase of the initial virus dose will result in a decrease of memory CTL numbers. Explanation: According to our model, the dominant component of effector response are helper-independent effector cells, E_D, dominate the peak CTL numbers in acute LCMV infection (Murali-Krishna et al., 1998) and ensure virus clearance. However, the first, smaller wave of CTL response are helper-dependent cells, E, which are less important for virus clearance but leave long-lived memory cells. An increase of the virus dose results in more extensive infection of helper cells and decreases the maximum value of E (but not E_D) and the number memory cells. Note that the prediction is specific for helper cell-tropic, non-persisting viruses.

We emphasize that we do not claim to offer a “correct” model, whose all assumptions follow directly from data, which includes all factors, explains all experiments, and ends all local debates. Such models do not exist, and such expectations are not realistic. The model is constantly in flux and subject to updates. The approach, fairly standard in physical sciences, is based on the old empiric observation that the simpler the model, given experiments under consideration, and the more experiments it agrees with, given the complexity level, the more plausible it is. Because a model is always under tight logical constrictions, its incorrect elements are easy to identify and fix once new data become available. The extreme case is the case of “total loss” when the entire model has to be replaced. In contrast, when a researcher uses a new simple model for each new experiment and ignores other facts, such models are not falsifiable, and the process does not converge anywhere. Our next step will be to include experiments on vaccination.

Appendix

A. Model notation and equations

The following equations describe the model blocks in Figures 2 to 4. A shaded oval represents a cell compartment characterized by the number of cell in it. A thick arrow represents a flux of cells from one compartment to another or from a source to a compartment, or the cell death. An arrow loop denotes proliferation of cells. A thin arrow from an oval to a thick arrow shows that the cell flux depends on a third, controlling compartment. The functional form of the dependence is shown at the thick arrow. A white oval represents not an independent variable but a linear combination of two or more compartments, as shown by thin arrows pointing to the oval.

We assume exponential rates for all processes (“radioactive isotope decay”) implying no time delay and Poisson distribution for each compartment lifetime. Each flux is assumed to be proportional to the current size of the compartment it is coming from. If we need to introduce a time delay, we include an additional compartment. E.g., compartments I_R and I_A in Figure 4 describe the time delay of virus production in an infected cell. We use the “well-stirred pot” (panmixia) approximation, i.e., neglect local changes of cell concentrations in the lymphoid tissue (Discussion).

The system of equations corresponding to the block of permissive and infected CD4 T cells (Figure 4) has a form

$$\begin{array}{cc}\hfill & dA∕dt=(1-T∕T_{\mathrm{i}})S_{\mathrm{A}}-(d_{\mathrm{A}}+p_{\mathrm{A}}{P}_{\mathrm{V}})A\hfill \\ \hfill & dR∕dt=d_{\mathrm{A}}A-p_{\mathrm{R}}{P}_{\mathrm{V}}R\hfill \\ \hfill & d{I}_{\mathrm{A}}∕dt=p_{\mathrm{A}}{P}_{\mathrm{V}}A-d_{\mathrm{I}}{I}_{\mathrm{A}}\hfill \\ \hfill & d{I}_{\mathrm{R}}∕dt=p_{\mathrm{R}}{P}_{\mathrm{V}}R-d_{\mathrm{I}}{I}_{\mathrm{R}}\hfill \\ \hfill & d{P}_{\mathrm{A}}∕dt=d_{\mathrm{I}}{I}_{\mathrm{A}}-k(E+E_{\mathrm{D}})P_{\mathrm{A}}-d_{\mathrm{P}}{P}_{\mathrm{A}}\hfill \\ \hfill & d{P}_{\mathrm{R}}∕dt=d_{\mathrm{I}}{I}_{\mathrm{R}}-k(E+E_{\mathrm{D}})P_{\mathrm{R}}-d_{\mathrm{P}}{P}_{\mathrm{R}}\hfill \end{array}$$ (1)

Here T = A + R + I_A + I_R + P_A + P_R is the total number of infectable or infected CD4 T cells, P_V = P_R + x P_A is the effective number of virus-producing cells regarding infection of new cells, and x is the ratio of virus productivity for activated versus resting cells.

Antigen-specific helper cells (Figure 2) constitute a small fraction of CD4 T cells and are described by a system of equations, as follows

$$\begin{array}{cc}\hfill & d{H}_{\mathrm{N}}∕dt=d_{\mathrm{N}}{H}_{\mathrm{Ni}}-[a_{\mathrm{N}}{P}_{\mathrm{V}}+d_{\mathrm{N}}]H_{\mathrm{N}}\hfill \\ \hfill & d{H}_{\mathrm{E}}∕dt=a_{\mathrm{N}}{P}_{\mathrm{V}}{H}_{\mathrm{N}}+[\alpha c_{\mathrm{H}}(1-H∕100)-(1-\alpha )d_{\mathrm{H}}-\alpha p_{\mathrm{A}}{P}_{\mathrm{V}}]H_{\mathrm{E}}\hfill \\ \hfill & d{H}_{\mathrm{I}}∕dt=\alpha p_{\mathrm{A}}{P}_{\mathrm{V}}{H}_{\mathrm{E}}-d_{\mathrm{I}}{H}_{\mathrm{I}}\hfill \\ \hfill & d{H}_{\mathrm{P}}∕dt=d_{\mathrm{I}}{H}_{\mathrm{I}}-k(E+E_{\mathrm{D}})H_{\mathrm{P}}\hfill \end{array}$$ (2)

Here H = H_E + H_I + H_P is the total number of primed helper cells, regardless of their infection status. Control switch α is the fraction of helper cells detecting virus, α = 1−exp(−P_H P_H0), where P_H = P_R + x³P_A is the effective number of virus-producing cells with respect to the antigen activation of helper cells.

Equations for antigen-specific CD8 T cells (CTLs) are

$$\begin{array}{cc}\hfill & dN∕dt=d_{\mathrm{N}}{N}_{\mathrm{i}}-\{d_{\mathrm{N}}+[\sigma +q(1-\sigma )]a_{\mathrm{N}}{P}_{\mathrm{V}}\}N\hfill \\ \hfill & d{E}_{\mathrm{D}}∕dt=q(1-\sigma )a_{\mathrm{N}}{P}_{\mathrm{V}}N+(1-\sigma )\beta c_{\mathrm{D}}M+[\beta c_{\mathrm{D}}-(1-\beta )d_{\mathrm{D}}]E_{\mathrm{D}}\hfill \\ \hfill & dE∕dt=\sigma a_{\mathrm{N}}{P}_{\mathrm{V}}N+\sigma \beta c_{\mathrm{D}}M+[\sigma (1-E∕E_{\mathrm{m}})(c-d)-(1-\sigma )r]E\hfill \\ \hfill & d{M}_{\mathrm{E}}∕dt=(1-\sigma )rE-d_{\mathrm{M}}{M}_{\mathrm{E}}\hfill \\ \hfill & dM∕dt=f{d}_{\mathrm{M}}{M}_{\mathrm{E}}-\beta c_{\mathrm{D}}M\hfill \end{array}$$ (3)

Here β is the fraction of direct effector cells in contact with virus-producing cells, given by β = 1−exp(−P/P₀), where P = P_R + P_A is the total number of virus-producing cells. Control function σ = 1−exp(−αH/H₀) is the fraction of indirect effector CTLs receiving a cytokine signal from helper cells.

In Equations 1 to 3, we use upper-case letters to denote compartment sizes (measured as percentile of the total CD4 or CD8 count in an average uninfected animal or human). Among them are 15 dynamic variables, whose derivatives are given by the left-hand sides of the equations. Parameters T_i, N_i and H_Ni are constant homeostatic counts of CD4 T cells, virus-specific CD8 T cells, and virus-specific CD4 T cells. We use them as initial sizes of compartments R, N, and H_N in an acute infection. Parameters H₀, P_H0, and P₀ are the characteristic numbers of helper cells and virus-producing cells in control functions σ, α, and β, respectively. The lower-case letters in Equations 1 to 3 denote constant model parameters (Figures 2 to 4 and Table 1). The terms 1−H/100 (Equations 2) and 1−E/E_m (Equations 3) introduce maximum limits for helper cells and CTLs.

B. Control functions

Control functions α, β, and σ determine the ability of different effector cell types to react to antigen or cytokines. These quantities express the probability of an effector cell receiving a signal, for three types of effector cells: Helper cells (H_E), helper-independent CTLs (E_D), and helper-dependent CTLs (E), respectively. The type and the source of a signal depends on a cell type: E_D cells recognize infected cells on contact; H_E cells recognize soluble virus peptides secreted by infected cells and presented by APCs in MHC-II context; E cells recognize cytokines secreted by H_E cells. When receiving a signal, a cell proliferates; a helper cell also secretes cytokines controlling CTL proliferation. We assume that effector CTLs can kill infected cells regardless of receiving a cytokine signal. It is also assumed that all cell types are uniformly distributed and that concentration of virus follows the concentration of virus-producing cells with proportionality factor v.

In all three cases, reception of a signal requires an effector cell being located within a critical radius of a source cell where the signal intensity exceeds a threshold level. The critical radius depends on the type of an effector cell. According to Poisson distribution, the probability of having at least one source cell within the critical radius around an effector cell, α, β, or σ, is given by 1−exp(−m), where m =nV* is the average number of source cells within the radius, V* is the critical sphere volume, and n is the source cell concentration.

For direct effectors requiring contact with infected cells, the source cell density n is given by n = (n_CD4/100) (P_R+P_A), where n_CD4 is the volume concentration of CD4 T cells in uninfected host, and P_A and P_R are measured as % of total CD4 T cell population. Critical volume V* is on the order of r_cell³, where r_cell is the cell radius. Hence, β = 1−exp[−P_R+P_A)/P₀], where P₀ ~ 100/(n_CD4r_cell³). A more accurate value of P₀ is determined from the steady-state virus load. Essentially, this control function implies that the expansion rate of direct effector cells saturates when the frequency of virus-producing cells is so high that every effector cell is in contact with an infected cell. Another version of the same biological argument based on a quasi-steady state between single E cells and P cells and E-P complexes (De Boer, 2007) leads to another form, β = 1/[1+(P_R+P_A)/P₀]. We did not find any essential differences between predictions of the two forms of the control function, and chose the exponential form only for the sake of similarity with the other two control functions. The saturation is also expected, when the frequency of effector cells, E_D+E, is very high. In the cited model, this effect is described, in our notation, as β = 1/[1+(E_D+E+P_R+P_A)/P₀]. In our work, which is not focused on this specific issue, we simply limit the maximum number of effector cells to 100%.

For helper cells, the critical radius is larger than r_cell due to diffusion of soluble antigen from an infected cell. It is assumed that soluble antigen diffuses from the cell much faster than APC with bound antigen, and thus we neglect the diffusion of APC. The critical volume V* is found considering uniform steady state diffusion from an infected cell (either resting or active), as follows. Local antigen concentration C(r) at distance r from an activated infected cell (P_A) is given by C(r) = c₀v/r, where v reflects proportionality to virus production per cell (for an active infected cell, v is replaced with xv), and fixed constant c₀ depends on the details of virion dynamics, cell geometry, and antigen presentation on cell surface. The critical radius r* is found from condition C(r*)=C*, where C* is the threshold antigen concentration. Hence, the critical volume around an infected cell is given by V_PA* = (4/3)π (c_oxv /C*)³ and V_PR* = (4/3)π (c_oxv /C*)³, respectively. Thus, for helper cells, we have m = (n_CD4/100)[P_AV_PA* + P_RV_PR*] = (x³P_A + P_R)/P_HO, where v³P_HO ~ (100/n_CD4)(c₀ /C*)⁻³, and α = 1−exp[−(x³P_A + P_R)/P_HO]. If APCs travel across tissue faster than soluble antigen, the same result will follow, but with a different constant c₀. Parameter v³P_H0 is determined from matching data approximately. The soft-threshold control of helper cells by antigen is likely to be more general than the simple antigen-diffusion we assumed above. Factor x³, however, is more model-dependent.

Derivation for indirect effector cells is similar, except instead of diffusion of antigen we have diffusion of cytokines, and source cells are now effector helper cells (infected and uninfected) that detect antigen. The source cell concentration is given by αH = α(H_E+H_I+H_P), which yields control function σ = 1−exp(−αH/H₀), where H₀ is determined from matching data.

C. Latently infected cells

When the total number of infected cells is less than one, as given by I_R+I_A+P_R+P_A < P_cut, infected cells are completely cleared. Estimating the total CD4 count at 10¹¹ cells per 7 kg animal, we set the lower cutoff for cell number, P_cut, at 10⁻⁹ %. To simulate small virus bursts from latently infected cells, at random times, we add a quantity CP_cut to I_R+I_A, where C ~ 1. The relative increase in I_R and I_A is determined by ratio p_RR/(p_AA). The average frequency of pulses is an external parameter (not shown in Table 1). In reality, many activation events may not produce enough virus to start an expansion. Our random-pulse procedure includes only successful virus bursts. We checked that changing the cutoff value, P_cut, or the pulse magnitude by a factor of 10 does not affect predictions for any experiment we considered. The average time between pulses is also not important, as long as it is shorter than the period of oscillations around the low-virus steady state (a few weeks) and longer than one day (for our parameter sets).

D. Simulated experiments

Our model can simulate a broad range of dynamic experiments by changing the initial values of some dynamic variables and introducing small modifications into Equations 1 to 3. For example, in the experiment on a primary acute infection, all compartment sizes are set at zero, with the exception of the initial virus dose, vP_V(0), which we used as a variable parameter to match data, resting CD4 T cells, R(0) = T_i, and naïve virus-specific cells, N(0) = N_i and H_N(0) = H_Ni. For vaccinated animals, we assumed two non-empty initial compartments, M(0) and H_E(0). To simulate a steady state, we simply run the simulation until the steady state was achieved with a high accuracy. To model antiretroviral therapy (ART), we can multiply the efficiency of cell infection (parameters p_A and p_R) by a factor of 1 – ε, where ε is the drug efficacy. To simulate a transient depletion of a cell type (e.g., CD8 T cells) with artificially introduced antibodies during a time interval, we can add to the right-hand sides of respective equations negative linear terms, such as −d_AbN, −d_AbE, …. The additional death rate d_Ab describes the effect of antibodies; d_Ab ~ 0.1/day (Jin et al., 1999). Also, we can describe a CTL vaccine vector administered already after infection by adding the appropriate terms to P and P_H. Finally, the model can be generalized to include immune response against several CTL and helper cells epitopes.

E. Parameter estimates

We solved Equations 1 to 3 numerically, using standard program ODE15S in MATLAB, for a set of initial compartment sizes, as described above. Altogether, we have 30 model parameters (Table 1). The complexity and scope of the model necessitates a large number of parameters, the origins of which vary. Parameters are divided into (I) those that are found in literature and (II) those that we estimated by matching data (approximately). These categories are then further subdivided into (a) parameters for which an accurate estimate is important and (b) those for which an order of magnitude estimate suffices.

Group I(a): (d_I, x, vu, T_i)

d_I: We identify the eclipse phase of virus replication cycle (before an infected cell becomes an effective target for CTLs) with the inverse decay rate of viremia in ART, 1/d_I = 1.0 day for humans and 0.7 day for simians (Brandin et al., 2006; Markowitz et al., 2003). We assume that the virus-producing phase is shorter (see parameter kE below) and contributes only to the initial shoulder of the decay. Note that

x: Virus RNA content was found to higher in activated cells (Ki67+) than in resting (Ki67−) cells by a factor of five (Zhang et al., 1999).

vu: The conversion factor between SIV p27 (gag protein) capture assay (Kuroda et al., 1999) and branched DNA amplification assay (Letvin et al., 2006), vu, is found by calculating the content of p27 in each virion containing 2 RNA copies and assumes the assays are equally efficient. Each virion contains ~1,400 gag proteins (Zhu et al., 2003) yielding a total 3·10⁷ RNA/p27 ng. In practice it is safer to average the virus maximum over the animals in the two assays separately from which a lower value is obtained, 6·10⁶ RNA/p27 ng.

T_i: Measurements of CD4 cells in GALT tissue show that approximately T_i = 7% of CD4 T cells are infected at the peak of virus load (Li et al., 2005). More recent reports show a higher percentage in humans (Bucy et al., 1999), which has the effect of raising the value of total infected cells at the peak of infection, and will therefore change the values of three parameters v, p_R, and p_A (below).

Group I(b): (N_i, H_Ni, d_N, d_H, E_M, P_cut, d_P)

N_i, HNi: Experiments in LCMV infected mice (Murali-Krishna et al., 1998) give an upper bound of 10³ naive CD8 T cells per spleen or N_i < 3·10⁻³ %CD8 count, given total ~3·10⁷ CD8 T cells per mouse spleen. We assume the same for CD4 T cells. A low bound can be obtained by a model developed by De Boer et al. to describe the CD4 and CD8 T cell responses during acute LCMV infection (De Boer et al., 2003; Homann et al., 2001). By back extrapolation they obtain initial values for each cell population N_i ~ H_Ni ~ 30 cell/spleen, or, 10⁻⁴ % CD8 or CD4count. Our model contains an activation delay, which necessitates a higher initial level of cells, thus we take this as a lower bound. We consider H_Ni and N_i in the range (0.1–3)10⁻³ % and fix the values at 10⁻³ %.

d_N: Zhang et al (Zhang et al., 1999) measured the exponential rate of regeneration of naïve T cells in HIV infected patients undergoing ART to be ~10⁻³ /day.

c_H, d_H: Based on data from (De Boer et al., 2003; Homann et al., 2001), De Boer et al (De Boer et al., 2003) model epitope specific CD4+ T cell responses to acute LCMV infection. Data show expansion followed with biphasic decline after antigen is cleared. Based on this work, we assume the expansion rate c_H in range (1.07–1.59) /day and combine the two decay phases into one phase, with the overall rate d_H in range (0.12 – 0.82) /day. For matching data from (Letvin et al., 2006), we take values slightly outside these ranges, c_H = 1.7 /day and d_H = 0.07 /day.

c_D, d_D: The same work interpolates epitope specific CD8+ T cell responses to acute LCMV infection with monophasic decline, c_D = (0.98 – 2.21)/day and d_D = (0.34–0.47)/day. We choose c_D = 1/day, d_D = 0.4/day for best match of data on various individuals.

E_m: This limits the expansion of the effector population to 100% of uninfected CD8 T cell level, and influences the dynamics in vaccinated individuals where the model predicts that this level is otherwise exceeded.

P_cut: This determines the sizes of the T cell populations. From extrapolation of mouse data based on relative size we determine ~10¹¹ of both CD4 T and CD8 T cells in monkeys. P_cut ~ 10⁻¹¹ determines when there is ~1 virus-producing cell left in the body.

d_P: Results for specific CD4 + cell lines such as Jurkat and CEM 5.25 estimate the death of infected cells due to necrosis and apoptosis (Bolton et al., 2002; Lenardo et al., 2002) d_P = 0.1 – 0.5 /day. We assume that rates for PBMC are in the same range we take d_P= 0.25/day.

Group II(a): (a_N, c, d, d_M, p_R, v, P_o, s_A)

a_N: The efficiency of naïve cell activation by virus influences primarily the timing of the effectors and hence the second virus peak (e.g. if a_N is reduced, effectors are delayed, allowing an earlier resurgence in virus). The value of a_N ~ (3·10^−3.v) is optimal for all previous and current animals

c – d: The expansion date of indirect CTLs can be inferred from the experiments of Kuroda et al. in acute SIV infection (Kuroda et al., 1999). The initial high death rate of CTLs necessitates large death rate, d. We assume for c the maximum division rate for eukaryotic cells, 3.5/d (5 divisions per day), which gives the largest value for d given expansion rate c–d.

d_M: The rate of retirement of effector memory CTL can also be inferred from the experiments of Kuroda et al (Kuroda et al., 1999). The CTL contraction rate after the peak is associated with a much lower death rate than that during the first expansion, and we take d_M a bit less than 1/day based on animal p88 from the cited work.

p_R: The efficiency of resting cell infection is determined to match the initial virus slope.

v: v determines the virus load per productive resting cell. This scales the height of the virus peak in RNA/ml and affects the turning-off point of the first virus peak through parameter P_HO.

P₀: The characteristic antigen threshold for the direct effector CTL response is determined from the effector level in the high steady state for individual animals: P_high = P₀d_D/(c_D + d_D), Given P_high in range (10⁻³ – 10⁻²)% CD4 (Kalams et al., 1999b), in can be estimated P₀ ~ (10⁻² – 10⁻¹)% CD4.

s_A: The intensity of the source of infectable cells, s_A, is known from the literature within a range and also can be determined from matching data. Studies of lymphocyte turnover in SIV infected macaques (Mohri et al., 1998) estimate the turnover time of resting cells, T_i/s_A, to be 30–40 days (cf. Table 2 except for two animals). In our model, the value of s_A is determined from matching individual dynamics of acute infection: It regulates the second peak of virus load; the results fall within the cited range (Table 2).

Group II(b): (d_A, k, P_HO, q, r, f, H₀, p_A)

d_A: The definition of “activated cell” and hence the estimates of its lifetime are controversial. In some works, it is defined based on surface markers, such as Ki67 (Haase et al., 1996). In the others, it is based on multi-phase dynamics of uninfected CD4 T cells measured by BrdU and deuterated glucose labeling and varies broadly between models (De Boer et al., 2006; Ribeiro et al., 2002). In contrast to these definitions, we define “activated cell” as the most infectable phase of cell cycle (probably, slightly ahead of S-phase when concentrations of nucleotides are maximum). Hence, the length of that phase is certainly shorter than 1 day. We choose it at the upper estimate, 1 day. As we discuss in the main text, Section 3.1, the lack of oscillations during virus rebound after brief ART, as well as the lower decay rate of the virus load in monotherapy than in ART also imply d_A ~ 1/day or shorter. In any case, the change in d_A affects mostly the levels of “highly infectable cells”, for which data are not readily available. Of course, there is continuous spectrum of cell phases with different infectivity, so that segregation into two types of cells, “resting” (low-infectable) and “activated” (highly-infectable) is an approximation.

k: In a high-virus steady state, the average lifetime of a virus-producing cell is given by 1/(kE_D,high) = P_high/s_A = (30–60 day)(P_high/T_i), where P_high/T_i is approximately equal to the ratio of virus-producing cells in the steady state and the viremia peak, P_A,high/P_R,max • V_high/(xV_max). On the average, for the eight monkeys considered here (Figure 5 and 6), we obtain 1/(kE_D,high) ~ 0.1 day. Then, the range of parameter k can be determined from the range of CTL number for SIV251 infected rhesus macaques, E_Dhigh = (1 – 20)%CD8 (Kuroda et al., 1999; Letvin et al., 2006; Newberg et al., 2006), which yields k ~ (0.5–10) /(%CD8 cell·day). In our simulation examples we fix k at 1/(%CD8 cell·day), which corresponds to E_Dhigh = 10%CD8, characteristic for MAMU*A01+ animals (Kuroda et al., 1999; Letvin et al., 2006; Newberg et al., 2006). Recently, Ganusov and De Boer (Ganusov and De Boer, 2008) estimated the lifetime of infected cells in spleen of C57BL/6 mice infected with LCMV Armstrong from data on adaptive transfer of epitope-prepulsed splenocytes. At the CTL peak, these authors obtained 1/(kE) = 3 min for the dominant epitope with E = 30%CD8 (Murali-Krishna et al., 1998) and 23 minutes for the subdominant epitope with E=7% (Murali-Krishna et al., 1998), which implies k • 10/(%CD8 cell·day). Thus, the killing efficiency inferred for LCMV is at the upper border of the range inferred for SIV.

Based on a deterministic single-site model and the measured rate of antigenic escape from CTL response, Asquith et al and Regoes et al (Asquith et al., 2006; Regoes et al., 2007) estimated that contribution of CTLs to the cell death is small as compared to the average lifetime of infected cells, as given by kE_D << 1/day. We believe that the conclusion may be an artifact of the single-site model neglecting physical linkage between many adapting sites. As it is well known, in finite populations of any realistic size, unless recombination is very strong, physical linkage can slow down adaptation rate by orders of magnitude [see (Rouzine et al., 2003; Rouzine and Coffin, 2005; Rouzine et al., 2008) and references therein].

P_H0: The threshold for expansion of helper cells is estimated from the low-virus steady state condition for virus, based on vaccinated monkeys infected with SHIV, < 10³ RNA/ml (Barouch et al., 2000) and human long term non-progressors, <10¹−10² RNA/ml.

q: The priming asymmetry, q, is necessary to explain the late emergence of direct effectors in SIV infection. Optimal timing of effectors is predicted for q ~ 10^{−2 −10}−4.

r: The helper-dependent (indirect) effector retirement rate is inferred from data (Kuroda et al., 1999). showing fast change in CTL phenotype at the CTL number peak. Assuming r ⪢1 is necessary to obtain an early peak in virus; we arbitrarily take r = 6.

f: In an LCMV Armstrong infection, it is estimated that (5 – 10)% of effectors become long-lived central memory cells (Kaech et al., 2002). This parameter affects the timing of the second virus peak

H₀: The threshold in helper cells for activation of helper-dependent CTLs determines the timing of helper cell expansion. Since helper cell dynamics is not separately measured in our data, we assume H₀ > 10⁻⁶ % CD4 cells in order for the high-virus state to be stable, and H₀ < 10⁻² to avoid delays in helper-dependent CTL response. Our specific choice H₀ ~ 10⁻⁵ is arbitrary.

p_A: That the probability of infecting a “resting” cell is much less than that of an activated cell is well established (p_A ⪢ p_R). The specific ratio p_A/p_R has not been measured; in our simulation, it affects only the steady-state level of highly-infectable cells; we assume p_A > 250 p_R to provide a broad stability of the high-virus state and obtain realistic values of the initial memory cell numbers required for a vaccinated animal to be in the low-virus state, M(0) ~ (0.1 – 1)% CD8.

As compared to the previous model (Rouzine et al., 2006), we introduced eight new parameters (d_P, x, v, a_N, c_H, q, P₀, c), and removed two parameters (the activation efficiency of direct effector cells, a, and the rate of the activation-induced death of helper cells, d_H). Although the total parameter count increased by six, only one new parameter, v, was variable. We also introduced a more consistent notation for three variables (E_T, V, and H_A are now denoted M_E, P_V = P_R+xP_A, and H_E, respectively) and five constant parameters (V₀, p, R_i, m, m_H are now denoted P_H0, p_A, T_i, d_M, d_H, respectively).

Parameter variation between individual animals

We found out that variation of five model parameters (p_R, s_A, v, P₀, c) and the effective infecting dose I_R(0)/P_cut, which is not necessarily equal to the census dose cited in the experimental work due to delay of virus replication and genetic variation of virus) can account for the differences between individual animals (Table 2). The remaining 25 parameters were fixed between animals. We manually adjusted the total of six values. Alternatively, we could use an automatic algorithm minimizing an objective function, such as the mean-square deviation (MSD). However, in a high-dimensional parameter space, an automatic procedure would end in one of the numerous secondary minima of MSD. In any case, manual isolation of the lowest minimum of MSD is required and represents the most labor-consuming part of the process based on detailed understanding of the system dynamics. Also, aiming at a high accuracy of parameter values determined from data from different animals is hardly meaningful. The manual procedure is reliable and efficient, because only a small subset of parameters affects dynamics in a specific time interval of an experiment. For example, the initial virus expansion depends only on the initial dose I_R(0)/P_cut and the efficiency of resting cell infection, p_R (at fixed parameters T_i, d_I and d_P). The maximum virus load determines v. The virus load decay signifies arrival of CTL effectors, which time point is sensitive, depending on the effector type, to either c–d or c_D–d_D. The threshold in antigen for direct effector CTLs, P₀, is adjusted to match the high-virus steady state level. The source intensity, s_A, regulates the height of the second maximum of the virus load, and so on.