Abstract
Harnessing electrical bias-induced mechanical motion on the nanometer and molecular scale is a critical step towards understanding the fundamental mechanisms of redox processes and implementation of molecular electromechanical machines. Probing these phenomena in biomolecular systems requires electromechanical measurements be performed in liquid environments. Here we demonstrate the use of band excitation piezoresponse force microscopy for probing electromechanical coupling in amyloid fibrils. The approaches for separating the elastic and electromechanical contributions based on functional fits and multivariate statistical analysis are presented. We demonstrate that in the bulk of the fibril the electromechanical response is dominated by double-layer effects (consistent with shear piezoelectricity of biomolecules), while a number of electromechanically active hot spots possibly related to structural defects are observed.
Keywords: amyloid, electro-mechanical coupling, double layer, PFM, SPM
Introduction
Development of nanoscale systems capable of “acting” on the nanoscale is rapidly emerging as one of the prominent directions in the nanoscience.1–4 While silicon-based electronics is now projected to scale down to sub-10 nm level,5 control of mechanical motion on these length scales presents an unresolved problem. A number of concepts based on optical,6–11 chemical 2, 12, 13 (including biological ATP-fueled motors) and electrical powering 14, 15 are being explored. Among all potential applications, electrically-driven molecular machines are emerging as primary candidates due to the fast operation unlimited by achievable photon densities or diffusion of chemical species. These machines can be considered as a natural evolution of molecular electronic concept to include manipulation and motion. 2, 16–21.
The examples include molecular nanocars 4 and molecular electromechanical machines. At the level of molecular assemblies, these include artificial muscles.2, 3 Despite the universally recognized role of electromechanical coupling in nanoscale systems manifesting themselves in changes of molecular shapes under electric field or during redox processes, the mechanisms of such phenomena until now have been inaccessible to experimental studies. The reason for this dearth of understanding is three fold and stems from (a) the need to establish a good electrical contact to molecule or molecular assembly, (b) the need to detect the resulting displacements and (c) the need for imaging in liquid environment. The latter requirement stems both from natural limitations inherent in unfolding spectroscopy 22 and the desire to mimic the natural functions of biological molecules and to control the performance at the molecular level. Thus, the tools to probe electromechanical activity on the molecular level are desperately needed.
In the last decade, significant progress in understanding of electromechanical coupling on the nanoscale has been achieved with the development of Piezoresponse Force Microscopy (PFM).23 Utilizing the intrinsic coupling between the electromechanical response of material and polarization order parameter, PFM has been broadly used to image domain structures down to ~3–10 nm resolution,24–27 study the mechanisms for domain nucleation and growth,28 and probe the mesoscopic mechanism for wall-defect interactions 29 and defect-mediated nucleation.30, 31 Recently PFM imaging of biological systems in ambient environment, including calcified tissues with ~sub 10 nm resolution has been demonstrated.32 In parallel, PFM imaging 25 and switching 33 of ferroelectrics in liquids has been demonstrated. However, much lower electromechanical response of biological materials (1–3 pm/V, as compared to 10–1000 pm/V for perovskites) combined with (a) much lower sensitivity of PFM in liquid due to viscous damping and added mass effects and (b) limitation on large voltage amplitudes have until now made the electromechanical imaging of biological and biomolecular systems in liquids impossible.
Here we report the measurements of electromechanical coupling in a prototypical biomolecular system – amyloid fibrils. Previously, the mechanical properties of fibrils 34–39 and their internal structure 40, 41 have been studied in order to elucidate the mechanisms of their formation and their role in amyloidosis,42, 43 diabetes,44–46 Alzheimer’s Disease.47, 48 In this work, we studied amyloid fibrils as a preparation step in understanding electromechanical coupling in live biological systems such as bacteria and cells. Specifically, we use the fibrils as a model soft system to study electromechanical coupling in liquid environment. In all studies to date, electromechanical response could not be unambiguously deconvoluted from the electrostatic interactions and contrast variations due to response variations in frequency dispersion of cantilever transfer function (i.e. topographic cross-talk 49). Here we use band excitation PFM (BE-PFM) 50 technique to measure electromechanical response of amyloid fibrils on mica and correlate it with the mechanical properties of the fibrils. We show that the mechanical properties of the fibril and the double layer at the fibril - water interface is responsible for the electromechanical response; however, a number of hot-spots corresponding to regions with enhanced electromechanical activity can be observed.
Electromechanical imaging in ambient and liquid environment
The amyloid fibrils were prepared using standard protocols 34 as described in the Methods section. Electromechanical response was probed using Piezoresponse Force Microscopy (PFM). In single frequency PFM, an oscillatory bias Vtip = V0·sin(ωt) is applied to the probe and electromechanical response is detected as a first harmonic of bias-induced tip displacement.49 As a logical extension of single frequency PFM, band excitation PFM utilizes the electrical excitation performed using broad band excitation signal containing multiple excitation frequencies and the mechanical response measured over the same frequency band as excitation signal.50, 51 Both of these techniques were used in our work for the characterization of the electromechanical coupling in amyloid fibrils.
Single frequency experiments
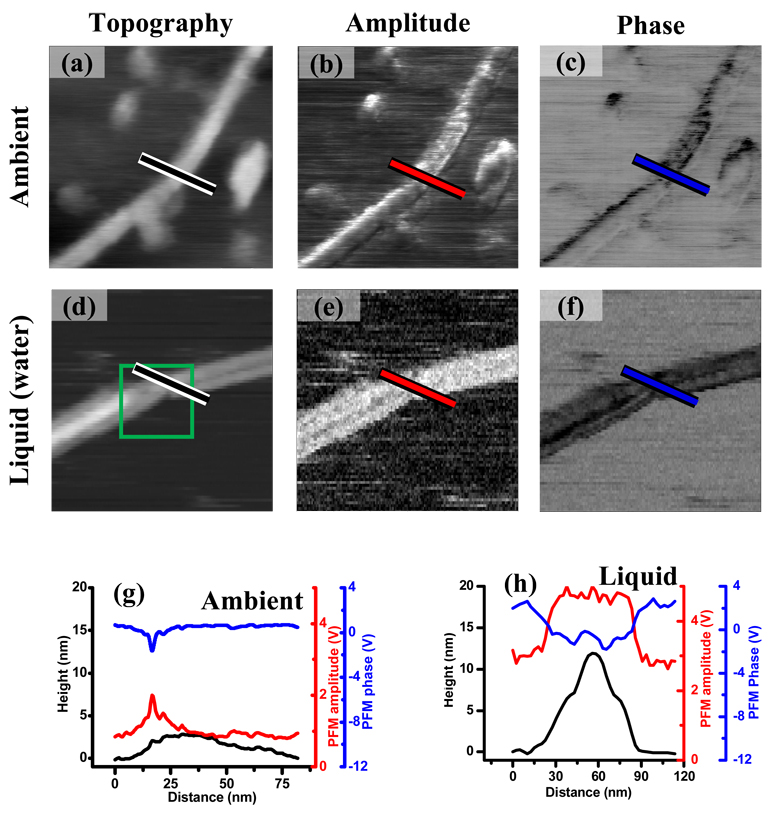
Spatially resolved mechanical response of amyloid fibrils to electrical excitation in air and in water are compared in Fig. 1. The width of the fibrils was found to be approximately the same in air and water, while the height illustrated a profound change from ~12 nm in water to ~ 3 nm in air. There are several possible reasons for this discrepancy, including dehydration of the fibrils in air and mechanical deformation of the fibril due to the larger tip-surface and fibril-surface adhesion forces inevitable for imaging in air. The minimum tip – sample force for imaging in air is ~ 100 nN, because of the capillary forces between the tip and the surface. Imaging in liquid environment allows for better control of the tip – sample force. We used 0.15 nN tip – sample force for our liquid measurements. The difference in indentation force in air and liquid is most likely responsible for the change in height. The indentation depth on amyloid fibrils in air is about 20 nm, while in liquid it is only 0.25 nm (see Table 1), thus, the amyloid fibril should appear several tens of nm lower, when imaged in air comparing to one imaged in liquid. The differences in amplitude and in phase of PFM signal between the fibril and the substrate is clearly visible both in ambient and in liquid environment. In ambient (Fig. 1(a), (b), (c)), amplitude and phase of PFM images show non-uniform contrast. The amplitude is larger on the left side of the fibril compared to the right side, and the phase is smaller on the right side of the fibril. There are at least two possible explanations for this behavior: the electromechanical properties of the fibril are non-uniform (left side has higher electromechanical response) or the error of the microscope’s feedback and surface tracking increases when the tip approaches boundary between substrate and fibril. Experiments in liquid (Fig. 1(f), (g)) do not show such non-uniformity of electromechanical response indicating that left and right sides of the fibrils have similar electromechanical properties. In our experiments the tip approached the fibril from the left side (the scanning was done from left to right) leading to the increase in the microscope’s feedback error on the left side of the fibril. Thus, it is logical to conclude that microscope’s feedback error along with other sources of errors makes a significant contribution to the contrast in Fig. 1(b), (c). In liquid the tip also scanned the area from left to right, and in this case the contrast in the amplitude and phase of PFM is similar on the left and right side of the amyloid fiber indicating that the contribution of the feedback error to the image is rather small. The almost three orders of magnitude decrease in tip indentation force for measurements in liquid compared to ambient measurements is most likely responsible for this difference. PFM amplitude and phase show structural features within the fiber (Fig. 1(f), (g)). Comparison of the images of the fibril’s topography and PFM amplitude and phase (Fig. 1(d), (e), (f)) indicates that changes in electromechanical contrast follow the changes in fibril height. In order to give a proper explanation of the contrast in our electro-mechanical measurements, it is important to remember, that PFM signal in is a convolution of several factors, most notably the electromechanical properties of the sample, electrostatic coupling between tip and the surface, contact mechanics of tip-surface junction and cantilever mechanics.52–54
Fig. 1.
Spatially resolved measurements of electromechanical coupling between tip and amyloidon-mica using single frequency PFM technique. Topography of the amyloid-on-mica sample measured by atomic force microscopy in air (a) and in water (d). Amplitude (b), (e) and phase (c), (f) of the mechanical signal excited by the AC electrical voltage applied to the tip measured in air (b), (c) and water (e), (f). All image sizes are 300 nm × 300 nm. Line profiles of the topography, amplitude and phase images, as marked in air (g) and in water (h). The green box shows the area where broadband electromechanical response presented on Fig. 2 (b–d) was measured.
Table 1.
Mechanical and electrical properties of the fibril and mica,59 estimated parameters of the contact of tip with the surface.
| Air (Findentation = 100 nN) |
Water (Findentati on = 0.15 nN) |
|||
|---|---|---|---|---|
| Amyloid | Mica | Amyloid | Mica | |
| Young’s modulus | 160 MPa | 150 GPa | 160 MPa | 150 GPa |
| Indentation depth (Hertzian model) | 19 nm | 0.20 nm | 0.25 nm | 0.0026 nm |
| Contact radius (Hertzian model) | 28 nm | 2.8 nm | 3.2 nm | 0.32 nm |
| Contact stiffness (Hertzian model) | 9 N/m | 840 N/m | 1.0 N/m | 96 N/m |
| Dielectric function | ~2 | 7 | ~2 | 7 |
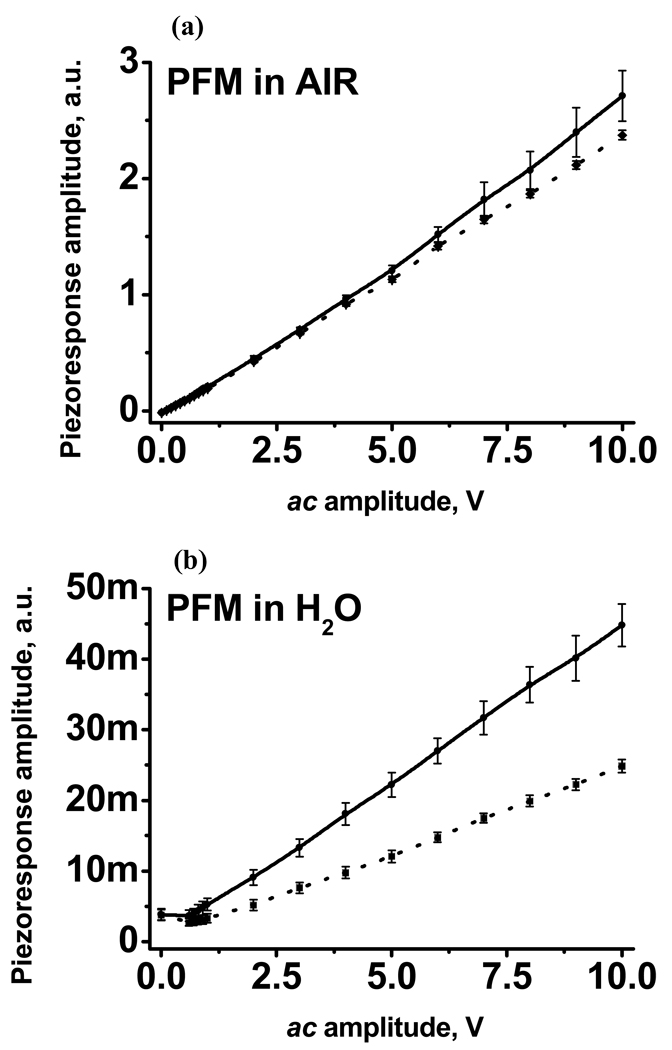
The dependence of single frequency piezoresponse as a function of the ac amplitude of tip voltage is shown for the mica and amyloid fiber measured in air (Fig. 2(a)) and in liquid (Fig. 2(b)). There are two mechanisms resulting in the linear dependence of the piezoresponse as a function of the ac amplitude of tip voltage, such as electro-mechanical properties of the sample or electrostatic coupling between tip and the surface.55 In liquid electrostatic coupling should be screened at the distances larger than Debye length (~ 10 nm in water with pH 7 if no electrolytes are present), the fact that similar behavior of piezoresponse observed in liquid as well as in air suggests that the main part of the piezoresponse signal should come from the electro-mechanical properties of the sample.
Fig. 2.
The strength of the single frequency PFM response as a function of the amplitude of tip voltage in air (a) and in liquid (b). Solid lines correspond to the PFM amplitudes on mica and dotted one correspond to amyloid fiber.
In our experiments we measure the mechanical response of the tip coupled to the surface, which has large frequency dispersion with several apparent resonance frequencies, quality factors for these frequencies, etc. Mechanical resonances of the tip – surface system are determined by electromechanical properties of the sample (amyloid), tip – surface contact properties and tip properties. All the factors listed above contribute to the PFM signal and single frequency measurements do not provide enough information to determine the main factor responsible for PFM contrast. To establish the origins of the contrast in an amyloid fibril – the variation of elastic properties of electromechanical response – we have used the band excitation PFM as described below. Band excitation PFM allows us to probe frequency dependence of the electromechanical response and, thus, to characterize the tip – surface contact resonance in much greater detail than single frequency measurements.
Band excitation PFM as a method for elimination of topographical cross-talk in electromechanical coupling measurements
The main source of the ambiguity in electromechanical measurements is the change in elastic properties between the fibril and mica, which results in the variation of tip-surface spring constant and hence in the effective resonant frequency. For single frequency electromechanical measurements the amplitude of the response is a convolution of the electromechanical coupling signal and the error signal from the shift of the contact resonance spectrum. In order to deconvolute an electromechanical signal from a signal arising from the changes in contact resonance parameters the whole frequency spectrum needs to be collected instead of a single frequency point.
Mechanical response of the amyloid-on-mica sample in a frequency range around tip – surface contact resonance (50 – 280 kHz) was collected using the band-excitation method. The mechanical resonance was excited by a broad band (50 – 280 kHz) electrical signal of constant amplitude of 10V (Materials and Methods). Fig. 3(a) shows the electromechanical response of amyloid fibrils on mica. This response has a complicated structure with several resonance peaks that can be analyzed using statistical methods56 or functional fit.
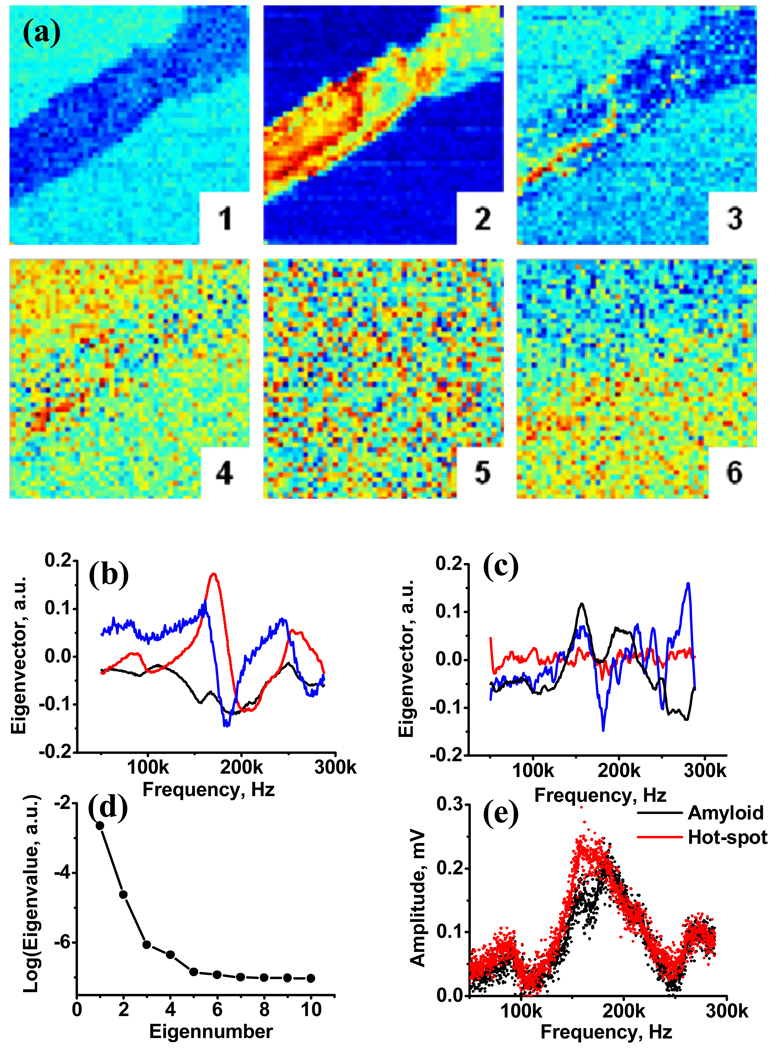
Fig. 3.
(a) Maps showing the spatial variations in magnitude of PCA components 1 through 9. (b) Eigenvectors for PCA components 1 (black), 2 (red), 3 (blue). (c) Eigenvectors for PCA components 4 (black), 5 (red), 6 (blue); (d) logarithm of the first 10 eigenvalues; (e) Amplitude spectra extracted from 5 “hot-spots” (red dots, solid red line is average response) and 5 points adjacent to them (black dots, solid black line is average response).
Multivariate statistical analysis of BE data
The band excitation method allows collecting full amplitude- and phase-frequency response spectra at each point of the sample surface. As is usual for imaging in liquids, the response in the 50–300 kHz range contains multiple response peaks related to both intrinsic materials responses and non-idealities in the cantilever and holder transfer functions. To avoid the uncertainty in data interpretation and establish the veracity of the fitting procedure, we analyze spectroscopic BE data using principal component analysis (PCA).56,57,58 The spectroscopic image of N×M pixels formed by spectra containing P points is represented as a superposition of the eigenvectors wj,
| (1) |
where aik ≡ ak(x,y) are position-dependent expansion coefficients, PRi(tj) ≡ PR(x,y,ωj) is the image at a selected time, and ωj are the discrete frequencies at which response is measured. The eigenvectors wk(ω) and the corresponding eigenvalues λk are found from the covariance matrix, C = AAT, where A is the matrix of all experimental data points Aij = PRi(ωj), i.e., the rows of A correspond to individual grid points (i = 1,.., N · M), and the columns correspond to frequency points, j = 1,.., P. The eigenvectors wk (wj) are orthogonal and are chosen such that the corresponding eigenvalues are placed in descending order,λ1 > λ2 >…..
The spatial maps of the first six PCA components (loading maps) of the piezoresponse data arrays and the corresponding eigenvectors and eigenvalues are shown in Fig. 3(a). Notably, the first 3 loading maps show pronounced spatial structure with the varying level of details. The PCA 1 map shows strong variation of contrast between the fibril and the surrounding mica, but very small contrast within the fibril. The PCA 2 map shows both strong variation of contrast between fibril and mica, and significant and clearly visible features within the fibril. Finally, the PCA 3 map shows a number of visible “hot spots” within the fibril, but only limited contrast between fibril and mica. These spots are also visible in the PCA 4 map. In comparison, the PCA 5 map is essentially structureless, and PCA 6 map shows the slope drift from the top left to bottom right corner of the image. The shape of λk (k) dependence (Fig. 3(d)) indicates that the first 3 PCA components contain the ~90% of significant information within the 3D spectral image, whereas remaining P − 5 components are dominated by noise. Based on the behavior of the Fig. 3(b), 3(c) plots and spatial correlations in the loading maps, the PCA maps 1–4 and 6 contain the significant information within the image.
Note that the PCA analysis is a purely statistical method and does not employ any assumption regarding the underlying physical behavior, ensuring its fidelity. However, in many cases the approximate interpretation of the data can be achieved based on the shape of corresponding eigenvector, wi(ωj), and simple physical model.56 The first eigenvector represents the gross difference in the electromechanical response amplitude between fibril and mica (note the similarity between the eigenvector and the overall response). The second and third eigenvector are reminiscent of the derivatives of the first one, and can be identified with the resonance frequency shift, i.e. variation of stiffness within the fibril. The 5th eigenvector is essentially noise-like, as expected. Finally, the 6th eigenvector represents the creep of resonance frequency (e.g. due to the changes in hydrodynamic damping induced by the changes in tip-surface separation).
The PCA analysis allows establishing the presence of the pints with anomalous response (“hot spots” in PCA 3 and 4 maps). The corresponding amplitude-frequency curves averaged over these locations are shown in Fig. 3(e), demonstrating the significant increase of electromechanical response amplitude in these regions.
Functional fitting
To quantify the BE data, we use a damped harmonic oscillator (DHO) model, which provides a reasonable fit for each of the resonance peaks as well as a clear physical meaning of all parameters calculated from the spectra; we also performed principle component analysis of the experimental data (for the protocol see ref. 56) and found that the system has three linearly independent variables similar to the number of variables DHO has. The DHO model (Eq. (3)) describes the movement of an object with mass m at the end of a system of a spring and a damper connected in parallel as a function of time after the object was displaced from the equilibrium position:
| (3) |
where m is the mass of the object, x is the displacement of the mass, t is time, ω0 is the angular resonance frequency is the damping ratio (ξ = c/2mω0), k is stiffness of the spring, and c is mechanical losses in the system (damping coefficient). In band excitation PFM the driving electrical band of frequencies is chosen to be around the mechanical resonance of the tip – surface system. Thus, the amplitude and phase spectra as a function of frequency provide characteristic parameters, such as resonance amplitude, resonance frequency and quality factor of the tip – surface resonance. Such an experimental set-up and analysis technique allows us to measure parameters of the electromechanical coupling between the tip and the sample. Note that the DHO model has 3 independent parameters, which is close to the estimated by the PCA analysis (strong variability in PCA 1–3 maps, except for “hot spot” regions).
The resonance frequency of the tip – sample contact is proportional to the contact stiffness, which in turn is related to the Young’s modulus and the contact area (Eq. 4)
| (4) |
where k2 is the contact stiffness, a is the radius of the contact, and Y is the indentation modulus of the material.
In this description, the resonance amplitude of the electromechanical coupling is a measure of electromechanical coupling free from topographical artifacts, because the changes in contact stiffness are compensated by the resonance frequency tracking. Quality factor is the measure of energy dissipation during the conversion of electrical energy into mechanical energy. Finally, resonance frequency is a measure of the local elastic properties of material.
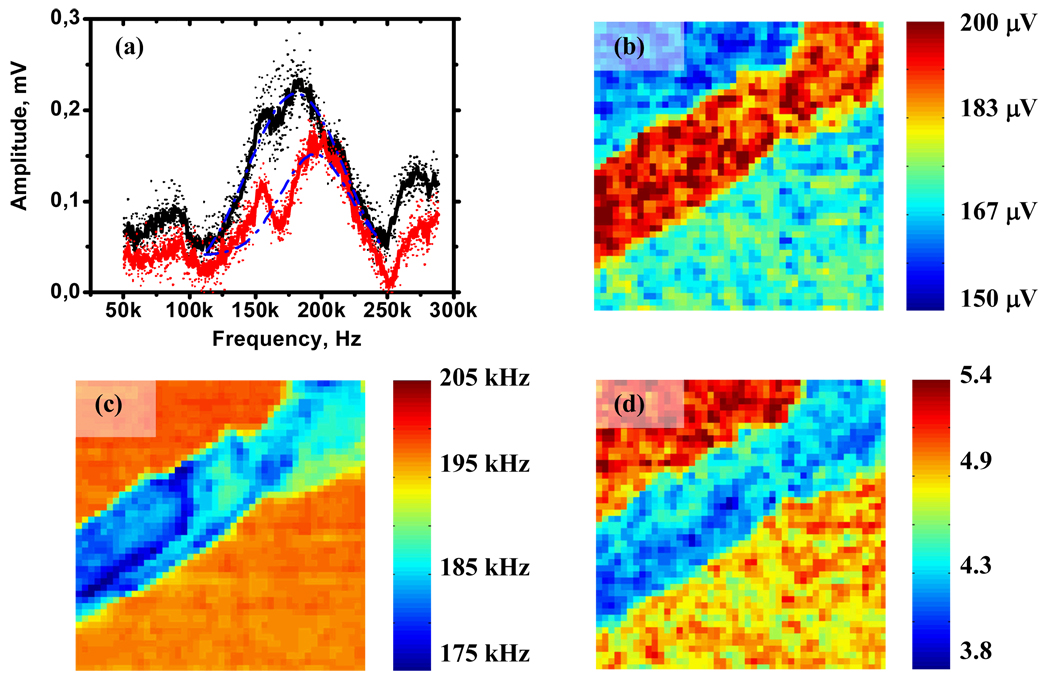
Spatially resolved measurements of resonance frequency (determined as functional fit of each spectrum with single damped harmonic oscillator) (Fig. 4(c)) show that the resonance frequency of tip-surface contact varies over a wide range (~15 kHz) within the amyloid fibril, while the amplitudes of piezoelectric responses of the amyloid fibril is almost constant (Fig. 4(b)).
Fig. 4.
(a) Examples of the broad frequency electromechanical response (red is typical spectrum of mica, black is typical spectrum for amyloid fiber). Blue lines are the fit of the spectrum using damped harmonic oscillator model. Spatially resolved maps of the amplitude (b), resonance frequency (c) and quality factor (d) of electromechanical response calculated as damped harmonic oscillator fit of the frequency spectra.
Experiment shows that tip – mica and tip – amyloid contacts have resonance frequencies and quality factors of 195 kHz and 4.9, and 185 kHz and 4.4, respectively. Such a small difference in quality factor (less than 15%) of amyloid fibril and mica suggests that the mechanism for electromechanical coupling is the same for these two materials. Under the experimental conditions the change in quality factor alone cannot explain the change in resonance frequency (in DHO model the resonance frequency and the quality factor are connected by the equation ), thus, the change in contact stiffness definitely affects the resonance frequency.
Table 1 shows indentation depth, contact radius and contact stiffness for ambient and liquid measurements estimated using the Hertzian model of the tip – surface contact using tip radius of 40 nm, Poisson ratio of 0.3 for mica and amyloid, and indentation forces of 100 nN (ambient) and 0.15 nN (liquid). The Hertzian model was used as the simplest model for tip – surface contact with the least amount of free parameters. All parameters used in modeling are close to those used in experiment. The large differences in Young’s modulus and contact stiffness between amyloid and mica explain the difference in observed contact resonance frequencies. Also the large indentation depth of the amyloid fibril in air explains the difference in the measured height of the fibrils in air and liquid.
The nature of electromechanical coupling in amyloid – mica system
Both mica and amyloid fibers are materials with small intrinsic piezoelectric effect. Mica is centro-symmetric, and hence bulk piezoeffect is zero, although surface electromechanical responses are possible.60 In amyloid fibrils, as in other biomolecular systems, the shear piezoeffect is expected.61 In this case for ideal fibril orientation the vertical PFM response is expected to be zero, with defects and structural irregularities providing regions with non-zero signal.
In addition to materials-related mechanisms, reproducibly observed electromechanical couplings between the metal-coated tip and amyloid-and-mica surface may involve
double layer coupling
dipole reorientation
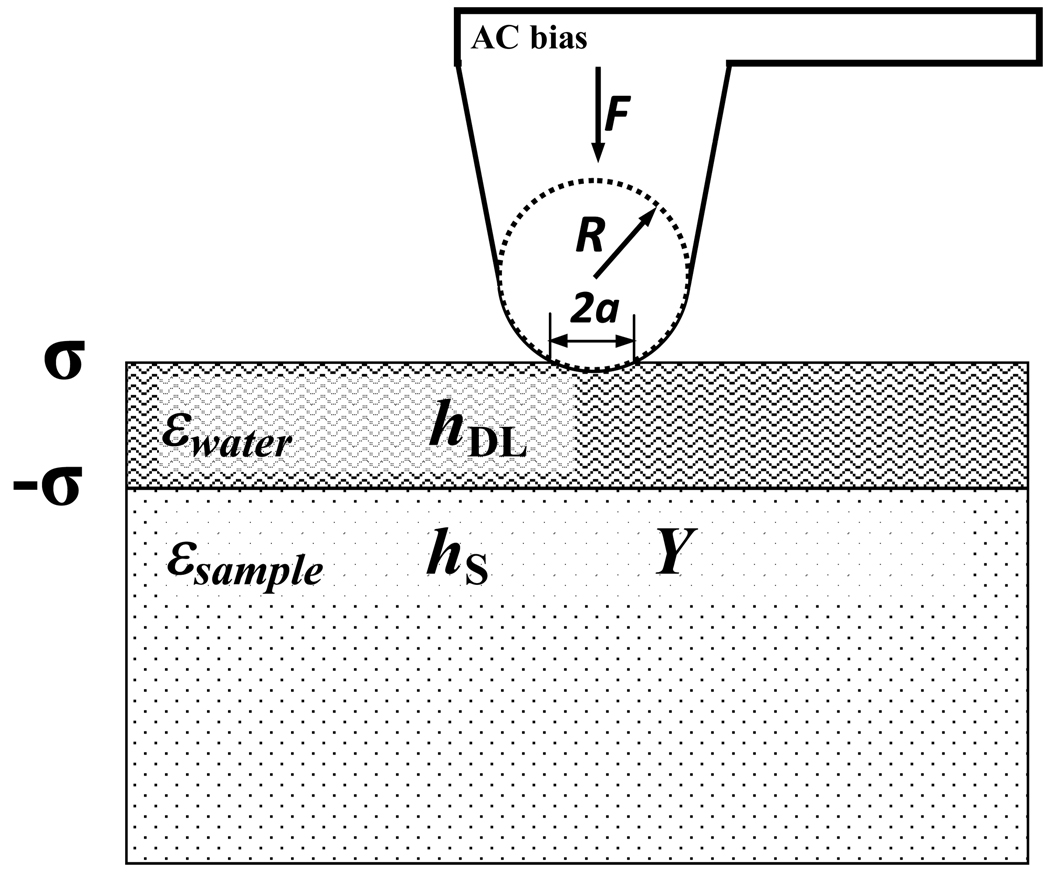
The exact equation for double layer coupling 62 model for electromechanical response d33 (the quantitative measure of the piezoelectric response in the direction perpendicular to the sample surface). can be adopted from the electromechanical response of electret films 63, 64 with the sample and one layer of charges (Fig. 5).
| (5) |
here ε is the permittivity of the solid material, hsample is the the thickness of sample, hDL is the the thicknesses of double layer, σ is the charge density of the double layer and Y is the Young’s modulus of the solid.
Fig. 5.
The schematics of the double layer model.
Relationship between measured parameters and parameters of the model
In our experiment absolute values of electromechanical amplitude are proportional to d33. The absolute value of d33 calculated from the experimental data is difficult to quantify,65 however, relative changes in d33 measured with atomic force microscope on one sample are very accurate. Thus, the ratio of d33(amyloid) to d33(mica) can easily be extracted from spatially resolved maps of amplitude of electromechanical resonance (Fig. 6(a)). This ratio [d33(amyloid)/d33(m ica)] can also be calculated using Eq. (6):
| (6) |
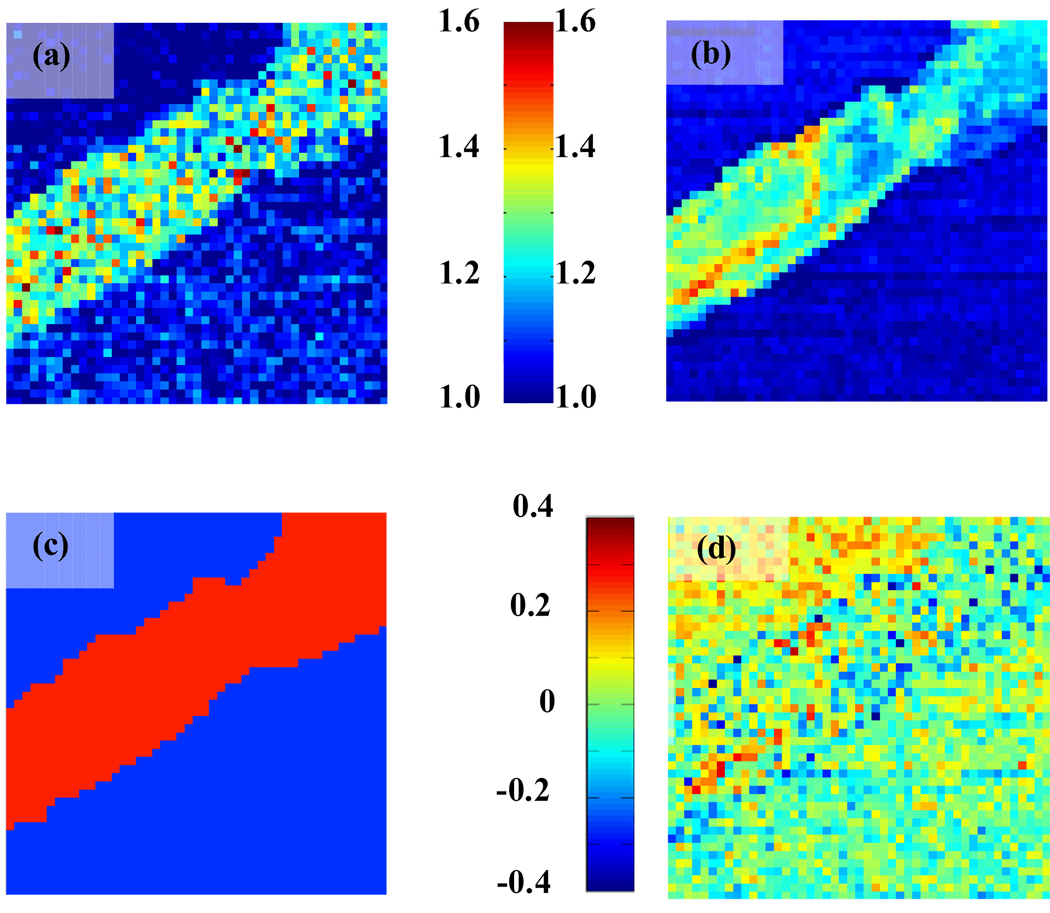
Fig. 6.
(a) Experimentally measured ratio of d33 to d33(mica). (b) Modeled ratio of d33 to d33(mica) assuming double layer coupling model. (c) The attribution of mica and amyloid fiber on the image. (d) The difference map between modeled and experimentally measured ratios.
Since the thickness of the sample is much larger than the thickness of the double layer and Eq. (6) can be simplified assuming hS → ∞ limit (Eq. (7)).
| (7) |
The Young’s modulus of the material can be calculated from the measured resonance frequency as Jesse et al. have already showed.66 Different contact resonances can be used to calculate contact stiffness as a function of frequency:
| (8) |
where fres is the resonance frequency of the tip – surface contact, i is the order of the resonance, f0BOUND is the resonance frequency of the tip in contact with infinitely stiff surface (this parameter depends only on the cantilever), k1 is the spring constant of the cantilever, k2 is the contact stiffness. The coefficients for the first 5 contact resonances were calculated (b1 = 7.7, b2 = 36.5, b3 = 80.4, b4 = 144.9, b5 = 230.8 …) based on the numerical analysis of contact resonance given in.51
Contact stiffness of the material in the first approximation is related to the Young’s modulus and contact area as k2 = 2aY, where a is the radius of the contact. After simple algebra, relationship for Young’s modulus as a function of resonance frequency can be deduced:
| (9) |
Substituting Eq. (7) into Eq. (5) we obtain:
| (10) |
Eq. (10) provides a functional relationship between electromechanical response and material stiffness assuming double layer mediated electromechanical response in the system. In order to test whether the electromechanical response is described completely by the elasticity effect, we calculate spatially resolved maps of the ratio d33(amyloid)/d33(mica) from amplitude of electromechanical response (left side of Eq. (10)) and from resonance frequency (right side of Eq. (10)).
Modeling electromechanical contrast image
Fig. 6(a) was created by dividing the spatially resolved values of electromechanical amplitude (Fig. 4(b)) by the average value of electromechanical amplitude of mica (~ 150 µV).
Modeling of the electromechanical coupling ratio from resonance frequency (Fig. 6(b)) was done as following:
The mask of the image with clear differentiation between mica (blue) and amyloid fiber (red) was created (Fig. 6(c)).
- The ratio of electromechanical coupling coefficients on mica area was calculated according to Eq. (11):
where f0BOUND − fitting parameter, fimageaverage − average resonance frequency of the image (f0BOUND = 242 kHz, fimageaverage = 195.5 kHz).(11) - The ratio of piezoelectric coefficients on amyloid fiber was calculated according to Eq. (12):
where f0BOUND − fitting parameter, fimageaverage − average resonance frequency of the image (f0BOUND = 242 kHz, fimageaverage = 195.5 kHz).(12)
The values for fmica and famyloid are taken from Fig. 2(c). f0BOUND − was adjusted to minimize the difference between modeled image and experimental map.
In order to understand the quality of the fit, a spatially resolved difference map was created (Fig. 6(d)). The fitting error is less than ±15%; also no apparent contrast on the difference image can be seen. This proves that the difference in electromechanical coupling between mica and amyloid fiber can be explained by the difference in the indentation moduli between those two materials. It also validates the use of double layer model for the description of the electromechanical contrast in the amyloid-on-mica system.
The reconstructed map in Fig. 6(d) exhibits a number of the "hot spots" of high electromechanical activity. These hot spot are represented correlated response at several adjacent locations, and thus cannot be attributed to pure noise response. The comparison with topography illustrates their correlation with the topographic inhomogeneities. Based on the fact the predominant piezoelectric coupling in these materials is shear, the disruption of fibril structure can create the regions of high electromechanical response, suggesting a possible explanation for observed phenomenon.
Conclusions
In this work we unraveled an origin of the electromechanical coupling observed on mica and amyloid fibers. The use of piezoresponse force microscope with broadband electrical excitation of the tip and signal detection allows for reliable study of electromechanical coupling in amyloid fibrils. Also, this methodology is directly transferrable to molecular systems, molecular assemblies and biological systems, which are crucial parts of the nanorobot devices for minimally invasive surgeries,67, 68 body functions monitoring 69, 70 etc. The electromechanical response of the double layer is responsible for this effect with the Young’s modulus of the material being the main parameter determining that determines the magnitude of electromechanical coupling. The double layer effect on electromechanical coupling extends to the other soft materials, such as polymer brushes etc.
MATERIALS AND METHODS
Sample preparation
For amyloid fibril samples, bovine insulin (Sigma-Aldrich #I5500) was reconstituted to 5 mg/ml in 10 mM HCl.34 This solution was incubated at 80 °C for 48 h. The fibril suspension was diluted to 0.5 mg/ml protein and was purified by 15 centrifugations at 3000g for 1 minute each to remove smaller aggregates. Ten microliters of a 0.05 mg/ml suspension was adsorbed onto freshly cleaved mica (EMS #71851-05) at room temperature for 1.5 minutes, followed by washing with copious amounts of Millipore-grade water. A stream of nitrogen was used to dry amyloid samples that were imaged in ambient air. Imaging was performed in air or in 1 mL Millipore water in a static fluid cell. Additional water was added as needed to compensate for evaporation.
Instrumentation for the measurements of electromechanical coupling
Single frequency experiments
Electromechanical coupling on amyloid and mica was measured using Asylum Research (Santa Barbara, CA) MFP3D Atomic Force Microscope (AFM). External function generator (SR DS345) was used to bias the tip with AC bias of 10 V amplitude and single frequency from 100 – 200 kHz range. For each experiment a single frequency in the 100 – 200 kHz range was chosen to maximize the amplitude of mechanical response. The amplitude of mechanical response was measured by feeding vertical deflection signal from photodetector of the microscope into lock-in amplifier (SR844 RF). Au coated tip (Olympus, RC800PB) with stiffness ~0.06 N/m and resonance frequency of 17 kHz was used for the experiments. The cantilever had a spring board shape with 20 µm width, 200 µm length and 0.8 µm thickness. The experiment was an exact replica of PFM experiments done in air; reference50 provides more details on the experiment configuration.
Band Excitation experiments
PFM and Band Excitation50 PFM was implemented on an Asylum Research (Santa Barbara, CA) MFP3D Atomic Force Microscope (AFM) and an in-house developed MatLab/LabView data acquisition and control system. A voltage excitation band spanning approximately 50 – 280 kHz (increasing chirp) with amplitude of 10 V was applied to the microscope tip. The mechanical response of the system was recorded by measuring and digitally storing the motion of the tip, taking the Fourier transform of the response. The amplitude, resonance frequency, and quality factor were extracted using a damped harmonic oscillator model at regular intervals during the tip biasing process. Au coated tip (Olympus, RC800PB) with stiffness ~0.06 N/m and resonance frequency of 17 kHz was used for the experiments. The cantilever had a spring board shape with 20 µm width, 200 µm length and 0.8 µm thickness.
Acknowledgements
The work was supported in part (MPN, SVK) by ORNL LDRD program. A portion of this research at the Oak Ridge National Laboratory’s Center for Nanophase Materials Sciences was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy. The research was also supported in part (VVR, AAV, SVK) by NIH grant RR024449.
References
- 1.Electromechanics on the Nanometer Scale: Emerging Phenomena, Devices, and Applications. MRS Bulletin; 2009. Sept., [Google Scholar]
- 2.Juluri BK, Kumar AS, Liu Y, Ye T, Yang YW, Flood AH, Fang L, Stoddart JF, Weiss PS, Huang TJ. A Mechanical Actuator Driven Electrochemically by Artificial Molecular Muscles. Acs Nano. 2009;3:291–300. doi: 10.1021/nn8002373. [DOI] [PubMed] [Google Scholar]
- 3.Madden JD. Mobile robots: Motor Challenges and Materials Solutions. Science. 2007;318:1094–1097. doi: 10.1126/science.1146351. [DOI] [PubMed] [Google Scholar]
- 4.Shirai Y, Osgood AJ, Zhao YM, Yao YX, Saudan L, Yang HB, Chiu YH, Alemany LB, Sasaki T, Morin JF, Guerrero JM, Kelly KF, Tour JM. Surface-Rolling Molecules. J. Am. Chem. Soc. 2006;128:4854–4864. doi: 10.1021/ja058514r. [DOI] [PubMed] [Google Scholar]
- 5.International Technology Roadmap for Semiconductors. 2008 [Google Scholar]
- 6.Balzani V, Credi A, Venturi M. Light Powered Molecular Machines. Chem. Soc. Rev. 2009;38:1542–1550. doi: 10.1039/b806328c. [DOI] [PubMed] [Google Scholar]
- 7.Ferris DP, Zhao YL, Khashab NM, Khatib HA, Stoddart JF, Zink JI. Light-Operated Mechanized Nanoparticles. J. Am. Chem. Soc. 2009;131:1686–1688. doi: 10.1021/ja807798g. [DOI] [PubMed] [Google Scholar]
- 8.Kim H, Goddard WA, Jang SS, Dichtel WR, Heath JR, Stoddart JF. Free Energy Barrier for Molecular Motions in Bistable [2]Rotaxane Molecular Electronic Devices. J. Phys. Chem. A. 2009;113:2136–2143. doi: 10.1021/jp809213m. [DOI] [PubMed] [Google Scholar]
- 9.Zheng YB, Yang YW, Jensen L, Fang L, Juluri BK, Flood AH, Weiss PS, Stoddart JF, Huang TJ. Active Molecular Plasmonics: Controlling Plasmon Resonances with Molecular Switches. Nano Lett. 2009;9:819–825. doi: 10.1021/nl803539g. [DOI] [PubMed] [Google Scholar]
- 10.Kumar AS, Ye T, Takami T, Yu BC, Flatt AK, Tour JM, Weiss PS. Reversible Photo-Switching of Single Azobenzene Molecules in Controlled Nanoscale Environments. Nano Lett. 2008;8:1644–1648. doi: 10.1021/nl080323+. [DOI] [PubMed] [Google Scholar]
- 11.Moore AM, Mantooth BA, Donhauser ZJ, Yao YX, Tour JM, Weiss PS. Real-Time Measurements of Conductance Switching and Motion of Single Oligo(phenylene ethynylene) Molecules. J. Am. Chem. Soc. 2007;129:10352–10353. doi: 10.1021/ja0745153. [DOI] [PubMed] [Google Scholar]
- 12.Soong R, Montemagno CD. Engineering Hybrid Nano-Devices Powered by the F-1-ATPase Biomolecular Motor. International Journal of Nanotechnology. 2005;2:371–396. [Google Scholar]
- 13.Choi HJ, Montemagno CD. Artificial Organelle: ATP Synthesis from Cellular Mimetic Polymersomes. Nano Lett. 2005;5:2538–2542. doi: 10.1021/nl051896e. [DOI] [PubMed] [Google Scholar]
- 14.Butt HJ. Towards Powering Nanometer-Scale Devices with Molecular Motors: Single Molecule Engines. Macromol. Chem. Phys. 2006;207:573–575. [Google Scholar]
- 15.Browne WR, Feringa BL. Making Molecular Machines Work. Nat. Nanotech. 2006;1:25–35. doi: 10.1038/nnano.2006.45. [DOI] [PubMed] [Google Scholar]
- 16.Rescifina A, Zagni C, Iannazzo D, Merino P. Recent Developments on Rotaxane-Based Shuttles. Curr. Org. Chem. 2009;13:448–481. [Google Scholar]
- 17.Gong XJ, Li JY, Lu HJ, Wan RZ, Li JC, Hu J, Fang HP. A Charge-Driven Molecular Water Pump. Nat. Nanotech. 2007;2:709–712. doi: 10.1038/nnano.2007.320. [DOI] [PubMed] [Google Scholar]
- 18.Yamaki M, Hoki K, Teranishi T, Chung WC, Pichierri F, Kono H, Fujimura Y. Theoretical Design of an Aromatic Hydrocarbon Rotor Driven by a Circularly Polarized Electric Field. J. Phys. Chem. A. 2007;111:9374–9378. doi: 10.1021/jp073953t. [DOI] [PubMed] [Google Scholar]
- 19.Flood AH, Ramirez RJA, Deng WQ, Muller RP, Goddard WA, Stoddart JF. Meccano on the Nanoscale - A Blueprint for Making Some of the World's Tiniest Machines. Aust. J. Chem. 2004;57:301–322. [Google Scholar]
- 20.Horinek D, Michl J. Molecular Dynamics Simulation of an Electric Field Driven Dipolar Molecular Rotor Attached to a Quartz Glass Surface. J. Am. Chem. Soc. 2003;125:11900–11910. doi: 10.1021/ja0348851. [DOI] [PubMed] [Google Scholar]
- 21.Vacek J, Michl J. Molecular Dynamics of a Grid-Mounted Molecular Dipolar Rotor in a Rotating Electric Field. Proc. Nat. Acad. Sci. USA. 2001;98:5481–5486. doi: 10.1073/pnas.091100598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Noy A. Handbook of Molecular Force Spectroscopy. Springer; 2007. [Google Scholar]
- 23.Gruverman A, Kholkin A. Nanoscale Ferroelectrics: Processing, Characterization and Future Trends. Rep. Prog. Phys. 2006;69:2443–2474. [Google Scholar]
- 24.Nikolaeva EV, Shur VY, Shishkin EI, Sternberg A. Nanoscale domain structure in relaxor PLZT x/65/35 ceramics. International Symposium on Micro- and Nano-Scale Domain Structuring Ferroelectrics (ISDS 2005); Nov 15–19, 2005; Ekaterinburg, RUSSIA. Ekaterinburg, RUSSIA: Taylor & Francis Ltd; 2005. pp. 137–143. [Google Scholar]
- 25.Rodriguez BJ, Jesse S, Baddorf AP, Kalinin SV. High Resolution Electromechanical Imaging of Ferroelectric Materials in a Liquid Environment by Piezoresponse Force Microscopy. Phys. Rev. Lett. 2006;96:237602. doi: 10.1103/PhysRevLett.96.237602. [DOI] [PubMed] [Google Scholar]
- 26.Calarco R, Meijers R, Stoica T, Luth H. Piezoresponse force microscopy for imaging of GaN surfaces; International Workshop on Nitrides Semiconductors (IWN 2004); Jul 19–23, 2004; Pittsburgh, PA. Pittsburgh, PA: Wiley-V C H Verlag Gmbh; 2004. pp. 785–789. [Google Scholar]
- 27.Bdikin IK, Shvartsman VV, Kholkin AL. In: Furuya Y, Quandt E, Zhang Q, Inoue K, Shahinpoor M, editors. Nanoscale ferroelectric properties of PZN-PT single crystals studied by scanning force microscopy; Symposium on Materials and Devices for Smart Systems held at the 2003 MRS Fall Meeting; Dec 01–05, 2003; Boston, MA. Boston, MA: Materials Research Society; 2003. pp. 147–152. [Google Scholar]
- 28.Tybell T, Paruch P, Giamarchi T, Triscone JM. Domain Wall Creep in Epitaxial Ferroelectric Pb(Zr0.2Ti0.8)O3 Thin Films. Phys. Rev. Lett. 2002;89:097601. doi: 10.1103/PhysRevLett.89.097601. [DOI] [PubMed] [Google Scholar]
- 29.Paruch P, Giamarchi T, Triscone JM. Domain wall creep in mixed c-a axis Pb(Zr0.2Ti0.8)O-3 thin films; 10th International Workshop on Oxide Electronics; Sep 11–13 2003; Augsbaurg, Germany. Augsbaurg, Germany: Wiley-V C H Verlag Gmbh; 2003. pp. 95–96. [Google Scholar]
- 30.Maksymovych P, Jesse S, Huijben M, Ramesh R, Morozovska A, Choudhury S, Chen LQ, Baddorf AP, Kalinin SV. Intrinsic Nucleation Mechanism and Disorder Effects in Polarization Switching on Ferroelectric Surfaces. Phys. Rev. Lett. 2009;102:017601. doi: 10.1103/PhysRevLett.102.017601. [DOI] [PubMed] [Google Scholar]
- 31.Jesse S, Rodriguez BJ, Choudhury S, Baddorf AP, Vrejoiu I, Hesse D, Alexe M, Eliseev EA, Morozovska AN, Zhang J, Chen LQ, Kalinin SV. Direct Imaging of the Spatial and Energy Distribution of Nucleation Centres in Ferroelectric Materials. Nat. Mater. 2008;7:209–215. doi: 10.1038/nmat2114. [DOI] [PubMed] [Google Scholar]
- 32.Kalinin SV, Rodriguez BJ, Jesse S, Thundat T, Gruverman A. Electromechanical Imaging of Biological Systems with sub-10 nm Resolution. Appl. Phys. Lett. 2005;87:053901. [Google Scholar]
- 33.Rodriguez BJ, Jesse S, Baddorf AP, Kim SH, Kalinin SV. Controlling Polarization Dynamics in a Liquid Environment: From Localized to Macroscopic Switching in Ferroelectrics. Phys. Rev. Lett. 2007;98:247603. doi: 10.1103/PhysRevLett.98.247603. [DOI] [PubMed] [Google Scholar]
- 34.Guo SL, Akhremitchev BB. Packing Density and Structural Heterogeneity of Insulin Amyloid Fibrils Measured by AFM Nanoindentation. Biomacromolecules. 2006;7:1630–1636. doi: 10.1021/bm0600724. [DOI] [PubMed] [Google Scholar]
- 35.Guo S, Akhremitchev BB. Investigation of Mechanical Properties of Insulin Crystals by Atomic Force Microscopy. Langmuir. 2008;24:880–887. doi: 10.1021/la7018605. [DOI] [PubMed] [Google Scholar]
- 36.Jansen R, Dzwolak W, Winter R. Amyloidogenic Self-Assembly of Insulin Aggregates Probed by High resolution Atomic Force Microscopy. Biophys. J. 2005;88:1344–1353. doi: 10.1529/biophysj.104.048843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Knowles TP, Fitzpatrick AW, Meehan S, Mott HR, Vendruscolo M, Dobson CM, Welland ME. Role of Intermolecular Forces in Defining Material Properties of Protein Nanofibrils. Science. 2007;318:1900–1903. doi: 10.1126/science.1150057. [DOI] [PubMed] [Google Scholar]
- 38.Knowles TPJ, Smith JF, Craig A, Dobson CM, Welland ME. Spatial Persistence of Angular Correlations in Amyloid Fibrils. Phys. Rev. Lett. 2006;96:238301. doi: 10.1103/PhysRevLett.96.238301. [DOI] [PubMed] [Google Scholar]
- 39.Smith JF, Knowles TPJ, Dobson CM, MacPhee CE, Welland ME. Characterization of the Nanoscale Properties of Individual Amyloid Fibrils. Proc. Nat. Acad. Sci. USA. 2006;103:15806–15811. doi: 10.1073/pnas.0604035103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sunde M, Serpell LC, Bartlam M, Fraser PE, Pepys MB, Blake CCF. Common Core Structure of Amyloid Fibrils by Synchrotron X-ray Diffraction. J. Mol. Biol. 1997;273:729–739. doi: 10.1006/jmbi.1997.1348. [DOI] [PubMed] [Google Scholar]
- 41.Geddes AJ, Parker KD, Atkins EDT, Beighton E. Cross-Beta Conformation in Proteins. J. Mol. Biol. 1968;32:343–344. doi: 10.1016/0022-2836(68)90014-4. [DOI] [PubMed] [Google Scholar]
- 42.Kyle RA. Amyloidosis: A Convoluted Story. British Journal of Haematology. 2001;114:529–538. doi: 10.1046/j.1365-2141.2001.02999.x. [DOI] [PubMed] [Google Scholar]
- 43.Sipe JD, Cohen AS. Review: History of the Aamyloid Fibril. J. Struct. Biol. 2000;130:88–98. doi: 10.1006/jsbi.2000.4221. [DOI] [PubMed] [Google Scholar]
- 44.Grudzielanek S, Jansen R, Winter R. Solvational Tuning of the Unfolding, Aggregation and Amyloidogenesis of Insulin. J. Mol. Biol. 2005;351:879–894. doi: 10.1016/j.jmb.2005.06.046. [DOI] [PubMed] [Google Scholar]
- 45.Swift B, Hawkins PN, Richards C, Gregory R. Examination of Insulin Injection Sites: An Unexpected Finding of Localized Amyloidosis. Diabetic Med. 2002;19:881–882. doi: 10.1046/j.1464-5491.2002.07581.x. [DOI] [PubMed] [Google Scholar]
- 46.Storkel S, Schneider HM, Muntefering H, Kashiwagi S. Iatrogenic, Insulin-Dependent, Local Amyloidosis. Lab. Invest. 1983;48:108–111. [PubMed] [Google Scholar]
- 47.Gasparini L, Dityatev A. Beta-Amyloid and Glutamate Receptors. Exp. Neurol. 2008;212:1–4. doi: 10.1016/j.expneurol.2008.03.005. [DOI] [PubMed] [Google Scholar]
- 48.Glenner GG, Wong CW. Alzheimers-Disease and Downs-Syndrome - Sharing of a Unique Cerebrovascular Amyloid Fibril Protein. Biochem. Biophys. Res. Co. 1984;122:1131–1135. doi: 10.1016/0006-291x(84)91209-9. [DOI] [PubMed] [Google Scholar]
- 49.Proksch R, Kalinin SV. Piezoresponse Force Microscopy with Asylum Research AFM. 2009 http://www.asylumresearch.com/Applications/PFMAppNote/PFMAppNote.shtml.
- 50.Jesse S, Kalinin SV, Proksch R, Baddorf AP, Rodriguez BJ. The Band Excitation Method in Scanning Probe Microscopy for Rapid Mapping of Energy Dissipation on the Nanoscale. Nanotechnology. 2007;18:435503. [Google Scholar]
- 51.Jesse S, Mirman B, Kalinin SV. Resonance Enhancement in Piezoresponse Force Microscopy: Mapping Electromechanical Activity, Contact Stiffness, and Q Factor. Appl. Phys. Lett. 2006;89:022906. [Google Scholar]
- 52.Kalinin SV, Karapetian E, Kachanov M. Nanoelectromechanics of Piezoresponse Force Microscopy. Phys. Rev. B. 2004;70:24. [Google Scholar]
- 53.Rabe U, Janser K, Arnold W. Vibrations of Free and Surface-Coupled Atomic Force Microscope Cantilevers: Theory and Experiment. Rev. Sci. Instr. 1996;67:3281–3293. [Google Scholar]
- 54.Hirsekorn S, Rabe U, Arnold W. Theoretical Description of the Transfer of Vibrations from a Sample to the Cantilever of an Atomic Force Microscope. Nanotechnology. 1997;8:57–66. [Google Scholar]
- 55.Kalinin SV, Rodriguez BJ, Jesse S, Seal K, Proksch R, Hohlbauch S, Revenko I, Thompson GL, Vertegel AA. Towards Local Electromechanical Probing of Cellular and Biomolecular Systems in a Liquid Environment. Nanotechnology. 2007;18:424020. doi: 10.1088/0957-4484/18/42/424020. [DOI] [PubMed] [Google Scholar]
- 56.Jesse S, Kalinin SV. Principal Component and Spatial Correlation Analysis of Spectroscopic-Imaging Data in Scanning Probe Microscopy. Nanotechnology. 2009;20:085714. doi: 10.1088/0957-4484/20/8/085714. [DOI] [PubMed] [Google Scholar]
- 57.Bonnet N. Some Trends in Microscope Image Processing. Micron. 2004;35:635–653. doi: 10.1016/j.micron.2004.04.006. [DOI] [PubMed] [Google Scholar]
- 58.Bosman M, Watanabe M, Alexander DTL, Keast VJ. Mapping Chemical and Bonding Information Using Multivariate Analysis of Electron Energy-Loss Spectrum Images. Ultramicroscopy. 2006;106:1024–1032. doi: 10.1016/j.ultramic.2006.04.016. [DOI] [PubMed] [Google Scholar]
- 59.Kracke B, Damaschke B. Measurement of Nanohardness and Nanoelasticity of Thin Gold Films with Scanning Force Microscope. Appl. Phys. Lett. 2000;77:361–363. [Google Scholar]
- 60.Tagantsev AK. Piezoelectricity and Flexoelectricity in Crystalline Dielectrics. Phys. Rev. B. 1986;34:5883–5889. doi: 10.1103/physrevb.34.5883. [DOI] [PubMed] [Google Scholar]
- 61.Minary-Jolandan M, Yu MF. Uncovering Nanoscale Electromechanical Heterogeneity in the Subfibrillar Structure of Collagen Fibrils Responsible for the Piezoelectricity of Bone. ACS Nano. 2009;3:1859. doi: 10.1021/nn900472n. [DOI] [PubMed] [Google Scholar]
- 62.Kacprzyk R, Dobrucki A, Gajewski JB. Double-Layer Electret Transducer. J. Electrostat. 1997;39:33–40. [Google Scholar]
- 63.Sessler GM, Hillenbrand J. Electromechanical Response of Cellular Electret Films. Appl. Phys. Lett. 1999;75:3405–3407. [Google Scholar]
- 64.Sessler GM, Hillenbrand J. Electromechanical response of cellular electret films; 10th International Symposium on Electrets; IEEE Service Center; 1999. [Google Scholar]
- 65.Kalinin SV, Rar A, Jesse S. A Decade of Piezoresponse Force Microscopy: Progress, Challenges, and Opportunities. IEEE T. Ultrason. Ferr. 2006;53:2226–2252. doi: 10.1109/tuffc.2006.169. [DOI] [PubMed] [Google Scholar]
- 66.Jesse S, Nikiforov MP, Germinario LT, Kalinin SV. Local Thermomechanical Characterization of Phase Transitions Using Band Excitation Atomic Force Acoustic Microscopy with Heated Probe. Appl. Phys. Lett. 2008;93:073104. [Google Scholar]
- 67.A R, J F. Nanomedicine, Vol. I: Basic Capabilities. Landes Bioscience; 1999. [Google Scholar]
- 68.Leary SP, Liu CY, Apuzzo MLI. Toward the Emergence of Nanoneurosurgery: Part III - Nanomedicine: Targeted Nanotherapy, Nanosurgery, and Progress toward the Realization of Nanoneurosurgery. Neurosurgery. 2006;58:1009–1025. doi: 10.1227/01.NEU.0000217016.79256.16. [DOI] [PubMed] [Google Scholar]
- 69.Sauer C, Stanacevic M, Cauwenberghs G, Thakor N. Power Harvesting and Telemetry in CMOS for Implanted Devices. IEEE T. Circuits Syst. 2005;52:2605–2613. [Google Scholar]
- 70.Kumar M. Nano and Microparticles as Controlled Drug Delivery Devices. J. Pharm. Pharm. Sci. 2000;3:234–258. [PubMed] [Google Scholar]