The basic reproductive ratio of life

Abstract

Template-directed polymerization of nucleotides is believed to be a pathway for the replication of genetic material in the earliest cells. We assume that activated monomers are produced by prebiotic chemistry. These monomers can undergo spontaneous polymerization, a system that we call “prelife.” Adding template-directed polymerization changes the equilibrium structure of prelife if the rate constants meet certain criteria. In particular, if the basic reproductive ratio of sequences of a certain length exceeds one, then those sequences can attain high abundance. Furthermore, if many sequences replicate, then the longest sequences can reach high abundance even if the basic reproductive ratios of all sequences are less than one. We call this phenomenon “subcritical life.” Subcritical life suggests that sequences long enough to be ribozymes can become abundant even if replication is relatively inefficient. Our work on the evolution of replication has interesting parallels to infection dynamics. Life (replication) can be seen as an infection of prelife.

1 Introduction

Evolution is based on replication, mutation, and selection. Replication proliferates information. Mutation results in errors in replication and thereby produces diversity. Selection occurs when some mutants are more fit than others. In order to understand the beginning of evolution, we must understand the origins of replication. In our earlier work, we studied “prelife” dynamics and the onset of replication (Nowak and Ohtsuki, 2008; Manapat et al., 2009; Ohtsuki and Nowak, 2009). Prelife is a model of a soup of activated monomers that undergo spontaneous polymerization. How might prebiotic replication occur in reality? Template-directed synthesis is believed to be a mechanism for copying nucleic acid sequences before enzymes evolved (Ninio and Orgel, 1978; Lohrmann et al., 1980; Joyce, 1987; Orgel, 2004). In this mechanism, the template sequence accelerates polymerization of a complementary strand through base-pairing interactions with the nucleotide monomers. This effect accelerates polymerization by at least one or two orders of magnitude (Kanavarioti and White, 1987). We model such synthesis as a three-step process: (1) association between primer and template, (2) template-directed elongation of the primer, and (3) dissociation of the double-stranded product. In addition, the grouping together of molecules (e.g., using vesicle membranes) is thought to be important for the evolution of replication enzymes (Szathmáry and Demeter, 1987; Szostak et al., 2001; Chen et al., 2006; Traulsen and Nowak, 2006). A recent experimental study demonstrated template-directed synthesis inside model protocells using activated monomers supplied from the exterior (Mansy et al., 2008). The system we study in this paper is in some ways similar to the system of nucleic acid sequences in a model protocell.

There have been many investigations of the origin of life, both experimental and theoretical (Oparin, 1953; Crick, 1968; Orgel, 1968, 1992; Eigen, 1971; Eigen and Schuster, 1982; Dyson, 1982, 1999; Kuppers, 1983; Stein and Anderson, 1984; Farmer et al., 1986; Fontana and Schuster, 1998; Lifson and Lifson, 1999; de Duve, 2005, 2007). The first step towards life must have been the synthesis of basic organic building blocks—amino acids, carbohydrates, and nucleotides—in primitive-Earth conditions (Miller, 1953; Allen and Ponnamperuma, 1967; Miller and Orgel, 1974; Hargreaves et al., 1977; Rao et al., 1982; Rushdi and Simoneit, 2001; Benner et al., 2002; Ricardo et al., 2004; Benner and Ricardo, 2005; Wachtershauser, 2007; Powner et al., 2009). After those basic components became available, mechanisms for storing information and catalyzing chemical reactions must have arisen. While other genetic polymers may have preceded RNA, it is generally accepted that an “RNA world” evolved at some point. In this world, RNA acted as both information carrier and enzyme (Woese, 1967; Crick, 1968; Orgel, 1986; Joyce, 1989, 2002; Ellington and Szostak, 1990; Cech, 1993; Sievers and von Kiedrowski, 1994; Johnston et al., 2001; Steitz and Moore, 2003; Hughes et al., 2004). Evidence supporting the RNA world theory comes from several sources, including the discovery that RNA forms the catalytic core of the ribosome (Nissen et al., 2000) and the discovery of RNA molecules that catalyze nucleic acid chemistry (Wilson and Szostak, 1999). A particularly noteworthy RNA molecule, evolved from a ligase ribozyme, catalyzes template-directed RNA polymerization, demonstrating a step toward a replication enzyme (Bartel and Szostak, 1993; Johnston et al., 2001). In a recent experiment, Lincoln and Joyce (2009) constructed paired RNA catalysts that can synthesize copies of each other when supplied with the right chemical precursors. This system resembles the “hypercycle” of Eigen and Schuster (1977, 1979), a cooperative network of enzymes that may have been one of the first forms of life. Here, we focus on a relatively early stage of life in which templating polymers (e.g., nucleic acids) existed but enzymes had not necessarily yet evolved.

One difficulty in the origin of life is the problem of combinatorial complexity. Very short RNA sequences generally do not have catalytic activity because they are not long enough to fold into active structures. Short ribozymes, for example, are about 30 bases long (Lee and Suga, 2001; Pan and Uhlenbeck, 1992). Hence, if (1) a molecule must be relatively long to have enzymatic activity and (2) most long molecules do not act as enzymes (Carothers and Szostak, 2006), then the probability that random polymerization will lead to a ribozyme is exceedingly small. One possible resolution to this problem is to somehow bias the formation of RNA sequences toward active sequences. For example, catalysis of RNA polymerization by montmorillonite clay appears to promote some lineages while suppressing others (Miyakawa and Ferris, 2003; Ferris et al., 2004). Such biases can dramatically reduce the effective size of sequence space. We investigated selection by differential rates of production (“selection before replication”) previously (Nowak and Ohtsuki, 2008). However, this mechanism does not necessarily bias the sequence pool toward active replicators. Another way to increase the chances of producing ribozymes is to bias the length distribution toward long sequences. Here we investigate how such a bias might arise.

This paper is organized as follows. In Section 2, we introduce our model. In Section 3, we present simulation results for a special case. In Section 4, we compute the first crucial quantities, the basic reproductive ratio of templates and the discriminant. In Sections 5, we generalize our model to allow for templates of multiple lengths, introducing the notions of subcritical life, the chain amplification ratio, and the cumulative basic reproductive ratio. In Section 6, we draw some analogies to infection dynamics. Finally, in Section 7, we summarize our findings.

2 The model

2.1 Basic setup

We consider “unary” sequences, Nⁱ. For example, N³ = N N N, where N represents an arbitrary monomer (e.g., the ribonucleotide A, C, G, or U). Here we focus on the efficiency of replication and the equilibrium length distribution, rather than mutation and diversity, so for simplicity we do not distinguish between different types of monomers. Sequences grow by incorporating activated monomers, *N, according to the chemical reaction Nⁱ + *N → Nⁱ⁺¹.

Let x denote the abundance of activated monomers and y_i the abundance of sequences of length i. The dynamics of these quantities are described by the following differential equations:

$$\begin{array}{l}\stackrel{.}{x}=\lambda -\alpha x-dx-ax\sum _{i=1}^{\infty }{y}_i,\\ {\stackrel{.}{y}}_1=\alpha x-(ax+d)y_1,\\ {\stackrel{.}{y}}_i={\mathit{axy}}_{i-1}-(ax+d)y_i,i=2,3,\dots .\end{array}$$ (1)

Activated monomers enter the system at the constant rate λ. They are deactivated (e.g., by hydrolysis) at rate α. When a sequence of length i and an activated monomer meet, the sequence may be extended to form a new one of length i + 1. Extension occurs at rate axy_i. All sequences are removed from the system at rate d. This system is what we call prelife (Nowak and Ohtsuki, 2008; Manapat et al., 2009; Ohtsuki and Nowak, 2009).

Now we introduce replication through template-directed synthesis (Figure 1). For simplicity, we first assume that only sequences of a particular length, n, can be templates. (Later, we consider the more realistic scenario in which all sequences with length between a minimum and maximum are templates.) Replication occurs when a primer of length k binds to a template so that their ends are aligned. The primer length, k, might be determined by salt concentrations, temperature, etc. Template-directed elongation occurs until the primer has been extended to length n. The strands then dissociate. The product sequences can then participate in prelife or replication reactions. For a given primer length k and template length n, the dynamics of the system are described by the following system of differential equations:

$$\begin{array}{l}\text{activated}\text{monomers}\{\stackrel{.}{x}=\lambda -dx-\alpha x-ax\sum _{i=1}^{\infty }{y}_i-\beta x\sum _{i=k}^{n-1}{z}_i,\\ \text{sequences}(\text{single}\text{strands})\{\begin{array}{l}{\stackrel{.}{y}}_1=\alpha x-(ax+d)y_1,\hfill \\ {\stackrel{.}{y}}_i={\mathit{axy}}_{i-1}-(ax+d)y_i,i=2,3,\dots ,i\ne k,n,\hfill \\ {\stackrel{.}{y}}_k={\mathit{axy}}_{k-1}-(ax+d)y_k-{By}_k{y}_n,\hfill \\ {\stackrel{.}{y}}_n={\mathit{axy}}_{n-1}-(ax+d)y_n-{By}_k{y}_n+2D{z}_n,\hfill \end{array}\\ \text{double}\text{strands}\{\begin{array}{l}{\stackrel{.}{z}}_k={By}_k{y}_n-\beta x{z}_k-d{z}_k,\hfill \\ {\stackrel{.}{z}}_i=\beta x(z_{i-1}-z_i)-d{z}_i,i=k+1,\dots ,n-1,\hfill \\ {\stackrel{.}{z}}_n=\beta x{z}_{n-1}-(D+d)z_n.\hfill \end{array}\end{array}$$ (2)

Figure 1.

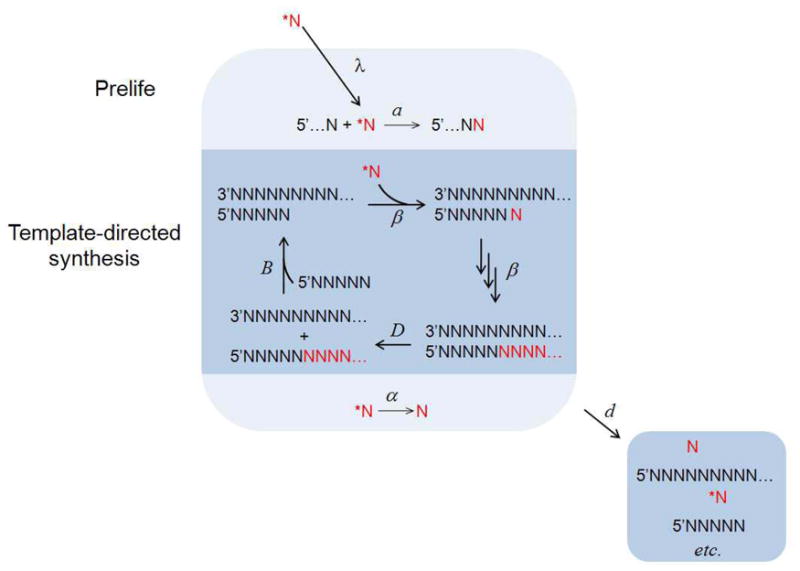
Non-templated polymerization and template-directed synthesis occur inside a model system using activated monomers supplied from the exterior. Replication begins when a primer (of length k) binds to a template (of length n) so that their ends are aligned. Template-directed elongation occurs until the primer has been extended to a sequence of length n. The pair then dissociates, yielding the original template and a copy. The two sequences can then begin a new cycle of replication. Activated monomers can be hydrolyzed, thereby losing activation, and all sequences are degraded at a fixed rate.

The abundance of activated monomers is x and the abundance of sequences of length i is y_i. Abundances of sequences other than primers and templates obey the prelife equations (1). The binding of a primer and template to form a reactive complex occurs at rate B. The variables z_i, where k ≤ i ≤ n, denote the abundances of double strands: z_k is the abundance of pairs in which one strand has length k and the other length n (formed after a primer binds to a template), z_k+1 is the abundance of pairs in which one strand has length k + 1 and the other length n (formed after one elongation step has occurred), and so forth. The parameter β is the template-directed elongation rate. The double-stranded complex dissociates at rate D. Such dissociation could be induced by thermal denaturation, which itself may be driven, for instance, by diurnal cycling. When B = 0, (2) reduces to the prelife system (1).

2.2 Model parameters and model protocells

Although prebiotic parameter values are unknown, several relevant rates have been determined in an experimental model system. Let us consider a model protocell consisting of a vesicle encapsulating nucleic acid sequences that replicate by template-directed synthesis (Mansy et al., 2008). In this case, the rate of input of activated monomers (λ) represents the rate of permeation of activated mononucleotides into the protocell. The equilibration half-time for a commonly used reactive monomer (5′-phosphorimidazolides) across model membranes based on fatty acids is on the order of seconds to hours, depending on the temperature (Mansy and Szostak, 2008; Mansy et al., 2008). A typical experimental concentration of activated monomers is on the order of 5–50 mM (Kanavarioti and White, 1987; Kozlov and Orgel, 2000; Mansy et al., 2008). Thus λ would be on the order of 10⁻³ to 10¹ M/hr in this system. We assume that monomers generated by prebiotic chemistry have similar properties so that the resulting sequences have similar binding, dissociation, and polymerization rates. For example, we do not consider the consequence of using monomers of different chirality (D-and L-nucleotides). Although this is a simplification, previous work has demonstrated physical and chemical mechanisms for obtaining high enantiomeric excess from a racemic mixture (Blackmond, 2004; Klussmann et al., 2006; Viedma et al., 2008)

Inactivation of phosphorimidazolide monomers during experiments is due to hydrolysis that yields the nucleotide monophosphate. The half-life of these monomers under template-directed polymerization conditions has been measured to be between 7 and 150 hours, depending on reaction conditions (Kanavarioti and White, 1987; Rajamani and Chen, 2009). Thus α would be roughly 0.005 to 0.1 hr⁻¹.

The presence of a template substantially enhances polymerization rates (Orgel, 2004). This effect was measured for activated ribonucleotides (Kanavarioti and White, 1987). In these experiments, the rate constant of non-templated polymerization was found to be 0.09 M⁻¹ hr⁻¹ when considering 3′-5′ linkages (0.7 M⁻¹ hr⁻¹ when including formation of 2′-5′ linkages). Addition of a template increased this rate constant to 13 M⁻¹ hr⁻¹ (3′-5′ linkages alone) or 14.9 M⁻¹ hr⁻¹ (2′-5′ and 3′-5′ linkages). A similar template effect was found in a study of RNA polymerization catalyzed by Pb²⁺ and Zn²⁺, in which the longest products of non-templated polymerization were trimers, but templated polymerization yielded products 30–40 bases long (Sawai and Orgel, 1975). More highly activated chemistries could increase these rate constants. Vogel et al. (2005) observed a rate of 40 M⁻¹ hr⁻¹ for templated polymerization, for example. In terms of the parameters of our model, these experiments suggest that the non-templated polymerization rate a would be on the order of 0.1 to 1 M⁻¹ hr⁻¹, and the template-directed elongation rate β would be on the order of 10 to 100 M⁻¹ hr⁻¹.

Annealing a primer to a template is generally a fast process compared with the other reactions in the system. For example, one measurement of the second order rate constant for annealing 20 bases is around 10⁴ M⁻¹ hr⁻¹ (Gartner et al., 2002). However, this rate depends on the temperature and the length of the annealing segment and can be very sensitive to buffer conditions, particularly ionic strength (Eun, 1996). A typical reaction for template-directed synthesis might allow a few minutes for annealing. Thus, the primer-template binding rate B is likely to be among the highest rate constants in the model, but its value may lie in a relatively large range. On the other hand, strand dissociation may be on the order of once per day (diurnal thermocycling), suggesting a value of D ≈ 0.04 hr⁻¹, although faster cycling could occur in thermal convection cells (Krishnan et al., 2002).

2.3 Model assumptions

For the purposes of simulation, it is useful to transform the infinite system (2) into a finite system. To do this, we introduce a new variable w,

$$w=\sum _{i=n+1}^{\infty }{y}_i,$$ (3)

representing the total abundance of all sequences of length greater than n. Then

$$\begin{array}{l}\stackrel{.}{w}=\sum _{i=n+1}^{\infty }{\stackrel{.}{y}}_i\\ =\sum _{i=n+1}^{\infty }({\mathit{axy}}_{i-1}-(ax+d)y_i)\\ ={\mathit{axy}}_n-dw.\end{array}$$ (4)

The complete system (2) can then be simulated with 2n − k + 3 differential equations. Extensive numerical simulations suggest that the equilibrium of (2) is globally stable.

In our model, the lengths of primers and templates are constrained in two ways. First, for the sake of analytic tractability, we assume that only sequences of a particular length, k, can act as primers. This simplification is justified because (1) a primer has a minimum length required for annealing, which depends on the environmental conditions, and (2) long primers are relatively rare (i.e., their abundance decreases exponentially with length in prelife; see below). We relaxed this assumption in numerical simulations in which sequences of many lengths acted as primers and obtained qualitatively similar results. Second, we assume that only sequences with lengths in a certain range can act as templates. We consider two versions of this assumption. We begin by doing our calculations for the simplified scenario of a single template length. However, our main focus is the realistic scenario in which templates have lengths in some range. The minimum length of a template is determined by the annealing length. For example, the annealing length—and thus the minimum possible primer length—is approximately 3 when the system is at less than 10 degrees C. The maximum length is determined by the relative rates of template-directed polymerization and of thermocycling-induced strand dissociation. If template-directed polymerization proceeds at one base per hour (Kanavarioti and White, 1987; Vogel et al., 2005), and thermocycling results in one dissociation event per day, then a typical template’s length will be somewhere between 20 and 30 bases. For sequences with lengths in the permissible range for templates, replication is generally completed before strands dissociate.

By studying unary sequences, we have ignored the effects of complementary base pairing. However, we can interpret our model in another way. Suppose we have a binary alphabet for our sequences, so a sequence is a string of 0’s and 1’s. We consider a particular polymerization lineage. For example, 0 → 01 → 011 → 0110 → · · ·. We then let x_i denote the sum of the abundance of the sequence of length i in this lineage and the abundance of its complement. The z_i’s are interpreted analogously. In this way, the results of our analysis below also describe the effect that replication with complementary base pairing has on the length distribution of sequences in a particular lineage.

3 Templates of a single length: numerical simulations

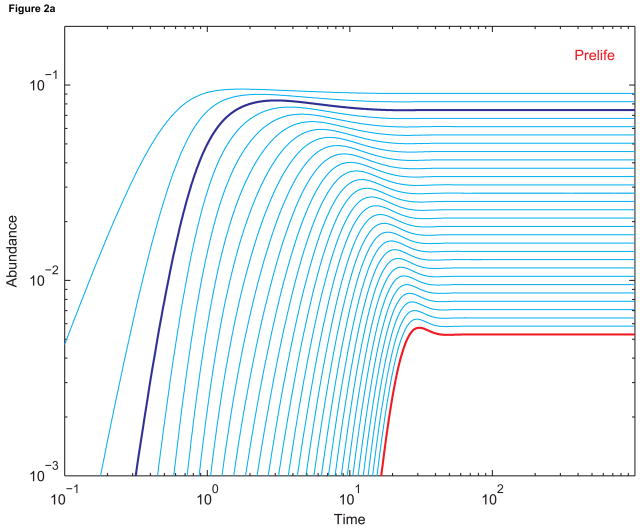
Figure 2(a) shows the prelife dynamics of sequences of lengths 1 to 30. There is no template-directed synthesis. All initial abundances are zero. At t = 0, activated monomers begin to enter the system. Some are hydrolyzed to form sequences of length 1. Longer and longer sequences are built as activated monomers are appended to the ends of existing sequences. At equilibrium, longer sequences are exponentially less common than shorter sequences.

Figure 2.

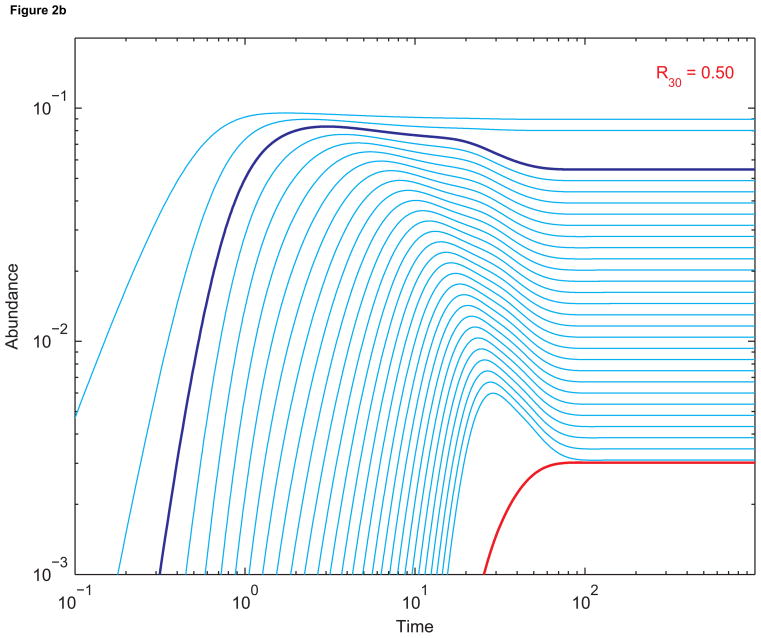
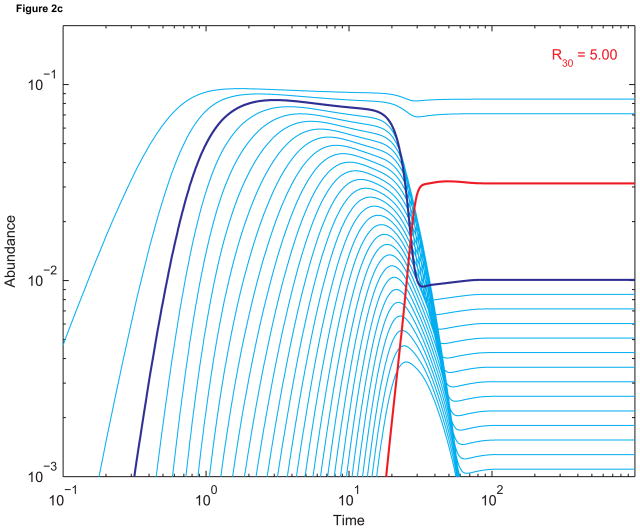
(a) Dynamics of sequences up to length 30 without replication. The abundance of length-3 sequences is in dark blue, and the abundance of length-30 sequences is in red. The single-strand elongation rate a is 10, the death rate d is 0.1, and all other constants are 1. Initial abundances are all zero. (b) The corresponding dynamics when sequences of length 30 (red) replicate using length-3 primers (dark blue). The primer-template binding rate B is 100; the double-strand dissociation rate D is 1; and the template-directed elongation rate β is 53.4. The basic reproductive ratio of length-30 sequenences, R₃₀, is 0.50, consistent with the fact that replication is not efficient enough to boost the abundance of length-30 sequences beyond its pre-replication value. (c) The dynamics when β has been increased to 455. Now R₃₀ = 5.00, and the equilibrium abundance of length-30 sequences is much greater than (almost ten times) its pre-replication value.

Figure 2(b) shows the corresponding dynamics when sequences of length 30 (red) replicate using length-3 primers (dark blue). As before, all abundances are initially zero. Prelife generates primers and templates. In this example, the parameter values allow only slow replication, corresponding to a scenario in which template-directed polymerization is not much more efficient than non-templated polymerization. Many templates get trapped in the double-stranded state, and at equilibrium sequences of length 30 are less abundant than they are in the absence of replication.

In contrast, for Figure 2(c), the template-directed elongation rate β has been increased by an order of magnitude. Now the relative rate of template-directed to non-templated polymerization is in the range of experimentally observed values for an RNA-based system (Kanavarioti and White, 1987). At t ≈ 10, the abundance of templates begins to increase sharply and the abundance of primers begins to decrease. A chain reaction has started: the more templates there are, the more primers are consumed in replication reactions. At equilibrium, the abundance of length-30 sequences is almost ten times its prelife value.

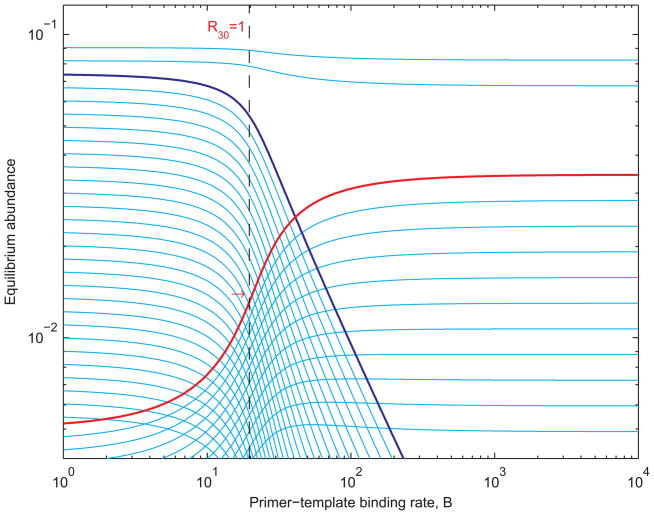
Figure 3 shows the equilibrium abundances of sequences of lengths 1 to 40, as functions of the primer-template binding rate B, when sequences of length 30 (red) replicate using length-3 primers (dark blue). As B varies, all other parameters are held constant. For small values of B, the equilibrium abundance of length-30 sequences remains close to its prelife value. Since primer-template binding is weak, double strands are slow to form and replication does not lead to a significant increase in the abundance of templates. For large values of B, the equilibrium abundance of templates is almost an order of magnitude greater than it is when B is 0. A high binding rate means that templates and primers associate rapidly to form double strands. Other factors, such as the rate at which double strands dissociate and the availability of primer and template precursors, then become rate-limiting. This is the reason for the saturation we observe at high B. As B increases through intermediate values, there is a dramatic increase in the equilibrium abundance of templates. The abundance is most sensitive to changes in B when B = 20.89.

Figure 3.

Equilibrium abundances of sequences of lengths 1 to 40 as functions of the primer-template binding rate, B. Sequences of length 30 (red) replicate using length-3 primers (dark blue). The broken line indicates where the basic reproductive ratio of length-30 sequences, R₃₀, equals 1 and the red arrow where the equilibrium abundance is most sensitive to changes in B. The single-strand elongation rate a is 10; the death rate d is 0.1; the double-strand dissociation rate D is 1; the template-directed elongation rate β is 500; and all other constants are 1.

We observe this transition from prelife to life, which is characterized by a high abundance of long replicating sequences, when other parameters are varied as well. For instance, as Figure 2 suggests, when β increases as all other parameters are kept constant, there is a critical range during which the equilibrium abundance of templates increases most rapidly. The same is true as D is increased. For fixed primer length k and template length n, the model parameter space—λ, α, a, d, B, D, and β take values in [0, ∞)⁷—consists of two regions. When the model parameters are in one region, the equilibrium structure is almost the same as for prelife. In the other region, template-directed polymerization dominates. The two regions are separated by a critical surface. As the parameters approach and cross this surface, there is a transition from prelife to life.

4 The critical surface

4.1 Calculation of the surface

Consider the following scenario. We start with the system (2), but the primer-template binding rate is zero and so no replication is possible. The system could be in a high temperature environment, for example. Sequence abundances settle to their prelife equilibrium values. Now the system’s environment cools, so binding of primers and templates can occur and replication begins. If the reaction rates cause templates to be more abundant at the new equilibrium than they were before replication was possible, then we are “above” the critical surface. For this to happen, the abundance of templates must increase from its prelife equilibrium value. If this increase is insignificant, then we are “below” the surface. Although replication is possible, the system essentially remains very close to its prelife equilibrium. Hence, we will find the critical surface by examining how the abundance of templates deviates from prelife equilibrium after double-strand formation becomes possible.

We assume that the template-directed elongation rate, β, is large enough to produce at least some complete copies before thermocycling results in strand dissociation. (This requirement motivated our restrictions on possible template length.) In this case, there is a separation of time scales, and we can make the steady-state assumption that ż_i = 0 for all i. Intuitively, if the elongation reactions are very fast, then the z_i adjust very quickly to the slower changes in x and the y_j.

At steady-state, we have

$$\begin{array}{l}{z}_k=\frac{{By}_k{y}_n}{\beta x+d},\\ z_{k+1}={\left(\frac{\beta x}{\beta x+d}\right)}^l{z}_k,l=2,\dots ,n-k-1,\\ z_n=\frac{\beta x}{D+d}{z}_{n-1}.\end{array}$$ (5)

It follows that

$$z_n=\frac{B}{D+d}{\left(\frac{\beta x}{\beta x+d}\right)}^{n-k}{y}_k{y}_n.$$ (6)

Equation (6) describes the relationship among the abundances x, y_k, y_n, and z_n at steady-state. The dynamical change of the template abundance is given by

$${\stackrel{.}{y}}_n={\mathit{axy}}_{n-1}-(ax+d)y_n-{By}_k{y}_n+2D{z}_n.$$ (7)

We evaluate (7) when x, y_k, y_n−1, and y_n are at their prelife equilibrium values. Longer sequences are exponentially less common than shorter sequences at prelife equilibrium, which is given by

$$\begin{array}{l}{x}^{\ast }=\frac{d}{2\alpha a}\left[\sqrt{{(\alpha +d)}^2+4\alpha \lambda \frac{a}{d}}-(\alpha +d)\right],\\ y_i^{\ast }=\frac{\alpha }{a}{\left(\frac{{ax}^{\ast }}{{ax}^{\ast }+d}\right)}^i.\end{array}$$ (8)

(A ^* denotes a quantity’s prelife equilibrium value.) Thus, for large n we can make the approximation ${\mathit{axy}}_{n-1}^{\ast }\approx 0$. After substituting (6), we find that the initial growth of templates at prelife equilibrium is

$${\stackrel{.}{y}}_n\approx \left[-{ax}^{\ast }-d+2D\frac{B}{D+d}{\left(\frac{\beta x^{\ast }}{\beta x^{\ast }+d}\right)}^{n-k}{y}_k^{\ast }-{By}_k^{\ast }\right]y_n.$$ (9)

The first two terms in brackets give the removal rate and the third and fourth terms the “production,” or replication, rate. The templates’ abundance will increase significantly when the production terms are larger than the removal terms. Let

$$R_n\equiv \frac{1}{{ax}^{\ast }+d}\left[\frac{2D}{D+d}{\left(\frac{\beta x^{\ast }}{\beta x^{\ast }+d}\right)}^{n-k}-1\right]{By}_k^{\ast }.$$ (10)

If R_n > 1, the production terms are larger than the removal terms, and the abundance of templates grows significantly. If R_n < 1, the removal terms are larger than the production terms, and the abundance of templates remains low, close to its prelife value. Thus the critical surface is R_n = 1. Note that we obtain a different surface for different values of the primer length k and the template length n.

Figure 2 shows how the abundance of sequences of length 30 (red) evolves in time for different parameter values. Figure 2(a) shows the progression towards prelife equilibrium. For Figure 2(b), sequences of length 30 replicate. Their equilibrium abundance is less than it is in prelife. This is expected since R₃₀ = 0.50, so the parameters that produce the dynamics lie below the critical surface. On the other hand, for Figure 2(c), R₃₀ = 5.00. The parameters are far above the critical surface, and the equilibrium abundance of templates is almost ten times its prelife value.

Figure 3 shows the equilibrium abundance of length-30 templates, in red, as a function of the primer-template binding rate B. The broken vertical line is the critical boundary R₃₀ = 1. The transition from low abundance to high abundance occurs as this boundary is crossed. The red arrow indicates the point at which the equilibrium abundance of templates is changing fastest as a function of B.

We can interpret R_n as a basic reproductive ratio (Anderson and May, 1979; May and Anderson, 1979; Nowak and May, 2000; Nowak, 2006). At prelife equilibrium, the average lifetime of a sequence is 1/(ax^* + d). Once replication begins, the rate at which a template is copied is

$$\left[\frac{2D}{D+d}{\left(\frac{\beta x^{\ast }}{\beta x^{\ast }+d}\right)}^{n-k}-1\right]{By}_k^{\ast }.$$ (11)

By multiplying this rate with the average lifetime, we obtain the basic reproductive ratio given by (10). Hence R_n is the expected number of templates that arise as copies of a single template, during its lifetime, at the onset of replication. R_n is an increasing, linear function of B—as more double strands are formed, more copies of the template are produced—and an increasing, saturating function of D (the dissociation rate) and β (the template-directed polymerization rate).

4.2 The discriminant

Let

$$\mathrm{\Delta }=\frac{2D}{D+d}{\left(\frac{\beta x^{\ast }}{\beta x^{\ast }+d}\right)}^{n-k}-1.$$ (12)

Observe that if Δ < 0, then R_n < 0. In particular, if Δ < 0, then R_n will never be greater than 1, regardless of how large B is. We call Δ the “discriminant.” The sign of the discriminant indicates whether selection of the templates is possible, regardless of the value of B.

We can write the condition Δ < 0 as

$$(n-k)log\left(\frac{\beta x^{\ast }}{\beta x^{\ast }+d}\right)<log\left(\frac{D+d}{2D}\right).$$ (13)

If we take d to be very small, then we can make the approximation

$$(n-k)log\left(\frac{\beta x^{\ast }}{\beta x^{\ast }+d}\right)\approx -(n-k)\frac{d}{\beta x^{\ast }}.$$ (14)

Hence we can rewrite (13) as

$$\frac{n-k}{\beta x^{\ast }}>\frac{1}{d}log\left(\frac{2D}{D+d}\right).$$ (15)

This says that if the average polymerization time (the time it takes to extend a primer to a full copy of the template) is too long, then the templates can never be selected. This is reminiscent of the “error threshold” of quasispecies theory if we rewrite the condition as

$$\frac{1}{\beta x^{\ast }}>\frac{C}{n-k},$$ (16)

where

$$C=\frac{1}{d}log\left(\frac{2D}{D+d}\right).$$ (17)

If the average time it takes to add one base (along the template) is greater than the inverse of the template length, then selection for the template is impossible, regardless of how fast double strands are formed. This limit leads naturally to our main scenario, in which the upper limit of template length is determined by the number of monomers that can be added before the next thermocycle.

5 Templates of many lengths

5.1 Reversals

For simplicity, we formulated the system (2) so that only sequences of length n can be templates, but we can extend the model so that all sequences with lengths in a certain range can replicate. We assume that the binding (B), dissociation (D), and elongation (β) rates are independent of a template’s length, and we continue to assume that primers have length k. R_n decreases as n increases because of the [βx^*/(βx^* + d)]^n−k term in (10). This means shorter templates have larger basic reproductive ratios than longer templates. Fewer monomers need to be polymerized to make a copy of a shorter template. Hence, the probability that a double-stranded intermediate is degraded during the replication process is smaller for shorter sequences.

Suppose all sequences with lengths between n₁ and n₂ can be templates. If n₁ ≤ n ≤ n₂, then a sequence of length n can arise in one of two ways: (1) it can be created as a direct copy of an already-existing sequence of length n (replication), or (2) it can be formed when a monomer is appended to the end of a sequence of length n − 1 (prelife extension). This coupling of templates by prelife extension can result in “reversals” in the length distribution in the sense that slower replicating, longer sequences become more abundant than faster replicating, shorter sequences (Manapat et al., 2009).

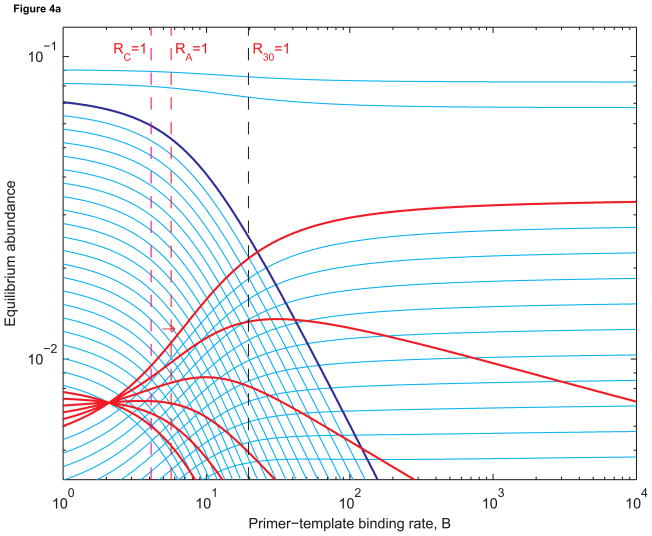
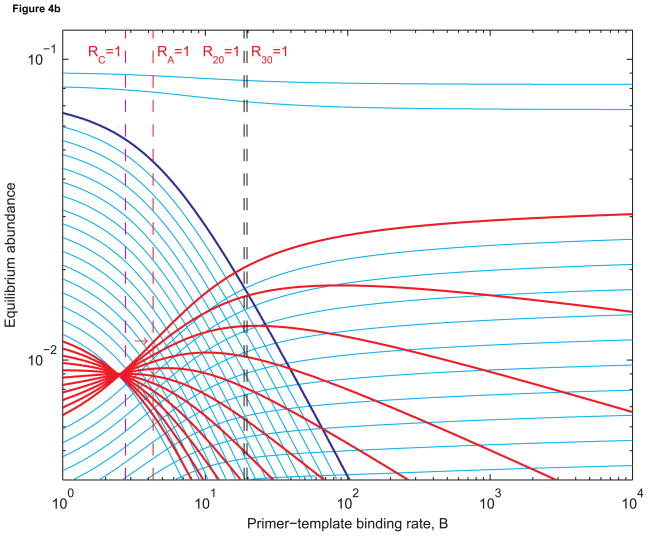
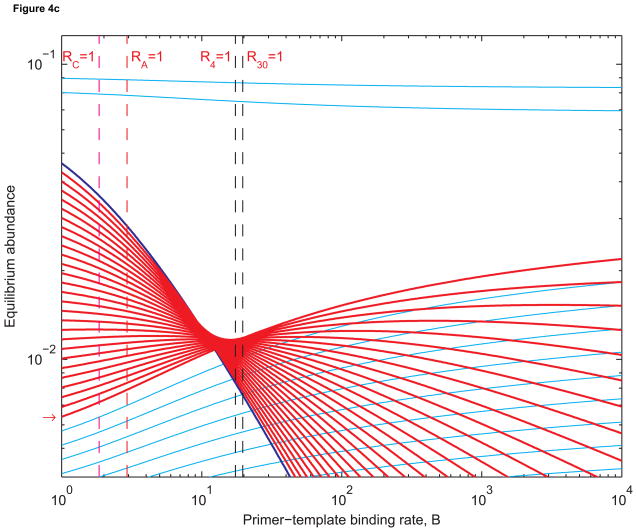
Figure 4 shows that the prelife equilibrium structure remains intact when B is small. In Figure 4(a), n₁ = 25 and n₂ = 30. In Figure 4(b), n₁ = 20 and n₂ = 30. In Figure 4(c), n₁ = 4 and n₂ = 30. Longer sequences are less abundant than shorter ones. This is expected since shorter sequences have larger basic reproductive ratios than longer sequences. As B increases, R_i increases for each i between n₁ and n₂. But it remains the case that R_i > R_j if i < j. When B is sufficiently large, however, the equilibrium abundance of length-j templates can be higher than that of length-i templates. When all templates are being replicated quickly, longer templates benefit from the fact shorter templates can be extended into longer ones by prelife polymerization. Hence we obtain reversals in equilibrium abundances such as the ones between B = 1 and B = 2 in Figures 4(a) and 4(b) and B = 10 and B = 11 in Figure 4(c).

Figure 4.

(a) Equilibrium abundances of sequences of lengths 1 to 40 as functions of the primer-template binding rate, B. Sequences of lengths 25 to 30 (red) replicate using length-3 primers (dark blue). The broken red line is where the chain amplification ratio R_A equals 1. In this case, the chain amplification ratio is the number of “second-generation” sequences of length 30 obtained from a single “first-generation” sequence of length 25. The broken magenta line is where the cumulative basic reproductive ratio, R_C, equals 1. The cumulative basic reproductive ratio is the total number of offspring produced by a single sequence of length 25 over its lifetime, even as it is extended to form longer sequences. The broken black line is where the basic reproductive ratios of sequence of length 25 to 30 are all (approximately) equal to 1. The red arrow indicates where the equilibrium abundance of length-30 templates is most sensitive to changes in B. The rate constants are as in Figure 3. (b) The same abundances when sequences of lengths 20 to 30 replicate. The broken black lines are where the basic reproductive ratios of sequences of length 20 and 30 equal 1. In both Figure 4(a) and 4(b), the equilibrium abundance of length-30 templates is increasing fastest close to where R_A = 1. (c) The abundances when sequencs of length 4 to 30 replicate: all sequences longer than the primer, up to the maximum length of 30, are templates. Here R_C = 1 is a better approximation of where the abundance of the longest templates is increasing most rapidly.

5.2 Subcritical life

When there are multiple templates linked together by prelife extension, we observe a phenomenon that we call “subcritical life.” Subcritical life is characterized by the existence of templates with R_n < 1 that nevertheless attain equilibrium abundances significantly greater than in prelife. In other words, there are templates for which the derivative of their equilibrium abundance, as a function of the binding rate B, is maximized at a value of B such that R_n < 1. Let ȳ_i(B) denote the equilibrium abundance of templates of length i as a function of B (all other parameters are held constant).

In Figure 3, only sequences of length 30 replicate, and the derivative ∂ȳ₃₀/∂B is maximized when B = 20.89 and R₃₀ = 1.06. In Figure 4(a), sequences of lengths 25 to 30 replicate. For large enough values of B, sequences of length 30 are most abundant. The derivative ∂ȳ₃₀/∂B is now maximized when B = 6.92 and R₃₀ = 0.35. In Figure 4(b), sequences of length 20 to 30 replicate, and ∂ȳ₃₀/∂B is largest when B = 4.50 and R₃₀ = 0.23.

Subcritical life has two interesting features. First, the value of B necessary to induce the transition from prelife to life decreases as the length of the chain of consecutive templates increases. Hence it is easier to select templates when there is a greater range of template lengths. For example, when there are six templates in the chain, the transition is steepest when B = 6.92 (Figure 4(a)). When there are eleven templates in the chain, the transition is steepest when B = 4.50 (Figure 4(b)). Second, the transition occurs at a value of B such that R_n < 1 not just for the template of maximal length but in fact for templates of all lengths in the chain. Subcritical life occurs because the abundance of the longest template is amplified not only by the replication of those sequences but also by the replication (and subsequent extension) of upstream sequences. Thus prelife can “jump-start” life.

We can now ask for a general condition that predicts the onset of subcritical life. When there are templates of just one length, this condition should reduce to R_n = 1. When sequences of many lengths can be templates, the condition should reflect the effects of prelife extension appropriately. We propose two candidates: the chain amplification ratio and the cumulative basic reproductive ratio.

5.3 The chain amplification ratio

Our first candidate is a quantity that reflects whether long sequences are amplified relative to short sequences. We begin with several definitions. A first-generation sequence of length n is one that is made by a prelife reaction (i.e., not by the copying of another sequence of length n). For example, a sequence that is obtained by extending one of length n − 1 is a first-generation sequence. A second-generation sequence is one that is a direct copy of a first-generation sequence. Consider a replicating sequence of length n. The basic reproductive ratio, R_n, is the expected number of second-generation sequences of length n that are obtained from a single sequence of length n at the onset of replication.

Suppose sequences of length n and n + 1 replicate. What is the expected number of second-generation sequences of length n + 1 that are obtained from a single sequence of length n (at the onset of replication)? We denote this quantity by R_n,n+1 and compute it as follows. Consider the initial sequence of length n. It will undergo one of three processes. (1) It can replicate at rate

$$r_n\equiv \left[\frac{2D}{D+d}{\left(\frac{\beta x^{\ast }}{\beta x^{\ast }+d}\right)}^{n-k}-1\right]{By}_k^{\ast }.$$ (18)

Each of the two resulting sequences will then yield R_n,n+1 second-generation sequences of length n + 1. (2) It can be lost through removal at rate d, yielding no sequences of length n + 1. Or (3) it can be extended to form a sequence of length n + 1 at rate ax^*. From the extended sequence, we eventually obtain R_n+1 second-generation sequences of length n. The probability of each of these events is proportional to the corresponding rate constant. Thus,

$$R_{n,n+1}=\frac{r_n}{r_n+d+{ax}^{\ast }}2R_{n,n+1}+\frac{d}{r_n+d+{ax}^{\ast }}·0+\frac{{ax}^{\ast }}{r_n+d+{ax}^{\ast }}{R}_{n+1},$$ (19)

from which we obtain

$$R_{n,n+1}=\frac{{ax}^{\ast }}{d+{ax}^{\ast }-r_n}{R}_{n+1}.$$ (20)

Since R_n = r_n/(d + ax^*), we can rewrite this as

$$R_{n,n+1}=\left(\frac{{ax}^{\ast }}{d+{ax}^{\ast }}\right)\left(\frac{1}{1-R_n}\right)R_{n+1}.$$ (21)

Suppose now that sequences of length n₁ to n₂ replicate. We define the chain amplification ratio, which we denote by R_A, to be the expected number of second-generation sequences of length n₂ obtained from a single sequence of length n₁. If R_A is greater than one, short sequences lead to more and more copies of long sequences. A generalization of (21) yields

$$R_A={\left(\frac{{ax}^{\ast }}{{ax}^{\ast }+d}\right)}^{n_2-n_1}\left(\prod _{j=n_1}^{n_2-1}\frac{1}{1-R_j}\right)R_{n_2}.$$ (22)

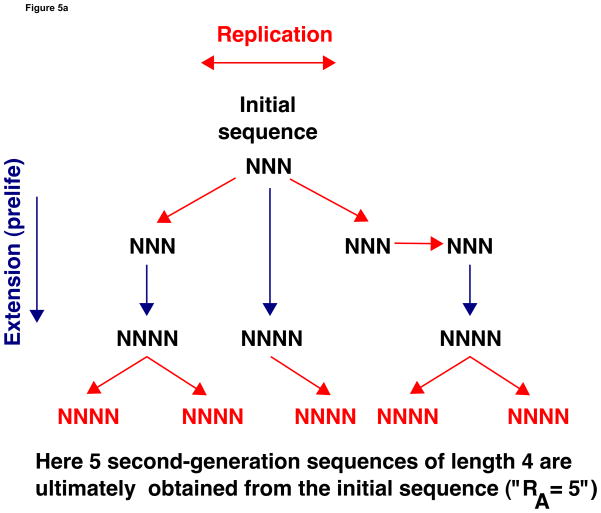
Figure 5(a) gives an example of the calculation of R_A when sequences of length 3 and 4 replicate. We start with a single template of length 3. This sequence replicates twice. One of the copies replicates again but then is lost (due to removal). There are three remaining sequences of length 3, each of which is extended to form a sequence of length 4. Thus there are three first-generation sequences of length 4. The offspring of these sequences—of which there are five—form the second generation. Hence R_A = 5 in this example, if the numbers are interpreted as averages.

Figure 5.

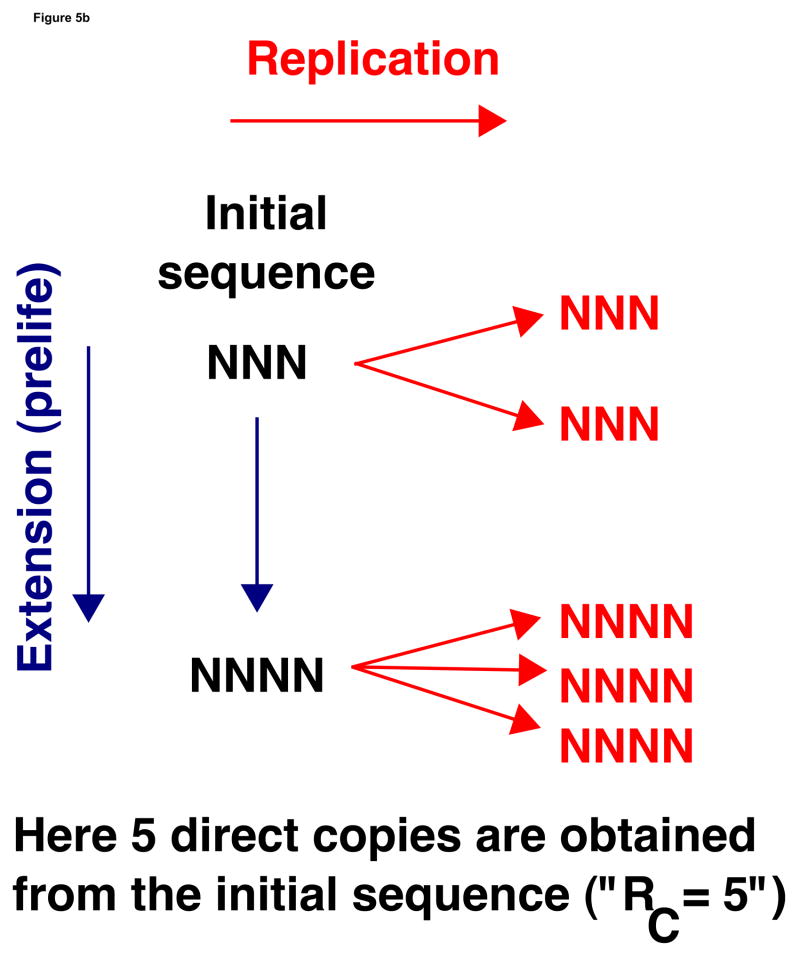
Suppose sequences of length n₁ to n₂ replicate and that a sequence of length i can be extended to form a sequence of length i + 1. (a) The chain amplification ratio R_A is the number of second generation templates of length n₂ obtained from a single template of length n₁. “Second generation” means that the sequence has exactly one other sequence of length n₂ in its production lineage. Here n₁ = 3, n₂ = 4, and R_A = 5, if the numbers are interpreted as averages. (b) The cumulative basic reproductive ratio R_C is the number of direct offspring of a sequence even as it is extended to form longer sequences. Again n₁ = 3 and n₂ = 4. The length 3 sequence is copied twice before being extended. The new length 4 sequence is copied three times before being extended. Thus R_C = 5, again if the numbers are interpreted as averages.

5.4 The cumulative basic reproductive ratio

Our second candidate is a quantity that reflects the number of copies made from a particular template throughout its entire lifetime in the system, even as it undergoes non-templated polymerization. We remain in the situation in which sequences of length n₁ to n₂ replicate. Suppose we tag a particular sequence of length n₁ just as replication begins. This is analogous to radioactive labeling of the 5′ end of an RNA sequence. Since extension occurs at the 3′ end, the tag is preserved as the sequence is extended, but copies of the RNA sequence do not have the tag. We can ask how many direct copies are made of the tagged sequence, even as it is extended to form longer and longer sequences. We call this quantity the cumulative basic reproductive ratio and denote it by R_C.

Consider first the case in which there are templates of just two lengths, so n₂ = n₁ + 1. The initial sequence of length n₁ will produce R_n1 direct copies before it is lost. When a sequence is lost, it is either removed completely, with probability d/(d + ax^*), or extended by non-templated polymerization, with probability ax^*/(d + ax^*). If it is extended, an additional R_n1 direct copies are made of the longer sequence. Hence,

$$R_C=R_{n_1}+\left(\frac{{ax}^{\ast }}{{ax}^{\ast }+d}\right)R_{n_1+1}.$$ (23)

Generalizing to arbitrary n₂ > n₁, we have

$$R_C=R_{n_1}+\left(\frac{{ax}^{\ast }}{{ax}^{\ast }+d}\right)R_{n_1+1}+{\left(\frac{{ax}^{\ast }}{{ax}^{\ast }+d}\right)}^2{R}_{n_1+2}+\cdots +{\left(\frac{{ax}^{\ast }}{{ax}^{\ast }+d}\right)}^{n-1}{R}_{n_2}.$$ (24)

Figure 5(b) gives an example of the calculation of R_C when sequences of lengths 3 to 4 are templates. We start with a template of length 3. Two copies of this length three sequence are produced. The tagged sequence is then extended, and three copies are made of the extension. In total, the sequence is copied five times, so R_C = 5, if the numbers denote averages.

In Figures 4, the broken red line indicates where R_A = 1 and the broken magenta line where R_C = 1. The red arrow indicates where the abundance of the longest templates is increasing fastest. We see that subcritical life begins close to R_A = 1 and R_C = 1. Thus, these quantities can be used to predict when the transition to subcritical life occurs. However, an analytical justification of this fact appears to be difficult.

6 The analogy with infection dynamics

The equations of our model suggest that life, characterized by highly abundant long sequences, can be viewed as an infection of prelife. Templates infect primers by turning them into other templates. But a primer can also be extended, by prelife, to form a template. This “spontaneous generation of infection” results in an equilibrium population structure that is much different from the structure when there is no “mutation” from uninfected hosts to infected hosts.

Bonhoeffer and Nowak (1994) study the following scenario. There are n types of infection, linearly ordered so that a host infected with type i can, by mutation of the pathogen, become a host infected by type i + 1. Pathogen i has basic reproductive ratio R_i. Let $w_i^{\ast }$ denote the equilibrium abundance of hosts infected by type i. They find that the equilibrium population is characterized as follows. If R_i < 1 for all i, then $w_i^{\ast }=0$ for all i. Suppose, on the other hand, that R_j > 1 for at least one j. Then $w_i^{\ast }>0$ for all i ≥ i₀ and $w_j^{\ast }=0$ for all j < i₀, where i₀ is such that R_i0 > R_k for all k ≠ i₀. In other words, if at least one of the pathogens has a basic reproductive ratio greater than one, then it is precisely the types that are downstream of the one with the highest basic reproductive ratio that survive at equilibrium.

Suppose now that there is spontaneous generation of infection. This means that uninfected hosts can spontaneously acquire an infection by type 1 (without having to come into contact with a host infected by type 1). It no longer makes sense to ask when the all-zeros equilibrium is stable. Since there is mutation from uninfected hosts, $w_i^{\ast }>0$ for all i. We can, however, ask the following. Suppose the transmissibility of all the pathogens is zero. There is a natural equilibrium in which $w_i^{\ast }>0$, for all i, due to mutation. How large do the transmissibilities have to be for the $w_i^{\ast }$ to be much greater than they are in the pre-transmission equilibrium?

We can frame this question in the context of our model (2). The system starts at prelife equilibrium. When template-directed synthesis becomes possible, templates can “infect” primers. What must be true of the parameters for the abundance of templates to increase significantly from the initial prelife values? We find that R_A = 1 and R_C = 1 are the crucial criteria in this case.

7 Conclusion

We have introduced a model of template-directed synthesis. Activated monomers enter the system and polymerize in a template-independent (slow) or template-dependent (fast) mechanism. For the purpose of analyzing this model, we have greatly simplified the scenario by neglecting the possibility of template-directed ligation (James and Ellington, 1997; Gao and Orgel, 2000), of a primer binding in the middle of a template to produce a shorter sequence, and of the breaking up of sequences to produce shorter sequences. Our assumptions correspond to an experimental scenario in which a defined primer sequence is used, activated polymers are scarce relative to activated monomers, and hydrolysis of the nucleic acid is relatively slow (Mansy et al., 2008). We also neglected the role of sequence diversity in order to focus on the length distribution.

We found that for some values of the kinetic rate constants, the equilibrium abundance of long templates remains low. This corresponds to a system with poor templating ability, where β is relatively low compared to a. For others, the equilibrium shifts rapidly toward long templates. A system with good templating ability, like RNA, would be characterized by a relatively large β. This shift in length distribution could be particularly important during the origin of life since a bias toward long sequences could increase the frequency of ribozymes in a protoell. We computed the critical surface in parameter space separating these two regions. In the case of a single template length, the surface is precisely the locus of points where the basic reproductive ratio equals one.

If there is a chain of templates, each being extended by non-templated polymerization into the next, long sequences can dominate even before the critical surface is reached. Even if each template is unviable on its own (i.e., has an R_n less than one), the equilibrium abundance of the longest templates in the chain can still be much larger than the equilibrium abundance of those sequences in prelife. This is not the result of Darwinian selection—all the sequences have basic reproductive ratios less than one and the differences in replication rate are minimal—but rather an effect of the interplay between chemical polymerization and replication. We have proposed two quantities, the chain amplification ratio and the cumulative basic reproductive ratio. These quantities are near one when then the transition from low to high abundance occurs for the longest templates. Prelife combines replication potentials: it links weak replicators together to jump-start life.