Internal Proton Transfer in the External Pyridoxal 5′-Phosphate Schiff Base in Dopa Decarboxylase

Abstract

Combined quantum mechanical and molecular mechanical (QM/MM) simulations of dopa decarboxylase have been carried out to elucidate the factors that contribute to the tautomeric equilibrium of the intramolecular proton transfer in the external PLP–L-dopa Schiff base. The presence of a carboxylate anion on the α-carbon of the Schiff base stabilizes the zwitterions and shifts the equilibrium in favor of the oxoenamine tautomer (protonated Schiff base). Moreover, protonation of the PLP pyridine nitrogen further drives the equilibrium toward the oxoenamine direction. On the other hand, solvent effects favor the hydroxyimine configuration, although the equilibrium favors the oxoenamine isomer with a methyl group as the substituent on the imino nitrogen. In dopa decarboxylase, the hydroxyimine form of the PLP(H+)–L-dopa Schiff base is predicted to be the major isomer with a relative free energy of −1.3 kcal/mol over that of the oxoenamine isomer. Both Asp271 and Lys303 stabilize the hydroxyimine configuration through hydrogen-bonding interactions with the pyridine nitrogen of the PLP and the imino nitrogen of the Schiff base, respectively. Interestingly, Thr246 plays a double role in the intramolecular proton transfer process, in which it initially donates a hydrogen bond to the phenolate oxygen in the oxoenamine configuration and then switches to a hydrogen bond acceptor from the phenolic hydroxyl group in the hydroxyimine tautomer.

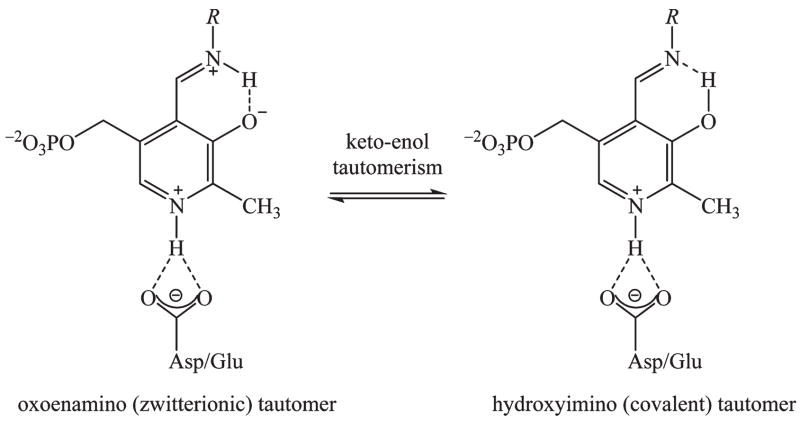
Pyridoxal 5′-phosphate (PLP),¹ derived from vitamin B₆, is a versatile enzyme cofactor that facilitates many chemical transformations, including racemization, decarboxylation, and transamination reactions (1). One important yet still not fully resolved question is the tautomeric equilibrium in the Schiff base of PLP, which involves an intramolecular proton transfer between the covalent hydroxyimine and zwitterionic oxoenamine configurations (Scheme 1). Here, we use the term “covalent” and “zwitterionic” to emphasize the difference in electronic structure between the tautomers. This equilibrium is a major factor affecting the reactivity of the PLP Schiff base in the active site (2). To understand the role of PLP cofactors in enzyme catalysis, it is critical to elucidate the position of the bridging proton in PLP-dependent enzymes (3). In this report, we present computational results from combined quantum mechanical and molecular mechanical (QM/MM) simulations to elucidate the factors that influence the tautomeric equilibrium of the external aldimine Schiff base, both in water and in the active site of dopa decarboxylase.

Scheme 1.

Tautomeric Equilibrium of an External PLP Aldimine in PLP-Dependent Enzyme

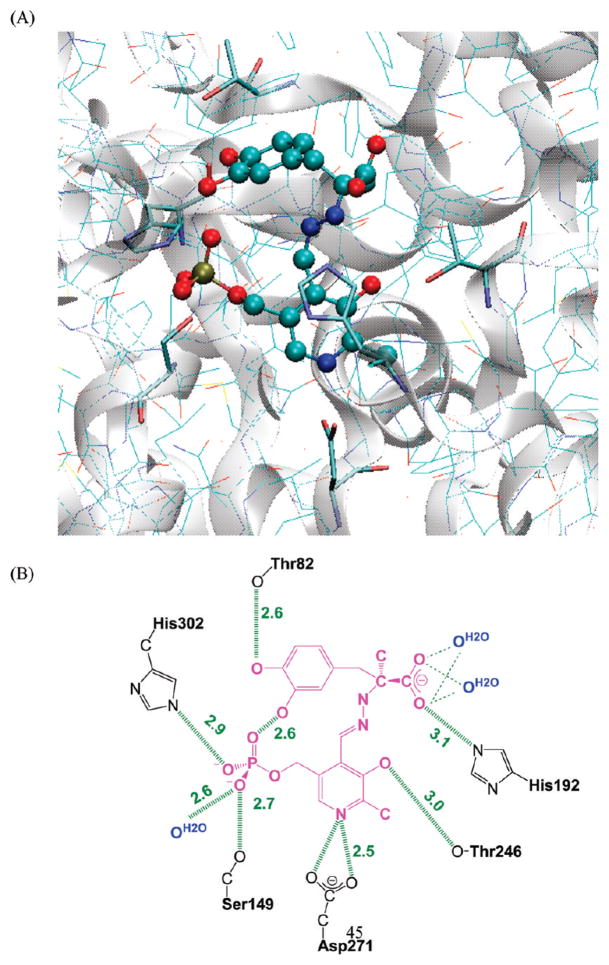
Dopa decarboxylase (DDC, EC 4.1.1.28) is a PLP-dependent enzyme, which catalyzes the irreversible decarboxylation reaction of aromatic L-amino acid substrates, such as dopa, phenylalanine, and tryptophan. DDC plays an important role in the conversion of the anti-Parkinson drug L-dopa into dopamine. The X-ray crystal structure (4) shows that the PLP cofactor forms an internal Schiff base with Lys303 in the absence of the substrate. The internal Schiff base is converted into the external PLP–L-dopa Schiff base, displacing Lys303 by the substrate L-dopa via a transaldimination process (4–6). The resulting PLP–L-dopa aldimine is embedded in an extensive hydrogen bond network in the enzyme (Figure 1), in which the side chain of Asp271 forms a salt bridge with the pyridine nitrogen of PLP (4). The active site residues, including Thr82, Ser149, Asn300, and His302, participate in hydrogen-bonding interactions with the phosphate group of the cofactor. Thr246 forms a hydrogen bond with the phenolic group of PLP, which plays a critical role in the hydroxyimine and oxoenamine tautomerization (4, 7, 8).

Figure 1.

Partial view of the active center of hog kidney dopa decarboxylase in complex with external PLP–carbiDopa Schiff base (PDB entry: 1JS3) (2). (A) PLP–carbiDopa Schiff base is shown in ball and stick. (B) Schematic depiction of hydrogen bond interactions (green dash lines), including structural water molecules (shown in blue) in the active site. The values indicate the hydrogen-bonding distances found in the X-ray structure. PLP–carbiDopa Schiff base is colored in magenta.

NMR, absorption, and fluorescence spectroscopic studies of model compounds for the internal and external aldimines showed that there is a keto–enol equilibrium, corresponding to an intramolecular proton transfer (3, 9–15). Kinetic and spectroscopic studies of aromatic amino acid decarboxylases with and without the substrate or a substrate analogue have been used to elucidate the physicochemical properties as well as the reaction mechanisms of the enzymatic processes (16–18). In the absence of substrate, PLP-dependent enzymes typically exhibit an absorption band in the range of 400–440 nm, corresponding to the oxoenamine configuration of the internal PLP–lysine aldimine (16). However, the absorption spectra of the internal PLP Schiff base of both rat liver and pig kidney DDCs show a prominent absorption maximum at 335 nm and a smaller absorption at 425 nm (16, 19–22). The former absorption has been attributed to the hydroxyimino aldimine tautomer (16). In addition, upon addition of the substrate, there is an increase in absorption at 425 nm, accompanied by a decrease at 335 nm. This variation is consistent with the formation of an initial L-dopa–enzyme complex that affects the tautomeric equilibrium of the internal aldimine (16). Subsequently, a new absorbance at 380–390 nm (16, 17) occurs, which has been suggested as the external aldimine in the oxoenamino conformation. It was proposed that the blue-shifted wavelength is due to a nonplanar structure of the oxoenamino PLP–aldimine cofactor. Alternatively, this new absorption band can be explained as the formation of an unprotonated form of the external PLP Schiff base (23), although it is catalytically inert in aspartate aminotransferase (24).

Several experimental studies have been reported to rationalize the tautomeric equilibrium and the intramolecular O···H···N hydrogen bond of small Schiff bases. Examination of X-ray structures of model compounds and analysis of Schiff bases reveal that the enol form is the dominant configuration (3,4,13,25,26), whereas there is a small number of examples with the bridging hydrogen on the imino nitrogen (25, 27). Furthermore, UV–vis and NMR show that the tautomeric equilibrium of Schiff bases is influenced by many factors, such as the substituent on the imino group (28–30), local polarity around the intramolecular hydrogen bond (28, 31), solvent polarity (3, 11, 31), temperature (11, 29), and the protonation state of the pyridine nitrogen (28, 30). Finally, hydrogen-bonding interactions with the phenolic oxygen of PLP cofactor can stabilize the keto tautomer (11, 31).

Previous theoretical investigations (15, 28, 31–35) focused on ab initio, DFT, and semiempirical calculations of Schiff bases in the gas phase with emphasis on substituent effects, intramolecular hydrogen bonds, and photochromic properties (15, 32–38). Kiruba et al. investigated solvent effects on PLP derivatives (39). Bach et al. (37) modeled the gas phase decarboxylation reaction of aminoformylacetic acid and the corresponding reaction in a cluster of six water molecules. Furthermore, the pyruvoyl-dependent enzymatic decarboxylation in histidine decarboxylase was investigated using ab initio and DFT methods (38). These calculations provided valuable insight into the electronic structure properties of the equilibrium and the effects of PLP cofactor on the decarboxylation.

Although a wealth of information has been accumulated on the hydroxyimine and oxoenamine tautomerism of PLP or PLP analogue Schiff bases, the location of the bridging proton of the intramolecular hydrogen bond in the enzyme active site remains elusive. Undoubtedly, this equilibrium is modulated by the specific electrostatic environment of a given enzyme. Our goal here is to understand the tautomeric equilibrium of the external PLP–L-dopa aldimine in dopa decarboxylase. Molecular dynamics (MD) simulation with a combined QM/MM potential is used to model the enzyme complexed with the external PLP Schiff base.

COMPUTATIONAL DETAILS

Model for the External PLP Schiff Base and Dopa Decarboxylase

The X-ray crystal structure of pig kidney DDC in a ternary complex with the PLP cofactor and carbiDopa inhibitor (PDB entry: 1JS3) (4) was used to generate the initial Michaelis complex structure containing the PLP–L-dopa external Schiff base. DDC is a homodimer, which consists of 486 amino acid residues in each subunit. There is only one active site and one PLP cofactor per dimer structure, located at the interface of the two monomers (16, 20, 41). The substrate, L-dopa, was constructed by modifying the structure of the carbiDopa inhibitor to yield the external Schiff base. The pK_a for the pyridine nitrogen of the external aldimine was recently established to be 5.8 in water due to the presence of the strongly electron-withdrawing imino group (3). This is significantly more acidic than the aldehyde form of the PLP cofactor itself, which has a pK_a of 8.5 (42, 43). In the active site, the crystal structure reveals that there is strong interaction between the pyridine nitrogen and the side chain of Asp271, a typical structural feature in PLP-dependent enzymes. However, the exact location of the proton, either on Asp271 or on pyridine, is unknown. Given that the pK_a of the pyridine of the external aldimine is somewhat more basic than a carboxylate group (3), we have kept the dopa-external aldimine protonated, (PLP(H+)–L-dopa), throughout the simulation. To study the intramolecular proton transfer reaction in the PLP(H+)-L-dopa Schiff base, we first built the structure of the oxoenamine tautomer. The residues in the missing loop (residue 328′–339′, where the prime indicates a residue from the second subunit) were modeled as follows. First, we reconstituted the missing loop in each monomer using the BUILD module in InsightII (Accelrys) (44). The phenol side chain of Tyr332′ forms a hydrogen bond with the carboxylate group of the substrate at a distance of 2.0 Å. The extended structure was subjected to 800 steps of the energy minimization using the adopted-basis Newton-Raphson method (45) (ABNR) with the side chain of Tyr332′ harmonically restrained and all the other residues held fixed using the CHARMM program (46). The active site residue Lys303, which is released from the internal aldimine Schiff base, was set neutral, ready for the next step in the reaction cycle. His192, His262, His348, His386, and His434 that form ion pairs or are exposed to the solvent were protonated, and we treated the remaining titratable residues corresponding to ionization states at pH 7. Although recent progresses have been reported on loop optimization (47–52), the computational results indicate that the procedure described above is adequate for the present study, which in turn validates the selection of the loop configuration in activity studies. This reconstructed enzyme system complexed with PLP(H+)–L-dopa Schiff base in the oxoenamino form was chosen as the initial structure in our simulations.

Potential Energy Function

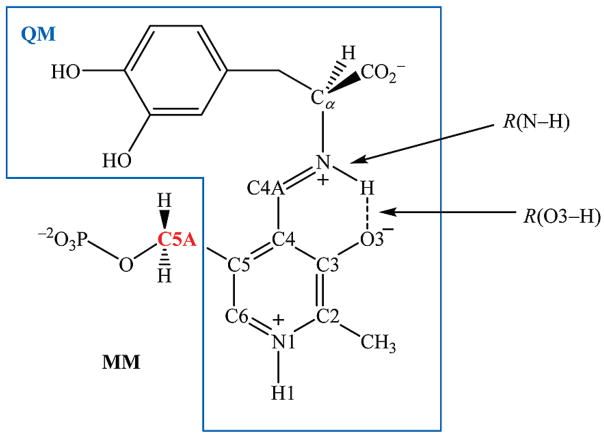
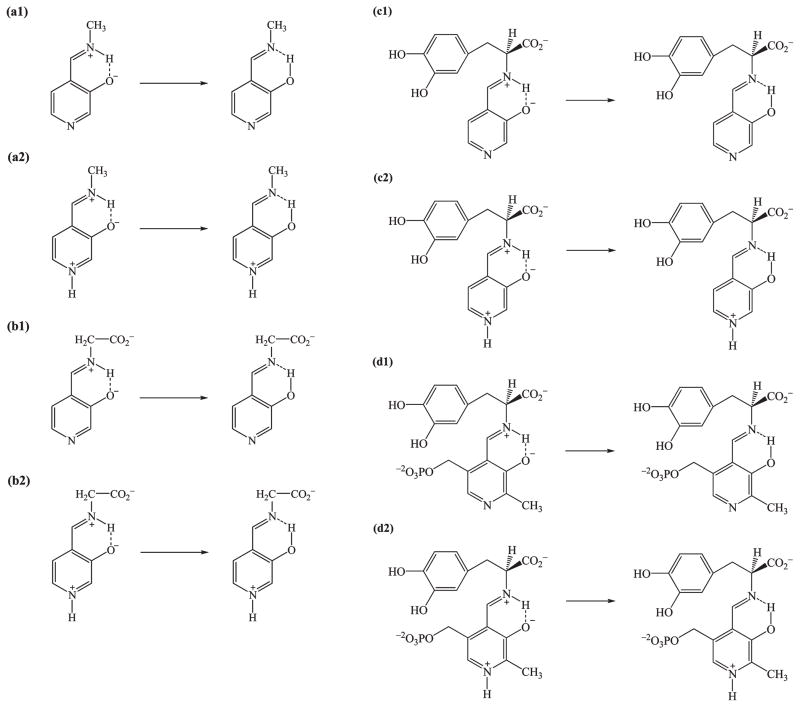
We used a dual-level (53–57) combined QM/MM (58–61) potential to describe the intramolecular proton transfer reaction of the PLP(H+)–L-dopa Schiff base in dopa decarboxylase. There are 39 atoms treated quantum mechanically by the Austin model 1 (AM1) (62) method (Figure 2). Previous calculations showed that the AM1 model can yield good geometrical results for the Schiff bases both in the ground and in the excited states in comparison with experiments and ab initio results (36, 63). To obtained accurate energetic results, we applied a dual-level approach (53–57), in which density functional theory (DFT) calculations were used as the high-level results to replace the semiempirical energies for the isolated “QM” species, while QM/MM interactions were determined at the lower level using the AM1/CHARMM potential. In hybrid QM/MM simulations, we placed the QM/MM boundary at the C5A position of the PLP(H+)–L-dopa Schiff base, which was treated with the generalized hybrid orbital (GHO) (64–66) method. All protein atoms and the phosphate group were modeled by the CHARMM22 all-atom force field (67), and water was represented by the three-point-charge TIP3P (68) model. To provide insight into solvation effects on the tautomeric equilibrium of the PLP Schiff base, we designed a total of eight model reactions, a1/a2, b1/b2, c1/c2, and d1/d2 (Scheme 2), for free energy simulations in aqueous solution. For reactions d1 and d2, the phosphate group was represented by the CHARMM22 force field (67), and the C5A atom was described as the GHO atom (65, 66).

Figure 2.

Partition of quantum and classical regions in combined QM/MM MD simulations for the PLP(H+)–L-dopa schiff base.

Scheme 2.

Model Reaction for Intramolecular Proton Trasfer Reaction in Aqueous Solution

Molecular Dynamics Simulations

Periodic boundary conditions along with the isothermal–isobaric (NPT) ensemble at 298.15 K and 1 atm were used, and long-range electrostatic effects are modeled using the particle-mesh Ewald method (PME–QM/MM) (69, 70). The leapfrog-Verlet integration scheme (71) was used in all simulations with a time step of 1 fs, and the nonbonded interaction list was updated on every 25 integration steps using a cutoff of 14 Å̇. The van der Waals energies were feathered to zero between 12 and 13 Å̇ with a shift function. All bonds involving hydrogen atoms, except those in the QM region, were constrained to their equilibrium distances using the SHAKE algorithm (72) during all dynamics simulations.

The initial enzyme system described above was embedded in a cubic box of water molecules about 89 × 89 × 89 Å̇³. Water molecules at distances less than 2.8 Å from any non-hydrogen protein atoms, the PLP(H+)–L-dopa Schiff base, or crystallographic waters were removed. The resulting system has a net charge of zero and no additional counterions were added. The final model of the enzyme system consists of 67518 atoms.

All water molecules were first minimized for 500 steps using the ABNR algorithm (45) to reduce initial close contacts, while the rest of the system was held constrained. This was followed by short simulations (5 ps) at 298.15 K to relax the water positions. Subsequently, we fixed the coordinates of all water molecules, the substrate PLP(H+)–L-dopa, and residues in the active site (Thr82, Ser149, His192, Thr246, Asp271, Asn300, His302, Lys303, Tyr332′, and Lys334′), and we optimized the rest of the system first by 500 steps of minimization to remove close crystallographic contacts. Then, the system was heated from 0 to 298.15 K in 30 ps of molecular dynamics simulations. After the initial setup, the entire system was relaxed and equilibrated at 298.15 K for 250 ps under harmonic restraints on non-hydrogen atoms of the PLP(H+)–L-dopa Schiff base and the active site residues listed above, and the force constants of these restraints were gradually changed from 50 to 5 kcal mol⁻¹ Å⁻². This ensures the relative positions of the external PLP aldimine and key residues in the active site to be maintained close to the X-ray structure. The structure at this stage was further equilibrated using the combined QM/MM potential for 100 ps without restraints, and the resulting structure was adopted as the starting configuration to perform the potential of mean force (PMF) calculations for the intramolecular proton transfer reaction in the enzyme.

For the eight model reactions in water, the center of mass of each reactant (i.e., oxoenamino tautomer) was placed at the center of a cubic water box. The lengths of edges for the cubic box for the smaller systems, a and b, are 30 and 45 Å for reactions c and d. In all QM/MM free energy simulations, each system was initially heated from 0 to 298.15 K within 30 ps, followed by an equilibration of least 60 ps with the solute restrained. Then, each system was equilibrated for an additional 250 ps in the absence of any restraint. The equilibrated structure of each model reaction was used for the following PMF calculations.

Free Energy Simulations

We carried out a series of umbrella sampling simulations to obtain the PMFs for the intramolecular proton transfer reaction of the PLP(H+)–L-dopa Schiff base in dopa decarboxylase enzyme and for each of the model reactions in aqueous solution. For each reaction, the bridging hydrogen was transferred from the imino nitrogen to the phenolic oxygen, corresponding to the tautomerization reaction of oxoenamino isomer → hydroxyimino isomer. The reaction coordinate, as depicted in Figure 2, is defined as z ≡ R(N–H) –R(O3–H). We used a total of 13–18 simulation windows for the model reactions in water and 29 windows for the enzymatic process. For the model reactions, each simulation window consisted of 50 ps for equilibration, followed by an additional 50 ps for averaging. For the enzymatic reaction, we performed 10 ps of equilibration, followed by 30 ps for averaging and trajectory collection for each window. Overall, a total of 1.55 ns of MD simulations for the enzyme system was performed. The weighted histogram analysis method (WHAM) (73) was used to analyze the probability density and to obtain the free energy profiles for the unbiased systems along the proton transfer reaction coordinate, z.

Interaction Energy Decomposition

The interaction energy decomposition method has been widely applied to enzymes (55, 74–81), which is adopted in the present study to probe electrostatic contributions from each residue on the tautomeric equilibrium of the external PLP(H+)–L-dopa Schiff base in the active site of DDC. We used 300 configurations to calculate the average interaction energies for each tautomer. For each configuration, we sequentially zeroed the MM charges of one residue and calculated the QM/MM energies in the order of the distance between the C_α atom of the residue and the bridging hydrogen of the Schiff base. The energy difference between the total QM energies that include (I) and exclude (I – 1) residue I corresponds to the electrostatic interaction energy between residue I and the QM system (PLP(H+)–L-dopa Schiff base):

$$\begin{array}{c}\mathrm{\Delta }{E}_{\text{elec}}(\text{I})=[E_{\text{QM}}(\text{I})+E_{\text{QM}/\text{MM}}(\text{I})]-[E_{\text{QM}}(\text{I}-\text{1})\\ +E_{\text{QM}/\text{MM}}(\text{I}-1)]\end{array}$$ (1)

where E_QM(I) is the energy of the “QM” subsystem and E_QM/MM(I) is the interaction energy between the QM region and the rest of the system in which residue I is included. The last two terms in eq 1 represent energies computed when residue I is excluded in the decomposition analysis (55, 74–81). Since the most interesting quantity is the differential electrostatic interaction energies in going from the oxoenamino to the hydroxyimino tautomer, we computed and reported the difference for this reaction in Figure 5:

$$\mathrm{\Delta }\mathrm{\Delta }{E}_{\text{elec}}(\text{I})=\mathrm{\Delta }{E}_{\text{elec}}^{\text{enol}}(\text{I})-\mathrm{\Delta }{E}_{\text{elec}}^{\text{keto}}(\text{I})$$ (2)

Figure 5.

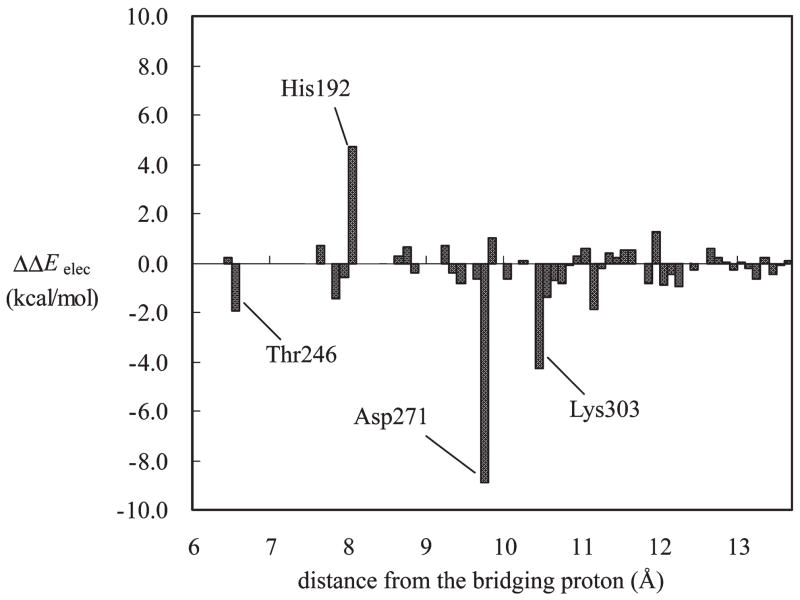
Residual contribution of dopa decarboxylase to the relative stabilization between the oxoenamino and hydroxyimino PLP-(H+)–L-dopa Schiff base as a function of the distance between the C_α atom of residue I and the bridging hydrogen of the intramolecular hydrogen bond in the dopa external aldimine. The residue numbers with contributions of more than 2 kcal/mol are indicated.

RESULTS AND DISCUSSION

We have studied the intramolecular proton transfer reaction of PLP(H+)–L-dopa Schiff base in dopa decarboxylase using a combined QM/MM potential with MD simulations. We used a dual-level approach to compute the potential of mean force for the intramolecular proton transfer reaction (tautomeric equilibrium), in which the intrinsic (gas phase) free energy change was determined using Gaussian03 (82) at the B3LYP/6–311 + G(d,p) level (83) and the semiempirical QM(AM1)/MM model was adopted to obtain solvation effects as the lower level model. For comparison, we also estimated the solvation effects by using the polarizable continuum model (PCM) (84,85), which provides a validation of the QM/MM simulations. In what follows, we first examine the effect of protonation at the pyridine ring in the external Schiff base and then functional group substitution on the imino nitrogen. We compare solvation results from the dual-level QM/MM simulations with those from PCM calculations. The PMF for the intramolecular proton transfer reaction of the PLP(H+)–L-dopa substrate in dopa decarboxylase is examined, with special emphasis on individual residue contributions in the active site. Finally, we discuss biological implications arising from these results.

(A) Hydroxyimine and Oxoenamine Tautomerism in the External PLP Aldimine

There are two main factors contributing to the tautomeric equilibrium of the PLP Schiff base: (a) the protonation state of the pyridine ring and (b) the substituent on the imino nitrogen of the Schiff base. The pyridine nitrogen of the external aldimine substrate has a pK_a of about 5.8 in aqueous solution (3), which is unprotonated under physiological conditions. However, in the active sites of most PLP-dependent enzymes, the pyridine nitrogen is assumed to be protonated due to stabilization through ion pair interactions with a basic residue such as Glu and Asp or hydrogen bonding to polar residues such as Ser and Thr. In the present case of DDC enzyme, Asp271 is the counterion of the pyridinium ion of PLP. In exceptional situations, such as in the active site of alanine racemase (81, 86, 87), the pyridine nitrogen is unprotonated and accepts a hydrogen bond from an arginine residue.

The protonation state of the pyridine nitrogen directly affects the tautomeric equilibrium between the hydroxyimino and oxoenamino isomers, which is reflected by the free energy difference between reactions 1 and 2 (Table 1). Protonation at the pyridine nitrogen shifts the intrinsic tautomeric equilibrium toward the oxoenamino direction with a free energy change of ca. 5 kcal/mol. In this case, the protonated pyridine ring acts as an electron sink, stabilizing the phenolate anion configuration through induction effects. Therefore, the positive charge of the protonated pyridine ring favors electrostatic stabilization of the zwitterionic configuration more than that of the covalent neutral tautomer.

Table 1.

Computed Free Energies of Tautomerization Reaction (Oxoenamino → Hydroxyimino) for the Model Reactions Located in the Gas Phase and in Aqueous Solution and for the Reaction in Dopa Decarboxylase at 298.15 K^a

reaction	ΔGgas	ΔGPCMe	ΔGPMF′f
a1	−4.4b	0.7	1.4
a2	0.4b	1.9	2.9
b1	2.3b	2.3	−0.1
b2	7.4c	3.6	−2.4
c1	0.9b	0.7	−0.7
c2	7.0c	1.4	−1.3
d1	5.0d	3.4	−0.9
d2	7.1c	9.4	−2.0
d2 in DDC			−1.3

^aAll energies are given in kcal/mol.

^bB3LYP/6–311+G(d,p)//B3LYP/6–311+G(d,p).

^cB3LYP/6–311+G(d,p)//HF/6–311+G(d,p).

^dB3LYP/6–311+G(d,p)//HF/6–31+G(d).

^ePolarizable continuum solvation free energies were calculated using B3LYP/6–311 +G(d,p) at the optimized structures indicated in the gas phase calculations.

^fCorrection of B3LYP/6–311+G(d,p) gas phase energy has been made to the lower level (AM1) energy; i.e., $\mathrm{\Delta }{G}_{\text{PMF}}=\mathrm{\Delta }{G}_{\text{PMF}}^{\text{AM}1}-\mathrm{\Delta }{G}_{\text{gas}}^{\text{AM}1}+\mathrm{\Delta }{G}_{\text{gas}}^{\text{B}3\text{LYP}/6-311+\text{G}(\text{d},\text{p})//\text{AM}1}$.

Substituent effects at the imino site of the PLP Schiff base are revealed in the series of reactions depicted in Scheme 2. Reaction b introduces a carboxylate group, whereas reaction c models the full L-dopa substrate. For reaction b, the α-carboxylate group stabilizes the oxoenamino isomer by about 7 kcal/mol both in the unprotonated and in the protonated pyridine systems in comparison with the parent compounds in reaction a. Similarly, the inclusion of the L-dopa group in reaction c results in similar effects, indicating that the oxoenamino tautomer gains greater stabilization in the presence of a carboxylate substituent at the imino nitrogen. The carboxylate effects can be attributed to ion pair interactions between the carboxylate ion and the zwitterionic Schiff base (b–d).

The results presented in the second column of Table 1 are consistent with recent experimental findings by Limbach, Toney, and co-workers (30, 31). Sharif et al. showed that the intramolecular proton transfer is coupled with hydrogen-bonding interactions at the pyridine ring. A protonated pyridine strongly favors the oxoenamino form of the Schiff base in the solid state and in polar aprotic solvents (30, 31). However, the intramolecular hydrogen bond is not coupled to the protonation state of the pyridine ring in aqueous solution (3). This has been attributed to competing hydrogen-bonding interactions with water, causing the imino group to rotate out of the aromatic plane. This observation is in accord with the results of reaction a1 (Scheme 2) in Table 1. In addition, the results in Table 1 show that solvation effects strongly favor the hydroxyimino configurations for reactions b–d when the pyridine nitrogen is protonated. This is because the carboxylate anion and pyridinium cation are separated without the interference of an internal zwitterion pair.

(B) Solvation Effects on the Tautomeric Equilibrium of PLP Schiff Base

The free energy results derived from the PMF for the intramolecular proton transfer in the hydroxyimine and oxoenamine tautomerization in aqueous solution, ΔG_PMF, are summarized in Table 1. Calculated dipole moments in the gas phase (μ_gas)and in aqueous solution (μ_aq) and the induced dipole moments from vacuum to water solution (Δμ_ind) are listed in Table 2.

Table 2.

Computed Dipole Moments (in D) in the Gas Phase (μ_gas) and in Aqueous Solution (μ_aq) Using DFT, ab Initio, and PCM Methods

reaction	tautomeric state	μgasa	μaqb	Δμindc
a1	oxoenamino	7.29	10.17	2.88
	hydroxyimino	5.05	6.78	1.73
a2	oxoenamino	4.37	6.64	2.27
	hydroxyimino	5.77	8.28	2.51
b1	oxoenamino	8.20	9.71	1.51
	hydroxyimino	11.11	13.41	2.30
b2	oxoenamino	18.64	23.06	4.43
	hydroxyimino	22.13	27.80	5.66
c1b	oxoenamino	7.15	8.71	1.56
	hydroxyimino	7.91	10.58	2.67
c2b	oxoenamino	19.11	23.68	4.57
	hydroxyimino	20.93	26.81	5.88
d1b	oxoenamino	12.45	16.41	3.96
	hydroxyimino	12.90	16.77	3.87
d2b	oxoenamino	15.76	20.48	4.72
	hydroxyimino	18.18	23.28	5.11

^aDipole moments μ_gas were calculated at HF/6–311 +G(d,p) with fully optimized geometries using the methods as described in the footnote of Table 1.

^bDipole moments μ_aq were calculated using thhe PCM method at HF/6–311 +G(d,p) with fully optimized geometries using the same method as described in the footnote of Table 1.

^cInduced dipole moment, Δμ_ind, is defined as Δμ_ind = μ_aq − μ_gas.

For the parent system, we found that solvation stabilizes the oxoenamino isomer of the PLP Schiff base by 5.8 and 2.5 kcal/mol for reactions a1 and a2, respectively, relative to the gas phase equilibrium. In the unprotonated pyridine system, the oxoenamino tautomer has a larger dipole moment than the hydroxyimino configuration, resulting in greater solvation effects in water (11). This is further reflected by a larger induced dipole moment in the oxoenamino isomer ( $\mathrm{\Delta }{\mu }_{\text{ind}}^{\text{keto}}=2.9\text{D}$) than that in the hydroxyimino tautomer ( $\mathrm{\Delta }{\mu }_{\text{ind}}^{\text{enol}}=1.7\text{D}$) for reaction a1. On the other hand, when the pyridine is protonated, solvent effects on the tautomeric equilibrium are less pronounced in a2 than in a1 since the dominant factor is the solvation of the cation. For comparison, the results from the PCM are in reasonable accord with explicit simulations (Table 1).

For reactions b and c, aqueous solvation stabilizes the hydroxyimino tautomer by −2.4 and −1.6 kcal/mol, respectively, when the pyridine ring is unprotonated, and the effects are increased to 8–10 kcal/mol if pyridine is protonated. Similarly, in the full PLP–L-dopa Schiff base model in reaction d, the proton transfer from oxoenamine to hydroxyimine is strongly favored by −5.9 and −9.1 kcal/mol in water for d1 and d2, respectively. The hydroxyimino form of the tautomer in reactions b–d can gain greater solvation stabilization of the carboxylate and pyridinium groups without the interference of an internal _witterions. Furthermore, we found that the induced dipole moments (Δμ_ind) for the hydroxyimino tautomers are greater than that for the oxoenamino isomers (Table 2). In comparison with the results from the PCM calculations, the trends from QM/MM simulations are reasonably reproduced, except that in reaction d2. In the latter case, the dihydroxyphenyl group in the optimized structures of the hydroxyimino and oxoenamino tautomers in reaction d2 is closer to the pyridine ring in the hydroxyimino conformation (see Supporting Information), resulting in a smaller solvent-accessible surface. Consequently, the hydroxyimino structure is poorly solvated in comparison with the more exposed configurations sampled in explicit simulations.

On the experimental side, Sharif et al. studied the chemical shifts of the Schiff base of PLP analogues in aqueous solution at different pHs (3). It was found that the pK_a values of the ring nitrogen and the imino nitrogen are 5.8 and 11.4, respectively, for methylated Schiff base systems. The computational results are consistent with experiments in that the oxoenamino form of the aldimine in reaction a is more stable in aqueous solution both in the protonated and unprotonated form of the pyridine ring (Table 1).

Listed in Table 3 are the average bond distances associated with the intramolecular hydrogen bond, i.e., between atoms O3–H (r_O3–H), N–H(r_N–H), and O3–N(r_O3···N), and the dihedral angle of φ_{N–C4A–C4–C3} (Figure 2) depicting out-of-plane torsion of the Schiff base. For all reactions, the donor–acceptor distances (r_O3···N)are shorter in _witterions configurations than neutral hydrogen bond pairs, thanks to electrostatic interactions. The intramolecular ion pair interactions restrict the protonated Schiff base to stay in the planar configuration characterized by relatively small dihedral fluctuations in a range of −5° to 7°. On the other hand, the average dihedral angles (φ_{N–C4A–C4–C3}) for the hydroxyimino isomers exhibit a greater degree of flexibility, ranging from ±17° to ±163°. Furthermore, in most cases, the average dihedral angles are far from planarity with the aromatic ring, suggesting that the PLP Schiff base does not maintain strong intramolecular hydrogen bonding in solution, consistent with the findings of ref 3. In contrast, geometry optimizations using the PCM continuum model always result in planar structures, favoring intramolecular hydrogen bonds, which is a clear illustration of the difference between a single structural optimization and dynamics simulations at a finite temperature.

Table 3.

Averaged Bond Distances and Dihedral Angle for the Intramolecular O3···H···N Hydrogen-Bonding Interaction in the Oxoenamino and Hydroxyimino Tautomers of the PLP Schiff Bases in Aqueous Solution^a,^b and in DDC Enzyme^a,^c

reaction	tautomeric state	rO3–H	rN–H	rO3···N	φN–C4A–C4–C3
a1	oxoenamino	2.16 ± 0.11	1.01 ± 0.03	2.84±0.08	1.6 ± 9.4
	hydroxyimino	0.98 ± 0.02	4.14±0.56	3.99±0.22	−66.2±126.6
a2	oxoenamino	2.20 ± 0.13	1.02 ± 0.03	2.86 ± 0.08	−4.6 ± 10.2
	hydroxyimino	0.98 ± 0.03	4.00±0.61	4.02±0.14	100.6±111.9
b1	oxoenamino	2.17 ± 0.10	1.01 ± 0.02	2.84±0.07	7.4±9.9
	hydroxyimino	0.98 ± 0.03	4.92±0.24	4.03 ± 0.11	−5.4±163.4
b2	oxoenamino	2.20±0.12	1.01 ± 0.02	2.85 ± 0.08	−3.2±12.5
	hydroxyimino	0.98 ± 0.03	3.05 ± 0.73	3.23 ± 0.25	−59.7±26.3
c1	oxoenamino	2.18 ± 0.13	1.01 ± 0.03	2.85 ± 0.10	−3.2±12.5
	hydroxyimino	0.97± 0.03	4.55 ± 0.58	4.05 ± 0.16	39.4±148.8
c2	oxoenamino	2.21 ±0.13	1.01 ± 0.03	2.87 ± 0.08	1.9±12.7
	hydroxyimino	0.98 ± 0.03	3.70 ±0.36	2.94±0.14	−41.6 ±17.4
d1	oxoenamino	2.15 ± 0.12	1.01 ± 0.03	2.80±0.07	7.2±10.6
	hydroxyimino	0.97±0.03	2.63 ± 0.46	3.05±0.17	46.9±20.8
d2	oxoenamino	2.17±0.12	1.02 ± 0.03	2.81 ± 0.08	4.2±17.0
	hydroxyimino	0.98 ± 0.02	2.55 ± 0.46	2.98±0.16	−15.3±44.2
d2 in DDC	oxoenamino	2.11 ± 0.11	1.03 ± 0.03	2.76±0.07	−14.6±10.3
	hydroxyimino	0.98 ± 0.03	3.29±0.57	3.26 ±0.31	79.8±34.7

^aAll distances are given in angstroms and angles in degrees. Standard deviations in the average distances and dihedral angles have been shown for each value.

^bAveraged over 50 configurations of the last 50 ps MD trajectories.

^cAveraged over 200 configurations of the last 100 ps MD trajectories.

(C) The PLP(H+)–L-Dopa External Schiff Base in Dopa Decarboxylase

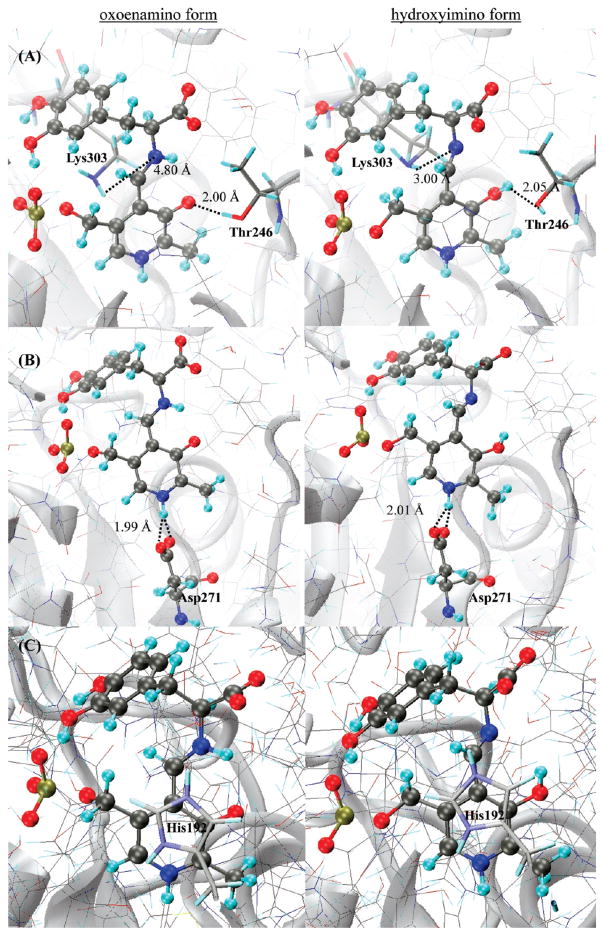
The active site of dopa decarboxylase is located at the interface of two monomers, in which the PLP(H+)–L-dopa Schiff base is embedded in a network of hydrogen bonds coupled with hydrophobic interactions. The hydrogen-bonding network between the PLP external aldimine and active site residues is crucial in controlling the cofactor reactivity. In PLP-dependent enzymes, the phenolic oxygen of the PLP is stabilized by various hydrogen bond-donating residues, such as tyrosine and asparagine in aspartate aminotrasferases. In DDC, Thr246 is in close proximity of the phenolic oxygen. For the oxoenamino tautomer, Thr246 donates a hydrogen bond to the phenolate anion, ^PLPO3⁻ ···Hγ1^Thr246, at an average distance of 2.0 Å (Table 4 and Figure 3A). Interestingly, we found that Thr246 becomes a hydrogen bond acceptor from the phenolic hydroxyl group in the hydroxyimino isomer. The average distance for the interaction, ^PLPO3–H ···Oγ1^Thr246, is 2.1 Å (Figure 3A). Thus, a conformational switch involving the hydroxyl group of Thr246 is coupled to the intramolecular proton transfer reaction. Moreover, the average φ_{N–C4A–C4–C3} dihedral angle changes from about −15 ± 10° in the oxoenamino configuration to 80 ± 35° (Table 3) in the hydroxyimino isomer, indicating that the intramolecular hydrogen bond with the Schiff base is disrupted. In the latter isomer, the imino nitrogen of the external aldimine forms a weak hydrogen bond with the side chain of Lys303 at an average distance of 3.0 Å (Figure 3A).

Table 4.

Selected Average Distances r_A–B (Å) between Oxoenamino or Hydroxyimino Tautomer of PLP(H+)–L-Dopa Schiff Bases and Enzyme Residues in the Active Site of DDC

PLP(H+)–L-dopa	residue	oxoenamine	hydroxyimine	X-ray
O3	Hγ1, Thr246	2.00±0.13	3.41 ± 0.21
H	Oγ1, Thr246	3.61 ± 0.25	2.05±0.29
O3	Oγ1, Thr246	2.83 ± 0.12	2.87±0.17	3.03
H1	Oδ1, Oδ2, Asp271	1.99 ± 0.23	2.01 ± 0.22
N1	Oδ1, Oδ2, Asp271	2.89 ± 0.16	2.91 ±0.17	2.78
C4A	Hε2, His192	3.95 ± 0.23	3.65±0.27	3.99
Cα	Hε2, His192	4.63 ± 0.23	5.19 ± 0.29
OCO2	Hε2, His192	3.77± 0.28	4.28±0.39
C4A	Nζ, Lys303	3.50± 0.18	4.01 ± 0.27	2.84
N	Hζ, Lys303	3.86 ± 0.27	3.00±0.41
H	Nζ, Lys303	4.80± 0.26	5.73±0.44
OCO2	Hη, Tyr332B	1.86±0.13	1.91 ±0.16

Figure 3.

Snapshots of active site pocket of dopa decarboxylase with oxoenamino and hydroxyimino PLP(H+)–L-dopa Schiff bases. PLP(H+)–L-dopa Schiff bases are displayed in ball and stick, and the specific amino acid residues, (A) His192, depicted in thick sticks, (B) Asp192, and (C) Lys303 and Thr246, are shown in ball and stick.

The pyridine nitrogen of the cofactor is protonated in DDC, forming an ion pair with Asp271, ^PLPN1⁺–H···Oδ^Asp271. A protonated pyridine ring is critical for catalysis and has been proposed to serve as an electron sink to stabilize the carbanionic intermediate produced in the catalytic step. The average H···Oδ^Asp271 distance is about 2.0 Å from the present QM/MM simulations (Table 4 and Figure 3B). Previously, Hayashi et al. (16,88) showed that both the protonated and unprotonated α-amino substrate L-dopa can bind to rat liver DDC to form the Michaelis complex, which is subsequently converted into the external aldimine. If the α-amino group is protonated, a basic residue is needed to remove the proton, and His192 can fulfill this role. Our MD simulations show that the imidazolium group of His192 is stacked above the pyridine ring of the PLP and interacts with the carboxylate group of the external aldimine at average distances of 3.8 and 4.3 Å (Table 4 and Figure 3C).

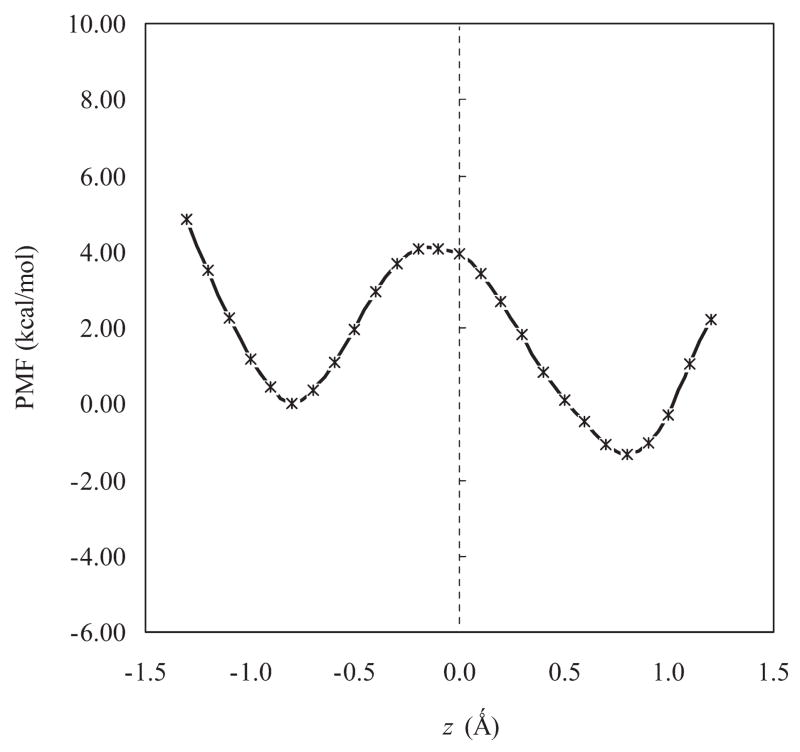
Figure 4 shows that the covalent hydroxyimino tautomer is preferred by −1.3 kcal/mol over the oxoenamino configuration in the active site, and a similar preference is found in aqueous solution for reactions b and c (Table 1). Note that the hydroxyimino configuration of the dopa external aldimine is not a local minimum using the hybrid DFT method, although a free energy of about 7 kcal/mol can be estimated at the HF/6-31+G(d) geometry.

Figure 4.

Computed dual-level potential of mean force for the tautomerization reaction (oxoenamino form → hydroxyimino form) of PLP(H+)–L-dopa Schiff base in dopa decarboxylase.

The relative interaction energies of individual residues with the hydroxyimino and oxoenamino tautomers are depicted in Figure 5. Not surprisingly, Asp271 makes the largest differential electrostatic contributions to the PLP(H+)–L-dopa tautomeric equilibrium thanks to the ion pair interactions with the protonated pyridine. However, in contrast to the findings for model compounds in the solid state and in polar aprotic solvents, in which intermolecular hydrogen bonds favor the oxoenamine configuration, Asp271 strongly stabilizes the hydroxyimino tautomer by nearly 9 kcal/mol. We attribute this finding to enhanced charge localization to favor ion pair interactions in the covalent configuration of the Schiff base (Scheme 1). Lys303 also has strong stabilizing contributions to the neutral imino nitrogen of the cofactor, whereas the interactions are repulsive in the protonated Schiff base. Interestingly, His192, which is stacked over the pyridine ring, interacts more favorably with the oxoenamino zwitterion configuration than with the hydroxyimino tautomer by 4.7 kcal/mol. We note that mutations of active site residues have significant effects on enzymatic activity (8).

Barboni et al. reported that the binding of L-dopa methyl ester (DopaOMe) in pig kidney DDC caused the appearance of a new absorbance at 390 nm (17). DopaOMe is an analogue of L-dopa, which forms the external aldimine with the PLP cofactor but is incapable of decarboxylation. Thus, it is used as a model for the Michaelis complex of the external aldimine. Hiyashi et al. found a similar phenomenon in the binding of L-dopa to rat liver DDC, accompanied by the appearance of an absorption band at 380 nm (16). The species at 380–390 nm absorption was suggested to be the oxoenamine tautomer of the external PLP Schiff base; however, oxoenamino PLP Schiff bases typically have an absorption peak in the range of 400–440 nm (16–19,21,22). The blue shift of the absorption has been proposed to be either due to a nonplanar structure of the PLP Schiff base with the imine group orthogonal to the pyridine ring or due to a special active site environment and hydrogen bonds to PLP (16). Although the present simulations show that the imine group and the pyridine ring of the oxoenamino form PLP(H+)–L-dopa Schiff base roughly maintain a coplanar configuration, there is a significant degree of conformational flexibility indicated by an average torsional angle (φ_{N–C4A–C4–C3})of −14.6 ± 10.3° (Table 3) in DDC. Thus, the blue-shifted absorption spectrum may be explained by the out-of-plane fluctuations about the imino moiety and the aromatic ring, which reduce the extent of π-electron delocalization.

The intramolecular proton transfer of the Schiff base has a low free energy barrier of about 5 kcal/mol at the B3LYP: AM1/QM/MM dual level of theory (Figure 4) with a preference for the hydroxyimine tautomer in the active site. Thus, the external PLP Schiff base is considered to be an equilibrium mixture of both tautomeric configurations. Simulations of the decarboxylation reaction of the PLP(H+)–L-dopa Schiff base in DDC (to be published) indicate that the hydroxyimine tautomer has a lower free energy barrier for the decarboxylation reaction than the oxoenamine form. It is possible that the catalyzed decarboxylation reaction is coupled with a low-barrier intramolecular proton transfer in the PLP-dependent enzymes and responsible for the observed spectral shifts.

Overall, our dual-level QM/MM simulations show that the tautomeric equilibrium of PLP(H+)–L-dopa Schiff base is strongly influenced by the hydrogen-bonding network in the active site of DDC. Although intrinsically the oxoenamino configuration is favored in the gas phase (Table 1) in all model reactions except a1 (Scheme 2), electrostatic interactions involving Asp271 and Lys303 favor the equilibrium shift toward the hydroxyimino side. In addition, a hydrogen bond switch of Thr246 from a hydrogen bond donor to the phenolate ion in the oxoenamine isomer to a hydrogen bond acceptor from the phenolic hydroxyl group in the hydroxyimine configuration further helps stabilization of the latter in the intramolecular proton transfer process.

CONCLUSIONS

We have carried out combined QM/MM molecular dynamics simulations to study the oxoenamino and hydroxyimino tautomeric equilibrium of PLP(H+)–L-dopa Schiff base in DDC. Eight model reactions (Scheme 2) have been investigated in the gas phase and in aqueous solution to elucidate the contributions of the intrinsic properties as well as solvent effects on the equilibrium. We employed a dual-level QM/MM approach in molecular dynamics simulations, in which density functional theory was used to represent the intrinsic free energy change in the tautomeric equilibrium and the semiempirical AM1 model was adopted to describe QM and MM interactions.

Both substituent effects on the Schiff base imine group and the protonation state of the PLP pyridine ring affect the tautomeric equilibrium of the PLP Schiff bases. The presence of a carboxylate anion on the α-carbon of the imino group helps to stabilize the zwitterionic configuration and shifts the equilibrium from the hydroxyimino tautomer to the oxoenamine isomer. Moreover, protonation of the PLP pyridine nitrogen further drives the equilibrium toward the oxoenamine direction. Solvent effects can favor either oxoenamino or hydroxyimino tautomer, depending on the electrostatic properties of the substituent on the imino nitrogen. With a carboxylate group on the α-carbon, solvent effects shift the equilibrium in the direction of the hydroxyimino tautomer; however, the equilibrium is driven toward the oxoenamino isomer when the substituent is a methyl group.

The present dual-level QM/MM MD simulations show that the hydroxyimino configuration of the PLP(H+)–L-dopa Schiff base is preferred over the oxoenamino isomer in the active site of DDC. The computed free energy barrier is about 5 kcal/mol from B3LYP: AM1/QM/MM simulations, suggesting that both tautomeric structures can be rapidly interconverted in the enzyme. Specific hydrogen-bonding and electrostatic interactions between the aldimine Schiff base and active site residues are important in controlling the keto–enol equilibrium of the PLP cofactor in PLP-dependent enzymes. In DDC, Asp271 forms an ion pair with the protonated pyridine nitrogen, while Lys303 helps to stabilize the Schiff base nitrogen in the hydroxyimino tautomer. Importantly, Thr246 plays a double role of hydrogen bond donor to stabilize the phenolate ion in the oxoenamino configuration and a hydrogen bond acceptor to favor the phenolic moiety of the oxoenamino tautomer.