The Comparison of Alternative Smoothing Methods for Fitting Non-Linear Exposure-Response Relationships with Cox Models in a Simulation Study

Abstract

We examined the behavior of alternative smoothing methods for modeling environmental epidemiology data. Model fit can only be examined when the true exposure-response curve is known and so we used simulation studies to examine the performance of penalized splines (P-splines), restricted cubic splines (RCS), natural splines (NS), and fractional polynomials (FP). Survival data were generated under six plausible exposure-response scenarios with a right skewed exposure distribution, typical of environmental exposures. Cox models with each spline or FP were fit to simulated datasets. The best models, e.g. degrees of freedom, were selected using default criteria for each method. The root mean-square error (rMSE) and area difference were computed to assess model fit and bias (difference between the observed and true curves). The test for linearity was a measure of sensitivity and the test of the null was an assessment of statistical power. No one method performed best according to all four measures of performance, however, all methods performed reasonably well. The model fit was best for P-splines for almost all true positive scenarios, although fractional polynomials and RCS were least biased, on average.

INTRODUCTION

Smoothing methods are widely used to analyze epidemiologic data, particularly in the area of environmental health where nonlinear relationships are not uncommon. These methods avoid parametric constraints on the shape of the exposure-response relationship and permit adjustment for cyclical patterns in the confounders. Most such applications fit cubic functions using splines (natural splines, restricted cubic splines, or penalized splines) or else apply fractional polynomials. There have been several recent examinations of the performance of these smoothing techniques. Steenland and Deddens (2004) described both penalized splines and restricted cubic splines in a review of alternative modeling approaches in occupational epidemiology. Höllander and Schumacher (2004) compared restricted cubic splines and fractional polynomials in Cox models through simulations and improved estimation of risk functions through bagging. In another report, we applied penalized splines, restricted cubic splines (stepwise), and fractional polynomials in survival models to data from two occupational cohort studies (Govindarajulu et al, 2007) and compared results. Restricted cubic splines (stepwise) and penalized splines were found to be closer to each other than either was to the fractional polynomial in both datasets where they were used to model lung cancer mortality as a function of lifetime exposure, to respirable crystalline silica (Checkoway et al, 1997) and to uranium, measured as radon progency (Samet et al, 1991). The distribution of exposure in both studies was skewed; bounded by zero with a long right tail, as is commonly observed in environmental and occupational studies (Johnson and Rappaport, 2007). Although the behavior of alternative smoothing techniques in relation to each other is of interest, their performance relative to the truth is of greater interest.

Motivated by these applications to real data, we turned to simulations in which we could create plausible exposure-response scenarios and evaluate model fit directly. In the present study we evaluated the performance of a broader range of smoothing techniques in simulated data, in which we know the exposure distribution and shape of underlying exposure-response curve. We first describe the alternative smoothing techniques we used to fit exposure-outcome data within a Cox model. These techniques were applied to data generated under six different scenarios, and the simulation framework is described in the next section along with the methods used to evaluate model fit. We then present results from the simulations. Finally, we draw conclusions regarding this work and future applications.

METHODS

Methods for fitting splines and fractional polynomials

We modeled non-linear exposure-response relationships using penalized splines, restricted cubic splines, natural splines, and fractional polynomials. We used the Cox proportional hazards regression model (Cox and Oates, 1985), where the model for the mortality rate for the ith subject at time t is:

$$\lambda (t | X_i)={\lambda }_0(t)\text{exp}(g(X_i))$$ (1)

where g is a smooth function of the cumulative exposure X_i defined by the particular smoothing method. Each smoothing method is described below in more detail.

1). Restricted cubic spline (RCS)

The RCS is a cubic regression spline constrained to have continuous first and second derivatives at the knots (Hastie and Tibshirani, 1990) for visual smoothness (Durrelman and Simon, 1989). RCS are further constrained to be linear above the last knot and below the first (Durrelman and Simon, 1989). The linearity in the tails allows for a more parsimonious model.

To model the dose-response relationship using a restricted cubic spline transformation, we first select H values, say (κ₁< κ₂< . . . < κ_H), within the observed range of the exposure. In the standard software implementation, these values, or knots, are located at a pre-specified number of evenly-spaced quantiles of the exposure distribution. We then assume the model in Eq. 1 is given by

$$g(X_i)={\beta }_0{X}_i+\sum _{h-1}^{H-2}{\beta }_h·X_{ih}$$ (2)

and the X_ih’s are non-linear functions determined by the position of the knots.

The H-2 spline variables created by the restricted cubic spline function are included in the Cox proportional hazard regression model, and standard modeling techniques can then be applied. We first implemented the RCS within R using the function, rcspline.eval, with a default of 5 knots, which uses a truncated power basis as described above (R 2.3.1, 2006).

We also implemented a stepwise RCS within a SAS macro written by one of us (D Spiegelman) and is described in Govindarajulu et al (2007). A stepwise selection procedure was used that starts with 25 knots to select spline variables that adhere to a specified entry and exit criteria determined by a user-defined significance level (default entry and exit levels are 0.05). The final model includes the exposure variable and whatever spline variables were retained using the stepwise selection procedure.

2). Penalized spline (P-spline)

P-splines were fit using the standard software implementation in R (R 2.3.1, 2006). P-splines offer an approach to selecting optimal smoothing via degrees of freedom (df) that is relatively robust to the choice of location and relatively large number of knots by modeling the smooth function, s, as defined in Eq. 2. The X_ih, where h=1,..,H-2, are non-linear basis functions corresponding to a large number of knots, H. In the pspline function in R, the X_ih’s are B-spline basis functions, piecewise polynomials joined by knots (R 2.3.1, 2006). The number and location of knots have little influence on the shape of the P-spline curve, as long as the knots are adequately spaced and the number of knots is sufficiently large (Ruppert, 2002).

We considered two implementatons of the pspline function within a Cox model fit in R, the standard implementation which uses df = 4 as the criterion for smoothing (R 2.3.1, 2006). and an alternative model selection criterion based on minimizing Akaike’s Information Criteria (AIC) (Akaike, 1974; Therneau and Grambsch, 1998) to select df. The AIC criterion, as implemented in the pspline function in R/Splus begins with a default of 15 spline terms in the B-spline basis expansion (R 2.3.1, 2006; Therneau and Grambsch, 2002). AIC then selects the optimal smoothing parameter that is used in the penalized partial likelihood fit, which is equivalent to selecting the optimal df (Therneau and Grambsch, 1998). The chosen knots are then evenly spaced across the range of X, i.e, the exposure variable.

3). Natural spline (NS)

The natural spline is essentially a restricted cubic spline as defined in Eq. 2 which instead of piecewise polynomials, uses B-splines basis functions, for X_ih, where h=1,..,H-2. B-spline basis functions were described in more detail in the previous section. We used the function, ns, in R to model the natural spline (R 2.3.1, 2006). We specified a usual default df of 4, where df = number of knots + 1 + 1 (if include intercept from the basis function). The ns function generates a basis matrix, which represents the family of piecewise-cubic splines with the specified sequence of interior knots and the natural boundary conditions. This constrains the function to be linear beyond the boundary knots, which default to the extremes of the data.

4). Fractional polynomials (FP)

Like P-splines and RCS, fractional polynomials may be used with any generalized linear model or Cox model for survival data (Royston and Altman, 1994). Although a global (rather than local) approach, the FP model has the advantage of being a simpler form than the other two options, and incorporating a wider range of functional forms than that permitted by the standard polynomial family. A greater range of possible dose-response relationships could be accommodated. An FP of degree m is defined as follows (Royston and Altman, 1994a):

$$g_m(X_i;\beta ,\mathbf{\text{p}})=\sum _{j=0}^m{\beta }_j{V}_j(X_i)$$ (3)

where m is generally taken to be either 1 or 2, p= {−2, −1, −0.5, 0, 0.5, 1, 2, 3} is a set of powers with p₁<…<p_m, and β = (β₁,. . ., β_m). An m=1 model would use a single value from p for V_j (X_i), whereas for an m=2 model, two values are selected (Govindarajulu et al, 2007). An m=1 model would use a single value from p, call it p_j so in Eq. 10,V_j(Xi) would be a single term,X_i^p_j, except when p_j=0, then it would be ln(X_i) (Royston and Altman, 1994a; Royston and Altman, 1994).

For an m=2 model, two values are selected from p, p_j and p_k. For example, if p_j =−2 then p_k can take on any of the values, {−2, −1, −0.5, 0, 0.5, 1, 2, 3}, to create all possible pairs with p_j or if p_j =1 then p_k can take any of the values, {1, 2, 3} to create the pairs, {(1,1), (1,2) or (1,3)} with p_j. In Eq. 10,V_j(X_i) would now contain 2 terms. If p_j ≠ p_k, the two terms in V_j(X_i) are X_i^p_j and X_i^p_k. If, p_j = p_k ≠ 0, than the two terms in V_j(X_i) are X_i^p_j and X_i^p_k ln(X_i). Finally, if p_j = p_k =0, then the two terms in V_j(X_i) are then ln(X_i) and ln(X_i)² (Royston and Altman, 1994a; Royston and Altman, 1994).

There are 44 possible combinations of m=1 and m=2 models, where the highest degree fractional polynomial considered is m=2. For a given m=1 or m=2 model, the best model is chosen to be the one with the lowest deviance. Since we are fitting Cox models we cannot simply define the deviance as −2*(log-likelihood) (Collett, 2003). Therefore, in this context, each Cox model is first ranked by the value of its partial log-likelihood. In R (R 2.3.1, 2006), using the fp function of the mfp function, the FP is tested against the straight-line model initially. If the test is significant at the specified alpha level, it continues else it selects the linear model. Next, the best m=1 model and best m=2 model are tested a stepwise RCS within a SAS macro written by one of us (D Spiegelman) and is described in Govindarajulu et al (2007). A stepwise against each other and the final model is made. In our analyses, we transformed the exposure variable to a fractional polynomial, g_m(X_i; β, p), which is then used as a predictor within the Cox model.

Simulation Framework

We first chose the distribution from which to simulate values for an exposure variable, x. In studies of environmental and occupational exposures, highly skewed exposure distributions are commonly encountered (Rosario et al, 2006). Exposure distributions are bounded by zero or the lower limit of detection of the measurement instrument and have no upper bound. Thus we employed the absolute value of the normal distribution with mean of 0 and standard deviation of 6 to simulate all exposure data. (It should be noted, that dose and exposure have different meanings in the field of environmental exposure assessment; “exposure” refers to a chemical or physical agent outside the body, whereas “dose” or “biomarker” refers to the amount of the agent that reaches the target organ inside the body (Johnson and Rappaport 2007). This simulation is equally relevant to both, and we will use the terms synonomously.)

For the dose-response curve, g(x), we generated the outcome under six different models: null, linear, quadratic, log, sine, and threshold. (Although a sine curve is not a biologically plausible exposure-response relationship, we included it because smoothing is often used to adjust for diurnal or seasonal patterns in epidemiologic data.).

The dose-response curve, g(x), for each different model is: null: 0, linear: β*x or 0.17*x, ln(x): β*ln(x+1) or 0.43*ln(x+1), sine: β*(sin(x/3)) or 0.71*(sin(x/3)), quadratic: β*x*(x–b)²or 0.005*x*(x–40)², and threshold: β*(x–b)₊ or 0.35*(x–2)₊. Depending upon g(x), we set b to be at a particular percentile of the exposure distribution. For the threshold dose-response, we chose the cutpoint based on the 25th percentile of exposure.

Since we were using a Cox proportional hazards regression, we generated the survival times using the hazard function. In proportional hazards form, the model containing g(x) is:

$$\lambda (t|x)={\lambda }_0(t)\text{exp}(g(x))$$ (4)

where λ₀(t) is the baseline hazard function and g(x) is the form of the exposure-response curve. We allowed for a baseline Weibull hazard (Klein and Moschberger, 1997), λ₀(t) = θνt^θ–1. Using the survival function, S(t) = 1-F(t), we obtained the baseline cumulative incidence function under the Weibull model at any time t, for a given exposure:

$$\begin{array}{l}{F}_0(t)=1-S_0(t)\\ F_0(t)=1-\text{exp}(-\nu {\text{t}}^{\theta }).\end{array}$$ (5)

Allowing F₀ to be average cumulative incidence among the unexposed, if there are 100 cases out of 2000 persons, then F₀=0.05. Solving for ν in Eq. 5, we obtained:

$$\nu =\frac{1}{t_{*}^{\theta }}(-\text{log}(1-F_0))$$ (6)

where t_*=20 years of followup time and θ=5 is the shape parameter, which is typical value for many types of cancer (Armitage and Doll, 1961; Breslow and Day, 1987; Zucker and Spiegelman, 2004).

In addition, we defined S₀(t) in terms of the baseline hazard:

$$S_0(t)=\text{exp}(-{\Lambda }_0(t))=\text{exp}\left[-\underset{0}{\overset{t}{\int }}{\lambda }_0(u)du\right]$$ (7)

We then modeled the survival times, t₀, from a Cox model via the following, using the baseline cumulative hazard function, Λ₀(t), the survival function, S(t), and the form of λ(t|x) (Eq. 4):

$$\begin{array}{l}S(t)=\text{exp}(-\Lambda (t))=\text{exp}\left[\underset{0}{\overset{t}{\int }}\lambda (u)du\right]\\ =\text{exp}\left[\underset{0}{\overset{t}{\int }}{\lambda }_0(u)\text{exp}(g(x))du\right]=\text{exp}[-{\Lambda }_0(t)\text{exp}(g(x))]\end{array}$$ (8)

F(t) was then defined in terms of S(t) for the Cox model, using the form of Λ₀(t) from the Weibull model, where 1 – S(t | x) = F(t | x) = 1 – exp(− exp(g(x))*vt^ϑ), and we used this equation to define t₀ in years:

$$t_0={(-\frac{\text{log}(1-F(t))}{\nu \text{exp}(g(x))})}^{1/\theta }$$ (9)

where F is generated from a standard uniform distribution and ν is defined per Eq. 6. After generating the survival times, we generated the competing risk times. We first obtained the cumulative incidence function from S(tw), similarly as for S(t) in Eq. 8, and generated the equation for competing risk time, tw, using an Exponential model:

$$tw=\frac{-\text{log}(1-U2)}{\gamma }$$ (10)

where F = U2 ~ Uniform(0,1) and γ was set to 10% which corresponds to 60% censoring per year. To obtain the follow-up time, t, we set t= min(t₀, tw) from Eq’s 9–10 and the event indicator, d=I[t₀<tw]. The final simulated datasets contain: (x, t, d): exposure variable, follow-up time, and event indicator.

Evaluating the Performance of Smoothing Approaches Fit to Simulated Data

We simulated exposure distributions and survival times under each of the six dose-response scenarios and and then compared each fitted curve (P-spline, RCS, NS, and FP) to the true curve. Each smoothed curve was fit in a Cox Model via standard software implementations. We simulated datasets of size n = 2,000, and ran N=1,000 iterations under each scenario. (We found that increasing iterations did not change significantly change results.) We selected parameter values for the true functions (see table above) in order to maintain a constant number of events, approximately 200 cases, under any scenario.

To compare the series of curves generated by each dose-response function, we evaluated four aspects of performance: 1) model fit as measured by Mean-Square Error (MSE), 2) the p-value for the test of linearity, calculated as the proportion of times that the test of linearity is rejected (power of method to reject the null hypothesis that association is linear), 3) the p-value for the test of null effect, calculated as the proportion of times the test of null hypothesis was rejected, and 4) bias (difference between the observed and true curves), as assessed by the rMSE and area difference. Each of these four aspects is described below.

The mean-square error calculation (MSE) involved taking the difference between log (hazard ratio) HR values predicted by each curve and values of the true dose-response curve at each observed data point along the x-axis. This was computed for each simulated dataset. We actually calculated the root MSE (rMSE)

$$rMSE=\sqrt{\sum _{i=1}^n(\text{log})\stackrel{̑}{H}{R}_i(x_i)-\text{log} H{R}_i(x_i){)}^2}$$ (11)

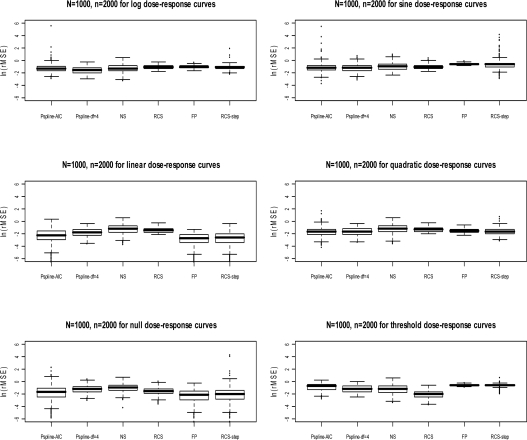
where log H̑R_j(x_i) is the estimated curve for the j^th simulated data set evaluated at the i^th subject’s exposure x_i and log HR_j (x_i) is the value of the true curve at x_i. The fit of each smoothing method applied to each exposure-response scenario was then summarized by the median rMSE score (across datasets), where a lower score reflects a closer relationship between the true and the estimated curves. The distribution of rMSE was presented in boxplots and the median was used to summarize model fit to reduce the influence of the tails.

We were also interested in the how often the test of linearity was rejected and how often the test of null effect was rejected by each smoothed model. For each hypothesis test, we estimated the proportion of times that the hypothesis was rejected in the 1000 replications for each smoothed function, fit to each dose-response function. In order to calculate the test of linearity for a given dataset, we computed the chi-square test:

$$X^2=-2l(x)-[-2l(g(x))]$$ (12)

where −2l(x) is −2*partial log-likelihood from the Cox model for x and −2l(g(x)) is the −2*partial log-likehood from the Cox model estimated for a particular g(x). We computed the p-value from Eq. 12 and reported the proportion of p-values less than or equal to the significance level of 0.05 across all simulations. In order to calculate the test of null effect, we computed the likelihood ratio chi-square test:

$$X^2=-2l(g(x))-[-2l(g(0))]$$ (13)

where −2l(g(0)) is the −2*partial log-likelihood from the null Cox model. We obtained the p-value from Eq. 13 and computed the proportion of p-values greater than or equal to 0.05 across simulations. We also computed a Wald chi-square to test the null effect.

The area calculations were computed using a method developed in a previous paper (Govindarajulu et al, 2007), based on summing across rectangles defined by a set of evenly-spaced values over the range of x. We computed the difference in area between the true and estimated dose-response curves (log HR) for each scenario. This allowed us to determine how close each spline curve was to the true dose-response curve over the entire span of the x-axis. In contrast with the MSE which summarizes the difference between curves at observed values of x, the area difference is measured giving equal weight to all x-values across the range of exposure. Thus the tails of the exposure distribution will give more weight in the estimation of bias (area difference) than in the calculation of model fit (rMSE).

RESULTS

To summarize model fit, the median root mean-square error, and interquartile range (IQR), are presented for each scenario in Table 1.

Table 1:

Median (IQR) root mean-square error for selected methods in 1000 simulated datasets (n=2000 subjects) generated for each of six scenarios of the true dose-response function

Dose-response function		Methods*
	g(x)	P-spline-AIC	P-spline-df-4	NS df=4	RCS nk=5	RCS stepwise	FP
log	βlog(x+1)	0.296 (0.183)	0.221 (0.176)	0.290 (0.279)	0.349 (0.155)	0.343 (0.148)	0.362 (0.118)
sine	βsin(x/3)	0.310 (0.232)	0.311 (0.249)	0.389 (0.321)	0.349 (0.190)	0.543 (0.295)	0.602 (0.108)
linear	βx	0.103 (0.151)	0.162 (0.155)	0.292 (0.290)	0.230 (0.135)	0.070 (0.090)	0.065 (0.078)
quadratic	βx(x–b)	0.182 (0.152)	0.182 (0.157)	0.293 (0.300)	0.253 (0.143)	0.187 (0.125)	0.121 (0.114)
null	0	0.187 (0.243)	0.291 (0.215)	0.368 (0.317)	0.213 (0.157)	0.138 (0.192)	0.121 (0.166)
threshold	β(x–b)+	0.478 (0.302)	0.307 (0.268)	0.291 (0.303)	0.132 (0.109)	0.571 (0.119)	0.579 (0.097)

^*AIC=Akaike’s Information Criteria was used as method of selection for optimal smoothness, df =degrees of freedom, and nk =number of knots. The df and nk represent default software settings used for each spline. IQR: interquartile ratio.

Corresponding boxplots are also presented for each scenario (Figures 1a–1f), transformed to the log scale in order to display the positive tails comprised of datasets with poorly fitting curves. All smoothing methods fit well when the true dose-response is linear, quadratic, or null, when summarizing across all results in Tables 1–4. P-splines (selected with df = 4) had the smallest median rMSE when the underlying exposure-response scenario was a logarithmic or sine function. Fractional polynomials fit the best for an underlying linear function, with the RCS-step not far behind. There was more variability in model fit for the P-spline (AIC) and RCS-step than the other methods for several different scenarios. The median df ranged from 1.0 to 2.9 across scenarios for Pspline-AIC and from 1.0 to 2.0 for RCS-step. Thus, P-spline-AIC fit poorly in several individual datasets, despite having lowest rMSE for sine scenario and moderate rMSE scores for the remaining scenarios. When the true dose-response model was a threshold, the restricted and natural splines fit better than FP or P-splines (Figure 1f).

Figure 1:

Boxplots of rMSE for selected methods in 1000 simulated datasets (n=2000 subjects) generated for each of the six scenarios of the true dose-response function

Table 4:

Proportion of times test of null effect was rejected (Wald test) for selected methods in 1000 simulated datasets (n=2000 subjects) generated for each of six scenarios of the true dose-response curve

Dose-response function		Methods*
	g(x)	P-spline-AIC	P-spline-df=4	NS df=4	RCS nk=5	RCS stepwise	FP
log	βlog(x+1)	0.938	0.843	0.750	0.775	0.995	1.000
sine	βsin(x/3)	0.762	0.693	0.538	0.570	0.616	0.004
linear	βx	1.000	1.000	1.000	1.000	1.000	1.000
quadratic	βx(x–b)	1.000	1.000	1.000	1.000	1.000	0.999
null	0	0.101	0.042	0.031	0.028	0.085	0.003
threshold	β(x–b)+	1.000	1.000	1.000	1.000	1.000	1.000

^*AIC=Akaike’s Information Criteria was used as method of selection for optimal smoothness, df =degrees of freedom, and nk =number of knots. The df and nk represent default software settings used for each spline.

The proportion of times the test of linearity was rejected is presented in Table 2 for each dose-response function. As expected, most methods rejected linearity a small proportion of times when the true exposure-response was linear, and a high proportion when the true exposure-response was a sine function. The test of linearity was rejected least often for the null scenario for all the splines except the P-spline-AIC. The P-spline-AIC was least consistent in how often the test of linearity was rejected across the different dose-response functions. The RCS-step and NS performed similarly well, while the RCS-nk=5 rarely rejects linearity under any scenario. We have omitted FP from these analyses because the models are non-nested and because the mfp function in R was not fully functional for Cox models in order to obtain results of this test.

Table 2:

Proportion of times test of linearity was rejected for selected splines in 1000 simulated datasets (n=2000 subjects) generated for each of six scenarios of the true dose-response function

Dose-response function		Methods*
	g(x)	P-spline-AIC	P-spline-df=4	NS df=4	RCS nk=5	RCS stepwise
log	βlog(x+1)	0.665	0.228	0.167	0.019	0.238
sine	βsin(x/3)	0.932	0.859	0.790	0.445	0.694
linear	βx	0.722	0.097	0.051	0.006	0.079
quadratic	βx(x–b)	0.679	0.300	0.227	0.036	0.369
null	0	0.747	0.076	0.052	0.006	0.082
threshold	β(x–b)+	0.682	0.241	0.236	0.052	0.160

^*AIC=Akaike’s Information Criteria was used as method of selection for optimal smoothness, df =degrees of freedom, and nk =number of knots. The df and nk represent default software settings used for each spline.

In Tables 3–4, we present the proportion of times the test of null was rejected using the likelihood ratio test or the Wald test. This test was rejected most often when the true exposure-response was linear, quadratic, or threshold, for all splines and fractional polynomials. The test was rejected least often when the true dose-response scenario was null, as expected, though it was rejected most often in that case for P-spline-AIC. FP rejected the test of null when the true scenario was a logarithmic function correctly, but performed poorly for the sine scenario.

Table 3:

Proportion of times test of null effect was rejected (likelihood ratio test) for selected methods in 1000 simulated datasets (n=2000 subjects) generated for each of six scenarios of the true dose-response function

Dose-response function		Methods*
	g(x)	P-spline-AIC	P-spline-df=4	NS df=4	RCS nk=5	RCS stepwise	FP
log	βlog(x+1)	0.954	0.876	0.840	0.769	0.940	1.000
sine	βsin(x/3)	0.911	0.853	0.796	0.697	0.733	0.008
linear	βx	1.000	1.000	1.000	1.000	1.000	1.000
quadratic	βx(x–b)	1.000	1.000	1.000	1.000	1.000	0.999
null	0	0.153	0.077	0.055	0.033	0.088	0.002
threshold	β(x–b)+	1.000	1.000	1.000	1.000	1.000	1.000

^*AIC=Akaike’s Information Criteria was used as method of selection for optimal smoothness, df =degrees of freedom, and nk =number of knots. The df and nk represent default software settings used for each spline.

We also computed the area difference between the true and estimated curves for each method and present the average for each scenario (Table 5). The area calculations, which incorporate the effect of the tails of exposure, show some interesting contrasts with the rMSE results (Table 1). Although the P-splines had smaller rMSE for several scenarios than the other methods, the P-spline, selected by AIC, was the most biased for the log and sine scenarios than all other methods. The RCS-step was more biased than the other methods for the threshold and linear scenarios. The FP had the smallest area difference from the truth for almost all scenarios, perhaps due to the global fit of this approach in contrast with the locally fit splines.

Table 5:

Average (sd) difference in area between true and estimated dose-response curves for selected methods in 1000 simulated datasets (n=2000 subjects) generated from six scenarios of the true dose-response function

Dose-response function		Methods*
	g(x)	P-spline-AIC	P-spline-df=4	NS df=4	RCS nk=5	RCS stepwise	FP
log	βlog(x+1)	30.43 (683.01)	7.02 (3.16)	8.47 (4.07)	8.16 (3.66)	8.38 (8.05)	7.17 (6.80)
sine	βsin(x/3)	29.50 (368.89)	16.10 (17.25)	13.38 (11.49)	15.18 (13.19)	42.46 (288.90)	7.23 (5.25)
linear	βx	4.63 (4.22)	5.26 (3.03)	14.55 (6.39)	5.46 (2.83)	3.23 (3.58)	2.89 (14.97)
quadratic	βx(x–b)	6.48 (6.58)	6.34 (3.38)	9.99 (4.57)	6.22 (2.91)	6.01 (42.49)	5.80 (8.85)
null	0	13.42 (58.16)	13.28 (11.76)	10.65 (8.09)	8.71 (7.65)	22.15 (466.00)	5.82 (4.92)
threshold	β(x–b)+	9.90 (5.56)	8.01 (4.84)	26.52 (8.37)	3.82 (2.34)	11.91 (5.37)	12.18 (27.66)

^*sd: standard deviation

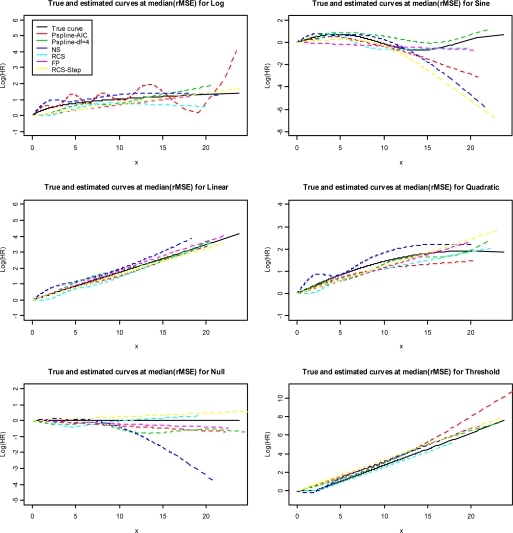
Visualization of the curves is represented in Figures 2(a–f), where for each scenario, the curve that generated the median rMSE is presented for each smoothing method. The curves deviate more from the true curve in the upper range of exposure for almost every scenario, except the linear. Since each curve represents the one that has the minimum median rMSE, for each method, the results cannot be directly compared to the summary measures of performance presented in Tables 1. Generally the plots indicate that all of the methods can capture the true dose-response curve well. However, the plots illustrate that even the best fitting example of each method, can deviate from the true curve, particularly in the sparsely populated tails of the distribution. This was particularly true in Figure 2b and 2e, for some of the methods in the null and sine scenarios Finally, it is interesting that the Pspline-AIC is quite wiggly (Figure 2a) for the log dose-response curve.

Figure 2:

The true dose-response curve for each scenario compared with the estimated curves selected for each method at the median rMSE based on 1000 simulated datasets (n=2000 subjects)

DISCUSSION

We observed the model fit of three alternative splines (penalized splines, restricted cubic splines, natural splines) and fractional polynomials with knowledge of the true exposure-response curve through simulations. By extending a previous study of the fit of various smoothing methods applied to actual data (Govindarajulu et al, 2007), we were better able to assess the accuracy (unbiasedness and reliability) of these methods for curve fitting under different dose-response scenarios.

The P-splines (AIC or df=4) had among the lowest rMSE when fit to log or sine functions, while fractional polynomial fit best for linear relationships. The typical fit was good for all methods across all scenarios, but P-splines tended to exhibit the best behavior. However, the model selected by Pspline-AIC rejected linearity more often than the other methods – even when the truth was linear. The type I error for p-spline selected by AIC was unacceptably large, whereas it was below 0.1 for all other methods. AIC also selected more poorly fitting p-spline models than did the default 4 degrees of freedom (df=4).

The RCS-step also performed well compared to the P-splines and FP based on rMSE. By contrast, the larger area difference (bias), for RCS, indicated that the fit was poorer in the higher exposure region. The RCS-nk=5 and NS were least consistent in all scenarios for all criteria, except in the threshold scenario, where they had smaller median MSE than the other methods. In all scenarios, we generated data from a skewed exposure distribution. It would be interesting to evaluate how the skewness of the exposure distribution affects the performance of these methods by repeating these simulations with the same exposure-response scenarios and uniform or normal exposure distributions.

In regards to the Pspline with 4 df, the Pspline in general has a fixed number of knots and the df modifies the degree of smoothness of the fit; this corresponds to roughly 10 knots. Thus, depending on placement, it could be more sensitive to the cutpoint with this many knots. We chose the cutpoint based on the 25th percentile of exposure because at the time having 25% of subjects with exposures below this seemed sufficient. To respond to the reviewer, we tested moving the changepoint to X=10 for the threshold dose-response instead. In fact, it seems that the RCS (nk=5) picks up this change better (rMSE=0.22) than the Pspline (df=4) (rMSE=0.32), which does even worse than the Pspline-AIC (rMSE=0.22). However, in terms of proportion of times test of linearity and test of null effect were rejected, all smoothing methods perform very poorly. It appears that moving the changepoint to a sparser area of data becomes more difficult to detect for the smoothing methods overall.

A number of authors have suggested stepwise regression as a way of optimizing the fit of restricted cubic spline regressions and related regression spline models (Durrleman and Simon, 1989; Eubank RL, 1984) while others have suggested an arbitrary fixed number of knots placed in a variety of a priori ways (Hess, 1994; Harrell et al., 1988; Heinzl, Kaider, Zlabinger, 1996). This is the first study we are aware of in which the performance of restricted cubic splines with fixed knot number and location, and with stepwise knot selection have been studied systematically by simulation. The nominal size and power of tests based upon the stepwise method appeared competitive with the other methods (Tables 2–4), despite the somewhat ad hoc nature of the approach, consistent with their utility as an exploratory data analysis tool.

Höllander and Schumacher conducted a simulation study to examine a number of methods for estimating dose-response curves that included fractional polynomials and restricted cubic splines. They examined two nonlinear exposure-response scenarios: a step function and an absolute value (v-shaped) function, in addition to the linear and null cases, and found that fractional polynomials were in general superior based on mean absolute errors and type I error rates. These results cannot be directly compared to ours, however, because of differences between the simulated distributions of exposures. Whereas they simulated exposures from a uniform distribution, we have generated right skewed exposure distributions to mimic real environmental exposures (Johnson and Rappaport, 2007).

In light of our findings, we may conclude that applying penalized splines to exposure-response data provides the most consistent fit. It is interesting that the best fitting Pspline-AIC was a wiggly curve for one of the scenarios, a problem found previously when this method was applied to real data (Govindarajulu et al, 2007; Therneau and Grambsch, 1998). For a biologic model, wiggliness in uninterpretable and the default model selection criteria for P-splines in R, based on degrees of freedom, df = 4, avoids this unattractive feature. The median fit of NS was worse in five of the six scenarios than RCS (nk=5). This was somewhat surprising given that NS employs B-spline basis functions. The rMSE measures overall performance but one may be interested in more specific aspects of the dose response curve such as whether a peak/dip/threshold is captured correctly, the % of times it is over/under estimated and so on. This is at least one drawback of using rMSE calculations.

It may be interesting to further compare these splines when fit by varying df rather than default software settings. Also, although the RCS and NS were least consistent in fit to the various scenarios, it would be worthy to see if their performances improve beyond standard settings. Finally, although the fractional polynomial was competitive with penalized splines in terms of all of the aspects of model performance, it should be kept in mind that FP are a polynomial model fit over the entire range of exposure, whereas the splines are locally fit over discrete intervals of the exposure variable. This difference may have implications for the robustness of the curves over different regions of the exposure range.