Why Match? Investigating Matched Case-Control Study Designs with Causal Effect Estimation

Abstract

Matched case-control study designs are commonly implemented in the field of public health. While matching is intended to eliminate confounding, the main potential benefit of matching in case-control studies is a gain in efficiency. Methods for analyzing matched case-control studies have focused on utilizing conditional logistic regression models that provide conditional and not causal estimates of the odds ratio. This article investigates the use of case-control weighted targeted maximum likelihood estimation to obtain marginal causal effects in matched case-control study designs. We compare the use of case-control weighted targeted maximum likelihood estimation in matched and unmatched designs in an effort to explore which design yields the most information about the marginal causal effect. The procedures require knowledge of certain prevalence probabilities and were previously described by van der Laan (2008). In many practical situations where a causal effect is the parameter of interest, researchers may be better served using an unmatched design.

1. Introduction

Individually matched case-control study designs are frequently found in public health and medical literature, and conditional logistic regression is the tool most commonly used to analyze these studies. Matching is intended to eliminate confounding, however, the main potential benefit of matching in case-control studies is a gain in efficiency. Therefore, when are these study designs truly beneficial? Given all the potential drawbacks, including extra cost, added time for enrollment, and increased bias, the use of matching in case-control study designs warrants careful evaluation. Discussion of the advantages and disadvantages of matching in the literature goes back more than 40 years.

In this paper, we focus on individual matching in case-control studies where the researcher is interested in estimating the marginal causal effect, and certain prevalence probabilities are known. Our procedure, first presented in van der Laan (2008), “targets” the parameter of interest rather than the distribution of interest, and is thus aptly named case-control weighted targeted maximum likelihood estimation. In order to eliminate the bias caused by the matched case-control sampling design, this technique relies on knowledge of the true prevalence probability $q_0\equiv P_0^{*}(Y=1)$, and an additional value ${\overline{q}}_0(M)\equiv q_0\frac{P_0^{*}(Y=0|M)}{P_0^{*}(Y=1|M)}$, where M is the matching variable. For unmatched designs, knowledge of only q₀ is required.

The case-control weighting scheme maps estimation methods developed for prospective sampling into methods for case-control sampling, and it produces efficient estimators when its prospective sample counterpart is efficient. Thus, both the matched and unmatched procedures are double robust and locally efficient: they perform well as long as $P_0^{*}(Y|A,\hspace{0.17em}W)$ or $P_0^{*}(A|W)$ is correctly specified, are consistent if either of these models are correctly specified, and efficient if both are correctly specified. (Here A is the exposure of interest and If is a vector of covariates.) We will compare the use of case-control weighted targeted maximum likelihood estimation in matched and unmatched case-control study designs as we explore which design yields the most information about the marginal causal effect. This paper will not address matching in cohort studies, and will concentrate solely on case-control studies. However, matching in cohort studies was briefly addressed in van der Laan (2008), and applying our methods to cohort studies is an area of future research.

2. Why Match? A Literature Review

There is a large collection of literature devoted to the topic of individual matching in case-control study designs. This overview attempts to capture the most important consideratons, and it is by no means exhaustive.

2.1. Individual Matching in Case-Control Studies

In an individually matched case-control study, the population of interest is identified, and cases are randomly sampled or selected based on particular inclusion criteria. Although, as Rothman and Greenland (1998) note, the definition of a case may implicitly define the population of interest for cases and controls. Each of these cases is then matched to one or more controls based on a variable (or variables) believed to be a confounder. Much of the literature on individual matching in case-control studies, particularly earlier texts, describes these designs as a way to reduce confounding in the sampling design. Reference to this is made in: Miettinen (1970), Breslow et al. (1978), Breslow and Day (1980), Kupper et al. (1981), Schlesselman (1982), Collett (1991), and Costanza (1995), among others. However, several authors (Breslow and Day, 1980; Kupper et al., 1981; Schlesselman, 1982; Rothman and Greenland, 1998; Vandenbroucke et al., 2007) point out that the goal of matching is to increase the study’s efficiency by forcing the case and control samples to have similar distributions across confounding variables. Rothman and Greenland (1998) go on to say that while matching is intended to control confounding, it cannot do this in case-control study designs, and can, in fact, introduce bias. Costanza (1995) agreed, stating that matching on confounders in case-control studies does nothing to remove the confounding, but frequently introduces negative confounding.

So, while some literature cites the purpose of matching as improving validity, later publications (Kupper et al., 1981; Rothman and Greenland, 1998) demonstrated that matching has a greater impact on efficiency over validity. Matched sampling leads to a balanced number of cases and controls across the levels of the selected matching variables. This balance can reduce the variance in the parameters of interest, which improves statistical efficiency. A study with a randomly selected control group may yield some strata with an imbalance of cases and controls. It is important to add, however, that matching in case-control studies can lead to gains or losses in efficiency (Kupper et al., 1981; Rothman and Greenland, 1998). This will be discussed further in later sections.

Breslow and Day (1980) note that matched case-control studies attempt to increase the informativeness of each of the subjects in the study. However, one should also note that matched studies discard not only a pool of unmatched controls, but the information in each exposure-concordant case-control pair. Additionally, matching has a substantial impact on the study sample, most notably, it creates a sample of controls that is not representative of exposure in the population or the population as a whole. The effect of the matching variable can no longer be studied directly, and the exposure frequency in the control sample will be shifted towards that of the cases (Rothman and Greenland, 1998). Matching in case-control studies also does not completely control for the variable or variables used for matching, in general. This means that researchers who implement matched designs must perform matched or stratified analyses (Seigel and Greenhouse, 1973; Schlesselman, 1982; Holland and Rubin, 1988; Rothman and Greenland, 1998; Rubin, 2006). If an unmatched analysis is performed on matched data, the validity of the case-control comparison may be decreased (Schlesselman, 1982).

2.2. Variable Selection

We revisit an earlier point made in this overview of individually matched case-control studies: matching variables are chosen a priori on the belief that they confound the relationship between exposure and disease. If controls are matched to cases based on a variable that is not a true confounder, this can impact efficiency. For example, if the matching variable is not associated with disease but is associated with the exposure, this will increase the variance of the estimator compared to an unmatched design. Here, the matching leads to larger numbers of exposure-concordant case-control pairs, which are not informative in the analysis, leading to the increase in variance. If the matching variable is only associated with disease, there is often a loss of efficiency as well (Schlesselman, 1982). If the matching variable is along the causal pathway between disease and exposure then matching will contribute bias that cannot be removed in the analysis (Vandenbroucke et al., 2007). Matching on a variable associated with exposure and not disease or a variable along the causal pathway are considered types of overmatching. Variables for matching should therefore be selected very carefully, and only those that are known to be associated with both exposure and disease should be considered. The number of matching variables should also be reduced to as few as possible. As the number of matching variables grows, the cases and controls will become increasingly similar with respect to the exposure of interest, and the study may produce a spurious result or provide no information (Breslow and Day, 1980). Additionally, when matching on more than one variable, matching variables should not be strongly correlated with each other (Schlesselman, 1982).

2.3. More on Efficiency

Kupper et al. (1981) performed a variety of simulations to demonstrate the impact of matching on efficiency. They found that in situations where confounding was present, the confidence intervals for matched studies were smaller than unmatched studies unless the odds ratio and the exposure of interest were large. However, the confidence intervals for the samples with randomly selected controls were always shorter when the number of controls was at least twice that of the cases. This is an important result, as efficiency is often touted as the benefit of an individually matched case-control study design. Simulations aside, Cochran (1953) is often cited as the theoretical paper that demonstrates the efficiency of matched designs. However, as noted by McKinlay (1977), Cochran’s result can be misleading. Comparisons between matched and unmatched study designs are often made with equal sample sizes and no other method of covariate adjustment (e.g. regression). In a matched design, controls may be discarded if they do not match a particular case on the variable or variables of interest. Multiple controls may be discarded per case, depending on the variables of interest (Freedman, 1950; Cochran and Chambers, 1965; McKinlay, 1977). In a typical randomly selected case-control study, these controls would be included. In many cases, if the discarded controls were available to be rejected in the matched study, they would be available for an unmatched design in the same investigation (Billewicz, 1965; McKinlay, 1977). Therefore, it may be more appropriate to compare the efficiencies of matched case-control studies of size n to randomly selected case-control studies of size n+number of discarded controls. Additionally, these randomly selected case-control studies should employ a method of analysis to reduce bias and variance. Therefore, the result from Kupper et al. (1981) is especially poignant, as all randomly selected case-control studies that had a size of at least 2n had shorter confidence intervals than their matched counterparts of size n.

2.4. Trends

Gefeller et al. (1998) performed a literature review of case-control studies published between 1955 and 1994 in three main epidemiology journals: American Journal of Epidemiology, International Journal of Epidemiology, and the Journal of Epidemiology and Community Health. They found that, among these journals, there was a decreasing trend in the percentage of individually matched case-control studies published (71.7% in the years preceding 1981, 65.5% in 1985, 46.9% in 1989, and 46.4% in 1994), and an increasing percentage of frequency matched studies (5.0% in the years preceding 1981, 9.1% in 1985, 16.3% in 1989, and 26.2% in 1994). Interestingly, the percentage of case-control studies using no matching stayed relatively constant with no obvious trend (averaging 29.3%, and ranging from 23.2% to 36.7%). Unfortunately, they found substantial evidence that individually matched studies were being performed without the appropriate matched analysis: only 74% of studies from 1994 used conditional logistic regression if logistic regression was the chosen method of analysis. A later analysis of medical literature in Medline, Rahman (2003), indicated that 5.3% of individually matched case-control studies used an unconditional logistic regression for those selecting logistic regression models. The review in Gefeller et al. (1998) indicates that unmatched case-control studies, at least in epidemiology, are in the minority. This should be questioned given the overwhelming agreement in the literature that matching is not frequently justified for case-control study designs.

2.5. Literature Review Discussion

The consensus in the literature indicates that there are very few circumstances where individual matching is indeed warranted. Case-control studies with a very small number of cases may benefit from individual matching, as a randomly selected control group from even a well-defined population of interest may be uninformative on many variables of interest (Schlesselman, 1982; Costanza, 1995). Individual matching moves from beneficial to required when variables such as sibship are included in the study (Rothman and Greenland, 1998; Costanza, 1995). Matching is also cited as necessary by many authors when the investigators expect the distribution of the matching variable to differ drastically between the cases and the controls. It may be this reason that draws many investigators towards a matched design, perhaps without appropriate consideration of the disadvantages or definition of the population of interest.

Methodologists in the literature stress that it is often possible for confounders to be adjusted for in the analysis instead of matched on in case-control designs (Schlesselman, 1982; Vandenbroucke et al., 2007). The development of effective methods to control confounding in analyses may have contributed to the drop in individually matched designs, but they are still quite common. It is therefore important to continue to disseminate the implications of individually matched case-control study designs to researchers, as Rothman and Greenland (1998) note that “people match on a variable (e.g. sex) simply because it is the ‘expected thing to do’ and they might lose credibility for not matching.” When researchers make design and analysis decisions based on these types of considerations, their research may suffer.

Our contributions to the vast literature on individual matching for case-control studies will be unique. We focus on scenarios where the researcher is interested in estimating a marginal causal effect, a parameter that cannot be estimated with conditional logistic regression, and certain prevalence probabilities are known. Thus, we will compare the use of case-control weighted targeted maximum likelihood estimation in matched and unmatched designs in an effort to explore which design yields the most information about the marginal causal effect.

3. Existing Methods

Model-based methods for the analysis of matched case-control studies are plentiful in recent literature (Breslow et al., 1978; Holford et al., 1978; Breslow and Day, 1980; Greenland, 1981; Schlesselman, 1982; Holland and Rubin, 1988; Benichou and Wacholder, 1994; Rothman and Greenland, 1998; Greenland, 2004). And, while it is not the only method of analysis for individually matched case-control studies, the predominant method of analysis is conditional logistic regression. This method provides a conditional estimate of the odds ratio of being diseased given the exposure of interest and baseline covariates. Conditional logistic regression will be discussed in more detail in the subsection below. Greenland (1981) and Holland and Rubin (1988) discuss another model-based method: the use of log-linear models to estimate the marginal odds ratio. Additionally, Rothman and Greenland (1998) and Greenland (2004) demonstrate the use of standardization in case-control studies, which estimate marginal effects with population or person-time averaging. Holland and Rubin (1988) note that the traditional two-way table and its extensions generally provide no causal insight for matched case-control studies. However, these methods are all distinctly different from the method we illustrate in this paper, discussed by van der Laan (2008), as our method is a nonparametric double robust locally efficient procedure that provides an estimate of the marginal causal odds ratio.

3.1. Conditional Logistic Regression

The logistic regression model for matched case-control studies differs from unmatched studies in that it allows the intercept to vary among the matched units of cases and controls. The matching variable is not included in the model (Breslow et al., 1978; Holford et al., 1978; Breslow and Day, 1980; Schlesselman, 1982). If the parameter of interest is the coefficient in front of the exposure A, the use of a matched study design and a conditional logistic regression analysis can yield increases in efficiency, compared to an unmatched design with a logistic regression analysis. It is important to note that in order to estimate an effect of exposure A with conditional logistic regression, the case and control must be discordant on A. Additionally, if information for a variable is missing; for a case (or control), the corresponding control (or case) information is discarded (Breslow and Day, 1980; Schlesselman, 1982). These two limitations do not occur in the new case-control weighted targeted maximum likelihood estimation methodology for causal effect parameters. More importantly, if a marginal causal effect is the parameter of interest, conditional logistic regression cannot be used as it can only estimate the conditional odds ratio.

4. Case-Control Weighted Targeted Maximum Likelihood Estimation

4.1. Background

We define $O*=(W,A,Y)\hspace{0.17em}\sim \hspace{0.17em}{P}_0^{*}$ as the experimental unit and corresponding distribution $P_0^{*}$ of interest. $P_0^{*}$ represents the population from which all cases and controls will be sampled. Here O* consists of baseline covariates W, an exposure variable A (referred to as the “treatment” variable in prospective studies), and a binary outcome Y, which defines case or control status. If we are interested in marginal causal effect parameters, we can define ${\psi }_0^{*}=\Psi *(P_0^{*})\in {\text{IR}}^d$ of $P_0^{*}\in M*$ as the causal effect parameter and define the risk difference, relative risk, odds ratio as follows for binary exposure A ∈ {0, 1}:

$$\begin{array}{ll}{\psi }_{0,RD}^{*}& \equiv E_0^{*}\{E_0^{*}(Y|A=1,\hspace{0.17em}\hspace{0.17em}W)-E_0^{*}(Y|A=0,\hspace{0.17em}\hspace{0.17em}W)\}\\ & =E_0^{*}(Y_1)-E_0^{*}(Y_0)\\ & =P_0^{*}(Y_1=1)-P_0^{*}(Y_0=1),\end{array}$$ (1)

$${\psi }_{0,RR}^{*}=\frac{E_0^{*}{E}_0^{*}(Y|A=1,\hspace{0.17em}\hspace{0.17em}W)}{E_0^{*}{E}_0^{*}(Y|A=0,\hspace{0.17em}\hspace{0.17em}W)}=\frac{E_0^{*}(Y_1)}{E_0^{*}(Y_0)}=\frac{P_0^{*}(Y_1=1)}{P_0^{*}(Y_0=0)},$$ (2)

and,

$${\psi }_{0,\hspace{0.17em}OR}^{*}=\frac{P_0^{*}(Y_1=1)P_0^{*}(Y_0=0)}{P_0^{*}(Y_1=0)P_0^{*}(Y_0=1)}.$$ (3)

These causal versions of the effect parameters require the specification of the counterfactual outcomes Y₀ and Y₁ for binary A and (W, A, Y = Y_A) as a time-ordered missing data structure on the full data structure (W, Y₀, Y₁). One must also make the randomization assumption: {A ⊥ Y₀, Y₁ | W}. Since these parameters are always well defined parameters of the distribution of the data, they can thereby be viewed as W-adjusted variable importance parameters. Then there is no need to make these assumptions. We refer to van der Laan (2006) for the details of this framework.

However, the observed data structure in matched case-control sampling is defined by:

$$\begin{array}{c}O=((M_1,\hspace{0.17em}{W}_1,\hspace{0.17em}{A}_1),\hspace{0.17em}(M_0^j=M_1,\hspace{0.17em}{W}_0^j,\hspace{0.17em}{A}_0^j:j=1,\dots ,J))\hspace{0.17em}\sim \hspace{0.17em}{P}_0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{with}\\ (M_1,\hspace{0.17em}\hspace{0.17em}{W}_1,\hspace{0.17em}\hspace{0.17em}{A}_1)\hspace{0.17em}\sim \hspace{0.17em}(M,\hspace{0.17em}\hspace{0.17em}W,\hspace{0.17em}A|Y=1)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{cases},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\\ (M_0^j,\hspace{0.17em}\hspace{0.17em}{W}_0^j,\hspace{0.17em}\hspace{0.17em}{A}_0^j)\hspace{0.17em}\sim \hspace{0.17em}(M,\hspace{0.17em}\hspace{0.17em}W,\hspace{0.17em}\hspace{0.17em}A|Y=0,\hspace{0.17em}\hspace{0.17em}M=M_1)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{controls}.\end{array}$$

Here M ⊂ W, and M is a categorical matching variable. The sampling distribution of the data structure O is described as above with P₀. Thus, the matched case-control data set contains n independent and identically distributed observations O₁,...,O_n with sampling distribution P₀. The cluster containing one case and the J controls is the experimental unit, and the marginal distribution of the cluster is specified by the population distribution $P_0^{*}$. The model $M*$, which possibly includes knowledge of q₀ or q̄₀(M), then implies models for the marginal distribution of cases (M₁, W₁, A₁) and controls $(M_1,\hspace{0.17em}{W}_2^j,\hspace{0.17em}{A}_2^j)$, j = 1,..., J.

Independent case-control sampling is described as sampling nC cases from the conditional distribution of (W, A), given Y = 1, and sampling nCo controls from (W, A), given Y = 0. The value of J used to weight each control is then nCo/nC. We refer to independent case-control sampling as Case-Control Design I, and matched case-control sampling as Case-Control Design II.

4.2. Methodology Summary

If one wishes to estimate marginal causal effects for Case-Control Design II, which correspond with the traditional parameters of interest in randomized trials, there is now a nonparametric double robust locally efficient procedure available. It performs well as long as $P_0^{*}(Y|A,\hspace{0.17em}\hspace{0.17em}W)$ or $P_0^{*}(A|W)$ is correctly specified, is consistent if either of these models are correctly specified, and efficient if both are correctly specified. The theoretical framework for case-control weighted targeted maximum likelihood estimation has been discussed in detail in van der Laan (2008), and step-by-step implementation for Case-Control Design I appears in Rose and van der Laan (2008). For the targeted maximum likelihood framework designed for prospective sampling, see van der Laan (2006), and for its implementation, see Bembom et al. (2007).

Case-control weighted targeted maximum likelihood estimation for Case-Control Design II incorporates estimates of $P_0^{*}(Y|A,\hspace{0.17em}\hspace{0.17em}W)$, $P_0^{*}(A|W)$, and knowledge of q₀ and q̄₀(M), where q̄₀(M) is defined as:

$${\overline{q}}_0(M)\equiv q_0\frac{P_0^{*}(Y=0|M)}{P_0^{*}(Y=1|M)}=q_0\frac{q_0(0|M)}{q_0(1|M)}.$$

The case-control weighted targeted maximum likelihood estimation procedure for Case-Control Design II uses $P_0^{*}(A|W)$ to update an initial estimate of $P_0^{*}(Y|A,\hspace{0.17em}\hspace{0.17em}W)$.

4.3. Implementation

Case-control weighted targeted maximum likelihood estimation for Case-Control Designs I and II can be implemented using existing software (including SAS, STATA, and R). The implementation of case-control weighted targeted maximum likelihood for Case-Control Design II is also very similar to the implementation for Case-Control Design I. Key differences will be stressed here, but for more detail, we refer to Rose and van der Laan (2008).

Weighting

Weights q₀ and ${\overline{q}}_0(M)\frac{1}{J}$ are assigned to the cases and corresponding J controls, respectively. This differs from Case-Control Design I in that $(1-q_0)\frac{1}{J}$ is used to weight controls in Case Control Design I instead of ${\overline{q}}_0(M)\frac{1}{J}$. In van der Laan (2008) it is suggested that in cases where q̄₀(M) is not known, 1 – q₀ can be used to approximate q̄₀(M).

Estimating $Q_0^{*}(A,\hspace{0.17em}\hspace{0.17em}W)$

Estimate $P_0^{*}(Y|A,\hspace{0.17em}W)\equiv Q_0^{*}(A,\hspace{0.17em}W)$ using the appropriate weights. This estimate is denoted Q̂*(A, W). Two methods for estimating Q̂*(A, W) include intercept adjusted logistic regression and case-control weighted logistic regression. Intercept adjusted logistic regression adds the intercept log q₀/(1 – q₀) to a logistic regression model. This yields the true logistic regression function $P_0^{*}(Y=1|A,\hspace{0.17em}\hspace{0.17em}W)$. If intercept adjusted logistic regression is used to obtain Q̂*(A, W), cases are weighted 1 and controls are weighted with ${\overline{q}}_0(M)\frac{1}{J}$. This is the only step and method where assigned weights are not q₀ and ${\overline{q}}_0(M)\frac{1}{J}$. In Rose and van der Laan (2008), we discussed disadvantages associated with using intercept adjusted logistic regression, and thus our simulations will focus on the use of case-control weighted logistic regression for estimating $Q_0^{*}(A,\hspace{0.17em}\hspace{0.17em}W)$.

Case-control weighted logistic regression uses the assigned weights and performs maximum likelihood estimation for prospective sampling (ignoring the case-control sampling design). Consider a nonparametric model for the marginal distribution of the covariates, and a model { $Q_{\theta }^{*}:\theta$} for $Q_0^{*}(A,\hspace{0.17em}\hspace{0.17em}W)$. Then the case-control weighted maximum likelihood estimator for $Q_0^{*}(A,\hspace{0.17em}\hspace{0.17em}W)$ in Case-Control Design II is given by:

$$\widehat{\theta }=\text{arg}\hspace{0.17em}\underset{\theta }{\text{max}}\sum _{i=1}^n{q}_0\text{log}{\widehat{Q}}_{\theta }^{*}(M_{1i},\hspace{0.17em}\hspace{0.17em}{W}_{1i},\hspace{0.17em}\hspace{0.17em}{A}_{1i})+{\overline{q}}_0(M_1)\frac{1}{J}\sum _{j=1}^J\text{log}(1-{\widehat{Q}}_{\theta }^{*}(M_{1i},\hspace{0.17em}\hspace{0.17em}{W}_{2i}^j,\hspace{0.17em}\hspace{0.17em}{A}_{2i}^j)).$$

If Q̂*(A, W) is obtained using case-control weighted logistic regression, it is weighted with q₀ and ${\overline{q}}_0(M)\frac{1}{J}$. For further discussion see van der Laan (2008) and Rose and van der Laan (2008).

Estimating $g_0^{*}(A|W)$

Estimate $P_0^{*}(A|W)\equiv g_0^{*}(A+W)$ using assigned weights. This estimate is denoted ĝ*(A | W), and may be obtained using case-control weighted logisitic regression, for example.

Calculating h(A, W)

Calculate the “clever covariate” for each subject based on $g_0^{*}(A|W)$. The covariate takes the form:

$$h(A,\hspace{0.17em}\hspace{0.17em}W)\equiv \left(\frac{I(A=1)}{\widehat{g}*(A=1|W)}-\frac{I(A=0)}{\widehat{g}*(A=0|W)}\right)$$

for the risk difference. Two covariates are used for estimation of other parameters, such as the odds ratio:

$$h_0(A,\hspace{0.17em}\hspace{0.17em}W)\equiv \left(-\frac{I(A=0)}{\widehat{g}*(A=0|W)}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{h}_1(A,\hspace{0.17em}\hspace{0.17em}W)\equiv \left(\frac{I(A=1)}{\widehat{g}*(A=1|W)}\right)$$

For further discussion see van der Laan and Rubin (2006) and Moore and van der Laan (2007).

Updating Q̂* (A, W)

Update Q̂*(A, W) by performing an additional weighted regression with h(A, W) as a supplementary covariate. The other coefficients in the initial fit Q̂*(A, W) are held fixed, and the intercept is suppressed in order to estimate the case-control weighted estimator of ε, the coefficient in front of h(A, W), which we denote as ɛ̂¹. The regression estimate Q̂*(A, W) is then updated and given by ${\widehat{Q}}_1^{*}(A,\hspace{0.17em}\hspace{0.17em}W)$:

$${\widehat{Q}}_1^{*}(A,\hspace{0.17em}\hspace{0.17em}W)=\widehat{Q}*(A,\hspace{0.17em}\hspace{0.17em}W)+{\widehat{\varepsilon }}^{1}h(A,\hspace{0.17em}\hspace{0.17em}W).$$

This step is iterated until convergence, although convergence is often achieved in one step.

Estimating Causal Parameters

Using q₀, q̄₀(M₁), and ${\widehat{Q}}_1^{*}(A,\hspace{0.17em}\hspace{0.17em}W)$, estimate causal parameters of interest (risk difference, relative risk, and odds ratio, defined in formulas (1), (2), and (3)) by averaging over the case-control weighted distribution of W. This mapping is performed by evaluating ${\widehat{Q}}_1^{*}(A,\hspace{0.17em}\hspace{0.17em}W)$ at A = 1 and A = 0 and applying weights q₀ to cases and ${\overline{q}}_0(M_1)\frac{1}{J}$ to the controls. This forms case-control weighted estimates of $E_0^{*}(Y_1)=P_0^{*}(Y_1=1)$ and $E_0^{*}(Y_0)=P_0^{*}(Y_0=1)$. The causal parameters of interest can then be calculated from these estimates. For example, the relative risk $E_0^{*}(Y_1)/E_0^{*}(Y_0)$ is estimated by:

$${\widehat{\psi }}_{RR}=\frac{\frac{1}{n}{\sum }_{i=1}^n{q}_0{\widehat{Q}}_{1,q_0}^{*}(M_1,\hspace{0.17em}\hspace{0.17em}{W}_{1i},\hspace{0.17em}\hspace{0.17em}1)+{\overline{q}}_0(M_1)\frac{1}{J}{\sum }_j{\widehat{Q}}_{1,q_0}^{*}(M_1,\hspace{0.17em}\hspace{0.17em}{W}_{2i}^j,\hspace{0.17em}\hspace{0.17em}1)}{\frac{1}{n}{\sum }_{i=1}^n{q}_0{\widehat{Q}}_{1,q_0}^{*}(M_1,\hspace{0.17em}\hspace{0.17em}{W}_{1i},\hspace{0.17em}\hspace{0.17em}0)+{\overline{q}}_0(M_1)\frac{1}{J}{\sum }_j{\widehat{Q}}_{1,q_0}^{*}(M_1,\hspace{0.17em}\hspace{0.17em}{W}_{2i}^j,\hspace{0.17em}0)}.$$

Calculating Standard Errors

Calculating standard errors, p-values, and confidence intervals for case-control weighted targeted maximum likelihood estimates requires the use of the case-control weighted influence curve. This methodology is discussed in detail in van der Laan (2008). We also refer to van der Laan and Robins (2002) for careful discussions of gradients and influence curve theory. The case-control weighted influence curve for matched case-control study designs is the influence curve for prospective targeted maximum likelihood with case-control weighting. We refer to van der Laan and Rubin (2006) and Moore and van der Laan (2007) for this methodology. A complete understanding of the derivation of infuence curves is not required to implement the case-control targeted maximum likelihood estimation procedure for Case-Control Design II.

For illustration, we present the unweighted influence curve for the risk difference of a prospective study ${\psi }_{0,RD}^{*}=P_0^{*}(Y_1=1)-P_0^{*}(Y_0=1)$, which is estimated by:

$$\begin{array}{ll}{\widehat{D}}_{RD}(\psi *,\hspace{0.17em}\hspace{0.17em}g*,\hspace{0.17em}\hspace{0.17em}Q*)(O)=& \frac{I(A=1)}{\widehat{g}*(1|W)}(Y-\widehat{Q}*(1,\hspace{0.17em}\hspace{0.17em}W))-\frac{I(A=0)}{\widehat{g}*(0|W)}(Y-\widehat{Q}*(0,\hspace{0.17em}\hspace{0.17em}W))\\ & +\widehat{Q}*(1,\hspace{0.17em}\hspace{0.17em}W)-\widehat{Q}*(0,\hspace{0.17em}\hspace{0.17em}W)-\widehat{\psi }.\end{array}$$

The case-control weighted double robust efficient influence curve for the risk difference ${\psi }_{0,RD}^{*}=P_0^{*}(Y_1=1)-P_0^{*}(Y_0=1)$ in a matched case-control study design is then:

$$\begin{array}{ll}{\widehat{D}}_{RD,q_0}(\psi *,\hspace{0.17em}\hspace{0.17em}g*,\hspace{0.17em}\hspace{0.17em}Q*)(O)=& q_0\widehat{D}*(g*,\hspace{0.17em}\hspace{0.17em}Q*)(M_1,W_1,\hspace{0.17em}\hspace{0.17em}{A}_1,\hspace{0.17em}\hspace{0.17em}1)\\ & +{\overline{q}}_0(M_1)\frac{1}{J}\sum _{j=1}^J\widehat{D}*(g*,\hspace{0.17em}\hspace{0.17em}Q*)(M_1,\hspace{0.17em}\hspace{0.17em}{W}_2^j,\hspace{0.17em}\hspace{0.17em}{A}_2^j,\hspace{0.17em}\hspace{0.17em}0)-\psi *,\end{array}$$

The asymptotic variance of $\sqrt{n}(\widehat{\psi }-{\psi }_0^{*})$ using the estimate of the efficient influence curve D_q0(ψ*, g*, Q*)(O) can be estimated by:

$${\widehat{\sigma }}^2=\frac{1}{n}\sum _{i=1}^n{D}_{q_0}^2(\psi *,\hspace{0.17em}\hspace{0.17em}g*,\hspace{0.17em}\hspace{0.17em}Q*)(O).$$

A 95% Wald-type confidence interval can then be constructed using the causal parameter estimate $\widehat{\psi }:\widehat{\psi }\pm z_{0.975}\frac{\widehat{\sigma }}{\sqrt{n}}$, as well as a p-value for $\widehat{\psi }:2[1-\Phi (|\frac{\widehat{\psi }}{\widehat{\sigma }/\sqrt{n}}|)]$.

5. Simulation Studies

5.1. Simulation 1

Our first simulation study was designed to illustrate the differences between independent case-control sampling (Case-Control Design I) and matched case-control sampling (Case-Control Design II) using the case-control weighting scheme for targeted maximum likelihood estimation proposed by van der Laan (2008). It was also designed to represent “ideal” situations where control information is not discarded (e.g. data collection is expensive, and covariate information is only collected when a control is a match). This simulation also demonstrates the use of weights q₀ and $(1-q_0)\frac{1}{J}$ with matched data, to represent situations where q̄₀(M) is not known. The population contained N = 35, 000 individuals, where we simulated a 9-dimensional covariate W = (W_i : i = 1,..., 9), a binary exposure (or “treatment”) A, and an indicator Y, which was 1 for cases and 0 for controls. These variables were generated according to the following rules:

$$\begin{array}{l}{P}_0^{*}(W_i=1)=0.5\\ g_0^{*}(A|W)=\frac{1}{1+\text{exp}(-(W_1+W_2+W_3-2W_4-2W_5+2W_6-4W_7-4W_8+4W_9))}\\ Q_0^{*}(A,\hspace{0.17em}\hspace{0.17em}W)=\frac{1}{1+\text{exp}(-(1.5A+W_1-2W_2-4W_3-W_4-2W_5-4W_6+W_7-2W_8-4W_9))}.\end{array}$$

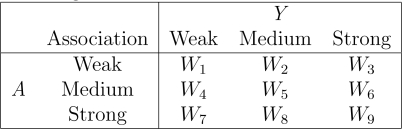
It can be seen in both $g_0^{*}(A|W)$ and $Q_0^{*}(A,\hspace{0.17em}W)$ that the covariates were generated with varied levels of association with A and Y. This was done to investigate the role of weak, medium, and strong association between a matching variable W_i and A and Y. The corresponding associations can be seen in Figure 1. For example, W₁ was weakly associated with both A and Y. One might recall that matching is potentially beneficial only when the matching variable is a true confounder; associated with both A and Y.

Figure 1:

Simulated Covariates

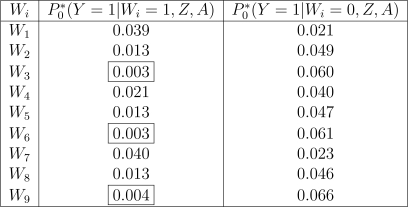
Another illustration of the varied association levels can be seen in Figure 2. Here, we display the probability an individual in the population was a case given W_i = 1, all the non-matching covariates (Z), and A. Likewise, probabilities for W_i = 0 are also shown. For example, let’s say matching variable W₂ is age with 1 representing ‘young’ (< 50 years) and 0 representing ‘old’ (≥ 50 years). In this population, it was not very likely (0.013) that someone who is young will become a case, while someone who is old has a much higher chance of becoming a case (0.047), given Z and A. Therefore, W₂, W₅, and W₈ represent situations where the distribution of W_i among cases and controls is very different. The covariates W₃, W₆, and W₉ represent situations where this difference is even more extreme.

Figure 2:

Simulated Covariates: Probabilities. Z represents the remaining eight non-matching covariates.

The simulated population had a prevalence probability q₀ = 0.030, and exactly 1045 cases. The true value of the odds ratio was given by OR = 2.302, with $P_0^{*}(Y_1=1)=0.055$ and $P_0^{*}(Y_0=1)=0.025$. We sampled the population using a varying number of cases nC = (200, 500, 1000) for both Case-Control Designs I and II, and for each sample size we ran 1000 simulations. For each simulation, the same sampled cases were used for Case Control Designs I and II. Controls were matched to cases on one variable (W_i) in Case-Control Design II for both 1:1 and 1:2 designs. The same number of controls were used in both Case-Control Designs I and II. Causal effect parameters were estimated using case-control weighted targeted maximum likelihood estimation (CCW T-MLE) for Case-Control Designs I and II with case-control weighted logistic regression for Q̂^* (A, W) discussed in Section 4.3. The initial fit for the estimate of $Q_0^{*}(A,\hspace{0.17em}\hspace{0.17em}W)$ was correctly specified as:

$$\begin{array}{l}\widehat{Q}*(A,\hspace{0.17em}\hspace{0.17em}W)=\frac{1}{1+\text{exp}(-({\widehat{\alpha }}_0+{\widehat{\alpha }}_{1}A+{\widehat{\alpha }}_2{W}_1+{\widehat{\alpha }}_3{W}_2+\dots +{\widehat{\alpha }}_9{W}_8+{\widehat{\alpha }}_{10}{W}_9))}.\end{array}$$

The initial fit for the exposure mechanism, which was the correct fit, was defined by:

$$\begin{array}{l}\widehat{g}*(A|W)=\frac{1}{1+\text{exp}({\widehat{\eta }}_0+{\widehat{\eta }}_1{W}_1+{\widehat{\eta }}_2{W}_2+{\widehat{\eta }}_3{W}_3+{\widehat{\eta }}_4{W}_4+{\widehat{\eta }}_5{W}_5+{\widehat{\eta }}_6{W}_6+{\widehat{\eta }}_7{W}_7+{\widehat{\eta }}_8{W}_8+{\widehat{\eta }}_9{W}_9)}.\end{array}$$

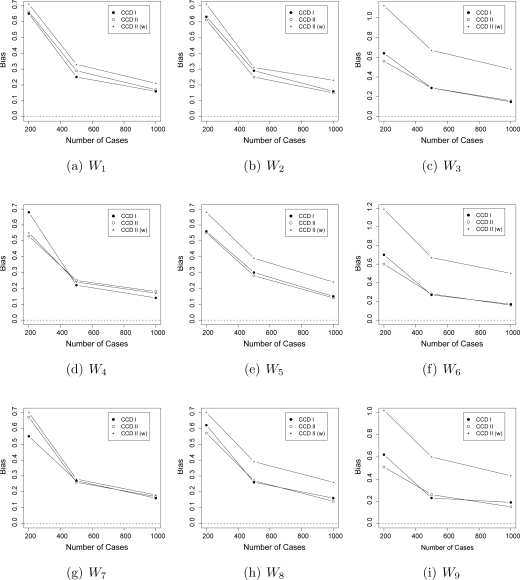
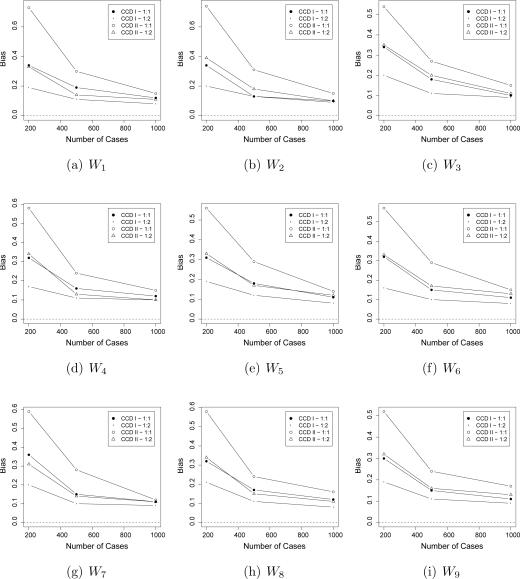
Case-Control Designs I and II performed similarly with respect to bias for the nine covariates. When examining efficiency, there were consistent increases in efficiency when the association between W_i and Y was high (W₃, W₆, and W₉), when comparing Case-Control Design II to Case-Control Design I. Results when association with W_i and Y was medium (W₂, W₅, and W₈) were not entirely consistent, although covariates W₅ and W₈ did show increases in efficiency for Case-Control Design II for all or nearly all sample sizes. These results were in line with the consensus found in our literature search: that matching may produce gains in efficiency when the distribution of the matching variable differs drastically between the cases and the controls.

Simulation 1 also demonstrates the use of weights q₀ and $(1-q_0)\frac{1}{J}$ with matched data, for situations where q̄₀(M) is unknown for Case-Control Design II. This weighting scheme provided a reasonable approximation, yielding larger standard errors, but similar levels of bias for covariates with a weak association with Y. As association with Y increased, the estimate of the odds ratio became more biased. Mean squared errors and relative efficiencies for the odds ratio can be seen in Table 1. Bias results can be seen in Figures 3 and 4.

Table 1: Simulation 1 – Efficiency.

II MSE is Mean Squared Error for Case-Control Design II with weights $(1-q_0)\frac{1}{J}$ for CCW T-MLE, II RE is relative efficiency of Case-Control Design II CCW T-MLE with q̄₀(M) weights is relative efficiency of Case-Control Design I CCW T-MLE, all REs are in comparison to II MSE, and nC is Number of Cases.

	nC	1:1 Matching			1:2 Matching
		200	500	1000	200	500	1000
W 1	II MSE	2.83	0.83	0.33	1.05	0.35	0.16
	II RE	1.06	1.08	1.10	1.07	1.10	1.13
	I RE	1.15	1.14	1.13	1.04	1.06	1.12
W 2	II MSE	3.02	0.77	0.38	1.22	0.45	0.18
	II RE	1.15	1.10	1.15	1.14	1.13	1.21
	I RE	1.16	1.03	1.34	1.14	1.38	1.33
W 3	II MSE	4.67	1.40	0.60	2.07	0.71	0.41
	II RE	2.40	2.38	2.56	2.22	2.48	3.09
	I RE	1.91	1.85	2.07	2.01	2.17	3.21
W 4	II MSE	2.27	0.65	0.31	1.06	0.33	0.14
	II RE	1.03	1.02	1.02	1.01	1.02	1.01
	I RE	0.80	1.08	1.13	1.01	0.97	0.94
W 5	II MSE	2.60	0.75	0.33	1.20	0.37	0.18
	II RE	1.24	1.23	1.18	1.23	1.23	1.26
	I RE	1.01	0.99	1.11	1.11	1.04	1.31
W 6	II MSE	5.25	1.44	0.64	2.17	0.70	0.38
	II RE	2.30	2.37	2.68	2.37	2.56	3.23
	I RE	1.71	2.27	2.10	2.23	2.22	2.74
W 7	II MSE	2.63	0.70	0.31	1.10	0.33	0.16
	II RE	1.03	1.01	1.02	1.02	1.02	1.02
	I RE	1.15	0.97	1.05	1.00	1.03	1.27
W 8	II MSE	2.40	0.79	0.31	1.07	0.35	0.17
	II RE	1.20	1.30	1.43	1.25	1.41	1.54
	I RE	0.93	1.14	1.08	1.11	1.11	1.30
W 9	II MSE	4.35	1.37	0.58	1.63	0.58	0.33
	II RE	2.46	2.35	2.39	2.30	2.39	2.70
	I RE	1.76	2.13	1.90	1.45	1.83	2.49

Figure 3:

Simulation 1 – Bias for 1:1 Matching. CCD I is CCW T-MLE for Case-Control Design I, CCD II is CCW T-MLE for Case-Control Design II with q̄₀(M) weighting, and CCD II (w) is CCW T-MLE for Case-Control Design II with (1 – q₀) weighting.

Figure 4:

Simulation 1 – Bias for 1:2 Matching. CCD I is CCW T-MLE for Case-Control Design I, CCD II is CCW T-MLE for Case-Control Design II with q̄₀(M) weighting, and CCD II (w) is CCW T-MLE for Case-Control Design II with (1 – q₀) weighting.

5.2. Simulation 2

Our second simulation study was designed to address less ideal, and perhaps more common, situations where control information is discarded. Controls were sampled from the population of controls in Simulation 1 until a match on covariate W_i was found for each case. Non-matches were returned to the population of controls. The number of total controls sampled to find sufficient matches was recorded for each simulation. This was the number of randomly sampled controls that was used for the corresponding Case-Control Design I simulation. The mean number of controls sampled to achieve 1:1 and 1:2 matching at each sample size is noted in Table 2 as nCo. For example, in order to obtain 200 controls matched on covariate W₁ in a 1:1 design, an average of 404 controls had to be sampled from the population. Thus, an average of 404 controls were used in the corresponding Case-Control Design I.

Table 2: Simulation 2 – Efficiency.

II MSE is Mean Squared Error for Case-Control Design II CCW T-MLE, I RE is Relative Efficiency of Case Control Design I CCW T-MLE Compared to Case-Control Design II MSE, nC is Number of Cases, nCo is Mean Number of Controls for Case-Control Design I.

	nC	1:1 Matching			1:2 Matching
		200	500	1000	200	500	1000
W 1	nCo	404	1006	2010	804	2011	4026
	II MSE	2.90	0.76	0.28	1.00	0.27	0.14
	I RE	2.89	2.24	2.14	2.12	1.70	2.16
W 2	nCo	404	1009	2016	808	2016	4031
	II MSE	2.91	0.77	0.30	1.15	0.36	0.16
	I RE	2.91	2.72	2.13	2.32	2.21	2.49
W 3	nCo	406	1016	2033	812	2034	4065
	II MSE	1.99	0.48	0.22	0.84	0.28	0.11
	I RE	1.82	1.43	1.65	1.81	1.78	1.85
W 4	nCo	403	1006	2010	806	2012	4023
	II MSE	2.47	0.67	0.29	1.09	0.28	0.13
	I RE	2.38	2.09	2.20	2.29	1.91	2.03
W 5	nCo	406	1010	2019	810	2019	4040
	II MSE	2.41	0.63	0.25	0.92	0.29	0.12
	I RE	2.24	2.00	1.92	1.95	1.89	2.10
W 6	nCo	411	1025	2046	819	2045	4094
	II MSE	2.08	0.64	0.23	0.88	0.27	0.13
	I RE	2.13	1.99	1.69	1.92	1.70	2.23
W 7	nCo	402	1001	2000	801	1999	4000
	II MSE	2.71	0.72	0.30	1.09	0.34	0.15
	I RE	2.54	2.42	2.18	2.19	2.25	2.18
W 8	nCo	407	1014	2028	811	2027	4055
	II MSE	2.28	0.56	0.23	0.97	0.25	0.11
	I RE	2.35	1.76	1.71	1.99	1.59	1.68
W 9	nCo	413	1030	2059	824	2061	4121
	II MSE	1.97	0.54	0.22	0.80	0.26	0.12
	I RE	1.91	1.77	1.69	1.62	1.69	1.84

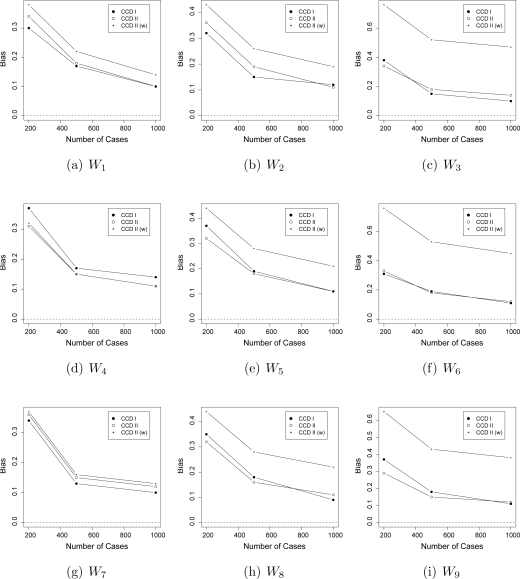
Case-control weighted targeted maximum likelihood estimation was performed for Case-Control Designs I and II. Case-Control Design I outperformed Case-Control Design II with respect to efficiency and bias for all sample sizes and both 1:1 and 1:2 matching. This was not surprising given the mean number of controls in each of the control samples for Case-Control Design I (on average, about two times the number of controls in each control sample for Case-Control Design II). Additionally, as association between W_i and Y increased, there was a trend that the number of controls necessary for complete matching also increased. A similar trend between A and W_i was not apparent. When returning to the bias results, one can see that they do not vary greatly with association between W_i and A or Y. Mean squared errors and relative efficiencies for the odds ratio can be seen in Table 2. Bias results are displayed in Figure 5.

Figure 5:

Simulation 2 – Bias. CCD I is CCW T-MLE for Case-Control Design I and CCD II is CCW T-MLE for Case-Control Design II.

6. Discussion

The main benefit of a matched case-control study design is a potential increase in efficiency. However, an increase in efficiency is not automatic. If one decides to implement a matched case-control study design, matching variable selection is crucial. Numerous publications in our literature review indicated that matching on non-confounding variables is not beneficial, including Kupper et al. (1981): “The futility of matching in [non-confounding situations] is clear...matching on [the variable] will have absolutely no effect on the distribution of the exposure variable in the diseased and nondiseased groups.” Therefore, increases in efficiency with a matched design depend heavily on the selection of a confounding variable as a matching variable. In practice, it may be difficult to ascertain the strength of the association between the matching variable, the exposure of interest, and the outcome. Our simulations for causal effect estimation confirmed the consensus in the existing literature: that in situations where the distribution of the matching covariate is drastically different between the case and control populations, matching may provide an increase in efficiency. Our simulations indicated that $P_0^{*}(Y=1|W_i=1,\hspace{0.17em}\hspace{0.17em}Z,\hspace{0.17em}\hspace{0.17em}A)$, for matching variable W_i and covariate vector Z, may need to be very small for an increase in efficiency using a matched design. These results were true, however, only for our simulations where no control subjects were discarded] it is very common for matched study designs to discard controls (Freedman, 1950; Cochran and Chambers, 1965; Billewicz, 1965; McKinlay, 1977).

This paper focused on the issue of individual matching in case-control studies where the researcher is interested in estimating the marginal causal effect and certain prevalence probabilities are known. Thus, we compared the use of case-control weighted targeted maximum likelihood estimation in matched and unmatched designs. We showed that in practical situations (e.g. when controls are discarded), an unmatched design is likely to be a more efficient, less biased study design choice. Since we also have a nonparametric double robust locally efficient procedure for the estimation of causal parameters in unmatched case-control study designs using q₀, it may be preferred to causal parameter estimation in matched designs. Furthermore, when q₀ is estimated, van der Laan (2008) demonstrated that one can incorporate the uncertainty surrounding the estimate of q₀ into the standard error of the parameter of interest. However, if controls will not be discarded, there is a priori information about the matching variable(s), or the circumstances only allow for a matched design, our double robust locally efficient procedure for the estimation of causal parameters in matched case-control study designs can then be used, as demonstrated in this paper. This design relies on the additional knowledge of q̄₀(M). Our simulations also indicated that when q̄₀(M) is unknown, 1 – q₀ may provide a reasonable approximation, although this should be examined further.