The evolution of growth rates on an expanding range edge

Abstract

Individuals in the vanguard of a species invasion face altered selective conditions when compared with conspecifics behind the invasion front. Assortment by dispersal ability on the expanding front, for example, drives the evolution of increased dispersal, which, in turn, leads to accelerated rates of invasion. Here I propose an additional evolutionary mechanism to explain accelerating invasions: shifts in population growth rate (r). Because individuals in the vanguard face lower population density than those in established populations, they should (relative to individuals in established populations) experience greater r-selection. To test this possibility, I used the ongoing invasion of cane toads (Bufo marinus) across northern Australia. Life-history theory shows that the most efficient way to increase the rate of population growth is to reproduce earlier. Thus, I predict that toads on the invasion front will exhibit faster individual growth rates (and thus will reach breeding size earlier) than those from older populations. Using a common garden design, I show that this is indeed the case: both tadpoles and juvenile toads from frontal populations grow around 30 per cent faster than those from older, long established populations. These results support theoretical predictions that r increases during range advance and highlight the importance of understanding the evolution of life history during range advance.

1. Introduction

When faced with unoccupied habitat, populations spread through space as a function of the rate of individual dispersal (D) coupled with the rate of population growth (r) (Skellam 1951). Most models of range spread assume that D and r are constant during range spread (Hastings et al. 2005). Recent theoretical and empirical results, however, show that dispersal evolves upwards on expanding range edges and that this predictable increase in dispersal can cause accelerating range advance (Travis & Dytham 2002; Simmons & Thomas 2004; Hughes et al. 2007; Phillips et al. 2008).

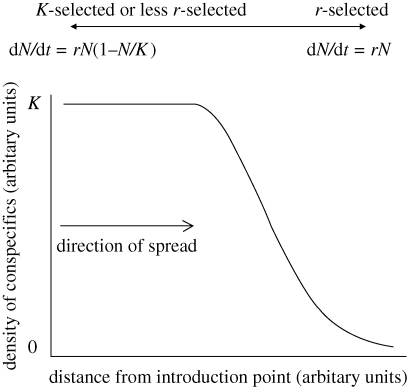
Here, I argue that we may also expect the rate of population growth (r) to increase on expanding range edges and thus drive accelerating range shift (Holt et al. 2006). Why do we expect this? The reason is that the invasion front is characterized by low conspecific density, gradually grading back to near-equilibrium density immediately behind the front (figure 1). This lowered conspecific density on the invasion front drives natural selection for increased reproductive rate (Lewontin 1965; Roff 1993). The reason for this is that any small advantage in the reproductive rate in an exponentially growing population will rapidly accumulate to a large advantage over time: classical r-selection (MacArthur & Wilson 1967). So, relative to individuals behind the front (which can be thought of as either less r-selected or K-selected), the highly dispersive individuals that make up the invasion front each generation face stronger r-selection.

Figure 1.

The shift between r- and K-selection on an invasion front. Populations behind the invasion front are near carrying capacity (K) and so exhibit logistic population growth: relative fitness is determined by variation in K. Populations on the invasion front are always below carrying capacity and exhibit exponential population growth: relative fitness is determined by the variation in r. Even if density regulation does not occur in the core of the range, individuals on the front will tend to spend longer at low density and, as a consequence, face stronger r-selection than individuals from the range core.

Life-history theory shows that the most effective way to increase the rate of population growth is to reproduce early (Cole 1954; Lewontin 1965; Roff 1993). So, all else being equal, individuals that grow faster (and thus attain reproductive size earlier) will be at a selective advantage as r-selection intensifies. Here I examine the evolution of individual growth rates during the invasion of cane toads across northern Australia. When toads were first introduced, they expanded their range at around 10 km yr⁻¹. In the north of their range, toads continue to spread, but now spread at around 55 km yr⁻¹ (Phillips et al. 2006). If toads on the expanding population front have been subject to r-selection (relative to toads in the interior of the range), then we would expect that individual growth rates would be higher as we move closer to the invasion front.

2. Material and methods

(a). Experimental design

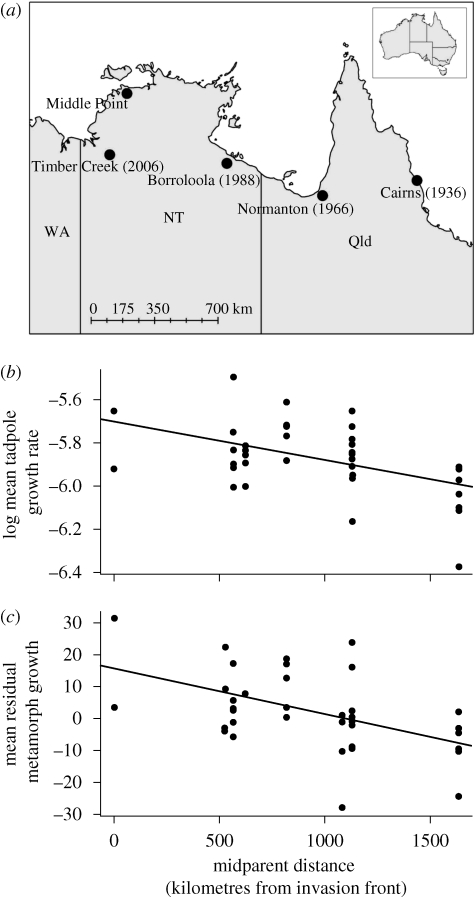
Toads were collected from four sites spanning the toads' invasion of northern Australia: Cairns (colonized 1936), Normanton (1966), Borroloola (1988) and Timber Creek (colonized 2006; figure 2a). These toads were held at Middle Point and maintained in captivity in sex-segregated, but population-mixed, containers for eight months before being bred.

Figure 2.

(a) Sampling localities. Cane toads colonized Cairns in 1936 and have spread westward, colonizing Normanton in 1966, Borroloola in 1988 and Timber Creek in 2006. Toads continue to spread westward. All laboratory work was conducted at Middle Point. The effect of midparent distance on the growth rate of (b) tadpoles (R² = 0.23) and (c) the growth of juvenile toads (R² = 0.22). Distance is measured relative to the invasion front (Timber Creek), so frontal populations have a low midparent distance. Points represent clutch means of log-transformed values with cohort and dam effects removed.

Breeding was elicited using a dose of leuprorelin acetate (Lucrin; Abbott Australasia—a synthetic gonadotrophin: 0.75 ml dose of 0.25 mg ml⁻¹). Where possible, I attempted to mate one dam with two sires (one from her population and one from another population). Multiple mating was achieved using the technique described in Howard et al. (1994). Thus, for 18 of 22 dams, multiple clutches and population crosses were obtained. For logistical reasons, breeding was done in four bouts (‘cohorts’). In each cohort, I attempted to generate clutches in a balanced way across the four sampled populations; however, many breeding attempts were unsuccessful, so the final design is unbalanced in this regard.

Following successful hatching of eggs, six tadpoles were chosen haphazardly from each clutch and reared individually in 1 l containers. Each tadpole was offered food (thawed frozen lettuce) ad libitum, and each container was cleaned twice weekly via an 80 per cent water change. Tadpoles were checked daily, and upon metamorphosis, each metamorph was weighed and placed into individual 1 l terrestrial containers. Metamorphs were fed daily on field-collected termites until they reached a weight of 0.3–0.4 g, at which point they were individually marked (with a toe clip) and transferred into larger (60 l) rearing containers with eight other similar-sized juvenile toads from a mixture of clutches. The mix of clutches in each container was haphazard—determined by the order of metamorphosis.

In these rearing containers, juvenile toads were fed to satiation (determined by no feeding for 1 min despite the abundant presence of food) each morning and evening. This feeding regime continued for 7 days, after which all animals were reweighed.

(b). Analyses

To determine whether individual growth rates varied with distance from the introduction point, I used midparent distance from Timber Creek as the independent variable of interest in all cases. If both parents were from Timber Creek, for example, the midparent distance was 0 km. If one parent was from Timber Creek and the other from Cairns, the midparent distance for that clutch was 818 km.

Tadpole growth was measured as the weight at metamorphosis divided by the days to metamorphosis, and this variable was log transformed to reduce skew prior to analysis. For juvenile toads, I used final weight as the dependent variable, but included initial weight as a covariate. Analyses then consisted of linear mixed models (Crawley 2007). To account for maternal and environmental effects, dam effects were nested within cohort. In all cases, the explanatory variable of interest was midparent distance, and because I had strong a priori hypotheses as to the effect direction, I used one-tailed tests.

3. Results

When raised in a controlled environment, tadpoles grew faster with increasing distance from the introduction point (Cairns; t = 2.43, d.f. = 163, p = 0.008; table 1 and figure 2b). This relationship corresponds to a 28 per cent increase in the tadpole growth rate between long-established (Cairns) and frontal (Timber Creek) populations. Similarly, when raised in a controlled environment and fed to satiation twice daily, juvenile toads grew faster with increasing distance from Cairns (t = 3.29, d.f. = 114, p = 0.0006; table 1 and figure 2c). For a toad starting at 0.3 g, this effect suggests a final weight of 0.65 g in Cairns compared with a final weight of 0.85 g in invasion front populations. Thus, within a single week of feeding to satiation, invasion front toads will tend to be 31 per cent larger than those from Cairns.

Table 1.

Parameter estimates for mixed models comparing growth of toads as a function of midparent distance from the invasion front, Timber Creek. Dependent variables are log-transformed ‘days to metamorphosis’ and log-transformed ‘size at metamorphosis’ for tadpole growth, and final mass (×100) for juvenile growth. The effect of midparent distance was significant in all cases.

model and parameter	estimate	standard error
tadpole growth
fixed effect
midparent distance	−1.55 × 10−4	6.40 × 10−5
variance due to random effects
cohort	0.128
dam within cohort	0.029
residual	0.082
juvenile growth
fixed effects
midparent distance	−0.013	0.004
initial weight	2.657	0.308
variance due to random effects
cohort	776.74
dam within cohort	13.00
residual	288.66

4. Discussion

The toads in this experiment came from populations spanning the toads' invasion history in Australia (toads were introduced in Cairns and are still spreading west of Timber Creek). When the offspring from these toads were raised under standardized conditions, tadpoles and juvenile toads from frontal populations grew substantially (28–31%) faster than those from older populations. The analysis removes dam and cohort effects, so the effect of midparent distance is independent of maternal or environmental effects.

If toads from frontal populations grow faster than conspecifics in older populations, all else being equal they will reach reproductive size (ca 90 mm in body length for females, Zug & Zug 1979) earlier. Earlier reproduction leads to an increased rate of population growth (r), and the rate of population growth (along with dispersal) determines the rate at which the population spreads. Toads historically expanded their range at 10 km yr⁻¹, but now do so at around 55 km yr⁻¹. While some of this acceleration is due to evolved shifts in dispersal (Phillips et al. 2008), the results here, in accordance with predictions by Holt et al. (2006), suggest that increased population growth rate in frontal populations may also be contributing to this accelerating invasion.

The terms r- and K-selection have generated significant controversy, primarily via species being assigned the status of r- or K-strategists based on aspects of their life history (Roff 1993). The controversy does not extend to the concept of r- and K-selection, however, which is a clear result of models of population growth: relative fitness is defined by individual variation in r when the population growth is exponential and in K when the population growth is logistic. Therefore, much of the controversy surrounding r and K is irrelevant to the work presented here because comparisons are being made within a single species, so the assumption that all else is equal (i.e. that all else being equal, faster growth will lead to earlier reproduction) is more justifiable. Nonetheless, if there is a very strong trade-off between juvenile growth rate and fecundity (unlikely) or survival (more likely) in this species, the increased growth rates observed here may not lead to increased population growth rate.

Additionally, it remains possible that the increased growth observed here has arisen as a consequence of adaptation to some unknown environmental variation across the toads' northern range or through correlated selection on other aspects of phenotype (e.g. body size) and is not a consequence of r-selection during range advance. Although environmental variation does not adequately explain the accelerated range advance of toads (Urban et al. 2008), reciprocal transplants and careful correlations between fitness and phenotype (e.g. Arnold & Wade 1984) will be necessary to rule out these possibilities.

With these caveats in mind, my results suggest that the life-history traits critical to the rate at which a population spreads (dispersal, and traits affecting population growth rate) may well evolve during range advance and do so in predictable directions. Dispersal is selected upwards during range advance, and traits affecting the rate of population growth also face upward selection on an expanding front simply because the expanding front is characterized by longer periods of exponential population growth. Thus, the process of range expansion drives the evolution of traits that accelerate that range expansion. Such rapid evolution has clear implications for our understanding of both species invasions and the way in which species can respond to climate change.