A censored beta mixture model for the estimation of the proportion of non-differentially expressed genes

Abstract

Motivation: The proportion of non-differentially expressed genes (π₀) is an important quantity in microarray data analysis. Although many statistical methods have been proposed for its estimation, it is still necessary to develop more efficient methods.

Methods: Our approach for improving π₀ estimation is to modify an existing simple method by introducing artificial censoring to P-values. In a comprehensive simulation study and the applications to experimental datasets, we compare our method with eight existing estimation methods.

Results: The simulation study confirms that our method can clearly improve the estimation performance. Compared with the existing methods, our method can generally provide a relatively accurate estimate with relatively small variance. Using experimental microarray datasets, we also demonstrate that our method can generally provide satisfactory estimates in practice.

Availability: The R code is freely available at http://home.gwu.edu/~ylai/research/CBpi0/.

Contact: ylai@gwu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Microarray technology is a powerful tool for studying complex diseases (Mootha et al., 2003) and for assessing the effects of drugs (Salvatore et al., 2008) at the molecular level. It is an experimental method by which thousands of genes can be printed on a small chip and their expression can be measured simultaneously (Lockhart et al., 1996; Schena et al., 1995). It can be used to detect changes in gene expression between normal and abnormal cells, which enables scientists to detect novel disease-related genes (Singh et al., 2002). Many statistical methods have been developed for this purpose (Cui and Churchill, 2003). Although other advanced genomics technologies, such as RNA sequencing (Nagalakshmi et al., 2008; Wilhelm et al., 2008), have been developed, microarrays have been continuously used for broad biomedical studies (Cancer Genome Atlas Research Network, 2008). Furthermore, since the structures of data from different genomics technologies are basically similar, methods for analyzing microarray data can also be useful for analyzing other similar genomics data.

Performing statistical tests for a large number of genes raises the need for an adjustment for multiple hypothesis testing (MHT). A widely used method to address this issue is the false discovery rate (FDR; Benjamini and Hochberg, 1995) that evaluates the proportion of false positives among claimed positives. FDR control is less stringent than the traditional family-wise error rate (FWER) control such as the Bonferroni correction, and provides more power for discovering differentially expressed genes. However, estimating FDR involves the estimation of π₀, the proportion of non−differentially expressed (null) genes [(1 − π₀) corresponds to the proportion of differentially expressed genes]. A reliable estimate of π₀ is also of great importance to the sample size calculation for microarray experiment design (Jung, 2005; Wang and Chen, 2004).

A variety of methods have been proposed for estimating π₀. Storey and Tibshirani (2003) proposed qvalue. This method uses the ordered P-values and a cubic spline, and estimates π₀ as the value of the fitted spline at a value close to 1. Pounds and Morris (2003) suggested BUM, a ‘beta-uniform’ mixture model with the estimate of π₀ being the value of the fitted model at 1. convest, a method introduced by Langaas et al. (2005), utilizes a non-parametric convex decreasing density estimation method and gives the value of the density at 1 as an estimate of π₀. A histogram-based method has also been proposed (Mossig et al., 2001; Nettleton et al., 2006). The above methods usually provide conservative estimates of π₀; in other words, they are expected to give positively biased π₀ estimates. This has been considered an advantage, since it protects against overestimating the number of differentially expressed genes.

Many other methods have also been proposed for estimating π₀. Lai (2007) proposed a non-parametric moment-based method coupled with sample-splitting to achieve the identifiability and obtained a closed-form formula for π₀. Scheid and Spang (2004) presented the successive exclusion procedure (SEP), which successively excludes genes until the remaining u-values (transformed P-values) are sufficiently close to a uniform distribution U[0, 1]. SEP estimates π₀ by J/m, where J is the estimated number of null genes, and m is the total number of genes. Guan et al. (2008) estimated the marginal density of P-values using a Bernstein polynomial density estimation, and gave a closed-form expression for their π₀ estimator. Liao et al. (2004) obtained an estimate of π₀ through Bayesian inference from a mixture model, which requires the distribution of P-values from non-null genes to be stochastically smaller than that from null genes. In addition to the above methods, there are still many other proposed methods for estimating π₀ (Broberg, 2005; Dalmasso et al., 2005; Jiang and Doerge, 2008; Lu and Perkins, 2007; Pounds and Cheng, 2004, 2006). Furthermore, π₀ can also be estimated through a normal mixture model based on the z-scores obtained from P-values (McLachlan et al., 2006).

In this study, to improve π₀ estimation, we propose a simple method, which is a modification of BUM. The novelty of our method is the introduction of artificial censoring to P-values so that an improved estimation can be achieved. Our motivation is based on the observation that a well-fitted BUM curve for the empirical P-value distribution may not be optimized for estimating π₀. In the following sections, we first introduce the statistical background and our method; then, we present the evaluation and comparison results from our simulation and application studies. Finally, we give some brief discussion to conclude our study.

2 METHODS

2.1 Detection of differential expression

In a typical microarray experiment, the gene expression in two groups of cells can be compared. On a microarray chip, a large number of genes can be monitored simultaneously, which provides researchers with measurement for each gene in each group. For example, to assess genes' involvement in tumor growth, the expression of tens of thousands of genes can be measured in normal and cancerous cells. Depending on the number of microarray chips available, multiple measurements for the expression of each gene are obtained.

For each gene, let μ₁ and μ₂ be the true mean intensities, in groups 1 and 2, respectively. To determine whether the gene is differentially expressed, the null and alternative hypotheses are:

A commonly used test statistic is the Student's t-test (assuming equal variances). A positive is claimed when H₀ is rejected in favor of H_a, and a negative when H₀ is not rejected. A positive means that the gene is declared differentially expressed; a negative means that the gene is declared non-differentially expressed.

If we knew the true state of each gene (i.e. whether it is truly differentially expressed or not), then the results of testing m genes simultaneously could be classified into four categories (each denoted by the random variable in parentheses): true positives (S), false positives (V), true negatives (U) and false negatives (T). Table 1 gives an illustration. Ideally, one would like to minimize V and T, and maximize S and U.

Table 1.

Numbers of true/false null hypotheses and negatives/positives in the situation of MHT

	True null	False null	Total
Negative	U	T	m−R
Positive	V	S	R
Total	m0	m−m0	m

The probability Pr(V > 0) is called the FWER. In MHT, strong control is defined as maintaining the FWER below a specified level α. The traditional strong-control method is the Bonferroni procedure; that is, rejecting each H₀ corresponding to a P-value less than α/m. However, in microarray studies, α/m is typically so small that it is unlikely that many null hypotheses will be rejected. A widely used alternative is to control the FDR, the expected proportion of false positives (V) among the claimed positives (R = V + S) (Benjamini and Hochberg, 1995):

Other versions of FDR have also been proposed: Tsai et al. (2003) considers the estimation of four other FDR versions. In general, controlling FDR provides higher statistical power for discovering differentially expressed genes. Let m₀ = U + V denote the total number of true null hypotheses, and π₀ = m₀/m denote the proportion of true null hypotheses (i.e. the proportion of non-differentially expressed genes; so the proportion of differentially expressed genes is 1 − π₀). Suppose that a researcher rejects H₀ for each gene with a P-value less than a prespecified level α. To estimate the corresponding FDR in this situation, Storey (2002) proposed

where 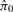is an estimate of π₀, and r(α) is the observed number of positives. From this equation, it is clear that the accuracy of an FDR estimate depends on the estimation of π₀, which is the parameter of interest in this study.

2.2 The beta-uniform mixture model

Pounds and Morris (2003) have proposed the beta-uniform mixture (BUM) model. It assumes the following model for the marginal distribution of P-values:

where 0 < p ≤ 1, 0 < γ < 1 and 0 < α < 1.

Based on this simple model, Pounds and Morris (2003) have proposed the following estimate of π₀:

where 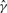and are the MLE estimates.

2.3 Our approach

To represent the marginal distribution of P-values, BUM uses a mixture of the uniform distribution U[0, 1] (also Beta(1, 1)) and a Beta distribution Beta(α, 1) with 0 < α < 1. However, BUM is too simplistic to achieve a robust performance in practice. Let p = {p₁, p₂,…, p_m} be the observed P-values. Under the independence assumption, the log-likelihood is given by

BUM estimates the fitted model curve by maximizing this log-likelihood. As p → 0, f(p) → ∞. Clearly, the smaller a p_i is, the larger its contribution will be to the log-likelihood. Therefore, to optimize the fitted curve, BUM places more weight on smaller P-values. However, π₀ is our focus and is estimated by 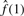, which depends more on the P-values close to 1. To solve this problem, we propose the following censored beta mixture model.

2.3.1 A censored beta mixture model

To improve BUM, we artificially censor the P-values that are less than a cut-off point λ. These P-values are considered ‘indistinguishable’. In other words, even though the actual P-values less than λ are available, we do not use those values; our model only uses the number of such P-values. (We do not consider P-values < λ as missing data). In this way, we aim to reduce the effect of very small P-values. Then, we have the mixture model:

where

is a left-censored uniform distribution U[0, 1] and,

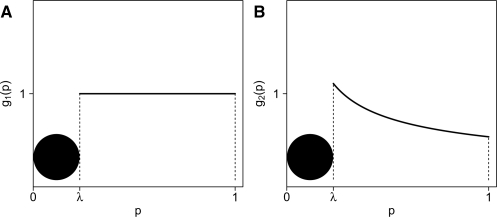
is a left-censored Beta(α, 1) distribution (0 < α < 1). Figure 1 provides an illustration of this model.

Fig. 1.

(A) Graph of g1, a censored uniform distribution U[0, 1]. (B) Graph of g₂, a censored beta distribution Beta(α, 1).

Remark 1. —

Note that although we do not assume a specific form for the density of f(p) in [0, λ), we know that Pr(0 ≤ p < λ|g₁) = λ and Pr(0 ≤ p < λ|g₂) = λ^α. The marginal probability is Pr(0 ≤ p < λ) = γ λ + (1 − γ)λ^α.

Remark 2. —

In this study, we assume that λ is given as 0.05, which is conventionally considered small (e.g. a threshold value for declaring statistical significance in practice). It is theoretically true that selecting a λ less than the minimum P-value is equivalent to using BUM. Furthermore, as pointed out by a reviewer, selecting a large λ is very similar to using qvalue or the histogram methods.

2.3.2 Estimating model parameters

Our model is a special case of the two-component mixture model in Ji et al. (2005). It consists of a censored Beta(1, 1) (equivalent to U[0, 1]), and a censored Beta(α, 1). Therefore, we can use the Expectation–Maximization (EM) algorithm (McLachlan and Krishnan, 2008) to estimate the parameters γ and α. Following Ji et al. (2005), we augment the data by introducing the latent indicator variables z_i, 1 ≤ i ≤ m (where m is the total number of genes) defined as:

Let z = {z₁, z₂,…, z_m}. The log-likelihood of our model given the ‘complete’ data {p, z}, is:

To maximize the log-likelihood with respect to γ and α, given the ‘complete’ data, we take the partial derivative of the above equation with respect to γ and set it equal to zero, and then do the same for α. Solving these two equations, we obtain the following maximum likelihood estimates of γ and α to be used in the M-step of the EM algorithm:

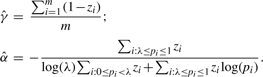In the E-step of the EM algorithm, we need to update the expected values of the {z_i}. Given the current estimates of γ and α, we can compute 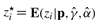. Since each z_i is an indicator variable, z_i^⋆ is the conditional probability (at each iteration of the algorithm) that p_i belongs to component g₂. Hence, we have the following formulas:

• For each censored P-value, that is, if 0 ≤ p_i < λ,

  
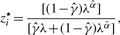
• For each non-censored P-value, that is, if λ ≤ p_i ≤ 1,

  

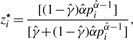
To start the EM algorithm, we select an initial value for γ; in general, we can use γ⁽⁰⁾ = 0.5, unless we have some empirical estimate of π₀ to use instead. Then, we initialize {z_i} by setting z_i⁽⁰⁾ = 1 − γ⁽⁰⁾ for 1 ≤ i ≤ m. With {z_i⁽⁰⁾}, we can obtain γ⁽¹⁾ and α⁽¹⁾, the estimates of γ and α after the first iteration. The convergence of EM algorithm is declared when

where γ^(k) is the estimate of γ at the end of the k-th iteration, and δ is a prespecified threshold (δ = 1 × 10⁻⁶ in this study). When the EM algorithm converges, let 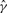and be the estimates of γ and α, respectively. Then, the estimate of π₀ is given by:

Remark 3. —

As suggested by a reviewer, it is necessary to consider multiple initial values for BUM. In our simulation study, for BUM's parameters (a and λ), we use a = λ = min(2 × mean of all P-values, 0.9) and 5 pairs of randomly simulated numbers from U[0, 1]. Although our method is robust to different initial values in this study, we still suggest that multiple initial values may be necessary to achieve a reliable estimate of π₀ in certain situations (e.g. π₀ ≈ 1). Furthermore, although the required computing time of our method is much longer than that of BUM (and several of other methods), it is still affordable with a general computer.

2.3.3 Confidence interval

Since the above EM algorithm does not provide us with any closed formulas of estimates, it is difficult to derive the theoretical confidence interval (CI) for the estimated π₀. Therefore, we use the bootstrap procedure (Efron, 1979) to obtain a CI for π₀ (we set B = 500 for both application studies):

1. Select a random sample of m P-values from { p₁, p₂,…, p_m} with replacement and equal probabilities;

2. Apply the EM algorithm to the sample generated in Step 1 and obtain a resampling estimate of π₀;

3. Repeat Steps 1 and 2 B times to obtain the resampling distribution of ;

4. For a 100(1 − α)% CI for π₀, find the (α/2)-th and (1 − α/2)-th quantiles of the resampling distribution.

Remark 4. —

A key assumption for bootstrapping P-values in the construction of CIs is that the observed P-values are independent. However, since genes are correlated in a expression dataset, a bootstrapped CI for π₀ should be considered as an approximation in practice. This issue has been discussed in Allison et al. (2002).

3 RESULTS

3.1 Simulation studies

3.1.1 Simulation configuration

We simulate gene expression data to evaluate the performance of our method. We also select several existing methods for a comparison study. BUM (Pounds and Morris, 2003) has to be included since it is the foundation of our method. Based on the consideration of the popularity and research history of the statistical methods for estimating π₀, the following methods are selected (notation in parentheses): (CB) our method; (BUM) Pounds and Morris (2003); (H) the histogram-based method (Mosig et al., 2001; Nettleton et al., 2006); (Q) qvalue (Storey and Tibshirani, 2003); (L) the method proposed by Liao et al. (2004); (S) the method proposed by Scheid et al. (2004); (C) convest (Langaas et al. 2005); (RDM) the method proposed by Lai (2007); (G) the method proposed by Guan et al. (2008). The notations defined above are used in Figure 2. (We have actually performed a simulation study to compare many more methods. However, due to the page limit, it is difficult to present all the results. The exclusion of other methods does not change our conclusion.)

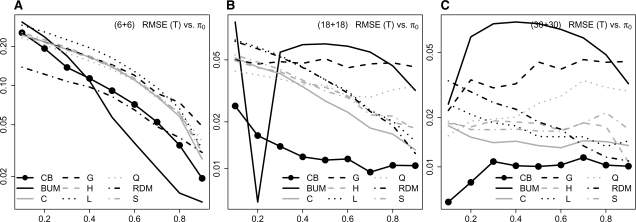
Fig. 2.

Simulation results: gene expression data are simulated based on a independence structure. RMSE in log-scale of the estimates from different methods with different sample sizes considered: n₁ = n₂ = 6 (A), 18 (B) and 30 (C).

For each dataset, we simulate expression observations for 5000 genes. In reality, genes work together in complicated gene networks. To study the impact of correlation among genes on different methods, we generate data with the assumption that genes interact in blocks (‘networks’) of equal size. We also assume that within each block, the correlation among any pair of genes is the same, and equal to ρ. We perform simulations for different sample sizes (n₁, n₂ = 6, 10, 18, 30 and 50); correlation strength (ρ = 0, 0.3, 0.5, 0.7 and 0.9); and number of blocks (b = 100, 200 and 500) [or, equivalently, number of genes per block (g_b = 50, 25 and 10)].

Remark 5. —

It is well-known that the sample size has an important impact on the estimation of π₀. As pointed out by one reviewer, the power of an α level test is the cumulative distribution function of the P-value evaluated at α. Since the power depends on the sample size, so does the distribution of P-values. Therefore, any non-trivial transformation of P-values (including π₀ estimators) depends on the sample size. For example, Pounds and Cheng (2005) have showed that when an estimate of the minimum of the assumed marginal distribution of P-values [e.g. f(1) for BUM] is used for estimating π₀, the estimator can be expressed as a function of the sample size.

Given a value of π₀ (0.1, 0.2,…, 0.9), a corresponding number of blocks are set to consist entirely of differentially expressed genes, with the remaining blocks consisting entirely of non-differentially expressed genes. For example, to generate a dataset with π₀ = 0.7 for the {b = 100, g_b = 50} configuration, we simulate 30 blocks with differentially expressed genes, and 70 blocks with non-differentially expressed genes. For each block, we use the covariance matrix Σ = (1 − ρ)I + ρE of size g_b × g_b, where I is the identity matrix and E is a matrix of ones. (Note that Σ is also the correlation matrix since all genes have unit variances.) Then, for each configuration mentioned above, we perform the following:

1. Simulate a gene expression dataset with 5000 genes.

   1. For a block of non-differentially expressed genes, generate observations from a multivariate normal distribution N(0, Σ) for both sample groups.
   2. For a block of differentially expressed genes, generate observations from a multivariate normal distribution N(0, Σ) for one sample group. Then, generate observations from a multivariate normal distribution N(μ, Σ) for the other group (where μ is a random vector, with elements coming from a uniform distribution U[0.5, 1.5]).

2. Apply the two-sample Student's t-test to the profile of each gene and obtain 5000 theoretical P-values.

3. Use different methods to estimate π₀.

3.1.2 Criteria for evaluation and comparison

We repeat the above steps B = 100 times for different values of π₀ (0.1, 0.2,…, 0.9). For each value of π₀ and each method, we compute the bias, standard deviation (SD) and root mean squared error (RMSE) as follows:

• ,

• ,

• ,

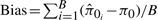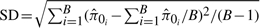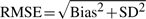where 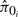is the i-th estimate of π₀. These criteria are used to evaluate the estimation performance of different methods and the impact of different λ.

3.1.3 Comparison of different methods

In all the results, the patterns in RMSE, bias and SD are very similar for all cases sharing the same sample size and correlation strength. In other words, the block size g_b in our configuration does not substantially affect the patterns in RMSE, bias and SD. In the Supplementary Materials, we present the simulation results based on 200 blocks with 25 genes in each block and different correlation values (ρ). In the following, we discuss the simulation results based on the simple independence structure (ρ = 0), which is representative of the other results. The simulation results are presented for samples sizes 6 +6 , 18 + 18 and 30 + 30. [In order to show a clear comparison among different methods, we use a log-scale for the y-axis in RMSE and SD graphs (with the option ‘log = “y” ’ in the R-function ‘plot’), and the cube root of Bias is actually used as the y-axis in the Bias graphs. All these comparison plots are given in the Supplementary Materials. However, in the following, we only give the RMSE-based comparison plots due to the page limit.]

When n₁ = n₂ = 6 (Fig. 2A), all the π₀ estimation methods show an overall decreasing pattern of RMSE as the value of π₀ increases. BUM gives the lowest RMSE when π₀ > 0.4; but its RMSE is among the worst when π₀ < 0.3, where RDM gives the lowest RMSE. Our method always gives a competitive low RMSE when π₀ > 0.1.

When the sample size increases to n₁ = n₂ = 18 (Fig. 2B), BUM shows an unstable performance: it gives a relatively high RMSE for all the values of π₀, except at π₀ = 0.2 and 0.9. The benefit of using our method is more apparent: its RMSE is lower than those of all the other methods, for all the values of π₀ except for π₀ = 0.2 (where BUM's RMSE is the lowest).

For n₁ = n₂ = 30 (Fig. 2C), BUM's RMSE displays a concave parabola pattern, and is always relatively high. Our method has the lowest RMSE for all π₀.

The figures in the Supplementary Materials also confirm a satisfactory performance in Bias and SD from our method. In general, most methods' bias decreases as the sample sizes and the value of π₀ increase. However, BUM quickly becomes the most negatively biased (which explains the observed large RMSE of BUM although the SD of BUM is among the smallest). A strongly negative bias leads to an undesirable overestimation of the number of truly differentially expressed genes. On the other hand, our method's bias becomes negligible as the sample sizes increase. Most methods' SD increases as the value of π₀ increases and decreases as the sample sizes increase.

In general, when the simulation results based on different dependent structure (independent, weakly/strongly dependent) are compared (Supplementary Materials), the higher the correlation, the higher becomes the SD. (The bias, on the other hand, remains mostly unaffected by the increase in correlation.) However, our results show that the increase in SD induced by positive correlation among test statistics does not render the existing π₀ estimation methods inappropriate.

3.1.4 Choice of λ

The above reported simulation configuration can also be used to understand the effect of λ. We simulate data with different sample sizes 6 + 6, 18 + 18 and 30 + 30 and compare the performance of our model for λ in the set {0.01, 0.03, 0.05,…, 0.25}. The figures in the Supplementary Materials shows that no single value of λ can be identified to minimize RMSE in a wide range of π₀. Furthermore, the RMSE patterns can change significantly when the sample sizes are changed. It is clear that a relatively large λ (e.g. λ = 0.25) is not a good choice. However, a relatively small λ (e.g. λ = 0.01) is also not an appropriate choice. In our simulation study, we have observed that λ = 0.05 is always a reasonable choice to achieve an overall satisfactory performance.

3.2 Applications to experimental data

We first consider the following two published experimental microarray datasets for our applications. The first dataset contains 22 283 gene expression profiles from kidney biopsies of 19 kidney transplant subjects with cyclosporine-based immuno-suppression and 22 kidney transplant subjects with sirolimus-based immuno-suppression. The second dataset consists of 12 488 gene expression profiles from pancreatic T regulatory (three subjects) and T effector cells (five subjects). Both datasets are publicly available in the Gene Expression Omnibus (GEO) database (Barrett et al., 2007) with accession numbers GSE1743 (Flechner et al., 2004) for the first (renal) dataset and GSE1419 (Chen et al., 2005) for the second (T cell) dataset.

Theoretical P-values based on the corresponding t-distributions are calculated for each dataset (two-sample Student's t-test is used for detecting differential expression). The true value of π₀ is unknown in the applications. Therefore, to compare different methods in each application, we obtain B = 500 bootstrap estimates of π₀ (see Section 2.3.3 for details) and construct a boxplot for the estimate from each method. Such a boxplot is useful to understand general CIs for an estimate.

Based on our simulation study, convest has consistently showed a relatively low RMSE. BUM should be considered since it is the foundation of our method. Therefore, for simplicity, we use boxplots to compare our method with BUM and convest. (The exclusion of other methods does not change our conclusion.) Figure 3 shows the P-value histograms and the estimates from these three different methods. For both datasets, the P-value distribution curves fitted by our method are close to the corresponding P-value histograms. Theoretically, π₀ cannot be higher than the marginal P-value distribution. This has been briefly discussed in one of our previous publications (Lai, 2007).

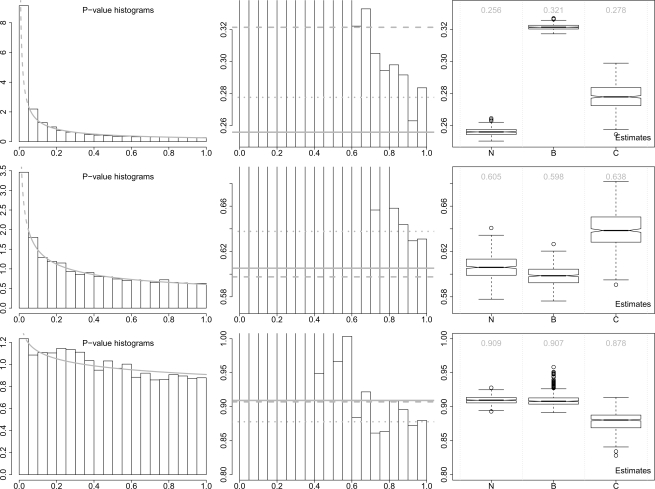
Fig. 3.

Application results: histograms of P-values and boxplots of bootstrap estimates of π₀. The P-values are calculated based on three experimental datasets: the renal data (upper panel), the T-cell data (middle panel) and the smoke data (lower panel). In the histograms (left panel), the gray curves represent the fitted censored beta mixture models (the dashed parts are artificially censored). The zoomed-in histograms (middle panel) are also shown to compare the estimate of π₀ from different methods. The gray solid, dashed and dotted lines represent the estimates from our method, BUM and convest, respectively. In the boxplots (right panel), N = our method, B = BUM and C = convest. The numbers in gray color are the estimates of π₀ based on the original data.

For the renal dataset, our method gives an estimate of π₀ 0.256 with a relatively tight CI (95% CI: 0.252–0.261). convest gives a higher estimate 0.278 with a wider CI (95% CI: 0.263–0.293), whereas BUM gives the highest estimate 0.321 although a slightly tighter CI (95% CI: 0.318–0.325). Notice that only the estimate from our method is under the whole P-value histogram. For the T-cell dataset, our method gives an estimate of π₀ 0.605 with relatively tight CI (95% CI: 0.586–0.626), whereas BUM gives a slightly lower estimate 0.598 and slightly tighter CI (95% CI: 0.583–0.616). Both estimates are under the whole P-value histogram. However, convest still gives a higher estimate 0.638 and wider CI (95% CI: 0.609–0.671).

We also use another experimental dataset to illustrate that our method (also BUM) does not always yield satisfactory estimation results. The third application is based on a dataset with 22 283 gene expression profiles from small airway tissues (five non-smokers versus six smokers). This dataset is also publicly available in GEO with accession number GSE3320 (Harvey et al., 2007). The estimation results are also given in Figure 3. A clear ‘bumped’ shape can be observed in the P-value range [0.15, 0.35], which causes the problematic estimation results from our method and BUM (these beta distribution based models do not allow any ‘bumped’ shapes). Our fitted model curve is not close to the P-value histogram. Although the CI from our method (95% CI: 0.899–0.921) and BUM (95% CI: 0.897–0.935) are clearly tighter (the one from our method is the tightest) than that from convest (95% CI: 0.850–0.902), both estimates from our method (0.909) and BUM (0.907) are clearly higher than the right end portion of P-value histogram. convest provides a more reasonable estimate 0.878 for this application, although the difference among the estimates from different methods is quite small.

Therefore, in practice, we suggest to check the histogram shape before applying any statistical methods for estimating π₀. If the histogram shape is roughly decreasing, then we expect satisfactory estimation performance from our method (and BUM in certain situations). If the histogram shape is not regular, then we may consider some non-parametric method like convest or the moment-based method (Lai, 2007).

4 DISCUSSION

Microarrays have been widely used in biological and medical studies. An accurate estimate of the proportion of differentially expressed genes is important in false positive control and experiment design. Therefore, the improvement of existing estimation methods still remains important.

Our proposed method for estimating π₀ provides an effective solution. Although it is arbitrary, the choice of λ = 0.05 provides an overall satisfactory performance. In our simulation study, the advantage of using our method is clear in the cases of moderate and large sample size (18 + 18 and 30 + 30). In these cases, our method outperforms (w.r.t. RMSE) the other methods considered in this study. In the case of small sample, BUM has a satisfactory performance. Our method may be improved if an efficient method for the automatic selection of λ can be developed. This issue will be pursued in our future research.

Although none of the π₀ estimation methods mentioned above considers the effect of gene networks and interactions, dependence among genes is still a difficult issue in microarray data analysis (Efron, 2007). However, as investigated by Benjamini and Yekutieli (2001), methods that are based on the independence assumption perform quite well in general situations of weak positive dependence, and a positive dependency structure is common in many situations. A satisfactory performance under weak positive dependence has also been confirmed in our simulation studies.