Non-linear vector summation of left and right vestibular signals for human balance

Abstract

The left and right vestibular organs always transduce the same signal of head movement, and with natural stimuli can only be activated simultaneously. To investigate how signals from the left and right vestibular organs are integrated to control human balance we electrically modulated the firing of vestibular afferents from each labyrinth independently and measured the resulting balance responses. Stimulation of one side at a time (monaural) showed that individual leg muscles receive equal inputs from the two labyrinths even though a single labyrinth appeared capable of signalling 3-D head motion. To deduce principles of left–right integration, balance responses to simultaneous stimulation of both sides (binaural) were compared with responses to monaural stimuli. The binaural whole-body response direction was compatible with vector summation of the left and right monaural responses. The binaural response magnitude, however, was only 64–74% that predicted by the monaural sum. This probably reflects a central non-linearity between vestibular input and motor output because stimulation of just one labyrinth revealed a power law relationship between stimulus current and response size with exponents 0.56 (force) and 0.51 (displacement). Thus, doubling total signal magnitude either by doubling monaural current or by binaural stimulation produced equivalent responses. We conclude that both labyrinths provide independent estimates of head motion that are summed vectorially and transformed non-linearly into motor output. The former process improves signal-to-noise and reduces artifactual common-mode changes, while the latter enhances responses to small signals, all critical for detecting the small head movements needed to control human balance.

Introduction

When an animal is at rest, vestibular primary afferent neurons discharge spontaneously with firing rates that vary across species. These have been reported as 5–10 s⁻¹ in frog (Myers et al. 1997), 13 s⁻¹ in stingray (Löwenstein, 1955), 30–40 s⁻¹ in rat and guinea pig (Courjon et al. 1987; Curthoys, 1982), 45–55 s⁻¹ in chinchilla (Goldberg et al. 1990), 65–90 s⁻¹ in squirrel monkey (Fernandez & Goldberg, 1971; Goldberg & Fernandez, 1971), and 90–115 s⁻¹ in macaque monkeys (Cullen & Minor, 2002). A resting discharge allows each afferent to signal acceleration in two directions with a decrease in firing rate signalling the opposite direction to an increase (Löwenstein & Sand, 1940; Goldberg & Fernandez, 1971). A higher resting rate allows each afferent to signal bi-directionally and symmetrically over a greater physical range. Therefore, the vestibular organs on just one side of the head should be capable of signalling linear and angular head accelerations equally in all directions. This and the fact that the left and right vestibular labyrinths are locked in the rigid structure of the skull would mean that each labyrinth transmits essentially the same information to the balance system.

Here we ask whether the balance system receives duplicate information from the two labyrinths, and if so, what advantage it offers. For example, does the duplication allow each labyrinth to project preferentially to different muscles? If not, how is the information from the two labyrinths combined? To investigate these questions we use galvanic vestibular stimulation (GVS). During human standing and walking, the brain interprets the GVS-evoked vestibular input as an unplanned body movement to which the balance system responds by moving the body in the opposite direction (Day et al. 1997; Fitzpatrick et al. 2006). The direction and size of this motor response can be used to infer properties of vestibular processing by the balance system. Using GVS allows separation of the actions of the left and right labyrinths by applying stimulus currents to each side independently or having both systems act together by applying stimuli bilaterally.

GVS acts to change the firing rates of vestibular afferents without physically moving the subject's head. We assume GVS produces analogous effects to those described for the squirrel monkey in which perilymphatic cathodal currents increase vestibular afferent firing linearly and anodal currents decrease it (Goldberg et al. 1984). Fitzpatrick & Day (2004) calculated that GVS activation of semicircular canal afferents would be equivalent to a continuous head rotation approximately about the roll axis of the head. This has received empirical support (Day & Cole, 2002; Day & Fitzpatrick, 2005; Fitzpatrick et al. 2006). The equivalent net linear acceleration from activation of otolith afferents is less certain. We restrict our analysis to the medium-latency component of the GVS-evoked response (Britton et al. 1993; Fitzpatrick et al. 1994), which appears to be driven primarily by semicircular canal afferents (Cathers et al. 2005) rather than the otolith organs. However, our arguments remain the same if otolith and semicircular canal afferents both contribute to the measured responses.

Methods

All procedures received UCL Research Ethics Committee approval and conformed to the Declaration of Helsinki. All participants gave written, informed consent.

A series of three independent experiments investigating specific aspects of left–right vestibular integration are described. There were minor changes in set-up and procedure between them as new questions arose. For completeness we describe the procedures separately below.

Experiment 1 was concerned with the effect of head position and changes in electromyographic (EMG) responses, which required a large number of trials per condition to obtain reliable waveforms. Experiment 2 was concerned with a wider range of stimulus polarity combinations but not individual muscle responses, requiring more experimental conditions but fewer trials per condition. As this experiment was concerned with balance reactions that can be obtained with smaller stimulus currents, we took the opportunity in this experiment to reduce the stimulation intensity and lessen the remote possibility of response saturation. We also changed our stimulation method to use independent parallel stimulus circuits for each labyrinth (Fig. 1A and B) to exclude the possibility of an unforeseen stimulus interaction that might occur using a single circuit to stimulate both labyrinths in series. (In retrospect, however, experimental conditions that were common to both experiments gave essentially the same results.) Experiment 3 was performed to investigate the effect of stimulus intensity on the balance response.

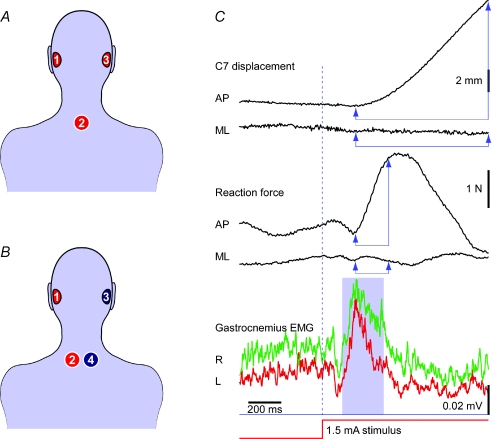
Figure 1. Method and analysis.

A, GVS electrode placement for Experiment 1. For binaural stimulation, the stimulus current was passed between mastoid electrodes 1 and 3, with either anode–right, cathode–left or cathode–right, anode–left. For monaural stimulation of either side, current was passed between electrodes 1 and 2 (T1 vertebra) or 3 and 2, with either the anode or cathode at the ear. B, GVS electrode placement for Experiments 2 and 3. Two stimulators were used so that binaural stimulation was achieved by independent stimulation of each side. Stimulus currents were passed between electrodes 1 and 2 for the left labyrinth and between 3 and 4 for the right labyrinth. C, typical mean response of one subject with head facing right to 1.5 mA binaural bipolar, anode–right, GVS. The stimulus evoked a medium-latency increase in the right (R) and left (L) rectified gastrocnemius EMG, measured as the area under the curve (blue areas, 120–370 ms). After an electromechanical delay this produced an increase in anteroposterior (AP) ground reaction force (middle) and a backward body sway at the level of C7 spinous process. There is little change in the mediolateral (ML) response with the head in this position. Force and displacement vectors were measured from amplitude changes between time points shown by vertical arrows (200–400 ms and 200–1000 ms respectively).

Experiment 1

Testing was spread across two sessions on separate days and involved 10 subjects (mean age 34 years, s.d. 10 years; 8 males). Three stimulating electrodes (2.5 cm diameter) were adhered to the skin overlying the left mastoid process, the right mastoid process and the T1 spinous process. Using a single constant-current stimulator, current was passed between the two mastoid electrodes for binaural stimulation, and between a mastoid electrode and the T1 electrode for monaural stimulation (Fig. 1A). Relays were used to select the appropriate electrode pair. There were six stimulation conditions consisting of four monaural configurations (anode right, cathode right, anode left, cathode left) and two binaural configurations (anode right and cathode left, cathode right and anode left).

The standing posture was either with the head rotated 90 deg to the right and feet 10 cm apart (session 1) or with the head facing forward and feet 0.5 cm apart (session 2) with head upright so that the roll balance response was maximal (Cathers et al. 2005). To ensure equal loading through each leg, subjects stood with each foot on a separate force plate (left leg: Kistler 9281B; right leg: Kistler 9287; Kistler Instrumente, CH-8408 Winterthur, Switzerland) and visual feedback from the force plates was available before trials (Marsden et al. 2002). Vision was obscured by liquid crystal glasses at the start of each trial (PLATO visual occlusion spectacles, Translucent Technologies, Toronto, Canada) and recording began after a 500–1000 ms random delay. Following a 500 ms baseline period, a 1.5 mA rectangular waveform stimulus was applied for 1 s. Within a session the subject received fifty trials of each of the six stimulus conditions presented in pseudo-random order.

Experiment 2

Testing took place during a single session and involved 10 subjects (mean age 31 years, s.d. 6 years; 5 males) who had not participated in Experiment 1. Two isolated constant-current stimulators were used, one for each side, to ensure independent influences on each labyrinth (Fig. 1B). Left vestibular stimulation was achieved by passing current between one electrode on the left mastoid process and the other placed 2 cm to the left of the T1 spinous process. Right vestibular stimulation was achieved using a mirrored electrode pair on the right side. Thus we could stimulate the two sides independently with any combination of polarities. Eight stimulation conditions were four monaural configurations (anode right, cathode right, anode left, cathode left) and four binauaral configurations, two of which were bipolar (anode right and cathode left, cathode right and anode left) and two monopolar (anode right and anode left, cathode right and cathode left).

Subjects stood on a single force plate (Kistler 9287) with the feet together and the head upright and facing forward. At the start of each trial they closed their eyes and data collection began after a random delay of 0.5–1.5 s. Following a 2 s baseline period, a 1.0 mA rectangular waveform stimulus was applied for 2 s. Twenty trials of each of the eight conditions were presented in pseudo-random order.

Experiment 3

Testing took place during a single session and involved 10 subjects (mean age 29 years, s.d. 7 years; 4 males) who had not participated in Experiments 1 or 2. Procedures were the same as those of Experiment 2 but the experimental conditions were different. There were 10 stimulation conditions in total consisting of two monaural configurations (anode right, cathode right) and five stimulus intensities (0.25, 0.5, 1.0, 1.5 and 2.0 mA). Ten trials of each of the 10 conditions were presented in pseudo-random order.

Measurement and analysis

Movement of the body was recorded in three dimensions using an optoelectronic motion capture system (CODA mpx30/cx1; Charnwood Dynamics, Rothley, UK) and sampled at 200 Hz. Measurements were taken from a marker placed over the C7 spinous process. Net ground reaction forces acting on the body in three dimensions were calculated from the force plate outputs sampled at 200 Hz. EMG from surface electrodes overlying the left and right medial gastrocnemius muscles were pre-amplified (gain 1000), transmitted wirelessly (FM time division multiplexed; channel bandwidth 1 kHz; MT8 MIE Medical Research, Leeds, UK), amplified further (×2) and sampled at 2 kHz. Without further filtering the signals were full-wave rectified prior to averaging.

Signals were aligned to stimulus onset and averaged for each experimental condition per subject. Measurements were made in the horizontal plane of the mean displacement vector at the level of C7 from 200–1000 ms post-stimulus onset (Fig. 1C top) and the mean ground reaction force vector from 200–400 ms post-stimulus onset (Fig. 1C middle). EMG responses were quantified by measuring the mean full-wave rectified signal from 120–370 ms and expressing it as a percentage of the mean pre-stimulus baseline level (Fig. 1C bottom).

To analyse EMG responses, the responses from both legs under different stimulation conditions were combined by first inverting the responses that were inhibitory through stimulus polarity and head orientation. They were then averaged across polarities and legs for each subject and head position. To assess laterality, the mean ipsilateral and contralateral responses were obtained from:

where L_leg= left leg, R_leg= right leg, L⁻= cathode left, L⁺= anode left, R⁻= cathode right, R⁺= anode right.

To assess whether the EMG responses to binaural stimulation were equivalent to the algebraic sum of the component monaural responses, the mean responses were obtained from:

Comparisons between these collapsed mean values were performed using Student's two-tailed paired t test with P_α set at 0.05.

For displacement and force responses, vector magnitude was calculated as (AP²+ ML²)^1/2 and vector direction as atan(ML/AP), where ML and AP denote mediolateral and anteroposterior components, respectively. The magnitudes and directions of the response vectors were analysed separately. Statistical comparisons of vector magnitudes were performed using Student's two-tailed paired t test. Summary measures of vector directions were calculated using circular statistical methods as recommended by Batschelet (1981), and statistical comparisons were performed using Hotelling's one-tailed test for paired angles (Zar, 2010).

Results

The results here are presented in order of the four questions asked:

• Are vestibular afferents functionally bi-directional for balance control?

• Does each labyrinth project symmetrically to both sides of the body?

• How are the left and right vestibular signals integrated?

• What is the vestibular input–motor output relationship?

Bi-directionality

We first tested whether the resting discharge of vestibular afferents allows them to transmit bi-directional information symmetrically. Starting from the premise that cathodal and anodal stimuli produce opposite changes in firing rate (increase and decrease respectively), and that oppositely directed head accelerations also produce opposite changes in firing rate, we reasoned that a reversal of stimulus polarity should have the effect of reversing the GVS-evoked virtual head-motion direction. If the afferents are functionally bi-directional, opposite polarities of monaural GVS should evoke balance responses of equal magnitude, albeit in opposite directions.

The magnitude of the balance response to monaural GVS was measured from the horizontal displacement of the top of the trunk (see Fig. 1) in 20 subjects standing with eyes closed and head facing forwards (data from Experiments 1 and 2 combined). For each subject, response magnitudes were measured from averaged traces for each monaural condition separately, and the mean magnitude computed from left and right-sided stimulation of the same polarity.

Mean magnitudes of evoked sway were 5.04 mm (s.e.m. 0.35 mm) for monaural anodal stimulation and 4.93 mm (s.e.m. 0.48 mm) for monaural cathodal stimulation. The difference was not significant (paired t₁₉= 0.29, P= 0.77). This result implies that the vestibular afferents contributing to the measured response are symmetrically bi-directional over the range of firing frequencies produced by GVS. If this result can be extrapolated to the whole population of vestibular afferents operating over the physiological range of firing frequencies it would effectively mean that a single labyrinth is capable of signalling accelerations in all directions equally, thus providing a complete description of 3-D head acceleration.

Bilateral projections

A muscle may either receive inputs exclusively from one labyrinth or receive weighted inputs from both labyrinths. This was investigated using monaural stimulation.

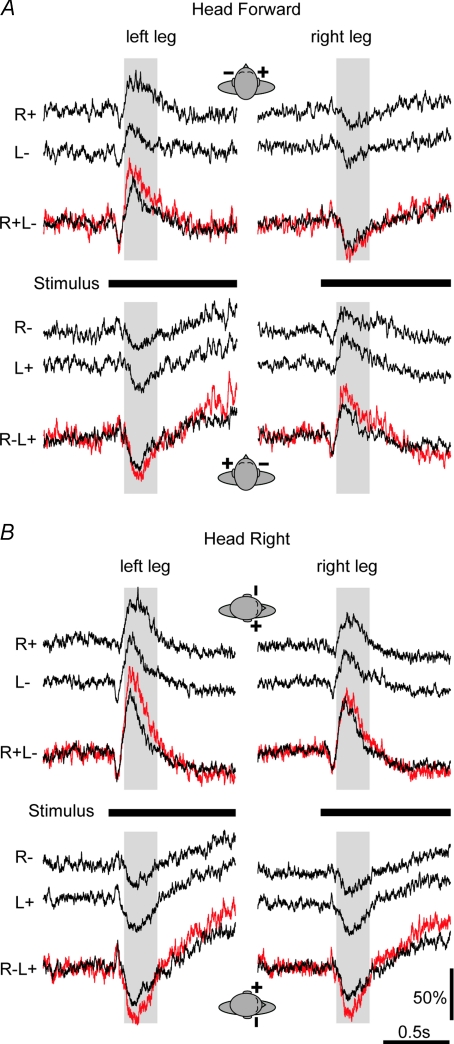
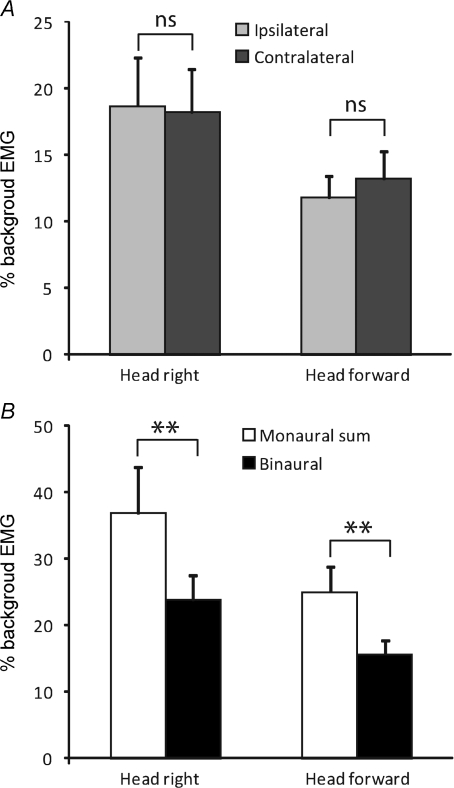
Monaural stimuli produced EMG responses in homonymous muscles of both legs, thus demonstrating a degree of bilateral connectivity (Fig. 2). However, it is not straightforward to deduce the relative weights of the ipsilateral and contralateral descending projections on the basis of these bilateral responses. With the head facing forwards the monaural stimulus evokes an excitatory response in one leg and an inhibitory response in the other (Fig. 2) making them difficult to compare. With the head facing to the side it evokes responses of the same sign in the two legs (Fig. 2) but in this position the two legs do not respond equally even with binaural stimuli (Britton et al. 1993; Watson & Colebatch, 1997). We therefore compared responses in the same muscle to monaural stimuli of opposite polarities to each labyrinth (paired traces in Fig. 2). These two stimuli produce responses of the same sign in a given muscle and evoke whole-body kinematic responses of the same magnitude (see previous section) and similar direction. A difference in the magnitudes of the two muscle responses would therefore indicate a lack of strict bilaterality. Figure 3A shows the mean EMG response sizes compared in this way after collapsing data across the two legs and polarities (see methods). There were no significant differences between the strengths of the ipsilateral and contralateral projections both with head right (paired t₉= 0.51, P= 0.620) and head forward (paired t₉= 1.96, P= 0.081). This indicates that individual leg muscles receive equal inputs from the two labyrinths.

Figure 2. GVS-evoked EMG responses.

Group mean GVS-evoked EMG response of medial gastrocnemius muscles. Mean rectified EMG from left leg (left) and right leg (right) with head facing forward (A) or to the right (B). Black traces in each panel show from top the response to right-sided monaural stimulation, left-sided monaural stimulation, and binaural stimulation. The polarity of each side is denoted by sign (+ for anode, – for cathode). Red traces show the result of summing the two respective monaural responses. Time of stimulation is shown by the thick horizontal bar. Shaded area starts at 120 ms latency and denotes the first 250 ms of the medium-latency EMG response, which is responsible for the observed body sway. Data from Experiment 1.

Figure 3. Group mean EMG responses.

Group mean (+s.e.m.) EMG responses to 1.5 mA GVS, normalised to background EMG levels. A, responses in the leg ipsilateral (light grey) and contralateral (dark) to the stimulated ear. B, responses to binaural stimulation (black) and the expected response based on the algebraic sum of the individual monaural responses (white). ns, not significant; **P < 0.01. Data from Experiment 1.

Left–right integration

To investigate how information from the two labyrinths is integrated when, as under natural conditions, they signal simultaneously to the balance system, we compared the responses obtained by stimulating both sides (binaural) with those based on individual monaural responses.

First, for a single muscle we took the rectified EMG response to monaural stimulation of a given polarity and added the response to monaural stimulation of the opposite side and polarity (Fig. 2, red traces). For all conditions this artificially summed response was larger than the equivalent binaural response produced by stimulating both ears simultaneously. As shown in Fig. 3B, when data were collapsed across the two legs and polarities (see Methods) this difference was highly significant both for the head right (paired t₉= 3.50, P= 0.007) and head forward (paired t₉= 4.19, P= 0.002) conditions, with the binaural response being only 64% (mean of both head positions) of that predicted by addition of the two monaural responses.

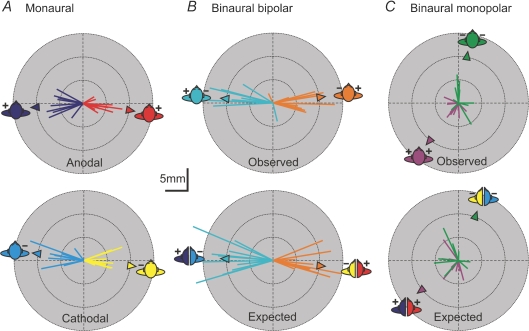
Because balance responses are coded for direction as well as magnitude, we tested whether the individual monaural responses summed vectorially rather than algebraically. For this we performed a calculation, similar to that above, but on displacement and force data with each subject's mean response treated as a two-dimensional vector. Figure 4 illustrates the displacement vectors obtained in Experiment 2. Each subject's mean displacement vector response to the four types of monaural stimuli is shown in Fig. 4A. The observed binaural response vectors to bipolar and monopolar stimuli are shown in the upper panels of Fig. 4B and C, respectively. The expected response vectors to binaural stimulation, defined as the vector sum of the corresponding monaural responses, are shown in the lower panels of Fig. 4B and C. These data suggest that the mean directions of the expected response vectors agree quite well with the observed vectors, but that the magnitudes differ.

Figure 4. GVS-evoked body displacement vectors.

Mean vectors of body displacement evoked by GVS are plotted for individual subjects. Each line represents the change in position in the horizontal plane of a marker at the level of the neck from 0.2 to 1 s after stimulus onset. Triangles represent the group mean direction calculated for each stimulation condition using circular methods with no weight given to vector magnitudes. A, responses to monaural stimulation with the active electrode as an anode (top) or a cathode (bottom). B, responses to binaural stimulation with a bipolar configuration showing observed response (top) and expected response (bottom) calculated as the vector sum of monaural responses for each subject independently. C, observed and expected responses to binaural monopolar stimulation. Colour coding indicates which of the monaural responses were used for expected response calculation. Data from Experiment 2.

The expected and observed vectors were compared for the complete data set comprising displacement and force data from Experiments 1 and 2. Table 1 summarises the vector magnitude comparisons. When the two labyrinths received opposite polarity stimuli (bipolar) the observed magnitude was significantly less than the expected magnitude for all four conditions and both measures. The displacement vector magnitudes were 66% (head right) and 74% (head forward) of the expected values. Similarly, the force vector magnitudes were 70% (head right) and 74% (head forward) of the expected values. When the two labyrinths received the same polarity stimuli (monopolar) the mean observed magnitudes were again less than the expected magnitudes but the differences were not significant.

Table 1.

Effects of head position and stimulus polarity on group mean magnitudes of individual response vectors measured from horizontal displacement of the trunk and horizontal ground reaction force

		Displacement (mm)		Force (N)
		Mean	s.d.	Mean	s.d.
Head right	Binaural L+R−	6.82	2.46	1.30	0.57
Bipolar (n= 10)	Monaural sum	9.69	3.18	1.68	0.71
		t9= 4.91	P < 0.001	t9= 3.32	P= 0.009
	Binaural L−R+	6.55	3.81	1.38	0.63
	Monaural sum	9.03	5.03	1.98	0.71
		t9= 4.42	P= 0.002	t9= 5.05	P < 0.001
Head forward	Binaural L+R−	7.36	3.57	1.44	1.01
Bipolar (n= 20)	Monaural sum	10.48	3.74	2.08	0.84
		t19= 6.96	P < 0.001	t19= 5.93	P < 0.001
	Binaural L−R+	6.53	3.18	1.40	0.69
	Monaural sum	8.92	4.10	1.85	0.66
		t19= 5.19	P < 0.001	t19= 3.82	P= 0.001
Head forward	Binaural L−R−	3.28	1.70	0.34	0.25
Monopolar (n= 10)	Monaural sum	3.48	2.13	0.47	0.23
		t9= 0.24	P= 0.813	t9= 1.01	P= 0.338
	Binaural L+R+	2.81	0.65	0.48	0.25
	Monaural sum	3.01	1.66	0.90	0.58
		t9= 0.36	P= 0.727	t9= 2.34	P= 0.044

Null hypothesis, response to stimulation of both labyrinths (binaural) has same magnitude as vector sum of component monaural responses, tested using the two-tailed paired t test. Probability less than 0.01 shown in bold. L = left labyrinth. R = right labyrinth. Positive and negative superscripts denote anode and cathode respectively. Head right, monopolar data from Experiment 1; head forward, bipolar data from Experiments 1 and 2; head forward, monopolar data from Experiment 2.

Table 2 summarises the vector direction comparisons. For 11 of the 12 comparisons comprising six experimental conditions and both measures there were no significant differences between the observed and expected vector directions. The one comparison (force vector, bipolar L⁺R⁻) that showed a difference was statistically weak (P= 0.04) and not significant with the Bonferroni correction for multiple comparisons.

Table 2.

Effects of head position and stimulus polarity on group mean directions of individual response vectors measured from horizontal displacement of the trunk and horizontal ground reaction force

		Displacement (deg)			Force (deg)
		Mean	AD	r	Mean	AD	r
Head right	Binaural L+R−	−4.33	12.34	0.977*	−3.19	9.33	0.987*
Bipolar (n= 10)	Monaural sum	−1.60	10.53	0.983*	3.23	21.63	0.929*
		F2,8= 3.01	P= 0.106		F2,8= 2.32	P= 0.160
	Binaural L−R+	−176.87	12.09	0.978*	−179.51	5.23	0.996*
	Monaural sum	−176.10	4.91	0.996*	−178.99	4.44	0.997*
		F2,8= 1.34	P= 0.315		F2,8= 0.25	P= 0.781
Head forward	Binaural L+R−	83.19	23.14	0.918*	85.64	10.83	0.982*
Bipolar (n= 20)	Monaural sum	87.66	16.11	0.960*	96.15	17.06	0.956*
		F2,18= 1.97	P= 0.168		F2,18= 3.95	P= 0.038
	Binaural L−R+	−81.52	26.59	0.892*	−89.96	15.73	0.962*
	Monaural sum	−91.82	17.02	0.956*	−96.24	18.95	0.945*
		F2,18= 1.91	P= 0.178		F2,18= 1.48	P= 0.254
Head forward	Binaural L−R−	−10.13	63.83	0.380	−67.05	63.47	0.386
Monopolar (n= 10)	Monaural sum	−20.50	76.67	0.105	−76.35	65.96	0.337
		F2,8= 0.81	P= 0.480		F2,8= 0.02	P= 0.976
	Binaural L+R+	142.35	42.79	0.721*	164.21	60.20	0.448
	Monaural sum	128.17	46.50	0.671*	119.71	53.56	0.563*
		F2,8= 0.21	P= 0.816		F2,8= 0.91	P= 0.439

Null hypothesis, response to stimulation of both labyrinths (binaural) has same direction as vector sum of component monaural responses, tested using the Hotelling's one-tailed test for paired angular differences (Zar, 2010). r is a measure of concentration, where bold values indicate significant deviation from a random distribution of directions (P < 0.05, Rayleigh's test). AD = angular deviation calculated from [2(1 −r)]^1/2 (Batschelet, 1981). Angular convention: zero degree is straight ahead, i.e. direction feet are pointing; positive angles measured in anticlockwise direction on floor. For other information, see Table 1 footnotes.

Input–output relationship

The smaller than expected response magnitude to simultaneous stimulation of both labyrinths might be due to either an active inhibitory mechanism or a non-linearity at some stage in the sensorimotor process. To investigate the latter we measured the response to monaural stimuli using a range of stimulating currents. In the monkey, Goldberg et al. (1984) showed that firing rate modulation of vestibular afferents is linearly related to stimulating current. If a non-linearity exists between vestibular input and motor output then it should be reflected in the monaural current–response curve.

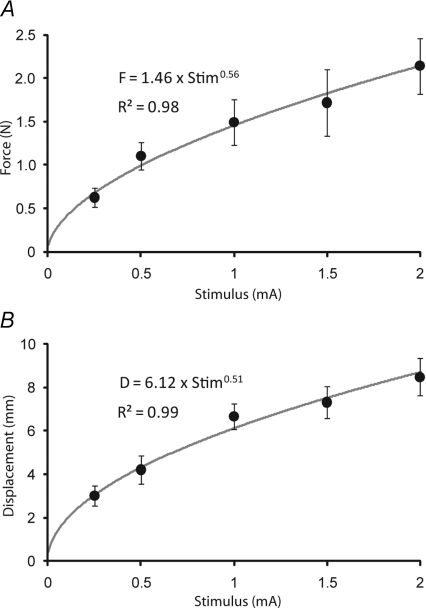
Both the force response and the body displacement response were non-linear functions of stimulus current (Fig. 5). For example, the force response to a 2 mA stimulus was only 72% of that expected by doubling the 1 mA response. The equivalent figure for the displacement response was 64%. A power curve was fitted to the complete data set. This was preferred to a linear fit because it gave higher R² values (force: 0.977 vs. 0.958; displacement: 0.988 vs. 0.944) and passed through the origin. The power curve exponents were 0.56 and 0.51 for the force and displacement responses respectively. From these curves it was calculated that a doubling of stimulation current would give 74% and 71% of response-size doubling for force and displacement, respectively.

Figure 5. Stimulus–response functions.

Group mean (±s.e.m.) GVS-evoked response magnitude as a function of GVS current. A, response measured from ground reaction shear force. B, response measured from horizontal displacement of the marker at C7. Shown are the equations and R² values of power functions fitted to the data. Data from Experiment 3.

Discussion

Bi-directionality

Because GVS produces movements of the same order of magnitude as standing body sway, we assume that the evoked vestibular afferent signals are not dissimilar from those encountered during standing. Also, with the relatively small GVS currents used here (1–1.5 mA), we assume that vestibular afferents behave linearly such that cathodal and anodal stimuli of the same intensity produce equal and opposite changes in vestibular afferent firing, as shown by Goldberg et al. (1984) in the monkey. Our results show that opposite polarity monaural GVS produces equal size responses. Thus, we are able to conclude that vestibular afferents are functionally bi-directional when their outputs are used to control standing balance.

This conclusion could appear at odds with the vestibulo-ocular reflex (VOR) literature. When a labyrinth or its nerve is destroyed on one side, imposed head movements towards the side of the lesion commonly produce smaller reflexive eye movements than head movements towards the intact side, a phenomenon often referred to as Ewald's second law after its discoverer (Ewald, 1892). This asymmetry implies that the intact labyrinth, which must be responsible for the eye movements in both directions, is not symmetrically bidirectional. It appears to respond less well to motion that decreases vestibular afferent firing than motion that increases it. However, there are two important differences between these types of experiments and ours. First, a unilateral vestibular lesion causes a central imbalance due to removal of tonic afferent input from one side. Secondly, and perhaps more importantly, the rotational stimuli used to demonstrate a sizeable asymmetry (around 3000 deg s⁻¹ s⁻¹; Halmagyi & Curthoys, 1988) is of a different order of magnitude from the head accelerations encountered during standing. Recordings made in our laboratory using a 3-D gyroscope on the subject's head have typically yielded angular accelerations less than 50 deg s⁻¹ s⁻¹ in subjects standing without instruction and interacting with others, and less than 10 deg s⁻¹ s⁻¹ during quiet stance. The dynamic range over which afferents remain bi-directional is limited by the resting firing rate since it can be decreased only to the point of silence. This non-linearity is most likely responsible for Ewald's second law. We therefore suggest that the high resting firing rate observed in primates coupled with the low head accelerations of standing results in a mirrored left–right pair of 3-D sensors that effectively deliver duplicate information to balance centres.

Sensor duplication

What benefit could this sensor duplication offer? As far as we know, the vestibular organs only transduce movement signals and as each organ covers all six degrees of freedom (3-D linear and 3-D angular) no additional quality of perception is possible by having two separated sensors in a rigid skull. A possible benefit could be that duplication offers redundancy. Loss of one side through injury or disease would leave a system still capable of sensing omnidirectional accelerations. However, the ensuing unilateral loss of tonic input imparted by the resting discharge causes a central imbalance that is very disabling in the acute state (Curthoys & Halmagyi, 1999). Rather than offering survival value this would leave the animal vulnerable for days to weeks until compensatory mechanisms were able to act.

Sensor duplication is not related to segregation of motor output whereby each labyrinth preferentially controls different muscles. The results show that individual muscles receive equal inputs from the two labyrinths. This strict bilaterality could arise from the properties of the descending pathways in the spinal cord. The motor tracts involved in GVS-evoked balance responses have yet to be established, but the vestibulospinal, reticulospinal and corticospinal tracts could all play a role (Britton et al. 1993; Marsden et al. 2005; Dakin et al. 2007). Alternatively, the bilaterality could arise from transfer of information between the two sides of the brain prior to motor output as occurs, for example, through reciprocal connections between the vestibular nuclei (Shimazu & Precht, 1966; Büttner-Ennever, 1992).

An appreciation of how signals from the two labyrinths are combined to produce the net response may provide a clue to the benefit of sensor duplication. At first glance, the hypothesis that the signals are summed did not appear to hold. The magnitude of the response was consistently smaller than expected from summation of the two component monaural responses having coincident directions (i.e. monaural stimuli of opposite polarities). This effect does not seem to have been observed before. Watson & Colebatch (1997) found that EMG balance responses to binaural stimulation were not different from the expected response based on the monaural sum. Similarly, Séverac Cauquil et al. (2000) did not find our non-additive effect in their balance centre-of-pressure responses, and MacDougall et al. (2003) did not find it in their ocular responses. However, in the present experiments the effect was highly significant for different initial postures, different stimulus polarities and different output measures taken from single muscle EMG through to ground reaction force and whole-body displacement. It is possible that the displacement response measured at 1 s after stimulus onset could have been corrupted by re-afferent signals arising from the initial part of the response, but that will not be so for the EMG and force responses measured at 370 ms and 400 ms (Day & Guerraz, 2007).

At around 70%, the binaural response was neither the sum nor the average of the two monaural responses, but somewhere in between. This is similar to the perceptual effects of combining brightness information from the two eyes or combining loudness information from the two ears (Lehky, 1983). It could be caused by the operation of an active inhibitory process. For example, the vestibular nuclei are reciprocally connected via inhibitory commissural connections (Shimazu & Precht, 1966). This could provide a mechanism whereby signals appearing simultaneously on the two sides would mutually inhibit each other to produce a smaller net effect than that expected from purely unilateral signals. However, the relationship we found between stimulus intensity and response magnitude from stimulation of just one labyrinth suggests an alternative mechanism.

Non-linear power law

The stimulus–response curves indicate a power-law relationship with an exponent of around 0.55. As the afferent signal is essentially a linear function of stimulus current (Goldberg et al. 1984), neurones in the pathway between sensory input and motor output must have non-linear transfer properties. With this non-linearity, a doubling of stimulus current, which presumably doubles the signal strength, would produce only 73% of an expected response doubling. This figure is similar to that seen when summing inputs from the two labyrinths, and this suggests a common mechanism. In the binaural case the doubling of input comes from a doubling of primary afferents transmitting the same signal rather than a doubling of signal strength in individual afferents. One way of thinking about such a non-linear gain function is that responses to small input signals will be disproportionally large. In other words the input–output gain increases with decreasing signal magnitude, which would give maximum sensitivity for small signals without saturating the response to large signals.

Power laws are commonly found relating perceptual magnitude to stimulus magnitude for a large variety of physical properties (Stevens, 1957). In such psychophysical experiments the power law exponents vary considerably depending on the physical property under investigation, for example 0.3 for loudness to 2.0 for visual flash rate (Stevens, 1957). In the present case the power law relates to behaviour rather than perception. However, it should be mentioned that there is little other evidence in the literature for such non-linear behaviour to GVS-evoked signals. For example, Popov et al. (2005) measured the long-lasting effect of GVS current on the centre of pressure displacement and reported an approximately linear response up to 4 mA. For GVS-evoked ocular movements, MacDougall et al. (2003) reported a linear relationship between GVS current up to 5 mA and ocular torsion position. The ocular torsion data presented by Séverac Cauquil et al. (2003) also show a linear relationship with GVS current over a lower intensity range of 0.1 to 0.9 mA. This linearity of the VOR reinforces the linearity of the primary afferent response to GVS, but why the oculomotor system should differ from the balance system is not certain. Perhaps it is necessary for the VOR to be a linear function of stimulus magnitude in order to maintain stability of the retinal image for a wide range of head motion.

It is interesting to note that Shaikh et al. (2005) observed non-linear behaviour similar to ours in vestibular network neurones in the monkey. They reported that neuronal responses recorded in the vestibular and fastigial nuclei to combined tilt and translation signals (in canal-plugged animals) produced only about 70% of that expected from linear summation of the individual tilt and translation responses. Because the canals were plugged and could not contribute, the combined response would have come from a doubling of signal strength in otolith afferents and thus would be closely analogous to the effect we observed as a result of doubling the stimulus current.

Vector summation of left and right signals

Consideration of response direction suggests that signals from the two labyrinths are treated as independent estimates of head acceleration and combined vectorially. As discussed above, this sum then undergoes non-linear transformation into the whole-body response. One benefit of vector summation of signals from each side would be an improvement in the signal-to-noise ratio as predicted by signal processing theories. Averaging or summing two channels that contain a common signal and uncorrelated noise increases the signal-to-noise ratio by a factor of 1.4 (the square root of 2). This modest increase in signal fidelity may be particularly relevant for the small head acceleration signals associated with balance.

Another important benefit would be the attenuation of particular types of unwanted signal through common-mode rejection, which is critical for small amplitude noise rejection. Synchronised modulation of firing rates across all afferents on both sides represents a signal not generated by a real head movement and therefore needs exclusion. Equivalent common-mode disturbances were effectively simulated in the present experiments by applying binaural monopolar GVS, which resulted in the opposing component of the vectors from each side being cancelled. Such common-mode changes in firing rates could originate from many sources, e.g. metabolic, hormonal, neural, thermal influences or changes in blood, CSF and endolymph pressure. Another possible source is suggested by a recent study by Plotnik et al. (2005). They showed that the resting afferent discharge rate of the movement-sensitive, irregularly firing afferents fluctuates markedly over long periods of many minutes in the decerebrate chinchilla, swinging between almost zero and maximal rates. This they attribute to a descending inhibition of a positive feedback control of afferents mediated by the vestibular efferent system. However, even in the anaesthetised intact animal, their Fig. 3B (Plotnik et al. 2005) shows large fluctuations in resting firing rate, ∼22% of the mean. Furthermore, these fluctuations are likely to be symmetrical across labyrinths, as suggested by the model in their Fig. 9. It is worth noting that the positive-feedback regulation of vestibular afferents proposed as the cause of the fluctuating baseline is also a means by which small-signal gain could be amplified.

Conclusions

In conclusion, during standing the two labyrinths provide duplicate head acceleration information that is summed vectorially and transformed non-linearly into motor output to control balance. The non-linearity can be described by a power law function with an exponent of around 0.55. Both these processes act to enhance the fidelity of small vestibular signals. When we consider the relatively low angular acceleration and velocity of the head that occurs during upright human behaviour we can appreciate that this could offer a crucial advantage to the balance system. There seems to be strong evolutionary pressure to improve vestibular sensitivity for upright balance control as shown by evolutionary enlargement of the human vertical canals (Spoor et al. 1994). The resting discharge coupled with vector summation and non-linear transformation may represent the neural manifestations of this evolutionary pressure.

Glossary

Abbreviations

EMG

electromyography, electromyographic

GVS

galvanic vestibular stimulation

Author contributions

B.L.D., J.F.M. and R.C.F. contributed to the conception and design of the experiments. All authors were involved in the analysis and interpretation of data and the writing or revising of the article. All authors approved the version to be published. The experiments were performed at the UCL Institute of Neurology (in the laboratory of B.L.D.).