Modeling Auxin-regulated Development

Abstract

The phytohormone auxin plays an essential role in many aspects of plant growth and development. Its patterning, intercellular transport, and means of signaling have been extensively studied both in experiments and computational models. Here, we present a review of models of auxin-regulated development in different plant tissues. This includes models of organ initiation in the shoot apical meristem, development of vascular strands in leafs and stems, and auxin-related functioning in roots. The examples show how mathematical modeling can help to examine expected and unexpected behavior of the system, challenge our knowledge and hypotheses, obtain quantitative results, or suggest new experiments and ways to approach a problem.

Computer simulations of plant responses to auxin explain previously perplexing aspects of the transport, regulation, and metabolism of this phytohormone.

The plant hormone auxin is important for a multitude of physiological processes regulating plant development. Since its discovery as a substance responsible for phototropism (Darwin 1880; Holland et al. 2009), auxin has been implicated in many other functions, including root gravitropism, phyllotactic patterning, and leaf vein and root hair formation (Blilou et al. 2005; Benkova et al. 2003; Blancaflor and Masson 2003). Auxin performs its actions by affecting, directly or with cooperation with other hormones, various aspects of cell functioning, such as growth or transcription of specific genes. Because it is such a critical substance for the plant, its concentration levels must be carefully controlled and adjusted to dynamic environmental and developmental factors. This is achieved by both metabolism and transport. The hormone is polarly transported within the plant by membrane-located proteins adjusting the rates of efflux from and influx into the cells. Although experimental work has improved our understanding of the mechanisms by which auxin is transported and how it is involved in regulating development within different tissues, there are still many aspects of these processes that are not fully understood or difficult to evaluate using current experimental methods (Friml and Palme 2002). Biological experiments often provide indirect information about the studied principle, e.g., phenotypic transformation after gene mutation or change in the concentration of some induced reporter. Taking into account the complexity of the system and multiplicity of variables that affect it, interpretation of such data is often not a straightforward task. Hence, there has been an increase of the use of computational modeling for elucidating our understanding of the role of auxin in plant development. Computational models offer the means of creating a simplified, but formal description of specific biological mechanisms while excluding nonessential (for the given mechanism) inputs. This idealized fully controllable environment with explicitly defined interactions facilitates the investigation of proposed concepts. It allows for gaining insight into the general nature of the biological process in hand, as well as for obtaining quantitative estimations of the parameters related to it. In particular, models have been used to predict cellular and subcellular concentrations of auxin, given the localizations of the transport mediators, something that cannot be directly measured in experiments. Also, the mechanisms that are used to localize transport mediators at the membranes of plant cells are mainly unknown, and modeling has been successfully used to explore the consequences of different hypotheses.

Here, we review various models that have been applied to different aspects of auxin-regulated plant development. Initially, we describe the biological mechanisms of polarized auxin transport, concentrating on the mathematical implementation. We are sparse with experimental references, and refer readers to the other contributions of this issue describing the experimental findings in more detail.

MODELING OF AUXIN

We use the term modeling for the creation of mathematical constructs representing dynamic processes within biological cells supplemented by computer simulations. Such models can be developed for problems at quite different scales, ranging from single molecular processes such as protein folding to large-scale descriptions of plant branching and even models of populations of plants. Because cells represent a natural discretization unit for molecular mechanisms that determine plant development at a tissue level, we focus on models describing a tissue with a cell-based discretization. The potential of this type of model is accentuated with the recent improvements in experimental techniques, in which confocal live imaging of fluorescently labeled molecular markers at cellular resolution represents a major input for building and testing models. The degree of discretization depends on the level of detail that is needed to resolve the problem addressed. In a simple case, individual compartments correspond to the cells, the apoplastic tissue is not represented, and membranes are either ignored or represented indirectly. Concentrations of auxin and other molecules are in this case considered constant within the cells. A more detailed discretization should be used if either internal gradients are of interest or if the distinction between cells and walls is of importance. An additional complication appears in simulations of a growing tissue, in which cell sizes increase and proliferation leads to the birth of new compartments as well as new neighborhood relations.

Auxin Metabolism

Auxin metabolism includes synthesis, degradation, and reversible conjugation of IAA (indole-3-acetic acid). Each of these processes can be carried out in multiple ways, contributing to complicated regulation of IAA levels in the cell. Local production and degradation can provide an inhomogeneous distribution of the auxin concentration in the tissue, and conjugation can be used to effectively buffer auxin in different cells. Although these aspects of auxin dynamics may be of great importance, current models are typically treating them either via boundary conditions or with simplistic homogeneous rules. Thus, in the future, when more detailed data become available, there is a great potential for a significant improvement of our models with respect to auxin metabolism.

Auxin Transport

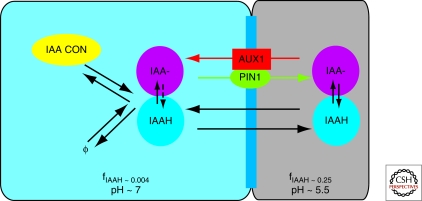
So far, models have been focusing on the dynamics resulting from auxin transport and we will discuss the underlying transport mechanisms in more detail. A conceptual comprehension of polar auxin transport in plants has been present for a long time, but the introduction of the chemiosmotic theory in the mid 1970s (Rubery and Sheldrake 1974; Raven 1975) is the mechanistic basis of our current understanding of the polar transport (Fig. 1). The idea is that auxin can exist in two forms, depending on the pH of the medium (its acid dissociation constant pK is 4.7). In the acidic extracellular space (pH 5.5), part of the auxin exists in its protonated, electrically neutral phase IAAH, and thus can freely enter the cells. In the cytoplasm (pH 7), auxin resides almost completely in its anion form (IAA⁻) and can no longer easily pass through the cell membrane. The ratio of concentrations of both forms of auxin can be expressed as (IAA⁻)/(IAAH) =10^pH−pK. This leads to the equations for the fraction of both types of auxin in the compartment in the form (IAA⁻) = Af_IAA⁻ = A(1+10^−pH+pK)⁻¹, in which A is the total auxin concentration, and f_IAAH=1−f_IAA⁻. Polar auxin transport from the cells was then hypothesized to result from polar localization of membrane proteins facilitating efflux of the anion form of auxin.

Figure 1.

Auxin transport across the cell membrane. Both forms of auxin (IAAH/IAA⁻) exist in cytoplasm (left/blue) and cell wall (right/grey) in different fractions (f_IAAH). Passive transport across the cell membrane is possible only for the electrically neutral form (IAAH). The auxin ion (IAA⁻) uses efflux (PIN1) and influx (AUX1) mediators to move between compartments. Active transport is especially important for efflux of auxin from the cell because of the strong dissociation of auxin in the cytosol. Synthesis, degradation (to and from ∅ in the figure), and reversible conjugation of auxin also regulate the amount of hormone available in the cell.

The mathematical description of auxin transport can be based on the elements of classic ion transport equations (Dainty 1962), in which transport mediators act as channel proteins. Hence, we will briefly introduce the ideas of passive ion transport based on an electrochemical potential across an membrane. The flux of the ions can be expressed as

$$j_A=-D_A(\frac{\mathit{dA}\left(x\right)}{\mathit{dx}}-A\left(x\right)\frac{n_{A}F}{\mathit{RT}}\frac{d\Phi \left(x\right)}{\mathit{dx}})\mathrm{,}$$ 1

in which D_A is diffusion coefficient of the ion A inside the membrane, A(x) its concentration at the point x, n_A its valence, RT is a molar thermal energy, and F is the Faraday constant (molar charge). Φ(x) is an electric potential and x changes across the membrane thickness. The first term corresponds directly to Fick’s law of diffusion and the second term represents flux of ions due to the electric potential. If Φ(x) is assumed to be linear within the membrane, we can integrate this equation and obtain

$$j_A=P_A\mu \frac{A_{\mathit{in}}{e}^{\mu }-A_{\mathit{out}}}{e^{\mu }-1}.$$ 2

We defined here P_A = D_A/L to be the permeability constant of the membrane and μ = n_A FV/RT is dimensionless energy ratio (V is the membrane potential). Auxin ion concentration on both sides of the membrane is given by A_in and A_out. If we introduce N(μ) = μe^μ/e^μ−1, we can simply write

$$j_A=P_A(N\left(\mu \right)A_{\mathit{in}}-N(-\mu )A_{\mathit{out}}).$$ 3

Adapting the ion transport equations to the movement of both forms of auxin between cytoplasm and wall compartments, we first note that for the negatively charged IAA⁻, the factor for the efflux is much higher than for the influx and the negative part can be neglected (the difference is in the order of two magnitudes). For this mechanism to be applicable to influx, the assumption is that IAA⁻ is accompanied by two protons. The change in sign results in high influx and the small efflux contribution can be neglected. Auxin flux across the membrane can then be described by

$$j_{c\to w}=j_{\mathrm{pass}}+j_{\mathrm{efflux}}+j_{\mathrm{influx}}\mathrm{,}$$ 4

in which j_pass describes passive transport of IAAH, and j_efflux and j_influx represent mediated efflux and influx of IAA⁻, respectively. Each of these contributions is given by

$$j_{\mathrm{pass}}=P_{\mathit{IAAH}}(f_{\mathit{IAAH}}^c{a}_c-f_{\mathit{IAAH}}^w{a}_w)$$ 5

$$j_{\mathrm{efflux}}=P_{{\mathit{IAA}}^{-}}{C}_{\mathrm{efflux}}N\left(\mu \right)\frac{f_{{\mathit{IAA}}^{-}}^c{a}_c}{K_{\mathit{efflux}}+f_{{\mathit{IAA}}^{-}}^c{a}_c}$$ 6

$$j_{\mathrm{influx}}=P_{{\mathit{IAA}}^{-}}{C}_{\mathrm{influx}}N\left(\mu \right)\frac{f_{{\mathit{IAA}}^{-}}^w{a}_w}{K_{\mathit{influx}}+f_{{\mathit{IAA}}^{-}}^w{a}_w}.$$ 7

Note that the above expressions can be simplified by combining constants, and that permeabilities of the membrane to the auxin ion, P_IAA⁻, get modified by the concentration of transport mediators C_{efflux/influx} as well. The mediated transport is saturable and here represented by a saturable Michaelis-Menten description with constants K_{efflux/influx}. Many models assume auxin concentrations far below these K values and hence use a linear term.

Experimental estimates for the transport parameters exist, and can be found in papers described later or in other reviews (e.g., Kramer and Bennett 2006). Although these values are good as a starting point, models need also to be tested for robustness when varying them. This is because estimated values do not always agree, they are often extracted from in vitro experiments, and they can be easily altered for specific tissues, for example by adjusting levels of expression of transport mediators.

When the chemiosmotic theory was proposed, active auxin transport mediators were hypothetical. Later experiments identified families of PIN proteins as the efflux facilitators and AUX1/LAX as proteins involved in influx of auxin into the cells. Current models for influx and efflux mediators use either a static expression-localization pattern from experimental findings, or define update rules when the expression and localization are dynamic. The regulatory mechanisms underlying the expression and localization of transport mediators are to a large extent unknown, but the dynamics can be described by production and degradation within the cells, and cycling between cytosol and membrane compartments. Auxin itself has been shown to both induce PIN and AUX/LAX expressions, and to be of importance for the cycling of PINs. This represents an additional layer of feedback between auxin and its polarized transport that needs to be resolved in the models.

MODELS FOR AUXIN-REGULATED DEVELOPMENT

Early Auxin Transport Models

Early auxin transport models addressed basipetal movement of auxin in a single file of cells. Leopold and Hall assumed a polar secretion of auxin facilitated by different permeabilities of the cell’s apical and basal membranes, and showed that this resulted in auxin moving against a gradient (Leopold and Hall 1966). Later models extended on the basis of chemiosmotic theory (Mitchison 1980; Goldsmith et al. 1981) and could account for more features observed in experiments such as auxin velocities in tissues. These models used a transport mechanism derived from the electrochemical potential gradient as described above, and described a static situation in which auxin was moved within a predefined geometry with constant transport parameters, very much like many of the modern root models. Another seminal early work, introducing a dynamic polarization of transport, was Mitchison’s implementation of Sach’s canalization idea (Sachs 1969; Mitchison 1981), which is discussed later.

Roots

There are several developmental aspects in the root that are dependent on auxin, and this is also reflected in the models that have been developed for root tissue. In the root auxin transport, mediators show a characteristic static pattern of expression and polarized location. This has been taken into account in several models in which a templated static location of transport mediators, extracted from experiments, have been used for predicting the auxin distribution in the tissue.

In a work by Swarup et al. (Swarup et al. 2005), experimental work was combined with modeling to show the importance of AUX1 expression in the epidermal tissue for mediating the signal from the root tip to the site of bending for a gravitropical response. The model represented the three outer cell layers of the root as a cylindrically shaped template in which cytosol and apoplastic tissue was discretized to obtain a subcellular resolution. The transport model was based on the chemiosmotic theory in which parameter values were taken from experimental estimates. Auxin was supplied asymmetrically at the root tip and removed at the boundary, simulating continuity with the geometry of older parts of the root. The model showed the importance of the AUX1 for retaining the auxin in the epidermal layer, and also for maintaining the asymmetry of the signal when propagating through the tissue.

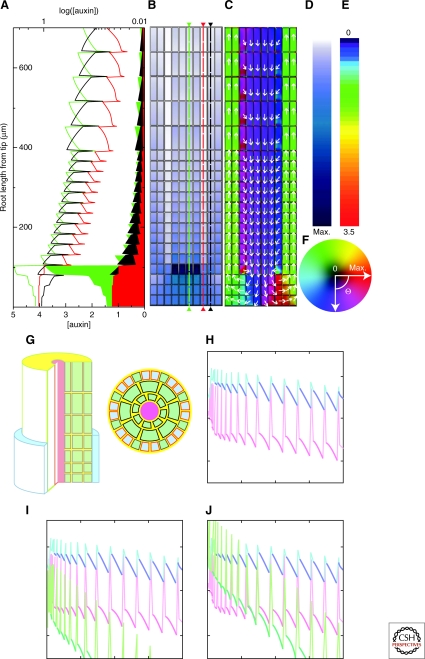
A similar setup was used in Jones et al. (Jones et al. 2008) for analyzing root hair growth in wild type and aux mutants (Fig. 2). Experiments showed that AUX1 is expressed more in the epidermal cells not producing root hairs. Inclusion of this expression pattern in the model showed that it could be a mechanism for producing longer auxin transport distances from the apex, explaining the differences of root hairs in an aux mutant compared with wild type (Fig. 2).

Figure 2.

Models of root transport. (A–F) Model from Grieneisen et al. (Grieneisen et al. 2007) showing that specific static localization of PIN efflux mediators is sufficient to create a reflux loop and generate an auxin peak at the quiescent center. Adapted by permission from Macmillan Publishers Ltd:Nature (Grieneisen et al. 2007), Copyright (2007). (G–J) Model for auxin distribution in the epidermal cell layer by Jones et al. (Jones et al. 2008). Adapted by permission from Macmillan Publishers Ltd.:Nature Cell Biology (Jones et al. 2008), copyright (2008). (G) Visualization of the template used in the simulations. (H–J) Auxin distribution in epidermal cells. Red is nonroot-hair cells and blue is root-hair cells auxin concentrantion for wild-type (H) and aux mutant (I, J) simulations. The difference between (I) and (J) is in the amount of auxin supplied to the tissue.

In a two-dimensional representation of the root, Grieneisen et al. (Grieneisen et al. 2007) used an experimentally extracted pattern of different PIN efflux mediators to analyze the auxin distribution within the root tip (Fig. 2). The root was compartmentalized using a lattice approach in which the tissue is divided into equally sized boxes. Basal localization of PINs within the internal root tissue and apical in the epidermal layers together with lateral PIN pointing inwards from the outer layers of cells indicate the reflux of auxin. The model showed that these PIN localizations were sufficient to create the known auxin peak at the root apex. Growth was also analyzed in the model and the auxin levels in different regions were used to control growth and proliferation, successfully representing the known patterns of this in the root.

A similar description was used in Laskowski et al. (Laskowski et al. 2008), in which the auxin distribution in relation to lateral root initiation was investigated. It has been shown that lateral root initiation is dependent on induced expression of LAX3 in pericycle cells underlying the new lateral root (Swarup et al. 2008), and that bending can induce the initiation (Laskowski et al. 2008; Ditengou et al. 2008). In the model, the root tissue was sharply bent (180°) and the geometrical change led to an increase of auxin in the pericycle cells on the outside of the bent root compared with the inside. This difference was then amplified by an auxin-induced influx expression at a sharp threshold.

Although the root models described so far have used the localization of transport mediators as inputs, a few models have also addressed the problem of mechanisms for the localizations of these proteins to the cell membrane (Likhoshvai et al. 2007; Stoma et al. 2008). The flux-based model (described in more detail later) by Stoma et al. was implemented on a root tissue, and was shown to be able to keep the efflux mediator pattern given that they were initiated from the experimental template.

Models of Venation and Phyllotaxis

Several aspects of plant development depend on a dynamic change of auxin transport polarity. In these cases, mechanisms for localizing the transport proteins need to be integrated in the models. This approach has been used in models to address the problems of venation and phyllotaxis. Because direct experimental evidence for mechanisms localizing transport mediators is to a large extent missing, models may fill the gap for testing the consequences of different hypotheses. Two main questions are: (1) what local mechanisms can explain the development of the global patterns? And (2) is it the same mechanism acting in all tissue types? In the following, we discuss models that approach these questions.

There are two main ideas for how auxin itself may influence localization of transport mediators to form patterns. One is the flux-based conception as first modeled by Mitchison (Mitchison 1981; Rolland-Lagan et al. 2005). It proposes that auxin flux between cells positively feeds back on transport permeability, leading to even higher fluxes. More recently, a concentration-based idea has been introduced (Jönsson et al. 2006; Smith et al. 2006). In this case, efflux mediators are localized from auxin concentrations in the neighboring cells, again leading to a positive feedback.

The key assumption used in Mitchison’s original flux-based model is that permeability of the membrane for auxin efflux is increasing with the flux of auxin between cells, such that instabilities in homogeneous flow of auxin through the tissue are amplified and form streaks. In nature, similar patterns of auxin can be observed as veins in the mature leaves or developing midvein in the leaf primordia. Mitchison showed that veins could form in a simplistic square cell template in which one side acted as a source and the other as a sink.

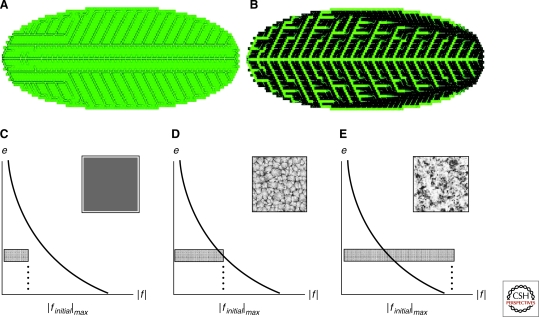
Mitchison already anticipated some criticism of flux-based models. One of them is that the veins are acting as sinks, relying on low auxin concentrations within them. He suggested that the vein-forming cells need to act as sinks only at the initiation of the path. Later, when the transport channel is already formed, auxin concentration could be increased without disturbing transport polarization. In the modern models, this scenario may be easily realized. First, the use of influx mediators (AUX1/LAX) allows for cells to act as sinks and still maintain high auxin concentrations (Kramer 2004). Alternatively, this can be achieved in simulations in which the flux influences efflux mediator cycling directly, i.e., a more realistic mechanism of regulation (Feugier et al. 2005; Fujita and Mochizuki 2006). Feugier et al. (2005) used a saturated transport mechanism and explicitly considered different dynamical rules for the efflux carrier PIN1. Simulations on an elliptically shaped lattice of hexagonal cells showed formation of various auxin patterns, some resembling branching structure of the leaf veins. They were able to achieve higher concentration of auxin in veins when the total number of PIN1 proteins within a cell was constant, i.e., the flux acted on the PIN1 cycling (Fig. 3).

Figure 3.

Models of vein formation. (A and B) Auxin patterns formed in the flux-based model by Feugier et al. (Feugier et al. 2005) (adapted with permission from Elsevier). In (A), the distribution of efflux mediator to each cell membrane is independent and veins show lower auxin concentration than the surrounding tissue. The auxin concentration is higher in the veins (as observed experimentally) when the efflux mediator is competitively reallocated between the cell membranes (B). (C–E) Analysis of pattern formation capabilities of the flux-based model depending on the initial conditions and parameters from Fujita and Mochizuki. The thick line represents a separatrix of the system. Only for a specific choice of initial conditions are veinlike patterns formed (D). Outside these conditions, the system switches to homogeneous auxin distribution (C) or patches of high auxin concentration (E). (Fujita and Mochizuki 2006) (adapted with permission from Elsevier.)

Another criticism of flux-based models is the existence of a flux-sensing mechanism. Mitchison himself noticed that because polarized transport produces an auxin gradient through the cell in direction of the flux, a flux sensor could be replaced by a gradient sensor, which may be easier to realize in nature. This idea was implemented by Kramer (Kramer 2009), who proposed that PIN1 is polarized by a cytoplasmic auxin gradient instead of flux. The author shows that the model based on chemiosmotic transport and including auxin influx mediators simulated on a rectangular lattice with specific source-sink boundary conditions is able to form a single canal of auxin containing cells. The concentration of auxin in the canal is elevated via activation of influx mediators. The model uses an abstract regulation of efflux mediators, not directly related to the cycling of PIN proteins.

One aspect of flux-based models is that they are very dependent on exact boundary conditions and quite sensitive to parameter perturbations, as analyzed in detail by Fujita et al. (Fujita and Mochizuki 2006). These authors based their model of vein formation on the concept of flux-enhanced auxin efflux polarization as well. In addition, they introduced a hypothetical diffusible substance in the veins enhancing PIN1 polarization. An analysis of the model parameters showed that forming channels was not the “natural” pattern for their implementation of the flux-based mechanism, but rather is the behavior in a region in between a no-pattern region and a region in which patches are formed (Fig. 3).

A classic patterning problem in plants is the positioning of new organs in the shoot apical meristem (SAM), leading to regular phyllotactic patterns. Models incorporating molecular rules based on recent experimental findings have been used to explain the global patterns. In the SAM, experiments suggest that auxin is localized mainly at the sites of newly forming primordia, and that this is sufficient to initiate primordia. Experimental studies have shown that polar transport via asymmetrically localized PIN1 is an essential part of this process (Reinhardt et al. 2003; Heisler et al. 2005). PIN1 and AUX1 expression in the SAM has been observed to be strongest in the epidermal layer, effectively making early primordia initiation two dimensional, which is reflected in the models.

Models have been used to verify the importance of transport for localizing auxin by extracting PIN1 polarization from experimental templates, and then simulating auxin transport models on these static templates (Barbier de Ruille et al. 2006, Jönsson et al. 2006). The model devised by de Reuille et al. assumed that active transport of auxin by PIN1 has a constant strength modulated by an auxin saturation term and that PIN1 is either present or absent on a membrane depending on the observed level of PIN1. The model incorporated passive auxin diffusion, degradation, as well as influx from the cells on the boundary of the simulated template and evacuation from cells manually marked as contributing to formation of provascular veins. Their simulations showed formation of auxin peaks at experimentally confirmed positions of new primordia. The model also predicted high auxin levels at the summit of the meristem, which was also detected using an IAA-specific monoclonal antibody. Jönsson et al. (2006) quantified intensity levels from a confocal template of PIN1 in cells and membranes. A model based on the chemiosmotic theory and explicitly taking into account apoplastic diffusion of auxin resulted in high auxin levels at the positions of primordia.

Experimental visualization of PIN1 localization in the epidermal layer of the SAM shows that PIN1 is polarized toward the newly forming primordia. This suggests that PIN1 may orient toward cells with high auxin content. Implementations of this idea led to models able to spontaneously generate auxin peaks at regular patterns (Jönsson et al. 2006; Smith et al. 2006). The regulation of PIN1 according to auxin levels in neighboring cells creates a positive feedback. Auxin flows up the gradient, enhances local maxima, and simultaneously produces a depletion zone around them. Jönsson et al. (2006) based the model on auxin regulating the PIN1 cycling, and verified the model’s capability of spontaneous pattern formation, both numerically and analytically. They simulated the model using spherical cells, confined on a half-sphere connected to a cylinder. Cells are continuously growing and dividing, pushing older cells down the surface. The model generated different phyllotactic patterns depending on supplied parameters, although the authors noticed that the patterns were quite unstable. This was partly attributed to imperfections of the mechanical growth and proliferation model, which caused abrupt changes of topology not present in real plants. An implementation of the model in a spatial continuum resulted in phyllotactic patterns (Newell et al. 2008). The relocalization of PIN1 during development was also predicted by the model. In a more recent work (Heisler and Jönsson 2006), Heisler and Jönsson refined the model including AUX1 influx mediator and apoplastic diffusion, with parameter values estimated from experiments. This showed that experimentally observed high levels of AUX1 in the epidermal layer can be sufficient to accumulate auxin to this layer and that auxin-induced expression of AUX1 stabilized the pattern. The influence of influx mediators was further analyzed in Sahlin et al. (Sahlin et al. 2009), in which it was found that influx mediators are not essential for pattern generation, but for stability of the patterns, something recently seen also in experiments (Bainbridge et al. 2008). Further, the authors could show that the model requires a relocation competition among PIN1 proteins, i.e., the regulation needs to be on the cycling of PIN1, and that feedback from auxin in the walls will not lead to patterning. Finally, the authors showed that the proposed mechanism of auxin concentration feedback is also able to generate patterns other than peaks, such as, e.g., stripes.

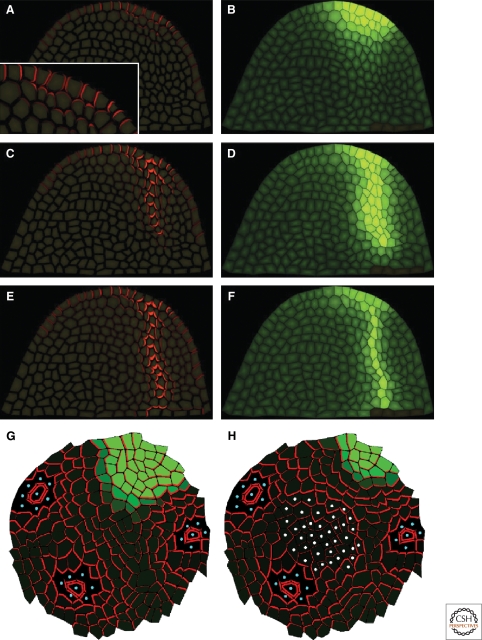
Smith et al. (Smith et al. 2006) also proposed feedback between auxin concentration in the cell and PIN1 polarization in the neighboring cells as the core of a pattern forming mechanism. In addition, they assumed an irreversible transition of the model rules for the cells committed to initiation of the primordium to stabilize the pattern. After reaching some auxin concentration threshold, those cells show increased auxin production adjusted by the distance from the forming primordium center and enhanced polarization of PIN1 toward the center of the primordia. The model was simulated on a two-dimensional curved surface using polygonal cells, which grow and divide according to a set of empirical rules. The parameters of the model were tuned to produce different phyllotactic patterns and the results show good agreement with experiments. In Bayer et al. (Bayer et al. 2009), the concentration-based model for the epidermal cell layer is integrated with a flux-based mechanism for the internal layers. An auxin peak is formed in the epidermal layer, and a transition to flux-based transport progresses continuously with the increase of auxin concentration in the cells, causing a basipetally directed outflow of auxin from the localized maximum in the epidermis. The model assumed the existence of two hypothetical signals. One is localized in cell membranes and accumulates with the flux across that membrane and controls the flux-based contribution to the PIN1 polarization. Another signal is in the form of a diffusible substance emanating from preexisting vasculature and directs the propagation of a developing vein toward it, similar to the one proposed by Fujita et al. (Fujita and Mochizuki 2006). Simulations of the model on a single template imitating a longitudinal section through a SAM showed good agreement with auxin and PIN1 dynamics observed in the experiment (Fig. 4). It also indicated an apical polarization of PIN1 toward the epidermal layer in the initial stages of primordia site specification, which was later confirmed experimentally by the authors.

Figure 4.

Examples of auxin transport models in the SAM. (A,C,E) PIN1 localization (red) at different stages of primordia specification followed by provascular vein formation. (B,D,F) Auxin concentration in cells (green) at times corresponding to A, C, E. From the model of Bayer et al. (Bayer et al. 2009) (adapted by permission from CSHL Press). (G,H) Model by Stoma et al. (Stoma et al. 2008) showing PIN distribution obtained in simulation initialized from experimental data. Blue dots mark existing primordia acting as auxin sinks. (H) Shows the importance of a central region (white dots). Degradation of auxin in the central region gives a PIN polarization much more closely corresponding to experimentally observed polarization.

Application of the flux-based model to different aspects of plant development was shown by Stoma et al. (Stoma et al. 2008). The authors argued that flux-based models show different behavior in two distinct regimes. When the coupling between auxin flux and PIN1 polarization is a function growing linearly or slower (weak regime), canals do not form, as observed already by Mitchison (Mitchison 1981). Instead, they noticed uniform convergence of auxin toward the sinks, which in turn produces auxin depleted zones around those points. In the strong regime, when the PIN1 polarizing function is increasing faster than linearly with auxin flux, the model produces auxin transporting canals like those seen in the case of provascular vein formation. Combining these properties, they proposed a unified model in which new primordia are specified by an auxin peak in the epidermal layer produced by the flux-based mechanism working in the weak regime. Once a threshold of auxin concentration is achieved at this maximum, the cells become capable of transporting auxin into inner layers, which triggers the initiation of a provascular strand. At the same time, the epidermal flux creates a depletion zone inhibiting creation of new primordia in the neighborhood of the existing one. Simulations of this model on different SAM templates showed good agreement with experimentally observed PIN1 distributions (Fig. 4). However, the emergence of a transient auxin minimum at the site of the developing primordia has yet to be verified.

Another model proposing a unified description of phyllotaxis and initial vein formation was introduced by Merks et al. (Merks et al. 2007). The autors extended the model by Jönsson et al. (Jönsson et al. 2006), supplementing it with auxin-induced PIN1 production. In addition to stable pattern of auxin peaks, they observed a traveling auxin wave forming a vein-like structure on a leaf-shaped template.

The list of models presented here is by no means exclusive and is intended just to highlight main directions of development in modeling of auxin transport phenomena. We should briefly mention other models falling beyond the scope of this review. An alternative approach to leaf venation using a reaction-diffusion mechanism has been proposed by Meinhardt (Meinhardt 1982). Worth noting is also the model by Runions et al., based on the set of geometrical rules loosely connected to transport principles (Runions et al. 2005) and achieving very realistic venation patterns. The idea of mechanics playing an integral role for phyllotactic patterning relates back to P. Green (Green et al. 1996), and have been further explored (Shipman and Newell 2004), also in models in which auxin and mechanical mechanisms are acting together (Newell et al. 2008; Hamant et al. 2008).

DISCUSSION AND OUTLOOK

Models of auxin transport have proved their usefulness. They have helped to formalize and evaluate hypotheses, spot inconsistencies and discrepancies with experiments in proposed ideas, quantify results, and introduce new concepts. Despite the successes and significant progress that has been made to deepen our understanding of auxin action and transport, there remains much to elucidate. In particular, the details of the regulation of auxin transport polarization bring a lot of controversy. It is possible that such a situation is because of the complexity of the system itself, which neither models nor experiments are able to resolve yet. Flux and concentration-based ideas are, at first sight, hard to reconcile because they are based on seemingly contradictory assumptions. The difficulty may be resolved if active influx of auxin is regulated. If a cell expresses a high level of influx mediators, it can attract auxin from neighboring cells regardless of its auxin concentration. So far, models only consider a coupling between auxin and its transport mediators, but other mechanisms could be included as well. For example, a connection between the localization of PIN proteins and PINOID and PP2A has been suggested experimentally (Michniewicz et al. 2007), but is not used in the models. Also, only trivial implementation of auxin metabolism has entered the models, whereas other factors such as mechanical forces could be prominent as well. Hopefully, with the advances in experimental techniques, visualization, and computational methods we will be able to analyze all the essential elements of auxin transport mechanisms both in models and experiments.

Evaluation of the models should always be done with respect to its ability to explain existing and predict future experimental data. Also, its connection to the underlying biological principles is of importance together with a robust behavior. Different modeling groups also need to reconcile and take advantage of each other's results. The proposed root models can serve as an example, in which some show the importance of AUX1, whereas others do not include influx mediators. On the other hand, the models including AUX1 do not include the recycling of auxin via internal tissue, which has been proposed as an important mechanism. In this respect, a simple method of sharing models would be a crucial element and the development of a common description, similar to SBML (Hucka et al. 2003) for systems biology models, would be very beneficial.