Avoiding Pitfalls in the Statistical Analysis of Heterogeneous Tumors

Abstract

Information about tumors is usually obtained from a single assessment of a tumor sample, performed at some point in the course of the development and progression of the tumor, with patient characteristics being surrogates for natural history context. Differences between cells within individual tumors (intratumor heterogeneity) and between tumors of different patients (intertumor heterogeneity) may mean that a small sample is not representative of the tumor as a whole, particularly for solid tumors which are the focus of this paper. This issue is of increasing importance as high-throughput technologies generate large multi-feature data sets in the areas of genomics, proteomics, and image analysis. Three potential pitfalls in statistical analysis are discussed (sampling, cut-points, and validation) and suggestions are made about how to avoid these pitfalls.

Introduction

Large multi-feature data sets to characterize tumors are being generated by new technologies in the areas of genomics (gene expression microarrays), proteomics (mass spectroscopy), image analysis (tissue microarrays), and others. These studies may provide information used for prevention, early detection, diagnosis, prognosis, and for prediction (to predict response to therapy). Traditional design issues involve specific patient subgroup representation, to address questions of interest. However, tumor heterogeneity provides challenges that have become even more acute in the era of large multi-feature databases. More data does not provide more useful information unless several pitfalls can be avoided. We discuss the statistical design and analysis of large multi-feature data sets with the goal of avoiding pitfalls, with an emphasis on pitfalls resulting from heterogeneity particularly of solid tumors in which it is more difficult to ensure that a representative tumor sample has been assessed.

The effect of intratumor heterogeneity in assessing biomarkers was considered by the Kananaskis working group on quantitative methods in tumor heterogeneity.¹ There was an emphasis on the sources of variability during various procedural steps:

1) representative tumor sampling/collection method (sequential or random; internal or external; back and forth, such as in needle-guided biopsy), 2) number of cells assessed by type of investigation (ranging from a few to millions), and 3) all or random cells versus targeted only cancer or “visually worst” cancer. These can lead to methodologic variability attributable to (surgical) extraction, inter-laboratory procedures, sample preparation, intra- and inter-reagent, inter-observer/inter-machine, and intra-observer/intra-machine.

Recommendations for reporting results of tumor biomarker prognostic studies (REMARK) have been outlined by The Statistics Subcommittee of the National Cancer Institute—European Organization for Research and Treatment of Cancer (NCI-EORTC) Working Group on Cancer Diagnostics.² The guidelines are aimed at clarifying the tenets of reporting in terms of study objectives, patient characteristics, therapies, specimen type and handling, assay methods with scoring, statistical test specifications and methods, data acquisition, analyses undertaken with results, and integrated discussion of results in the context of the potential for the study design to address relevant questions. The implementation of these reporting recommendations would be a large step forward in improving the ability to evaluate biomarker results, including apparent inconsistent results arising from assays of heterogeneous tumors.

Heterogeneity

Heterogeneity of cells within individual tumors (intra-tumor heterogeneity) has long been recognized.^3,4 Recognition of morphological differences between tumors by histopathologists is the basis of grading tumors. Solid tumors may contain recognizable subpopulations that differ morphologically, biochemically, functionally, and dynamically. This is most dramatically revealed in tumors such as teratomas in which several different recognizable tissue types are present. More subtley, groups of cells (perhaps clones) may express different immunohistochemical staining properties than other cells within the same tumor. There may be differences between cells within the same tumor in terms of resistance to chemotherapeutic drugs.⁵ Subclones of tumor cells may have different probabilities of metastases and show a different proliferating fraction of cancer stem cells.^6,7 Individual premalignant neoplasms such as ductal carcinoma in situ of the breast exhibit heterogeneity of nuclear grade.^8–11 Individual breast cancer tumors may contain a mixture of multiple grades of malignant cells, which has implications for understanding the pathways for progression of heterogeneous tumors.^12,13

The term heterogeneity has two meanings—it may refer to distinct subpopulations or to a continuous range of differences (Webster’s New World Dictionary College Edition, 1957. World Publ., Cleveland). An example of two distinct patient subpopulations are those who are alive and those who are dead at some point in time. An example of a continuous range of differences is the spectrum of colors. Although the colors may be given different names such as red, orange, yellow, green, blue, indigo, and violet, these are an arbitrary number of classes within a continuum of wavelengths. The classes may be defined, but they are not the only possible classes. Tumors probably can be most accurately considered as containing cells with a variety of phenotypes. These phenotypes can be analytically characterized and reported with biomarkers. There may be a continuous spectrum (distribution) of values of biomarkers. The distribution may be unimodal, bimodal, or multimodal. A unimodal distribution may be symmetrical such as a Gaussian (normal) curve, or asymmetrical such as a Poisson or lognormal distribution.

In summary, the challenge of tumor heterogeneity is to provide information about a patient’s tumor that is reliable and useful for prognosis and therapeutic guidance. The new era of large multi-feature data sets can provide numerical descriptions of the variety of cells within each tumor that are amenable to objective statistical analysis. However, for the results to be reliable the pitfalls posed by heterogeneous tumors must be taken into account.

Pitfall 1: Sampling

Since solid tumors may be heterogeneous, it is important to analyze multiple samples to get a comprehensive picture of a patient’s entire tumor. Fine needle aspirates and core needle aspirates may under or over represent high grade areas in the tumor. Even in excision biopsy specimens, microscopic examination of limited amounts of a tumor may miss high grade areas. Analysis of portions of tumors by biochemical or molecular biology assays may provide quantitative data about a tumor sample that is an average or aggregate value, but the contribution of a minor fraction of high grade cells may be hidden by a large fraction of low grade cells.

Several methods are available to obtain quantitative information about the heterogeneity within a solid tumor by analyzing many separate cells or multiple regions of interest. These include flow cytometry, static image cytometry, and laser capture microdissection. Flow cytometry has the advantage that measurements can be made on tens of thousands of individual cells, but has the disadvantage that the histological architecture of tissues is lost because the cells are dispersed. Static image cytometry^14–16 and laser capture microdissection¹⁷ each have the advantage of allowing the correlation of measurements of individual cells, or regions of interest, with intact histological structure. This allows quantitative measurements to be related to traditional histopathological grades and other histopathologic details. For instance, quantitative image cytometry has revealed heterogeneity within individual breast ducts by detecting differences between different nuclei in breast ducts that were scored as having the same grade by the Van Nuys criteria.¹⁸

Heterogeneity within tumors has been a concern in the sampling of tumors for the construction of tissue microarrays (TMA), and the subsequent analysis of the samples.^19,20 In this technique small cores of tissue (0.6 mm–2 mm in diameter) are obtained from donor paraffin blocks and are assembled in a recipient paraffin block. The advantage of tissue microarays is that a single paraffin block can potentially contain hundreds of tissue samples. Tissue microarray slides prepared from the blocks will contain samples from all those samples of tissue which can then be processed together and analyzed by high-throughput image analysis.²¹ Multiple samples from the same tumor, or samples from tumors of different patients, that are arrayed on the same slide can be compared. However, the question arises about how many samples from a heterogeneous tumor are necessary to adequately characterize such a tumor. Several groups have considered that issue and concluded that while two samples from a tumor are sufficient for population studies, for individual patients the two samples may differ significantly.^22,23 It has been suggested that full sections rather than TMAs should be used for accurate assessment of some factors, for example for assessment of progesterone receptor, or human epidermal growth factor receptor 2 (HER-2) in breast cancer patients.²⁴ In our TMA studies, we have found that less than 10% of patients have two samples that would result in classifying a patient as different.⁴³ However, Miller et al.¹⁸ found that there were significant differences in digital image analysis features between all ducts assigned the same nuclear grading. Comparison of intra- and interclass correlations is a method suitable for determining whether two samples from a heterogenous population of tumor cells are more similar to each other than two samples from different heterogeneous tumors.^5,26 Ideally, the values of a biomarker measured in pairs of samples from the same patient would be more similar to each other (intraclass correlation) than pairs of samples from different patients (interclass correlation). If not, then tumor heterogeneity and/or measurement variation may be obscuring important differences.

Quantitative measurements of protein expression, RNA expression, or nuclear image features of tumors are frequently reported in comparison to a pathologist’s description of the tumor grade and stage. However, traditional histopathology has limitations as a predictive biomarker.²⁷ One such limitation is the interobserver variation in grading by pathologists (categorical classification) as expressed analytically by the kappa statistic.²⁸ Intraobserver variation has also been observed. Considerable effort has been made to devise systems that reduce the interobserver variation in grading, for instance, in the grading of in situ duct carcinoma of the breast.^29–31 Quantitative molecular and image analysis with coefficients of variation of less than 3% can provide useful information that is complementary to the descriptive information provided by the pathologist. The pathologist, can also assist the molecular biologists by determining what regions of abnormal and normal tissue are best assessed by the molecular biologist.

In summary, it is important to recognize that heterogeneity within each assessment system may have a variable effect on an assessed outcome. Investigators need to more routinely examine the effects of tumor and laboratory assessment heterogeneity with a view that this could have a substantive impact on study conclusions, introducing unnecessary inconsistencies in the literature.

Pitfall 2: Cut-points

When there is a continuous distribution of biomarker values with no obvious modal values, then a good alternative to using cut-points to derive discrete subgroups of patients with different outcomes, is to consider a biomarker as a continuous rather than a dichotomous variable in multivariate analyses. For example, Chapman et al³² reported the multivariate results obtained by use of continuous hormonal receptor factors, followed by multivariate examination of various cut-points. They showed there was no best cut-point for estrogen receptor (ER) or for the progesterone receptor (PgR) in breast cancer patients and suggested that they be considered as continuous rather than dichotomous (negative, positive) variables for prognosis. Thompson et al³³ report the percent risk of prostate cancer as a continuous dependent variable and prostate specific antigen (PSA) as a continuous independent variable, in contrast to the previous discrete risk groups with cut-points of 4.0 ng/mL and 10 ng/mL.

If two cut-points are more informative than one cut-point, then this raises the question whether more cut-points, or different cut-points would be an improvement. That is, should one search among a variety of possible cut-points until the difference between groups of patients becomes statistically significant with the minimum p-value? Altman et al³⁴ have shown that seeking an optimal cut-point among several cut-points causes an inflation of type I error rate, and that this requires corrections for multiple testing; they also advocate against use of a data set to determine a factor cut-point, followed by use of the cut-point in the same data to determine its (multivariate) significance.

However, if the distribution of the values of a biomarker appears by inspection and/or outcome to have subgroups, e.g. bimodal, i.e. Mobbs et al³⁵ or trimodal, then it is reasonable to consider multivariate investigations aimed at definition of appropriate cut-points, i.e. Chapman et al.³² This requires that the number of subgroups be chosen, e.g. 2 or 3, so that the patients will be aggregated to minimize overlap between subgroups.

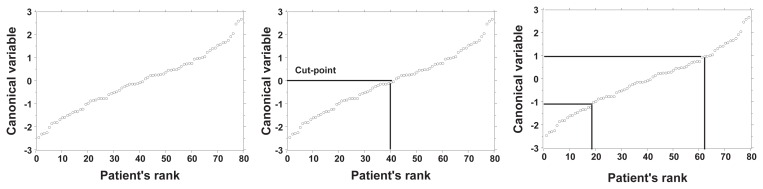
Alternatively, a population of patients who have a continuous distribution of values of a quantitative biomarker can be separated into two groups by specifying a neutral to investigation cut-point of its distribution. For instance, one cut-point at the mean value would separate patients into two groups, one with a higher and the other with a lower value of the biomarker. Or, the population can be separated by two cut-points into three groups, low, medium, and high values of the biomarker (Fig. 1). These groups are not necessarily intrinsically different biological classes,³⁶ but they may be informative. These new discrete groups can be compared to patient outcome; for one cut-point, the patients might be described graphically as healthy or sick, good or poor survival, and for two cut-points good, moderate, and poor survival, using univariate Kaplan-Meier or cumulative incidence,³⁷ or multi-variately with Cox or log-normal survivor plots.³⁸ Recently, Royston et al³⁹ demonstrated that a visual display of length of survival accomplished with a log-normal distribution of survival times would complement a Kaplan-Meier plot.

Figure 1.

Cut-points of a continuous distribution of breast cancer patients. Eighty patients with in situ duct carcinoma of the breast were ranked by a canonical variable derived by weighting 39 nuclear features of 200 cells per patient.²⁵ Left panel: there is a continuous distribution of patients. Middle panel: one cut-point at the mean separates patients into two groups (Low and High). Right panel: two cut-points separate patients into three groups (Low, Intermediate, and High). The choice of the number of cut-points, and the value of the cut-points, produces different groups of patients. Such discrete groups of patients are useful for comparing the outcome of the groups of patients, for instance by Kaplan-Meier survival analysis. However, the discrete groups are not distinct biological classes recognized from the distribution of their canonical variable of nuclear features.

There are several caveats to the application of cut-points. The first is in the use of visual subjective estimates of values rather than of objective measurements. In some cases qualitative information is combined with quantitative information to derive a score. The score is then separated into discrete classes. For example, grading of invasive carcinoma of the breast⁴⁰ by the Nottingham histologic score, combines visual estimates of degree of acinus formation (1, 2, 3) and nuclear atypia (1, 2, 3) with numerical count of mitoses(converted to score 1, 2, 3) to create a total score which determines the grade (Total score of 3, 4, or 5 = grade 1, 6 or 7 = grade 2, and 8 or 9 = grade 3.). Two cut-points are then used to give three discrete nuclear grades.

In a series of patients with in situ duct carcinoma of the breast, objective quantitative image analysis measurements of 39 nuclear features including size, shape, texture, and stain intensity were combined in a dimension reduction method, Fisher discriminant analysis, to derive a single value, the canonical variable, for each of 80 patients.²⁵ Figure 1 (left) This result indicates that there is a continuous distribution of values. Figure 1 (middle) shows two groups of patients resulting from one cut-point, and Figure 1 (right) shows three groups of patients resulting from two cut-points. Since the distribution of nuclear values is continuous without obvious groups, the number of cut-points and position of the cut-points are arbitrary and not derived from distinct subpopulations. The two or three groups are not intrinsic biological classes.³⁶ Although cut-points may not provide classes of patients with distinctly different nuclei, the grouping (binning) of patients can be useful. For instance, it was determined that one cut-point at the mean resulted in two groups of patents that differed in recurrence of ductal carcinoma in situ and in development of invasive cancer.^25,41

A notable example of the use of two cut-points to derive three informative groups of patients is given by Camp et al.⁴² The amount of p53 staining in breast cancer biopsies was determined by immunohistochemistry. Two cut-points were determined by a method that allows the effects of scanning many cut-points and simultaneously visualizing the histogram of the distribution of p53 staining and of the Kaplan-Meier survival plots. The surprising result was that the survival was not proportional to the amount of p53, but rather that patients with intermediate values of p53 survived better than patients with low and high values of p53. We have confirmed this non-linear dependence of survival on p53.⁴³ In addition we have shown that two groups of patients, produced by one cut-point at the mean, do not differ in survival.

In addition to grouping patients by cut-points of the amounts of proteins measured by immunohistochemistry, patients have been grouped by cut-points of the amounts of messenger RNA measured in gene expression microarrays. A multivariable method, Logical Analysis of Data (LAD) has been used to group breast cancer patients for good and poor prognosis,⁴⁴ and for diagnosis of lymphoma patients as having diffuse large B-cell lymphoma or follicular lymphoma⁴⁵ based on gene expression data. LAD is a method that uses combinatorics and optimization to derive one or more cut-points for each of many individual variables.⁴⁶ LAD has recently been extended to prognosis of censored survival data.⁴⁷

If two cut-points are more informative than one cut-point, then these results raise the question whether more cut-points, or different cut-points would be an improvement, which brings us back to the beginning of this discussion that it could be appropriate to examine the effects of continuous factors without categorization, as continuous factors in multivariate modeling.

In summary, while there is frequently an impetus to assign cut-point(s) at an early investigational point to facilitate scientific or medical application, this assignment may be detrimental to progress if it is not robust over a broad range of data. Good work-ups of a continuous factor’s multivariate effects on outcome, with repeated testing of (externally) generated hypothesized cut-points will avoid confounding of apparent effect that may arise from cut-points applied inappropriately in some future contexts.

Pitfall 3: Validation

Information about a set of tumors and the corresponding patient’s outcome may be used to develop models that make predictions about the outcome of new patients. In order to be useful, the models must be validated both statistically and clinically.⁴⁸ Intratumor heterogeneity requires the same considerations previously noted,^49,50 and additional considerations.

Previously, studies with cut-points of continuous values of the biomarker utilized ROC curves⁵¹ and with dichotomous outcome typically reported specificity (negative test of true negatives), sensitivity (positive test of true positives), positive predictive value (chance that a positive test is really positive) and negative predictive value (chance that a negative test is really negative). The goal of 100% specificity and 100% sensitivity is almost never achieved, and when reported should be viewed with skepticism. The positive and negative classes of the test may be determined by using cut-points of continuous quantitative biomarker data, as discussed above; however, recalculation is required for each cut-point considered. Recently, there has been a movement of medical practice in diagnostic testing towards the use of likelihood ratios and nomograms like that of Fagan’s⁵² which permit a simpler and more efficient handling of continuous data.⁵³ The reliability of conclusions about continuous data may be made by estimating the error of the predicted outcomes by cross-validation, e.g. comparing repeated subsets of the original population. For instance, in k-folding, the patients may be divided into two groups such as 1/3 and 2/3 and the analysis is repeated with many different groups; or leave-one-out in which all the patients but one are repeatedly analyzed. Large inter-tumor heterogeneity and outliers will be indicated if the error estimates are not uniform. However, intra-tumor heterogeneity will not be detected once the data for many cells or many regions within each tumor are combined to characterize each patient’s tumor.

Intra-tumor heterogeneity can be detected when multiple regions within each tumor are measured and recorded separately rather then reported as an “average” or aggregated value to characterize a patient’s tumor. This can be achieved quantitatively by image cytometry that records different values for different regions of a tumor ^25,41 or qualitatively by pathologists who report all nuclear grades within each tumor, including the occurrence of more than one grade in a tumor. For instance, for breast ductal carcinoma in situ, Goldstein and Murphy⁵⁴ reported 45% (68/150), Miller et al⁵⁵ reported 50% (62/124) and Allred et al.⁵⁶ reported 44% (53/120) of patients having more than one nuclear grade. The grades 1, 2, and 3 are categorical groups that are assigned to nuclei whose deviation from normal nuclei is continuous.²⁵ The reliability of interobserver variability (concordance) in assigning nuclear grades is expressed as the kappa statistic.²⁸ It ranges from slight (kappa = 0.29) to substantial (kappa = 0.9)^29–31 depending on the classification system. This indicates that the exact proportions of each of the nuclear grades within a heterogeneous tumor that are reported may depend upon the classification system used and the judgment of the pathologist. Although the reported proportions of each nuclear grade within a heterogeneous tumor may not be perfectly relied upon, the heterogeneity among the nuclear morphologies within many tumors certainly exists. This may be seen in the examples shown in the valuable supplement to the paper by Allred et al.⁵⁶

Data sets from gene expression microarrays, mass spectroscopy, and image cytometry include measurements of multiple features of each tumor. Dimension reduction methods, such as discriminant analysis or logistic regression, may reduce the measurements of multiple features to a single value. This requires criteria to select informative features, to eliminate highly correlated features, and to calculate weights of each feature. The subset of selected informative features may not be unique, several different subsets may yield models with similar results.^44,45 Where feasible, it is important to include more patients than features to avoid over fitting the data.^57–59 The reliability of the conclusions from one set of patients can be determined by testing them on a second independent set of patients that were not used to obtain the first set of conclusions, e.g. by comparison of a model from a “training set” with a “test set”. Even with low p-values on the training set, there may be failures to replicate results on a comparable test set,⁶⁰ especially due to differences in patients assessed in each set. Care must be taken to obtain a test set that is similar to the training set.⁶¹ Camp et al⁴² have given a good example of this type of external validation that was necessitated by their comparison of various cut-points which might have lead to an overestimate of statistical significance.³⁴ External validation is important when there is inter-tumor heterogeneity, and especially when there is intra-tumor heterogeneity.

To avoid bias, the training set and the test must be comparable, including having the same proportion of patients with intra-tumor heterogeity. The validation methods discussed above consider the effects of patient heterogeneity. Heterogeneous results may be derived in the same patients due to system instability with known or unknown factors which alone, or in combination, may have similar effects on outcome. Where feasible, considering a (restricted) all subset analysis may indicate the existence of groups of factors with very similar effects.³⁸ Such a situation may be expected in competing molecular or genetic pathways. With a reasonably manageable number of factors in targeted investigations, it is better to avoid over simplification to a few factors to avoid biasing the results.^62–64

This becomes impractical in large multi-feature databases in the areas of genomics (gene expression microarrays), proteomics (mass spectroscopy), image analysis (tissue microarrays and mammography), and others where it is essential to consider some type of reduction in the number of factors under consideration. Readers are directed in particular to the comprehensive and expanding NIH website coverage of this large topic which is beyond the scope of this paper. Examples are the book of Simon et al⁶⁵ and the extensive free software available in BRB-Array Tools (http://linus.nci.nih.gov/pilot/index.html) as well as the knowledge-base linkages of the NIH Pharmacogenetics Research Network (http://www.nigms.nih.gov/Initiatives/PGRN).

In summary, internal cross-validation and statistical factor subgroup checking is an important first step to assess the stability of results within a single data set, to maximize the prospects of consistent inference between data sets.

Conclusion

Considerations of sampling, cut-points and validation must be taken into account when analyzing large multi-features data sets, and especially when analyzing and interpreting data that describe heterogeneous tumors. At each step—assembling an appropriate cohort of patients, selecting regions of biopsy specimens, extracting quantitative data, reducing and interpreting the data—there are additional considerations that must be taken into account when there is tumor heterogeneity. This requires the collaboration of biostatisticians, pathologists, and laboratory scientists who have complementary expertise. Since most, if not all, solid tumors are heterogeneous at some stage of progression the challenges of heterogeneity must be kept in mind to avoid potential pitfalls.