Outer hair cell piezoelectricity: Frequency response enhancement and resonance behavior

Abstract

Stretching or compressing an outer hair cell alters its membrane potential and, conversely, changing the electrical potential alters its length. This bi-directional energy conversion takes place in the cell’s lateral wall and resembles the direct and converse piezoelectric effects both qualitatively and quantitatively. A piezoelectric model of the lateral wall has been developed that is based on the electrical and material parameters of the lateral wall. An equivalent circuit for the outer hair cell that includes piezoelectricity shows a greater admittance at high frequencies than one containing only membrane resistance and capacitance. The model also predicts resonance at ultrasonic frequencies that is inversely proportional to cell length. These features suggest all mammals use outer hair cell piezoelectricity to support the high-frequency receptor potentials that drive electromotility. It is also possible that members of some mammalian orders use outer hair cell piezoelectric resonance in detecting species-specific vocalizations.

I. INTRODUCTION

Early in the 1880s, Jacques and Pierre Curie reported that the application of mechanical stress to one of a variety of crystalline materials produced electricity and coined the term piezoelectricity (from the Greek, piezein—to press). After considering the thermodynamics of the process, Gabriel Lippmann concluded that applying an electric field across the crystals should produce mechanical stress. The Curie brothers quickly confirmed the converse piezoelectric effect predicted by Lippmann (Cady, 1946). Crystalline piezoelectric materials have been used in applications that range from marine sonar to mechanical actuators to electronic delay lines. Noncrystalline, biological piezoelectricity has been observed in bone (Fukada and Yasuda, 1957) and ligament (Korostoff, 1977; Fukada, 1982).

Outer hair cell (OHC) electromotility (Brownell et al., 1985) is a direct conversion of membrane potential to cell length change and is functionally equivalent to the converse piezoelectric effect. The mechanism responsible for electromotility resides in the OHC lateral wall, a nanoscale composite of membranes and cytoskeletal proteins (Brownell et al., 2001). The OHC lateral wall also supports a mechanoelectrical conversion (the direct piezoelectric effect) (Gale and Ashmore, 1994; Zhao and Santos-Sacchi, 1999), which further strengthens the view that the lateral wall is piezoelectric. Several theoretical treatments of the OHC and its role in hearing have assumed the OHC to be piezoelectric (Mountain and Hubbard, 1994; Tolomeo and Steele, 1995; Spector et al., 1998, 1999; Raphael et al., 2000; Iwasa, 2001; Spector et al., 2002). The models all infer or assume Maxwell reciprocity (Cady, 1946) in which the coefficients for the direct and converse effects are equal. Recent experimental evidence provides quantitative support for this thermodynamic requirement for piezoelectricity (Dong et al., 2002).

Electomotility makes a major contribution to the sensitivity and frequency selectivity of mammalian hearing (Brownell et al., 2001; Liberman et al., 2002). The motor mechanism responsible is membrane based, does not depend on calcium or cellular stores of ATP, and is capable of generating mechanical force at frequencies >50 kHz (Brownell and Kachar, 1986; Kachar et al., 1986; Frank et al., 1999; Brownell et al., 2001). The functional significance of electromotility has been questioned because an equivalent circuit analysis based on conventional membrane resistance and capacitance predicts a low-pass frequency response that would limit the membrane voltage and therefore force production only to low frequencies (Hudspeth and Logothetis, 2000). We show that the inclusion of piezoelectricity into the equivalent circuit of the outer hair cell pushes the corner frequency to higher values. In addition, piezoelectric materials can be driven into resonance and we present an analysis predicting resonance in OHCs in the ultrasonic range. The predicted values are, however, compatible with those used for echolocation in chiroptera (bats) and cetaceans (whales and dolphins).

II. METHODS

Lateral wall piezoelectricity is modeled for two different representations of the outer hair cell lateral wall, a rectangular slab and a cylindrical shell. The piezoelectric and material properties are assumed to be homogenous for both geometries. The rectangular slab is known as a length-thickness extension (LTE) resonator in the piezoelectric literature. Most of our analysis is developed for the LTE model because its properties are the most thoroughly studied. The cylindrical shell more closely matches the geometry of the OHC lateral wall and it is called a radial-poled cylinder (RPC) resonator.

III. RESULTS

For the purpose of analysis, the OHC lateral wall is split along its length and rolled out to form a rectangular slab detached from other cellular elements (Fig. 1). The slab is laid out along three Cartesian axes. The circumference of the cylinder is represented by the width (w) of the slab, parallel to x₂; the cell length (l) and wall thickness (t) are parallel to x₁ and x₃, respectively. The lateral wall is a composite structure composed of the plasma membrane, cortical lattice, and subsurface cisterna. OHC electromotility involves electromechanical coupling between all three layers (Brownell et al., 2001) and we assume a thickness of 100 nm (seen in electron micrographs). An electric field across the lateral wall defines the direction of poling or net polarization across the thickness (t) of the slab (x₃ direction) and the resonance mode of interest induced by this field is along the length of the cell (x₁ direction). This is a LTE resonator the properties of which are fully described in the IEEE standard (Rosen et al., 1992). The pertinent constitutive piezoelectric equations are

$$S=s^{E}T-dE,D=dT+{\epsilon }_0{\epsilon }^{T}E,$$ (1)

where S is the strain, D is the electric polarization (or displacement), s^E is the elastic compliance at constant electric field, ε₀ is the permittivity of free space, ε^T is the permittivity coefficient of the slab at constant stress, T is the stress, E is the electric field, and d is the piezoelectric constant of the slab. Equation (1) is a set of tensor equations, having electrical and mechanical properties in three dimensions where the mechanical properties include shear. The off-diagonal coefficients (d) are the same, as required by Maxwell reciprocity, and, specifically, d₃₁=d₁₃ in the complete LTE tensor representation (Rosen et al., 1992). For a thin plate, t ≪ l, the LTE resonator can be represented by a plane electrical wave propagating in the thickness direction coupled to a plane mechanical wave propagating in the length direction and Eq. (1) becomes

$$S_1=s_{11}^E{T}_1-d_{31}{E}_3,D_3=d_{31}{T}_1+{\epsilon }_0{\epsilon }_{33}^T{E}_3.$$ (2)

For unclamped standing waves in the length-direction, stress is zero at the ends of the specimen and S₁ becomes a function only E₃. The two parts of Eq. (2) are used to solve for D₃. Current as a function of frequency (f) is determined by integrating D₃ with respect to time. Dividing by voltage, we obtain the admittance of the specimen:

$$\begin{array}{cc}\hfill Y\left(f\right)=& i\frac{2\pi flw}{t}\left({\epsilon }_0{\epsilon }_{33}^T-\frac{d_{31}^2}{s_{11}^E}\right)\hfill \\ \hfill +& i\frac{2w{d}_{31}^2}{t{s}_{11}^E\sqrt{\rho s_{11}^E}}\tan \left(\pi fl\sqrt{\rho s_{11}^E}\right).\hfill \end{array}$$ (3)

See Table I for definitions of the symbols. The first term in Y(f) after expanding the right side, reveals a conventional dependence on the E field while the 2nd and 3rd terms result from the dependence of S on E. Note that the quantity $\sqrt{\rho s_{11}^E}$ is the inverse of the speed of sound in the lateral wall.

FIG. 1.

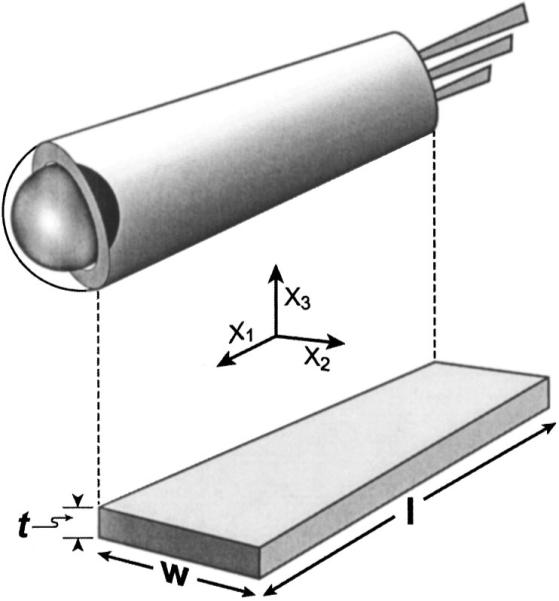
Schematic of cylindrical OHC lateral wall (above) and its LTE representation (below).

TABLE I.

Coefficient values. LW—lateral wall; PE—piezoelectric

Coefficient	Symbol	Value	Unit
Length	l	20,40,60,80	μm
Radius	r	4.5	μm
Width (circumference)	w	28.5	μm
Thickness (LW & PE plate)	t	100a	nm
Density	ρ	1a	g/ml
PE plate permittivity	${\epsilon }_0{\epsilon }_{33}^{\mathrm{T}}$	5.0×10−11	C2/Nm2
PE plate elastic compliance	${\mathrm{S}}_{11}^{\mathrm{E}}$	3.1×10−5	m2/N
PE constant	${\mathrm{d}}_{31}^2$	6.8×10−16	C2/N2
LW resistance	Rpm	100	Ωm2
LW capacitance	Cpm	1.7×10−2	F/m2
Basal membrane resistance	Rba	1	Ωm2
Basal membrane capacitance	Cba	1.7×10−2	F/m2
Apical area (cuticular plate)	Acp	8.2×10−11	m2
Apical membrane resistance	Rap	5.0×10−4	Ωm2
Apical membrane capacitance	Cap	1.7×10−2	F/m2

^aEstimated—this paper.

Experimental values for the coefficients (Table I) are obtained from the literature (Halter et al., 1997; Spector et al., 1998, 1999). There have been no direct measures of the elastic compliance ($s_{11}^E$) and the piezoelectric coefficient ($d_{31}^2$) for the lateral wall. The first may be calculated from a one-dimensional determination of the axial Young’s modulus (Y₁₁) for the OHC modeled as a spring with spring constant (k₁). A range of values for the axial Young’s modulus has been reported and we choose one that is near the mean. It was obtained by compressing the OHC with a calibrated cantilever without controlling the membrane potential (Holley and Ashmore, 1988). The elastic compliance of a hollow cylinder of length (l), width w), radius (r), and thickness (t) is

$$s_{11}^E=Y_{11}^{-1}=\frac{\text{strain}}{\text{stress}}=\frac{\Delta L_1∕L_1}{F_1∕A}=\frac{\Delta L_1∕L_1}{k_1\Delta L_1∕A}=\frac{A}{k_1{L}_1},$$ (4)

where A=π(r)²-π(r-t)²≈2π rt=wt and L₁=l. The piezoelectric coefficient $d_{31}^2$ is calculated from

$$d_{31}=\frac{{\text{strain}}_1}{{\text{ElectricField}}_3}=\frac{\Delta L_1∕L_1}{V_3∕t}=\frac{S_1}{V_3}t.$$ (5)

The values for S₁ /V₃ (Where V₃ is the potential difference across the wall thickness) are available from the literature (Tolomeo and Steele, 1995).

An equivalent circuit of the OHC that included piezoelectricity was developed to evaluate its influence on the membrane potential. A model of current flow across OHC membranes for a cell held in a microchamber (Dallos and Evans, 1995) was adapted. The model retained the two-dimensional radially symmetric RC circuit of the original, with a piezoelectric element (Sherrit et al., 1997) added in parallel to the lateral wall membrane resistance (Fig. 2). The admittance of the element is that defined for the LTE model in Eq. (3). The element is added in parallel because the piezoelectric element is assumed to be an ideal material with no losses so that there would be no current at DC. Two simulations were performed (1) with piezoelectricity and (2) with a capacitor (the membrane capacitance alone).

FIG. 2.

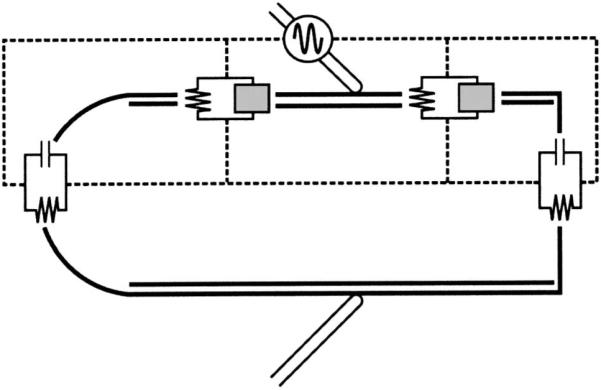
Equivalent circuit diagram for microchamber recording conditions. Gray box impedance in the lateral wall represents either a piezoelectric element [from Eq. (3)] or pure capacitance for the conventional RC analysis.

The results of these simulations are seen in Fig. 3 in which the voltage-divider equivalent impedance is plotted against frequency. Piezoelectricity pushes the corner frequency to a higher value and diminishes the magnitude of dampening. Figure 3 also provides a comparison between cells of different length (20 vs 80 μm). Resonance and corner frequencies are increased in the shorter cell while the overall electrical behavior is similar.

FIG. 3.

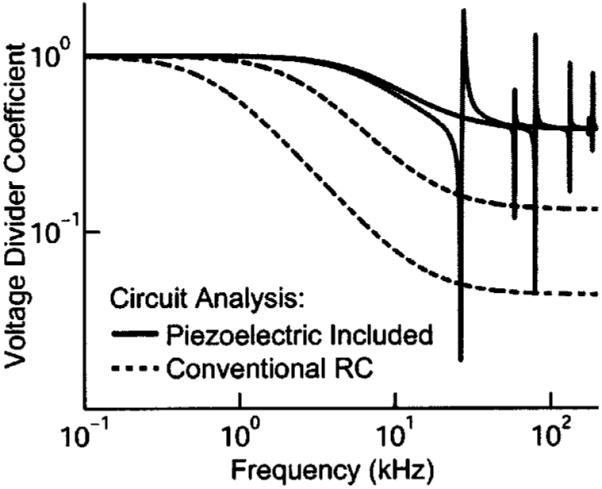
Equivalent circuit analysis for 20 and 80 μm OHCs with 1% of the cell in the microchamber. The solid and dashed gray lines with the lower cutoff and resonance frequency represent the 80 μm cell.

Based on the IEEE-defined formula for the series resonance frequency $f_s=(1∕2l)\sqrt{1∕\rho s_{11}^E}$, the first resonance frequency for the piezoelectric slab (80 μm) is predicted at 37 kHz. An iterative solution of

$$\frac{{\left(k_{31}^l\right)}^2}{1-{\left(k_{31}^l\right)}^2}=\frac{\pi }{2}\frac{f_p}{f_S}\tan \left(\frac{\pi }{2}\frac{\Delta f}{f_S}\right)$$

predicts the anti-resonance frequency (f_p) at 46 kHz, where ${\left(k_{31}^l\right)}^2=d_{31}^2∕{\epsilon }_{33}^T{s}_{11}^E$ is the electromechanical coupling constant. Additional confirmation of OHC piezoelectricity would come from comparing impedance and admittance in isolated cells to confirm a shift between resonance (f_s) and antiresonance (f _p). Resonance frequencies increase with decreasing cell length (Fig. 4). This is intuitive as resonance frequency is inversely proportional to length for most materials. An inverse relationship was also found between resonance frequency and slab thickness (Fig. 5).

FIG. 4.

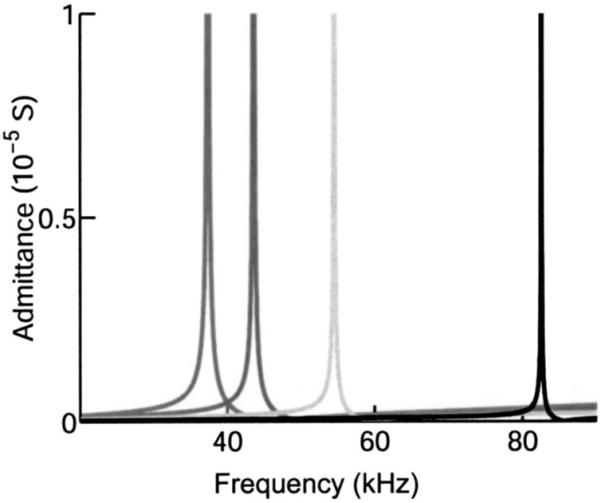
Admittance resonance peaks for LTE model of different lengths. The frequency of the resonance peaks are higher for shorter cells. The cell lengths are 80, 60, 40, and 20 μm proceeding from left to right.

FIG. 5.

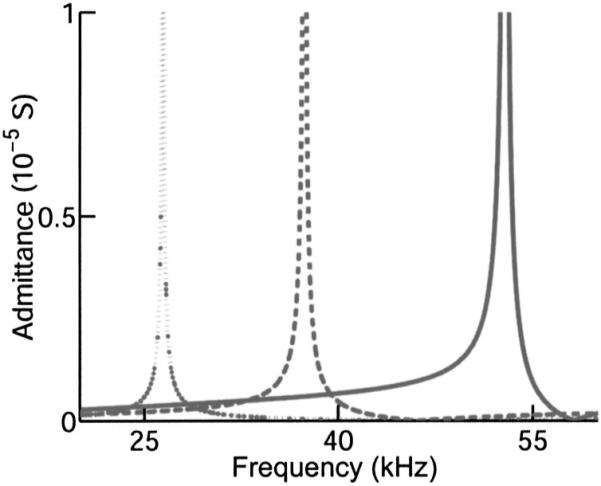
Effect of lateral wall thickness on admittance resonance spectrum for an LTE model of an 80-μm-long cell. All other parameters as in Fig. 4. Resonance frequency increases with decreasing thickness. The wall thickness is 200, 100, and 50 nm proceeding from left to right.

A radial-poled cylinder (RPC) resonator (Ebenezer and Sujatha, 1997) was also examined. It allowed an assessment of not considering the contribution of S₂ resonance mode in the development of the LTE model. The RPC model consists of a cylindrical shell where the diameter of the cylinder is much greater than the thickness of the shell and the electric field acts across the shell thickness. The d₃₁ coefficient defined in the LTE mode) couples to the circumferential direction causing a displacement (described by $s_{11}^E$) manifesting itself as a hoop or breathing mode. This then couples to the length of the cylinder through $s_{12}^E$ to result in the radialpoled cylinder resonator. The resonance spectra of different length radial-poled cylinders were nearly identical to those of the rectangular slab model when l (Cell length)>60 μm. The resonance of shorter cylinders was less than that of the same length LTE model (Fig. 6), showing that inclusion of an S₂ resonance mode becomes more important in the LTE model as l becomes shorter.

FIG. 6.

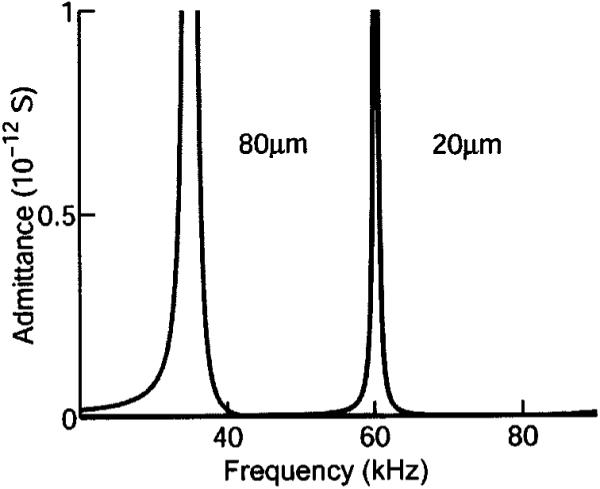
Radial poled cylinder (RPC) model. All parameters are the same as those used in the LTE model. The elastic compliance in the circumferential direction was chosen to be the same as that for the axial direction. Resonance frequency is similar to the LTE at 80 μm length, but at 20 μm length the resonance is not as high a frequency as that of the LTE model.

IV. DISCUSSION

An unresolved challenge to the OHC’s role as the cochlear amplifier has been the fact that a conventional circuit analysis based on passive resistive and capacitive elements predicts a low-pass behavior as with the dashed curves in Fig. 3 (Hudspeth and Logothetis, 2000). This should restrict OHC electromotility to low frequencies below a corner frequency determined by the length of the cell. A thermodynamic approach suggests a piezoelectric augmentation of the OHC receptor potential that results from the OHC deformation that occurs during normal cochlear vibrations (Spector et al., 2002, 2003). The present results, based on an engineering analysis of the lateral wall, reveal that OHC piezoelectricity would also extend the frequency range of stereocilia mediated sensory receptor currents. Electromotility is mediated by the transmembrane receptor potential. Future cochlear modeling should consider the contributions to the OHC receptor potential from both ionic currents and piezoelectric modulation of the membrane potential by acoustically driven cell deformation.

The extended frequency range predicted from our model is consistent with the corner frequencies measured for mechanically unloaded OHCs when stimulated in the microchamber configuration (Dallos and Evans, 1995; Frank et al., 1999). Even though a mechanical resonant peak has not been observed in isolated OHCs, Frank et al. (1999) attributed the electrically induced displacement response, with its elevated cutoff frequency, to the presence of a second-order resonance. This conclusion was based on fitting the displacement response, in both amplitude and phase, with that of an over-damped second-order resonant system, in which the resonant frequency was found to depend on cell length. Their data required the presence of a length-dependent resonance similar to that shown in Fig. 4.

The OHC is mechanically loaded in the fluid filled organ of Corti. It is firmly anchored to supporting cells by tight junctions in the reticular lamina. The tectorial and basilar membranes introduce additional mechanical loads. The in vivo OHC is therefore a viscous-damped mechanically loaded resonator in contrast to the unloaded or free resonator in our analysis. Radiation damping of the resonance would be expected to result in a broadening and weakening of the impedance peak as a function of frequency. The observation of a broad, ultrasonic mechanical resonance in electrically evoked basilar membrane vibrations near the round window of the guinea pig inner ear (Grosh et al., 2003) is consistent with this expectation. The OHCs near the round window are all short and close to the same length. By inference they should have similar resonance behavior. Electrical stimulation around this frequency would result in a summed response that would be broader than that expected in an unloaded OHC. Many rodents display ultrasonic vocalizations during mating (White et al., 1998). The broad electrically evoked ultrasonic vibrations observed in the guinea pig ear (Grosh et al., 2003) contain these mating frequencies.

Outer hair cells appeared with mammals over 200 million years ago. The OHCs of the small rodentlike early mammals enabled them to hear frequencies above 50 kHz. They were the basis of a cochlear amplifier that counteracted viscous damping and refined the passive mechanical filtering of the organ of Corti (Brownell et al., 2001). Hair cell resonance would not benefit hearing in most mammals and it is of interest that the predicted resonance frequencies are generally beyond the frequency range that OHCs at a specific location on the basilar membrane would operate. In addition, the impedance mismatch between the OHCs and the organ of Corti is so severe that any resonance would be expected to remain confined within the cell and have little impact on the vibrations of the organ of Corti. The importance of OHC biological piezoelectricity for all mammals appears to be its ability to improve the high-frequency electrical response and allow the cochlear amplifier to work throughout the mammalian frequency range.

The first bats appeared over 60 million years ago with an elegant echolocation mechanism that allowed them to navigate in a nocturnal environment. An additional resonance has been invoked to explain their enhanced hearing sensitivity at the echolocation frequencies (Kossl and Russell, 1995; Russell and Kossl, 1999). Bats may have co-opted OHC piezoelectric resonance to achieve this. Some 10 million years later cetaceans adopted a remarkably similar specialization (Ketten, 1997). The organ of Corti in echolocating members of the orders chiroptera and cetacea is greatly expanded at the region devoted to the echolocation frequencies. The OHCs in the region are short and of uniform length so that the reticular lamina is parallel to the basilar membrane. This organization would allow OHC resonance to be summed, overcoming the impedance mismatch that normally obscures the resonance. While echolocating mammals may be the only ones to utilize the cellular resonance, the piezoelectric mechanism that underlies it helps to support high-frequency receptor potentials throughout the entire class mammalia.