Application of Machine Learning Algorithms to Predict Coronary Artery Calcification With a Sibship-Based Design

Abstract

As part of the Genetic Epidemiology Network of Arteriopathy study, hypertensive non-Hispanic White sibships were screened using 471 single nucleotide polymorphisms (SNPs) to identify genes influencing coronary artery calcification (CAC) measured by computed tomography. Individuals with detectable CAC and CAC quantity ≥70th age- and sex-specific percentile were classified as having a high CAC burden and compared to individuals with CAC quantity <70th percentile. Two sibs from each sibship were randomly chosen and divided into two data sets, each with 360 unrelated individuals. Within each data set, we applied two machine learning algorithms, Random Forests and RuleFit, to identify the best predictors of having high CAC burden among 17 risk factors and 471 SNPs. Using five-fold cross-validation, both methods had ~70% sensitivity and ~60% specificity. Prediction accuracies were significantly different from random predictions (P-value <0.001) based on 1,000 permutation tests. Predictability of using 287 tagSNPs was as good as using all 471 SNPs. For Random Forests, among the top 50 predictors, the same eight tagSNPs and 15 risk factors were found in both data sets while eight tagSNPs and 12 risk factors were found in both data sets for RuleFit. Replicable effects of two tagSNPs (in genes GPR35 and NOS3) and 12 risk factors (age, body mass index, sex, serum glucose, high-density lipoprotein cholesterol, systolic blood pressure, cholesterol, homocysteine, triglycerides, fibrinogen, Lp(a) and low-density lipoprotein particle size) were identified by both methods. This study illustrates how machine learning methods can be used in sibships to identify important, replicable predictors of subclinical coronary atherosclerosis.

INTRODUCTION

Coronary artery disease (CAD) is the leading cause of death in the United States, accounting for more than 650,000 deaths per year [Rosamond et al., 2007]. Atherosclerosis is the major cause of CAD and coronary artery calcification (CAC) is a measure of subclinical coronary atherosclerotic calcified plaque burden that can be detected and quantified non-invasively by computed tomography [Peyser et al., 2002; Wexler et al., 1996]. CAC quantity predicts future CAD events in asymptomatic [Arad et al., 2000; Budoff et al., 2007] and symptomatic adults [Keelan et al., 2001].

Many environmental and genetic factors are involved in the atherosclerotic process. Older age, male sex as well as many traditional CAD risk factors have been associated with CAC quantity [Wexler et al., 1996; Wilson et al., 1998]. Several recent studies identified novel CAD risk factors including C-reactive protein levels, Lp(a), plasma fibrinogen, plasma homocysteine and low-density lipoprotein particle size associated with CAC quantity in various study groups [Bielak et al., 2000; Cassidy et al., 2004; Kuller et al., 1999; Kullo et al., 2004, 2006; Wang et al., 2002].

In a study of the heritability of CAC quantity, age, sex, measures of body size, blood pressure, diabetes, hypertension and smoking explained ~40% of the variability in CAC quantity and more than 40% of the unexplained interindividual variation was attributable to genetic factors [Peyser et al., 2002]. Several studies showed statistically significant or suggestive associations of candidate genes, such as the apolipoprotein E (ApoE) gene, and the soluble epoxide hydrolase (sEH) gene, with variation in CAC quantity [Fornage et al., 2004; Kardia et al., 1999]. Many of the genes involved in CAC susceptibility, however, remain unidentified [Lange et al., 2002].

Traditional statistical regression modeling requires specification of the exact relationship between predictor variables and outcome including any interactions between predictor variables. When modeling with many predictor variables and their interactions, it is unrealistic to test all possible regression models. Alternatives to traditional statistical modeling include ensemble learning methods which construct a set of prediction models in a training data set and then test these models on new observations in a second data set (i.e., the testing data set). This approach captures the inherent etiologic heterogeneity and interactions underlying the complex architecture of the outcome of interest without the need for a prior model specification. Random Forests [Breiman, 2001] and RuleFit [Friedman and Popescu, 2005] are ensemble learning methods with similar advantages of good predictability, insensitivity to outliers, limited effort of model tuning and insensitivity to uninformative predictors.

We used Random Forests and RuleFit in two replicate data sets of non-Hispanic White individuals using 17 traditional and novel CAD risk factors and 471 single nucleotide polymorphisms (SNPs) in 114 candidate genes, as well as 287 tagSNPs in these candidate genes, to predict high CAC burden. The predictability of each method was evaluated using five-fold cross-validation; both predictability as well as predictor variables were compared between methods.

METHODS

STUDY GROUP

The study was approved by the Institutional Review Boards of all participating institutions. Each participant gave written informed consent.

Participants were enrolled in the Genetic Epidemiology Network of Arteriopathy (GENOA) study, a multicenter community-based study of hypertensive sibships, whose main goal is to identify genes influencing blood pressure levels and development of target organ damage due to hypertension [O’Meara et al., 2004; Turner et al., 2006]. Only GENOA participants from the Rochester field center were considered for the present analyses because only these participants had CAC measured. In the first phase of the GENOA study (June 1996 to October 2000), the Mayo Clinic diagnostic index and medical record linkage system of the Rochester Epidemiology Project were used to identify all non-Hispanic White residents of Olmsted County, MN diagnosed with essential hypertension by 60 years of age. Eligible probands were contacted and questioned about their siblings. If they had siblings living in the area, the siblings were contacted and asked if they had been diagnosed with hypertension. If at least one sibling of the proband reported a previous diagnosis of hypertension before age 60, all available siblings were invited to participate.

Between December 2000 and February 2004, 1,241 of the original GENOA participants in the Rochester field center returned to undergo risk factor and target organ damage measurement. Individuals with a history of coronary revascularization and women who were pregnant or lactating were excluded from measurement of CAC quantity with electron beam computed tomography. Participants with a history of myocardial infarction, stroke or a coronary angiogram that indicated a blockage (n = 75) were excluded from the current analyses. Participants (n = 2) with outlier values (±4 standard deviations from the mean for quantitative risk factors) and low rate of SNP genotyping calls were also excluded. The final study group included 935 individuals in 400 sibships with both genotypic and phenotypic data. The sibship size ranged from 2 to 11 siblings and there were 80 singletons.

We took advantage of the sibship-based study design and created two data sets, each with 360 unrelated individuals, to test for replication of risk factor and SNP associations in study groups with similar genetic and environmental backgrounds. We randomly sampled one sib from each sibship with at least two sibs without replacement to create the first data set (referred to here as data set 1). From the remaining participants, we randomly sampled a second sib from each sibship with at least two sibs to establish the second data set (referred to here as data set 2). The same number of singletons (total n = 80) was randomly assigned to each data set. Therefore, the subjects within each data set were independent from each other.

MEASUREMENT OF RISK FACTORS

Standard enzymatic methods were used to measure total cholesterol, high-density lipoprotein cholesterol (HDL-C) and triglycerides after overnight fasting [Kottke et al., 1991]. Plasma glucose was measured by the glucose oxidase method. Low-density lipoprotein cholesterol was calculated using the Friedwald equation [Executive, 1993]. Body mass index (BMI) was calculated (weight/height²; kg/m²). Systolic blood pressure (SBP) and diastolic blood pressure levels were measured in the right arm with a random-zero sphygmomanometer (Hawksley and Sons, West Sussex, UK). Three measures at least 2 min apart were taken and the average of the second and third measurements was analyzed. Fibrinogen was measured by the Clauss (clotting time-based) method [Clauss, 1957] and C-reactive protein by a highly sensitive immunoturbidimetric assay [Keevil et al., 1998]. Low-density lipoprotein particle size was measured by polyacrylamide gel electrophoresis [Hoefner et al., 2001]. Plasma homocysteine was measured using a liquid chromatography electro-spray tandem mass spectrometry method as previously described [Magera et al., 1999]. Lp(a) was measured in serum by an immunoturbidimetric assay using the SPQTM Test System (Diasorin, Stillwater, MN) [Levine et al., 1992].

MEASUREMENT OF CAC

CAC was measured using an Imatron C-150 electron beam computed tomography scanner (Imatron Inc., San Francisco, CA) using a standard protocol [Bielak et al., 2001]. CAC was defined as a hyperattenuating focus in a coronary artery that was at least four adjacent pixels in size (i.e., 1.04 mm²), with a radiograph attenuation coefficient (Computed tomography number) above 130 Hounsfield Units throughout the focus. An experienced radiologist inspected the technical quality and scoring accuracy of each tomogram and interpreted their findings. Quantity of CAC was defined as the CAC score described by Agatston et al. [1990]. Individuals with detectable CAC and CAC scores ≥70th percentile for their age and sex based on CAC scores from a community-based sample of asymptomatic adults unselected for risk factors were classified as having a high CAC burden and compared to individuals with CAC <70th percentile [Lange et al., 2002]. The 70th percentile identifies those considered to be in the highest risk group for a future event.

SNP GENOTYPING

Genes were selected to represent biological pathways or positional candidate genes from systems known to be associated with hypertension and CAD, including ion transport, inflammation, vascular wall biology, the renin-angiotensin system and lipid metabolism. SNP genotyping was obtained using a combination of two genotyping platforms: mass spectrometer-based detection system implemented on a Sequenom MassARRAY System and the fluorogenic TaqMan assay implemented on an ABI Prism 7900 Sequence Detection System. Primer and probe sequences are available from the authors upon request.

MISSING DATA IMPUTATION

The average genotype missing rate was 4.5% in data set 1 and 4.2% in data set 2. Because the current version of RuleFit requires complete data, we imputed missing genotypes from neighboring markers using an extension of the expectation-maximization (EM) algorithm [Chiano and Clayton, 1998] implemented in HelixTree^® (Golden Helix Inc., Bozeman, MT). The 20 highest linkage disequilibrium (LD) SNPs were selected within a window of 30 SNPs centered about the SNP of interest. Missing genotypes were computed through the 20-SNP haplotypes with EM convergence tolerance of 0.001 and maximum EM iteration number of 50. In a simulation study, this method achieved imputation accuracy above 95% with missing rates ranging from 1 to 10% [Sun and Kardia, 2008]. The same complete data set was analyzed with Random Forests and RuleFit methods.

RANDOM FORESTS

There are three unique characteristics in how the trees are grown with the Random Forests algorithm: (1) the method randomly selects, with replacement, n samples to form a training data set; (2) a small subset of all predictor variables (here a subset of the 471 SNPs and 17 risk factors) are randomly selected for each tree and (3) then each tree is grown, independently of the other trees, to the largest extent possible to classify the outcome status (here CAC score < or ≥70th percentile) [Breiman, 2001]. Next, the algorithm makes predictions for each observation in the testing data set using only the predictor variables and a classification is determined for every tree in the forest. Finally, the algorithm rates the importance of each variable in predicting the outcome based on the most votes over all the trees in the forest. The Random Forests method is robust with respect to unimportant predictor variables (such as genetic factors without any predictive power), and overfitting, and it provides estimates of what variables are important in the classification [Breiman, 2001]. In this study, we applied the original Random Forests implementation [Breiman, 2001] that uses the classification and regression tree to grow the individual trees and uses bootstrapping to randomize the sample. To rank the importance of the predictors, we used the Gini index which measures the average decrease in node impurities from splitting on the variable [Breiman, 2001].

RULEFIT

RuleFit has the same advantages of the Random Forests algorithm but adds more interpretability to the model [Friedman and Popescu, 2005]. Each rule’s influence on the predictive model and the relative importance of each independent variable can be assessed by the algorithm. RuleFit provides: (1) an accurate prediction model for the outcome; (2) a set of simple rules which could reflect gene-gene, gene-risk factor and risk factor-risk factor interactions and (3) a variable selection method by ranking the relative importance of all independent variables considered.

STATISTICAL METHODS

In this study, we used data sets 1 and 2; each included 360 independent subjects with 17 risk factors and 471 SNPs, and two machine learning methods to predict CAC burden. Descriptive statistics for risk factors, CAC and SNPs were generated using the statistical software R. Based on results from diagnostic plots and Kolmogorov-Smirnov tests for normality, triglyceride and Lp(a) levels were transformed using the natural logarithm in order to reduce skewness. Student’s t-test and χ²-test were used to confirm that risk factor distributions and prevalence of high CAC burden in the two data sets were not statistically significantly different (P-value of 0.05 on two-sided tests). Population genetic parameters for all SNPs were calculated, including minor allele frequencies (MAFs), genotype frequencies and either a χ² test or the Fisher exact test for departures from expectations under Hardy-Weinberg equilibrium (HWE).

We used the tagSNP selection method [Carlson et al., 2004] to remove highly redundant SNP predictors. There were 287 tagSNPs which had no pair-wise LD R² > 0.5 and had MAF > 0.05. Thus, we could remove unnecessary SNPs and retain the most informative SNPs for analysis as well as improve computation speed which is a critical issue for higher dimensional genome-wide association data.

To evaluate the overall performance of the model predictive ability, we did not use the default point estimate, 50% voting rate as the threshold, to classify the binary outcome. Instead, we evaluated the sensitivity and specificity at all possible voting rate thresholds using the vector of all votes from the ensemble, and then plotted the receiver operating characteristic (ROC) curve based on these values.

For both the Random Forests and RuleFit analyses, each data set was partitioned into five exhaustive, mutually exclusive, cross-validation subsets of 72 individuals each by random sampling. In five-fold cross-validations, four of the five subsets were combined and used as the training data set for the purpose of “learning”. The remaining subset was used for testing. Five times the ROC curve was calculated based on the vectors of sensitivity and specificity based on the votes from each method. The values of area under the curve (AUC) of the ROC curves of five cross-validation subsets were averaged to compare the predictability and stability of the models. Within each of data sets 1 and 2, the entire model building procedure was repeated in each of the five-fold cross-validation steps.

All statistical analyses were performed with R statistics environment version 2.3.0 from R Project (http://www.r-project.org/). R libraries of Random Forests (randomForest 4.5.-15) and RuleFit (rulefit) [Friedman and Popescu, 2005] were utilized to predict CAC burden using risk factors and SNPs as predictors. The modeling parameters used for Random Forests (function “randomForest”) were importance = TRUE, ntree = 2,000 and mtry = 30. The parameters used for RuleFit (function “rulefit”) were rfmode = “class”, max.rules = 10,000 (10,000 rules) and tree.size = 4 (four levels of tree depth). Other parameters used in the functions of “randomForest” and “rulefit” were same as the default settings if not specified above. The parameters of both methods were chosen by optimizing the prediction performance.

PERMUTATION TESTS

The null distribution of AUCs was generated for a total of 1,000 permutations for each machine learning method separately. For each permutation test, the prediction model was built (as described above) and the predictive ability was estimated by the AUC of the ROC curve using a data set with randomly shuffled high CAC burden status. Then, the observed AUC of the ROC curve was compared to the null AUC distribution to calculate empirical P-values reported here.

RESULTS

EVALUATION OF MODEL PREDICTABILITY OF RANDOM FORESTS AND RULEFIT USING ROC CURVE

The descriptive statistics of all 17 risk factors and the outcome were summarized in supplemental Table I. Only HDL-C and triglyceride were significantly different between the two data sets. The MAFs, genotype frequencies and HWE P-values of 471 tested SNPs in both data sets were summarized in supplemental Table II.

The AUC results of Random Forests and RuleFit considering all 17 risk factors and all 471 SNPs are summarized in Table I. Using the 287 tagSNPs (pair-wise LD R² < 0.5) instead of all 471 SNPs led to a slightly increased AUC (i.e., the predictive ability improved) in data set 1 for both methods but not in data set 2 (Table I).

TABLE I.

The impact of tagSNP selection on model predictability

		Data set 1		Data set 2
Method	SNPs used	AUC mean	AUC STD	AUC mean	AUC STD
Random Forests	All 471 SNPs	0.734	0.044	0.747	0.048
	287 tagSNPs	0.760	0.016	0.744	0.064
RuleFit	All 471 SNPs	0.678	0.065	0.692	0.060
	287 tagSNPs	0.703	0.047	0.692	0.054

SNP, single nucleotide polymorphism; AUC, area under the curve.

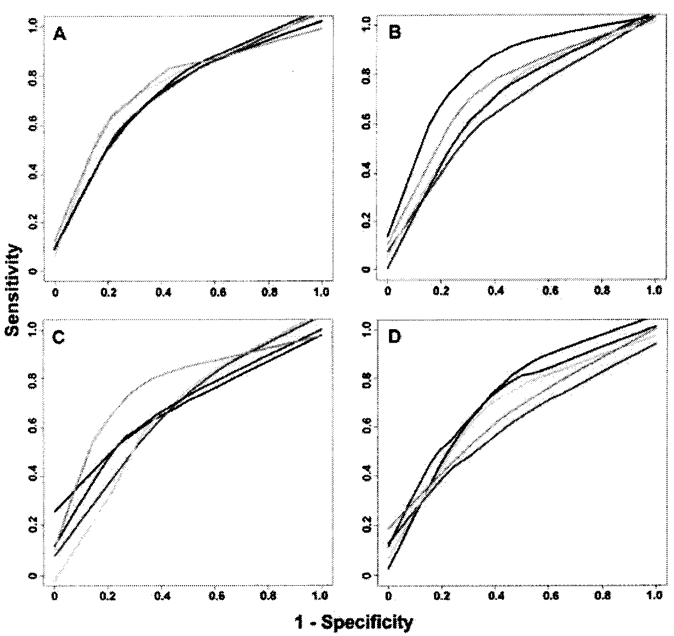
Considering all 17 risk factors and just the 287 tagSNPs, the ROC curves and AUC results of the two methods are summarized in Figure 1 and Table II with results from five-fold cross-validation. Using Random Forests, the mean (STD) AUC of the five ROC curves was 0.760 (0.016) for data set 1 and 0.744 (0.064) for data set 2. Using RuleFit, the mean (STD) AUC was 0.703 (0.047) and 0.692 (0.054) for data sets 1 and 2, respectively. The largest mean AUCs among the 1,000 permutation tests were 0.559 and 0.543 for Random Forests, and 0.632 and 0.640 for RuleFit for data sets 1 and 2, respectively. The observed AUCs of ROC curves from both Random Forests and RuleFit were statistically significantly different from the permuted values with empirical P-value less than 0.001, for each data set.

Fig. 1.

ROC curve of Random Forests and Rulefit with five-fold cross-validation. (A) Random Forests on dataset 1. (B) Random Forests on dataset 2. (C) RuleFit on dataset 1. (D) RuleFit on dataset 2. 17 clinical predictors and 287 tagSNPs were used to predict the presence of higher CAC burden in two datasets with 360 unrelated individuals in each. Each ROC curve represents one subset result of the five-fold cross-validation procedure. [Color figure can be viewed in the online issue which is available at www.interscience.wiley.com]

TABLE II.

Summary of predictability of Random Forests and RuleFit with five-fold cross-validation using 17 risk factors and 287 tagSNPs

	Random Forests						RuleFit
	Data set 1			Data set 2			Data set 1			Data set 2
	AUC	Sensitivity (%)	Specificity (%)	AUC	Sensitivity (%)	Specificity (%)	AUC	Sensitivity (%)	Specificity (%)	AUC	Sensitivity (%)	Specificity (%)
Subset 1	0.746	80.8	60.0	0.843	89.1	61.5	0.690	71.2	60.0	0.746	73.9	61.5
Subset 2	0.746	70.7	71.0	0.675	71.2	60.0	0.681	73.2	61.3	0.614	71.2	50.0
Subset 3	0.778	79.6	61.1	0.718	74.5	61.9	0.667	70.4	61.1	0.696	76.5	61.9
Subset 4	0.752	75.0	61.5	0.718	71.9	69.2	0.692	68.8	65.4	0.739	78.1	61.5
Subset 5	0.777	77.5	71.4	0.766	81.3	68.2	0.786	85.0	71.4	0.665	68.8	59.1
Mean	0.760	76.7	65.0	0.744	77.6	64.2	0.703	73.7	63.8	0.692	73.7	58.8
STD	0.016	4.0	5.7	0.064	7.6	4.2	0.047	6.5	4.7	0.054	3.8	5.1

SNP, single nucleotide polymorphism; AUC, area under the curve.

In Table II, the sensitivity and specificity for each cross-validation subset, data set and analysis method are presented. For Random Forests, the average sensitivities were 76.7 and 77.6%, and the average specificities were 65.0 and 64.2% for data sets 1 and 2, respectively. For RuleFit, the average sensitivities were 73.7 and 73.7% and the average specificities were 63.8 and 58.8% for data sets 1 and 2, respectively.

VARIABLE SELECTION

We compared the 50 top-ranked variables from Random Forests and RuleFit models and identified 31 (62%) common variables from both methods in data set 1 and 32 (64%) in data set 2. Additionally, 23 (46%) common variables were identified by Random Forests in both data sets and 20 (40%) by the RuleFit method. There were 14 (28%) common variables identified by both methods that showed replication in both data sets 1 and 2. These variables were age, BMI, sex, serum glucose, HDL-C, SBP, cholesterol, homocysteine, triglyceride, fibrinogen, Lp(a) and low-density lipoprotein cholesterol particle size and two SNPs including GPR35_rs3749172 and NOS3_rs1800780 (the ranks are summarized in Table III). The mean, standard deviation and t-test P-value of the risk factors (χ² P-value for sex) are summarized in Table IV. The mean levels of HDL-C and triglyceride were significantly different in the two data sets (Table IV). Besides GPR35_rs3749172 and NOS3_rs1800780, six other tagSNPs were found to be top-ranked in three out of four tested models. The allele frequencies, genotype frequencies and the HWE P-values of the eight SNPs are summarized in Table V. MAFs of the SNPs did not differ between data sets.

TABLE III.

Predictors with replicable effects and their importance ranks in data sets 1 and 2 from Random Forests arid RuleFit

	Rank in Random Forests		Rank in RuleFit
Predictor	Data set 1	Data set 2	Data set 1	Data set 2
Age	1	1	1	1
Serum glucose	2	2	3	3
BMI	3	4	2	2
HDL-C	4	3	14	4
Fibrinogen	8	8	5	7
Homocysteine	7	5	13	5
log(Lp(a))	11	9	8	12
Systolic blood pressure	5	6	7	25
log(triglyceride)	6	7	15	20
Cholesterol	10	11	28	14
Sex	12	16	20	16
LDL-C particle size	13	14	9	41
NOS3_rs1800780	16	47	31	34
GPR35_rs3749172	19	41	38	45

The rank is based on the total of 304 variables including 287 tagSNPs and 17 risk factors. BMI, body mass index; HDL-C, high-density lipoprotein cholesterol; LDL-C, low-density lipoprotein cholesterol; SNP, single nucleotide polymorphism.

TABLE IV.

Descriptive statistics of the identified risk factor predictors with replicable effects and the hypertension status and the outcome in the two data sets

	Data set 1 (n = 360)		Data set 2 (n = 360)
Variables	Mean	STD	Mean	STD	t-Test P-valuea
Age (years)	59.12	10.06	59.20	9.80	0.914
BMI (kg/m2)	30.87	5.83	30.38	6.35	0.283
SBP (mmHg)	131.08	17.04	131.57	16.54	0.695
HDL-C (mg/dL)	50.73	14.03	53.06	15.39	0.034
Cholesterol (mg/dL)	199.63	34.30	198.44	31.11	0.626
Fibrinogen (mg/dL)	316.33	76.38	318.73	81.13	0.684
log_Lp(a)	2.69	1.24	2.63	1.18	0.523
log_triglyceride	4.98	0.54	4.87	0.51	0.005
Homocysteine (md/dL)	9.98	2.77	9.82	2.51	0.427
LDL-C particle size (Å)	269.93	5.13	270.36	4.84	0.247
Serum glucose (mg/dL)	105.29	23.35	104.43	24.60	0.630
	n	%	n	%	χ2 P-value
Male gender	153	42.5	147	40.8	0.701
Hypertension	269	74.7	266	73.9	0.865
High CAC burdenb	251	69.7	245	68.1	0.687

BMI, body mass index; SBP, systolic bleed pressure; HDL-C, high-density lipoprotein cholesterol; LDL-C, low-density lipoprotein cholesterol; CAC, coronary artery calcification.

^aThe t-test was used to assess whether the variables’ means of the two data sets are significantly different from each other.

^bHigh CAC burden is defined as having detectable CAC and being ≥sex- and age-specific 70th percentile for CAC score.

TABLE V.

Descriptive statistics of the important SNPs with replicable effects in the two data sets

		Data set 1					Data set 2
SNP name	Major/Minor allele	MAF	Nii	Nij	Njj	HWE P-value	MAF	Nii	Nij	Njj	HWE P-value
NOS3_rs1800780	A/G	0.494	85	194	81	0.143	0.486	88	194	78	0.136
GPR35_rs3749172a	A/C	0.403	125	180	55	0.511	0.403	134	162	64	0.223
FGB_rs1800788	C/T	0.193	234	113	13	1.000	0.201	231	113	16	0.631
GPC6_rs1886928	A/G	0.415	123	175	62	1.000	0.433	113	182	65	0.585
SELP_rs6131a	G/A	0.189	236	112	12	0.872	0.172	251	94	15	0.136
rs7944706	G/A	0.426	125	163	72	0.168	0.449	110	177	73	0.914
NOS3_rs891511	G/A	0.325	164	158	38	1.000	0.315	171	151	38	0.538
COL19A1_rs1736	G/A	0.363	148	163	49	0.733	0.385	140	163	57	0.369

^aNon-synonymous SNP. SNP, single nucleotide polymorphism; MAF, minor allele frequency; HWE, Hardy-Weinberg equilibrium.

CAC ASSOCIATIONS OF IDENTIFIED PREDICTORS AND THE INTER-RISK FACTOR CORRELATION (KGRAPH)

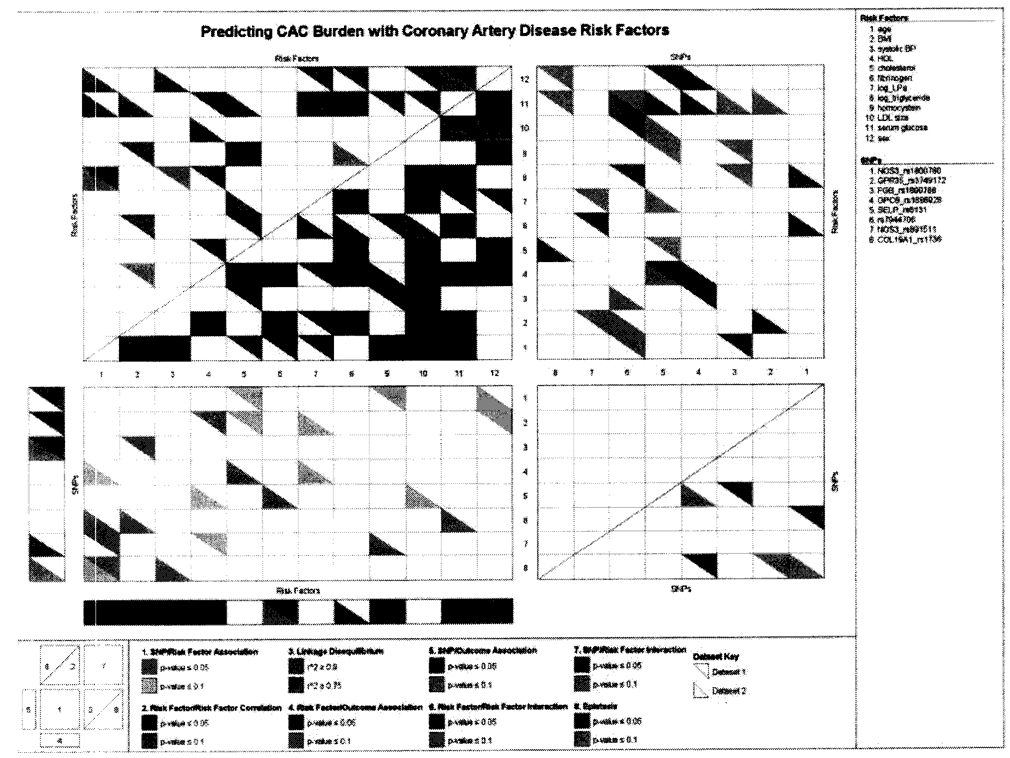
Pair-wise correlations and interactions among replicable predictors and their associations with CAC burden are presented in Figure 2 using KGraph [Kelly et al., 2007]. The figure simultaneously displays both significant univariate associations and pair-wise interaction associations with CAC burden, as well as the underlying correlation structure among the predictor variables (SNPs and risk factors). Although these variables have replicable effects in prediction, most of their univariate associations (regions 4 and 5) and pair-wise interactions (region 6: risk factor-risk factor interaction; region 7: SNP-risk factor interaction; region 8: SNP-SNP interaction) are not significant in replicate. Seven univariate associations, age, BMI, SBP, HDL-C, homocysteine, serum glucose and sex, are significant in both data sets (P < 0.05). Furthermore, three risk factor-risk factor interactions, cholesterol and homocysteine, Lp(a) and serum glucose, triglyceride and serum glucose, are significantly associated with CAC burden in both data sets.

Fig. 2.

Summary of CAC burden associations and correlations (KGraph) of all risk factors and SNPs with replicable effects. AC, coronary artery calcification; SNP, single nucleotide polymorphism.

DISCUSSION

Due to the complicated cellular and molecular processes involved in complex diseases, the contributing genetic factors may function in an interdependent network fashion instead of independently. Therefore, traditional methods that study one factor at a time could be highly biased and misleading. Random Forests and RuleFit both provide the functionality to evaluate the relative importance of the predictors. In the current study, both methods were robust and were reasonably consistent (over 60% variables were highly ranked in both data sets) for variable selection.

Although methods such as Random Forests have been shown to be robust to insignificant variables [Breiman, 2001], with the scale of current genome-wide association studies involving hundreds of thousands of SNPs and future studies involving millions of genotypes, the signal-to-noise ratio has to be considered to achieve better performance. Several knowledge-based approaches can greatly reduce the dimensionality for specific biomedical questions. For example, SNPs from candidate genes that are associated with a certain disease or a disease-related trait can be analyzed separately. In addition, a spectrum of SNPs can be analyzed based on the disease-related pathways and networks. These approaches, however, are limited by a priori understanding of the disease process and can hardly be used to discover novel SNPs and/or genes. Alternatively, by ranking the single SNP association test results, researchers are able to prescreen the SNPs using a priori criteria (e.g., the 1% most strongly associated with the outcome of interest) for further pattern recognition analyses. This approach is biased toward univariate effects and ignores the possibilities of epistasis and/or gene-environment interactions. As an advantage, tree-based ensemble learning methods such as those applied here include the main effects as well as the interaction effects in each of the individual trees. Assuming the feature selection results from each method define a part of the true classification boundary in some hyperspace, combining the results from several methods will provide much higher confidence in finding the truly important predictors. Therefore, combining multiple methods is crucial to accurately identify the disease-related SNPs and risk factors.

The Random Forests method is known to be insensitive to uninformative predictors [Breiman, 2001]. Removing the redundant information as much as possible, however, benefits the predictability of the machine learning process as well as the computation speed. Although both algorithms run very fast for hundreds of SNPs, the computation of hundreds of thousands [Gunderson et al., 2006; Matsuzaki et al., 2004] of SNPs from whole genome association studies might be a deterrent for applying such machine learning methods. Utilizing the tagSNP selection strategy eliminates redundant SNPs and accelerates the modeling process while maintaining the accuracy of predictability.

In this study, we used a five-fold external cross-validation procedure to assess the predictive ability of Random Forests and RuleFit. Because of the re-sampling procedure applied in the ensemble learning methods, such as Random Forests, it may not be necessary to use external sample to cross-validate the prediction model [Breiman, 2001]. This recommendation is based, however, on the observation that the ensemble learning methods, such as Random Forests, do not overfit and are robust with respect to unimportant predictors. Recent studies have demonstrated that the external cross-validation step is necessary to accurately evaluate the predictive ability using the Random Forests algorithm [Konig et al., 2007; Sun et al., 2007]. In addition, using the cross-validation procedure is important to fairly compare the predictive ability across multiple machine learning methods, especially when one of the methods does include the re-sampling process.

We found evidence for an association of SNPs in two genes (NOS3 and GPR35) with higher CAC burden. The NOS3 gene has been associated with atherosclerosis [Hingorani et al., 1999; Kuhlencordt et al., 2001; Wang et al., 1996]. The NOS3 gene encodes endothelial nitric oxide synthase which synthesizes nitric oxide (NO) in endothelial cells from L-arginine. NO is an important endogenous anti-atherogenic molecule, and the NOS3 gene may influence bioavailability of NO and thereby predispose to atherosclerotic vascular disease. NOS3_rs1800780 is located on the intronic region between the 12th and the 13th exons of NOS3 gene. There is no known non-synonymous SNP in the flanking region of this SNP with strong LD. Genetic variation in NOS3 (Glu298Asp; rs1799983) has been associated with reduced blood pressure fall after exercise training [Rankinen et al., 2000], lower basal coronary blood flow and reduced coronary vasodilation to adenosine [Naber et al., 2001] and reduced flow-mediated dilatation of the brachial artery [Savvidou et al., 2001]. However, NOS3_rs1799983 was not a significant predictor of high CAC burden using either statistical method in the current study.

GPR35_rs3749172 is a non-synonymous SNP that causes the serine (A allele) to arginine (G allele) conversion on the amino acid position of 294 of G-protein-coupled receptor 35 (GPR35). Although the function of GPR35 and its role in CAC burden is not clear, it was suggested to be a receptor for the kynurenine pathway intermediate kynurenic acid [Wang et al., 2006]. The intermediates of the kynurenine pathway are present at micromolar concentrations in blood and are regulated by inflammatory stimuli. Using sequence alignment and membrane protein topology analysis, we found that the non-synonymous GPR35_rs3749172 encodes a Ser (Ser294) to Arg change which may alter the protein function. GPR35_rs3749172 is located on the cytosolic c-terminal, which is the phosphorylation domain of the GPR proteins [Okumura et al., 2004]. The Ser294 is conserved by comparing human, mouse and rat GPR35 protein sequences. As the c-terminal phosphorylation sites are critical to the function of the G-protein receptors and there are only four conserved sites for phosphorylation on the c-terminal of human GPR35, the Ser294Arg polymorphism may be functionally related to the modification of the GPR35 signal transduction pathway. The role of GPR35 in the biology of CAC burden is still unclear and needs to be further investigated.

The original implementation of Random Forests [Breiman, 2001] used a bootstrapping procedure which introduced bias in variable selection [Strobl et al., 2007]. The bootstrapping procedure artificially favors quantitative variables and categorical variables with more categories (i.e., the more categories the variable has, the more likely it is to be selected). However, “re-sampling with replacement” (i.e., down-sampling) reduces the bias. In the task of SNP selection, such a bias is not an issue due to the identical three-class data type of SNPs. However, variable selection tasks comparing phenotypic and other genotypic variables need to consider the potential bias introduced by different re-sampling procedures and importance measurements [Strobl et al., 2007].

It is known that the non-random missing data patterns can alter the results of machine learning. Concern regarding non-random missing data is elevated when the missing data rate is non-trivial. Necessary procedures of controlling the data quality and removing predictors with non-random missing patterns can help to identify the true predictors and improve the predictive ability of the models.

This study demonstrates how two machine learning algorithms can be applied to identify SNP and risk factor associations that are replicable both between data sets using the same method and between methods using the same data set. The use of multiple methods and data sets provides increased confidence in the accuracy of the predictors. Two novel SNP associations for CAC burden were identified in the present study. The approaches implemented here provide alternatives to methods that rely on pre-specified models.