Observed Enhancement of the Catalytic Activity of a Biomimetic Diiron Complex by the Addition of Water - Mechanistic Insights from Theoretical Modeling

Abstract

The biomimetic diiron complex [Fe^IIIFe^IV(μ-O)₂(5-Me₃-TPA)₂](ClO₄)₃ (TPA = tris(2-pyridylmethyl)amine) has been found to be capable of oxidizing 9,10-dihydroanthracene in a solution of acetonitrile. Addition of water up to 1M makes the reaction 200 times faster, suggesting that the water molecule in some way activates the catalyst for more efficient substrate oxidation. It is proposed that the enhanced reactivity results from the coordination of a water molecule to the iron(III) half of the complex, converting the bis-μ-oxo structure of the diiron complex to a ring-opened form where one of the bridging oxo groups is transformed into a terminal oxo group on iron(IV). The suggested mechanism is supported by DFT (B3LYP) calculations and transition state theory. Two different computational models of the diiron complex are used to model the hydroxylation of cyclohexane to cyclohexanol. Model 1 has a bis-μ-oxo diiron core (diamond core) while model 2 represents the “open core” analogue with one bridging μ-oxo group, a terminal oxo ligand on iron(IV), and a water molecule coordinated to iron(III). The computational results clearly suggest that the terminal oxo group is more reactive than the bridging oxo group. The free energy of activation is 7.0 kcal/mol lower for the rate limiting step when the oxidant has a terminal oxo group than when both oxo groups are bridging the irons.

I. Introduction

Enzymes containing non-heme diiron active sites play important roles in the binding and activation of molecular oxygen for biochemical oxidations (1,2). High-valent intermediates have been identified as the active oxidants for non-heme diiron enzymes such as methane monooxygenase (MMO) and ribonucleotide reductase (RNR) and proposed for Δ⁹-desaturase (Δ9D) (1,3,4). A diiron(IV) intermediate called Q has been identified in the catalytic cycle of MMO, which converts methane to methanol (5-8). A similar oxidant is proposed for Δ9D in the dehydrogenation of saturated fatty acids such as stearic acid (9). On the other hand, an iron(III)iron(IV) intermediate X is observed in the R2 subunit of RNR to generate a catalytically essential tyrosyl radical that then initiates the conversion of ribonucleotides to deoxyribonucleotides (10-12). All three enzymes possess a common diiron center that is coordinated by the side chains of histidine, glutamate and aspartate amino acids and reacts with dioxygen to form these high-valent intermediates. It is proposed that these intermediates may have an Fe₂(μ-O)₂ diamond core (9,13,14).

Spectroscopic, structural and mechanistic insights from biomimetic diiron complexes can give a better understanding of the detailed functions of diiron enzymes like MMO, RNR and Δ9D (15,16). There have been a number of efforts to synthesize complexes with a formal Fe^IIIFe^IV oxidation state (17-21), only for one series of complexes with the general formulation [Fe^IIIFe^IV(μ -O)₂(5-R₃-TPA)₂](ClO₄)₃ (TPA = tris(2-pyridylmethyl)amine) (21) is an Fe₂(μ -O)₂ diamond core shown to be present to serve as a synthetic precedent for the core structures proposed for high-valent diiron enzyme intermediates. The crystal structure of the 5-ethyl derivative was obtained, representing the only example of a structurally characterized high-valent bis(μ-oxo)diiron complex (22). Also, the TPA complex was shown to effect oxo transfer and H-atom abstraction reactions in the presence of added water (23), but no rationale was given for the effect of water. In the present contribution it is shown that the addition of water activates this complex for substrate oxidation. It is suggested that the added water binds to the [(L)₂Fe₂(μ-O)₂]³⁺ complex and converts it to a much more reactive ring-opened structure, i.e. [(L)Fe^IV(O)-Fe^III(OH₂)(L)]³⁺, with a terminal oxo-group bound to iron(IV) (Scheme 1). The plausibility of this mechanism for activation is tested and supported by DFT (B3LYP) calculations and transition state theory.

Scheme 1.

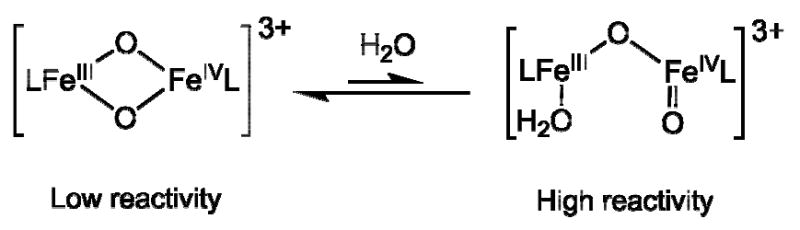
Proposed opening of the diamond core in the presence of water. The open core analogue is formed which possesses a terminal Fe^IV=O group. For these two complexes the hydroxylation of cyclohexane was modeled.

II. Methods and Models

A. Computational Methods and Models

Most calculations were done using the hybrid density functional B3LYP (20% exact exchange) (24-28). A few calculations were done with B3LYP* (15% exact exchange) (29) to investigate how the computed results depend on the amount of exact exchange included in the hybrid density functional. The software package Jaguar 5.5 (30) was used for geometry optimizations and for the calculation of the final energies. Hessian matrices (i.e. matrices of force constants) were calculated using Gaussian 03 (31). Because an explicit Hessian is needed in saddle point optimizations, the geometries of the transition states were also determined using the Gaussian program. The Hessians were also needed to evaluate zero point effects, entropic- and thermal corrections to the Gibbs free energy. In the construction of the reaction free energy profile, thermal effects from the separated species have been used exclusively, since for loosely bound intermediates the harmonic approximation gives poor results. As experiments are done at -30°C, the Gibbs free energy was calculated for 243 K.

The double zeta basis set lacvp was used for geometry optimizations, for zero point effects and thermal corrections. This basis set has a 6-31G description for all atoms except iron. The core orbitals of iron (except the outermost) are described by an effective core potential (32). The final energies for the fully optimized structures were calculated with the lacv3p** basis set, which includes polarization functions on all atoms except iron. Experience has shown, that geometries obtained from calculations using the double zeta basis are quite adequate for the calculation of the final energetics (33, 34).

In a recent publication a case was reported, in which the self-interaction error (SIE) in DFT, caused severe errors in the modeling of reactivity by stabilizing artificially delocalized states. This had the effect that fractional numbers of electrons where transferred from the closed-shell substrate molecule to the iron complex, and in the worst case lead to the disappearance of the barrier for hydrogen abstraction (35). It was found that delocalization effects of the SIE can be avoided by lowering the total charge of the iron complex through addition of a counter-ion. In the present investigation this was done by including a ClO₄^- ion in the computational model complexes, since it is the counter ion present in the experimental study.

To reproduce the polarization effects of the solvent used in the experiments, the self-consistent reaction field (SCRF) method implemented in Jaguar 5.5 was employed (36, 37). The solvent was modeled as a macroscopic continuum with a dielectric constant of 36.6 (corresponding to acetonitrile), and the solute was placed in a cavity contained in this continuous medium. Final energies of the optimized structures were corrected for the solvent effects by employing the lacvp basis set. The dielectric medium has a very small effect on the reaction energetics as long as no substantial charge separations are involved (38, 39).

Special consideration was made concerning the position of the ClO₄^- ion, since the charge distribution of the system depends on the position of the counter-ion. However, in all calculations the distance between the counter-ion and the iron complex remained almost unchanged (i.e. moved less than 0.3 Å), why the presence of the ion should not have any significant effect on the relative solvent energies. Only for the final product after the hydroxylation step the distance between counter-ion and complex had to be fixed since otherwise the counter-ion will move towards the complex due to the large structural change after the hydroxide transfer.

The spin populations indicate the spin- and oxidation state of the metal ions and were derived from Mulliken population analysis. Antiferromagnetically (AFM) coupled spin states are not pure spin states since they are contaminated by ferromagnetically (FM) coupled states. In order to correct the energy of these AFM states, it is possible to apply the Heisenberg spin-Hamiltonian formalism (40). However, for the systems investigated here, the corresponding FM and AFM states were found to have almost the same energy, differing with less than 3 kcal/mol for all interesting (energetically low lying) spin states. Which means that a correction for spin contamination would not significantly change the energy.

The computational model complexes were built upon the X-ray structure reported for [Fe₂(μ-O)₂(5-Et₃-TPA)₂]³⁺. After initial calculations on this complex it was concluded that the 5-ethyl-substituents can be neglected for the computational model complexes, since they did not affect the ordering of the spin states. Also the effect on the spin splitting is very small. The difference between the ground state and the two next higher lying states are 2.4 and 2.6 kcal/mol including the ethyl-substituents, and 3.6 and 4.0 kcal/mol without them. Thus, the two model complexes contain the parent TPA ligand. The diamond core complex [Fe₂(μ-O)₂(TPA)₂(ClO₄)]²⁺ (1) and the corresponding water containing open core analogue [Fe₂(μ-O)(O)(H2O)(TPA)₂(ClO₄)]²⁺ (2) are shown respectively in Figures 1 and 2.

Figure 1.

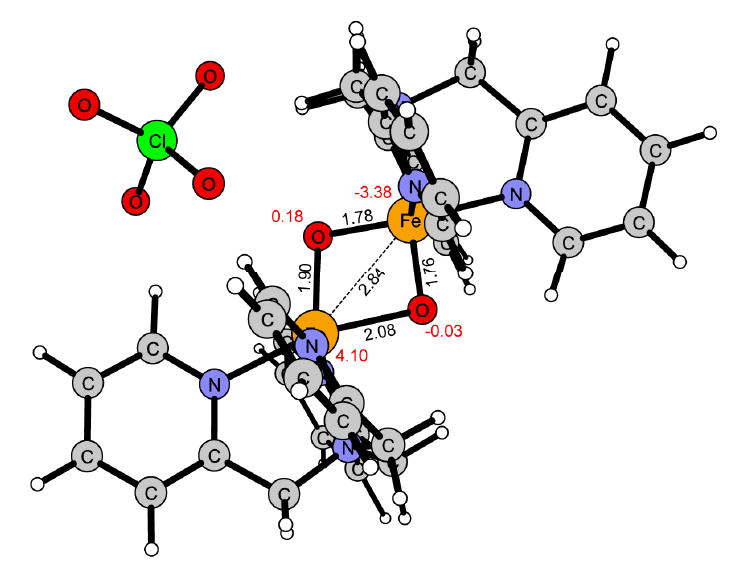
Reactant [Fe₂(μ-O)₂(TPA)₂(ClO₄)]²⁺ (1) in the S = 1/2 spin state (5α4β). Distances are given in Ångström, red numbers represent the calculated Mulliken spin.

Figure 2.

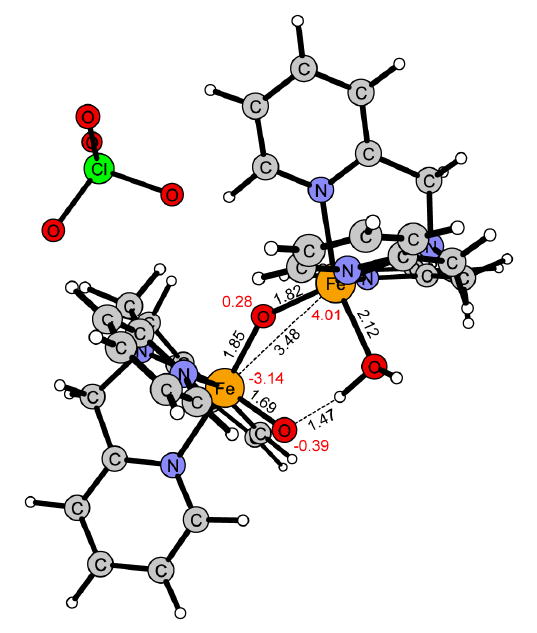
Reactant [Fe₂(μ-O)(O)(H₂O)(TPA)₂(ClO₄)]²⁺ (2) in the S = 1/2 spin state (5α4β). Distances are given in Ångström, red numbers represent the calculated Mulliken spin.

Cyclohexane was used as substrate in order to reduce the computational cost and to avoid effects of the delocalization error in DFT (cyclohexane has a higher ionization potential than DHA and is therefore less likely to be affected by the delocalization error (35, 41). For oxidation of DHA to anthracene the first transition state for hydrogen abstraction (HAT) is clearly rate limiting (35), and the difference in reactivity observed with the presence of water should be compared to the HAT step in the modeled hydroxylation of cyclohexane.

III. Results and Discussion

A. Experimental Results

In a previous communication, we demonstrated that [Fe^IIIFe^IV(μ-O)₂(TPA)₂]³⁺ can oxidize the side chains of ethylbenzene and cumene in MeCN with 0.75% added water at -30°C (23). However the fact that this complex can only be generated in situ makes it difficult to control the other components present in the solution and determine the inherent reactivity of the [Fe^IIIFe^IV(μ-O)₂]³⁺ core. Furthermore, the required addition of water was puzzling. To investigate a better defined system, we have instead focused on the reactivity of the more stable [Fe^IIIFe^IV(μ-O)₂(5-Me₃-TPA)₂]³⁺ complex (5-Me₃-TPA = tris(5-methyl-2-pyridylmethyl)amine)), which can be isolated as a solid (21). As in the previous study (23), the progress of substrate oxidation by [Fe^IIIFe^IV(μ-O)₂(5-Me₃-TPA)₂]³⁺ can readily be monitored by the loss of its intense green chromophore (λ_max = 616 nm, ε = 5200 M^-1 cm^-1) that arises from its valence-delocalized [Fe^IIIFe^IV(μ-O)₂] core. We note that addition of 1 M water to an MeCN solution of [Fe^IIIFe^IV(μ-O)₂(5-Me₃-TPA)₂]³⁺ did not affect its characteristic intense visible chromophore nor did its signature EPR signals change. We have also reported in a previous study that the characteristic vibration of the [Fe₂(μ-O)₂] diamond core at ∼666 cm^-1 was unchanged by the addition of water (21). Taken together, these spectroscopic results indicate that the [Fe₂(μ-O)₂] diamond core remains essentially intact in MeCN solution even in the presence of 1 M water.

Interestingly, the reactivity of [Fe^IIIFe^IV(μ-O)₂(5-Me₃-TPA)₂]³⁺ is quite low in anhydrous acetonitrile, as only oxidation of the weak C-H bond of dihydroanthracene (DHA, BDE = 78 kcal.mol^-1) (42) is fast enough to be distinguished from the self-decay of the diiron complex. However the addition of water significantly activates [Fe^IIIFe^IV(μ-O)₂(5-Me₃-TPA)₂]³⁺ for C-H bond oxidations. As shown in Figure 3, the rate for DHA oxidation increases linearly as a function of water concentration, changing almost 200-fold from zero to 1 M added water. This unprecedented observation of water-dependent oxidation of a C-H bond by a high-valent [Fe₂(μ-O)₂] diamond core has stimulated us to explore the water activation mechanism. An attractive hypothesis is shown in Scheme 1, where water acts as a Lewis base to open up the diamond core and generate an oxidant with a terminal oxo group. This idea was suggested by a comparison of different oxoiron(IV) units where we found that the H-atom abstraction reactivities of complexes with the same supporting ligand increase in the order [Fe^IIIFe^IV(μ-O)₂]³⁺ < [Fe^IV₂(μ-O)₂]⁴⁺ ≪ [Fe^IV=O]²⁺ (43). This observed reactivity progression lends credence to the mechanism shown in Scheme 1, and DFT calculations were carried out to assess the reactivity of the hypothetical Fe^III-O-Fe^IV=O unit relative to that of the [Fe₂(μ-O)₂]³⁺ diamond core.

Figure 3.

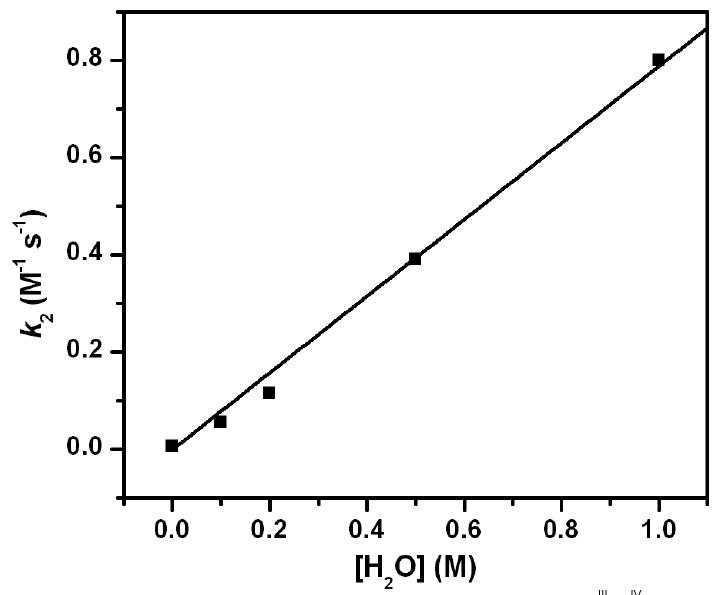
Second order rate constants for the oxidation of DHA by [Fe^IIIFe^IV(μ-O)₂(5-Me₃-TPA)₂]³⁺ in MeCN under Ar at -30 °C as a function of added water. The second order rate constants k₂ in the presence of 0, 0.01, 0.2, 0.5 and 1 M added water are 0.0050, 0.056, 0.12, 0.39 and 0.80 M^-1.s^-1, respectively.

B. Computational Results

Spin states

Open-shell transition metal dimers can possess a number of different spin states and it is necessary to know the energetic splittings of these states along the reaction coordinate. In the present investigation the systems initially consist of one iron(III)- and one iron(IV)-ion, bridged by one (2) or two (1) oxo groups. Iron(III) can in principle have a spin of 5/2, 3/2 or 1/2. Similarly, iron(IV) can have a spin of 2, 1 or 0. Considering the possibility of both FM and AFM coupling results in 15 different spin states that could be accessible. An analysis was done in order to understand which spin states could be important during the reaction to be modeled. A state that lies high in the reaction intermediate is quite unlikely to be involved in the reaction and to affect the kinetics.

Since all states having zero spin on iron(IV) were found to be high in energy (16 kcal/mol higher than the ground state or even impossible to obtain as solutions of the SCF procedure), these will not be considered in the following discussion. In order to make the text more readable, the spin states will from now on be denoted by a generalization of the rule that 5α4β denotes the reactant spin state having five unpaired electrons on iron(III), AFM-coupled to four unpaired electrons on iron(IV).

The reactant

For the bis-μ-oxo complex 1, the spin ground state predicted by B3LYP is 5α4β (Table 1). Two close lying states are 1α4β (+ 0.6 kcal/mol) and 1α4α (+ 0.7 kcal/mol) formed by AFM and FM coupling between low-spin iron(III) and high-spin iron(IV). However, experimentally it has been found that the reactant of 1 is best described as a ferromagnetically coupled mixed-valence low-spin iron(III) – low-spin iron(IV) pair with an S = 3/2 ground state (22). This experimentally suggested quartet, i.e. 1α2α, lies 9.5 kcal/mol above the calculated ground state.

Table 1.

B3LYP free energies (including dielectric effects) in kcal/mol for the splitting of the spin states in the reactant [Fe₂(μ-O)₂(TPA)₂(ClO₄)]²⁺(complex 1) and [Fe₂(μ-O)(O)(H₂O)(TPA)₂(ClO4)]²⁺ (complex 2) as well as for the intermediate resulting after hydrogen abstraction. (a) The energy of the intermediates is set in relation to the reactant ground state.

Reactant			ΔE		Intermediate			ΔEa
Fe1(III)	Fe2(IV)	S	Complex 1	Complex 2	Fe1(III)	Fe2(III)	S	Complex 1	Complex 2
1α	2α 2β	3/2 1/2	9,5 6,4	11,5 12,7	1α	1α 1β	1 0	12,6 10,6	18 18,5
	4α 4β	5/2 3/2	0,7 0,6	8,6 9,3		3α 3β	2 1	14,6 13,0	20,4 23,8
3α	2α 2β	5/2 1/2	11,9 8,2	14.7 -		5α 5β	3 2	7,0 10,4	6,4 7,4
	4α 4β	7/2 1/2	10,7 -	8,8 9,5	3α	3α 3β	3 0	21,5 -	29.5 -
5α	2α 2β	7/2 3/2	1,2 2,0	1,2 4,5		5α 5β	4 1	12,4 12,4	13,3 12,4
	4α 4β	9/2 1/2	2,0 0,0	0,9 0	5α	5α 5β	5 0	3,7 2,3	-1,2 -2,6

Obtaining the correct ground state for this type of complex is a difficult task for quantum chemical methods. To investigate the situation in more detail, calculations were also performed with other functionals. In a previous work on spectroscopic properties of 1 using a non-hybrid functional it was possible to obtain the correct ground state, S = 3/2, resulting from valence delocalization (a symmetric complex with two Fe^+3.5 centers, formally 1α2α) (44). In the present study the amount of Hartree-Fock exchange in the functional was therefore varied. Five different fractions of Hartree-Fock exchange in the B3LYP functional were tried: 20% as in B3LYP, 15% as in B3LYP*, 10%, 5%, and 0% as in non-hybrid functionals. For further comparison the non-hybrid functional BLYP was included in this series and the results are shown in Table 2. The energetic difference between the reactant in its experimental ground state and the ground state predicted by DFT is given for the different functionals. It can be seen that 1α2α becomes the ground state when the amount of Hartree-Fock exchange is decreased. Also the corresponding Mulliken spin on the two low-spin iron centers becomes more equal, thus moving towards a valence delocalized state. However, the barriers for hydrogen abstraction become unrealistically high with decreasing Hartree-Fock exchange. This means that even if B3LYP and B3LYP* predict the wrong ground state for 1 and cannot reproduce the observed valence delocalization, they still provide the most reasonable reaction energetics. B3LYP has proved its suitability for the calculation of reaction energetics many times. The results in the table also indicate that a spin crossing from 1α2α to 5α4β will occur prior to the HAT. This behavior is well known for transition metal complexes and is sometimes referred to as two-state-reactivity (45).

Table 2.

Free energies in kcal/mol (including dielectric effects) for the splitting between the experimental ground state of the reactant S=3/2 (1α2α) and the calculated ground state S=1/2 (5α4β). (a) The amount of Hartree-Fock exchange in B3LYP is 20%, for B3LYP* it is 15%, and for the other functionals presented here it was set to 10%, 5% and 0%, respectively. BLYP is not a hybrid functional and contains no Hartree-Fock exchange.

	State			Mulliken Spin		ΔE	HAT versus
Functional(a)	Fe1(III)	Fe2(IV)	S	Fe1	Fe2	Reactants	ground state	own spin state
B3LYP	1α 5α	2α 4β	3/2 1/2	0,84 4,10	1,56 -3,38	9,5 0,0	47,1 22,0	37,6 22,0
B3LYP*	1α 5α	2α 4β	3/2 1/2	0,94 3,98	1,30 -3,15	2,7 0,0	44,9 24,7	42,2 24,7
B3LYPX10	1α 5α	2α 4β	3/2 1/2	0,90 3,94	1,39 -3,04	0,0 4,6	44,5 31,2	44,5 26,6
B3LYPX5	1α 5α	2α 4β	3/2 1/2	0,94 3,87	1,33 -2,93	0,0 10,8	46,6 39,0	46,6 28,2
B3LYPX0	1α 5α	2α 4β	3/2 1/2	1,08 3,73	1,16 -2,76	0,0 22,6	47,5 52,6	47,5 30,0
BLYP	1α 5α	2α 4β	3/2 1/2	0,97 3,84	1,22 -2,90	0,0 18,9	39,3 35,7	39,3 16,8

It is interesting to note that among ten synthetic and biological Fe(III)Fe(IV) complexes characterized thus far, complex 1 is the only one found possessing a low-spin configuration on Fe(III) (high-spin in all other cases) (46). The low-spin iron(III) state in 1 may be enforced by double exchange coupling that leads to the observed valence delocalization (21)

The transformation of 1 to 2 during water binding can give two isomers. The terminal oxo group generated from one of the bridging oxygens can either be trans to an amine nitrogen of the TPA ligand, or trans to a pyridine nitrogen of the same (Figure 4). The calculated free energy difference between these two isomers is small, 3.2 kcal/mol in favour of the isomer with the oxo group trans to the amine nitrogen, which is the isomer chosen for this investigation. The choice is based not only on this small energetic difference in the reactant, but also on the fact that the corresponding isomer for the reaction intermediate (after hydrogen abstraction from the substrate) has been observed in an x-ray structure (21). Another question that arises for complex 2 is the relative proton affinities of the oxo group on iron(IV) and the hydroxo group on iron(III). The calculated proton affinity is 3.4 kcal/mol larger for the hydroxo group on iron(III), a free energy difference that corresponds to a difference of more than 2 pKa units. This means that the most stable protonation state of 2 is that in which iron(IV) has a terminal oxo group and iron(III) has a coordinated water molecule. Since this energy difference is rather small it can be worth to mention that when the first hydrogen atom is transferred from the substrate to the protonated iron(IV)=OH⁺ group the proton moves back to the OH group on iron(III) before the transition state is reached. This further justifies the choice of protonation state in 2 since starting from the alternative protonation state does not affect the activation energy.

Figure 4.

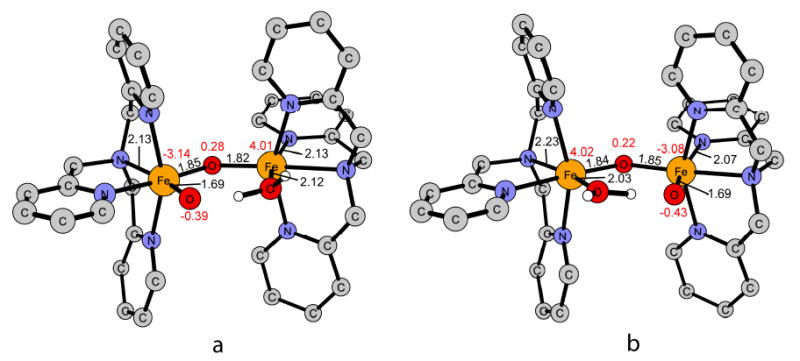
The two possible isomers after ring opening of the diamond core by coordination of a water molecule to Fe(III) (S = 1/2). The ClO₄^- counter-ion and the hydrogen atoms of the TPA ligand are omitted for clarity. a) the terminal oxo group is coordinated trans to the amine nitrogen of the TPA ligand. b) the terminal oxo group is coordinated trans to a pyridine nitrogen of the TPA ligand.

The calculated spin ground state of the reactant 2 is the same as for 1, 5α4β, almost degenerate with the corresponding AFM coupled state 5α4α (0.9 kcal/mol higher). The states 5α2α and 5α2β are very close to the ground state (1.2 and 4.5 kcal/mol higher). Spin states having one unpaired electron on iron(III) and either two or four unpaired electrons on iron(IV), are 8.6 to 12.7 kcal/mol higher than the ground state, and all states having three unpaired electrons on iron(III) lie more than 8.8 kcal/mol above the ground state.

The reaction intermediate

For 1, the reaction intermediate has a B3LYP ground state with five unpaired electrons on each iron(III), AFM coupled to give a singlet (5α5β, Table 1). The formation of this intermediate is slightly endergonic, it lies 2.3 kcal/mol above the reactant. The corresponding FM coupled state (5α5α) is separated by 1.4 kcal/mol. At about 5-8 kcal/mol higher lie the 1α5α and 1α5β states. The remaining states are even higher in energy, so it is probably quite safe to assume that these states are not involved in the reaction mechanism. Support for the calculated 5α5β ground state of the reaction intermediate comes from a series of diiron(III) complexes with the same bridging groups (oxo and hydroxo) that experimentally were found to have an AFM coupled high-spin diiron(III) spin state (47).

The reaction intermediate for hydroxylation of cyclohexane by 2 has at the B3LYP level also a 5α5β ground state (S = 0, Table 1). The corresponding ferromagnetic state 5α5α (S = 5) lies only 1.4 kcal/mol higher. For this intermediate B3LYP predicts the same spin ground state as that found by Mössbauer spectroscopy for the H₂O-Fe^III-O-Fe^III-OH complex that serves as the precursor for 1 (21). From the calculated spin splitting, it seems quite safe to assume that only those states which have five unpaired electrons on at least one of the irons and either five or one on the other can be involved in the reaction, since all other spin states of the intermediate are 12.4 to 29.5 kcal/mol higher in energy than the reactant ground state.

Hydroxylation of cyclohexane by 1: [(Fe^IIIFe^IV(μ-O)₂(TPA)₂(ClO₄)]²⁺

Hydroxylation is initiated by hydrogen atom transfer from cyclohexane to one of the bridging oxo groups with iron(IV) being reduced to iron(III). It was found that the activation free energy is unreasonably high (33 kcal/mol or more) for all states except S = 9/2 (5α4α) and S = 1/2 (5α4β). The lowest free energy barrier of 22.0 kcal/mol was found for S = 1/2 with an AFM spin pairing of 5α4β (the optimized TS is shown in Figure 6). The free energy barrier on the FM coupled 5α4α surface is only 2.7 kcal/mol higher (Figure 5). The reaction energy for HAT of 5α4β is very small (2.3 kcal/mol), so this step could be regarded as thermoneutral.

Figure 6.

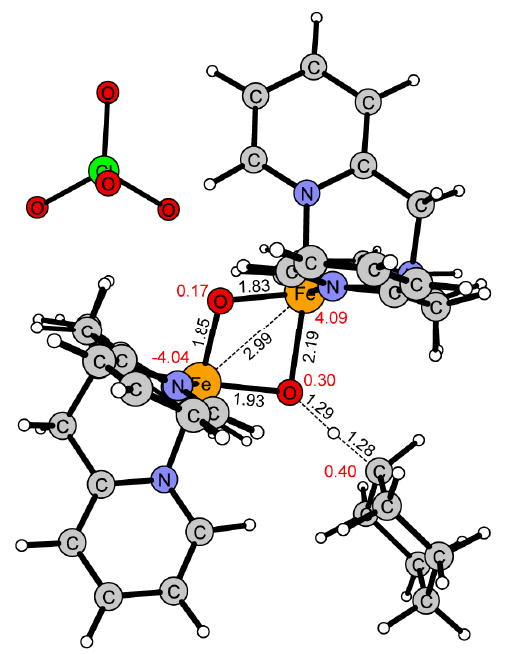
Transition state of the hydrogen atom transfer (HAT) of 1 in the S = 1/2 spin state.

Figure 5.

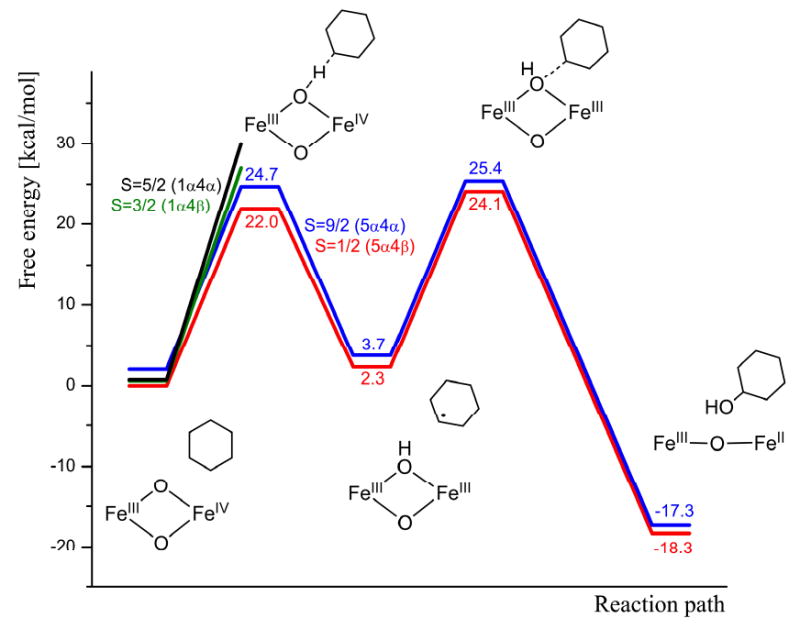
Gibbs free energy profile (B3LYP level) for the hydroxylation of cyclohexane by 1 at -30°C.

In the hydroxyl group transfer (OHT), the cyclohexane radical formed by HAT is transformed into cyclohexanol. When the OH group is removed, one of the iron(III) ions is reduced to iron(II). The free energy of activation at the B3LYP level is 21.8 kcal/mol, i.e. very similar in magnitude to the initial HAT. The optimized transition state for OHT is shown in Figure 7. As for the HAT step, it was found that the only spin states for which the reaction has a reasonable free energy of activation are those that have both irons in their high-spin states (e.g. 5α5α and 5α5β). In contrast to the HAT, which is slightly endergonic, the OHT is found to be very exergonic, the reaction free energy being -23.6 kcal/mol at the B3LYP level.

Figure 7.

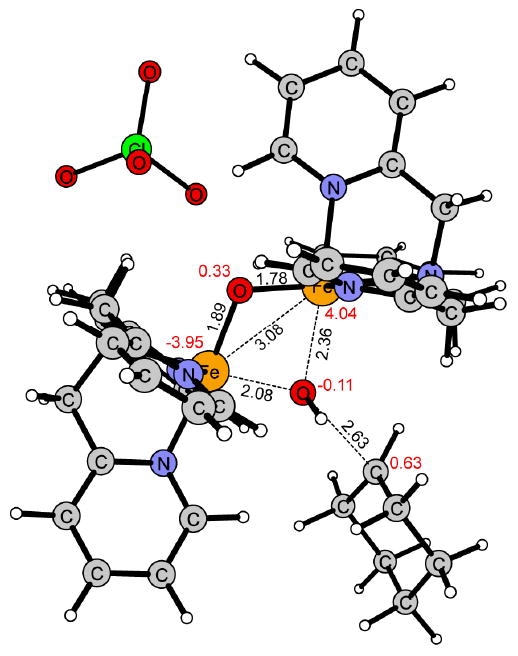
Transition state for hydroxyl group transfer (OHT) of 1 in the S = 1/2 spin state.

It can thus be concluded that during the entire hydroxylation reaction, 1 stays on the potential energy surface corresponding to S = 1/2 5α4β (B3LYP level), i.e. the AFM coupling of the two iron ions in their high-spin states. For both steps (HAT and OHT) the free energy barrier at the B3LYP level is about 22 kcal/mol, corresponding to a turn-over frequency (TOF) of about 10^-4 s^-1 for each step.

Hydroxylation of cyclohexane by 2: [Fe₂(μ-O)(O)(H2O)(TPA)₂(ClO₄)]²⁺

When a water molecule coordinates to iron(III) in 1, one of the two bridging μ-oxo groups is released from iron(III) and becomes a terminal oxo group on iron(IV). As a consequence, the iron cluster is opened up and the iron-iron distance increases from 2.84 Å in 1 (Figure 1) to 3.48 Å in 2 (Figure 2). Despite these significant structural changes, the spin ground state remains the same in 2 as in 1, i.e. S = 1/2 (5α4β). The HAT from cyclohexane to 2 requires an activation free energy of 15.0 kcal/mol at the B3LYP level and the HAT step is slightly exergonic (ΔG = -2.6 kcal/mol, Figure 8). The optimized transition state for HAT is shown in Figure 9. As in 1, the reaction surface of the corresponding FM coupled spin state S = 9/2 (5α4α), lies very close to the reaction surface of the ground state. The activation free energy is 18.5 kcal/mol in the reactant state S = 9/2 (5a4a), while in the S = 3/2 and S = 7/2 states the free energy of activation is above 30 kcal/mol.

Figure 8.

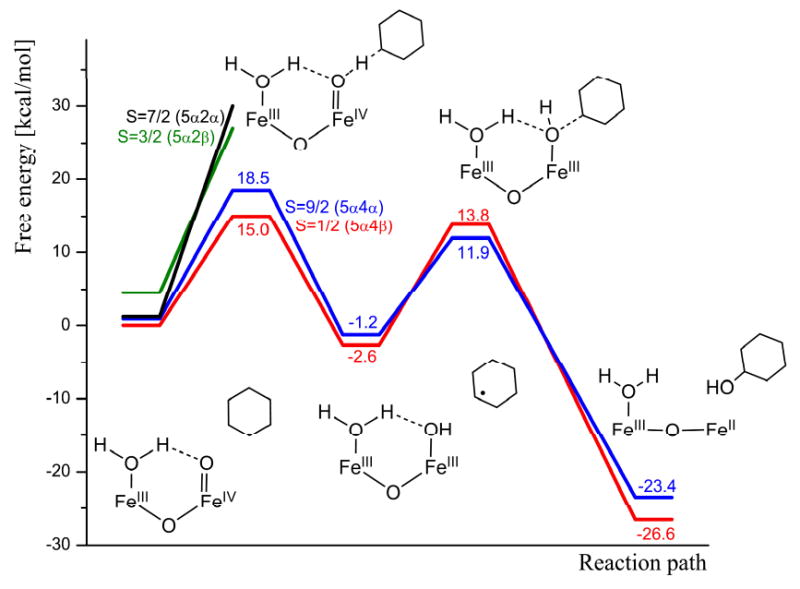
Gibbs free energy profile (B3LYP level) for the hydroxylation of cyclohexane by 2 at -30°C.

Figure 9.

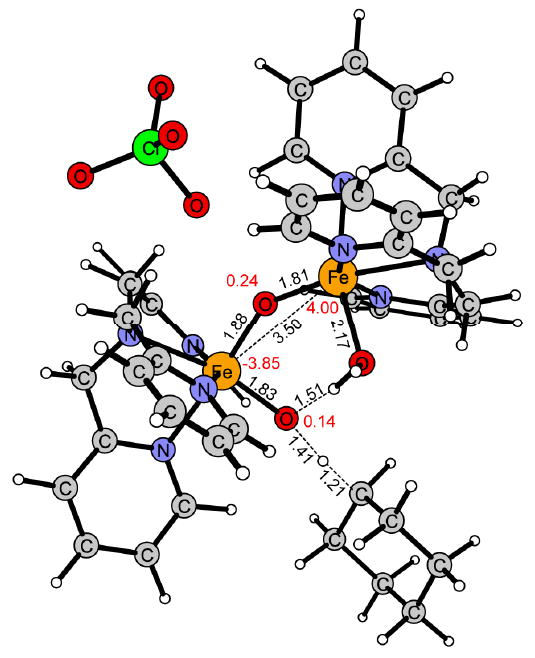
HAT transition state for 2 in the spin state S = 1/2.

For the OHT step, the reaction surfaces of the 5α5α and 5α5β states are so close that B3LYP predicts a spin crossing to occur before the transition state of OHT. However, the transition states are close in energy and at the end of the reaction the product comes back to the initial state again. On the lowest free energy surface (5α4α), the free energy of activation is 16.4 kcal/mol, and the reaction step is exergonic by about 22 kcal/mol. The optimized transition state for OHT is shown in Figure 10.

Figure 10.

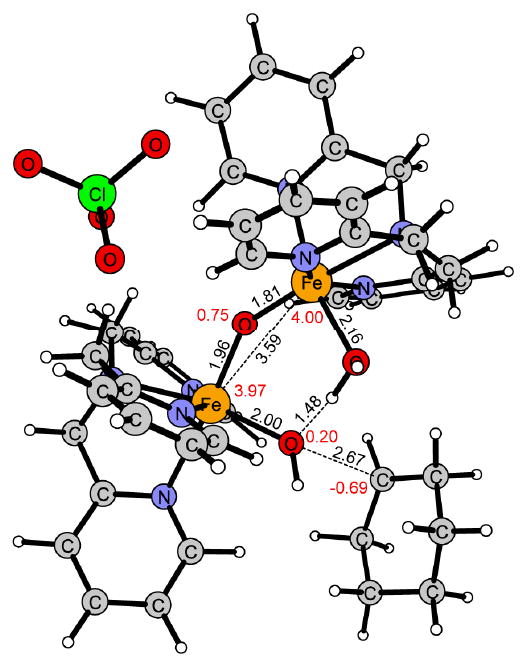
Transition state of the hydroxyl group transfer (OHT) for 2 in the spin state S = 9/2.

It can thus be concluded that during the HAT step, 2 stays on the free energy surface corresponding to the reactant ground state, while in the OHT the corresponding FM coupled state may also be involved in the reaction. For both steps, HAT and OHT, the free energy barrier is about 15 kcal/mol at the B3LYP level, corresponding to a turn over frequency (TOF) of about 2 s^-1 for each reaction step.

Comparison of the two models (1 and 2) and with experimental results

The computational results obtained for the hydroxylation of cyclohexane to cyclohexanol by 1 and 2 show that the (H₂O)Fe^III-(μ-O)-Fe^IV=O center of 2 is much more reactive than the Fe^III-(μ-O)₂-Fe^IV center of 1. For the hydrogen atom transfer (HAT), the free energy of activation is about 7 kcal/mol lower for 2 than for 1. This difference in reactivity is explained by the unpaired spin density on the reactive terminal oxo-group in 2 (S = -0.39, Figure 2), which is higher than that on the reacting μ-oxo group in 1 (S = -0.03, Figure 1). The difference in reactivity is also reflected by the thermodynamic driving force for HAT, which is larger for 2 than for 1, ΔG_HAT at 243 K being 2.6 kcal/mol exergonic in 2, while 2.3 kcal/mol endergonic in 1 (Figure 5 and 8).

Also for the hydroxyl group transfer (OHT) 2 is more reactive than 1, the free energy of activation being 6 kcal/mol lower for 2 than for 1 (Figure 5 and 8). For this step the difference in reactivity can be understood by the requirement that two Fe-OH bonds (2.14 and 2.04 Å) need to be broken in 1 (Figure 11), while only one (1.95Å) is broken in 2 (Figure 12). This is also correlated with the reaction energy since the reaction with 1 (ΔG = 18.3 kcal/mol) is 8.3 kcal/mol less exergonic than with 2 (ΔG = 26.6 kcal/mol).

Figure 11.

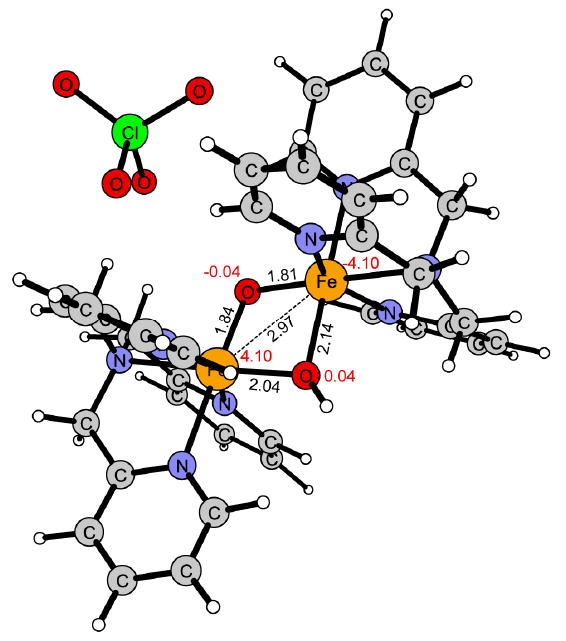
Reaction intermediate of 1 with the two high-spin iron centers antiferromagnetically coupled (5α5β).

Figure 12.

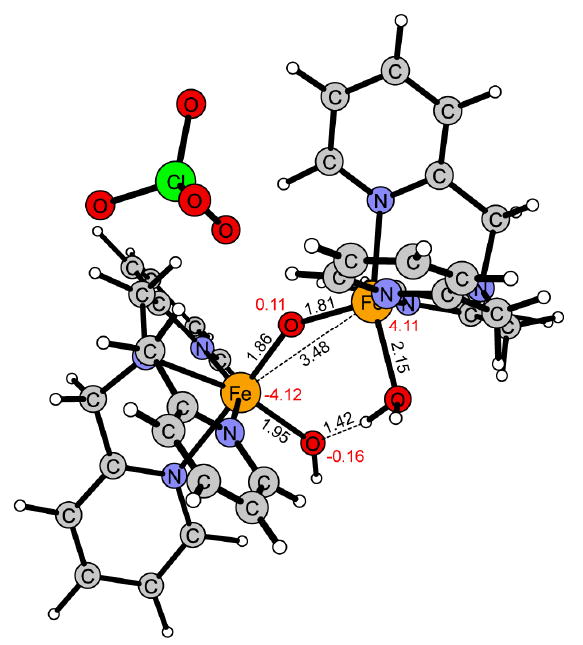
Reaction intermediate of 2 in the high-spin antiferromagnetically coupled ground state (5α5β).

The experimentally found increase of the turn-over frequency (TOF) for HAT from DHA by a factor of 200 corresponds to a difference in the activation barrier of about 3 kcal/mol. This should be compared to the 7.0 kcal/mol predicted by the computational approach. A possible explanation for the larger enhancement obtained computationally relative to that observed experimentally could be that the experimental rate obtained in ‘dry’ acetonitrile may not be low enough due to a trace amount of water present in the ‘dry’ acetonitrile solvent. In addition, there are also methodological limitations/uncertainties as pointed out above. However, the qualitative agreement between calculations and the experimentally observed water effect supports the suggested explanation for the enhanced reactivity.

IV. Conclusions

Experimentally, we have observed that increasing the concentration of water in acetonitrile from 0 to 1 M, enhanced the oxidative reactivity of the complex [Fe^IIIFe^IV(μ-O)₂(5-Me₃-TPA)₂](ClO₄)₃ towards dihydroanthracene by a factor of 200 (Figure 1). To rationalize this interesting trend, we postulate that the introduction of water favors the conversion of the Fe^IIIFe^IV(μ-O)₂ diamond core to a ring-opened form where a water molecule coordinates to iron(III), resulting in the conversion of one of the bridging oxo groups into a terminal oxo group on iron(IV). This explanation is qualitatively supported by the present computational investigation. For both reaction steps (HAT and OHT) the computed free energy of activation is lower for [(H₂O)Fe^III(L)(μ-O)Fe^IV=O(L)], the water activated complex, than for its [Fe^III(μ-O)₂Fe^IV] precursor. For the HAT, the difference in reactivity is explained by the fact that the terminal oxo group in [(H₂O)Fe^III(L)(μ-O)Fe^IV=O(L)] has a higher unpaired spin density than the bridging oxo groups of [(L)Fe^III(μ-O)₂Fe^IV(L)]. For the OHT, two Fe-OH bonds must be broken in the Fe^III(μ-O)(μ-OH)Fe^III intermediate to form the alcohol product, while only one Fe-O bond is broken in the (H₂O)Fe^III(μ-O)Fe^III-OH intermediate.

The computational results predict the rate limiting step for the hydroxylation of cyclohexane to be 7 kcal/mol lower when the oxidant has a terminal oxo group, but the observed rate enhancement corresponds to a free energy difference of only about 3 kcal/mol, so the computational approach appears to overestimate somewhat the difference in reactivity. There could be a few reasons for this discrepancy. The first and most obvious reason could be that the binding of water is endergonic, which would decrease the computed effect of adding a water. This is supported by the experimental finding that the intense green chromophore still exists in the presence of water, and disappears only during substrate oxidation. This could possibly be modeled by calculations, but it is a non-trivial task and was therefore not done in the present study. A second reason might be that the B3LYP-functional artificially overestimates the effect. However, reducing the amount of exact exchange from 20% to 15% gives a similar result. The barriers for the hydrogen abstraction and hydroxylation go up in energy for both model complexes 1 and 2, but the difference between them stays the same. So far there are no known cases where the functional fails when there is no effect of reducing the amount of exact exchange. A third reason for the overestimation of the experimentally observed effect might be the chemical model itself. The modeling of a highly positively charged complex in the presence of counter-ions is a difficult problem as already indicated above. Lastly, there could be a problem with the experimental measurements, since there could be trace water already present in the solvent before water addition that would enhance the rate for the zero-water measurement and thus decrease the measured rate enhancement.

Figure 13.

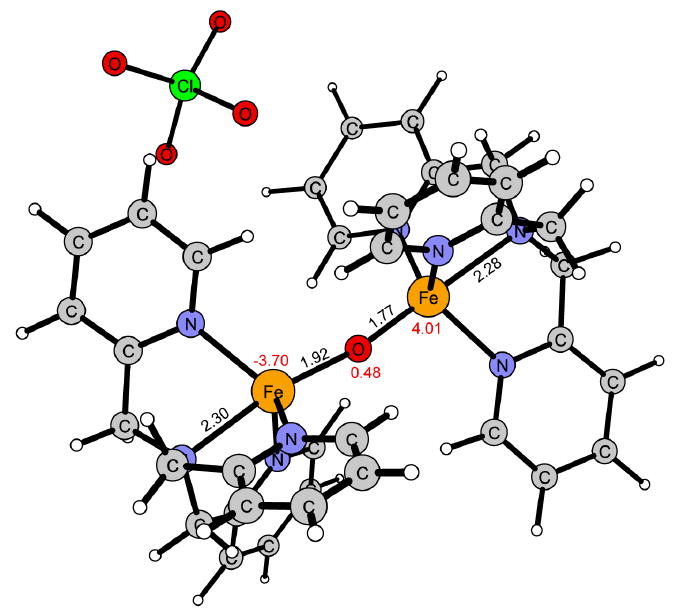
Reaction product of 1 in the ground state 5α4β.

Figure 14.

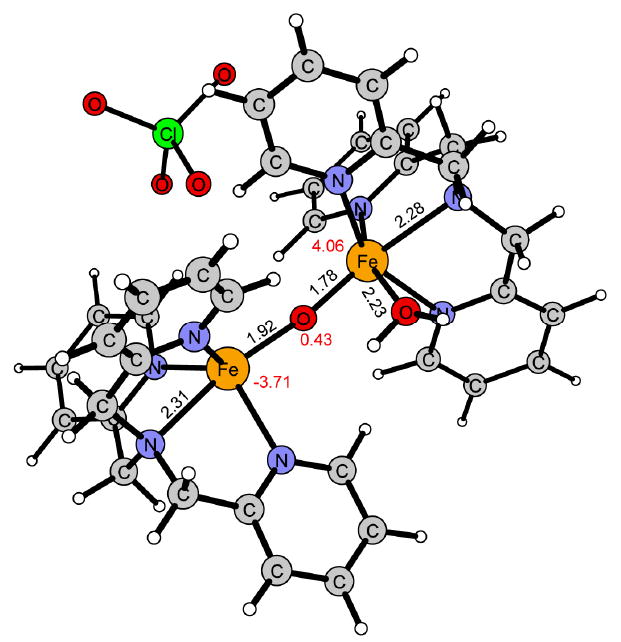
Reaction product of 2 in the ground state 5α4β.