Prediction equations for human thoracic and lumbar vertebral morphometry

Abstract

Statistical correlations between anatomical dimensions of human vertebral structures have indicated a potential for the prediction of vertebral morphometry, which could be applied to the creation of simplified geometrical models of the spine excluding the need for preliminary processing of medical images. The aim of this study was to perform linear and nonlinear regressions with published anatomical data to generate prediction equations for 20 vertebral parameters of the human thoracic and lumbar spine as a function of only one given parameter that was measured by X-ray. Each parameter was considered individually as a potential predictor variable in terms of its correlation with all of the other parameters, together with the readiness with which lateral X-rays could be obtained. Based on this, the parameter vertebral body height posterior was chosen and the statistical analyses described here are related to this parameter. Our linear, exponential and logarithmic regressions provided significant predictions of anterior vertebral structures. However, third-order polynomial prediction equations allowed an improvement on these predictions (P-values < 0.001), e.g. endplates and spinal canal (R², 0.970–0.995) as well as pedicle heights and the spinous process (R², 0.811–0.882), in addition to a reasonable prediction of the posterior vertebral structures, which have shown a low or no correlation in previous studies, e.g. pedicle inclination and transverse process (R², 0.514–0.693) (anova). Comparisons of the theoretical predictions with two other sets of experimental data indicated that the predictions generally agree well with the experimental data. A time-efficient approach for obtaining anatomical data for the description of human thoracic and lumbar geometry was provided by this method, which requires the measurement of only one parameter per vertebra (vertebral body height posterior) from a lateral X-ray and the set of developed prediction equations. Vertebral models based on this type of parameterized geometry could be used in biomechanical studies that require geometry variation, such as in spinal deformations, including scoliosis.

Introduction

During recent decades, finite element analyses have been performed to provide a better understanding of the biomechanics of the human spine. Several finite element models have been developed and are summarized in Gilbertson et al. (1995) and Fagan et al. (2002). As geometrical factors exert a noticeable influence on the behavior of the spine (Robin et al. 1994), reliable simulations of human spine behavior require complex 3D modeling of the main anatomical structures, e.g. vertebrae, intervertebral discs and ligaments.

Human vertebral geometry has typically been obtained, in vivo, through the 3D reconstruction of medical images, such as computed tomography or magnetic resonance imaging. This technique provides accurate vertebral assessment but requires a long processing time and considerable computational power is required for the manual or semi-automatic segmentation of the images. Moreover, the patient has to be submitted to relatively high doses of ionizing radiation. Alternative procedures have included stereo-radiographic approaches using X-rays (Aubin et al. 1997; Dumas et al. 2004). However, these require a long and tedious process of identification of numerous anatomical landmarks. Some semi-automatic methods have shown fast vertebral reconstruction (Pomero et al. 2004) but they require specific software and hardware.

In-vitro measurements with cadaveric vertebrae have been taken directly from bony specimens or have been obtained from medical images (Krag et al. 1988). These studies have focused on only one specific anatomic structure, such as the dimensions of the vertebral body (Hall et al. 1998), spinal canal, pedicles (Zindrick et al. 1987; Marchesi et al. 1988; Moran et al. 1989) and facet joints (Masharawi et al. 2004); a limited set of structures (Berry et al. 1987); or a limited set of vertebrae such as thoracic (Cotterill et al. 1986; Scoles et al. 1988; Aharinejad et al. 1990) or lumbar vertebrae (Semaan et al. 2001). The most complete collection of quantitative 3D-surface anatomy of the main vertebral parameters for the thoracic and lumbar human spine has been provided in Panjabi et al. (1991, 1992). As this dataset has been used in the current study, a detailed description of the measured parameters is provided in the Materials and methods.

Investigations of correlations between anatomical dimensions of the human vertebral structures have indicated that vertebral relationships could be used to predict vertebral morphometry without the preliminary processing of medical images. Statistical analyses that were performed using simple linear regression analyses between the main vertebral parameters and the vertebral body height (e.g. Scoles et al. 1988; Breglia, 2006) have found low or no correlations for some important parameters, such as pedicle dimensions. Scoles et al. (1988) described the posterior structures as being highly variable and largely unpredictable.

X-rays are frequently used in clinical diagnosis for patients as well as in biomechanical experiments with human vertebral samples. Some studies have used multiple-linear regression analyses (e.g. Lavaste et al. 1992; Laporte et al. 2000) to provide methods for the reconstruction of the human vertebrae from two X-rays (anterior–posterior and lateral). However, to explain 100% of the variability for each parameter, the measurement of six to 15 initial parameters per vertebra on X-rays was needed. Moreover, none of these previous studies have performed an evaluation of the predictability of the generated equations with another set of experimental measurements.

The aim of this study was to perform linear and nonlinear regression analyses with published anatomical data to generate prediction equations for 20 vertebral parameters of the human thoracic and lumbar spine as a function of only one given parameter measured by X-ray.

Materials and methods

Study population

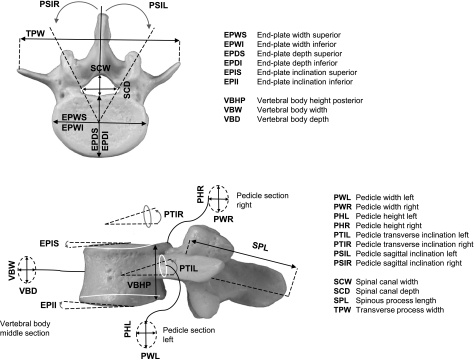
Vertebral anatomical data were collected from the studies of Panjabi et al. (1991, 1992) and included in this study. This dataset was considered as being an approximate average for nonpathological human spines. It provided linear and angular dimensions of the main parameters from human cadaveric thoracic and lumbar vertebrae. The mean age of the subjects (n = 12) was 46.3 years (range: 19–59 years), weight was 67.8 kg (range: 54–85 kg), height was 167.8 cm (range: 157–178 cm) and the male : female ratio was 8 : 4. In order to carry out statistical analyses, 15 linear and six angular vertebral parameters were selected from this dataset to describe the size and shape of the human thoracic (T1–12) and lumbar (L1–4) vertebrae (Fig. 1). The values of the vertebral parameters related to the vertebral level L5 were not included in the analysis.

Fig. 1.

Schematic representation of the vertebral anatomical parameters that were considered for linear and nonlinear regression analyses.

Statistical analysis

The initial assumption for this study was that 20 vertebral parameters on each level of the thoracic (T1–12) and lumbar (L1–4) spine could be considered as a variable that can be predicted (Fig. 1). All vertebral parameters that were selected for this study were tested as a possible predictor variable. Each vertebral parameter was individually regressed against the possible predictor variable by a least-squares estimation process. Based on the level of correlation with the other parameters and ease of measurement on lateral X-rays, the parameter vertebral body height posterior (VBHP) was chosen and the statistical analyses described in this study are related to this parameter. Linear and nonlinear regression analyses were employed to find the best functions to fit each parameter in a prediction equation.

During the statistical analyses, several hypotheses were tested for each parameter: (i) a function could not fit the data significantly better than a horizontal line (no relationship between the two selected variables); (ii) a second-order equation could not fit the data significantly better than a linear equation; (iii) a third-order equation could not fit the data significantly better than a second-order equation, and so on. The statistical procedure performed on each parameter corresponds to a four-step procedure that is illustrated as an example in Fig. 2.

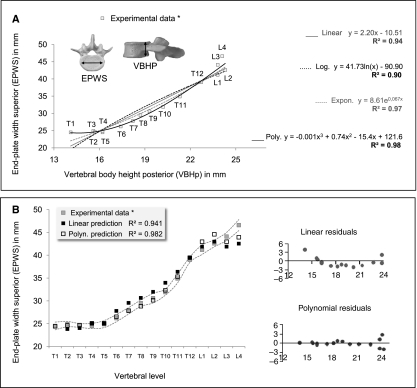
Fig. 2.

Description of the statistical procedure performed for two vertebral parameters. (A) Correlation of experimental data of the thoracic and lumbar spine (in this case, VBHP vs. EPWS) and set of prediction equations generated from linear, logarithmic, exponential and polynomial regression analyses (y is the value of EPWS and x is the value of VBHP on each vertebral level). (B) Values of EPWS predicted using linear and polynomial equations are superimposed on experimental data to allow the selection of the best equation. Dotted curve indicates SD of the experimental data. Residual plots evaluation shows that the polynomial equation is significantly better.

In the first step, least-squares estimation was used to find equations to describe the relationship between two vertebral parameters, e.g. the variables (EPWS) and VBHP; each data point represents the mean value in different vertebral levels of 12 cadavers. Initially, a linear regression was performed, fitting an equation of the form y = C₁ + C₂x to the data. The fraction of the overall variance of the EPWS that was reduced by this line was determined by the R² value. A logarithmic and an exponential curve with equations of the form y = C₁ + C₂ln(x) and y = C₁e^C2x, respectively, were then used to test the increase in R². Next, polynomial equations including more coefficients (C₁, C₂, C₃, C₄, etc.) were used to find the best fit of the data points. This was continued until adding another higher-order term did not significantly increase R² (Fig. 2A).

The second step was to perform an anova to select an equation from the generated set, which could predict the EPWS values significantly better. It was based not only on quality of fit but also on the physical meaning of the prediction equations (Motulsky & Christopoulos, 2004). High values of R² associated with a P-value < 0.01 indicated the third-order polynomial as the best-fitting equation that could provide the best approximation to the experimental values of EPWS.

In the third step it was evaluated how the selected best-fitting, in this case the polynomial equation fits the EPWS data significantly better than a linear equation. Linear and third-order polynomial predictions of the EPWS were superimposed on experimental values together with their respective SD (Fig. 2B). The quality of these regressions was assessed by examining the respective residual plots. The linear equation was inappropriate for the description of the EPWS data because residuals clustering indicated that the data differed systematically (not just randomly) from the prediction curves. Positive residuals tended to cluster together at the first thoracic and the last lumbar vertebrae, whereas negative residuals clustered together in the transition zone from the thoracic to the lumbar region. In contrast, polynomial residual plots had a random arrangement of residuals, which was more appropriate to predict EPWS (Fig 2B).

The fourth step corresponds to the evaluation of the predictability of the best-fitting equation of the set of equations developed in the third step using experimental data from two further datasets. The dataset of Berry et al. (1987) includes 12 vertebral parameters of three thoracic vertebrae (T2, T7 and T12) and four lumbar vertebrae (L1–4). The dataset of Scoles et al. (1988) includes 10 vertebral parameters of five thoracic vertebrae (T1, T3, T6, T9 and T12) and two lumbar vertebrae (L1 and L3) of male and female data.

Results

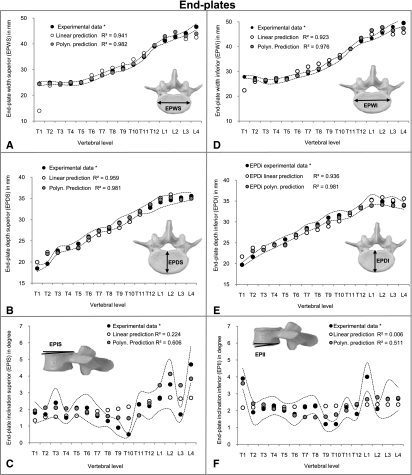
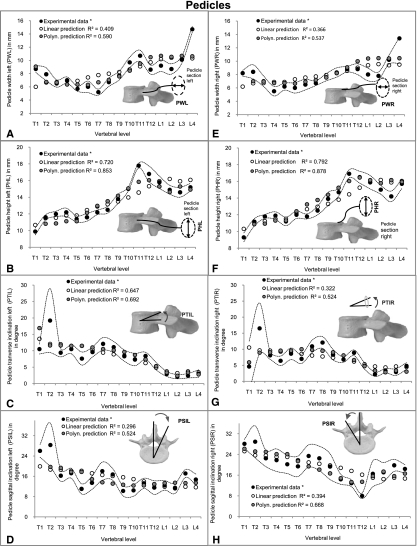
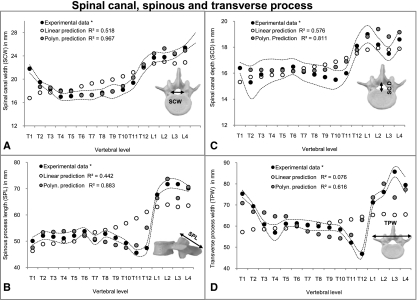
In general, there were no large differences for the correlations of each of the individual 20 vertebral parameters with VBHP when comparing linear, exponential and logarithmic regressions with each other. For this reason, only the linear predictions are provided from these results (Figs 3, 4 and 5). High correlations were found for parameters related to endplates (EPWS, EPWI, EPDS and EPDI) and vertebral bodies (VBW and VBD) (R², from 0.923 to 0.959) (Fig. 3) (please see Fig. 1 for all abbreviations). Moderate values of R² (from 0.520 to 0.793) were achieved in pedicle heights (PHL and PHR) and transverse inclination left (PTIL) (Fig. 4) as well as in the spinal canal (SCW and SCD) (Fig. 5). However, about 50% of the investigated parameters showed low or no correlation with VBHP. These were the dimensions of endplate inclinations (EPIS and EPII) (Fig. 3), pedicles (PWL, PWR, PTIR, PSIL and PSIR) (Fig. 4) and other posterior structures (SPL and TPW) (Fig. 5).

Fig. 3.

Linear and polynomial predictions of parameters related to endplates and vertebral body (EPWS, EPWI, EPDS, EPDI, EPIS and EPII) (A-F) superimposed on experimental data of Panjabi et al. (1991, 1992)*. Dotted curve indicates SD of the experimental data.

Fig. 4.

Linear and polynomial predictions of parameters related to pedicles (PWL, PWR, PHL, PHR, PTIL, PTIR, PSIL and PSIR) (A-H) superimposed on experimental data of Panjabi et al. (1991, 1992)*. Dotted curve indicates SD of the experimental data.

Fig. 5.

Linear and polynomial predictions of other vertebral posterior structures (SCW, SCD, SPL and TPW) (A-D) superimposed on experimental data of Panjabi et al. (1991, 1992)*. Dotted curve indicates SD of the experimental data.

In contrast to the above regressions, third-order polynomial regressions provided the best results with significant correlations between all selected parameters and VBHP (Table 1). As the dataset of Panjabi et al. (1991, 1992) does not include VBW and VBD, an alternative method for the prediction of these parameters was used. The inclusion of more than four coefficients increased the R² values but anovas indicated that the obtained correlations did not significantly improve parameter predictions. For instance, fourth- and fifth-order polynomial regressions between the PWL and VBHP resulted in P-values > 0.05.

Table 1.

Polynomial coefficients (C₁, C₂, C₃ and C₄) for prediction equations of 20 parameters per vertebral level of the human thoracic and lumbar spine.

Vertebral parameter		Abbreviation	C1	C2	C3	C4	SD	R2	P-value
Endplate	Width	EPWS	121.650	−15.403	0.742	−0.010	1.195	0.982	1.07E−10
		EPWI	300.140	−43.509	2.206	−0.035	1.454	0.976	5.19E−10
	Depth	EPDS	−60.076	8.983	−0.293	0.004	0.852	0.981	1.31E−10
		EPDI	−63.590	9.473	−0.300	0.003	0.769	0.981	1.26E−10
	Inclination	EPIS	−66.833	12.035	−0.691	0.013	0.699	0.606	0.008981
		EPII	66.233	−9.095	0.418	−0.006	0.606	0.514	0.030367
Vertebral body	Width	VBW*	4.1409	0.748	–	–	1.287	0.969	5.69E−05
	Depth	VBD**	−80.223	10.313	−0.350	0.004	0.523	0.995	0.000666
Pedicle	Width	PWL	230.261	−34.915	1.777	−0.029	1.682	0.590	0.011194
		PWR	157.740	−23.284	1.168	−0.019	1.446	0.537	0.022469
	Height	PHL	168.200	−27.194	1.522	−0.027	0.954	0.853	2.80E−05
		PHR	105.820	−17.256	0.999	−0.018	0.872	0.879	8.65E−06
	Transverse inclination	PTIL	−10.658	2.9889	−0.099	−0.001	2.741	0.693	0.002089
		PTIR	−202.510	31.347	−1.496	0.023	2.877	0.524	0.026147
	Sagittal inclination	PSIL	305.290	−39.194	1.734	−0.025	4.064	0.524	0.026141
		PSIR	−275.130	53.937	−3.119	0.057	3.403	0.669	0.003290
Spinal canal	Width	SCW	206.750	−26.838	1.218	−0.017	0.634	0.964	6.76E−09
	Depth	SCD	−2.449	3.8232	−0.254	0.006	0.573	0.811	0.000123
Spinous process	Length	SPL	−947.110	168.10	−9.310	0.170	3.472	0.882	7.43E−06
Transverse process	Width	TPW	−343.670	80.885	−5.090	0.102	7.259	0.616	0.007667

SD in mm (for linear dimensions) or in degree (for angular dimensions).

The basic form of the prediction equations is y = C₁ + C₂x+C₃x² + C₄x³ where y is the value of the parameter to be predicted and x is the value of the VBHP on each vertebral level.

S, superior; I, inferior; L, left; R, right.

^*For VBW, x is the value of EPWS/EPWI on each vertebral level.

^**For VBD, x is the value of EPDs/EPDI on each vertebral level.

The parameters EPWS, EPWI, EPDS, EPDI, VBW and VBD that showed high correlations by linear, logarithmic and exponential regressions exhibited, after third-order polynomial regressions, an increase of R² (from 0.970 to 0.982, P-values < 0.01) (Fig. 3). Similarly, the correlations with PHL, PHR, PTIL, SCW and SCD were improved and R² values ranging from 0.693 to 0.964 were achieved (Figs 4 and 5). Furthermore, for those parameters that displayed low or no correlation with anterior procedures (EPIS, EPII, PWL, PWR, PTIR, PSIL, PSIR, SPL and TPW), polynomial regressions achieved reasonable correlations (R², from 0.514 to 0.693, P-values < 0.05) (Figs 3, 4 and 5). An exception was PTIL, for which the best results were obtained after exponential regression (R² = 0.757) (Fig. 4C).

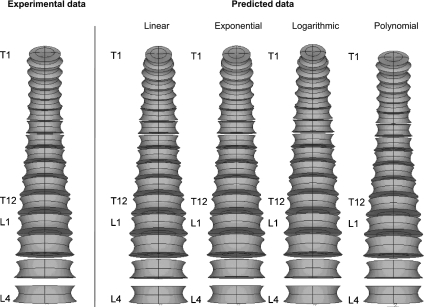
The prediction of the vertebral parameters related to anterior vertebral structures using linear, exponential, logarithmic and polynomial prediction equations did not demonstrate significant differences (Fig. 6). Moreover, polynomial prediction equations were required to predict the parameters related to posterior vertebral structures. The polynomial predictions are generally within or close to the regions of the 95% confidence intervals of the experimental data of Panjabi et al. (1991, 1992).

Fig. 6.

Geometric models of the human thoracic (T1–12) and lumbar (L1–4) vertebrae constructed with parameters related to endplates and vertebral bodies (EPWS, EPWI, EPDS, EPDI, EPIS, EPII, VBW and VBD). The first model corresponds to the data of Panjabi et al. (1991, 1992) and was created using eight parameters per vertebral level (a total of 128 parameters). The other models were generated using only the values of the VBHP of each vertebral level and predicted parameters from linear, exponential, logarithmic and polynomial equations.

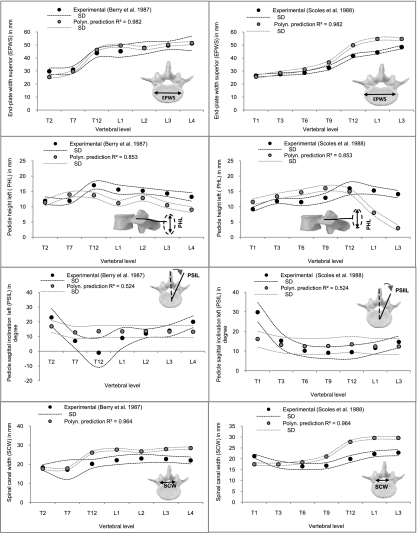
Using the dataset of Berry et al. (1987), a comparison of predicted EPWS and EPDI showed mean percent errors of −14.93 and 31.86%, respectively for T1; all other levels were very close to experimental data with mean percent errors of −0.32 to 9.68% (Fig. 7A). Predictions of PHL showed better results for thoracic levels with the smallest error being −0.05 mm (−0.8%) for PHL (T2) and a mean percent error of approximately 22.5% for thoracic and 24.6% for lumbar levels (Fig. 7B). Polynomial pedicle predictions showed a high error for PSIL (T12) (Fig. 7C). Predictions related to the SCW and SCD also displayed better results for thoracic levels with the largest error being 1.19 mm (7.93%). Lumbar levels showed an approximate mean percent error of 23% (SCW) and 31% (SCD) (Fig. 7D).

Fig. 7.

Comparison of some predicted vertebral parameters (EPWS, PHL, PSIL and SCW) with corresponding experimental data from Berry et al. (1987) (left column, A–D) and Scoles et al. (1988) (right column, E–H) in selected vertebral levels. The means and 95% confidence intervals (dotted lines) of the experimental and predicted values are shown.

With the dataset of Scoles et al. (1988), predictions of EPWS and VBD showed a range of mean percent errors of −2.68 to 23.48%, with the largest errors occurring in EPWS (L1) (Fig. 7E). The shortest error for PHL was −0.69 mm (−4.66%) for T12 and a mean percent error of approximately 18.5% for thoracic and 45.6% for lumbar levels was found (Fig. 7F). Polynomial pedicle predictions showed a high error for PSIL (T1) (Fig. 7G). Predictions of SCW and SCD showed similar results to the prediction with the dataset of Berry et al. (1987), with the largest error being 4.25 mm (22.1%) for thoracic levels (Fig. 7H).

Discussion

Linear and nonlinear regression analyses were performed with the anatomical data of Panjabi et al. (1991, 1992) to generate prediction equations for 20 vertebral parameters per vertebral level of the human thoracic (T1–12) and lumbar (L1–4) vertebrae as a function of the VBHP. The parameters corresponding to the vertebra L5 were not included in the analyses because L5 shows remarkable morphological differences for some parameters when compared with the other lumbar vertebrae (Berry et al. 1987; Zindrick et al. 1987; Scoles et al. 1988). This is probably due to the position of L5 being localized in the final transition zone, from lumbar to sacral region (Panjabi et al. 1989, 1992).

In this study two assumptions were necessary. First, despite the high anatomical variability of the human vertebrae, the dataset of Panjabi et al. (1991, 1992) was assumed to be representative of the adult population without spinal pathology. Second, it was assumed that the dimensions of the vertebral structures described in this dataset were obtained precisely. As the three datasets used in this study were provided from in-vitro measurements, further investigations are necessary to evaluate the predictability of the regression equations with a dataset from patients.

Third-order polynomial equations represented the best regression approximation as indicated after analysis of covariance (Table 1). SEs indicated that, with few exceptions, such as for pedicle inclinations, the best fit values for the prediction equations were accomplished with reasonable certainty. Pedicle inclinations showed a wide variation that can be observed in the wide confidence interval of the sagittal plane angle for the mid-thoracic vertebrae (Fig. 4C,D,G,H).

Our results were compared, when possible, with existing published data. All correlation coefficients generated using polynomial regressions were considerably better than the values obtained by Breglia (2006) using simple linear regressions on the data of Panjabi et al. (1991, 1992). The parameters related to posterior structures that could not be predicted with the regressions of Breglia (2006) have shown a moderate correlation after polynomial regressions. Linear regression procedures are straightforward and the results appear to be readily evaluated statistically. However, the relationships between the vertebral variables follow a curved line, not a straight line. Although the methods used for fitting a nonlinear equation such as polynomial regression are extensions of linear regression, the results are better because polynomial equations can be used to create a generic curve through the data points; more coefficients create a more flexible curve, which could better fit the data.

Comparisons of the theoretical predictions with two other sets of experimental data (Berry et al. 1987; Scoles et al. 1988) indicated that the predictions generally agree well with the experimental data. Although the differences in the predictions of pedicle inclination (Fig. 7C,G) have been relatively great, a reasonable correlation between the main posterior elements and VBHP was found. This is not in accordance with Scoles et al. (1988) who declared that it was not possible to establish useful predictors for pedicle dimensions based on the size of the vertebral body. Differences in predicted values may also be attributed to technical factors related to obtaining these anatomical data, such as different protocols of preparation and measurement. Furthermore, there are individual variations and aging that can induce substantial changes in each individual's vertebrae (Bernick & Cailliet, 1982; Diacinti et al. 1995).

Lavaste et al. (1992) developed a method to reconstruct lumbar vertebral geometry from two X-rays (anterior–posterior and lateral) using multiple-linear regression analysis. However, to predict the vertebral geometry, six given parameters per vertebra were required. A digitalization process to define these parameters showed a relative error of approximately 15%. Moreover, the orientation and width of the pedicles were not taken into consideration. Laporte et al. (2000) performed a similar study in thoracic vertebrae, which required the measurement of 15 parameters per vertebra by X-ray in order to explain 100% of the variability for each parameter.

The advantage of using the generated set of prediction equations (Table 1) is the capability to model vertebral geometry in each level of the thoracic and lumbar spine, with the exception of L5, using only one parameter per vertebrae (VBHP), which can be easily measured on conventional lateral X-rays.

Conclusion

The present study shows that nonlinear regression analyses provide a time-efficient approach for modeling of the human vertebrae, allowing a better understanding of statistical correlations between vertebral dimensions. The geometry that was reconstructed using the predicted vertebral parameters may be applied for the construction of finite element models of the spine without the need for expensive, invasive and time-consuming data collection, such as medical images. Another advantage is that this approach allows the values of the vertebral parameters to be changed, producing different vertebral morphologies. This could be used for the development of parameterized models of the spine to perform studies based on geometry variation, such as in spinal deformations, including scoliosis.

Conflict of interest statement

Each author of this study did not and will not receive benefits in any form from a commercial party related directly or indirectly to the content of this study.