Alternative splicing, gene duplication and connectivity in the genetic interaction network of the nematode worm Caenorhabditis elegans

Abstract

We examined the relationship between gene duplication, alternative splicing, and connectedness in a predicted genetic interaction network using published data from the nematode worm Caenorhabditis elegans. Similar to previous results from mammals, genes belonging to families with only one member (“singletons”) were significantly more likely to lack alternative splicing than were members of large multi-gene families. Genes belonging to multi-gene families lacking alternative splicing tended to have higher connectedness in the genetic interaction network than did genes in families that included one or more alternatively spliced members. Moreover, alternatively spliced genes were significantly more likely to interact with other alternatively spliced genes. These results support the hypothesis that certain key proteins with high degrees of network connectedness are subject to selection opposing the occurrence of alternatively spliced forms.

It has become increasingly apparent that alternative splicing is a major mechanism for enhancing protein diversity in eukaryotes (Blencowe 2006; Kim et al. 2007; Lareau et al. 2004; Stetefeld and Ruegg 2005). However, the evolution of alternative splicing remains mysterious (Ast 2004). The mechanisms by which alternative splicing arises are not well understood, and the evolutionary advantages (if any) of alternative splicing as opposed to gene duplication as a mechanism of generating protein diversity remain elusive. One key idea guiding recent studies of the evolution of alternative splicing has been that of a trade-off between alternative splicing and gene duplication. This idea has received support from the observation that, in the human genome, there is a negative correlation between the incidence of alternative splicing and gene family size (Kopelman et al. 2005; Su et al. 2006). However, it is not known whether the same sort of trade-off is seen in non-mammalian eukaryotes or even in all mammals.

Alternative splicing is expected to have a major impact on how genes and proteins interact in biological networks (Blencowe 2006), as does gene duplication (Hughes and Friedman 2005; Wagner 2001). One important generalization regarding biological networks is that they tend to be scale-free (Barabási and Albert 1999; Zhu et al. 2007). Unlike a random network, a scale-free network has the property that a small proportion of nodes have a large number of connections, while the other nodes have smaller numbers of connections. Moreover, many biological networks consist of numerous small modules of densely interconnected nodes, while connections between modules are sparser (Ravasz et al. 2002; Zhu et al. 2007).

Gene duplication will increase the scale-free property of networks if genes involved in networks are duplicated differentially, are deleted differentially after duplication and/or if interactions are retained differentially after duplication (Hughes and Friedman 2005; Wagner 2003). Consistent with this prediction, in the yeast genetic network, highly connected “hubs” are often unduplicated genes (“singletons”), while members of large multi-gene families frequently have few connections in these networks (Hughes and Friedman 2005). Furthermore, in yeast, 44% of singletons with multiple network connections were found in regions of the genome presumably duplicated by an ancient polyploidization event (Hughes and Friedman 2005). In these cases, presumably the gene was originally duplicated in the polyploidization, but one copy was subsequently deleted. These results support the hypothesis that duplication of highly connected hubs can be selectively disadvantageous and that, as a consequence, differential deletion of duplicates has played a role in shaping the scale-free property of biological networks.

Here we analyze data on alternative splicing and gene family membership in the nematode worm Caenorhabditis elegans, a species in which the overall level of alternative splicing is much lower than it is in mammals (Kim et al. 2007). First we test the hypothesis that there is a trade-off between alternative splicing and gene duplication in C. elegans as in human by examining the relationship between gene family size and the incidence of alternative splicing. Zhong and Sternberg (2006) present a predicted genetic interaction network among approximately 2000 genes of C. elegans, based on both yeast two-hybrid screens and a survey of published literature. Using this preliminary genetic interaction network, we examine the relationship between alternative splicing and network connectedness. Specifically, we test the prediction that alternatively spliced genes, like members of large gene families, will tend to have reduced network connectedness.

Methods

The complete set of protein translations (WormPep 140) for C. elegans was downloaded from the Sanger Institute website: http://www.sanger.ac.uk/Projects/C_elegans/WORMBASE/current/wormpep_download.shtml. We obtained information on numbers of exons and alternative splicing from database annotations. WormPep data on alternative splicing comes from EST/mRNA data, published papers, and personal communications. Alternative splicing information is categorized as “confirmed” if there is transcript evidence for every base in every exon; as “partially confirmed” if transcript evidence in incomplete; and as “predicted” if transcript evidence is lacking. Of 19,542 genes analyzed here (see below), the information on the presence or absence of alternative splicing was categorized as confirmed in 4,872 cases (24.9%) and as partially confirmed in 10,037 cases (51.4%). Of 1,717 genes annotated as alternatively spliced, 872 (50.8%) were confirmed; 841 (49.0%) were partially confirmed; and only 4 (0.2%) were predicted.

Protein families were assembled using the BLASTCLUST computer program (Altschul et al. 1997) by amino acid sequence homology search (E-value of 10⁻⁶) and the single-linkage method. To score a match between two proteins, we further required that 30% of amino acids be identical, and that 50% of amino acids at aligned sites be shared. We used the complete set of predicted protein translations (including all alternatively spliced forms) in assembling protein families. Then, in order to count the number of genetic loci in each family, we filtered the data so that a unique transcript was counted for each locus. We excluded from the analysis 29 loci for which data on the number of exons was not available and 178 loci at which different transcripts were assigned to membership in different families by BLASTCLUST. The data set used in analyses included 19,542 loci (genes) assigned to 11,741 families. 2,209 of these genes, belonging to 1,579 gene families, were matched with genes in the C. elegans genetic network (Zhong and Sternberg 2006). Note that in analyses of these genes, family size refers to the number of family members in the entire C. elegans genome, not just in the subset included in this network. The genetic interaction network (Zhong and Sternberg 2006) identified the genetic loci involved but did not identify the individual alternative splice variant in the case of loci with two or more splice variants.

The genetic interaction network of Zhong and Sternberg (2006) was based on both experimental data from yeast two-hybrid screens and on a survey of the literature, including data on orthologs in Drosophila melanogaster and Saccharomyces cerevisiae. Zhong and Sternberg (2006) used a logistic regression procedure to estimate the overall probability of an interaction between two C. elegans genes. Only gene pairs with an estimated probability of 0.9 or better were counted as interaction. The probability of interaction predicted by Zhong and Sternberg's (2006) algorithm was highly correlated with prediction of interactions by an independent method (called “systematic genetic interaction analysis”) using RNAi (Byrne et al. 2007).

Two measures of network interactions were used for a given vertex (gene) v: (1) the number of single-step interactions (n) between v and other vertices (also known as the “degree” of v); and (2) the clustering coefficient (CC), given by the formula CC = 2E/[n(n−1)] where E is the number of lines among nodes in a 1-neighborhood of v (Zhu et al. 2007). CC was computed by the Pajek program (Batagelj and Mrvar 2006).

Statistical analyses used the gene family, the individual gene, or the individual network interaction as unit of analysis. The variables examined here were generally not normally distributed, Therefore, we used the median as a measure of central tendency, and in hypothesis tests we used nonparametric statistical methods, which make no assumptions regarding the form of the underlying distribution (Hollander and Wolfe 1973). Variables describing network interactions were not strictly independent since genes interacted with other genes in the network. Therefore, permutation (randomization) tests were used for testing hypotheses regarding these variables. In each permutation test, we created 1,000 pseudo data sets by random sampling (with replacement) from the data under analysis.

Given N units classified into k groups by some classificatory variable X, in order to conduct simultaneous pairwise comparisons between groups with respect to the median of some continuous scalar variable Y measured on each of the N units, we created 1,000 pseudo data sets of N units each by randomly sampling (with replacement) independently from the vector of X values and from the vector of Y values. The level of significance of the difference between two group medians was obtained by comparing the observed absolute difference with the distribution of absolute differences obtained for the corresponding groups in the 1,000 pseudo data sets. Because in these permutation tests, values of the classificatory variable X were sampled at random from the data, the proportions of the units in the pseudo data sets belonging to each of the k groups are expected to approximate those in the original data. To test the hypothesis of correlation between two continuous variables (Y₁, and Y₂), the correlation coefficient (r) was compared with the distribution of r values computed for 1,000 pseudo data sets generated by randomly sampling (with replacement) independently from the vector of Y₁ values and from the vector of Y₂ values.

To test the hypothesis that network interactions occurred randomly between alternatively spliced genes, the expected value under random association was computed on the basis of the occurrence in the data set of genes with alternative splicing and of genes lacking alternative splicing. The chi-square statistic was computed by comparing observed and expected numbers of interactions between alternatively spliced genes and observed and expected numbers of other interactions. The chi-square statistic was then compared with values of the same statistic computed for 1,000 pseudo data sets.

Results of randomization tests were generally similar to those of standard nonparametric and parametric procedures (assuming independence of the units of analysis), which were applied to the same data sets in preliminary analyses. However, the randomization tests tended to be more conservative in several cases, as is expected because of the lack of independence. Statistical analyses were conducted using the Minitab statistical package, release 13 (http://www.minitab.com/).

Results

Comparison of gene families

We analyzed data on 19,542 protein-coding loci (genes) of C. elegans, of which 1,717 (8.8%) had reported evidence of alternative splicing. By protein sequence homology, we assigned these genes to11,741 families, 10,143 of which (86.4%) included only a single member (“singletons”). Of the remaining families (“multi-gene families”), a majority included 2 members (831 or 7.1% of the total) or 3 members (263 or 2.2% of the total). Only 17 families (0.09%) had more than 50 members.

Of 9,399 genes in multi-gene families, 647 (6.9%) were alternatively spliced. This proportion was lower than that (1,070 of 10,143 or 10.5%) observed in singletons, and the difference was statistically significant (χ² = 81.8; 1 d.f.; P < 0.001). In an additional analysis, we placed gene families in four size categories following Kopelman et al. (2005): singletons; families with 2–3 members; families with 4–9 members; and families with ≥10 members. The proportion of alternatively spliced members was 10.5% in singletons; 231/2,435 (9.5%) among genes belonging to 2–3 member families; 171/1,900 (9.0%) among genes belonging to 4–9 member families; and 245/5,064 (4.8%) among genes belonging to families with ≥10 members. The difference among categories was highly significant (χ² = 139.4; 3 d.f.; P < 0.001). When each of the three other family size categories was compared separately with singletons, the only significant difference was between singletons and families with ≥10 members (χ² = 139.5; 1 d.f.; P < 0.001, corrected for multiple testing by the Bonferroni procedure). Thus, as in the results of Kopelman et al. (2005) with mammals, the incidence of alternative splicing was a decreasing function of family size; but a marked reduction was seen in the largest families.

One factor that would cause a reduced incidence of alternative splicing would be a high frequency of single-exon (intronless) genes. Of the 10,143 singletons, only 187 (1.8%) were intronless, while 298 of 9,399 (3.2%) genes from multi-gene were intronless. The difference in proportions was highly significant (χ² = 35.5; 1 d.f.; P < 0.001). However, when intronless genes were excluded from the analysis, the proportion of alternatively spliced genes still was a decreasing function of family size. Excluding intronless genes, alternative splicing was found in 1,070/9,956 (10.7%) of singletons; 231/2,369 (9.8%) of genes from 2–3 member families; 171/1,854 (9.2%) of genes from 4–9 member families; and 245/4,633 (5.3%) of genes from families with ≥10 members. The difference among categories was highly significant (χ² = 133.0; 3 d.f.; P < 0.001). Excluding intronless genes, the median number of exons was significantly greater in alternatively spliced genes (21.0 exons) than in genes lacking alternative splicing (5.0 exons; P < 0.001; Mann–Whitney test). The same trend was seen when singletons and members of multi-gene families were analyzed separately (Fig. 1).

Fig. 1.

Median numbers of exons of singletons and multi-gene family members, classified as lacking (AS−) or possessing (AS+) alternative splicing. Numbers of genes in each category are indicated. In each case, medians differed significantly between the AS− and AS+ groups (Mann-Whitney test; P < 0.001)

Network connectedness

Information on genetic network interactions was available for 2,209 genes (designated the “network data set”). The genes in the network data set belonged to 1,579 families, of which 1,240 (78.5%) were singletons. For the 2,209 genes in the network data set, the raw number of network interactions and the clustering coefficient (CC) were highly correlated (r_S = 0.902; P < 0.001). We compared medians of these two measures between alternatively spliced genes (N = 381) and genes lacking alternative splicing (N = 1,828). The median number of network interactions was higher in genes without alternative splicing (7.0) than in genes with alternative splicing (5.0), but the difference was not significant at the conventional level (P < 0.057; randomization test). Median CC was also higher in genes without alternative splicing (0.0200) than in alternatively spliced genes (0.0133); and the difference was statistically significant (P < 0.025; randomization test).

We further examined the relationship between alternative splicing and network connectedness by categorizing singletons with regard to the presence or absence of alternative splicing and by categorizing members of multi-gene families by the presence or absence of alternative splicing in the gene itself and in other members of the same family (Fig. 2). Genes lacking alternative splicing and belonging to multi-gene families without alternative splicing showed higher median values of both measures of network connectedness than did any other category of genes (Fig. 2). The median number of interactions for genes lacking alternative splicing and belonging to multi-gene families lacking alternative splicing was significantly greater than that for any other category except singletons lacking alternative splicing (Fig. 2a). Furthermore, the median CC for genes lacking alternative splicing and belonging to multi-gene families lacking alternative splicing was significantly greater than that for any other category (Fig. 2b).

Fig. 2.

Median (a) number of network interactions and (b) clustering coefficient (CC) of 2209 C. elegans genes categorized by family size and by presence (AS+) or absence (AS−) of alternative splicing in the gene itself and/or other family members. Numbers in each category are indicated at the top of each bar. Randomization tests of the hypothesis that a median value equals the corresponding value for AS− genes in AS− multi-gene families: *P < 0.05; **P < 0.01; ***P < 0.001

Patterns of interaction

In order to examine whether alternatively spliced genes tended to interact disproportionately with other alternatively spliced genes, we examined 16,593 interactions in the network that occurred between genes of different families. In interactions between singletons, interactions between alternatively spliced genes occurred significantly more frequently than expected based on the frequency in the data set of singletons with and without alternative splicing (Fig. 3; P < 0.001; randomization test). Similarly, in interactions between a singleton and a member of a multi-gene family, interactions between alternatively spliced genes occurred significantly more frequently than expected (Fig. 3; P < 0.001; randomization test). The same pattern was seen in interactions between two members of different multi-gene families (Fig. 3; P < 0.001; randomization test).

Fig. 3.

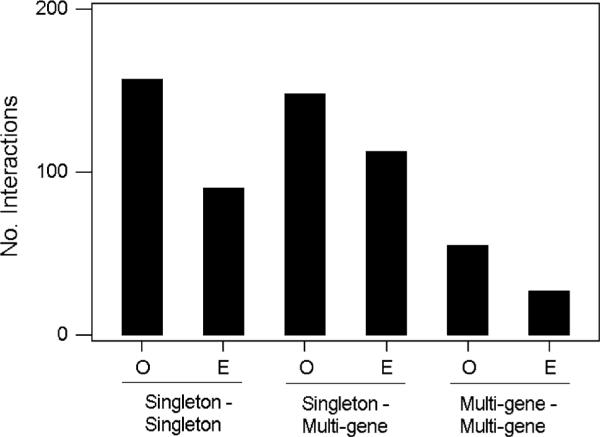
Observed (O) and expected (E) numbers of network interactions between alternatively spliced genes, categorized by the family sizes of the genes involved. The difference between observed and expected was significant in each case (P < 0.001; randomization tests)

Discussion

In the human genome, there is evidence of a negative relationship between alternative splicing and gene duplication, since alternative splicing is more prevalent in smaller gene families (Kopelman et al. 2005; Su et al. 2006). It has been estimated that about 42% of genes in the human genome are alternatively spliced (Kim et al. 2007). The proportion of alternatively spliced genes in C. elegans is only about 12% (Kim et al. 2007). Consistent with the overall frequency of alternative splicing in C. elegans, annotations indicative of alternative splicing were available in only about 9% of the C. elegans genes analyzed here. Some cases of alternative splicing have probably been missed by current annotation. However, even if all the multi-exonic genes currently predicted not to be alternatively spliced on the basis of computer models alone (see Methods) turn out to be alternatively spliced, the incidence of alternative splicing would still be much lower than that in mammals. In spite of the difference between C. elegans and mammals with regard to the overall level of alternative splicing, a negative association between family size and alternative splicing was found to characterize C. elegans as well.

Rukov et al. (2007) presented evidence that there has been little change in alternative splicing pattern in the 85–110 million years that separate C. elegans from C. briggsiae. Thus, these authors suggest that mechanisms such as gene duplication may have been more important in differentiation between the two species. This hypothesis is consistent with the present results in supporting the hypothesis of an evolutionary trade-off between gene duplication and alternative splicing as mechanisms of functional differentiation.

Genes that lacked alternative splicing tended to be more highly connected in the genetic network than alternatively spliced genes, and this was particularly true of genes without alternative splicing that were members of multi-gene families lacking any alternatively spliced members. Only 10 families of the 205 multi-gene families without alternative splicing had as many as 7 members included in the network data set: H2A histones (19 members total, 18 in network data set); H3 histones (20 members total, 17 in network data set); H2B histones (17 members total, 16 in network data set); H4 histones (16 members total, all in network data set); tubulins (16 members total, 15 in network data set); CCCH-type zinc-finger proteins (10 members total, all in network data set); ubiquitin conjugating enzymes (20 members total, 9 in network data set); NADH:flavin oxidoreductases (8 members total, all in network data set); long-chain fatty acid elongases (8 members total, all in network data set); and proteasome α subunits (7 members total, all in network data set).

Hughes and Friedman (2005) reported evidence that purifying selection acts to oppose the duplication of genes with large numbers of network interactions, presumably because of the disruptive effects on cellular function of duplicating highly connected network “hubs” (Papp et al. 2003; Wagner 2003). The present data set included a number of highly connected singletons; there were 12 singletons with 100 or more predicted network connections, including byn-1, fib-1, lpd-7, nol-1, pro-2, rpa-0, and ubq-1. In addition to selection against duplication of highly connected singletons, the present results suggest that certain key proteins with high degrees of network connectedness may likewise be subject to selection opposing the occurrence of alternatively spliced forms.

We further observed that alternatively spliced genes tended to interact in the network with other alternatively spliced genes to a greater extent than expected by chance. This was true in the case of interactions between two singletons, interactions between a singleton and a multi-gene family member, and interactions between two multi-gene family members. The genetic interaction network data of Zhong and Sternberg (2006) did not identify which alternatively spliced variants were involved in interactions. Nonetheless, these results suggest one explanation for the fact that in C. elegans alternatively spliced genes tend not to be highly connected in the network; namely, that these genes constitute a small subset of all genes and interact preferentially with other alternatively spliced genes.

The understanding of genetic interaction networks in its infancy, particularly in the case of multi-cellular eukaryotes (Byrne et al. 2007). The network data analyzed here (Zhong and Sternberg 2006) involved only about a tenth of the genes in the C. elegans genome; and, although only interactions strongly supported by the algorithm of Zhong and Sternberg (2006) were included in the network, the extent of error in the prediction of interactions remains uncertain. In spite of the limitations of currently available data, our results suggest that the study of network interactions will play an important role in the elucidating the biological role and evolutionary origin of alternative splicing.