A Statistically Rigorous Test for the Identification of Parent−Fragment Pairs in LC-MS Datasets

Abstract

Untargeted global metabolic profiling by liquid chromato-graphy−mass spectrometry generates numerous signals that are due to unknown compounds and whose identification forms an important challenge. The analysis of metabolite fragmentation patterns, following collision-induced dissociation, provides a valuable tool for identification, but can be severely impeded by close chromatographic coelution of distinct metabolites. We propose a new algorithm for identifying related parent−fragment pairs and for distinguishing these from signals due to unrelated compounds. Unlike existing methods, our approach addresses the problem by means of a hypothesis test that is based on the distribution of the recorded ion counts, and thereby provides a statistically rigorous measure of the uncertainty involved in the classification problem. Because of technological constraints, the test is of primary use at low and intermediate ion counts, above which detector saturation causes substantial bias to the recorded ion count. The validity of the test is demonstrated through its application to pairs of coeluting isotopologues and to known parent−fragment pairs, which results in test statistics consistent with the null distribution. The performance of the test is compared with a commonly used Pearson correlation approach and found to be considerably better (e.g., false positive rate of 6.25%, compared with a value of 50% for the correlation for perfectly coeluting ions). Because the algorithm may be used for the analysis of high-mass compounds in addition to metabolic data, we expect it to facilitate the analysis of fragmentation patterns for a wide range of analytical problems.

Metabolic profiling^1,2 combines the application of modern spectroscopic techniques with statistical analyses in the study of biofluids, cells, and tissues. The discipline typically employs either nuclear magnetic resonance (NMR) or mass spectrometry (MS) to profile biological samples for the levels of thousands of small molecules (<1 kDa). Liquid chromatography time-of-flight mass spectrometry (LC-TOF MS)(3) has become an increasingly popular technology in this area, because of its relatively low cost, high sensitivity, and good resolution.

Because of the high sensitivity of this analytical platform and the complex nature of metabolic samples, LC-MS experiments result in large numbers of signals that are due to unknown compounds and whose assignment forms a major challenge to the subsequent data analysis. The two primary measurements used to narrow down the possible identities of the unknown compounds are their elution times and their mass estimates. For modern TOF mass spectrometers, the latter may be accurate to within a few parts per million (ppm), under optimal conditions.(4)

An important piece of complementary information may be obtained through the use of tandem mass spectrometry,(5) whereby molecules of predetermined masses are fragmented through collision-induced dissociation. The estimated masses of the fragments produced can then be used to place further constraints on the possible identity of the metabolite from which they are derived. Various studies have suggested methods for improved chemical formula elucidation, based on variations of this technique.⁶⁻⁸ Fragmentation patterns may also result from in-source fragmentation, especially in the case of “hard” ionization techniques such as electron ionization (EI).

There are fundamental differences in the manner in which fragmentation patterns are used in metabolomics, compared to their use in proteomics. The fact that proteins are composed of a finite set of amino acids has allowed for the development of elaborate mathematical techniques for the interpretation of their fragmentation patterns. While equivalent methods are not available in metabolomics, metabolite databases such as the Human Metabolome Database(9) or Metlin(10) provide extensive mass spectral libraries, including MS/MS data, which constitute important tools for metabolite identification.

More modern and higher-throughput fragmentation procedures do not restrict the analysis to metabolites of prespecified masses, but attempt to simultaneously analyze the fragmentation patterns of all metabolites across a wide range of masses. One example, known as MS^E, attempts to do so by rapidly alternating between a high- and a low-energy fragmentation, with the objective of producing a low-energy spectrum that contains few or no fragments so that the original metabolite can easily be identified, using its corresponding fragments observed in the high-energy spectrum.(11) However, this approach can be confounded by the production of in-source fragments, as well as those produced by low-energy collisions.

A key challenge to the reliable use of any high-throughput approach lies in establishing which fragments are derived from which metabolite when several distinct metabolites are coeluting from the column. The development of improved chromatographic techniques, such as Ultra-Performance Liquid Chromatography (UPLC),(12) has allowed for greater separation efficiency; however, given the large number of compounds found in metabolic samples, coelution remains an important obstacle. The problem is typically addressed by exploiting the fact that compounds derived from the same underlying metabolite will have very similar chromatographic elution profiles, and consequently should have an approximately constant ratio of intensities. One measure that has been used to quantify this property is the Pearson correlation,^13,14 which has the advantage of being easily interpretable and widely used in many different contexts. Other methods proposed include comparing the chromatographic peak profiles using neural networks(15) and, rather more simply, testing whether the apices of coeluting chromatographic peaks share the same retention time.(16)

While these methods are highly valuable to researchers, they are fundamentally heuristic in that they provide intuitive but poorly understood rules of thumb to data analysis. There are a number of reasons for avoiding the use of heuristic methods. Since they are not built on a comprehensive understanding of the system to which they are applied, they may, without warning, perform poorly under “unusual circumstances” (e.g., for very high ion counts). Moreover, it is difficult to establish the “optimality” of heuristic methods: they may be designed to maximize a score function that makes some intuitive sense but whose propriety for the system studied is difficult to ascertain, since the system is not understood. Finally, if a score function is used to quantify the degree of peak similarity, then some “acceptance threshold” for this score must be chosen, above which the peaks are deemed to stem from the same underlying metabolite, and below which they are deemed to be unrelated. The choice of this threshold is generally quite arbitrary as the distribution of the score function is rarely understood.

In this paper, we develop a statistically rigorous approach to the problem of coelution based on an underlying model of the ion counts that is derived directly from the distribution of the ion arrivals and the properties of the detection system. In particular, the method developed is tailored to LC-TOF MS systems employing a time-to-digital converter (TDC) to measure the time-of-flight of incoming ions and count the number of ion arrivals. Consequently, the method is not expected to work on instruments employing the alternative analog-to-digital converters (ADCs), although it is quite likely that analogous techniques might be developed for such instruments.

Theory

Methodological Approach

Despite the elaborate nature of the technology involved in the generation of LC-TOF MS data, many of the mechanisms whereby the data are produced can be described with a high degree of accuracy by means of relatively simple mathematical models. It may be useful to exploit this feature and aim for a more rigorous approach to the analysis of LC-TOF MS data, wherein all the aspects of the data generation process that are relevant to the eventual analysis are understood and accounted for—in a sense, an ab initio approach to data generation and analysis. Such an approach should be set in contrast to the much more widely studied heuristic techniques for mass spectral data analysis.

When adopting a rigorous approach, it may be helpful to regard the raw recorded ion counts in an LC-TOF MS experiment as being derived from three components:

(1) A systematic element directly due to the compounds in the sample and in the chromatographic column. This may, to a first approximation, be regarded as a function of the concentration and ionization propensity of these compounds.

(2) The fundamental noise due to the fluctuating numbers of molecules that are ionized.

(3) The effects of the physical architecture of the mass spectrometer used, such as the type of detector it employs. This includes the effects of background electronic noise, because its severity is highly dependent on the type of detector used.

What is typically of interest to the analytical researcher is the systematic element (1), because this is the component that carries information regarding the biological system under study, although it will often also carry chemical noise. Components (2) and (3) are nuisance effects that introduce uncertainty into the data and are of no direct interest. Therefore, a good framework for data analysis should account for the uncertainty introduced by the nuisance components as accurately as possible, in order to draw inferences about the biological information in the sample.

It turns out that component (2) is very easy to characterize mathematically, because the arrival times of the ions are governed by the well-known Poisson distribution,(17) which is a property that has previously been used as the basis for a noise model for quadrupole TOF MS data.(18) If a highly advanced mass spectrometer were available—one capable of measuring to an arbitrary degree of accuracy the numbers and arrival times of all incoming ions—then the development of a comprehensive statistical framework for the analysis of LC-TOF MS data might be within reach. At present, however, a model based solely on a Poissonian distribution of ion arrivals is not entirely appropriate, because current technology does not allow for the detection of the precise number of incoming ions.

Different manufacturers employ different detection methods, each having its own advantages and drawbacks. Many mass spectrometers make use of a TDC as part of their detection system. TDCs are capable of blocking out most electronic noise, and therefore, provide good signal-to-noise ratios when the rate of ion arrivals is low.^19,20 However, they are easily saturated, so that for higher rates of ion arrivals, only a fraction of the ions are counted and the mass estimates are biased toward lower values.(21) In the following, the expression “detector saturation” will be used to denote any deviations from a linear response, caused by an excess of ion arrivals at the detector system. While such saturation can be induced by components of the detection system other than the TDC, it is typically the latter that has the most impact on dynamic range.

Thus, for LC-TOF MS systems employing a TDC, significant deviations from the Poisson distribution should be expected at higher ion counts. Both statistical^21–23 and physical(24) methods for correcting for detector saturation are available. But while the “corrected” ion count will thereby be rendered closer to the true count, it will generally not adhere to a Poisson distribution. Rather, it will adhere to a much more complex distribution for which a truly rigorous statistical analysis would be very difficult. The same may be said of most of the standard preprocessing steps that are routinely applied to LC-MS data (e.g., normalization, retention time alignment, etc.)—such measures make the data easier to analyze on a superficial level, but the actual statistical distribution of preprocessed data is extremely complex and may not be suitable for rigorous statistical analysis.

Initially, it may therefore be preferable to restrict the analysis to more moderate ion counts, for which the Poisson approximation is good. On that basis, a statistically rigorous test of hypothesis for identifying related fragment pairs on TDC mass spectrometers is presented in the following section.

A Goodness-of-Fit Test for Exact Coelution

In the following, it will be assumed that the chromatographic peaks studied are pure; that is, they are derived from only one molecular species. As long as the mass peaks are pure, they may be centroided without the loss of important information, because the shape of the mass peak is largely determined by factors such as the velocity and spatial distribution of the ions at the time the electric field is applied,(17) which are of little interest. Moreover, the count of a centroided mass peak will remain Poissonian, because the sum of independent Poisson distributed random variables is itself Poissonian.

The probability of obtaining the count k from a Poisson-distributed random variable with rate λ is given by

For LC-MS data, the rate of ion arrivals of a particular molecular species will be a function of its elution time, t, so that we may write

For a Poisson distribution, the rate parameter (λ) is equal to the mean. The centroided rate function, λ(t), therefore describes the mean number of ion arrivals of a particular molecular species within one scan, as a function of retention time. The rate function may be regarded as the product of the concentration and the ionization propensity of the compound, and consequently may be written

where π is a measure of the compound’s ionization propensity, and Q(t) is a measure of its concentration in the retention time dimension. Supposing a metabolite were to fragment into multiple ions after eluting from the chromatographic column, these would all share the same Q(t) as the original metabolite. This provides the basis for constructing a test of hypothesis for exact coelution.

Suppose we wish to test whether a proposed fragment pair is “legitimate”, rather than the result of close but partial coelution. The two ion counts will be referred to as k₀(t) and k₁(t) and their rate functions can be written λ₀(t) = π₀Q(t) and λ₁(t) = π₁Q(t). A matching pair of ion counts, (k₀(t), k₁(t)), will be referred to as a “data point”. The joint distribution of the counts at a given retention time is then given by

where, for the sake of conciseness, the dependence on t has been omitted. However, if

we may, following Przyborowski and Wilenski,(25) rewrite the joint probability as

which is the joint probability of a Poisson distribution with mean μ (which determines the sum of the ion counts, n) and a binomial distribution of n trials with probability ρ (which determines what portion of the sum is due to k₀ in particular). If the two ions under investigation exhibit exact coelution and, hence, share the same Q(t), then this term cancels out from the expression for the binomial probability, which, when reinstating the dependence on t, can be written as

which will therefore be constant across retention time. Under the null hypothesis of constant binomial probabilities, Pearson’s χ² goodness-of-fit statistic,

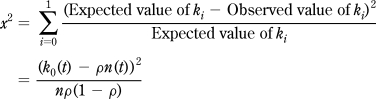approximates a χ² distribution with one degree of freedom (see, for example, Wackerly et al.,(26) p 682). We can evaluate this statistic for all N data points across the chromatographic peak and sum them to obtain a pooled statistic, X² = Σx², which approximates a χ² distribution with N − 1 degrees of freedom, since ρ must be estimated from the data. The approximation to the χ² distribution works best when n is large and ρ is moderate. A standard test of validity is to require that nρ ≥ 5 and n(1 − ρ) ≥ 5; data points for which this is not the case should be left out or pooled together.

If there is partial coelution, so that the binomial probability varies from data point to data point, then the value of the X² will generally be considerably greater than what would be expected by chance, a property that can easily be quantified by calculating the corresponding p-value. Therefore, given a set of ion counts across two coeluting chromatographic peaks, the goodness-of-fit (GOF) test indicates the probability of obtaining deviations from the estimated binomial probability that are at least as extreme as those observed, under the null hypothesis that chromatographic peaks examined exhibit exact coelution. The fact that the test quantifies the uncertainty of this assignment with a relevant p-value is its main advantage over the alternative heuristic techniques that measure peak similarity by means of poorly understood score functions, and consequently define their acceptance thresholds in an essentially arbitrary manner. The acceptance threshold of the GOF test may simply be given by the chosen significance level, which is easily interpretable and relates straightforwardly to the researcher’s aversion to false positives.

Statistics other than the one previously proposed may be used to detect deviations from exact coelution. Similar to the X²-statistic, the likelihood ratio test statistic (see, for example, Wackerly et al.,(26) p 517) is approximately χ²-distributed and, in addition, has certain asymptotically optimal properties. However, it has been argued that the likelihood ratio test is less reliable than the X²-statistic for small sample sizes,(27) so that considerably higher n(t) values would be required by the former for the resulting p-value to be accurate. This is consistent with our findings from applying the two statistics to the counts of simulated chromatographic peaks. Therefore, the X²-statistic is preferable for low counts, and because detector saturation becomes increasingly severe with higher counts, the use of the likelihood ratio test statistic is generally not recommended.

To calculate X², the binomial probability must be estimated. A very simple estimator may be constructed by dividing the sum of all the counts of one ion by the sum of all the counts of both ions:

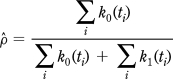If this estimator is used, then the overall computational requirements of the test will be very low, and generally comparable to those of the Pearson correlation. Computational efficiency is an important property, considering the size of typical LC-MS datasets.

The GOF test can easily be generalized so that it simultaneously tests for the exact coelution of an arbitrary number of chromatographic peaks. When doing so, it becomes necessary to work with multinomials rather than binomials; however, the general approach, including the estimation of multinomial probabilities, is closely analogous to the procedure just described. It should also be noted that confidence intervals can be constructed for the estimated probabilities. This can be useful when the ions investigated are isotopologues, in which case the multinomial probabilities describe the isotopic abundance pattern, knowledge of which can be helpful in identifying unknown compounds.

Nevertheless, note that the GOF test is not a clustering algorithm: it does not identify each set of exactly coeluting peaks over a given range of retention times. Like the Pearson correlation, it can provide a similarity score (the p-value) to measure the degree of coelution of each pair of peaks, and on the basis of these scores a clustering algorithm might be constructed. In addition, if the GOF test were to be used in an automated fashion, it would require a separate peak-picking algorithm to define the retention times and corresponding ion counts to which the test were to be applied. Thus, the computational requirements of an automated algorithm would, to a large extent, be dependent on the nature of the peak-picking and clustering algorithms. The fact that the GOF test can be used to simultaneously test for the coelution of multiple peaks might well make the associated clustering algorithm faster than methods that are based exclusively on pairwise comparisons.

Illustration of the GOF Test on Simulated Data

It may be instructive to illustrate the use of the GOF test on simulated chromatographic peaks. The GOF test makes no assumptions regarding shape of the chromatographic peaks under investigation, so we may, for simplicity, assume a Gaussian peak shape. The centroided rate function at the ith chromatographic scan (lasting from t_i−1 to t_i) can then be written

where I is the mean number of ion arrivals over the entire chromatographic peak. For given values of μ, σ, and I, we may then simulate Poisson-distributed random variables according to this model, for each of the N scans over which the chromatographic peak is to be investigated. If two simulated chromatographic peaks share the same μ and σ, then the result of applying the GOF test to their counts will be a p-value that is approximately uniformly distributed. A discrepancy in the μ values, for instance, would tend to inflate the X² statistic and result in a correspondingly low p-value.

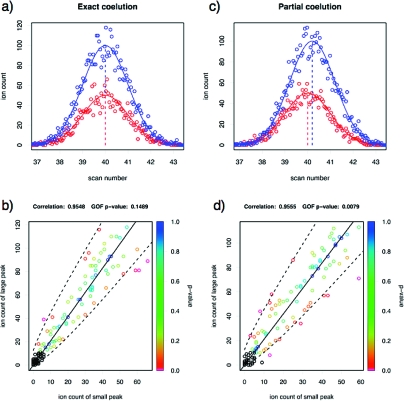
The data thus simulated in Figure 1 illustrate the ability of the GOF test to detect discrepancies from exact coelution (p = 0.0079) that are so small that the resulting Pearson correlation (0.9555) is essentially the same as what would be expected for exact coelution. In addition to the highly significant GOF p-value, the excessive deviation from the estimated binomial probability under partial coelution can be seen on the scatterplot from the comparatively large number of data points with very low p-values, which is a feature that would be difficult to spot by eye, without the color coding.

Figure 1.

(Top) Two simulated chromatographic peaks exhibiting exact coelution (a) and two simulated chromatographic peaks exhibiting very close but partial coelution (c), as indicated by the shifted means (10% of the standard deviation of the peaks). (Bottom) The corresponding scatterplots with the p-values of the x²-statistics of each data-point indicated by color-code. Low counts for which the distribution of the x²-statistics may deviate substantially from the χ₁²-distribution are excluded, and these data points are indicated in black. While the correlations are approximately the same in either scenario, the p-value of the pooled X²-statistic is highly significant under partial coelution (p = 0.0079), but quite moderate under exact coelution (p = 0.1489).

Illustration of the GOF Test on Experimental Data

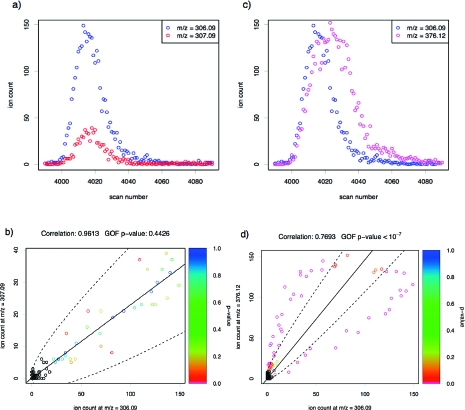
Figure 2 illustrates the same scenarios of exact and partial coelution using real metabolic data. As with the simulated data, the X²-statistic results in a moderate p-value under exact coelution (p = 0.4426) but a highly significant one under partial coelution (p < 10⁻⁷). In practice, when analyzing metabolic samples, the total number of partially coeluting peaks, and the closeness of their coelution, may vary considerably, depending on the nature of the sample and on the experimental setup. The GOF test is likely to be most valuable when the coelution is very close.

Figure 2.

Similar to Figure 1, except, in this case, real LC-MS data derived from synthetic urine are used. The left-hand side shows the chromatographic peaks (a) and scatterplot (b) of a pair of isotopologues, which, like related fragments, may be expected to exhibit exact coelution; the right-hand side shows the chromatographic peaks (c) and scatterplot (d) of two presumably unrelated compounds. The difference in the estimated means is 6.34 times the estimated standard deviation.

Experimental Section

The validity of the theory described above rests on two fundamental assumptions: (i) that the recorded ion counts are approximately Poisson-distributed, and (ii) that the ratio of the rate functions at the two m/z values investigated is approximately constant when there is exact coelution.

It is only if these two assumptions hold that we would expect the x²- and the X²-statistics obtained from the observed ion counts of exactly coeluting compounds to adhere to the distributions predicted under the null hypothesis. Any departure from the two assumptions (because of detector saturation, interference from unrelated ions, or indeed, errors in the theoretical framework) would likely result in inflated statistics. Therefore, the validity of the test may be evaluated by applying it to pairs of compounds known to exhibit exact coelution and by comparing the distributions of the resulting test statistics to the predicted ones. On that basis, the validity of the GOF test was evaluated on real metabolomic data that have been derived from synthetic urine.

The validity of the test was examined under varying ranges of ion counts, to evaluate the effects of detector saturation. Here, it should be noted that in LC-TOF MS experiments, the number of ion counts obtained will be dependent on the duration of the chromatographic scan time: the longer the scan time is, the higher the count. However, the only factor affecting detector saturation is the rate of ion arrivals, so that a longer scan time does not induce greater detector saturation, despite the higher count. Consequently, ion counts will in the following be classified as “low”, “moderate”, or “high”, with these categories corresponding roughly to the tertiles of the full ion count range.

Preparation of Synthetic Urine

Eighty-three of the most abundant endogenous mammalian metabolites, ranging in molecular weight from 30−625 Da, were weighed into a 1-L bottle and then dissolved in 1 L of HPLC-grade water (Sigma−Aldrich, St. Louis, MO). Any remaining solids were removed by vacuum filtration. Approximate final metabolite concentrations were targeted to fall between 1 mM and 20 mM, with sodium azide added at 0.05% v/v as a preservative. The normally high levels of inorganic salts found in urine were not added, in order to eliminate the effect of salt suppression in the various sample introduction interfaces. The stock solution was stored at −80 °C.

Instrumentation

Synthetic urine samples (5 μL) were injected onto a 2.1 mm × 100 mm (1.7 μm) HSS T3 Acquity column (Waters Corporation, Milford, CT) and eluted using a 18-min gradient of 100% A to 100% B (A = water, 0.1% formic acid, B = acetonitrile, 0.1% formic acid). The flow rate was 500 μL/min, the column temperature was 40 °C, and the sample temperature was 4 °C. Samples were analyzed using a UPLC system (UPLC Acquity, Waters Ltd. Elstree, U.K.) coupled online to a Q-TOF Premier mass spectrometer (Waters MS Technologies, Ltd., Manchester, U.K.) in positive- and negative-ion electrospray mode with a scan range of m/z 50−1000 and a scan time of 0.08 s. Three technical replicates were run. To obtain data that were as raw as possible, the spectrometer was run in continuum mode and the detector saturation correction was switched off. A feature of the Q-TOF Premier is that it employs a “DRE lens”, which is a mechanism for defocusing the ion beam to minimize detector saturation.(24) This defocusing mechanism was also switched off.

Results

Selection of Test Datasets

Clusters of isotopologues provide convenient test sets, because they can be expected to exhibit exact coelution.(15) Eleven prominent clusters of isotopologues were investigated in this analysis. In all cases, plots of the mass peaks (see Figure 3) were closely inspected to reduce the risk of “contamination” from closely coeluting compounds with similar mass. While this procedure cannot guarantee the resulting dataset to be one composed exclusively of pure chromatographic peaks, it is quite conservative, because any contamination would tend to inflate the resulting x²-statistics, which, in turn, would lead us to reject the validity of the GOF test. Heavier isotopologues were excluded if their signal was weak enough to be comparable to the background noise. A total of sixteen peak pairs were included in the final analysis. The masses and scan numbers of their apices are listed in Table 1.

Figure 3.

Continuum plots of a pair of isotopologues. The x-axis indicates the chromatographic scan number, while the y-axis indicates each of the individual “ticks” of the clock that measures the time-of-flight of the ions, along with the corresponding m/z values. The number of ions counted at each tick is indicated by the color code. In these two cases, there are no apparent signs of interference from other compounds of similar masses.

Table 1. Scan Numbers and m/z Values of the Peaks Used in the Evaluation of the GOF test at Their Apices^a.

cluster	compound	scan number/retention time (min)	m/z	isotopologueb
1	N-acetyl-l-glutamic acid	857/1.652	188.0426	[M−H]−
		868/1.672	189.0572	[M+1−H]−
		877/1.690	190.0615	[M+2−H]−
2	uridine	1096/2.114	243.0537	[M−H]−
		1104/2.129	244.0672	[M+1−H]−
3	4-aminohippuric acid	1677/3.234	193.0507	[M−H]−
		1681/3.241	194.0653	[M+1−H]−
		1681/3.241	195.0645	[M+2−H]−
4	glutaric acid	1724/3.323	131.0251	[M−H]−
		1755/3.382	132.0381	[M+1−H]−
5	methylsuccinic acid	2471/4.763	132.0384	[M+1−H]−
		2414/4.654	133.0376	[M+2−H]−
6	3-nitro tyrosine	2877/5.546	225.0399	[M−H]−
		2871/5.535	226.0579	[M+1−H]−
7	adipic acid	2952/5.689	145.0464	[M−H]−
		2951/5.687	146.0554	[M+1−H]−
8	indoxyl sulfate	2971/5.725	211.9924	[M−H]−
		2965/5.714	213.0030	[M+1−H]−
		2975/5.733	213.9970	[M+2−H]−
		2972/5.727	214.9968	[M+3−H]−
9	suberic acid	3635/7.007	173.0707	[M−H]−
		3617/6.973	174.0842	[M+1−H]−
		3623/6.985	175.0832	[M+2−H]−
10	salicylic acid	4096/7.895	138.0239	[M+1−H]−
		4100/7.903	139.0298	[M+2−H]−
11	sebacic acid	4615/8.893	202.1097	[M+1−H]−
		4610/8.884	203.1155	[M+2−H]−

^aThis may not correspond to the global maximum of the peak, because, for many clusters, parts of the chromatographic peaks were left out, to avoid “contamination” from distinct compounds of similar masses.

^bHere, “[M−H]⁻” denotes the negatively ionized lowest-mass isotopologue of the metabolite in question.

To allow for an approximately constant ratio of counts, all the pairs of isotopologue mass peaks that were accepted as “pure” were centroided over a matching number of mass bins. The binomial probabilities were then estimated, and the resulting x²-statistics calculated. Given the large number of data points available for each pair of isotopologues, the distribution of each statistic should approximate a χ²-distribution with one degree of freedom. Thus, the validity of the algorithm may be tested by evaluating whether or not the empirically calculated x²-statistics conform to this distribution. Note that the binomial probabilities could have been calculated theoretically from the known isotopic abundance patterns, but this was avoided, because their estimation will always be required when the test is applied to putative parent−fragment pairs.

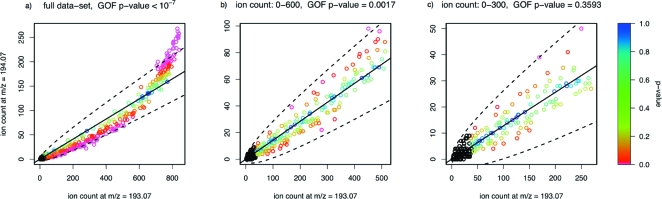
To evaluate the effects of detector saturation, the GOF test was applied to the data at various cutoffs. The cutoff was applied to the sum of the paired ion counts rather than to each one individually, because this reduces the bias caused to the resulting distribution of x²-statistics. In this way, three datasets were constructed: the full dataset (6090 data points), a dataset consisting of low and moderate paired ion counts, namely those of less than 600 (4029 data points), and one consisting only of low paired ion counts, namely those of less than 300 (2986 data points). In all cases, low ion counts for which the x²-statistics might be unreliable (those with nρ̂ < 5 or n(1 − ρ̂) < 5) were excluded. Figure 4 shows the resulting GOF scatterplots for one pair of mass peaks (derived from 4-aminohippuric acid), with the approximate p-values of the x²-statistics indicated by color code. The effects of detector saturation are very clear for the full dataset, where there is a very strong deviation from linearity and a correspondingly low GOF p-value. The deviation is difficult to see by eye for the dataset of low and moderate counts, although the GOF p-value remains significant. The dataset of low counts results in a moderate p-value and only a few data points show possible signs of detector saturation.

Figure 4.

Scatterplots for the three datasets derived from 4-aminohippuric acid: (a) the full data set, (b) the dataset with low and moderate counts, and (c) the dataset with only low counts. The approximate p-values of the x²-statistics are indicated by color code, and the p-values of the pooled X²-statistics are listed.

Validation

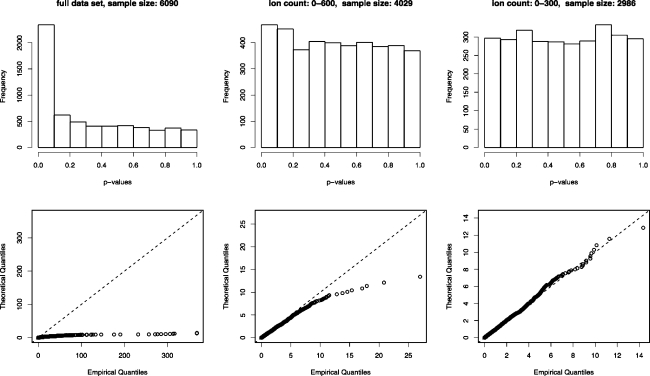
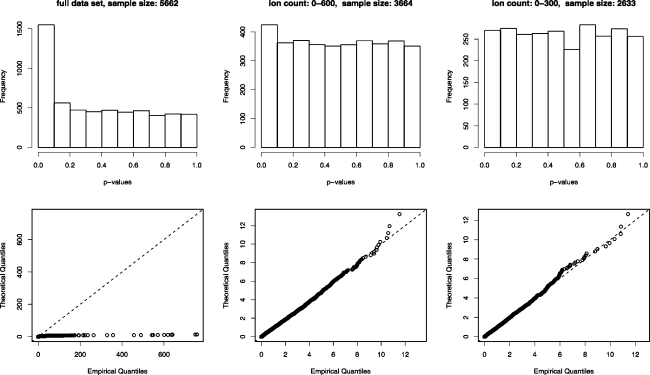
To determine whether the x²-statistics of the three datasets adhere to the χ₁²-distribution, quantile−quantile plots were drawn, along with histograms of the corresponding p-values (see Figure 5). The percentage of the x²-statistics that fell within the 5% and 1% critical regions of the χ₁²-distribution were also calculated (see Table 2). The full dataset clearly shows very strong deviation from the predicted distribution, with far more high values than would be expected from a χ₁²-distribution and consequently a distribution of p-values that is strongly biased toward lower values. The same is true of the dataset with the cutoff at 600, although, here, the deviation is more moderate. However, the final dataset seems to be consistent with a χ₁²-distribution.

Figure 5.

(Top) Histograms of the p-values corresponding to the x²-statistics derived from the three datasets and (bottom) quantile−quantile plots of the x²-statistics themselves, compared to the theoretical χ₁²-distribution. Only the dataset of low counts seems to closely approximate the χ₁²-distribution.

Table 2. Data Regarding the x²-Statistics Derived from the Three Datasets.

	full dataset	ion count: 0−600	ion count: 0−300
percentage of x2-statistics in 5% critical region	31.13% (1896/6090)	6.45% (260/4029)	4.99% (149/2986)
percentage of x2-statistics in 1% critical region	21.51% (1310/6090)	1.51% (61/4029)	0.87% (23/2986)
GOF p-value for X2-statistics	<10−7	<10−7	0.5642

To test the validity of the X²-statistics of the three datasets, all of the x²-statistics of each group were summed, providing three X²-statistics. Their distributions should adhere to the χ²-distribution, with the number of degrees of freedom being equal to the total sample size minus sixteen (the number of parameters estimated). As shown in Table 2, the two larger groups yield extremely low p-values, but the group with a cutoff at 300 yields a p-value that is consistent with a uniform distribution.

As was mentioned earlier, there are statistical methods for correcting for the effects of detector saturation. While these do not restore the Poisson distribution of the data, they may extend the range over which the Poisson approximation is valid. To investigate such an effect, Coates’ correction algorithm(23) was applied to the continuum data, after which it was centroided and the GOF test applied once more. The results are shown in Figure 6 and Table 3.

Figure 6.

(Top) Histograms of the p-values corresponding to the x²-statistics derived from the three datasets after they had been corrected for detector saturation and (bottom) quantile−quantile plots of the x² statistics themselves, compared to the theoretical χ₁²-distribution. Only for the dataset of low and moderate counts does the correction seem to cause the distribution of the x²-statistics to be substantially closer to the χ₁²-distribution than it was for the raw data, although some deviations remain.

Table 3. Data Regarding the x²-Statistics Derived from the Saturation-Corrected Datasets.

	full dataset	ion count: 0−600	ion count: 0−300
percentage of x2-statistics in 5% critical region	20.89% (1183/5662)	5.70% (209/3664)	5.24% (138/2633)
percentage of x2-statistics in 1% critical region	13.49% (764/5662)	1.06% (39/3664)	0.72% (19/2633)
GOF p-value for X2-statistics	<10−7	0.0074	0.3190

Despite the correction, the distributions of the x²- and X²-statistics for the full dataset remain significantly different from the appropriate χ²-distributions. For the dataset of low and moderate counts, the distribution of x²-statistics is made considerably closer to acceptable, although the p-value of the X²-statistic remains significant. There is no indication that the distributions of the statistics change substantially for the dataset of low counts.

Note that, in cases where the ion count ratio is very close to one, the degree of detector saturation will be approximately the same for both counts, which will have the effect of preserving the approximate constancy of the ion count ratio, even for high counts. This can potentially induce a lower-than-expected X²-statistic for high counts and a correspondingly inflated p-value; however, the application of Coates’ correction algorithm increases the variance of the counts beyond what would be expected for Poissonian data, so that this form of bias does not arise.

An important issue regarding the validity of the GOF test is the manner in which the rate function of a given fragment may be influenced by the coelution of a distinct metabolite through ionization suppression. If ionization suppression were to reduce the rate functions of all the fragments studied by the same proportion, then the GOF test would remain valid, as the linear relationship between the fragments would be unaffected. However, if the nature of ionization suppression is such that the rate functions of different fragments are reduced by different proportions, then even very mild suppression effects might induce the GOF test to return a low p-value when it should not. If this is the case and if such suppression effects are common under coelution, then the GOF test should only be expected to return a uniformly distributed p-value when a single metabolite is eluting, which would limit its value as an analytical tool.

To test for the presence of such suppression effects, the GOF test was applied to the chromatographic peaks of a number of known parent−fragment pairs for which there was partial coelution with a distinct metabolite. Validating the GOF test in this setting is more problematic than for isotopologues, because it requires the identification of the fragment and because of the risk that the fragment investigated may, in fact, be derived from the coeluting compound. As with the isotopologues, any contamination of the mass peaks from unrelated compounds would tend to inflate the resulting x²-statistics, which, in turn, would lead us to reject the validity of the GOF test. In addition to validating the GOF test under partial coelution, this procedure illustrates how the test would, in practice, be applied to pairs of ions.

The parent−fragment pairs that were investigated are listed in Table 4. As with the isotopologues, the continuum data were inspected, Coates’ correction was applied, and three datasets of differing ion counts were constructed. The chromatographic peaks of an example parent−fragment pair are shown in Figure 7, along with that of the coeluting compound.

Table 4. Parent−Fragment Pairs Used To Test for the Presence of Ionization Suppression Effects on the GOF Test^a.

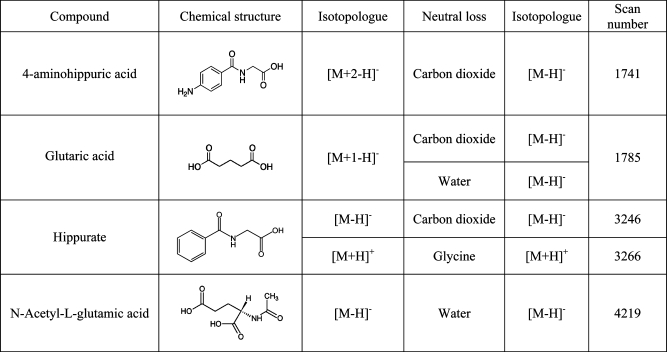^aIn all cases, a distinct metabolite was coeluting with the above pairs. The scan numbers of the apices of the chromatographic peaks used in the evaluation of the GOF test are listed.

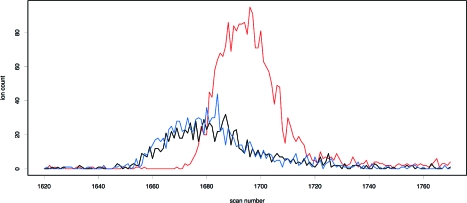
Figure 7.

Ion counts of 4-aminohippuric acid (blue), the fragment formed by the loss of carbon dioxide (black), and a partially coeluting compound (red) used in the ionization suppression test. If the rate functions of 4-aminohippuric acid and its fragment were reduced by significantly differing factors by the partially coeluting compound, we would expect their ratio to start shifting near scan number 1680, but no such effect is observed.

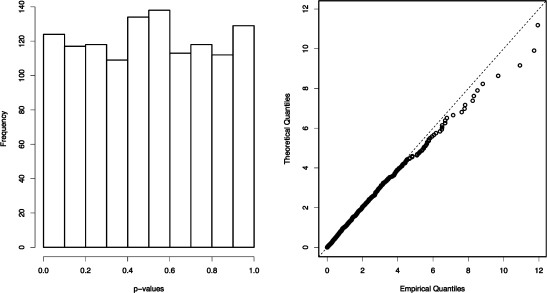
The results are similar to those obtained for the isotopologues. As shown in Figure 8, the resulting x²-statistics for the “low” ion counts are consistent with a χ²-distribution, and the overall GOF p-value for the X²-statistics is consistent with a uniform distribution at 0.3705. Thus, there is no evidence that the coelution of distinct compounds affects the validity of the GOF test. Nevertheless, given that the detailed mechanics of ionization suppression remain poorly understood, we cannot decisively exclude the possibility that coeluting compounds could interfere in such a manner that the GOF test might be rendered biased. Any technique that identifies related fragments based on the degree of linearity of their ion count ratios would be adversely affected by such interference.

Figure 8.

Histogram of the p-values returned by the GOF test when applied to the low ion counts of the six parent−fragment pairs (left), and quantile−quantile plot of the corresponding x²-statistics (right). The results are consistent with those obtained for the isotopologues, and there is no evidence that the coelution of distinct compounds affects the validity of the GOF test.

Performance Comparison

The false positive and false negative rates of the GOF test and of the Pearson correlation were compared using the data derived from the pairs of coeluting isotopologues. Because the null hypothesis of the GOF test is that the compounds investigated exhibit exact coelution, a false positive will occur when two exactly coeluting peaks are deemed to be partially coeluting, whereas a false negative is the failure to classify two partially coeluting peaks as such. The set of isotopologues contains only exactly coeluting peaks, and therefore allows only for an evaluation of the false positive rate. However, artificial coelution can be introduced by shifting the paired peaks away from each other scan by scan, thus producing semiempirical data to imitate partial coelution, and allowing for the false negative rate of the two tests to be evaluated as a function of “increasingly partial” coelution. Although the coelution is introduced artificially, this procedure allows for a level of control over the degree of coelution that would be impossible to achieve through the use of purely raw data.

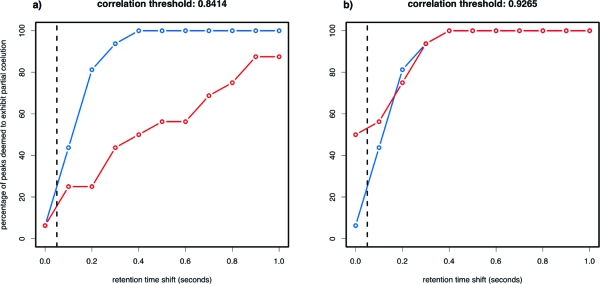
The significance level of the GOF test was set to 0.05, which is, by definition, also the theoretical false positive rate. Unlike the GOF test, the theoretical false positive rate of the correlation approach is very likely dependent on factors such as the peak heights and shapes and cannot be straightforwardly linked to its “acceptance threshold”. To allow for a fair comparison, two values for the acceptance threshold of the correlation were investigated: one that resulted in an identical number of false positives for the two tests and another that resulted in a closely comparable number of false negatives across the retention time shifts. Coates’ correction was applied to the data and the cutoff of 300 ion counts was used. The retention times of the sixteen pairs of exactly coeluting peaks were shifted by up to ten scans, giving a maximum retention time difference of 1 s, which is approximately a third of the median full width at half-maximum (fwhm) of these chromatographic peaks.

The percentages of peak pairs deemed to exhibit partial coelution are shown in Figure 9, as a function of the retention time shift. The empirical false-positive rate of the GOF test is 6.25% (1/16), and the empirical false-negative rate reaches zero after a shift of just four scans. When the empirical false-positive rate of the correlation is fixed to 6.25%, its empirical false negative rate is substantially higher than that of the GOF test throughout the retention time range investigated and takes over ten scans to reach zero. When the false-negative rates of the two tests are matched, the correlation has a false-positive rate of 50%, as opposed to the 6.25% for the GOF test. Clearly, the results suggest the performance of the GOF test to be considerably better than that of the correlation at these low counts. This is in addition to the inherent advantages that come with using a test of hypothesis.

Figure 9.

Plots of the percentage of the isotopologue pairs that are classified as exhibiting partial coelution by the GOF test (blue) and the correlation (red), as a function of “increasingly partial” coelution. Only the leftmost point corresponds to exactly coeluting peaks and thereby indicates the false-positive rate. False-negative rates correspond to 100 minus the ordinate for nonzero retention time shifts. Plot (a) standardizes the two tests by matching their false positive rates, while plot (b) matches their false negative rates. Clearly, the performance of the GOF test is considerably better than that of the correlation.

Discussion and Conclusion

The results suggest that when the analysis is restricted to low ion counts, the GOF test for exact coelution provides a good approximation to a genuine test of hypothesis. Because of detector saturation, the distribution of the test statistic used does not adhere exactly to the predicted distribution; however, for low ion counts, the approximation seems to be good enough for the p-values produced to be of satisfactory quality and, here, the test compares very favorably to a test based on the Pearson correlation. There is evidence that the range of ion counts over which the test is valid may be extended by applying Coates’ correction algorithm(23) to the continuum data.

Given the requirement of undistorted Poisson-distributed data, the GOF test is only expected to work with mass spectrometers employing a TDC to measure the time-of-flight of the ions. It seems likely that a similar type of test based on the magnitude of the deviations from the estimated chromatographic peak ratio might be designed for other types of detectors. The fact that low ion counts are required for the test to be valid represents another important constraint on its use. However, it is one that can often be overcome by making use of the ion counts of mass peaks of less abundant isotopologues, or by restricting the sampling to the edges of the chromatographic peaks. Moreover, this constraint is likely to become less severe as the technology advances. Also note that the GOF test is, a priori, just as valid as heuristic methods such as the Pearson correlation at higher ion counts. The p-value of the GOF test can still be used as a similarity score, only it can no longer be assumed to adhere to a uniform distribution under the null hypothesis and, therefore, its acceptance threshold will have to be chosen in a manner that is as arbitrary as that for the heuristic methods.

The GOF test addresses one very specific problem in the analysis of LC-MS data. There are several software packages, such as XCMS,(28) MetAlign,(29) and MZmine,(30) that provide much more extensive tools for the analysis of LC-MS data. These are based on a rather different philosophy than the GOF test, because they are generally designed to work with any type of LC-MS data, irrespective of factors such the type of detector employed by the mass spectrometer. Nevertheless, the GOF test could quite easily be incorporated into software packages such as these, although, given its requirements, it should only be used when detailed knowledge of the instrument is available. While the GOF test is expected to become a useful analytical tool, it does also, in the opinion of the authors, have considerable value as a proof-of-concept that the data analytical tasks encountered in the analysis of LC-MS data can, in at least some cases, be addressed using a mathematically more rigorous approach.

At this point, the prospects of extending the use of rigorous statistical methods not only to the region of high ion counts, but also to address other questions of interest, such as quantifying the uncertainty of mass estimates, seem quite realistic. However, such a broad theoretical framework would almost certainly have to incorporate, in detail, the effects of the architecture of the specific type of mass spectrometer used, and consequently a distinct mathematical model would have to be developed for each class of mass spectrometer. The development and assessment of such a model for a single type of mass spectrometer, as a proof-of-concept, will be the objective of future research. The fact that only rather limited documentation is publicly available on most modern mass spectrometers will form an important obstacle.

In summary, we have demonstrated and validated the feasibility of addressing an important problem in the analysis of LC-MS data by means of a rigorous statistical method derived directly from the fundamental distribution of the incoming ions. In cases where there is close chromatographic coelution of distinct metabolites, the algorithm will allow for a substantially improved analysis of their fragmentation patterns, as it provides a powerful means for distinguishing between different groupings of related fragments and includes a rigorous measure of the uncertainty of this assignment. The technique may thereby greatly facilitate the elucidation of the molecular formulas of unknown compounds, and it moreover constitutes an important step toward a more rigorous approach to mass spectrometry data analysis.