DTI Fiber Tracking with Local Tissue Property Sensitivity: Phantom and In Vivo Validation

Abstract

Diffusion tensor imaging (DTI) provides directional information that can be used to delineate brain white matter connections non-invasively via fiber tracking. The most commonly used methods for tractography are based on the streamline tracking algorithm for track propagation and a set of empirically and globally defined criteria for track termination. In this study, we propose a streamline tracking algorithm with high order propagation accuracy and a single termination criterion based on tissue property to minimize user intervention and biases introduced during tracking process. These advantages and the agreement with histological reports are demonstrated in our tracking results in phantoms and in humans.

Introduction

One of the most important advantages of diffusion tensor imaging (DTI) (1) is its capability to determine fiber tracks in a noninvasive manner. A typical set of DTI data is composed by diffusion-weighted images sensitized in six or more non-collinear gradient directions, followed by pixel-by-pixel determination of the diffusion tensor. The resultant diffusion tensor, which characterizes the self-diffusion of water, is represented by a rank-2 symmetrical 3 × 3 matrix consisting of six independent variables, resembling an ellipsoid in a three-dimensional space. The eigenvector of the largest diffusion tensor eigenvalue (i.e., direction of the fastest diffusion) is generally assumed as the local fiber orientation, which can in turn be used to help establish connectivity among various brain regions (2-7). The goal of DTI fiber tracking is thus to generate continuous, reliable and robust fiber tracks from the diffusion tensors.

Most tracking techniques can be loosely assigned to two groups: streamline propagation and global energy minimization approaches. While both attempt to estimate the best route of a fiber, the global energy minimization approach (5,7) delineates the tracks by minimizing a specific cost function, as opposed to the streamline tracking technique which determines the trajectories from local information. As such, global energy minimization techniques are computationally intensive and slow in general, especially when the algorithms needs to avoid local minimums. On the other hand, streamline tracking approach, which is one of the most widely used techniques in today's research and clinical applications, is usually straightforward and fast. When starting points and propagation rules are given, the tracks can readily propagate forward in a 3D vector field (2,4). Oftentimes procedures that perform image registration, noise removal and tensor or vector field regularization before initiating the tracking process are integrated as a part of the fiber tracking process to improve the vector field quality and tracking reliability.

In this report, we separated the field adjustment and smoothing steps from the core tracking algorithms, and focused on the streamline tracking algorithm only. Because streamline tracking has been studied extensively in physics and engineering disciplines, there are many algorithms that can be selected for DTI fiber tracking when the discrete fiber directional information is given. For example, the fiber assignment by continuous tracking (FACT) algorithm is widely adopted and has been implemented in several fiber tracking software packages (4). It uses the conventional voxel concept and its core propagation algorithm is close to Euler's method for extremely fast tracking speed. Basser et al. proposed a field interpolation and regularization method in conjunction with a numerical integrator which can be Euler's method or the preferred Runge-Kutta method (2).

While selecting an effective streamline propagation algorithm is similar to other physics and engineering problems, the termination conditions which determine whether a fiber track should continue are unique in brain white matter. It is common for most fiber tracking algorithms to use a set of globally applied criteria. However, it can be a difficult task to keep a set of rules in a coherent and consistent manner for all fiber tracks in different brain regions. Because of the lack of a gold standard in fiber tracking, user intervention based on a priori information or experiences plays an important role in determining the termination parameters, rendering inconsistent tracking results.

To achieve fast and reliable fiber tracking results, an improved streamline method is described in this report that tracks nerve fibers with high propagation accuracy, minimizes human intervention and preset criteria, and can start and end based on the internal property of the vector field and tissue characteristics. This streamline tracking technique can also be preceded by tensor field adjustment techniques for an improved field quality, along with a propagation modulation method such as tensor deflection (TEND) during tracking by extending TEND into the continuous tensor field model (8).

Theoretical Framework

Discrete vs. Continuous Fiber Tracking

The DTI tensor and the subsequent directional information are typically computed from diffusion weighted images on a pixel-by-pixel basis. It is common in medical imaging that the smallest data point in a three dimensional volume, i.e. a voxel, is treated as a homogeneous block which contains no information of fiber curvature, making it impossible to bend a fiber within the voxel. Theoretically, however, a voxel can be considered as a point source and the imaging data can be generalized into a continuous framework by interpolating between the discrete data points to form a continuous volume in 3D. In this manner, a continuous field can be flexibly constructed from the discrete DTI data when a proper connection method is used to provide an effective model to match the physical brain. Generally, any common interpolation method, such as linear, cubic or spline interpolation, can be a candidate for the field construction. The naturally accepted concept of voxel can in turn be seen as the nearest neighbor interpolation in a continuous field framework.

Streamline Tracking in a Continuous Field

In this report, the direction and magnitude of a principle eigenvector are treated as the pseudo-velocity after continuous field construction. The uniqueness of neuronal fiber tracking is that the white matter tracking can be bidirectional and the rules for track monitoring and termination should be provided.

The trajectory evolution algorithm controls the course of fiber tracking. When the DTI vector field is interpolated into a continuous framework, the streamline tracking is numerically equivalent to solving an ordinary differential equation (ODE)

$$\begin{array}{l}\frac{d\mathbf{\text{r}}\left(x,y,z,t\right)}{dt}=\mathbf{\text{v}}\left(x,y,z\right)\\ \mathit{\text{with}}\mathbf{\text{r}}\left(x,y,z,0\right)={\mathbf{\text{r}}}_0\end{array}$$

where r is the streamline track, v the pseudo-velocity derived from the directional eigenvector of the diffusion tensor, x, y, z the spatial coordinates, t the pseudo-time, and r₀ the initial positions of seed points. While most streamline tracking algorithms directly take the normalized magnitude of eigenvector v₀ during tracking, the velocity perspective of the tensor directional field allows us to flexibly construct the vector field by combining tissue property information, such that the termination criteria can be made more sensitive to the difference between gray matter and white matter. In this report, the vector field was simply weighted by FA values.

Typically, the simplest solution to solve an ODE numerically is to use Euler's method. Starting from a given initial condition, the fiber track propagates along the direction of the principal eigenvector from one position to the next. This process is repeated until one of the termination criteria is met. The advantage of Euler's method is that it is extremely fast by approximating a curve with a series of straight lines (9). However, it has only first order accuracy. Reducing the step size or increasing matrix size by hyper-sampling the original matrix volume would introduce stability issues. In numerical computing, the de facto standard of solving an initial value ODE problem to achieve higher order accuracy is the Runge-Kutta method, which uses trial steps at the midpoint of an interval to cancel out lower-order error terms (9). In our implementation, the fourth order Runge-Kutta algorithm with direct feeding of the intermediate data is used for fiber track propagation. The vector directions also need to be flipped in order to achieve tracking in both directions.

Termination Criteria for Streamline Tracking

The termination criteria are used to stop a track when it is likely to leave the white matter region and enter another region where the tensors are not well defined. These criteria are important to white matter fiber tracking because the false-positive tracks must be suppressed to reach meaningful results. Most fiber tracking algorithms to date have the following three criteria to terminate a track: 1) when the track reaches a segmented boundary or image boundary; 2) when the track reaches the maximum number of propagation steps; 3) when the track turns any degree larger than a user-defined angle. While the first criterion is more objective using well established imaging or segmentation techniques, the last two criteria are mostly based on the users' experience or preference, and can be biased especially in the case of determining a maximum turning angle. Furthermore, because these termination criteria are universally applied to all fiber tracks, there is no a priori information for the tracking algorithm, which is always driven by local data in streamline tracking, to judge if a sharp turn comes from a real fiber, or a voxel with corrupted directional information, or is simply caused by the low coherence of gray matter. As a result, a compromise between setting high criteria to discourage false-positive tracks and lowering the criteria to avoid truncating sharp-turning fibers often introduces difficulties into the fiber tracking process. Thus, globally applied termination criteria increases the human involvement and requires a priori information to adjust mutually nonexclusive termination conditions for meaningful tracking results to be reached in different regions.

We present here a single unified termination criterion to address this problem. This criterion is based on the fact that the diffusion tensor principal eigenvectors are more collimated inside the white matter fibers and more randomly oriented in gray matter and CSF regions. Thus, the distance the track moves in the white matter regions is longer than the distance it moves in the gray matter regions for the same number of time steps (Fig. 1). A track can then be naturally terminated when it moves slowly than it does in white matter by setting a minimum speed limit. This unified termination criterion conceptually illustrated in Fig. 2 is based on the intrinsic local information by monitoring the local tracking speed to evaluate the tracking situation. This intrinsic difference between white matter and gray matter provides a way to set a proper minimum speed limit. In our implementation, the threshold to label low FA region was set at 0.3 (10,11). A Monte Carlo simulation on the eigenvector field was also carried out to find the low coherence region such that a coherence factor was determined at 0.85v₀ in regions with low FA. Thus, the minimum tracking speed was set at 0.25v₀ by combining the coherence factor and the FA weighting. As a result, it is not necessary to segment out the gray matter regions or to monitor the curvature of the track. As long as the principal eigenvector field of DTI and the starting points are given, the tracking can start and stop automatically by monitoring the track propagating behavior only. In addition, this unified termination criterion still has the ability to integrate with all three aforementioned termination criteria if a priori information justifying these criteria is available.

Fig. 1.

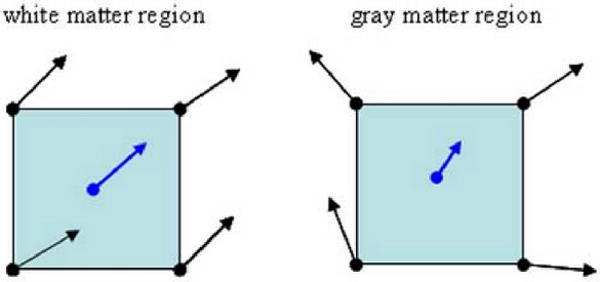
Pseudo-speed in a continuous field becomes an indicator or measurement of local vector field coherence. Tracking speed will be slower in gray matter regions.

Fig. 2.

A schematic illustration of the unified termination criterion based on the pseudo-speed. The red point represents a corrupted vector which could produce incorrect fiber forks when tracks pass nearby. With the unified termination criterion, track A survives a sharp turn because it has high tracking speed. Track B and C illustrate wrong forks which have less sharp turning angles than track A, but would terminate automatically in gray matter due to their slow tracking speed. Should a turning angle limit be used, track A could be terminated prematurely while tracks B or C could survive, leading to a premature termination or a false positive.

Experiments

Because of the present lack of a gold standard for fiber tracking in human DTI, a simulated curvature phantom was generated to demonstrate the tracking algorithms. The phantom was a 3D elliptical band in a 128 × 128 × 128 volume with cubical voxels. Each voxel inside the band, simulated as white matter, had the same FA value set at 0.34, and the fiber orientation was in the tangential direction of the ellipse. The ratio between the two semi axes of the ellipse was 1:2. The cross section of the 3D elliptical band was 5 × 4 voxels. The voxels outside the band were simulated as gray matter with FA = 0.1. The intensity of gray matter and white matter in the base image was the same. The base image and 15 diffusion weighted images, acquired with the same diffusion directional scheme as the in vivo data collected on a GE Excite 3T scanner, were generated from the diffusion signal attenuation equation. The SNRs of the base image and the diffusion weighed images were approximately 30 and 14 respectively by adding Gaussian noise into the clean image. We assumed that diffusion weighted images had the same level of noise but lower SNR in comparison to the base image because of signal attenuation. The b factor was set to 800 s/mm². The diffusion tensor was then computed back from the noisy diffusion weighted images with the Levenberg-Marquardt nonlinear fitting algorithm. The tensors were decomposed into eigenvectors and eigenvalues for DTI fiber tracking. The eigenvectors had unit magnitudes after normalization.

The simulated fibers were tracked from the same starting points by 1) Euler's method with FA=0.15 thresholding and 30 degree turning angle limit, 2) Euler's algorithm with FA=0.15 thresholding but without the curvature limit, and 3) the proposed streamline fiber tracking with the minimum speed as 0.25v₀ which was moving averaged over the most recent 3 consecutive tracking steps. Averaging with more tracking steps will increase the moving average window for better stability, but it will also increase the risks of entering a neighboring fiber and generate a wrong fork before the fiber can be terminated. The continuous field was constructed from tri-cubic interpolation on the weighed discrete DTI directional field described above. The averaging from 3 recent steps provides good stability and sensitivity for fiber tracking in a continuous field.

To demonstrate our new streamline fiber tracking method in vivo, healthy human brain DTI images were acquired with a resolution of 128 × 128 × 68 giving 1.9mm × 1.9mm × 1.9mm voxel size with a single shot diffusion weighted EPI sequence on a GE 3T Signa Excite scanner at TR = 17000 ms, TE = 70.3 ms, FOV = 24 cm with 8-channel SENSE encoding. The SNRs of the base image and 15 diffusion weighted images were approximately 29 and 12 respectively with a b factor of 1000 s/mm². The tensor computation procedure was the same as the procedure in the phantom simulation. The white matter tracking procedure was carried out in the right uncinate fascicle, a well-known fiber bundle with an arch in the middle (12). The starting and target ROIs were selected manually by referencing the images presented in other fiber tracking reports (13). Both ROIs were large enough to ensure that the whole uncinate fascicle passed through the two regions. The fibers were tracked by both our method and Euler's method without a turning angle limit under FA=0.15 thresholding from the same field and ROIs for easy comparison. The ratio between the survival tracks, the tracks passed through two ROIs, and total tracks was used to assess the effectiveness of the tracking method.

To better illustrate the agreement between the fiber tractography and anatomical structure, we examined the sizes of fiber cross sections on a coronal slice passed by the tracks from both methods and compared with the data presented in anatomical and histological research. For the reason of consistency with published histological results, the cross section of tracks was investigated on the coronal slice 2 mm in front of the base arch of the uncinate fascicle. The size of the fiber was measured as the area circumscribed by the pixels through which the tracks passed. The measured sizes were then evaluated by comparing with the reference value found in the histological literature for the healthy controls' combined cross-sectional area of the right uncinate fascicle, to assess the agreement of the spatial coverage of tracked fibers (14).

Results

The tracking results in the half ellipse phantoms are shown in Fig. 3. The top and bottom of the elliptical band in the figure are transparent to demonstrate the track pathways inside the band. Fig. 3a shows a set of fiber tracking results using Euler's method with a typical 30° turning limit. The combination of the vector field noise, insufficient tracking accuracy and global curvature thresholding can terminate all fiber tracks early when the turning-angle limit is stringent. That is, the caution exercised here to suppress the false-positive fibers would almost always lead to truncations of sharp-turning fibers above the threshold. Subsequently, Fig. 3b shows the tracking results using Euler's method without curvature limit to exam the tracking accuracy only. Under such a condition, the accumulated errors still lead to deviations from the actual tracks, resulting in fewer surviving fiber tracks in the white matter region as the streamline propagation goes on. Our streamline tracking algorithm tracked continuously inside the band of ellipses with a higher survival rate for better fiber spatial trajectories and representation (Fig. 3c). Starting from the same ROI with 20 seeds in the experiment, 90% of tracks (18 out of 20) failed to track the whole half ellipse with Euler's method while only 35% of tracks (7 out of 20) failed with our tracking method.

Fig. 3.

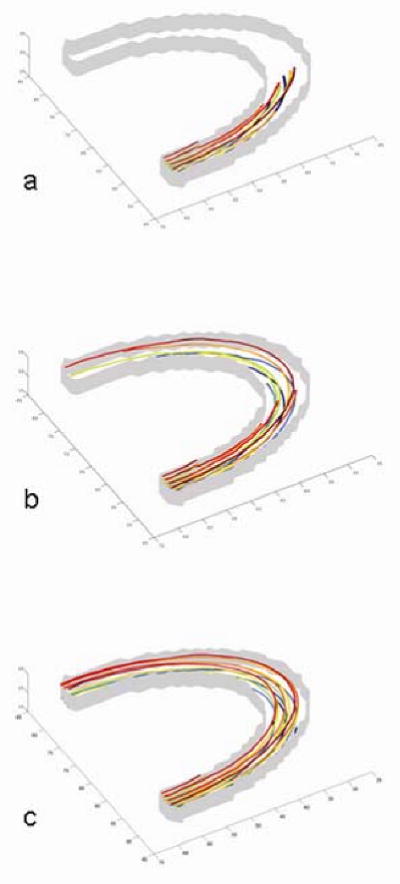
Tracking results inside the half elliptical band. The top and bottom of the 3D band are transparent to demonstrate the track pathways inside the band. a) Euler's method with FA=0.15 thresholding and turning angle limit at 30°. b) Euler's method with FA=0.15 thresholding but without turning angle limit. The deviation is mainly caused by the noisy tensor field and accumulated propagation errors. Fewer tracks stay inside the white matter region as the streamline propagation goes on. c) Proposed fiber tracking method. Most fiber tracks are recovered from the noisy tensor field.

To validate the tracking algorithm in vivo, the streamline tracking procedure was carried out in the human brain to determine the uncinate fascicle. The tracking starts from a large slab with 388 starting seed points to ensure that the ROI holds the entire intersection of the uncinate fascicle. The results show that both methods produce successful tracks from the seed region to the target ROI (Fig. 4). However, only 6 out of 388 seeds tracks reached the target with Euler's method with no preset curvature limit while 34 out of 388 tracks reached the target with our method.

Fig. 4.

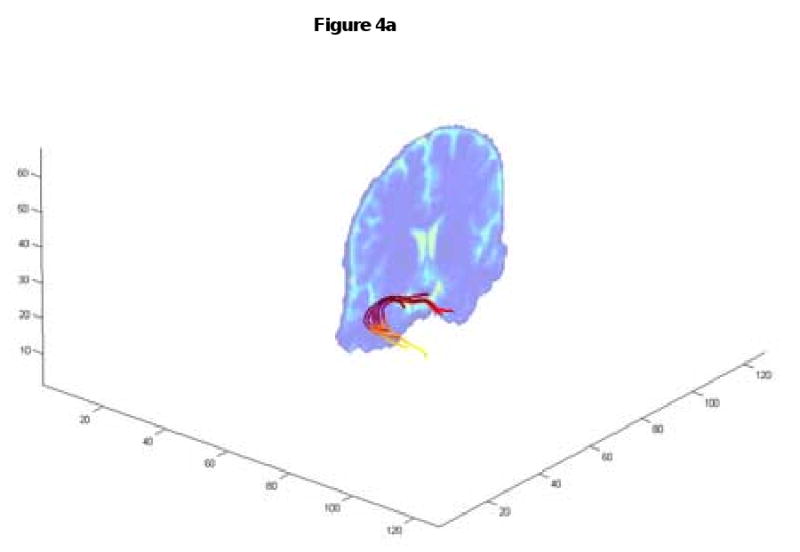
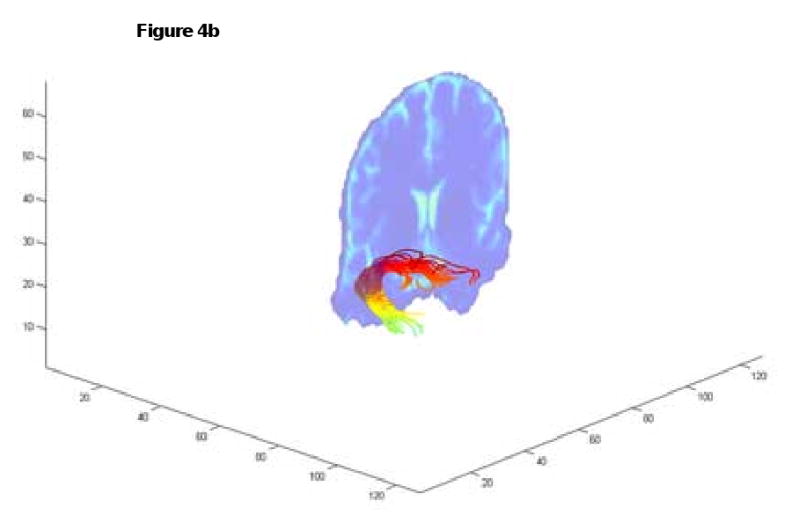
Tracking the uncinate fascicles. Euler's method allowed 6 successful tracks (4a) while our method led to 34 successful tracks with improved spatial details (4b). The coronal slice is the same as the slice shown in Fig.5 and Fig. 6.

Because the uncinate fascicle forms a solid fiber bundle near its turning arch, it presents a suitable location to assess the validity of fiber tracking by comparing the cross-sectional areas of the tracked fibers with the data presented in histological reports. Fig. 5 shows the location of the coronal slice described in the Experiments section. The cross-sectional areas of both tracking results are shown in Fig. 6. The overlay between the two cross sections suggests that the survived tracks from both methods share similar trajectories in the main white matter fibers. The pixel spatial arrangement and the circumscribed areas are shown in Fig. 7. The area circumscribed by the intersected pixels is approximately 108.3 mm² with our method and 52.34 mm² with Euler's method in the frontal lobe anterior to the turning arch, and is approximately 97.47 mm² and 52.34 mm² respectively in the temporal lobe region. The average cross-sectional area in healthy humans for this region is 98.7 ± 28.4 mm² in the histological report (14). Thus, our result shows high agreement with the histological data while that computed from Euler's method is lower than the referenced mean value by 1.8 standard deviations. This preliminary result suggests that our method has similar spatial coverage compared to the true white matter fiber bundle, and delivers accurate spatial trajectory information of fibers.

Fig. 5.

The coronal slice location used to investigate the cross-sectional area circumscribed by tracked fibers.

Fig. 6.

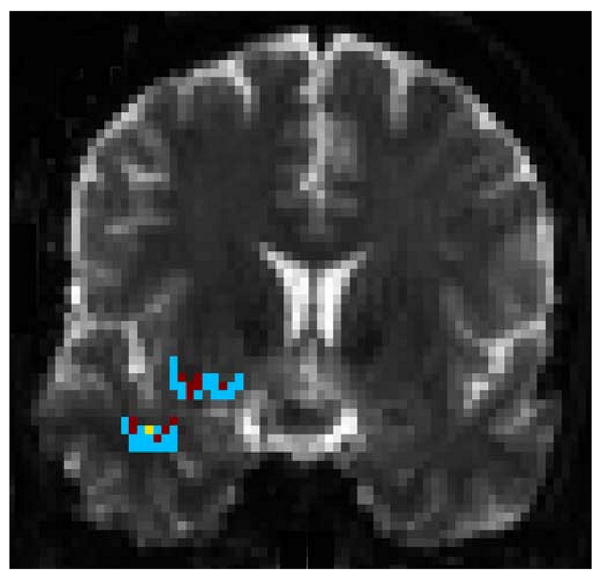
The regions where the tracks pass through the coronal slice in Fig. 5. The pixel arrangement is shown in Fig. 7.

Fig. 7.

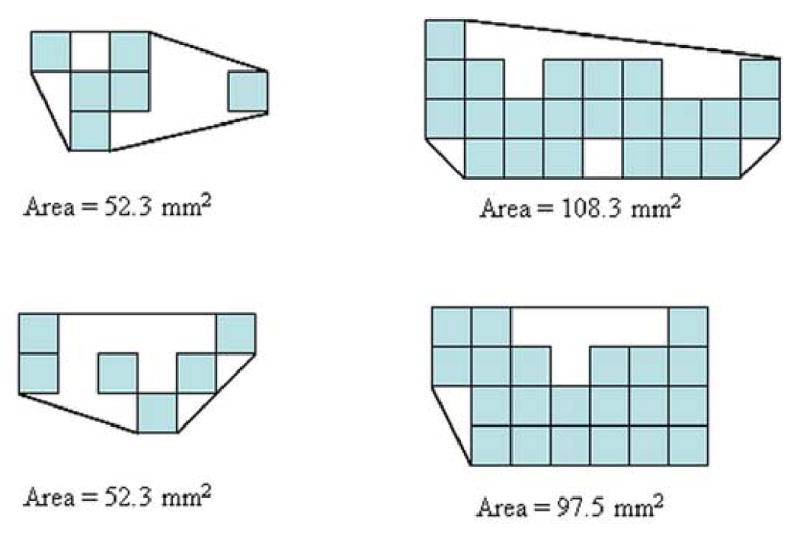
A graphic illustration of the cross-sectional area determination. The left column shows the cross-sectional pixels tracked by Euler's method, and the right column shows the cross-sectional pixels tracked by our method.

Discussions and Conclusions

While fiber tracking with DTI is an effective method to quantitatively reveal white matter tracts in vivo non-invasively, and most fiber tracking techniques successfully deliver reasonably good results in tracking brain white matter fibers, myocardiac fiber and muscle fibers, the lack of a gold standard for in vivo fiber tracking makes the validation of tracking results and comparisons among different tracking techniques a difficult task. In addition, the gap between the complexity of brain white matter fibers and the limited information from the DTI images makes fiber tracking a formidable problem. For example, the relatively low resolution and the limitations of the DTI model have raised questions as to its ability for revealing thin and short fibers or the fibers in complex regions.

The method described in this report aims to track fibers using the typical acquisition methods found in today's DTI experiments and obtain reliable tracking results. The high accuracy tracking algorithm dramatically reduces propagation errors. The reference to neighboring information, rather than relying on the information of one voxel alone, reduces the sensitivity to corrupted local information in the directional field computed from the diffusion tensor. This also helps to reduce erroneous forks and recovers some of the actual trajectories masked by partial volume effects. Further, the unified termination criterion based on sensing the local tissue properties instead of setting global thresholds could reduce potential biases. The consistency with known fiber structures in the brain and better spatial coverage of tracked fibers demonstrate that DTI fiber tracking has the potential to reveal the volume size of relatively large fiber bundles.