The beak of the other finch: coevolution of genetic covariance structure and developmental modularity during adaptive evolution

Abstract

The link between adaptation and evolutionary change remains the most central and least understood evolutionary problem. Rapid evolution and diversification of avian beaks is a textbook example of such a link, yet the mechanisms that enable beak's precise adaptation and extensive adaptability are poorly understood. Often observed rapid evolutionary change in beaks is particularly puzzling in light of the neo-Darwinian model that necessitates coordinated changes in developmentally distinct precursors and correspondence between functional and genetic modularity, which should preclude evolutionary diversification. I show that during first 19 generations after colonization of a novel environment, house finches (Carpodacus mexicanus) express an array of distinct, but adaptively equivalent beak morphologies—a result of compensatory developmental interactions between beak length and width in accommodating microevolutionary change in beak depth. Directional selection was largely confined to the elimination of extremes formed by these developmental interactions, while long-term stabilizing selection along a single axis—beak depth—was mirrored in the structure of beak's additive genetic covariance. These results emphasize three principal points. First, additive genetic covariance structure may represent a historical record of the most recurrent developmental and functional interactions. Second, adaptive equivalence of beak configurations shields genetic and developmental variation in individual components from depletion by natural selection. Third, compensatory developmental interactions among beak components can generate rapid reorganization of beak morphology under novel conditions and thus greatly facilitate both the evolution of precise adaptation and extensive diversification, thereby linking adaptation and adaptability in this classic example of Darwinian evolution.

1. Reconciling adaptation and adaptability: g matrix meets darwin's finches

Geometric simplification of an organism's complexity, with its multitude of interacting traits and effects (Thompson 1917; Fisher 1930; Rice 2004), and its environment (Wright 1932; Simpson 1944; Lande 1979; Arnold et al. 2001) has been a powerful tool in evolutionary biology. Subject to usual assumptions of quantitative genetics, geometric investigation of additive genetic covariance matrix (G matrix)—a statistical summary of allelic effects in a population—can provide important insights into foundational questions on the nature and maintenance of genetic variation in natural populations (Steppan et al. 2002; Roff 2007; Arnold et al. 2008). Because the G matrix is a static imprint of many population processes—in particular drift, selection, mutation, recombination and migration, which are, in turn, affected by a multitude of organismal development and functional effects (Turelli 1988; Hansen 2006)—it should be useful as both a historical probe, inferring past evolutionary events in a population, and a future predictor of evolutionary change (Schluter 1996; Steppan et al. 2002; Björklund 2004; McGuigan 2006; Arnold et al. 2008). The crucial assumption in these applications is persistence of the G matrix in relation to dynamic processes that create and maintain it, which is, proximately, a question of the nature and directionality of the relationship between genetic, developmental and functional integration of phenotypic traits (Cheverud 1982, 1996; Atchley 1984; Riska 1989; Wagner & Altenberg 1996).

Whether recurrent co-selection of traits—their functional integration—is eventually translated into their co-inheritance—genetic integration—is determined by developmental dynamics of these traits. On the one hand, persistent co-selection can reduce variance in developmentally linked traits preventing further evolution of their genetic integration (Bulmer 1971; Slatkin & Frank 1990); on the other hand, the selected variance can be replenished by developmental and functional interactions among traits, e.g. in geometric sense, projections from correlated structures to the direction of the most persistent selection (Rice 2004; Blows & Walsh 2009). Thus, functional integration does not necessarily equal genetic integration and vice versa, even for repeatedly co-selected traits, either because of compensatory interactions between traits during development or because of the accumulation of neutral genetic and developmental variation in trait complexes (Hermisson & Wagner 2004). Two ubiquitous phenomena are central to these patterns: (i) functional interchangeability and redundancy—where different combinations of traits result in the same fitness or physiological output (Arnold 1983; Alfaro et al. 2005; Collar & Wainwright 2006; Young et al. 2007)—and (ii) emergent and compensatory developmental interactions among traits whose steps and progression are not the subject of natural selection on resulting functional phenotype (Baldwin 1902; Müller & Newman 2003; West-Eberhard 2003; Forgacs & Newman 2005; Gerhart & Kirschner 2007).

Few groups of traits illustrate the diverse relationships between developmental and functional integration better than do foraging structures—complexes of traits that combine exaggeration with variability and precision of local adaptation with exceptional evolutionary diversification. Avian beaks, in particular, are textbook examples of both precise adaptation and extreme evolutionary diversification. Importantly, for the focus of this study, distinct developmental precursors of beak's components (see below) are routinely under strong natural selection for close functional integration, making them an ideal system to study the mechanisms that link development and evolution of local adaptation and evolutionary change.

Darwin's finches, in particular, are one of the best-studied morphological radiations (Lack 1947; Grant 1986; Grant & Grant 1989; Schluter 2000) providing well-established examples of rapid adaptation and evolutionary diversifications in relation to ecology (Boag & Grant 1981; Schluter 1984; Schluter & Grant 1984; Grant & Grant 2006), functional and developmental mechanisms (Bowman 1961; Grant 1981; Abzhanov et al. 2006; Grant et al. 2006) and quantitative genetics and evolution (Grant & Grant 1995, 2002; Schluter 1996). However, Darwin's finches also illustrate the paradox, where rapid, and essentially unconstrained (Gibbs & Grant 1987; 1995; Grant & Grant 2002), evolution of precise local adaptation (that is expected from close genetic integration of beak components (Grant 1994) and the modularity of developmental processes and their phenotypic outcomes) nevertheless coexists with a rapid evolutionary diversification (Grant 1986) that close correspondence between genetic and developmental integration should prevent. A key to resolution of this paradox lies in understanding the developmental dynamics of beak components.

Although the three commonly measured beak components—beak length, width and depth—form a closely integrated functional unit in adult birds, they have different ontogenies. For example, beak depth has an important function of forming nestling gape, resulting in its relatively later ossification, greater developmental variability and lesser ontogenetic integration with other beak components (Badyaev & Martin 2000a; Badyaev et al. 2001). Beak length, as measured in adult birds, includes not only the premaxillary bone, but also the continuously growing horny rhamphotheca that accounts for greater variability and compensatory functional interactions of this trait across an individual's lifetime. Beak depth and its major component—the dentary bone—are more affected by postontogenetic remodelling by muscle attachment than the other two components (A.V.B. 2009, unpublished data). More specifically, recent studies of developmental biology of avian beaks have identified a major role of emergent and self-regulatory processes in beak morphogenesis (Eames & Schneider 2008; Jheon & Schneider 2009), where heterochronic expression of the same developmental modules produce both environment-specific fine-tuning within a species and extensive evolutionary diversification (Wu et al. 2006; Abzhanov et al. 2007).

During beak development, cells derived from cranial neural crest and mesodermal mesenchyme migrate into embryo's facial region and form several condensations or prominences covered by an ectoderm-derived layer of epithelium. There is evidence of pronounced compensatory growth both within and among these prominences where spatial and temporal distribution of cell proliferation is regulated by conserved regulatory factors (Helms & Schneider 2003). For example, Bmp4 regulates early mesenchyme commitment of neural crest cells to osteogenic pathway (Abzhanov et al. 2007), general cell proliferation in localized zones within the prominences (Wu et al. 2004) and fine-tuning of the outgrowth (Abzhanov et al. 2004). The outgrowths induce reciprocal (Geetha-Loganathan et al. 2009; Hu & Marcucio 2009) regulatory feedback between mesenchyme and epithelium, with epithelium layer providing both axial information and bounding effect for cell proliferation (MacDonald et al. 2004; Jheon & Schneider 2009). Such ectomesenchymal interactions direct orientation and outgrowth of the frontonasal and paired maxillary primordia giving rise to upper beak and of the mandibular primordia producing lower beak. Importantly, different axes of growth within the same cell proliferation zone can have different phenotypic outcomes—for example, Bmp4 and calmodium, when overexpressed in the same domain, cause outgrowth along beak depth and length axes correspondingly (Abzhanov et al. 2006). While such outgrowth is unlikely to result in developmental independence of beak components (because the same tissue is partitioned between the two growth directions), the similarity in precursor tissue allocation among relatives can account for positive genetic correlations between beak components (Grant 1994) despite their antagonistic growth (see §4c).

With this background in mind, I studied multivariate coevolution of genetic, developmental and functional integration in beaks of house finches (Carpodacus mexicanus) during 19 generations after colonization of a novel environment at the northwestern edge of this species' geographical range. In particular, I was interested in reconciling extensive developmental variability in beak morphology with precise local adaptation and extensive diversification among populations (Badyaev & Martin 2000a; Badyaev et al. 2000, 2008). Here, I show that compensatory and facultative interactions among beak components are evident in all aspects of their developmental evolution, producing rapid expression of locally adaptive phenotypes, likely accounting for abrupt changes in phenotypic appearance across generations and polymorphism within generations, and overall functional redundancy of beak configurations. The role of directional selection in this process is largely confined to elimination of phenotypic extremes formed by compensatory developmental interactions, while long-term consistent stabilizing selection along a single axis of beak morphology—beak depth—is mirrored in the structure of beak's G matrix. I suggest that ubiquitous compensatory interactions between beak components can greatly facilitate both the evolution of precise local adaptation and extensive diversification in avian beaks, thereby linking development with evolution and adaptation with adaptability in this classic example of Darwinian evolution.

2. House finch establisment in northwestern montana

(a). Brief history of population establishment

The present range of house finches in continental North America is a result of natural expansion of native populations in the western USA in the 1950s and human introduction of finches through pet trade in the northeastern USA in the 1930s (for details see Badyaev 2009). House finches first reached northwestern Montana from the south and west of the Continental Divide in the 1950s (P. L. Wright 1994, personal communication) and started breeding at the study site—an isolated area of suitable nesting habitat located in an open prairie at the confluence of three mountain valleys—in 1988 (R. McCue 1993, personal communication).

The data for this study were collected continuously from 1994 to 2009 and include n = 7932 individuals (detailed description of study site and protocols are in Badyaev & Martin 2000a). Briefly, all resident finches were trapped, measured, photographed under standardized settings, sampled for DNA and plasma, and individually marked with a unique combination of one aluminium and three coloured plastic rings. Pairing and nesting affiliations of breeding adults were reliably determined with observations, filming on the nests, and confirmed with genotyping (Oh & Badyaev 2006). Complete census of marked individuals, strong fidelity of adult house finches to the location of previous breeding and the isolation of the study site allowed us to follow individual birds from hatching to up to 10 years of age, monitor population size precisely and construct accurate pedigrees (references in Badyaev 2005). Breeding resident population (breeding pairs and single adults between nesting attempts) averaged n = 324 birds per year and varied from n = 218 birds during the fifth generation to n = 628 birds in the 11th generation. In addition, the population included offspring of these parents (sample sizes in table 1), immigrant males and females that transit through the study site and, late in the season, flocks of dispersing juvenile finches from adjacent populations. About 15 per cent of offspring measured in each year after 1995 were progeny of offspring hatched in the previous year (Sæther et al. 2004). Data on first generations of house finches breeding in the study site prior to 1995 (here combined into ‘arrival group’—‘generations 1–4’) were from birds measured at the time of collection and subsequently held at the University of Montana's P. L. Wright Zoological Museum (fig. 1 in Badyaev 2009). For subsequent generations, locally hatched juveniles were measured in each generation from the cohort hatched in 1995 (‘fifth generation’ hereafter) to the cohort hatched in 2009 (‘19th generation’).

Table 1.

Multivariate allometry of beak morphology in locally born fully grown house finches during first 19 generations (n = 5074) following population establishment in northwestern Montana, USA. Eigenvectors and eigenvalues are from correlational matrix with the effects of sex controlled statistically in general linear model.

	generations
	1–4 (n = 39)			5 (n = 323)			6 (n = 396)			7 (n = 355)			8 (n = 252)			9 (n = 411)			10 (n = 294)			11 (n = 374)
	PC1	PC2	PC3	PC1	PC2	PC3	PC1	PC2	PC3	PC1	PC2	PC3	PC1	PC2	PC3	PC1	PC2	PC3	PC1	PC2	PC3	PC1	PC2	PC3
BL	0.27	0.93	0.22	0.72	−0.57	−0.04	0.75	−0.68	−0.08	0.51	0.82	−0.27	0.78	−0.48	0.05	0.80	−0.58	0.08	0.33	−0.04	0.94	0.22	0.64	0.74
BD	0.63	−0.35	0.75	0.49	0.77	−0.49	0.59	0.72	−0.43	0.31	0.12	0.94	0.38	0.42	0.82	0.34	0.58	0.74	0.74	−0.65	−0.27	0.64	0.48	−0.61
BW	0.79	−0.05	−0.68	0.38	0.19	0.87	0.35	0.26	0.90	0.80	−0.56	−0.19	0.52	0.66	−0.63	0.48	0.56	−0.67	0.62	0.79	−0.19	0.74	−0.60	0.29
λ	2.44	1.47	0.63	2.42	1.45	0.71	2.50	1.67	0.83	1.83	1.42	0.48	1.50	0.81	0.38	1.84	0.71	0.51	1.60	1.10	0.61	1.57	1.03	0.64
%	45.4	38.0	16.6	56.4	30.4	13.2	50.1	33.5	16.3	49.1	38.1	12.8	55.8	25.9	18.3	60.3	23.2	16.6	48.5	33.1	18.5	48.4	32.1	19.7
	12 (n = 421)			13 (n = 425)			14 (n = 434)			15 (n = 459)			16 (n = 324)			17 (n = 242)			18 (n = 317)			19 (n = 62)
BL	0.44	0.73	0.68	0.61	0.39	−0.68	0.78	−0.56	0.58	0.80	−0.47	−0.36	0.71	0.44	−0.54	0.82	0.04	−0.57	0.61	−0.10	0.78	0.78	−0.11	0.62
BD	0.46	0.51	−0.82	0.68	−0.71	0.19	0.60	−0.19	−0.78	0.47	0.88	−0.10	0.70	−0.45	0.55	0.33	0.84	0.42	0.81	−0.13	−0.63	0.41	−0.28	−0.79
BW	0.77	−0.63	0.04	0.40	0.59	0.82	0.55	0.80	0.23	0.37	0.09	0.93	−0.01	0.77	0.63	0.46	−0.54	0.70	0.17	0.97	−0.04	0.48	0.82	0.17
λ	1.47	0.59	0.41	1.47	0.58	0.52	1.14	0.55	0.48	1.35	0.55	0.29	1.47	1.20	0.49	1.50	1.29	0.19	0.91	0.48	0.29	1.36	0.75	0.69
%	59.4	23.8	16.9	57.1	22.6	20.3	55.6	25.2	22.5	61.8	25.1	13.1	46.5	37.8	15.7	48.2	32.3	19.5	54.2	28.6	17.2	51.9	24.9	23.1

BL, beak length; BD, beak depth and BW, beak width.

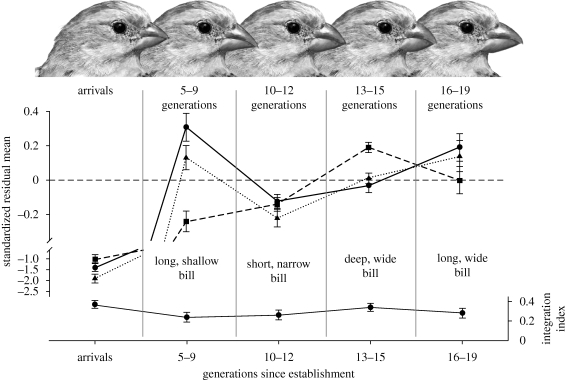
Incubation progress and embryonic development were continuously monitored with incubation probes installed in nests during nest building (Badyaev & Oh 2008), nestlings were individually marked within a few hours of hatching, sexed molecularly by amplification of an intron of the CHD1 gene, and longitudinal growth data were collected every second day to fledging (day 16). After fledging, individually marked juveniles were recaptured at least once a week (references in Badyaev 2005) and juvenile survival selection was measured as survival from 40–45 days of age (fully grown) to 70–80 days of age because no significant juvenile dispersal takes place before that age. This is a period of the strongest selection on beak morphology (Badyaev et al. 2001) as juvenile finches start to feed on seeds independently. We measured (with digital calipers to an accuracy of 0.05 mm): beak length from an angle of the skull to the tip of upper mandible, beak width at the anterior end of nostrils, and beak depth in a vertical plane at the anterior end of nostrils over both mandibles (see Badyaev & Martin 2000b for measurement error and interobserver variance assessment). For illustration of microevolutionary transformations of beak morphology, coordinates of 10 homologous landmarks were digitized from standardized photographs of 20 randomly selected adults in each of the 19 generations. The transformation of the original images was obtained with Procrustes superimposition with tpsSuper 1.03 (Rohlf 1997) and shown, for illustration only, as landmark displacement from the consensus position (figure 1).

Figure 1.

Distinct, but similarly integrated beak morphologies during 19 generations following establishment of house finches in northwestern Montana, USA. Upper drawings illustrate reconfiguration of beak morphology by tpsSuper (v. 1.03) from a consensus position based on displacement of 10 homologous landmarks (black circles in the arrivals group) within each group of generations and is shown for illustration only. Middle graph shows microevolutionary change in standardized (mean = 0, s.d. = 1) beak length (circles, solid line), depth (squares, dashed line) and width (triangles, dotted line) across generations. Lower graph shows integration index (mean ± 1 s.e.) calculated for three beak components as I = [∑(λ_i−1)²/6]^1/2 (Cheverud et al. 1983), where λ_i is an eigenvalue of the correlation matrix of the normalized data (table 1). Statistical significance of the integration coefficient was obtained by resampling, with replacement, of the within-principal component loadings (n = 500).

(b). Material and methods

(i). Pedigree and estimation of variance components

To estimate an overall additive genetic variance–covariance matrix, we constructed a fully resolved pedigree consisting of full- and half-sib groups (n = 429 birds, 90 families, distributed across 11 generations under this study). Parental identities were established through direct observations in the field and subsequently confirmed with genotyping at 16 highly polymorphic microsatellite loci that we developed for this species (for details of parentage analysis see Oh & Badyaev 2006, 2009). Pooling data across several generations minimized the effect of fluctuations in population size (see §2a) on estimation of overall G matrix.

Additive genetic (G) and common environmental (E; e.g. nest effects) variance–covariance matrices were derived by fitting phenotypic data to a multivariate animal model of the general form

where y is a vector of trait values, b a vector of fixed effects, a a vector of additive genetic effects, c a vector of common environmental effects and e a vector of residual variation, and X, Z and E are incidence matrices for the fixed, additive genetic and common environmental effects, respectively (Lynch & Walsh 1998). Analysis was carried out using restricted maximum likelihood implemented in ASReml (2.0) software. We used univariate general linear models (PROC GLM, SAS Inc.) to identify significant fixed effects, and any fixed effect term that was significant in at least one trait was included in the final multivariate model. This resulted in the inclusion of year, offspring sex and age. Nest identity (nested within dam identity) was included as a random effect representing variance owing to common environment (e.g. nest environment and parental effects).

(ii). Measurement of natural selection

I used three methods to estimate multivariate selection on beak morphology. First, to measure the full extent of nonlinear and correlational selection, I fitted the full second-order polynomial (Lande & Arnold 1983; Phillips & Arnold 1989; Arnold et al. 2001)

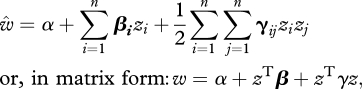where z are original traits, w is juvenile survival associated with the onset of independent foraging (from 40 to 80 days), β is the vector of standardized directional selection gradients, and γ is the matrix of quadratic and cross-product terms among the traits (table 2).

Table 2.

Standardized directional selection gradients (β) and the matrix of standardized quadratic and correlational selection gradients (γ) during first 19 generations following population establishment in northwestern Montana, USA. The effects of sex controlled statistically in general linear model. Last data for selection were collected for the 18th generation.

	generations
	5 (n = 342)				6 (n = 276)				7 (n = 435)				8 (n = 285)
	β	BL	BD	BW	β	BL	BD	BW	β	BL	BD	BW	β	BL	BD	BW
BL	0.013	0.042	−0.020	−0.031	0.006	0.01	−0.038	−0.02	−0.071	0.067	−0.071	0.019	0.031	0.02	−0.063	0.015
BD	0.109		0.073	0.012	0.185		0.085	0.001	0.056		−0.020	0.031	0.005		0.036	0.024
BW	−0.022			−0.022	−0.035			−0.001	0.019			0.014	0.035			0.023
	9 (n = 463)				10 (n = 474)				11 (n = 498)				12 (n = 664)
BL	−0.035	−0.038	0.010	0.053	0.118	0.018	0.070	0.011	0.013	−0.027	0.028	−0.017	0.023	0.016	0.071	−0.045
BD	−0.073		−0.032	0.038	−0.088		−0.016	−0.040	0.042		0.001	0.033	−0.032		−0.047	0.008
BW	−0.013			−0.005	0.018			0.017	0.049			0.013	−0.070			−0.02
	13 (n = 603)				14 (n = 563)				15 (n = 339)				16 (n = 414)
BL	−0.024	−0.011	0.003	0.004	0.043	−0.018	−0.038	0.011	0.102	0.009	0.021	−0.055	−0.079	0.003	−0.054	0.078
BD	0.007		0.017	−0.035	0.078		0.067	0	−0.049		−0.021	−0.032	0.099		0.046	−0.063
BW	−0.020			0.022	0.006			0.017	−0.121			0.023	−0.023			−0.056
	17 (n = 524)				18 (n = 284)				overall (n = 6164, 18 years)
BL	0.034	0.014	−0.063	−0.03	−0.024	−0.01	−0.018	−0.011	−0.02	−0.01	−0.01	0.01
BD	−0.103		0.042	0	−0.006		−0.054	0.052	−0.01		0.01	0
BW	−0.043			−0.02	0.014			−0.013	−0.03			−0.01

Bold values are significant at α < 0.05.

Second, I performed canonical rotation of γ matrix (Box & Draper 1987; Blows & Brooks 2003) to create M matrix whose eigenvectors m_i describe the shape of the response surface and the direction of its principal orientation (table 3). The largest eigenvalues λ_i are associated with the greatest curvatures in the survival response surface; positive eigenvalues describe upward curvature of fitness response and negative eigenvalues indicate downward curvature of response (Phillips & Arnold 1989; Arnold et al. 2001).

Table 3.

Directions of the strongest selection on beak morphology during first 19 generations following population establishment in northwestern Montana, USA. Shown are eigenvalues (λ_i) and eigenvectors (m_i) of the M matrix from the canonical rotation of γ (table 2) and the direction of the strongest natural selection (a₁) estimated by the projection pursuit regression. Additional directions were not significantly different.

	generations
	5				6				7				8
	λi	BL	BD	BW	λi	BL	BD	BW	λi	BL	BD	BW	λi	BL	BD	BW
m1	0.06	−0.32	0.54	−0.16	0.05	−0.41	0.89	−0.17	0.06	0.86	−0.32	0.40	0.07	0.41	0.86	0.31
m2	0.01	0.67	0.31	−0.47	0.01	0.69	0.42	0.58	0.01	−0.09	0.67	0.73	−0.03	−0.73	0.32	0.65
m3	−0.03	0.12	0.41	0.31	−0.02	−0.59	−0.12	0.80	−0.02	0.51	0.66	−0.55	0.01	−0.12	0.31	0.21
a1	—	0.11	0.18	0.77	—	0.36	0.19	0.56	—	0.48	−0.14	0.58	—	0.39	0.01	0.59
	9				10				11				12
m1	0	0.53	0.67	0.52	0.02	0.54	0.15	0.83	0	0.53	0.02	0.85	0.02	0.92	0.39	−0.09
m2	−0.03	0.84	−0.29	−0.47	0	0.46	0.78	−0.44	−0.01	0.20	0.97	−0.15	0	0.13	−0.08	0.99
m3	−0.09	0.16	−0.68	0.71	−0.07	−0.71	0.61	0.36	−0.07	0.82	−0.25	−0.51	−0.03	−0.37	0.92	0.12
a1	—	0.24	0.04	0.35		0.52	0.82	0.11	—	0.39	0.23	0.87	—	0.53	0.21	0.42
	13				14				15				16
m1	0.02	0.08	0.84	−0.53	0.06	−0.65	0.05	0.76	0.03	−0.17	0.96	−0.21	0.07	0.60	0.27	0.75
m2	−0.01	0.36	0.46	0.81	0.01	0.28	0.94	0.19	0	−0.32	0.14	0.94	−0.01	0.75	0.65	0.14
m3	−0.03	0.93	−0.25	−0.26	−0.06	0.70	−0.33	0.63	−0.05	0.93	0.23	0.28	−0.06	−0.28	0.87	0.12
a1	—	0.63	0.11	−0.54	—	−0.15	0.03	−0.47	—	0.25	0.24	0.71	—	0.16	0.37	0.65
	17				18				overall
m1	0.01	0.52	0.01	0.84	0.01	0.79	0	−0.61	0.01	0.18	0.98	0.01
m2	−0.01	0.17	0.84	−0.14	0	0.22	0.27	0.94	0	0.69	−0.13	0.71
m3	−0.06	0.76	−0.24	−0.49	−0.02	0.27	0.74	−0.35	−0.01	−0.70	0.11	0.70
a1	—	0.49	0.07	0.67	—	0.54	−0.16	0.58	—	0.57	0.19	0.45

Bold a₁ values are significant at α < 0.05 and s.e. is determined by 500 bootstraps.

Third, I used the projection pursuit regression to find the fitness surface that maximizes the contribution of trait combination to juvenile survival without the assumption of the specific shape of fitness surface (table 3; Schluter & Nychka 1994). Here, a linear combination of the original traits y_i = a^Tz, where a is projection delineating the fitness contribution of each original trait (Schluter & Nychka 1994). A range of smoothing parameter (lambda) values was tested and the one that minimized the generalized cross-validation score was retained. I used PP program (Schluter & Nychka 1994) to calculate the projections and associated statistics. Only one projection is reported because the second projection was not statistically different from the first for any generations.

3. Microevolutionary trends: evidence for compensatory developmental and functional interactions among beak components

Across 19 generations since establishment in northwestern Montana, house finches expressed a wide spectrum of beak morphologies (figure 1) with beak depth showing the most consistent trend across generations compared with width and especially length (for univariate analysis of microevolutionary trends see fig. 1 in Badyaev 2009).

Three lines of evidence suggest that phenotypic variability within each generation was a result of compensatory developmental and functional interactions among beak components. First, morphological integration was similar for widely distinct beak morphologies across generations (table 1; within generations, each eigenvector was commonly aligned with only a single (and, importantly, different across generations) beak component) pointing to adaptive equivalence of distinct beak configurations in figure 1.

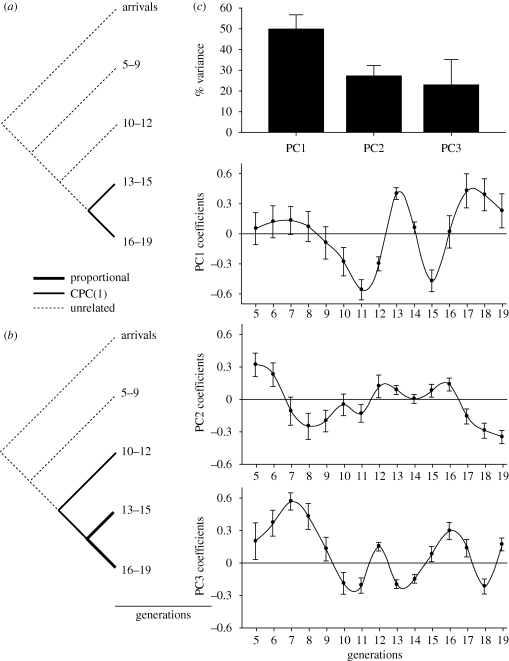
Second, morphological covariance structure, evaluated with the common principal component (CPC) analysis and Flury's (1988) decomposition of χ²-tests (Phillips 1998), was dissimilar across generations in both sexes, despite very short microevolutionary scale and sufficient statistical power to detect difference (figure 2, table 1). In males, with the exception of the last six generations that shared one common principal component (CPC1: χ² = 0.84, p = 0.66), all earlier generations had unrelated covariance structures (unrelated versus CPC1: χ² > 20.18, p < 0.001). In females, only the last six generations had proportional covariance structure (χ² = 0.31, p = 0. 57) and shared one CPC with generations 10–12 (χ² < 2.15, p > 0.65), while all other generations had unrelated covariance structures (χ² > 22.0, p < 0.001).

Figure 2.

Microevolutionary trends in covariance structure of beak morphology illustrate widespread interchangeability and compensatory variation in beak components during microevolutionary change. The CPC analysis of shared covariance structure in (a) males and (b) females during 19 generations after population establishment. Line thickness indicates the hierarchy of shared covariance structure. (c) Eigenanalysis of changes in covariance structure across generations (conventional PC analysis of the covariance matrices of CPC1 scores of each generation). Shown is percentage of variance accounted by the first three eigenvalues across all generations and coefficients of corresponding eigenvectors. Error bars are bootstrapped s.e. (n = 100). High covariation among generations would produce consistently increasing or decreasing PC loadings across generations, while fluctuating PC loadings among generations indicate negative covariation among some generations and might be produced by compensatory growth of different beak components in different generations (table 5).

Third, a detailed eigenanalysis combining within-generation covariance patterns with across-generation trends (figure 2c) showed that despite widely distinct beak phenotypes across generations, the change (i.e. across-generation fluctuations in principal component (PC) coefficients of within-generation CPC1; figure 2c) was gradual between adjacent generations, the pattern expected when consistent microevolutionary change in one beak component (i.e. beak depth; figure 1) is associated with compensatory growth in the other two components. Monotonically increasing or decreasing PC coefficients across generations would indicate proportional changes in covariance structure (e.g. variation in beak size would be needed to accomplish changes in individual dimensions of beak), whereas fluctuating PC coefficients across generations would suggest the lack of the link between within- and among-generation variation in beak morphology. That all three eigenvalues were needed to explain the link between within- and across-generation change in beak morphology (figure 2c, top) as well as dimensionality of P (figure 3) indicates that different beak components show compensatory variation in different generations, the pattern that also explains abrupt changes in beak phenotypes (figure 1, top) and the lack of shared covariance structure (figure 2a) despite somewhat gradual microevolutionary changes in phenotypic covariance structure (figure 2c).

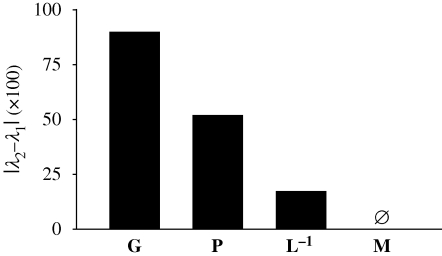
Figure 3.

Relative difference between the first (λ₁) and the second (λ₂) eigenvalues of additive genetic covariance matrix (G, table 4), phenotypic covariance matrix (P, table 1), matrix of ontogenetic variation (L⁻¹, table 5) and matrix describing adaptive landscape (M, table 3) in Montana house finches over 19 generations after population establishment. Smaller values indicate greater dimensionality of variability. The third eigenvalues were not significant in any of the matrices.

The major evolutionary significance of compensatory developmental interactions and functional versatility in configurations of beak components is that they would shield from natural selection and, thus, maintain substantial developmental and genetic variation in individual beak components (see §4a), thereby enabling rapid microevolutionary changes during population establishment, such as shown by long and shallow beaks of finches during generations 5–9 followed by short and narrow beaks of finches in subsequent generations (figure 1). Such channelled and facilitated changes in beak phenotypes not only can enable rapid expression of suitable morphology and exploitation of resources in novel environments, but can also reconcile the necessity for specialization and close functional integration in beaks with extensive evolutionary diversification following changes in natural selection. Whether such facilitated developmental variation is an evolved property or an emergent phenomenon of generative mechanisms of beak morphogenesis can be examined by direct comparisons of genetic covariance structure in beak morphology with fluctuations in natural selection and developmental interactions as house finches adapt to novel environments of northwestern Montana.

4. Genetic covariance structure in relation to adaptive equivalence and developmental dynamics

(a). G matrix

Beak depth had higher additive genetic variance than other beak components (table 4). All beak components, but particularly beak width and length, showed nearly perfect genetic correlations, the pattern most likely representing genetic similarity in allocation to the shared developmental precursor (see §4c). The eigenstructure of G was described by two significant eigenvalues that together explained 94 per cent of variance: the first eigenvector was aligned with variation in beak depth and accounted for more than 85 per cent of variance, and the second eigenvector was aligned with equal expression of beak length and width and accounted for about 9 per cent of additive genetic variance. Such structure is consistent with beak depth showing most continuous microevolutionary trends in both multivariate (figure 1) and univariate (fig. 3d in Badyaev 2009) analyses and emphasizes the lesser dimensionality of G compared with phenotypic covariance matrix (figure 3; see also Kirkpatrick 2009).

Table 4.

Overall additive variance–covariance matrix (G) for untransformed beak traits. Genetic covariances are below the diagonal, genetic variances on the diagonal and genetic correlations are above the diagonal. g_i are eigenvectors associated with λ_i eigenvalues.

	beak length	beak depth	beak width	g1	g2	g3
beak length	0.022	0.654	1.01a	0.18	0.69	−0.71
beak depth	0.059	0.366	0.834	0.95	−0.32	−0.07
beak width	0.045	0.098	0.038	0.27	0.65	0.71
λ				0.39	0.04	0.02
% var				85.2	8.7	6.1

Bold genetic variances are significantly different from zero. Bold eigenvalues values explain significant amount of variation (see text for details).

^aNot significantly different from unity.

(b). Natural selection

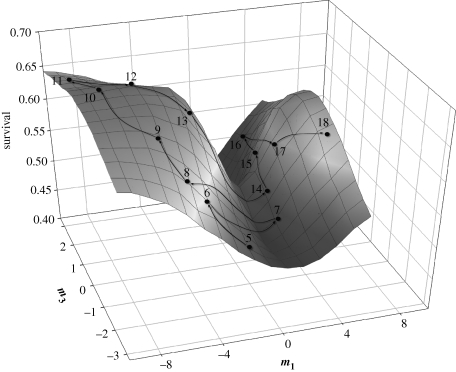
All three methods of multivariate selection assessment produced similar results—fitness surface had the shape of a saddle (mixture of positive and negative eigenvalues in table 3) where the valley of the saddle was oriented along the axis of beak depth variation and the hills framing the saddle oriented along the proportional expression of beak length and depth (figure 4). Comparisons of the eigenvalues in table 3 shows that in five generations (5–8 and 16), the effect of beak depth on juvenile survival (i.e. the curvature of the valley) was greater than the effect of proportional expression of beak length and width in relation to beak depth (curvature of the hills forming the valley), while in all other generations the survival contribution of proportional expression of beak length and width for a given beak depth was greater than or equal to the effect of beak depth. Importantly, the estimated response surface did not have a single optimum either within (not shown) or across generations (figures 3 and 4). Across generations, adaptive proportional expression of beak length and width differed (i.e. was under fluctuating directional selection), while beak depth was most commonly under stabilizing selection (tables 2 and 3). The projection pursuit regression analysis similarly showed that within most generations and overall, natural selection acted on the relative expression of beak length and width (table 3).

Figure 4.

Overall fitness surface (juvenile postfledging survival) defined by the canonical axes m₁ (variation in beak depth) and m₃ (relative expression of beak length and beak width) (table 3). Dots show average coordinates of m₁, m₃ and survival for each generation (shown by numbers), starting with generation 5. Arrows connect subsequent generations. G matrix orientation (85% along m₁ and 8.7% along m₃) largely coincides with the orientation of M matrix.

Magnitude of selection was similar between the estimates obtained from γ and M, and both methods identified quadratic selection on beak depth as the most common selection pressure (tables 2 and 3). However, by elimination of correlational selection gradients, the canonical rotation of γ enabled better interpretation of quadratic selection on beak depth in relation to relative expression of length and width (i.e. a saddle shape in figure 4) and provided an important insight into developmental variability and functional redundancy of discrete morphologies formed by beak components (figure 1).

(c). Developmental variability

Developmental variability was assessed in two steps. First, we constructed age-specific correlation matrices for the growth sequence of all traits from age 1 to age 16 (typically eight measures per trait; Badyaev & Martin 2000a) and calculated overall correlational matrix (L) and associated eigenvalues and eigenvectors for the entire growth sequence, separately for each generation. Eigenstructure of L identifies similar allometric relationship across ontogenetic stages and the directions of most consistent ontogenetic integration in size and shape of growing structure (Cock 1966). Second, to assess multivariate directions of greatest independent developmental variation (i.e. lowest ontogenetic integration) of the three beak components, we calculated negative inverse L for each generation (L⁻¹; table 5). Eigenvectors of L⁻¹ reflect projections of traits with greatest independent variation during growth. In each generation, there were two significant directions of independent ontogenetic variation (table 5, figure 3). In 13 out of 16 generations (5, 7, 8, 10, 11 and 14–16), these directions were antagonistic growth of beak length and depth, and growth of beak width. In other generations, these directions were antagonistic growth of beak length and width, and growth of beak depth (table 5). The most consistent directions of greatest ontogenetic variability across all generations were antagonistic growth of beak length and depth, and independent variation in beak width (table 5).

Table 5.

Lines of greatest developmental variance and least integration during early ontogeny (1–16 days post-hatch) of beak morphology during 16 generations following population establishment in northwestern Montana, USA. Shown are eigenvectors and eigenvalues of the negative inverse matrix of ontogenetic allometry (L⁻¹) with the effects of sex removed in general linear model. Data on ontogenetic covariance structure were not available for generations 17–19.

	generations
	5 (n = 43)		6 (n =148)		7 (n = 215)		8 (n = 113)		9 (n = 82)		10 (n = 229)		11 (n = 196)
	l1	l2	l1	l2	l1	l2	l1	l2	l1	l2	l1	l2	l1	l2
BL	0.79	−0.15	0.72	0.16	−0.65	−0.45	0.69	−0.22	0.30	0.77	0.67	−0.44	0.68	−0.45
BD	−0.67	−0.29	0.02	−0.98	0.73	−0.16	−0.70	−0.49	−0.80	−0.12	−0.73	−0.30	−0.73	−0.34
BW	−0.13	0.87	−0.70	0.13	−0.19	0.89	0.07	0.85	0.52	−0.63	0.08	0.85	0.06	0.83
λ	2.77	1.74	2.68	1.16	2.61	1.26	2.53	1.79	2.77	2.30	2.40	1.58	2.89	2.16
	12 (n = 172)		13 (n = 204)		14 (n = 158)		15 (n = 174)		16 (n = 74)		overall (n = 1808)
BL	−0.56	−0.59	0.81	−0.04	0.70	−0.45	0.76	0.37	0.74	−0.21	0.69	−0.43
BD	−0.24	−0.79	−0.45	−0.68	−0.72	−0.40	−0.64	0.52	−0.57	0.43	−0.72	0.38
BW	0.79	0.18	0.38	0.73	0.02	0.82	−0.06	0.86	−0.09	0.81	0.12	0.81
λ	3.18	2.87	3.75	2.73	3.52	1.92	2.74	1.84	2.24	1.54	2.52	2.08

The finding of high genetic correlation between beak components (table 4) that show variable and frequently antagonistic developmental interactions (table 5), low additive genetic variance (table 4) and might be regulated by non-overlapping gene cascades (e.g. Abzhanov et al. 2006) is surprising. It further emphasizes that genetic and developmental integration are not necessarily equal, even for frequently co-selected traits (e.g. Badyaev 2004; Frankino et al. 2007). However, when variation in developmental partitioning of precursors among traits is consistently greater than variation in fitness consequences of their final configurations—as is expected in adaptively equivalent combinations of traits (figure 4)—the developmentally interacting traits will evolve genetic correlations even when their relative expression is antagonistic and additive genetic variance is low (Bulmer 1971; Houle 1991; Björklund 2004).

5. Generative and selective variation in avian beak form

(a). Orientation of genetic variance–covariance matrix in relation to the fitness surface and developmental variation

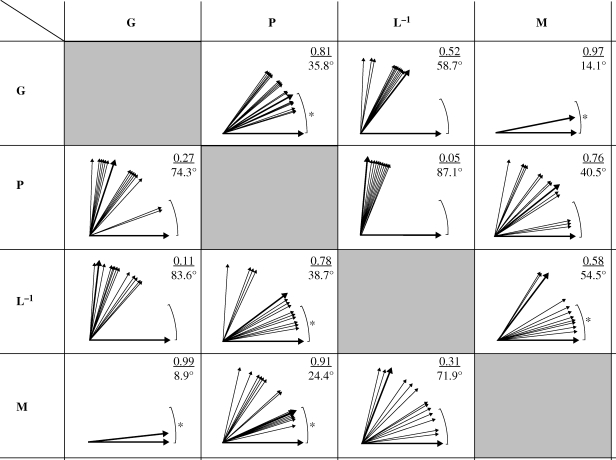
Both main eigenvectors, g₁ and g₂, of G matrix were indistinguishable from the two main eigenvectors, m₁ and m₂, of the overall adaptive landscape (i.e. the most recurrent selection, figure 4; α = 14.1° and 8.9° correspondingly; figure 5). Overall g₁ had similar direction as the first eigenvector (p₁) of phenotypic covariance matrix calculated across all generations (α = 35.8°), but correlation between g₁ and p₁ was highly variable across generations (α = 21–53°; figure 5 above diagonal). There was pronounced temporal clustering in G and P correlations (figure 5), corresponding to discrete beak morphologies expressed across generations (figures 1, top and 2c). There were no similarities between G and P in second eigenvectors (overall α = 74.3°; figure 5, below diagonal). Main directions of the greatest ontogenetic variability, eigenvectors l₁ and l₂, were largely orthogonal to both g₁ and g₂ (α = 56–88° and 48–88° correspondingly, figure 5), which is expected from the short-term contingent nature of compensatory interactions among the beak components that L⁻¹ describes.

Figure 5.

Concordance of G, additive genetic covariance matrix (table 4); P, phenotypic covariance matrix (table 1); L⁻¹, negative inverse covariance matrix of ontogenetic integration (table 5) and M, matrix of multivariate selection (table 3) of beak morphology during 19 generations following population establishment. Drawn are the first (above diagonal) and the second (below diagonal) eigenvectors and the corresponding vector correlations and angles (in degrees) between them. All vectors are drawn the same length for illustration only (see tables 1–5 for actual length in corresponding eigenvalues). Thick lines show overall vectors calculated across all generations; thin lines show within-generation vectors. For L⁻¹ versus G, and P versus G comparisons, within-generation vectors of L⁻¹ and P are compared with the vectors of overall G. For all other comparisons (L⁻¹ versus P, L⁻¹ versus M, and P versus M), vectors are compared within each generation. Brackets show bootstrapped limits (n = 100) within which the vectors are not distinct. Asterisks indicate similarity of overall vector correlations (if thick vectors are within the bracket) or similarity of within-generation vectors (if most of the within-generation vectors are within the bracket).

(b). The relationship between developmental variability, natural selection and beak phenotypes

The primary target of natural selection was developmental variation arising from compensatory interactions between beak components in each generation—the direction of greatest developmental variability (l₁) was highly similar to the direction of strongest natural selection (m₁) in all but two generations: in generation 8 and 15, α = 57° and 69°; in all other generations α = 16–27°; average for all generations α = 32° (vectors within bracket, figure 5, above diagonal). However, because these compensatory interactions were distinct among generations (table 5), there was no concordance between overall m₁ and overall l₁ calculated by combining all generations (α = 54.5°, figure 5). Similarly, while there was no concordance between overall m₂ and overall l₂ (α = 71.9°, figure 5), these directions were similar in half of all generations (vectors within bracket, figure 5, below diagonal). Nearly all unintegrated trait variation arising during growth was eliminated (either by mortality or by functional adjustment) in final beak phenotypes because l₁ was orthogonal to p₁ in all generations (α = 87.1°, figure 5, above diagonal), regardless of the diversity in generation-specific patterns of growth and selection (tables 2 and 5). However, within-generation l₂ and p₂ showed concordance in all but six generations (vectors in bracket, figure 5, below diagonal), primarily because the secondary dimension of developmental variability was aligned with variation in a single original trait—typically beak width (see loadings of λ₂ in table 5)—the trait that forms nestling gape and has an important independent function during ontogeny.

(c). Evolution of genetic architecture in avian beaks

Compensatory adjustments of beak components (table 5) and adaptive equivalence of beak configurations (figure 4) have important consequences for evolution of genetic architecture that facilitates both adaptation and evolutionary change in beak morphology. First, the extended phenotypic range of locally adaptive morphologies converts overall disruptive selection during colonization of novel environment to overall stabilizing selection where several adaptive phenotypes are maintained both within and between generations—a condition that favours stability in genetic architecture (Lande 1976; Brodie et al. 1995; Jones et al. 2004; Kopp & Hermisson 2006). Second, compensatory adjustments among beak components should shield genetic variance in individual traits, such that modulation of a small number of conserved developmental modules can produce both locally adaptive morphology and evolutionary diversifications (Kopp & Hermisson 2006). For example, in Darwin's finches, controlling for compensatory and correlational interactions in evolutionary changes in beak morphology revealed that beak shape, but not beak size, was the target of selection and the most diverging trait (Schluter 2000, p. 233). Third, compensatory developmental interactions among beak components and adaptive equivalence of several beak configurations might explain the puzzling result where the dimensions of the strongest and most persistent stabilizing selection coincide with the dimensions of greatest additive genetic variance while traits under fluctuating directional selection had low additive genetic variance (figure 5, table 4). Our results show that diverse phenotypic adjustments among beak components can either replenish genetic and developmental variation along the axis of most consistent selection or shield variance in the trait that is most consistently subject to selection (Blows & Walsh 2009).

In this study, the compensatory interactions between beak length and width in accommodating a particular beak depth might maintain high additive genetic variation in beak depth despite strong and consistent selection on this trait and large microevolutionary changes along the axis aligned with variation in beak depth. Such diverse and contingent compensatory interactions along the beak length–width axis, as well as the consistent selection on beak depth, can maintain the stability of G matrix (analogously to the maintenance of G by mutational variance aligned with G axes; Jones et al. 2007). Thus, whereas the most consistent evolutionary trends are associated with the direction of maximum variance in G (figure 4), the local adaptive adjustments in each generation are produced by relative expression of beak length and width—which is a direction of the minor axis of G (for similar findings on evolutionary divergence aligned with g₁ and functional adjustment aligned with g₂ see McGuigan et al. 2005).

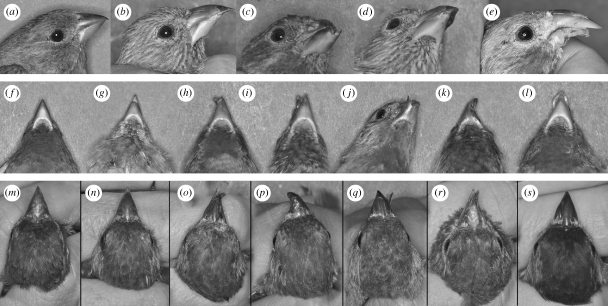
Proximately, compensatory interactions among beak components capitalize on multiple developmental pathways by which the same beak phenotype can be produced—the configuration made possible by self-regulatory and modular generative processes in beak ontogeny, where spatial and temporal variation in the regulation of only a few conserved signalling modules and reciprocal feedback between ectoderm and mesenchyme can accomplish a range of changes, from adaptive fine-tuning, to global size upregulation, to evolutionary diversifications (Helms & Schneider 2003; Eames & Schneider 2008; Jheon & Schneider 2009). For example, changes in relative rates of cell proliferation among the facial prominences and compensatory growth among the zones of cell proliferation within the prominences can induce regulatory inputs from facial ectoderm and lead to asymmetric outgrowth and variable curvatures of beaks within species (Wu et al. 2006) and to species-specific changes in beak depth (Abzhanov et al. 2004). Additional evidence of emergent, weakly integrated and self-regulatory developmental dynamics comes from patterns of expression of beak abnormalities during early generations following establishment of house finches in the novel environment (figure 6). In addition, developmental redundancy and interconnectiveness means that selection on beak length, for example, can involve upregulation of several growth zones producing, by compensatory interactions, different shape of beaks (figure 1)—a phenomenon that can induce directional changes in a complex of traits even when individual components are under stabilizing selection (Rice 2004).

Figure 6.

Developmental abnormalities in house finch beaks illustrating errors in coordinated growth of beak components. Upper row: (a) normal phenotype, (b) overbite—elongated upper beak (frequency: 14 per 15 000 captures = 0.09%), (c) ‘crossbill’ phenotype (total: 0.11% of which right crossing: 0.08%, left-crossing: 0.03%), (d) ‘shoveler’ phenotype—widened and flattened upper beak (0.02%) and (e) outgrowth/modifications on lower or upper beak (0.23%). Middle row: (f) normal phenotype, (g) overbite, (h–i) ‘crossbill’ phenotype, (j) ‘skimmer’ phenotype—widened and overlapping lower beak (0.01%), (k) both upper and lower beaks are curved in the same direction (0.017%) and (l) ‘shoveler’ phenotype. Lower row: (m) normal phenotype, (n) underbite—longer lower beak (0.12%), (o) right-crossing ‘crossbill’ phenotype, (p) both upper and lower beaks curved in the same direction, (q) ‘skimmer’ phenotype, (r) incomplete right-curving (0.18%) and (s) outgrowth on upper or lower beaks (e.g. pronounced groves, ridges and condensations).

6. Are the ‘lines of least resistance’ the ‘lines of most recurrence’?

Close alignment of G to the adaptive landscape, as found in this study (figure 5), could be either a cause or a consequence: long-term stabilizing selection is expected to create such alignment (Lande 1980; Cheverud 1984; Schluter 1996), whereas G's direction of greatest variability should be aligned with the direction of the long-term ‘least selective resistance’ (i.e. the negative inverse of overall γ matrix, table 3; Arnold et al. 2001). Indeed, the reviews of G matrix persistence produced a number of contrasting results—from long-term stability across populations and species to function- and sex-specific expression within species (Steppan et al. 2002; McGuigan 2006; Arnold et al. 2008)—findings that are not surprising considering the multitude of factors that influence allelic distribution that shape G and variation in the relative importance of these factors across time and space. More important empirical considerations are the actual formation of the G matrix and historical changes in its dimensionality and, thus, the extent to which it can be used as a historical probe of population processes influencing a complex of traits. For example, are the lines of ‘least genetic resistance’ (Björklund 1996; Schluter 1996) the lines of greatest recurrence of organism–environment associations that reflect the evolved correspondence between developmental and functional integrations (Badyaev 2007) stabilized by genetic circuitry and accomplishing evolutionary integration (Baldwin 1902; Müller & Newman 2005)? Or are these lines the lines of ‘the least selective resistance’ (Arnold et al. 2001) that delineate the direction of the least depleted additive genetic variance? Or are these lines the lines delineated by the complexity of multitrait structures that reflect projections from functional and developmental correlations among the trait's components and thus define the directions of both developmental accommodation and evolutionary diversification (Whyte 1965; West-Eberhard 2003)? In relation to beak evolution, or any structure under persistent selection for functional integration, genetic integration among traits can represent: (i) domains of the most conserved regulatory modules; (ii) directions of the most recurrent selection on a complex of traits, where the variance is maintained by functional interchangeability and compensatory interactions; (iii) directions most consistently shielded from selection; or (iv) directions delineated by migration or hybridization between populations. The results of this study support the first two of these explanations, but explicitly historical comparisons of evolving G both in relation to changes in other components of variance (e.g. matrices of maternal and environmental effects), and empirically examined selective pressures are needed to understand the sensitivity and inertia of G in reflecting population history.