PERFORMANCE EVALUATION OF A 32-ELEMENT HEAD ARRAY WITH RESPECT TO THE ULTIMATE INTRINSIC SNR

Abstract

The quality of an RF detector coil design is commonly judged on how it compares with other coil configurations. The aim of this article is to develop a tool for evaluating the absolute performance of RF coil arrays. An algorithm to calculate the ultimate intrinsic signal-to-noise ratio (SNR) was implemented for a spherical geometry. The same imaging tasks modeled in the calculations were reproduced experimentally using a 32-element head array. Coil performance maps were then generated based on the ratio of experimentally measured SNR to the ultimate intrinsic SNR, for different acceleration factors associated with different degrees of parallel imaging. The relative performance in all cases was highest near the center of the samples (where the absolute SNR was lowest). The highest performance was found in the unaccelerated case and a maximum of 85% was observed with a phantom whose electrical properties are consistent with values in the human brain. The performance remained almost constant for 2-fold acceleration, but deteriorated at higher acceleration factors, suggesting that larger arrays are needed for effective highly-accelerated parallel imaging. The method proposed here can serve as a tool for the evaluation of coil designs, as well as a tool to guide the development of original designs which may begin to approach the optimal performance.

INTRODUCTION

Parallel MRI methods exploit the local nature of the reception pattern of the individual elements of coil arrays to extract spatial information about the detected magnetization ^1-3. When this coil sensitivity information is combined with the spatial information obtained from externally applied magnetic field gradients, images can be reconstructed from under-sampled datasets acquired in less time than would otherwise have been required with gradient encoding alone. Despite the many advantages of parallel imaging, one disadvantage is that parallel MR image reconstructions require the inversion of a non-unitary encoding matrix, which leads to spatially dependent amplifications of noise. This additional source of signal-to-noise ratio (SNR) loss has been used to assess the performance of coil arrays in parallel MRI applications and has been referred to as the geometry factor (g), since it depends on the shape of the coil sensitivity functions ².

The dependency of baseline SNR and g upon coil array geometry suggests that the final SNR of the reconstructed image can be improved by optimizing the design of the receiver coil array. Nowadays it has in fact become common practice to include simulations of SNR and g in the design process ^4,5. Although effective in improving existing array configurations, such a method does not necessarily aid in developing innovative designs and, furthermore, it gives no indication of how well a given design performs in comparison to the maximum achievable SNR.

Prior work has shown that there is in fact an inherent electrodynamic limit to the achievable SNR for any physically realizable receiver coil, and the behavior of ultimate intrinsic SNR (assuming sample-dominated noise) has been modeled both in the absence ⁶ and in the presence ^7,8 of parallel acceleration. In these prior studies ultimate intrinsic SNR was calculated by performing a mode expansion of the electromagnetic (EM) field inside the object, without making any assumption about the origin of each EM field in the basis set. In this work we propose a different approach, using a mode expansion to express the general current distribution on a surface surrounding the sample and deriving the EM field inside the object associated with each current basis function. The resulting basis of EM fields is then employed to calculate the best possible SNR as in the other studies. However, with our method we can also derive and display the optimal current patterns associated with the ultimate intrinsic SNR.

The existence of an upper bound, independent of coil array design, on the performance of parallel MRI may be very useful for coil optimization. The comparison of the ultimate SNR with the SNR of a coil array under development can indicate whether there is room for further improvement and can help in selection of the best design for given field strengths and sample properties. Ocali et al. introduced a method to express the SNR performance of a coil as a percentage of the best possible performance, in the case of standard gradient-encoded MRI ⁶. The aim of the present work, following preliminary results presented at the 2006 meeting of the ISMRM in Seattle, Washington ⁹, is to extend this method to include the effects of parallel imaging, and to compute absolute coil performance for a particular many-element array which is expected in principle to approach the ultimate limit.

In order to achieve absolute comparisons, it was necessary to scale computed ultimate intrinsic SNR values by all known experimental factors influencing baseline SNR. Coil performance maps, which at each pixel display the experimentally measured SNR value divided by the corresponding scaled ultimate achievable value, were used to evaluate a close-fitting 32-element head array design ¹⁰.

METHODS

Review of the theoretical basis for ultimate intrinsic SNR

The source of noise that inherently limits the SNR performance of MRI systems is electromagnetic fluctuations caused by thermal agitation of particles in the sample, as the contribution of other noise sources can in principle be diminished through technological improvements. For this reason, our derivation of the best possible SNR starts from the concept of intrinsic SNR, which is defined as the ratio of the NMR signal to the RMS noise voltage produced by the randomly fluctuating noise currents in the sample ^6-8,11. The complex-valued signal voltage induced in a receiving coil by a nuclear magnetic moment M precessing at position r₀ with the Larmor frequency ω about the z-axis, immediately after a 90° pulse, can be expressed, using the principle of reciprocity ¹², in terms of the RF magnetic field that would be transmitted at the same position by a unit current of frequency ω flowing around the coil (see Ref. 12 for notational conventions):

$${\nu }_{\mathrm{S}}=\omega M\cdot {\tilde{\mathcal{B}}}_1^{-}{\left({\mathbf{r}}_0\right)}^{\ast }=\omega M_0\left({\mathcal{B}}_{1,x}\left({\mathbf{r}}_0\right)-i{\mathcal{B}}_{1,y}\left({\mathbf{r}}_0\right)\right),$$ [1]

where M₀ is the equilibrium magnetization (magnetic moment of a unit volume) and the net coil sensitivity is defined as the complex conjugate of ${\tilde{\mathcal{B}}}_1^{-}\left({\mathbf{r}}_0\right)$, the left-hand circularly polarized component of the RF magnetic field. The RMS noise voltage per unit square root receiver bandwidth is given by:

$${\nu }_{\mathrm{N}}=\sqrt{8k_{\mathrm{B}}T{P}_L}=\sqrt{4k_{\mathrm{B}}T{\int }_{\text{sample}}\sigma \left(\mathbf{r}\right){\mid \mathcal{E}\left(\mathbf{r}\right)\mid }^2{d}^3\mathbf{r}},$$ [2]

where k_B is Boltzmann's constant, T is the absolute temperature of the sample and P_L is the power loss per unit current within the load (or sample). Assuming isotropic conductivity in the sample, and invoking again the principle of reciprocity, P_L can be calculated with a volume integral as the Ohmic loss due to the RF electric field $\mathcal{E}$, which would be generated within a sample with conductivity σ by the coil if it were driven by a unit current ¹³.

An expression of the intrinsic SNR received by the coil, per unit sample volume and unit square root receiver bandwidth, can be found by combining Eq. [1] and [2]:

$$\mathrm{SNR}{\left({\mathbf{r}}_0\right)}_{\text{intr}}=\frac{\omega M_0\left({\mathcal{B}}_{1,x}\left({\mathbf{r}}_0\right)-i{\mathcal{B}}_{1,y}\left({\mathbf{r}}_0\right)\right)}{\sqrt{4k_{\mathrm{B}}T{\int }_{\text{sample}}\sigma \left(\mathbf{r}\right){\mid \mathcal{E}\left(\mathbf{r}\right)\mid }^2{d}^3\mathbf{r}}}$$ [3]

The ultimate value of intrinsic SNR at any particular position r is found by maximizing the ratio in Eq. [3]. The net coil SNR is directly related to the electromagnetic fields responsible for both signal reception and Ohmic losses in the sample; therefore signal and noise are linked by Maxwell's equations and cannot be treated separately in the search for the optimum SNR. The EM field can be expanded in a complete set of basis functions, each representing a valid solution of Maxwell's equations within the object:

$$\begin{array}{cc}\hfill & {\mathcal{B}}_1\left({\mathbf{r}}_0\right)=\sum _{c=1}^{+\infty }{\alpha }_c\left({\mathbf{r}}_0\right){\mathcal{B}}_{1c}\left({\mathbf{r}}_0\right)\hfill \\ \hfill & \mathcal{E}\left({\mathbf{r}}_0\right)=\sum _{c=1}^{+\infty }{\alpha }_c\left({\mathbf{r}}_0\right){\mathcal{E}}_c\left({\mathbf{r}}_0\right)\hfill \end{array}$$ [4]

and every EM mode can be associated with a hypothetical coil, so that it is possible to specify a complete basis of coil sensitivities and the total noise power associated with any linear combination of them. The best possible SNR would then be given by the weighting coefficients α_c (r₀) that result in the highest intrinsic SNR ^6-8. In Cartesian parallel imaging, undersampling during signal acquisition leads to aliasing in single-coil image data, so the weighting coefficients must also serve to remove aliasing in the combined image. In the present work we computed the coefficients α_c (r₀) using the weak Cartesian SENSE algorithm ², which is an SNR-optimal reconstruction algorithm for parallel imaging that yields unit net coil sensitivity at the reconstructed voxel position r₀ and zero at all aliasing positions r_n. For this particular case, the search for maximum SNR is therefore equivalent to finding the reconstruction weights that minimize the total noise power in the denominator of Eq. [3], subject to the following constraint:

$${\mathcal{B}}_{1,x}\left({\mathbf{r}}_n\right)-i{\mathcal{B}}_{1,y}\left({\mathbf{r}}_n\right)={\delta }_{n0}\text{for}n=0\dots R\text{-}1,$$ [5]

where δ is the Kronecker delta and R is the reduction, or acceleration, factor. The solution was given by Pruessmann et al. ² and an expression for the ultimate intrinsic SNR per unit volume and unit bandwidth at any pixel position r₀ was derived in Ref. 7 and 8:

$$\mathrm{SNR}{\left({\mathbf{r}}_0\right)}_{\text{ult intr}}=\frac{\omega M_0}{\sqrt{4k_{\mathrm{B}}T{\left[{\mathbf{S}}^H{\Psi }^{\text{-}1}\mathbf{S}\right]}_{0,0}^{\text{-}1}}}$$ [6]

In this expression, from which any scaling factor related to the particular pulse sequence has been removed, the superscript ^H indicates conjugate (Hermitian) transpose and S denotes the encoding matrix ² containing the sensitivities of all basis elements at the reconstructed voxel position r₀ and all aliased positions in case of undersampling:

$${\mathbf{S}}_{cn}={\mathcal{B}}_{1c,x}\left({\mathbf{r}}_n\right)-i{\mathcal{B}}_{1c,y}\left({\mathbf{r}}_n\right)$$ [7]

For a complete basis, the encoding matrix S would be infinite-dimensional (dim(S) = ∞×R). In practice, the ultimate intrinsic SNR may be shown to converge for a finite number L of suitably-chosen basis elements ^6-8, and S has dimension [L×R]. Ψ is the [L×L] noise covariance matrix, which characterizes the noise received by each coil and the correlated noise between coils ¹⁴:

$${\Psi }_{c,c^{\prime }}={\int }_{sample}\sigma \left(\mathbf{r}\right){\mathcal{E}}_c\left(\mathbf{r}\right)\cdot {\mathcal{E}}_{c^{\prime }}{\left(\mathbf{r}\right)}^{\ast }{d}^3\mathbf{r}$$ [8]

The “0,0” subscript in the denominator of Eq. [6] indicates the diagonal element of the matrix in square brackets with an index associated with the target position r₀.

Ultimate intrinsic SNR depends on the modeled object geometry and dielectric properties, but is independent of the particular choice of the basis functions. However, previous authors have shown that the numerical complexity involved in calculating SNR from Eq. [6] is affected by the choice of basis functions, and have selected basis functions tailored to the object geometry ^7,8. In the present study, the EM modes inside a spherical object were derived by performing a full-wave EM field expansion into vector spherical harmonics.

Ultimate intrinsic SNR calculation

Ultimate intrinsic SNR was calculated inside a sphere with uniform electrical properties. The net EM field was derived by performing a mode expansion with dyadic Green's functions (DGF) ¹⁵, following a method recently described that enables calculation of the optimal field and current patterns associated with the best possible SNR ¹⁶. Given any spatial current distribution J, the electric field can be calculated as:

$$\mathcal{E}\left(\mathbf{r}\right)=i\omega {\mu }_o{\int }_{sample}\mathbf{G}(\mathbf{r},{\mathbf{r}}^{\prime })\cdot \mathbf{J}\left({\mathbf{r}}^{\prime }\right)d^3{\mathbf{r}}^{\prime },$$ [9]

where μ_o is the magnetic permeability in free space and G(r,r′) is the branch of the DGF associated with the region indicated by r. The expression of G(r,r′) used for this work is defined in Ref. 16 in terms of a double series of vector wave functions in spherical coordinates:

$$\begin{array}{cc}\hfill & {\mathbf{M}}_{l,m}(\mathbf{r},k)=j_l\left(kr\right){\mathbf{X}}_{l,m}(\theta ,\phi )\hfill \\ \hfill & {\mathbf{N}}_{l,m}(\mathbf{r},k)=(1∕k)\nabla \times {\mathbf{M}}_{l,m}(\mathbf{r},k)\hfill \end{array}$$ [10]

where l, m are the expansion indices, X_l,m is a vector spherical harmonic ¹³, k is the complex wave number, r is the radial coordinate and j_l is a spherical Bessel function of order l.

We started by defining a complete basis set of surface current modes, distributed on a spherical surface at 5 mm distance from the surface of the modeled sphere, in order to mimic the case of previously-constructed close-fitting coil geometries. The generic surface current mode was expressed as:

$${\mathbf{K}}_{lm}=W_{lm}^{\left(M\right)}{\mathbf{X}}_{l,m}(\theta ,\phi )+W_{lm}^{\left(E\right)}\widehat{r}\times {\mathbf{X}}_{l,m}(\theta ,\phi ),$$ [11]

where and $W_{lm}^{\left(M\right)}$ and $W_{lm}^{\left(E\right)}$ are the series expansion coefficients representing divergence-free and curl-free surface current contributions, respectively. As in Ref. 8, a subset of the infinite basis with L = 13,122 basis elements (corresponding to an expansion order of l_max = 80) was used in the calculation of Eq. [6], to ensure convergence. For each mode, the electric field was computed using Eq. [9] and the magnetic field was then derived as $\mathcal{B}\left(\mathbf{r}\right)=(-1∕i\omega )\nabla \times \mathcal{E}\left(\mathbf{r}\right)$. The individual EM fields were used to construct the encoding matrix and the noise covariance matrix in Eq. [7] and [8], respectively. It is worth noting that, by adjusting the relative scaling between the electric and the magnetic field, it is possible to obtain for these matrices precisely the same expressions as in Eq. [B8] and [B7] of Ref. 8 (after multiplying Eq. [B7] by the conductivity of the sample, to correct for a minor typographical error). Wiesinger et al. in Ref 8 used a multipole expansion to compute the EM fields inside a dielectric sphere, independent of the underlying details of surface current patterns. In this work, we chose for convenience to take advantage of our previously derived DGF software, which has the additional advantage of allowing computation of optimal current patterns for comparison with particular coil designs, and enabling prediction of conductor losses and other current-related effects ¹⁶.

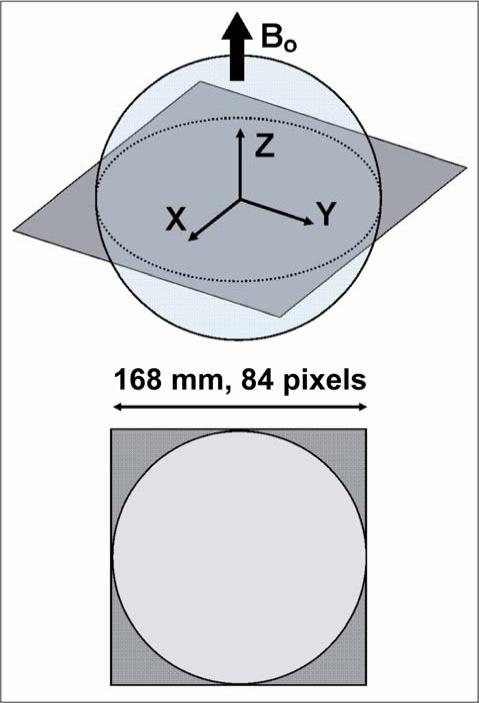
The modeled sphere was chosen to match the geometry and the electrical properties of two existing spherical MR phantoms, henceforward referred to as “Phantom 1” and “Phantom 2”. Phantom 1 is a “Braino” phantom (GE Medical Systems, Milwaukee, WI, USA), containing 12.5 mM of N-acetyl-L-aspartic acid [NAA], 10 mM of creatine hydrate [Cr], 3 mM of choline chloride [Ch], 7.5 mM of myo-inositol [mI], 12.5 mM of L-glutamic acid [Glu], 5 mM of DL-lactic acid [Lac], sodium azide (0.1%), 50 mM of potassium phosphate monobasic [KH₂PO₄], 56 mM of sodium hydroxide [NaOH] and 1 mL/L of Gd-DPTA [Magnevist]. Phantom 2 is a low-conductivity phantom (Siemens Healthcare, Erlangen, Germany), filled with a solution of 1.25 NiSO₄ × 6 H₂O, per 1000 g of distilled H₂O. Both phantoms have diameter equal to 16.9 cm (Figure 1). T1 relaxation time was measured to be 450 ms for Phantom 1 and 200 ms for Phantom 2. Water solutions equivalent to the content of each phantom were mixed and their conductivity and permittivity at 123.22 MHz (the operating frequency of the 3T scanner used in our experiments, whose actual operating field strength is 2.89T) were measured using an Agilent 85070E dielectric probe (Agilent Technologies, Palo Alto, CA, USA). Conductivity was 0.97 Ohm⁻¹m⁻¹ and relative permittivity was 81.3 for Phantom 1, whereas for Phantom 2 conductivity was 0.084 Ohm⁻¹m⁻¹ and relative permittivity was 80. Magnetic permeability of free space was used in both cases. A transverse section through the center of the sphere was divided into an 84×84 grid of square pixels with 2 mm side (Figure 1) and ultimate intrinsic SNR was calculated at each position, using 2.89 T static magnetic field strength and a temperature of 298 degrees Kelvin, as measured with a thermometer in the scanner room where the experimental part of this work was conducted. Calculations were implemented in Matlab (MathWorks, Natick, MA, USA).

Figure 1.

Schematic diagram of the image plane and the FOV used to calculate ultimate intrinsic SNR for the spherical phantoms used in this study. The FOV is a square with a side of 16.8 cm, just large enough to contain the entire circular section. It is uniformly divided into an 84×84 grid of pixels.

Experimental data acquisition

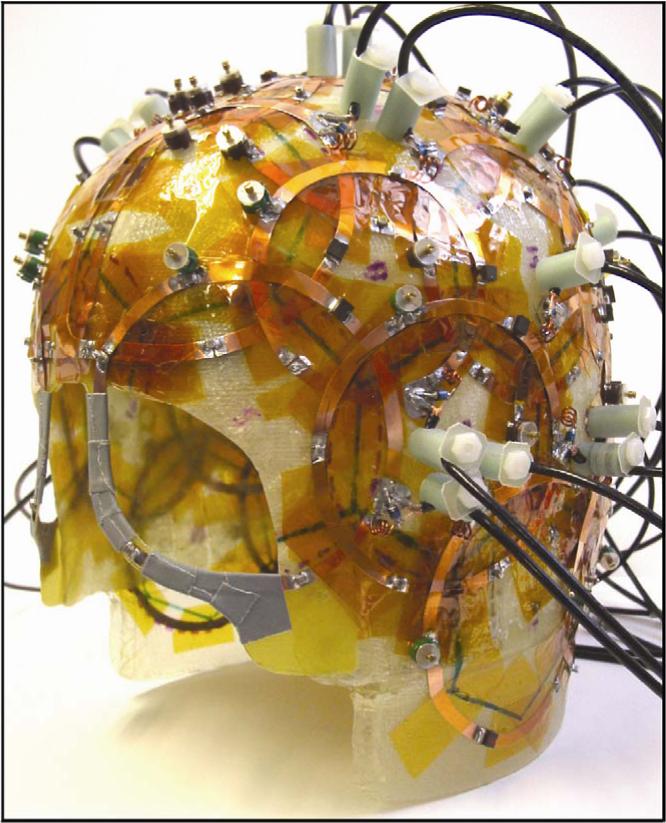
The spherical phantoms were scanned on a Siemens TIM Trio 3T scanner (Siemens Healthcare, Erlangen, Germany) using the same image planes modeled in the ultimate intrinsic SNR simulations (see Figure 1). The RF receive coil used in the SNR measurements was a receive-only head coil array (Figure 2) consisting of 32 overlapping circular surface coil elements arranged over the entire dome of the head ¹⁰, with the scanner body coil used for transmit. The receive array was tuned and matched for a human head. A single proton density weighted two-dimensional gradient echo image was obtained with parameters TR = 2000 ms, TE = 3.8 ms, flip angle = 20°, slice thickness = 3 mm, 128×128 matrix, FOV = 256 mm, pixel half-bandwidth = 25.6 kHz (line bandwidth = 200 Hz/pixel). With the known T1s and our chosen flip angle of 20 degrees, the selected TR was computed to be sufficient for full relaxation between excitations. To map the flip angle distribution over the phantom, eight additional images were acquired with slice-selective excitations, using identical pulse sequence parameter values but with increasing transmit voltages to achieve several nominal flip angles ranging from 60° to 150° in 15° increments and receiving with the body coil, including an additional zero signal point.

Figure 2.

32-element receiver coil array employed in the experimental study. The surface coils are packed on a thin helmet-shaped fiberglass frame that minimizes the distance from the sample.

For each acquisition, raw k-space data were saved for offline analysis, and magnitude images reconstructed online were also saved for comparison. Each image acquisition was accompanied by a noise reference measurement obtained by recording complex-valued data with the array coil during the same pulse sequence used for the image acquisition but with no RF excitation. This ensured that the noise samples were bandwidth-matched with the image acquisition and that a sufficient number of noise samples were acquired to accurately estimate the noise statistics.

Experimental SNR calculation

All image reconstruction and analysis was performed offline with custom software written in Matlab. Image data were acquired with a Cartesian k-space sampling and two-dimensional Fourier imaging, thus a standard image reconstruction consisting of standard FFT operations for each individual coil channel was carried out as a start. No apodization or filtering was applied at any stage of the image reconstruction, other than for the processing of coil sensitivity estimates for SENSE reconstruction.

Due to the dielectric properties of the spherical phantoms, the flip angle of the RF excitation varied spatially over the phantom, with higher flip angles at the center of the phantom ^17,18. Since the flip angle distribution affects image SNR, these transmit effects were identified and removed from the empirical SNR calculation. To compute the flip angle distribution, we fit a sinusoid model of image intensity as a function of transmit voltage across the eight body coil reference images to each image pixel with the Matlab function fminsearch. In this model, the magnitude image intensity I is given by I = p₁ sin(v · p₂), where v represents the applied transmitter voltage for the given reference image, parameter p₁ captures both the object magnetization contributing to the signal as well as the receive coil sensitivity profile, and parameter p₂ captures the flip angle per unit voltage. Given the eight reference images and corresponding eight voltages, the fit produced the two estimated parameter values at each pixel that yielded the minimum mean squared discrepancy between the model and the reference image data. The achieved flip angle map $\widehat{\theta }(x,y)$ was then calculated at each pixel as the product v₀ · p₂, where v₀ is the desired voltage applied during the final image acquisition. Individual coil images were then divided by the spatially varying function $\text{sin}\left(\widehat{\theta }(x,y)\right)$ to normalize the effect of the intensity non-uniformity caused by the flip angle distribution, giving rise to a compensatory intensity increase in the periphery of the phantom. Because the phantoms contained no internal structure, the resulting image from a given coil element after flip angle normalization provided a good approximation to the element's sensitivity profile.

The noise covariance matrix Ψ was calculated from the statistics of the noise samples scaled by dividing the sample covariance matrix $\widehat{\Psi }$ by the scalar-valued noise equivalent bandwidth b_noise to account for noise autocorrelations within each channel due to the filtering introduced by the data acquisition electronics and receiver, i.e. $\Psi =\widehat{\Psi }∕{b_{noise}}^{19}$.

With coil sensitivity estimates and channel noise covariance estimates in hand, composite images in absolute SNR units were obtained following the general procedure outlined by Kellman & McVeigh ¹⁹. Component coil images were combined using a Cartesian SENSE reconstruction algorithm ², which in the unaccelerated case corresponds precisely with the optimal matched filter SNR combination method described by Roemer et al. ²⁰. Note that, because the MR signal is defined to be complex-valued, we adopted an observation model where the signal is assumed complex-valued and thus the image SNR calculated from the imaging data does not require an additional $\sqrt{2}$ scaling (see, e.g., Ref. 19 and 21). In order to eliminate any phase variation in the experimental data (so as to match the simulated results, for which M₀ is assumed real in Eq. [6]), the absolute magnitude of the complex-valued combined SNR image was taken. To account for the SNR bias introduced by this final magnitude operation, a correction was applied to the resulting image SNR as detailed in Ref. 19 (following Ref. 21 and 22, which generalize the well-known Rician distribution correction ²³ to the case of multi-element coil arrays).

SNR and g maps for acceleration factors 2, 4, and 6 were obtained from the fully sampled dataset, using the SENSE reconstruction algorithm ² with one-dimensional undersampling on the x-y plane. To give a true measure of g for various acceleration rates, and to provide the best match between simulated and experimental conditions, the images were cropped, before undersampling, to produce a tight FOV around the phantom, resulting in a cropped image size of 84×84. Estimates of the coil sensitivity profiles were generated by low-pass filtering the resulting image intensities with a two-dimensional Hanning filter (normalized for unity noise gain) with a cutoff set to include only the central 25% of k-space. Noise covariance matrices were estimated as described above, and the geometry factor was calculated directly from the analytic expression ².

Coil performance maps

The ultimate intrinsic SNR is calculated considering the effects of a net EM field acting at particular positions inside a sample, and deliberately ignoring all experimental factors which are not considered “intrinsic,” The units of an ultimate intrinsic SNR calculation are therefore arbitrary – useful for investigating relative behavior of the optimum as a function of key parameters such as acceleration factor and field strength ^6-8, but not suitable for evaluation of actual coil performance.

On the other hand, in order to compare the experimental SNR data with the simulated data, the ultimate intrinsic SNR values must be properly scaled to account for the specific pulse sequence parameters and system characteristics ⁶:

$${\mathrm{SNR}}^{\prime }{\left({\mathbf{r}}_0\right)}_{\text{ult intr}}=\mathrm{SNR}{\left({\mathbf{r}}_0\right)}_{\text{ult intr}}\cdot \frac{V_{\text{voxel}}\sqrt{{\mathrm{N}}_{\text{acq}}\mathrm{NEX}}\text{sin}\left(\theta \right)}{\sqrt{\mathrm{F}\Delta f}}$$ [12]

where V_voxel is the volume of the voxel, N_acq is the number of the acquired k-space samples, which accounts for the signal summation resulting from Fourier transform, NEX is the number of signal averages, θ is the nominal flip angle, F is the system noise factor and Δf is the receiver bandwidth. The system noise figure (NF), which is the noise factor expressed in dB, was calculated from noise power measurements, obtained experimentally for one of the system receiver channels using the “hot-cold resistor” method ²⁴. The noise factor F was then derived using NF = 10log₁₀ F. The NF is a measure of the degradation of the SNR of an RF coil introduced by downstream components in the RF signal chain, including the preamplifiers. For this work, the published hot-cold resistor method ²⁴ was followed closely. Metal film resistors, which have a low thermal coefficient of resistivity, were used, and it was confirmed, using a network analyzer, that these resistors had the same value at room temperature and when cooled with liquid nitrogen. The resulting measured noise factor of F = 1.22 is consistent with the manufacturer's specifications. Note that the inclusion of a single noise factor correction to ultimate intrinsic SNR in Eq. [12] assumes that all receiver channels share the same noise factor. If this is not the case (e.g. due to differential source impedances seen by distinct preamplifiers), a single multiplicative correction is not possible, and the effects of receiver-chain noise must instead be removed from experimental SNR measurements through modification of each element of the measured noise correlation matrix, since ultimate intrinsic SNR calculations do not refer to particular receive channels. Potential effects of neglecting channel-to-channel variations in noise factor are addressed in the Discussion.

Table 1 summarizes the numerical values of the scaling factors, as well as the values of the phantom's dielectric properties and of the other quantities used in the calculations. These quantities include the operating frequency ω and the equilibrium magnetization M₀ at the field strength of interest, here 2.89 T. M₀ appears in Eq. [6] for ultimate intrinsic SNR, and must be accounted for correctly. The final value of M₀ listed in Table 1 was computed using the expression ²⁵:

$$M_0=\frac{N{\gamma }^2{\mathrm{h}}^{2}I(I+1)B_0}{3k_{\mathrm{B}}\mathrm{T}}$$ [13]

with the gyromagnetic ratio γ = 2.68×10 ⁸ rad T⁻¹ s⁻¹, the temperature of the sample T = 298 K, the main magnetic field B₀ = 2.89 T, I = 1/2 for hydrogen and the number of nuclear spins per unit volume N = 6.691×10 ²⁸ m⁻³, assuming that the signal due to non -water components of the phantom liquids is negligible. k_B is Boltzmann's constant and ħ is Planck's constant divided by 2π. It is also important to notice that, although the final matrix size is 128×128, N_acq is equal to (256×128)/R_accel, with R_accel being the acceleration factor, because there were 256 k-space samples for each readout, due to an automatic 2-fold oversampling performed by the MR system. The total bandwidth, including the oversampling, was 51.2 kHz.

Table 1.

Dielectric properties, constants and scaling factors used in the calculations

Larmor frequency	ω/2π	123.22	MHz
Equilibrium magnetization	MO	9.03 × 10−3	A·m−1
Boltzmann constant	kB	1.381 × 10−23	J·K−1
Sample temperature	T	298	K
Conductivity	σ	0.97 Phantom 1 0.08 Phantom 2	Ω−1·m−1
Relative permittivity	εr	81.3 Phantom 1 80 Phantom 2	-
Vacuum permittivity	εo	8.85 × 10−12	C2·N−1·m−2
Permeability	μ	1.2566 × 10−6	Wb·A−1·m−1
Volume of the voxel	Vvoxel	1.2 × 10−8	m3
Receiver bandwidth	Δf	51.2	kHz
Flip angle	θ	0.3421	rad
Noise factor	F	1.22	-
Signal averages	NEX	1	-
Acquired data points	Nacq	(256 × 128)/Raccel	-

An accurate scaling of ultimate intrinsic SNR is critical to the absolute significance of coil performance maps, which are defined as the ratio of the experimental SNR images to the corresponding scaled ultimate intrinsic SNR images:

$$\mathrm{CPM}\left({\mathbf{r}}_0\right)=\frac{\mathrm{SNR}{\left({\mathbf{r}}_0\right)}_{\text{array}}}{{\mathrm{SNR}}^{\prime }{\left({\mathbf{r}}_0\right)}_{\text{ult intr}}}$$ [14]

Performance maps provide a measure of the efficiency of each coil array for the specific imaging task, as a function of position inside the sample of interest. Performance maps for the 32-element head array were generated for various acceleration factors, with the computational grid adjusted to match the voxel positions of the 84×84 cropped experimental image matrix.

Performance maps were also synthetically generated for a 32-element array of loop coils, which was modeled in simulation with a linear combination of the current modes, using appropriate weighting coefficients to constrain the current patterns to be similar to the configuration in Figure 2. The noise model for this simulation included a body noise contribution as for the ultimate intrinsic case, as well as a coil noise contribution accounting for the finite conductivity of the coil conductors ¹⁶. In this case, it was not necessary to scale the ultimate intrinsic SNR, as the simulated coil SNR was calculated within the same framework and using the same basis functions as the ultimate intrinsic SNR.

RESULTS

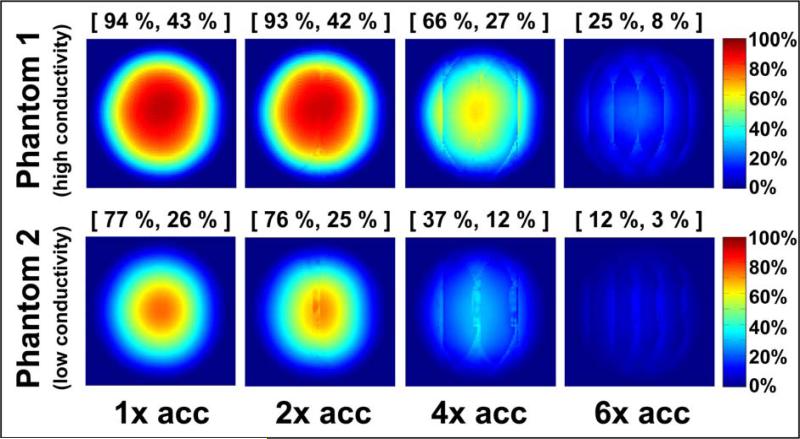
Coil performance maps for the 32-element head array are shown in Figure 3, for both phantoms at various acceleration factors. In all cases the performance relative to the ultimate intrinsic SNR was highest near the center of the object and approached zero near the surface, where the ultimate SNR assumes its largest values.

Figure 3.

Coil performance maps at 2.89 T for a central axial slice through each of two homogeneous spherical phantoms with equal dimensions and different electrical properties (“high conductivity”: σ = 0.97 Ohm⁻¹m⁻¹, ε_rel = 81.3; “low conductivity”: σ = 0.084 Ohm⁻¹m⁻¹, ε_rel = 80). The performance of the 32-element head array with respect to the ultimate SNR is shown for each phantom at various acceleration factors. Each pixel represents the experimental SNR divided by its corresponding ultimate SNR value. Above each map, the maximum and the mean performance are indicated in brackets and reported as a percentage of the optimum. The mean is computed including only the pixels inside the circular cross-section of the object.

A peak performance of 85% and 70% for Phantom 1 and Phantom 2, respectively, was observed in the unaccelerated case. The maximum and mean performance (reported in square brackets above each map) both decreased as the acceleration factor was increased. For 2-fold acceleration, the performance relative to the ultimate SNR was almost equal to that in the fully-sampled reconstruction (i.e. the array demonstrated the minimal allowed degradation in absolute SNR with acceleration), whereas for 6-fold undersampling, noise amplifications substantially degraded image SNR and the maximum performance decreased to 22% and 11% of the ultimate SNR for phantoms 1 and 2, respectively.

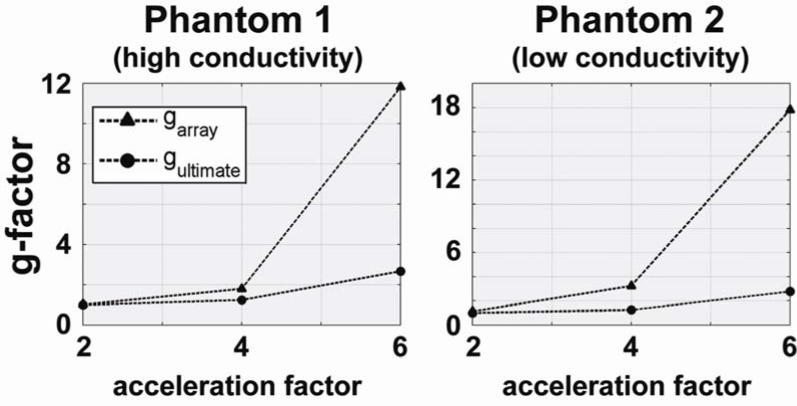
Figure 4 shows the g-factor performance of the coil array relative to the ultimate intrinsic case. We notice that, in terms of g-factor performance, the 32-element array is almost equivalent to a hypothetical infinite array for 2-fold acceleration, whereas its efficiency in accelerating by a factor of 6 is on average less than 20% of that predicted for the ultimate case. It is important to note that the g-factor performance maps are only a measure of how well the finite array preserves SNR with parallel imaging acceleration as compared to the ultimate case. g-factor performance values can approach 100% even in the case of overall poor coil performance, i.e. when the baseline unaccelerated SNR is very small compared to the ultimate intrinsic SNR. Nevertheless, although the maps in Figure 4 do not provide an absolute measure of coil performance, they are useful in investigating the capabilities of the coil array for parallel imaging tasks, and they can be calculated more easily than absolute performance maps, without reference to the scaling factors in Eq. [12].

Figure 4.

Geometry factor performance for various parallel imaging acceleration factors at 2.89 T for a central axial slice through each of the two uniform spherical phantoms. Since the g-factor in the ultimate intrinsic case is always smaller than the g-factor for the 32-element array (or indeed any finite array), g_ultimate is shown as a percentage of g_array in these maps.

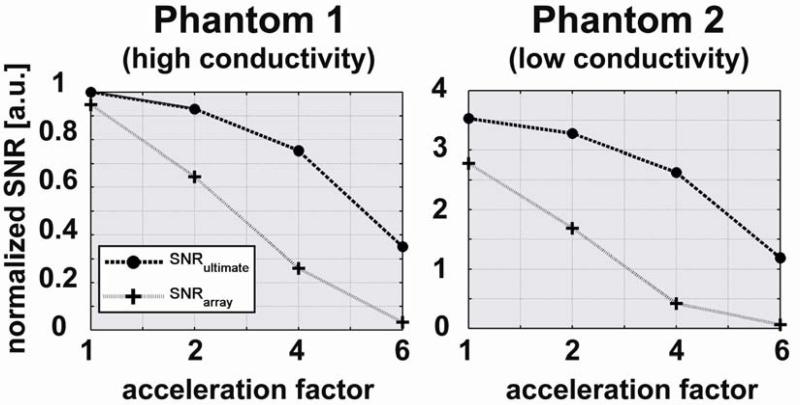
Comparisons with the ultimate intrinsic SNR and g-factor in the center of the sample are shown as a function of acceleration factor in Figures 5 and 6, respectively. In Figure 5 we see that absolute SNR (both for the 32-element array and in the ultimate case) is more than three times higher for Phantom 2 than for Phantom 1. However, the relative performance of the coil array is worse for Phantom 2, and the difference between the SNR of the coil array and the ultimate intrinsic SNR increases more rapidly with increasing acceleration for Phantom 2. This is confirmed by the graphs in Figure 6, which show that for 2-fold acceleration ultimate intrinsic g-factor and g of the array overlap for both phantoms, whereas for 6-fold acceleration g of the array becomes 12 for Phantom 1 and 18 for Phantom 2, though ultimate intrinsic g remains almost equal in both plots.

Figure 5.

SNR as a function of acceleration factor for a voxel in the center of each spherical phantom. The SNR obtained with the 32-element head array is compared with the corresponding ultimate intrinsic SNR for each of the two phantoms. Both plots are normalized to the value of ultimate intrinsic SNR at an acceleration factor of 1 for the phantom with the highest electrical conductivity (i.e. Phantom 1).

Figure 6.

Geometry factor as a function of acceleration factor for a voxel in the center of each spherical phantom. The geometry factor of the 32-element head array is compared with the corresponding optimal values.

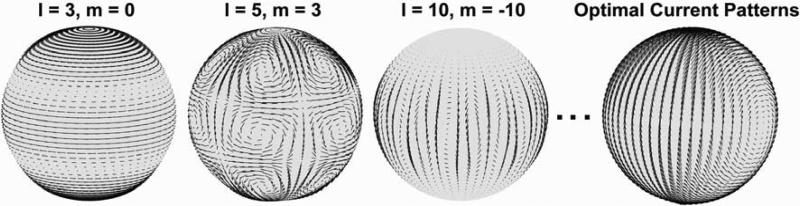
Figure 7 provides an example of the surface current patterns that can be calculated with the DGF formalism. The rightmost plot shows the net optimal surface current pattern resulting in ultimate intrinsic SNR at a voxel at the center of the sphere. The optimal current patterns were derived by summing the contributions of the individual current modes in Eq. [11], each weighted by the corresponding coefficient from the SNR-optimal reconstruction. For the other plots, three current modes (order l = 3, m = 0; l = 5, m = 3; l = 10, m = −10) were arbitrarily chosen as examples of individual contributions to the net ultimate pattern. The current patterns of the individual modes actually have more apparent structure than does the optimal combination, which consists of a large distributed current loop with its axis in the transverse plane.

Figure 7.

Illustration of the process by which optimal surface current patterns are generated. The first three plots from the left show current patterns for three arbitrarily chosen modes (l = 3, m = 0; l = 5, m = 3; l = 10, m = −10). The rightmost plot show the optimal current patterns, evaluated at every arrow position as the sum of the contributions of all current modes, weighted by the combination coefficients resulting in maximum SNR at a voxel in the center of the object. Optimal current patterns can be similarly computed for other voxel positions.

Figure 8 shows (at right) a simulated performance map for our synthetically generated 32-element array with Phantom 1, for comparison with experimental results. The simulated peak performance in the unaccelerated case was 97%. Difference between simulated and experimental performance are addressed in the Discussion. To the left of the performance map in Figure 8 are a schematic of the array and a plot of the simulated current patterns.

Figure 8.

Simulation of the performance of a 32-element head array with respect to the ultimate intrinsic SNR. Loop coils were arranged in software around a spherical object to obtain a configuration similar to the array in Figure 2 (left plot). Current modes in our basis set were then weighted with appropriate coefficients in order to reproduce the current patterns corresponding to this conductor geometry (center plot). The SNR of the array was calculated using the DGF method on a transverse FOV and the resulting values were reported as a percentage of the optimum by means of a performance map (right plot). The maximum and the mean performance are indicated in brackets above the map.

DISCUSSION

As the number of available receiver channels on modern MR systems increases, greater attention will be paid to the design and performance of many-element RF coil arrays. Questions regarding the balance of coil-noise and sample-noise, or the suitability of any particular array design for parallel imaging, promise to take on new significance as the number of elements increases. In the present work a method has been described to evaluate the performance of any particular coil array against a well-defined absolute benchmark. Coil performance is strictly constrained by the behavior of electromagnetic fields within the sample ^6-8. For a chosen imaging task, the best possible SNR achievable for any coil configuration can be computed using a complete set of coil sensitivity basis functions. In this study, we used ultimate intrinsic SNR as a reference to assess the efficiency of a 32-element head receive array.

It should be noted that, although our experiments were performed only at 2.89 T, the basis functions used in this work take full account of the frequency-dependence associated with operation at different field strengths, and that coil performance maps are possible at arbitrary field strength. That said, simple phantom geometries with uniform electrical properties are expected to become an increasingly poor approximation of in vivo SNR behavior with increasing field strength. The characterization of coil performance for arbitrary electrically inhomogeneous objects remains possible with appropriate choices of surface-based field or current basis functions, but such characterization would likely require extensive computational effort. In fact, the calculation of ultimate intrinsic SNR would require a full-wave numerical solution, for example using the Finite Difference Time Domain (FDTD) technique, for each current mode, as well as detailed knowledge of the dielectric structure and spin distribution of the object.

In simulating the ultimate SNR we are effectively using an infinite number of coils surrounding the object, and we expect a very high signal close to the surface. As a consequence, the ultimate SNR rises rapidly at the edges, and relative coil performance is higher near the center of the object. A similar spatial variation was reported in a previous paper which showed coil performance maps in the case of non-parallel MRI ⁶. The performance values presented in that study are slightly lower than those found for the unaccelerated case in this investigation, but the results are not directly comparable as the phantom, the image section, and the imaging system were different. Coil performance maps for parallel MRI were presented for the first time at the 2006 meeting of the International Society for Magnetic Resonance in Medicine ⁹, for the case of a cylindrical phantom. In that preliminary work, we reported performance values of less than 50% in the center of the sample, for a coil array with fewer elements that was more poorly matched to the phantom than was the case in this work.

In the current work, the overall maximum performance, corresponding to the unaccelerated case with Phantom 1, was more than 80% in the central portion of the phantom, implying that there is little room for improvement in coil array design for the case of fully-sampled acquisitions. A slightly higher performance in the center of a uniform spherical sample was predicted by a prior simulation study which modeled receive arrays of circular coils distributed around the surface of the sphere ²⁶. In that work the electrical properties of the sphere were chosen to approximate values in the human brain and they were consistent with the properties measured for Phantom 1. In order to investigate whether the higher performance values in the center were due to the fully encircling configuration of the coil elements in Ref. 26, as opposed to the open-faced configuration of our 32-element array, we also simulated (see Figure 8) the performance with respect to the ultimate intrinsic SNR of a 32-element array, with loop coils arranged similarly to the head array in Figure 2. The simulated unaccelerated peak performance of 97% is similar to the values reported in Ref. 26, which suggests that removing coils at the bottom and front of the array has little effect on the SNR in the central region of the phantom. The difference in values between the map in Figure 8 and the corresponding map in Figure 3 must be then linked to other factors.

1. A minor contribution may traced to our expression for voxel volume in Eq. [12]. In reality the signal contributions to a given reconstructed voxel value are weighted by the point-spread function (PSF), whose integrated volume may differ somewhat from simple cuboid voxels. However, the Cartesian SENSE reconstruction we used maintains a nearly sinc-shaped PSF, whose integrated volume is the same as that for a cuboid voxel. To the extent that the phantom is uniform, that the sensitivities vary slowly within a given voxel, and that partial volume effects are limited to positions near the edges of the object, the voxel volume is not expected to differ from that used in Eq. [12].

2. Another minor effect may be related to our assumption of uniform noise factor for all receiver channels. In practice, variations in noise factor are expected to be modest (e.g. ~10%), resulting in still smaller variations in measured SNR for any given channel (~5%). Meanwhile, differing values in different receiver channels will be averaged to some extent by inclusion in the noise correlation matrix, resulting in even smaller effects on combined SNR.

3. An additional complication is that, while we do account for body-derived noise correlation between array elements (see Eq. [8]), we do not model inductive coupling, which may also contribute to noise statistics. In fact, measured noise correlations between coil elements are on average higher than predicted by our DGF method (ratio of off-diagonal to diagonal elements of the noise correlation matrix 55% maximum and 9% average for simulations versus 53% maximum and 12% average for experiments). To the extent that this increased correlation reflects pure linear inductive coupling, it is not expected to have a significant effect on SNR when the noise correlation matrix is included in the reconstruction ²⁷. However, some degradation due to extensive coupling cannot be ruled out.

4. The most significant contribution to the discrepancy between simulated and measured performance is likely due to the presence of additional noise sources that are not taken into account by our DGF formulation. The weights used for our 32-element DGF calculations produce a relatively simple current distribution inside the conductors, neglecting current concentration effects along edges and around capacitors.

The particular contributions of each of these effects to the observed discrepancy between simulated and experimental coil performance may be investigated in detail. However, one of the explicit advantages of ultimate performance maps is that, when combined with appropriate simulations of particular array geometries, they can indicate now much of the room for improvement in coil performance relates to practical as opposed to theoretical limits.

Phantom 2 was included in this study to illustrate the effects of electrical properties upon coil performance, and also to provide data from a phantom which is widely available to the research community. Absolute SNR values were higher for Phantom 2 (see Figure 5) due to its smaller electrical conductivity, which results in lower sample noise (see Eq. [2]). On the other hand, smaller electrical conductivity corresponds to larger standing wave effects, which are partly responsible for the lower performance of the 32-element head array with Phantom 2. In fact, as the array was tuned and matched for the human head, better loading with Phantom 1 might have positively affected the performance results because the array was designed to provide the correct noise match to the preamplifiers with a human head-type load, and because the higher conductivity of Phantom 1 increases loading and leads to a smaller relative contribution of coil noise. The fact that coil performance was lower with Phantom 2 does not imply that the head array design is suboptimal for its target clinical applications, as Phantom 2 is filled with a solution whose electrical properties are not meant to approximate human tissue, but rather to minimize susceptibility artifacts.

The average performance of the coil array (see Figures 3 and 4) was almost constant for 2-fold acceleration, but rapidly decreased for larger acceleration factors. This suggests that 32 elements, arranged as in Figure 2, are not enough for effective highly-accelerated parallel imaging and that larger arrays, or a different configuration of the conductors, are needed in order to approach the acceleration efficiency of the ultimate intrinsic case.

The examples shown in this work demonstrate that the method proposed here can serve as a tool for the evaluation of coil designs. Ultimate intrinsic SNR defines an absolute performance target for coil designers, and coil performance maps provide useful and immediate feedback on how far a particular array configuration is from this target. Ultimate SNR need be computed only once for each particular geometry and object composition, which facilitates its use as an effective evaluation instrument for coil engineers.

Given the comparatively large set of basis functions required for convergence of the ultimate intrinsic SNR at multiple positions, it is unlikely that all the modes used to simulate the optimum can be practically realized with an actual coil array. However, the asymptotic growth of the ultimate intrinsic SNR with increasing number of modes (see Ref. 6-8), and our results showing that 32 elements nearly saturate the ultimate SNR in the unaccelerated case, demonstrate that a smaller subset of the larger basis can capture the dominant SNR behavior. It may even be possible to build an array targeted to that subset of modes in order to approach the simulated optimal sensitivity patterns, using the weighting factors generated by the ultimate SNR optimization to directly compute these ideal EM fields. For example, the distributed optimal current pattern shown in Figure 7 could in principle be approximated with a comparatively small number of concentric loops. However, the optimum will be different for every point in the sample and thus only a tradeoff solution might exist for the conductor patterns needed to approach optimal performance at a large number of positions. Genetic algorithms have been already applied to a similar optimization problem ²⁸ and, with an accurate and robust parameterization, they might be employed also for the design of optimized coil arrays for different parallel MRI applications.

Since such arrays should in principle perform very close to the optimum, any substantial discordance could be linked to noise other than that coming from the sample. The development in recent years of arrays with very many elements ²⁹ has raised to practical priority the question of what is the smallest size for array elements before the final SNR begins to be dominated by the noise coming from the electronic components. Compared to other methods previously proposed to calculate ultimate intrinsic SNR (see Ref. 6-8), the DGF approach used in this work allows convenient modeling of arbitrarily-shaped finite arrays within the same framework.

In conclusion, the capability of parallel MRI to accelerate image acquisitions is fundamentally limited by electrodynamic constraints, but the knowledge of such limitations can be exploited to evaluate current coil design and eventually to guide the development of innovative receivers that may operate close to the optimum performance.

ABBREVIATIONS

MR

Magnetic Resonance

MRI

Magnetic Resonance Imaging

SNR

Signal-to-Noise Ratio

g

geometry factor

ISMRM

International Society for Magnetic Resonance in Medicine

NMR

Nuclear Magnetic Resonance

RMS

Root Mean Square

RF

Radiofrequency

EM

Electromagnetic

DGF

Dyadic Green's Function

FOV

Field Of View

FFT

Fast Fourier Transform

FDTD

Finite Difference Time Domain

PSF

Point-Spread Function